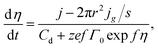DOI:
10.1039/D0RA00608D
(Paper)
RSC Adv., 2020,
10, 6979-6984
Theoretical modeling of electrochemical nucleation and growth of a single metal nanocluster on a nanoelectrode
Received
20th January 2020
, Accepted 8th February 2020
First published on 14th February 2020
Abstract
Theory of the initial stages of electrochemical formation and growth of a single metal nanocluster on an indifferent nanoelectrode has been developed and analyzed. General theoretical time dependences of the current and nanocluster size have been presented for the case of diffusion controlled growth at potentio- and galvanostatic deposition, and cyclic voltammetry.
1. Introduction
Nucleation and growth processes are the key phenomena in the theory of phase transitions. From a practical position, nucleation and growth of metal nanoparticles on conducting supports are of considerable interest for creating advanced functional interfaces with myriad applications.1 Future advances in the control of materials and processes at the nanoscale are largely dependent on the understanding of the fundamental regularities of nucleation and growth (thermodynamics and kinetics of nucleation, size distribution and growth rate of nanoclusters, rate-determining steps of nucleation and growth, the influence of non-steady-state and size effects, etc.), since they determine the initial stages of the formation of nanomaterials and nanostructures. Theoretical and experimental studies of the nucleation and growth processes clarify the mechanism and kinetics of the synthesis of nanosized objects and thereby contribute to the development of nanomaterial science. In particular, detailed elucidation of the nature of the nucleation phenomena and the early growth stages of new-phase nanoparticles on a foreign substrate is extremely important for success in the field of nanoelectrochemistry when developing approaches to the electrodeposition of monodisperse nanoparticles and various nanomaterials with predetermined characteristics, including nanowhiskers, nanofilms, and nanocluster sets.
It is highly convenient to study the processes of nucleation and growth by electrochemical methods, because they allow setting, controlling and measuring current, electrode potential, charge and, thus, it is possible to affect supersaturation (overpotential) in the system, i.e. to affect the conditions of new phase formation from the nanoscale to the microscale.2–4 The most detailed information on the kinetics of electrocrystallization may be obtained via the studies of the formation and growth of a single crystal, because side processes and interaction between nuclei do not complicate the phase formation in this case. The use of nanoelectrodes simplifies significantly the realization of a single nucleation because of the purely geometrical reasons. This allows us to study nanoobjects from one atom to several nanolayers.5–10
Different approaches are used now to model the electrochemical nucleation and growth processes. New data may be obtained both by the computational methods (methods of quantum chemistry, molecular dynamics, Monte Carlo, etc.)11 and by the mathematical analysis based on the classical nucleation theory (CNT) or the atomistic theory.12–14
The present work is aimed at the theoretical analysis and modeling of the formation and growth of a single metal nanocluster (the assembly of metal atoms) on a nanoelectrode by basic electrochemical techniques (potentiostatic and galvanostatic deposition, cyclic voltammetry). This is important as the mentioned methods are widely used for the experimental study and obtaining of nanomaterials and nanostructures.5–7,15–20
2. Analysis of theoretical models
Kinetics of ions discharge at the electrolyte/cluster interface differs significantly from the regularities of discharge on the planar electrolyte/electrode interface. Activation energies of the forward and backward reactions (attachment and detachment of a one particle to the g-atomic cluster) may be presented as follows:21–23| |
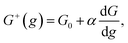 | (1) |
| |
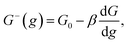 | (2) |
where G0 (J) is activation energy for electrolyte/cluster equilibrium, α and β are the transfer coefficients (α + β = 1), and G is the new-phase cluster formation work (Fig. 1).
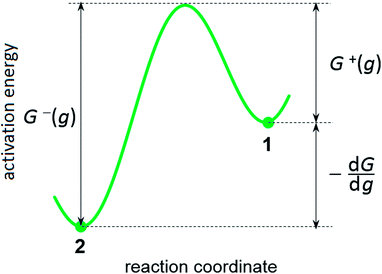 |
| | Fig. 1 Scheme of energy barriers at the increase (decrease) in the cluster size by one particle: (1) – ion in the electrolyte, (2) – atom in the supercritical new-phase cluster. | |
If nucleation proceeds at the moderate supersaturation, than its regularities may be analyzed within the frames of CNT approximations, which suppose a usage of macroscopic parameters to characterize a new-phase properties. Then, G is expressed as follows:22–24
where
z is the valence of depositing ions,
e (C) is the elementary electric charge,
η (V) is the overpotential (in this paper, the cathodic overpotential and current density are considered positive),
η =
E∞ −
E,
E∞ is the equilibrium potential of bulk metal,
E is the potential of the cathode, and
a is a coefficient depending on the geometric shape of the cluster. For hemispherical cluster,
a = (18π
υ2)
1/3σ,
υ (cm
3) is the volume of one new-phase atom, and
σ (J cm
−2) is the surface tension of the electrolyte/cluster interface. The driving force of the electrochemical phase formation can be expressed by the formula
where
ηp = 2
συ/
zer. The term
ηp, which can be called phase overpotential, considers the Gibbs–Thomson effect on the growing cluster. The cluster of radius
r exists in unstable equilibrium with the electrolyte at the overpotential equal to
ηp. For the critical cluster, d
G/d
g = 0 and
rc = 2
συ/
zeη.
In the case of electrochemical nucleation, the frequencies of attachment of one particle to the g-atomic cluster and detachment from the (g + 1)-atomic cluster are proportional to the densities of cathode and anode currents, that is why the equation of transition through the electrolyte/cluster interface may be written in the form22
| |
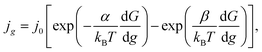 | (5) |
where
jg (A cm
−2) and
j0 (A cm
−2) are the current density and the exchange current density at the electrolyte/cluster interface, respectively,
kB is the Boltzmann constant, and
T (K) is the absolute temperature. Under mixed (charge transfer and diffusion) control:
22,23| |
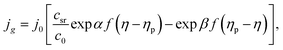 | (6) |
where
c0 (cm
−3) is the bulk concentration of the depositing ions,
csr (cm
−3) is their concentration on the cluster surface, and
f =
ze/
kBT. Hills
et al.25 studied the electrochemical phase formation kinetics using similar approach. Considering the dependence of cluster size on the overpotential,
eqn (6) may be transformed to
| |
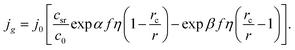 | (7) |
This formula shows that the Gibbs–Thomson effect can be neglected at r >> rc. There are two important aspects in these model representations: (1) the exchange current density at the electrolyte/cluster interface does not depend on the overpotential and (2) both cathode current and anode current depend on the overpotential and cluster size (see Fig. 1).
For the hemispherical cluster of radius r, we have
| |
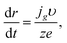 | (9) |
where
q (C) is the charge required for electrodeposition of this cluster, and
t (s) is time. As we demonstrated above, the Gibbs–Thomson effect can be neglected at the growth stage (see
eqn (7)). Then from
eqn (6), taking into account the stationary approximation of the Fick equation in spherical coordinates,
26–28 we can find the current density to the growing small cluster:
| |
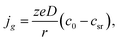 | (10) |
where
D (cm
2 s
−1) is the diffusion coefficient of the depositing metal ions, and
csr =
c0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
exp(−
fη).
The combination of eqn (6) and (10) provides the general expression that describes the growth of a new-phase cluster under mixed kinetic-diffusion control:
| |
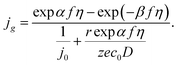 | (11) |
Then for pure kinetic (charge transfer) control, we have the Butler–Volmer equation,
| |
jg = j0[exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αfη − exp(−βfη)], αfη − exp(−βfη)],
| (12) |
and for pure diffusion control, we have the following formula:
| |
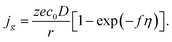 | (13) |
Diffusion control is typical in the cases of electrodeposition from aqueous solution with low concentration of depositing ions; that is why we will analyze further only the regularities of diffusion controlled cluster growth at different variants of changes in supersaturation (overpotential) in the system.
3. Results and discussion
3.1. Potentiostatic electrodeposition
The time dependence of the radius of a hemispherical nanocluster, which formed at time t0 and grows under constant overpotential (growth is controlled by diffusion), may be easily obtained from eqn (9) and (13):| | |
r = (2c0υD)1/2[1 − exp(−fη)]1/2(t − t0)1/2.
| (14) |
Then for the current, I = 2πr2jg, we have6,26,28
| | |
I = πze(2c0D)3/2υ1/2[1 − exp(−fη)]3/2(t − t0)1/2.
| (15) |
The value of the [1 − exp(−fη)] multiplier is close to unity at high values of cathode overpotential; the current and nanocluster size will depend only on time.
Fig. 2 illustrates time dependences of nanocluster size (Fig. 2a) and current (Fig. 2b) under potentiostatic conditions. These dependences were calculated according to eqn (14) and (15) at z = 1, T = 300 K, η = 40 mV, c0 = 1.2 × 1017 cm−3, D = 10−5 cm2 s−1, υ = 1.7 × 10−23 cm3, and t0 = 50 ms. This values corresponding to the formation and growth of a single Ag nanocluster on a 100 nm-radius Pt electrode.6 Theoretical curves reflect qualitatively accurately the experimental time dependences of current and nanocluster size. The moment of supercritical (capable of stable growth) cluster formation is clearly visible by the abrupt increase in current. Let us note that the current splash associated with the charging of the double electric layer is recorded on experimental potentiostatic current transients immediately after stepping the potential. Besides, the nucleation time lag in the experiment depends on the nanoelectrode size, overpotential and electrolyte concentration and varies within the relatively wide limits even for the same values of electrodeposition parameters.6 Quantitative conformity between theoretical and experimental curves may be provided by selection of the diffusion coefficient value.
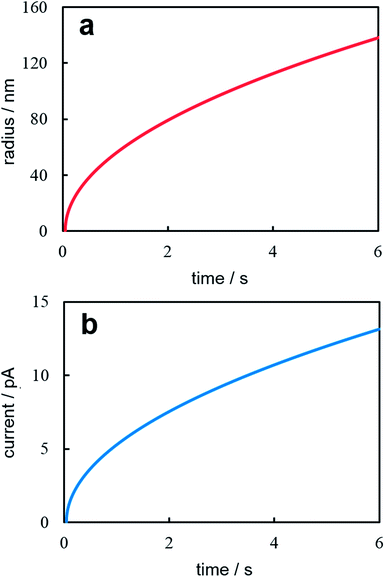 |
| | Fig. 2 Time dependence of the nanocluster radius (a) and the potentiostatic current transient (b). Calculation parameters are reported in the text. | |
3.2. Cyclic voltammetry
In cyclic voltammetry, the time dependences of overpotential η(t) is given as: η = νt, 0 ≤ t ≤ tλ (forward scan), η = ν(2tλ − t), t ≥ tλ (reverse scan), where ν is the scan rate, and tλ is the reversal time (Fig. 3). Taking into account the dependences of cluster growth rate and current on the overpotential,| |
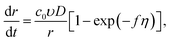 | (16) |
| | |
I = 2πzec0rD[1 − exp(−fη)],
| (17) |
the following equations were obtained for the forward scan29,30| |
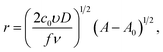 | (18) |
| | |
I = πze(2c0D)3/2(υ/fν)1/2(A − A0)1/2[1 − exp(−fη)],
| (19) |
and for reverse scan| |
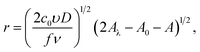 | (20) |
| |
I = π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ze(2c0D)3/2(υ/fν)1/2(2Aλ − A0 − A)1/2[1 − exp(−fη)], ze(2c0D)3/2(υ/fν)1/2(2Aλ − A0 − A)1/2[1 − exp(−fη)],
| (21) |
where A(η) = fη + exp(−fη), A(η0) = fη0 + exp(−fη0), A(ηλ) = fηλ + exp(−fηλ). In the derivation these formulas, we assumed that r(t0) = 0. The analysis of the expressions for the radius and current shows that the maximum nanocluster size is| |
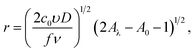 | (22) |
and the positions of the cathodic maximum and anodic minimum of the cyclic voltammogram may be found from the condition that dI/dt = 0:| |
2fηm + exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fηm + 3exp(−fηm) = 2(2Aλ − A0 + 1), fηm + 3exp(−fηm) = 2(2Aλ − A0 + 1),
| (23) |
where ηm is the overpotential corresponding to an extremum. A similar approach can also be found in Pritzker's work.31
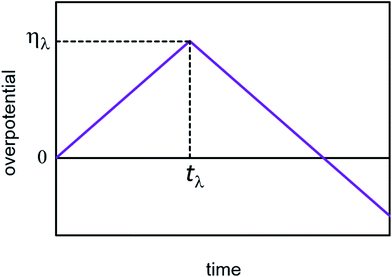 |
| | Fig. 3 Scheme of the time dependence of overpotential in cyclic voltammetry. | |
Fig. 4 presents the dependences of the nanocluster size and current on overpotential under cyclic potential sweep. These dependences were calculated from eqn (18), (20) (Fig. 4a) and eqn (19), (21) (Fig. 4b). The calculations were performed at ν = 0.05 V s−1, t0 = 0.8 s (η0 = 0.04 V), tλ = 2.4 s (ηλ = 0.12 V) and the same values of z, υ, c0, D, T as for Fig. 2. A sharp rise in current (point A) is associated with the formation of a supercritical nanocluster (Fig. 4a). After the reverse (point B), the overpotential decreases but the cluster continues growing in the cathode region and reaches the maximum size in the crossover point at η = 0 (point D). Then it begins to dissolve and disappears completely at ηF (point F). This overpotential may be determined from the fηF + exp(−fηF) = 2Aλ − A0 condition. The current increases on the forward scan (Fig. 4b). The maximum current is observed after the reverse (point C) because the current is affected by both an increase in the crystal size and a decrease in overpotential after reverse. For this reason, in the cathode region there is a nucleation loop on the cyclic voltammogram, i.e. the current value on the reverse scan is higher than that on the forward scan at the same overpotential.32 In the anode region, the peak corresponding to the cluster dissolution is observed (point E). From the above said it follows that the method suggested allows predicting changes in the nanocluster size at the known value of the diffusion coefficient of depositing ions in the electrolyte.
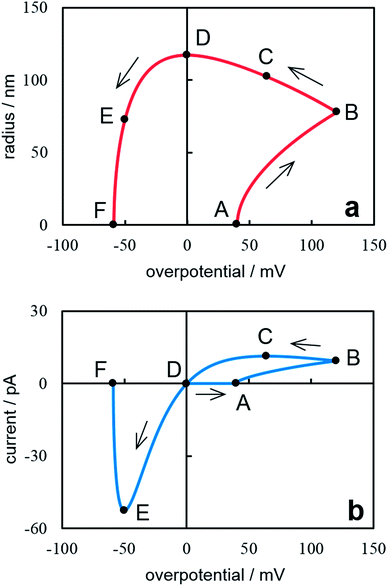 |
| | Fig. 4 Dependence of the nanocluster radius on the overpotential (a) and the cyclic voltammogram (b). Calculation parameters are reported in the text. The points mentioned in the text are marked on the cyclic voltammogram. | |
3.3. Galvanostatic electrodeposition
In this case, the overpotential in the system changes in a complicated way. Some factors (charge/discharge of the double electric layer; changes in the adatoms concentration; changes in mass transfer conditions; mutual influence between the kinetics of formation and kinetics of cluster growth) make the analysis of the experimental results difficult at the multiple nucleation on the conventional electrodes.23,33–35 The solution to problem is somewhat simplified when a single nanocluster is formed and grows on the nanoelectrode.
The balance equation for electrolyte/nanoelectrode interface can be written as23,33
| | |
jt = Cdη + ze(Г − Г0) + q/s,
| (24) |
where
j (A cm
−2) is the applied current density (
j = const),
Cd (F cm
−2) is the specific capacity of the double electric layer,
Γ and
Γ0 (cm
−2) are the single adatom (monomer) concentration and its initial value at
t = 0, respectively,
Γ =
Γ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
exp
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fη
fη,
q (C) is the charge spent on the nanocluster growth, and
s (cm
2) is the nanoelectrode surface area. We do not take into consideration planar diffusion to the electrode in
eqn (24). Therefore, we obtain equation for changing the overpotential in the system
| |
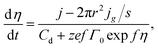 | (25) |
where the term 2π
r2jg/
s = 0 until the appearance of the cluster of supercritical size.
Eqn (16) and
(17) may be used considering the phase overpotential to determine the nanocluster growth rate and the growth current.
Fig. 5 illustrates the results of the numerical solution of the aforementioned equations system at I = 10−13 A, s = 3.14 × 10−10 cm2 (100 nm-radius electrode), Cd = 80 μF cm−2, Г0 = 1.2 × 1013 cm−2, σ = 10−5 J cm−2, and the same values of z, υ, c0, D, Т as for Fig. 2 and 4. The supercritical nanocluster was introduced at η = 40 mV. The calculations demonstrate that when the constant current is switched on, the double electric layer starts charging, the overpotential (Fig. 5a) and the adatoms concentration increases. After the nanocluster appearance, a part of current is consumed on his growth. The overpotential reaches maximum, when the growth current of nanocluster becomes equal to the preassigned current. When the growth current is greater than the preassigned one, overpotential and the adatoms concentration decreases, the double electric layer is discharged; the prevailing ions flux from the electrode surface into the electrolyte bulk arises. Afterwards only the diffusion controlled growth of nanocluster takes place under low overpotential. The modeling demonstrates that the nanocluster growth rate during the galvanostatic deposition is significantly lower than that under potentiostatic conditions, because of the overpotential drop (Fig. 5b) after nanocluster formation. At the higher values of preassigned current, the multiple nucleation will take place; in addition, the increase in the concentration of the depositing ions will results in an decrease in the number of clusters and an increase in the cluster size.23
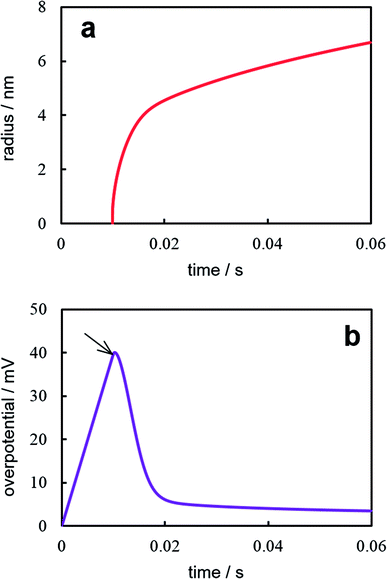 |
| | Fig. 5 Time dependences of the nanocluster size (a) and current (b) under galvanostatic electrodeposition. Calculation parameters are reported in the text. | |
4. Conclusion
Theoretical aspects of thermodynamics and kinetics of initial stages of electrochemical phase formation are briefly analyzed. The electrochemical methods was shown to be very useful for obtaining and studying single metal nanoclusters on an indifferent nanoelectrode. The models of formation and diffusion controlled growth of a new-phase nanocluster were proposed for the following methods:
(1) potentiostatic electrodeposition;
(2) cyclic voltammetry;
(3) galvanostatic electrodeposition.
It has been demonstrated that the use of these models allows us to determine the mechanism and parameters of nucleation and growth of a single metal nanocluster on a nanoelectrode by interpreting the time dependences of such macroscopic quantities as electric current and electrode potential.
Conflicts of interest
There are no conflicts of interest to declare.
References
- S. C. S. Lai, R. A. Lazenby, P. M. Kirkman and P. R. Unwin, Nucleation, aggregative growth and detachment of metal nanoparticles during electrodeposition at electrode surfaces, Chem. Sci., 2015, 6, 1126–1138 RSC.
- G. Staikov and A. Milchev, The Impact of Electrocrystallization on Nanotechnology, in Electrocrystallization in Nanotechnology, ed. G. Staikov, Wiley-VCH, Weinheim, 2007, pp. 1–29 Search PubMed.
- A. Milchev, Electrocrystallization: Nucleation and growth of nano-clusters on solid surfaces, Russ. J. Electrochem., 2008, 44, 619–645 CrossRef CAS.
- L. P. Bicelli, B. Bozzini, C. Mele and L. D'Urzo, A Review of Nanostructural Aspects of Metal Electrodeposition, Int. J. Electrochem. Sci., 2008, 3, 356–408 CAS.
- M. V. Mirkin, Nanoelectrodes and liquid/liquid nanointerfaces, in Nanoelectrochemistry, ed. M. V. Mirkin and S. Amemiya, CRC Press, Boca Raton, FL, 2015, pp. 539–572 Search PubMed.
- J. Velmurugan, J.-M. Noёl, W. Nogala and M. V. Mirkin, Nucleation and growth of metal on nanoelectrodes, Chem. Sci., 2012, 3, 3307–3314 RSC.
- J. Velmurugan, J.-M. Noёl and M. V. Mirkin, Nucleation and growth of mercury on Pt nanoelectrodes at different overpotentials, Chem. Sci., 2014, 5, 189–194 RSC.
- Y. Y. Peng, R. C. Qian, M. E. Hafez and Y. T. Long, Stochastic Collision Nanoelectrochemistry: A Review of Recent Developments, ChemElectroChem, 2017, 4, 977–985 CrossRef CAS.
- M. A. Edwards, D. A. Robinson, H. Ren, C. G. Cheyne, C. S. Tan and H. S. White, Nanoscale electrochemical kinetics & dynamics: the challenges and opportunities of single-entity measurements, Faraday Discuss., 2018, 210, 9–28 RSC.
- I. Valov and W. D. Lu, Electrochemistry at the nanoscale, Nanoscale, 2016, 8, 13825–13827 RSC.
- J. W. Weidner, P. B. Balbuena, A. Z. Weber, J. P. Meyers and V. Subramanian, Mathematical Modeling of Electrochemical Systems at Multiple Scales, J. Electrochem. Soc., 2014, 161, Y9 CrossRef CAS.
- A. Milchev, Electrochemical phase formation: classical and atomistic theoretical models, Nanoscale, 2016, 8, 13867–13872 RSC.
- A. Milchev, Nucleation phenomena in electrochemical systems: kinetic models, ChemTexts, 2016, 2, 4 CrossRef.
- I. Valov and G. Staikov, Nucleation and growth phenomena in nanosized electrochemical systems for resistive switching memories, J. Solid State Electrochem., 2013, 17, 365–371 CrossRef CAS.
- J. Ustarroz, X. Ke, A. Hubin, S. Bals and H. Terryn, New Insights into the Early New Insights into the Early Stages of Nanoparticle Electrodeposition, J. Phys. Chem. C, 2012, 116, 2322–2329 CrossRef CAS.
- H. S. Toh, C. Batchelor-McAuley, K. Tschulik, M. Uhlemann, A. Crossley and R. G. Compton, The anodic stripping voltammetry of nanoparticles: electrochemical evidence for the surface agglomeration of silver nanoparticles, Nanoscale, 2013, 5, 4884–4893 RSC.
- L. Jiujuan, Z. Guoyun, W. Jinzhong, H. Yan, H. Wei, W. Shouxu, W. Chong, C. Yuanming, Y. Wenjun, M. Chaoying, M. Hua, Z. Jinqun and C. Qingguo, Nickel-nanoparticles-assisted direct copper-electroplating on polythiophene conductive polymers for PSB dielectric holes, J. Taiwan Inst. Chem. Eng., 2019, 100, 262–268 CrossRef.
- B. Pérez-Fernández, D. Martín-Yerga and A. Costa-García, Galvanostatic electrodeposition of copper nanoparticles on screen-printed carbon electrodes and their application for reducing sugars determination, Talanta, 2017, 175, 108–113 CrossRef PubMed.
- M. Miyake, T. Ueda and T. Hirato, Potentiostatic Electrodeposition of Pt Nanoparticles on Carbon Black, J. Electrochem. Soc., 2011, 158, D590–D593 CrossRef CAS.
- D. Kong, Z. Zheng, F. Meng, N. Li and D. Li, Electrochemical Nucleation and Growth of Cobalt from Methanesulfonic Acid Electrolyte, J. Electrochem. Soc., 2018, 165, D783–D789 CrossRef CAS.
- D. Turnbull and J. C. Fisher, Rate of nucleation in condensed systems, J. Chem. Phys., 1949, 17, 71–73 CrossRef CAS.
- V. A. Isaev and O. V. Grishenkova, Kinetics of electrochemical nucleation and growth, Electrochem. Commun., 2001, 3, 500–504 CrossRef CAS.
- V. A. Isaev, Electrochemical phase formation, UB, Russian Academy of Science, Ekaterinburg, 2007, (in Russian) Search PubMed.
- Y. I. Frenkel, Kinetic Theory of Liquids, Oxford University Press, Oxford, 1946 Search PubMed.
- G. J. Hills, D. J. Schiffrin and J. Thompson, Electrochemical nucleation from molten salts – II. Time dependent phenomena in electrochemical nucleation, Electrochim. Acta, 1974, 19, 671–680 CrossRef CAS.
- G. J. Hills, D. J. Schiffrin and J. Thompson, Electrochemical nucleation from molten salts – I. Diffusion controlled electrodeposition of silver from alkali molten nitrates, Electrochim. Acta, 1974, 19, 657–670 CrossRef CAS.
- S. Fletcher, Electrochemical deposition of hemispherical nuclei under diffusion control. Some theoretical considerations, J. Chem. Soc., Faraday Trans. 1, 1983, 79, 467–479 RSC.
- S. Fletcher, Some formulae describing spherical and hemispherical diffusion to small crystals in unstirred solutions, J. Cryst. Growth, 1983, 62, 505–512 CrossRef CAS.
- V. A. Isaev, O. V. Grishenkova, A. V. Kosov, O. L. Semerikova and Y. P. Zaykov, On the theory of cyclic voltammetry for formation and growth of single metal cluster, J. Solid State Electrochem., 2017, 21, 787–791 CrossRef CAS.
- V. A. Isaev, O. V. Grishenkova and Yu. P. Zaykov, Theory of cyclic voltammetry for electrochemical nucleation and growth, J. Solid State Electrochem., 2018, 22, 2775–2778 CrossRef CAS.
- M. D. Pritzker, Voltammetric response for the diffusion controlled electrodeposition onto growing hemispherical nuclei, J. Electroanal. Chem., 1988, 243, 57–80 CrossRef CAS.
- S. Fletcher, C. S. Halliday, D. Gates, M. Westcott, T. Lwin and G. Nelson, The response of some nucleation/growth processes to triangular scans of potential, J. Electroanal. Chem., 1983, 159, 267–285 CrossRef CAS.
- V. A. Isaev and O. V. Grishenkova, Galvanostatic phase formation, J. Solid State Electrochem., 2014, 18, 2383–2386 CrossRef CAS.
- A. Milchev and M. I. Montenegro, A galvanostatic study of electrochemical nucleation, J. Electroanal. Chem., 1992, 333, 93–102 CrossRef CAS.
- V. A. Isaev and O. V. Grishenkova, Galvanostatic nucleation and growth under diffusion control, J. Solid State Electrochem., 2013, 17, 1505–1508 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Olga V. Grishenkova
*a,
Olga V. Grishenkova a and
Yurii P. Zaykov
a and
Yurii P. Zaykov ab
ab
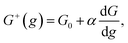
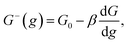

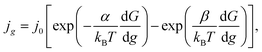
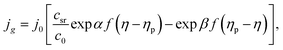
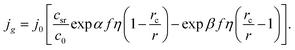
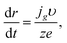
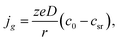
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−fη).
exp(−fη).
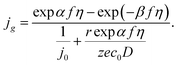
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αfη − exp(−βfη)],
αfη − exp(−βfη)],
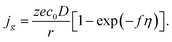

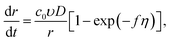
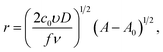
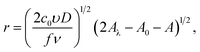
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ze(2c0D)3/2(υ/fν)1/2(2Aλ − A0 − A)1/2[1 − exp(−fη)],
ze(2c0D)3/2(υ/fν)1/2(2Aλ − A0 − A)1/2[1 − exp(−fη)],
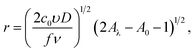
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fηm + 3exp(−fηm) = 2(2Aλ − A0 + 1),
fηm + 3exp(−fηm) = 2(2Aλ − A0 + 1),
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp
exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fη, q (C) is the charge spent on the nanocluster growth, and s (cm2) is the nanoelectrode surface area. We do not take into consideration planar diffusion to the electrode in eqn (24). Therefore, we obtain equation for changing the overpotential in the system
fη, q (C) is the charge spent on the nanocluster growth, and s (cm2) is the nanoelectrode surface area. We do not take into consideration planar diffusion to the electrode in eqn (24). Therefore, we obtain equation for changing the overpotential in the system