Open Access Article
Open Access ArticleSpatially-varying inversion near grain boundaries in MgAl2O4 spinel
Blas P. Uberuaga *a and
Romain Perriot
*a and
Romain Perriot b
b
aMaterials Science and Technology Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA. E-mail: blas@lanl.gov
bTheoretical Division, Los Alamos National Laboratory, Los Alamos, NM 87545, USA
First published on 24th March 2020
Abstract
Complex materials, containing multiple chemical species, often exhibit chemical disorder or inversion. Typically, this disorder is viewed as spatially homogeneous throughout the material. Here, we show, using a simple grain boundary in MgAl2O4 spinel, that this is not the case and that the level of inversion at the grain boundary plane is different than in the bulk. This has ramifications for the energetics of the boundary and how defects interact with it, as exemplified by the relative formation energy of vacancies. Using these results as motivation, we construct a simple model of inversion versus grain size that captures the salient behavior observed in experiments and allows us to extract inversion-relevant properties from those same experiments, suggesting that grain boundaries in the experimentally prepared material are essentially fully inverse. Together, these results highlight the role that microstructure plays on the inversion in the material.
Introduction
As nanostructured materials become ever more ubiquitous and important in the quest to develop advanced materials, it is imperative to understand the role that the interfaces play in dictating their properties. This includes describing the structure–property relationship of these interfaces down to the atomic scale, as it is the atomic scale details of their structure that often determine their properties. Thus, since the early 1970s,1–3 one primary focus area of computational materials science has been the atomic structure of interfaces, in particular grain boundaries, and how those structures impact the properties of the material. However, despite this long history, most studies have focused on metallic systems, and the relatively few studies that have examined interfaces and grain boundaries in ionic materials have tended to limit themselves to simple oxides, such as rocksalts4–7 (e.g. NiO, MgO) or fluorites8–11 (e.g. CeO2, UO2).This is not to say that there have been no atomistic scale studies of grain boundaries in more complex ionic ceramics.12–15 Indeed, work out of the CEA in France16 has comprehensively examined the structure of grain boundaries in complex systems such as spinels. These studies have revealed that the stability of grain boundaries in spinels such as NiCr2O4 and FeCr2O4 is driven by the cation coordination at the boundary. Grain boundary formation energies ranged form 2–6 J m−2 (with the interatomic potential used in the study). They linked higher energies to those grain boundaries in which the local coordination of cations deviated the most from bulk values. The mechanical response of grain boundaries in these same materials was later examined.17 There, the authors found that grain boundaries in the Ni spinel tend to exhibit an overall higher critical stress to cleavage than in the Fe spinel.
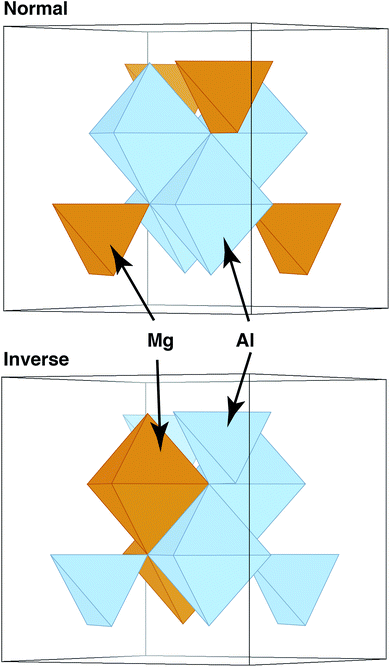
In these and other similar studies, the grain boundaries were constructed by bringing two slabs of spinel together, minimizing the energy versus rigid-body translations, and then minimizing the ionic positions and the cell parameters. However, one aspect that has still been neglected is how the chemical structure of the material might vary in the presence of a grain boundary. Complex oxides such as spinels and pyrochlores are often characterized by their level of inversion i or disorder. Often measured experimentally, this parameter describes the fraction of, for example, A cations that reside on the octahedral, or B sublattice, in an AB2O4 spinel. Some spinels, such as MgAl2O4, exhibit a relatively small amount of inversion, with natural spinels having i = 0.05–0.1218–20 and synthetic spinels reaching higher levels of inversion, i = 0.33.21,22 In contrast, other spinels have greater propensity for inversion,23 and some, such as MgIn2O4 are fully inverse (i ∼ 1),24 where all of the tetrahedral sites (A sublattice) contain In and the Mg cations are all on the octahedral, or B, sublattice. These structures are schematically illustrated in Fig. 1.
While inversion is typically thought of as an average parameter for a given chemistry, recent experimental work has revealed that, in the case of nanocrystalline MgAl2O4, inversion is a function of grain size.25,26 As the grain size is reduced, the inversion in the material increases. This suggests that inversion is not constant throughout the material, but spatially varies near, in this case, the grain boundaries of the material. This grain-boundary-localized inversion has been linked with increase strength of the material.25
Inversion and disorder in materials such as spinels27–29 and pyrochlores30–33 have been extensively studied computationally. However, these studies have invariably looked only at bulk behavior and not at the role of microstructural features such as grain boundaries in modifying that inversion, with the exception of one study that looked at the formation of antisites near a grain boundary in pyrochlore.34 Here, using a simple grain boundary we studied in past work,35 we show, using atomistic calculations, that inversion does indeed vary spatially, with higher levels of inversion found near the grain boundary than in the bulk. Further, this difference in structure has a direct impact on the thermodynamics of at least some potential defects in the system. We then use these results as the foundation of a simple model of inversion versus grain size, showing that the basic behavior reproduces the trends observed in experiment. Overall, our results point to the need to consider chemical inversion or disorder near grain boundaries in multicomponent materials.
Methodology
Our methodology is rather straight forward. We start with a Σ3 twin grain boundary in MgAl2O4, the same boundary we have used in a previous study on dopant segregation.35 This is admittedly the simplest boundary one could consider, and one can argue that it is not very representative of higher energy boundaries. However, it serves as a limiting case, a lower bound on behavior that might be expected for more general boundaries. Further, constructing low energy structures for arbitrary Σ boundaries in materials such as spinel is a challenge.Using a Buckingham potential with parameters as determined by Bacorisen et al.36 and reported in Table 1, we then perform a canonical Monte Carlo (MC) simulation, swapping Mg and Al cations. After each swap, we minimize the energy and apply a standard Metropolis acceptance criterion on whether to accept the swap or not. We do this 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times (each referred to as a “MC step”), at which point we see that the energy of the system tends to settle around an average value, suggesting that the system has reached some sort of quasi-equilibrium. The MC simulations were performed at 1000 K. The simulation cell, containing two grain boundaries, had dimensions of 2.30 × 1.99 × 5.17 nm3 and contained a total of 2464 ions. (Of course, we can never be certain that another lower energy state space exists in the system. That is, the MC simulations could get stuck in a set of states without being able to reach another set of states that is more representative of the system at this temperature. This is always an issue with a finite number of iterations.)
000 times (each referred to as a “MC step”), at which point we see that the energy of the system tends to settle around an average value, suggesting that the system has reached some sort of quasi-equilibrium. The MC simulations were performed at 1000 K. The simulation cell, containing two grain boundaries, had dimensions of 2.30 × 1.99 × 5.17 nm3 and contained a total of 2464 ions. (Of course, we can never be certain that another lower energy state space exists in the system. That is, the MC simulations could get stuck in a set of states without being able to reach another set of states that is more representative of the system at this temperature. This is always an issue with a finite number of iterations.)
| Interaction | A (eV) | ρ (Å) | C (Å6 eV) |
|---|---|---|---|
| Mg–O | 1279.69 | 0.29969 | 0 |
| O–O | 9547.96 | 0.21916 | 32.0 |
The potential used assigns full formal charges to the ions, even though it is known from both theory and experiment that, in reality, the ions only obtain partial charges.37 However, in a comparative study between this potential and density functional theory, Murphy et al.38 showed that, while the numbers certainly differ, the two approaches agree on the relative stability of different defect reactions in MgAl2O4. Thus, we expect that the basic physical trends reported here are qualitatively representative of the real material.
Using the lowest energy structure found during the course of one MC simulation, we then compute the relative formation energies of vacancies in both this ‘minimized’ structure and compare them to the ‘ideal’ structure we started with. We consider all three types of vacancies – Mg, Al, and O. We remove each atom in the system, one at a time, minimizing the energy to determine the relative formation energy as a function of distance from the two grain boundaries in the material (since we are using periodic boundary conditions in all three dimensions, there are necessarily two grain boundaries in the simulation cell). Both the MC simulations and the minimizations were performed using LAMMPS,39 though the MC simulations used the extension developed by Sadigh et al.40 This extension enables the use of LAMMPS as an engine to perform Monte Carlo simulations of various types. Here, we have used it simply to perform canonical MC simulations. In the electrostatic calculations, we used the particle–particle particle–mesh (PPPM) method.41 The cutoffs for the short-range terms in the potential were set to 8 angstroms.
Results and discussion
The central result from this work is highlighted in Fig. 2, which shows the structure of the grain boundary before and after the MC simulations. As is clear from the figure, there is a greater degree of inversion near the grain boundaries than in the bulk. In fact, at this temperature and potential, there is no inversion or antisites created in the bulk. All antisites form at or near the grain boundaries. This enhanced inversion extends just over 1 nm at each grain boundary and lowers the grain boundary energy by 1.35 eV nm−2, or 0.21 J m−2, from 2.51 to 2.30 J m−2. While not a very large change, as will be discussed, the change in inversion for this boundary is also not particularly large, and this change does represent a 10% lowering of the energy. Finally, the spatial extent of the antisites is greater than the structural disorder inherent to the grain boundary and, thus, the inversion, in some sense, increases the physical width of the grain boundary.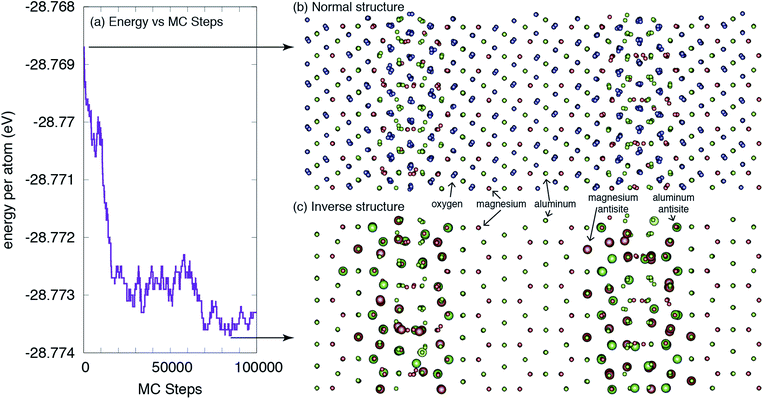 | ||
| Fig. 2 The structure of a Σ3(111) grain boundary in MgAl2O4. (a) The energy of the system versus Monte Carlo steps is reduced as more antisites are formed near the GBs. (b) The ideal ‘normal’ structure, as constructed in ref. 35, without consideration of any change in local inversion. (c) The lower-energy ‘inverse’ structure, as determined from the Monte Carlo simulations. The larger spheres indicate antisites relative to the ideal structure. For clarity, oxygen ions are not shown in (c). The large black arrows indicate where the structures were extracted from the MC simulations. | ||
From the result shown in Fig. 2, we can define both a grain boundary width and a grain boundary inversion. We define the width, w, as simply the distance between the planes that contain any antisites on one side of the boundary to the other. For the grain boundary inversion, iGB, we count the number of Al antisites (AlMg) – Al cations that reside on what, in the original structure, was a Mg site – and divide that by the total number of A sites (the sum of AlMg and MgMg in the same grain boundary region defined by the width w). That is, the inversion at the grain boundary is defined as iGB = AlMg/(AlMg + MgMg) for those sites within the region defined by w. We do this for both grain boundaries and average the values, which are given in Table 2. We find that, in contrast to the bulk, where the inversion from these simulations is ibulk = 0, the inversion at the boundaries is, on average, iGB = 0.26. The average width of the inverse grain boundary is 1.2 nm.
The behavior depicted in Fig. 2 also suggests a relatively simple model for the average inversion of the sample as a function of grain size. If we assume that all grain boundaries have a similar width as we find for the Σ3 boundary studied here, and that they also all have a similar grain boundary inversion, we can view the material as comprised of bulk grains surrounded by a skin of grain boundary region, of width w. A schematic of this structure is given in Fig. 3a. If we assume either cubic or spherical grains (the result is insensitive to this choice), we can derive the average inversion of the material as a weighted average of that of the bulk and that of the grain boundary, arriving at the following relationship:
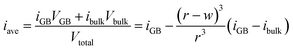 | (1) |
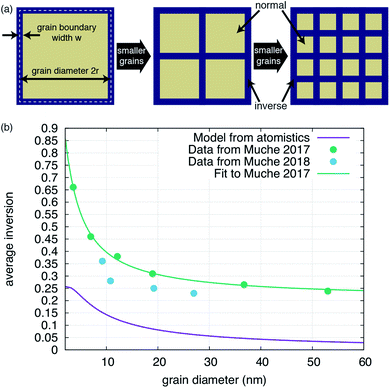 | ||
| Fig. 3 Impact of grain boundary inversion on the average inversion within the material. (a) Schematic of how the structure of the material changes as grains are made smaller. Motivated by the results shown in Fig. 2, each grain is treated as being comprised of an interior bulk-like region, with a bulk level of inversion (‘normal’ for MgAl2O4) and a level of inversion at the grain boundary. The diameter of the grain is 2r while the width of the grain boundary is w. As the grain size is reduced, the relative volume taken by grain boundaries increases. (b) Inversion versus grain size as determined by using eqn (1) (purple line) with parameters determined from the atomistic simulations or (teal line) parameters determined by fitting eqn (1) to the data in ref. 25, shown as the teal points. The blue points, from ref. 26, are shown for completeness, but were not used to fit a separate set of parameters simply because a good fit was not obtainable for this small dataset. | ||
We also compare our result with previous experimental data in Fig. 3b. It is clear that the average inversion we predict versus grain size follows the basic trend of the experiment but is systematically lower. Fitting eqn (1) to the experimental data in ref. 25, we can extract effective w, iGB, and ibulk from the experiment. As reported in Table 2, the experimentally-fitted inversions, both for the bulk and the grain boundary, are significantly higher than extracted from our simulations. The bulk value, ibulk = 0.21, is reasonably close to experimentally determined values for synthetic spinels, as noted previously.21,22 The grain boundary inversion and width of iGB = 1.00 and w = 0.44 nm are larger and smaller, respectively, than what we extract from our simulations. This suggests that, in the experiment, grain boundaries are not nearly as wide as our simulations suggest and that they exhibit a much higher degree of inversion. Of course, in the values extracted from our simulations, we considered the width to include the region containing any antisites, even if the last plane only had one. It is possible that we would obtain a better agreement with the experimentally derived values if we limited the width of the grain boundaries to only those planes with a relatively high concentration of antisites.
That said, it is reasonable that the experimentally derived grain boundary inversion is higher than that extracted from the simulations. In the simulations, we considered a Σ3 twin boundary, which, at least in metals, has essentially no interaction with defects.42 Thus, of all grain boundaries one might consider, this one interacts most weakly with defects and, by extension, inversion and antisites. Any other grain boundary would be expected to exhibit much stronger interactions and, thus, a greater degree of inversion. Further, experiments reveal inversion levels of on the order of 0.2–0.3 in the bulk, while our simulations predict a bulk inversion of 0. This is likely a limitation of both the potential, which over-penalizes the formation of antisites, and the methodology, which, while accounting for configurational entropy, neglects vibrational entropy. Past work has shown that accurate predictions of inversion require the treatment of vibrational entropy and short range order.29
What this simple model does reveal, however, is that we can accurately fit the experimental data and obtain physically-meaningful properties of the grain boundary. We conclude that the grain boundaries are essentially fully inverse, at least in this particular set of samples. This model assumes that the grain boundary inversion is constant versus grain size. It is possible that, as the grain size shrinks, the interactions between grain boundaries leads to a further modification of the inversion. However, the results presented here suggest that such behavior is not necessary to explain the experimentally observed trends.
Finally, to provide some sense of whether the spatially dependent inversion has any consequences for the properties of the grain boundary, we examine the formation energy of defects at both the original boundary and the MC-minimized boundary. We calculated the formation energy of the Mg, Al, and O vacancies as a function of distance from the two boundary planes. These results are presented in Fig. 4. Interestingly, the relative formation energies of Mg and O vacancies are not significantly perturbed by the inversion. In the case of the O vacancy, the formation energy is lower at one boundary when inversion is introduced, but not the other. In fact, there are sites a few planes away from the central plane of symmetry where the inversion leads to a greater repulsion of the vacancies. However, any behavior observed at one boundary is absent in the other, obscuring any systematic trends. The same is true of the Mg vacancy, where the formation energy of the vacancy is significantly reduced at one boundary but not at the other, again rendering any solid conclusions difficult to extract.
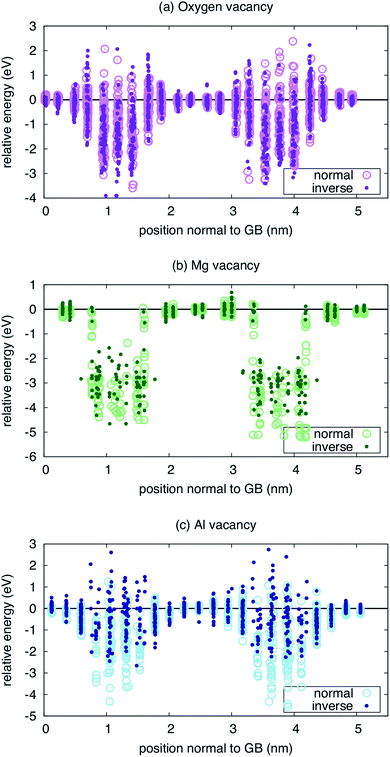 | ||
| Fig. 4 Energetics of vacancies near both the ideal (normal) and minimized (inverse) Σ3(111) grain boundary for three types of vacancies: (a) oxygen, (b) magnesium, and (c) aluminum. | ||
Only for the Al vacancy do we see consistent trends at the two boundaries in the simulation supercell. At both boundaries, the Al vacancy is effectively repelled, with higher formation energies when inversion is introduced than when it is not. Further, there are more sites with positive energy, indicating repulsion compared to the bulk reference. Thus, while the interaction of Mg and O vacancies can be enhanced or not when the inversion is considered, the Al vacancies consistently show a weaker interaction with the inverse boundary.
One might suspect that the defect mobility would also be significantly modified due to the inversion. To gain some sense of this might be the case, we examined the landscape of O vacancies within the boundary plane for the first boundary in Fig. 4 (results not shown). In this case, even though there are lower energy sites for the vacancy when the inversion is present, we do not see a significant shift of the landscape within the boundary plane. That is, the relative energy of different sites that connect the lowest energy sites in the boundary plane are similar in both the inverse and normal boundaries. While this is not conclusive, it suggests that the chemical disorder represented by the inversion does not dominate over the structural disorder represented by the boundary itself in terms of the landscape defects might experience as they migrate.
What does all of this tell us? The primary conclusion is that inversion is indeed spatially dependent and will vary with the microstructure in the material. Thus, considering only one level of inversion, or more generally cation disorder, in complex oxides such as spinels or pyrochlores or, indeed, any multicomponent ionic oxide is probably, at best, incomplete. To understand the properties of these materials more completely, one must consider these effects. This is true not only of grain boundaries, but any microstructural feature, such as internal surfaces due to porosity or dislocations. The fact that experiments reveal size-dependent average inversion and correlate this behavior with, for example, the strength of the material highlights the importance of understanding these effects. At this point, we have only provided proof-of-principle results that highlight the reality of spatially-dependent inversion and its potential importance. Further work is necessary to fully realize the impact of this behavior on properties of interest.
Conclusion
To conclude, we have used atomistic simulations to examine the relative inversion residing at and near a grain boundary in MgAl2O4 spinel. We find that, consistent with experimental results, the inversion is not spatially homogeneous and that a higher level of inversion exists at the boundary than in the bulk. This inversion modifies the interaction of at least a subset of defect types with the boundary, altering the thermodynamic equilibrium defect content that would be present. A simple model of inversion as a function of grain size captures the trends observed in experiment and, further, allows us to extract grain boundary-relevant inversion parameters. Overall, this work highlights the importance of considering the spatial variations in chemical order in complex microstructures for a more complete view of the properties of complex, multicomponent materials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
B. P. U. and R. P. acknowledge support by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001).References
- G. Hasson, J.-Y. Boos, I. Herbeuval, M. Biscondi and C. Goux, Surf. Sci., 1972, 31, 115 CrossRef CAS.
- M. Weins, H. Gleiter and B. Chalmers, J. Appl. Phys., 1971, 42, 2639 CrossRef CAS.
- R. Cotterill, T. Leffers and H. Lilholt, Philos. Mag., 1974, 30, 265 CrossRef CAS.
- P. Tasker and D. Duffy, Philos. Mag. A, 1983, 47, L45 CrossRef CAS.
- D. Duffy, J. Phys. C: Solid State Phys., 1986, 19, 4393 CrossRef CAS.
- D. Harris, G. Watson and S. Parker, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 11477 CrossRef CAS.
- B. P. Uberuaga, X.-M. Bai, P. P. Dholabhai, N. Moore and D. M. Duffy, J. Phys.: Condens. Matter, 2013, 25, 355001 CrossRef.
- L. Van Brutzel and E. Vincent-Aublant, J. Nucl. Mater., 2008, 377, 522 CrossRef CAS.
- P. V. Nerikar, K. Rudman, T. G. Desai, D. Byler, C. Unal, K. J. McClellan, S. R. Phillpot, S. B. Sinnott, P. Peralta and B. P. Uberuaga, et al., J. Am. Ceram. Soc., 2011, 94, 1893 CrossRef CAS.
- J. A. Purton, N. L. Allan and D. S. Gunn, Solid State Ionics, 2017, 299, 32 CrossRef CAS.
- A. Symington, M. Molinari, J. Statham, J. Wu and S. C. Parker, J. Phys.: Energy, 2019, 042005 Search PubMed.
- V. Ravikumar, V. P. Dravid and D. Wolf, Interface Sci., 2000, 8, 157 CrossRef CAS.
- R. Astala and P. Bristowe, J. Phys.: Condens. Matter, 2002, 14, 13635 CrossRef CAS.
- T. Oyama, N. Wada, H. Takagi and M. Yoshiya, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134107 CrossRef.
- S. Von Alfthan, N. A. Benedek, L. Chen, A. Chua, D. Cockayne, K. J. Dudeck, C. Elsässer, M. W. Finnis, C. T. Koch and B. Rahmati, et al., Annu. Rev. Mater. Res., 2010, 40, 557 CrossRef CAS.
- A. Chartier, B. Golovchuk, S. Gossé and L. Van Brutzel, J. Chem. Phys., 2013, 139, 134702 CrossRef PubMed.
- L. Van Brutzel, A. Chartier, B. Sicaud and M. Sauzay, J. Chem. Phys., 2019, 151, 014701 CrossRef PubMed.
- G. Gobbi, R. Christoffersen, M. Otten, B. Miner, P. Buseck, G. Kennedy and C. Fyfe, Chem. Lett., 1985, 14, 771 CrossRef.
- U. Schmocker, H. Boesch and F. Waldner, Phys. Lett. A, 1972, 40, 237 CrossRef CAS.
- U. Schmocker and F. Waldner, J. Phys. C: Solid State Phys., 1976, 9, L235 CrossRef CAS.
- E. Brun, S. Hafner, P. Hartmann and F. Laves, Naturwissenschaften, 1960, 47, 277 CrossRef CAS.
- F. Docherty, A. Craven, D. McComb and J. Skakle, Ultramicroscopy, 2001, 86, 273 CrossRef CAS.
- K. E. Sickafus, J. M. Wills and N. W. Grimes, J. Am. Ceram. Soc., 1999, 82, 3279 CrossRef CAS.
- T. F. Barth and E. Posnjak, Z. Kristallogr. - Cryst. Mater., 1932, 82, 325 CAS.
- D. N. Muche, M. A. Marple, I. Hung, Z. Gan, R. H. Castro and S. Sen, J. Phys. Chem. C, 2017, 121, 13898 CrossRef CAS.
- D. N. Muche, M. A. Marple, S. Sen and R. H. Castro, Acta Mater., 2018, 149, 302 CrossRef CAS.
- A. Cormack, G. Lewis, S. Parker and C. Catlow, J. Phys. Chem. Solids, 1988, 49, 53 CrossRef CAS.
- A. Seko, K. Yuge, F. Oba, A. Kuwabara, I. Tanaka and T. Yamamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 094116 CrossRef.
- C. Jiang, K. E. Sickafus, C. R. Stanek, S. P. Rudin and B. P. Uberuaga, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 024203 CrossRef.
- L. Minervini, R. W. Grimes and K. E. Sickafus, J. Am. Ceram. Soc., 2000, 83, 1873 CrossRef CAS.
- C. R. Stanek and R. W. Grimes, J. Am. Ceram. Soc., 2002, 85, 2139 CrossRef CAS.
- C. Jiang, C. Stanek, K. Sickafus and B. Uberuaga, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 104203 CrossRef.
- S. Finkeldei, P. Kegler, P. Kowalski, C. Schreinemachers, F. Brandt, A. Bukaemskiy, V. Vinograd, G. Beridze, A. Shelyug and A. Navrotsky, et al., Acta Mater., 2017, 125, 166 CrossRef CAS.
- R. Perriot, P. P. Dholabhai and B. P. Uberuaga, Nanoscale, 2017, 9, 6826 RSC.
- M. M. Hasan, P. P. Dholabhai, S. Dey, B. P. Uberuaga and R. H. Castro, J. Eur. Ceram. Soc., 2017, 37, 4043 CrossRef CAS.
- D. Bacorisen, R. Smith, J. Ball, R. Grimes, B. Uberuaga, K. Sickafus and W. Rankin, Nucl. Instrum. Methods Phys. Res., Sect. B, 2006, 250, 36 CrossRef CAS.
- P. Thibaudeau and F. Gervais, J. Phys.: Condens. Matter, 2002, 14, 3543 CrossRef CAS.
- S. Murphy, C. Gilbert, R. Smith, T. Mitchell and R. Grimes, Philos. Mag., 2010, 90, 1297 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- B. Sadigh, P. Erhart, A. Stukowski, A. Caro, E. Martinez and L. Zepeda-Ruiz, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184203 CrossRef.
- R. W. Hockney and J. W. Eastwood, Computer simulation using particles, Hilger, Bristol, 1988 Search PubMed.
- M. J. Demkowicz, O. Anderoglu, X. Zhang and A. Misra, J. Mater. Res., 2011, 26, 1666 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |