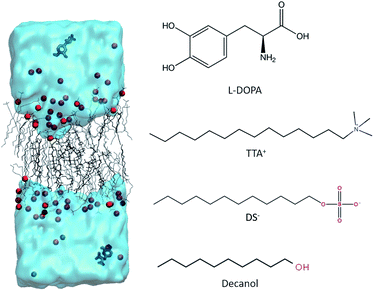
Open Access Article
Open Access ArticleL-DOPA modulates the kinetics but not the thermodynamic equilibrium of TTA+ amphiphiles forming lyotropic nematic liquid crystals†
Álvaro R. Ruiz-Fernández‡
 ab,
Felipe Villanelo‡
ab,
Felipe Villanelo‡ ac,
Sebastian E. Gutierrez-Maldonado
ac,
Sebastian E. Gutierrez-Maldonado ac,
Claudia Pareja-Barruetoac,
Boris E. Weiss-López*b and
Tomas Perez-Acle
ac,
Claudia Pareja-Barruetoac,
Boris E. Weiss-López*b and
Tomas Perez-Acle *acd
*acd
aComputational Biology Lab, Fundación Ciencia & Vida, Santiago, Chile. E-mail: tomas@dlab.cl
bUniversidad de Chile, Facultad de Ciencias, Departamento de Química, Casilla 653, Santiago, Chile. E-mail: bweiss@uchile.cl
cCentro Interdisciplinario de Neurociencia, Universidad de Valparaíso, Valparaíso, Chile
dUniversidad San Sebastian, Carmen Sylva 2444, Santiago 7510156, Chile
First published on 17th April 2020
Abstract
Lyotropic liquid crystals (LLCs) are mixtures of amphiphile molecules usually studied as mimetic of biological membrane. The equilibrium dynamics of tetradecyltrimethyl ammonium cation (TTA+) molecules forming nematic LLCs (LNLCs) is guided by a dive-in mechanism where TTA+ molecules spontaneously leave and re-enter the bicelle. Of note, this dynamic behavior could be exploited to produce drug nano-delivery systems based on LNLCs. Therefore, the understanding of the effect of pharmaceutically interesting molecules in the dynamics of the dive-in mechanism should be crucial for drug delivery applications. In this work, we studied the effects of L-DOPA in the equilibrium dynamics of TTA+ bicelles forming LNLCs, employing a transdisciplinary approach based on 2H-NMR together with molecular modeling and molecular dynamics simulations. Our data suggest that L-DOPA perturbs the kinetic of the dive-in mechanism but not the thermodynamics of this process. As whole, our results provide fundamental insights on the mechanisms by which L-DOPA govern the equilibrium of LNLCs bicelles.
1 Introduction
Parkinson's disease (PD) is a neurodegenerative disorder characterized by continuous neuronal death producing a lack of dopamine in the Substantia nigra of the human brain.1 Dopamine is a catecholamine neurotransmitter derived from L-3,4-dihydroxyphenylalanine, commonly known as L-DOPA. As a precursor of dopamine, L-DOPA has become the most used treatment for PD due to its ability to cross the blood–brain barrier, reaching the Substantia nigra. Despite its wide use, L-DOPA administration it is not an issue-free therapy for the treatment of PD. L-DOPA is very unstable compound. Near 99% of L-DOPA administered orally is degraded either via oxidation or decarboxylation.2,3L-DOPA administration also produces side effects such as nausea, sleepiness and dyskinesia4 and, due to its high metabolic clearance, maintaining a constant L-DOPA plasma concentration requires both elevated and continuous dosage, exacerbating its side effects.5 To deal with these issues, different delivery systems have been developed including microspheres, dendrimers, and micelles for infusion and transdermal delivery.5,6 Recently, the use of biodegradable copolymers of glycolic and lactic acids used via nasal L-DOPA administration, have attract the attention of many investigators7 In recent years, mixtures of amphiphilic molecules in solutions received significant attention as potential delivery systems. Among these, solutions made of orientationally ordered discotic aggregates (bicelles8 among others), termed as lyotropic nematic liquid crystals (LNLCs), exhibit several uses such as, to grow oriented carbon nanotubes,9–11 to synthetize silica and metals containing regularly oriented nanopores and,12–17 as membrane mimetics,18–20 and as micro-lubricants.21,22 Of note, more recently, LNLCs has been proposed as simple but versatile carriers for pharmaceutical formulations to avoid the metabolic clearance and to maintain constant plasma concentration of drugs.23–26 Due to their geometry, bicelles have an anisotropic diamagnetic susceptibility that makes them spontaneously align in magnetic fields, with the symmetry axis of the disk perpendicular to the direction of the field. This enables the obtention of valuable experimental information such as quadrupole splittings that helps to understand its intrinsic dynamics nature. In a previous work, a mechanism for the insertion and expulsion of an amphiphile molecule from a bicelle, called the dive in mechanism, has been proposed.27 Considering that LNLCs could be used as delivery systems for drugs, particularly L-DOPA, we performed an experimental and theoretical study aimed to determine how the presence of L-DOPA modulates the dive in mechanism of the amphiphiles forming the LNLC. Notably, our data suggest that, while the inclusion of L-DOPA in the media actually modulates the kinetics of the dive in mechanism generating additional micro-states where several more TTA+ amphiphiles could be out of the bicelle, the thermodynamics of this process, remain unaltered. Therefore, future applications of LNLC to the development of drug delivery systems, should consider the effect of the drug concentration on the dynamical behavior of bicelles.
2 Methodology
2.1 Mesophase preparation
L-DOPA was purchased from Santa Cruz Biotechnology and used as received. L-DOPA-d3 was purchased from ISOTEC. Fully deuterated sodium dodecylsulphate (SDS-d25), tetradecyltrimethyl ammonium chloride (TTAC) and decanol (DeOH) were purchased from Aldrich. HPLC-grade water and sodium chloride (NaCl) at the highest purity available were purchased from Merck. All compounds were used as received. The base solution (BS) for this study was taken from a previous work from our group.27 It was prepared by dissolving 0.3448 g of TTAC, 0.1094 g of NaCl and 0.0730 g of DeOH in 1 ml of H2O, and was equilibrated 48 hours at 300 K, before any measurements were performed. To study the effect of L-DOPA in this system three different solution were prepared. System 1: BS + 18 mg SDS-d25 + 5 μL of D2O. System 2: BS + 18 mg SDS-d25 + 7.5 mg L-DOPA + 5 μL of D2O. System 3: BS + 7.5 mg of L-DOPA-d3 + 5 μL of D2O. In the preparation of the three systems when SDS-d25 and D2O were included, SDS and H2O were removed in the same amount to maintain the concentration of BS.SDS-d25 is added because it is used to test the effect of L-DOPA in the aggregate structure, following modifications in the dynamics of the aliphatic chains of SDS-d25 at different depths towards the interior of the hydrophobic core. D2O is added because ΔνQ of water deuterium gives valuable information about the interface dynamics. L-DOPA-d3 will provide information about the interaction of the drug with the aggregate components.
2.2 2H-NMR spectra
2H-NMR spectra were obtained in a Bruker Avance 400 NMR spectrometer, located at the Universidad de Santiago de Chile, using a broadband probe tuned to 61.425 MHz, at 300 K. The 2H 90° pulse was 19 μs long and more than 1000 transients from a spectral window of 40 kHz were accumulated in 32 kB files.2.3 Polarized light microscopy (PLM)
A Motic series B microscope with crossed polarizers was employed to observe the textures. The samples were placed in a concave slide with a depth of 1 mm and were allowed to orient in a 1.4 T magnet for 15 min. The photos were taken with a 20-fold magnification, from the center of the concavity, avoiding variations in the thickness of the sample due to the curvature of the slide. Photos were obtained at 300 K.2.4 MD simulations
Of note, SDS is a salt that in aqueous solution dissociates in its cation and anion, thus in the solution used for NMR experiments, SDS becomes dissociated in SD− and Na+. Thus, the NMR results are from SD−. For this reason, the MD simulation protocols used SD−.
The amount of L-DOPA in system 2 is close to the saturation point, thus no additional concentration-response experiments, could be performed. However, for theoretical simulations, an increased number of L-DOPA molecules can be included.
Therefore an additional simulation containing exactly the same molecules as Box 1, but adding four L-DOPA molecules was generated and named Box 3. Thus Box one is basically a bilayer of TTA+, and; Box 2: is Box 1 + 2 L-DOPA and Box 3: is Box 1 + 4 L-DOPA. Atomic charges of all simulated molecules are presented in Table S3† along with Fig. S6.† The equilibrium condition reached by the simulations, studied specifically for Box 3, is presented in Fig. S4 and S5.†
3 Results and discussion
3.1 Experimental data, 2H-NMR and PLM
2H-NMR spectra of the three studied systems (see Section 2.1) with their PLM textures are shown in Fig. 2. The spectra profile and the textures observed in PLM correspond to Schlieren textures, confirming that the three systems are in the same lyotropic nematic phase.29–34 The Schlieren texture is the name given to the colored texture observed when a polarized light is applied on a lyotropic liquid crystal, when it is in a nematic phase. Thus, the addition of L-DOPA did not change the phase of the system.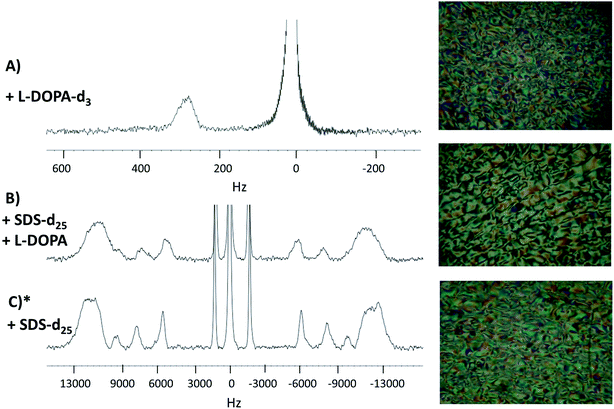 | ||
| Fig. 2 2H-NMR spectra and the PLM textures. Panel (A), L-DOPA-d3 in system 2. Panel (B), SDS-d25 in system 2. Panel (C), SDS-d25 in system 1. * System 1 spectrum and PLM texture were obtained in a previous work and are reproduced with permission from ref. 27. | ||
As seen in Fig. 2A, the signal on the left corresponds to the deuterium from L-DOPA-d3 and the signal on the right is from DHO. In Fig. 2B and C, the signal in the middle, near 0 Hz, is from DHO, and the remaining signals are from SDS-d25. The separation in Hz between two signals coming from the same deuterium corresponds to the quadrupole splitting (ΔνQ). ΔνQ can be obtained from the following expression:
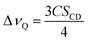 | (1) |
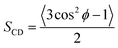 | (2) |
Table 1 shows ΔνQ of SDS-d25 of systems 1 and 2. In both systems, ΔνQ decreases as the carbons of SDS-d25 get closer to the hydrophobic core. This is expected because the orientational order given by the interface interaction decrease towards the hydrophobic core. The addition of L-DOPA has an effect in the dynamics of the first 8 carbons of SDS, as can be observed in Table 1; ΔνQ of system 2 decrease around 2 kHz respect to system 1. For the rest of the carbons, the change in ΔνQ is not significant. These observations imply that L-DOPA must be interacting with the interface of the aggregate without reaching the hydrophobic core. Moreover, considering that Fig. 2A indicates that L-DOPA remains in the isotropic domain of the systems, the interaction with hydrophobic core, if exist, must be too weak to be detected.
| Carbon | ΔνQ (Hz) | |
|---|---|---|
| System 1* | System 2 | |
| 1 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
| 2 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
| 3 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
| 4 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
| 5 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
| 6 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
| 7 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
| 8 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 402 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 621 621 |
| 9 | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 470 470 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 924 924 |
| 10 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 080 080 |
15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 352 352 |
| 11 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714 714 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 225 225 |
| 12 | 2967 | 2788 |
Other possible explanation for the decrease in ΔνQ when L-DOPA is added, is that L-DOPA could affect the system inducing macroscopic changes in the aggregates that affects macroscopic measurements, such as viscosities. An increment in viscosity could explain the widening of the 2H-NMR signals from spectra in Fig. 2B with respect to Fig. 2C, and the decrease in ΔνQ is given by a lost of orientation of the complete aggregate.21,22 To check for this phenomena a study on the effects of L-DOPA in other lyotropics nematic systems, approaching the sensitivity of these kind of systems, is added in ESI, Section 1 (Fig. S1†). Unfortunately, since the concentration of added L-DOPA (7.5 mg per ml of water) is saturating, conducting a study similar to those exposed in the ESI Section 1,† is not viable because increasing the concentration of L-DOPA in this systems will produce precipitation, so no phase change could be observed.
3.2 Equilibrium molecular dynamics
To determine if our molecular models is capable to recover the experimentally bicelle dynamics, we rely on the calculations of ΔνQ. For this purpose, we use the order parameter of the C–D bond of DS− with respect to the direction of the magnetic field applied (xy plane). As observed in Fig. 3, the first five C–D bond splittings are correctly reproduced by the MD simulation of Box 2. Despite the disagreement from carbon 7 to 11, the experimental and simulated values of ΔνQ are similar. The general trend of the experimental ΔνQ are well reproduced by the calculation, suggesting that the general dynamics behavior of the simulated bilayer mostly reflects that of the experimental aggregate.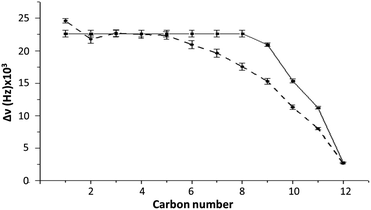 | ||
| Fig. 3 Comparison of ΔνQ between experiment (system 2) (continuous line) and MD simulations (Box 2) (dashed line) as a function of the carbon number. Error bars represent the standard deviation. See Table S1† for exact numbers. | ||
Individual ΔνQ values can be seen in Table S1 of the ESI.† Importantly, the reproduction of the experimental ΔνQ was achieved using a temperature of 328 K and halving the DS− charges of the experimental system in order to compensate for the absence of polarizability. As proposed in the literature, this change corrects the overestimation of the electrostatics interactions that is present in common MD force fields.36–42
During simulation of both Box 2 and Box 3, L-DOPA establish a dynamic process, passing from the bulk aqueous phase to interact with the interface of the aggregate (Fig. S2†). These fast L-DOPA exchange denotes a weak interaction with the bilayer: there is a cumulative loss of 115 kJ mol−1 of short range LJ and coulombic interaction energy when L-DOPA is transferred from bulk to the surface of the bicelle (see Table S2 at the ESI†). Notably, this energy loss shown by our MD simulations is in agreement with 2H-NMR results (Fig. 2A) explaining why L-DOPA interaction with the bicelle is too weak to produce a ΔνQ.
Fig. 4 shows the distance, between the center of mass of the bilayer and the center of mass of the TTA+ molecules leaving the bilayer, as a function of simulation time in boxes 1, 2 and 3. These data indicates that adding two L-DOPA (Fig. 4, Panel B) to the system, apparently do not perturb the exchanges dynamic of TTA+ between the bulk and the bicelle. As noted, the addition of two L-DOPA do not change significantly the time that TTA+ molecules remain in the bulk after leaving the bicelle, neither changes the frequency of TTA+'s insertion and expulsion. When two L-DOPA molecules are added, the time that TTA+ molecules remain in the bulk is on average 65 ns, similar to the average time of 68 ns without L-DOPA. During the simulation without L-DOPA, 14 TTA+ molecules were expelled and 13 were inserted; with two L-DOPA molecules, 13 TTA+ molecules were expelled and inserted along the simulation. Thus, the addition of two L-DOPA molecules do not perturb the exchange dynamics of TTA+, resulting average in 0.72 and 0.74 molecules in the bulk, for systems without L-DOPA and with two L-DOPA, respectively.
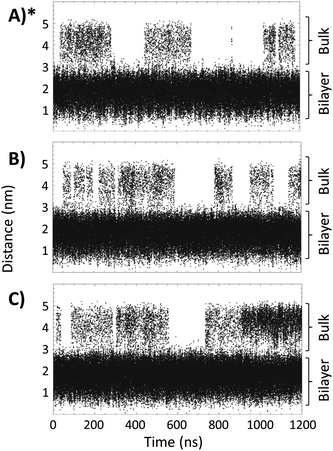 | ||
| Fig. 4 Distance, as a function of time, between the TTA+ center of mass and the center of mass of the bilayer of the bicelle. Panels (A), (B) and (C), represent Box 1, Box 2 and Box 3, respectively. (*) Reproduced with permission from ref. 27. | ||
However, the addition of 4 L-DOPA molecules (Fig. 4C) increases the number of TTA+ molecules present in the bulk. During the MD simulation, 19 TTA+ molecules were expelled and 18 were inserted, with an average time in the bulk of 87 ns, corresponding to an average of 1.65 TTA+ molecules in the bulk.
To check if TTA+ molecules reach a thermodynamic equilibrium in the bulk (after expulsion from the bilayer), we define an internal order parameter as the inner vector going from the first to the second carbon of TTA+ (Fig. 5), and compare its behavior in the bulk of our simulations with that of a control simulation where the bilayer is absent. The control simulation consisted of a box of 4 × 4 × 4 nm3 with 1 TTA+, 1 Cl− and 2126 molecules of H2O, using the same simulation parameters of Box 2, but executed for 200 ns. Fig. 5 shows the probability distribution of the inner vector angle of TTA+ with respect to the z axis in three different scenarios: bulk TTA+ in Box 2, bulk TTA+ in Box 3 and a TTA+ in the control box. As noted, the angular sampling distributions for all systems resulted similar without statistically significant differences, according to a Kruskal–Wallis non-parametric test, suggesting the achievement of a thermodynamic equilibrium. The same histogram was constructed to evaluate if L-DOPA changes the inner angle distribution of a TTA+ molecule in water (Fig. S7†).
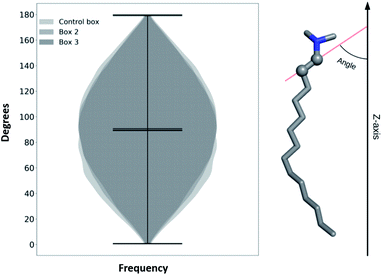 | ||
| Fig. 5 Histogram of a characteristic inner angle of a TTA+s when are in the bulk solution of Box 2, Box 3 and from 1 TTA+ in water for 200 ns. | ||
In a thermodynamic equilibrium, the standard free energy of a process depends on the equilibrium constant, according to eqn (3):
ΔG0 = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Keq Keq
| (3) |
Assuming that our simulation is an equilibrated system, qualitative information about the insertion/expulsion process could be obtained considering that this equilibrium is properly represented by eqn (4):
 | (4) |
Therefore, ΔG0 of insertion of a TTA+ molecule can be calculated from eqn (3), assuming that the equilibrium constant Keq can be estimated using the quotient between the amount of TTA+ present in the bilayer and in the bulk. Table 2 summarizes the TTA+ insertion/expulsion events, the average time of TTA+ molecules in the bulk, the average number of TTA+ molecules present in the bulk and the ΔG associated with the TTA+ insertion/expulsion process.
| Insertion/expulsion events | Avg. time of TTA+ in the bulk (ns) | Avg. number of TTA+ in the bulk | ΔG of insertion (kJ mol−1) | |
|---|---|---|---|---|
| Box 1 | 12/14 | 68 | 0.72 | −11.00 |
| Box 2 | 13/14 | 65 | 0.74 | −10.95 |
| Box 3 | 18/19 | 87 | 1.65 | −8.89 |
As seen on Table 2, for all simulation boxes both the number of insertion/expulsion events and the average time that TTA+ molecules remain in the bulk are different. However, the ΔG0 calculated according to eqn (3), in all three cases was quite similar, with differences falling within the thermal noise (around 2 kJ mol−1). These ΔG0 values also support our assumption of thermodynamic equilibrium, suggesting that the presence of L-DOPA will only perturb the kinetics of the TTA+ insertion/expulsion mechanism but not its thermodynamics.
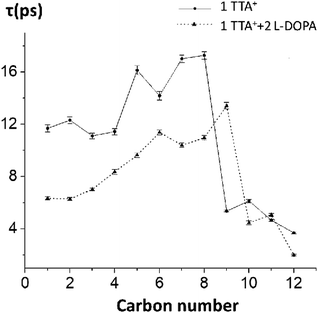
To test the hypothesis of a kinetic effect of L-DOPA on the studied systems, we analyze the autocorrelation function of the order parameters, SCH, of every carbon–hydrogen bond on TTA+. This analysis is computationally expensive because the trajectory must be saved with a higher frequency, to rigorously catch the dynamic behaviour of the atoms. Attending to this cost, we perform the analysis on the control box decribed in the preceding section (one TTA+, one Cl− in a water box, without the bilayer, simulated for 200 ns) with and without L-DOPA. The autocorrelation curves were fitted to a mono-exponential decay, to obtain the representative τ of the SCH decay of each C–H bond, with and without L-DOPA (Fig. 6), see Table S5† for the exact numbers and Fig. S8† to see the autocorrelation curves. Interestingly, the τ with L-DOPA is significantly shorter than τ without L-DOPA for the first eight carbons. This can be interpreted as an effect of L-DOPA on the dynamics of the C–H bonds, specially for the first carbons that are near the polar head of TTA+. In Table S4† we present the SCH of TTA+ obtained for Box 2, and using a Box containing only water molecules.
3.3 Steered molecular dynamics
To analyze the possible effect of L-DOPA in the thermodynamics of insertion/expulsion mechanism of TTA+ molecules from the bicelle, we performed steered molecular dynamics (SMD) on individual TTA+ molecules belonging to Box 2. To do so, we defined an insertion/expulsion reaction coordinate as the distance in the z-axis from the C12/N atoms of the steered TTA+ molecule with respect to the center of mass of all the N atoms belonging to the proximal TTA+ monolayer. To further determine the influence of L-DOPA on the steered TTA+ molecule, we applied two additional restrictions to keep L-DOPA in the surface of bilayer: a distance restraint to keep it close to the steered TTA+ molecule, and an angular restraint to keep the aromatic ring of L-DOPA parallel to the surface. As a control simulation we performed a similar protocol in the system lacking L-DOPA that was described in ref. 27.From every simulations we calculate the work performed and then calculate the energy (ΔF) using Jarzynsky equation:
ΔF = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈exp−W/kT〉 ln〈exp−W/kT〉
| (5) |
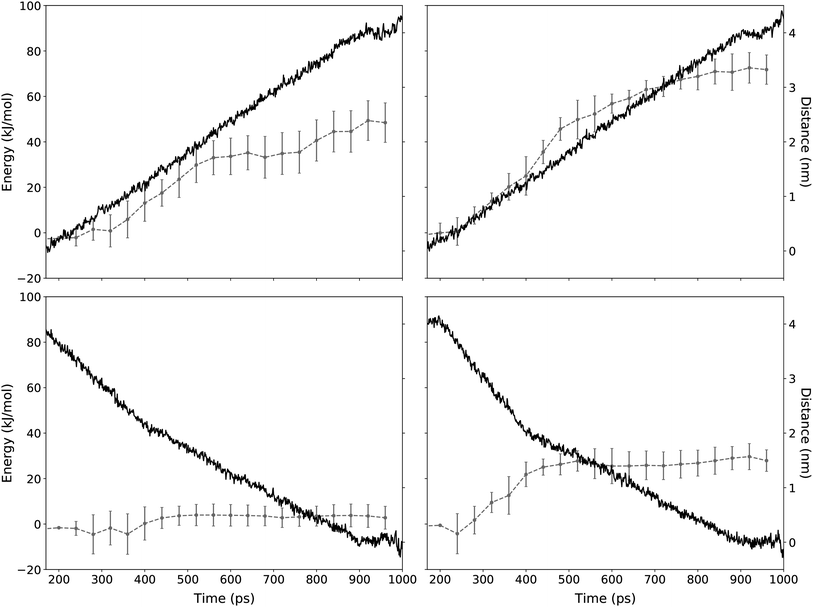 | ||
| Fig. 7 Distance and energy of a TTA+ molecule during the SMD protocol. The application of the SMD protocol simulating the expulsion and the insertion mechanism is presented in the top and bottom panels, respectively. Red line corresponds to the energy as function of simulation time (left y-axis). Left panels shows SMD experiments without L-DOPA and right panels with L-DOPA. Error bars represent the standard deviation of n independent steering experiments for TTA+ molecules according to Table 3 (see Methods). Blue line shows the distance between the steered TTA+ molecule and the rest of the bilayer (right y-axis). | ||
| ΔF (kJ mol−1) | n | ||
|---|---|---|---|
| Expulsion | Without L-DOPA | 48.45 ± 8.69 | 48 |
| With L-DOPA | 66.18 ± 7.32 | 35 | |
| Insertion | Without L-DOPA | 2.77 ± 5.01 | 40 |
| With L-DOPA | 27.90 ± 4.74 | 23 |
Regarding the interaction of L-DOPA with the interphase, Fig. S3† shows an alternative insertion/expulsion mechanism given by the interaction of L-DOPA with the amphiphile molecule that is being inserted or expelled.
To further analyze these results, it is important to address the differences between the energies obtained from the equilibrium MD and the SMD simulation protocols. Free energy values obtained from equilibrium MD using eqn (3) represent a function of state for a molecular system in a near-to-equilibrium condition: the TTA+ molecules that become expelled from the bicelle describe a conformational sampling in the solvent equivalent to that of TTA+ molecules in solution (Fig. 5).
On the other hand, ΔF values are obtained from the ensemble of trajectories generated by the irreversible work of the SMD protocols executed to either insert or expulse a TTA+ molecule from the bilayer. Therefore, the SMD protocol assume an out of equilibrium condition where irreversible work is performed between the two states: a TTA+ molecule embedded in the bilayer and its counterpart embedded in the solvent. As a consequence, these energies can not be compared directly as they represent different thermodynamic processes.
However, ΔF implies that the balance between the insertion and the expulsion process, considered as a whole, is tilted towards the insertion and, as we increase the concentration of L-DOPA, the cost of the insertion process increases, an observation that is in agreement with the increase of ΔG shown in Table 2.
Likewise, SMD results are useful to better describe the “dive in mechanism” of TTA+ molecules.27 Thus, in the absence of L-DOPA, the ΔF of expulsion of a TTA+ molecule is more than 17 times higher than the value of its ΔF of insertion, the latter being near to thermal noise. This is a clue about how energetically costly is the expulsion mechanism of an amphiphile from its aggregate, compared to that of the insertion value. Notably, this observation in agreement with the spontaneity of the insertion process denoted by ΔG values in Table 2. It is important to remark that L-DOPA was inserted in the interphase with some restriction as was describe in the last part of Section 2.4.2. These restrictions are much needed because during the insertion/expulsion of the TTA+ under study, is possible that L-DOPA leave the interphase, as is suggested by the loose of 115 kJ mol−1 when L-DOPA pass from the bulk to the interphase, as is exposed in Fig. S2.†
Even more interesting is the apparent contradiction between the values of ΔF and ΔG when L-DOPA is added. In SMD, both cases, expulsion and insertion, have a 20 kJ mol−1 increase in ΔF compared to condition without L-DOPA (Table 3). To better comprehend these results, it should keep in mind that the ΔG from equilibrium MD implies both process simultaneously, insertion and expulsion. Instead SMD considers both process independently. In SMD with L-DOPA both process have a similar increase in energy, so both increases are canceled when they are considered together, because they act in opposite sides of the eqn (4). As whole, our data supports the notion that adding L-DOPA will affect the kinetic of the “dive in mechanism” rather than its thermodynamics.
4 Conclusions
Previously, it have been shown that TTA molecules have an equilibrium between the bilayer and the bulk, when placed in a bilayer with TTA+ as the main component.27 The bilayer simulated (Box 2) reproduce the dynamics of the bicelles that form the lyotropic nematic liquid crystal (system 2), see Fig. 2.NMR analysis shows that L-DOPA does not seems to significantly affect overall TTA+ bicelle dynamic properties (see Fig. 2) but it affects the exchange kinetic of TTA+ between bulk and bilayer. Simulation experiments support this conclusion because L-DOPA do not change ΔG0 (see Table 2). L-DOPA affects the autocorrelation time of C–H order parameters from TTA+ chain, which are related with the re-orientational order of the carbon chain of these molecules (see Fig. 6). These evidences suggest that L-DOPA intervenes in the kinetic of the dive in mechanism, but deeper analysis are required to known the exact mechanism.
It is interesting that the L-DOPA affects the kinetics of the process without affecting its thermodynamics. There is a kind of robustness in the TTA+'s insertion/expulsion equilibrium that was not expected, considering the intervention of L-DOPA. SMD experiments support this conclusion and favors kinetic perturbation.
Bicelles with TTA+ as main component, are interesting models of potential new drug delivery systems. This work contributes to the understanding of how a pharmacological interesting molecules like L-DOPA affects the dynamic properties of a bilayer.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are pleased to acknowledge financial support from FONDECYT (Grant 1150138 and 3190594). The authors also acknowledge the National Laboratory for High Performance Computing (NLHPC), Universidad de Chile, Powered@NLHPC. This work was partially supported by the Programa de Apoyo a Centros con Financiamiento Basal AFB 170004 to Fundación Ciencia & Vida, the Air Force Office of Scientific Research under award number FA9550-19-1-0368, Instituto Milenio Centro Interdisciplinario de Neurociencia de Valparaíso ICM-ECONOMIA P09-022-F. Research was partially sponsored by the Army Research Laboratory and was accomplished under Cooperative Agreement Number W911NF-19-2-0242. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.References
- D. Elgueta, M. S. Aymerich, F. Contreras, A. Montoya, M. Celorrio, E. Rojo-Bustamante, E. Riquelme, H. González, M. Vásquez and R. Franco, et al., Neuropharmacology, 2017, 113, 110–123 CrossRef CAS PubMed.
- Y. Z. Zhou, R. G. Alany, V. Chuang and J. Wen, Chromatographia, 2012, 75, 597–606 CrossRef CAS.
- T. Tahvanainen and A. Haraguchi, Eur. J. Soil Biol., 2013, 54, 41–47 CrossRef CAS.
- K. J. Black, J. L. Carl, J. M. Hartlein, S. L. Warren, T. Hershey and J. S. Perlmutter, J. Neurosci. Methods, 2003, 127, 19–29 CrossRef CAS PubMed.
- N. Ngwuluka, V. Pillay, L. C. Du Toit, V. Ndesendo, Y. Choonara, G. Modi and D. Naidoo, Expert Opin. Drug Delivery, 2010, 7, 203–224 CrossRef CAS PubMed.
- S. Tang, L. J. Martinez, A. Sharma and M. Chai, Org. Lett., 2006, 8, 4421–4424 CrossRef CAS PubMed.
- P. Gambaryan, I. Kondrasheva, E. Severin, A. Guseva and A. Kamensky, Exp. Neurol., 2014, 23, 246–252 CAS.
- C. R. Sanders and J. Prestegard, Biophys. J., 1990, 58, 447–460 CrossRef CAS PubMed.
- G. Scalia, ChemPhysChem, 2010, 11, 333–340 CrossRef CAS PubMed.
- D. Vijayaraghavan, J. Mol. Liq., 2014, 199, 128–132 CrossRef CAS.
- M. Casavant, D. Walters, J. Schmidt and R. Smalley, J. Appl. Phys., 2003, 93, 2153–2156 CrossRef CAS.
- A. Takai, Y. Yamauchi and K. Kuroda, J. Am. Chem. Soc., 2009, 132, 208–214 CrossRef PubMed.
- S. Warren and U. Wiesner, Pure Appl. Chem., 2009, 81, 73–84 CAS.
- X. Zhang, W. Lu, J. Dai, L. Bourgeois, J. Yao, H. Wang, J. R. Friend, D. Zhao and D. R. MacFarlane, Sci. Rep., 2014, 4, 7420 CrossRef CAS PubMed.
- S. Che, Z. Liu, T. Ohsuna, K. Sakamoto, O. Terasaki and T. Tatsumi, Nature, 2004, 429, 281–284 CrossRef CAS PubMed.
- H. Lin and C. Mou, Acc. Chem. Res., 2002, 35, 927–935 CrossRef CAS PubMed.
- S. Umadevi, H. Lee, V. Ganesh, X. Feng and T. Hegmann, Liq. Cryst., 2014, 41, 265–276 CrossRef CAS.
- V. Bahamonde-Padilla, J. López-Cascales, R. Araya-Maturana, M. Martínez-Cifuentes and B. Weiss-López, ChemPhysChem, 2014, 15, 1422–1431 CrossRef CAS PubMed.
- U. H. Durr, M. Gildenberg and A. Ramamoorthy, Chem. Rev., 2012, 112, 6054–6074 CrossRef CAS PubMed.
- D. E. Warschawski, A. A. Arnold, M. Beaugrand, A. Gravel, É. Chartrand and I. Marcotte, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 1957–1974 CrossRef CAS PubMed.
- A. Ruiz-Fernández, J. López-Cascales, J. Giner-Casares, R. Araya-Maturana, F. Díaz-Baños, D. Muñoz-Gacitúa and B. Weiss-López, RSC Adv., 2016, 6, 7455–7464 RSC.
- A. Ruiz-Fernández, J. López-Cascales, J. Giner-Casares, R. Araya-Maturana, F. Díaz-Baños and B. Weiss-López, RSC Adv., 2016, 6, 85411–85419 RSC.
- H. K. Bisoyi and S. Kumar, Chem. Soc. Rev., 2010, 39, 264–285 RSC.
- L. Mäler and A. Gräslund, Macromolecular Drug Delivery, Springer, 2009, pp. 129–139 Search PubMed.
- C. Müller-Goymann, Eur. J. Pharm. Biopharm., 2004, 58, 343–356 CrossRef PubMed.
- C. Kang, C. G. Vanoye, R. C. Welch, W. D. Van Horn and C. R. Sanders, Biochemistry, 2010, 49, 653–655 CrossRef CAS PubMed.
- A. Ruiz-FernaÍĄndez, J. Phys. Chem. C, 2018, 122, 1192–1196 CrossRef.
- G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185(2), 604–613 CrossRef CAS.
- G. Raffard, S. Steinbruckner, A. Arnold, J. H. Davis and E. J. Dufourc, Langmuir, 2000, 16, 7655–7662 CrossRef CAS.
- L. S. Vermeer, B. L. De Groot, V. Réat, A. Milon and J. Czaplicki, Eur. Biophys. J., 2007, 36, 919–931 CrossRef CAS PubMed.
- M. Bloom, J. H. Davis and A. L. Mackay, Chem. Phys. Lett., 1981, 80, 198–202 CrossRef CAS.
- K. Merz, B. Roux and B. Membranes, A Molecular Perspective from Computation and Experiment, Birkhäuser, Boston, 1996 Search PubMed.
- M. Brown, R. Thurmond, S. Dodd, D. Otten and K. Beyer, J. Am. Chem. Soc., 2002, 124, 8471–8484 CrossRef CAS PubMed.
- K. Hiltrop, Lyotropic liquid crystals in topics in physical chemistry, Springer New York, 1994, vol. 3 Search PubMed.
- A. Seelig and J. Seelig, Biochemistry, 1974, 13, 4839–4845 CrossRef CAS PubMed.
- B. Jonsson, O. Edholm and O. Teleman, J. Chem. Phys., 1986, 85, 2259–2271 CrossRef.
- E. Egberts, S. Marrink and H. Berendsen, Eur. Biophys. J., 1994, 22, 423–436 CrossRef CAS PubMed.
- P. Ahlstrom and H. Berendsen, J. Phys. Chem., 1993, 97, 13691–13702 CrossRef CAS.
- J. López Cascales, J. De la Torre, S. Marrink and H. Berendsen, J. Chem. Phys., 1996, 104, 2713–2720 CrossRef.
- P. David, W. van Gunsteren and A. Mark, J. Comput. Chem., 2010, 31, 1117–1125 CrossRef PubMed.
- T. Heinz, W. van Gunsteren and P. Hünenberger, J. Chem. Phys., 2001, 115, 1125–1136 CrossRef CAS.
- V. Bahamonde-Padilla, J. Espinoza, B. Weiss-Lopez, J. L. Cascales, R. Montecinos and R. Araya-Maturana, J. Chem. Phys., 2013, 139, 14703–14711 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra00764a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2020 |