Open Access Article
Open Access ArticleSynthesis and high-pressure studies of strontium diazenide by synchrotron X-ray diffraction and DFT calculations†
Yue Liab,
Huanpeng Bub,
Qinglin Wang c,
Jiani Linab,
Xiaoli Wanga,
Jianfu Lia,
Pinwen Zhu*b and
Hongyang Zhu
c,
Jiani Linab,
Xiaoli Wanga,
Jianfu Lia,
Pinwen Zhu*b and
Hongyang Zhu *ab
*ab
aSchool of Physics and Electronic Engineering, Linyi University, Linyi 276005, P. R. China
bState Key Lab of Superhard Materials, College of Physics, Jilin University, Changchun 130012, P. R. China. E-mail: hongyangzhu@jlu.edu.cn; zhupw@jlu.edu.cn
cShandong Key Laboratory of Optical Communication Science and Technology, School of Physics Science and Information Technology, Liaocheng University, Liaocheng 252059, P. R. China
First published on 13th July 2020
Abstract
In this work, strontium diazenide (SrN2) was synthesized using strontium azide as a starting material in a Walker-type module under high-pressure and high-temperature conditions. The synthesized SrN2 was further studied under high pressure up to 43.2 GPa using in situ synchrotron X-ray diffraction to supplement the high-pressure exploration of alkaline earth diazenides. The SrN2 underwent a possible phase transition from a tetragonal structure into an orthorhombic structure at 12.0 GPa. SrN2 shows anisotropic compressibility due to the orientation of the diazenide anions. The bulk modulus of SrN2 is 132.4 (10.2) GPa, which is larger than that of Sr(N3)2. The larger bulk modulus of SrN2 is attributed to the stronger covalent strength between Sr and N atoms in SrN2, which is confirmed by our theoretical calculations.
Introduction
Metal–nitrogen compounds have attracted extensive attention in recent years due to their outstanding physical and chemical properties including high energy density,1,2 superior hardness,3,4 and high luminous efficiency.5,6 Among them, only the nitride (N3−) and azide ([N3]−) based compounds have been known for a long time in spite of the fact that numerous theoretical studies have shown that all-nitrogen anions with different valences might be stable.7–9 In recent years, the progressive developments of high-pressure synthesis of new materials have greatly expanded the class of metal nitrides and stimulated the study of nitrogen compounds. Several novel nitrides with remarkable properties have been synthesized under high pressure and high-temperature conditions. One type of the compounds consists of nitrogen and noble metals (such as osmium, iridium, or platinum) named metal pernitrides.3,4,10–12 The other is named alkaline earth diazenide containing alkaline earth metals (such as calcium, strontium, and barium) and nitrogen.13–17 The alkaline earth diazenides and the metal pernitrides have the same formula of MN2, but the anionic dinitrogen units are not identical. In contrast to metal pernitrides which contain the pernitride units [N2]4− with N–N single bonds, alkaline earth diazenides incorporate quasi-molecular units [N2]2− with N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double bonds with two surplus electrons within the antibonding
N double bonds with two surplus electrons within the antibonding 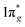 molecular orbital.11,15,18 Metal diazenides have good conductivities similar to metal. Vajenine et al. theoretically calculated interactions of Ba 5d and N 2p and concluded that the significant width of the π* band is responsible for the metallic nature of the diazenides.14 Subsequently, Schneider et al. confirmed alkaline earth diazenides are of temperature-dependent true metallic behavior by conductivity measurements.9 Lithium diazenide (Li2N2) exhibits characteristics of both electron conduction and ionic conduction due to the ion pathways and relatively smaller radius of lithium ions.9
molecular orbital.11,15,18 Metal diazenides have good conductivities similar to metal. Vajenine et al. theoretically calculated interactions of Ba 5d and N 2p and concluded that the significant width of the π* band is responsible for the metallic nature of the diazenides.14 Subsequently, Schneider et al. confirmed alkaline earth diazenides are of temperature-dependent true metallic behavior by conductivity measurements.9 Lithium diazenide (Li2N2) exhibits characteristics of both electron conduction and ionic conduction due to the ion pathways and relatively smaller radius of lithium ions.9
In 2012, Schneider et al. successfully synthesized metal diazenides (CaN2,17 SrN2,17 BaN2,17 and Li2N2 (ref. 8)) employing the controlled thermal decomposition of the corresponding azides at high-pressure and high-temperature conditions. The phase stabilities, structures, chemical bonding, optical, and electronic properties of metal diazenides have been theoretically predicted under high pressure.18–21 Li2N2 has been predicted with density functional theory to have three phase transitions of Pmmm → Immm → Pnma → Cmcm in the pressure range of 0–100 GPa,8,22,23 and the nitrogen was polymerized with further compressed to 242 GPa.23 BeN2 were predicted Be and adjacent N connect with covalent bonds to enhance the structural stability using performed using density functional theory.24 Wessel and Kulkarni et al. calculated and found that the bulk moduli of alkaline earth diazenides are smaller than those of the metal pernitrides.11,15,18,25,26 Although extensive theoretical high-pressure studies on metal diazenides have been carried out, the experimental high-pressure study of metal diazenides is a challenge and has not been reported due to the difficulty of synthesis of sample and the property of sensitive to moisture.
Therefore, the significance and absence of a high-pressure study of SrN2 prompted our endeavor to explore its structural properties under high pressure and compressibility. In this work, SrN2 was synthesized by controlled decomposition of Sr(N3)2 in a Walker-type module under high-pressure and high-temperature conditions. The high-pressure structure and compressibility properties of the synthesized SrN2 were investigated by measuring synchrotron angle-dispersive X-ray diffraction (XRD) patterns under high pressure up to 43.2 GPa using a symmetric diamond anvil cell (DAC). The crystal orbital Hamiltonian populations (COHP) and integral crystal orbital Hamiltonian populations (ICOHP) values were calculated to obtain deeper insight into the nature of chemical bonding and bonding strength between metal and N atoms.
Experimental and theoretical section
Synthesis of SrN2
The SrN2 was synthesized under high-pressure and high-temperature conditions in a Walker-type module in combination with a 1000 t pressure. MgO-octahedra with edge lengths of 14 mm (14/8 assembly) were used as the pressure medium. Eight tungsten carbide cubes with truncation edge lengths of 8 mm compressed the octahedra Sr(N3)2 was carefully ground and filled into a cylindrical boron nitride crucible in the glovebox. The process of assembling the sample is given in Fig. S1 in the ESI.† The assembly was pressurized to 9.0 GPa within 214 minutes at room temperature, then heated to 823 K in 30 minutes and held at this temperature for 15 minutes, and then cooled down to ambient temperature in 10 minutes. After that, the pressure was released within 623 minutes. The black metallic bulk SrN2 was obtained from the boron nitride crucible and kept in silicone oil as SrN2 is highly sensitive to moisture.17 The synthesized sample is shown in Fig. S2.†Synchrotron XRD measurements under high pressure
High-pressure experiments were performed in a symmetric diamond anvil cell with flat anvils of 300 μm in diameter. The synthesized SrN2 powders were loaded into a 120 μm diameter sample chamber of a T301 steel gasket which was pre-indented to 70 μm thickness. Pressures were measured by the ruby luminescence method.27 Silicon oil was chosen as a pressure-transmitting medium as the sample is sensitive to moisture. The in situ high-pressure synchrotron XRD experiment was carried out at the 4W2 beamline (λ = 0.6199 Å) of Beijing Synchrotron Radiation Facility and the average time of a collecting spectrum was 300 seconds. The images were collected by a Pilatus image panel detector. CeO2 was used to calibrate the distance and geometric parameters between the sample and the detector. The diffraction patterns were transformed into one-dimensional diffraction angle and diffraction intensity using Fit2D software. The crystal structure was refined using Rietveld refinements packages of Materials Studio software.Theoretical calculations
The electronic structure calculations for the SrN2 were performed via density functional theory (DFT) within the generalized gradient approximation Perdew–Burke–Ernzerhof (GGA-PBE)28 as executed in the Vienna Ab initio Simulation Package (VASP) code.29 The projector-augmented wave (PAW)30 method was performed for Sr 4p65s2 and N 2s22p3 as valence states adopted from the VASP potential library. Plane-wave cutoff energy of 600 eV and appropriate Monkhorst–Pack31 k-mesh (k-point grid of 0.03 Å−1) was chosen to ensure the convergence of less than 1 meV per atom. The COHP and ICOHP values were calculated using the LOBSTER program.32Results and discussion
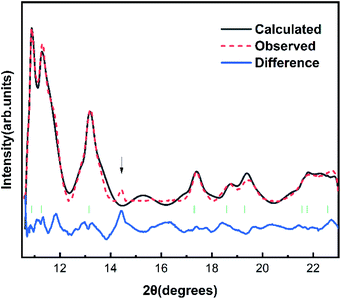
The Fig. 1 shows the refinement of synchrotron XRD pattern of the synthesized SrN2 measured at 0.4 GPa, which was indexed with the tetragonal structure (I4/mmm, Z = 2, Fig. 2) based on the positions of nine diffraction peaks using Rietveld refinements packages of Materials Studio software, yielding a = b = 3.8187 Å, c = 6.279 Å, and V = 91.56 Å3. These cell parameters are in good agreement with the reported results.17 The Wyckoff positions of Sr atoms and N atoms are assigned to 2a and 4e, respectively. SrN2 structure is occupied by all octahedral voids consisted of the strontium ions with [N2]2− units along [001]. Each strontium ion is coordinated “end-on” by two and “side-on” by four diazenide units, and each diazenide unit is surrounded by six strontium ions as illustrated in Fig. 2. The distance of the N–N bond is 1.226 Å, which is shorter than that of the Sr–N bond of 2.528 Å and 2.764 Å.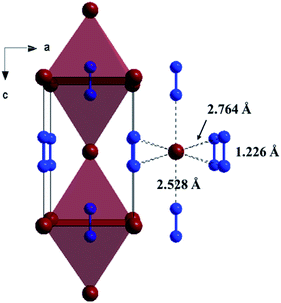 | ||
| Fig. 2 Crystal structure of the ambient condition tetragonal phase (space group: I4/mmm, Z = 2) of SrN2 along [010]. Red colour represents Sr atoms, and blue colour represents N atoms. | ||
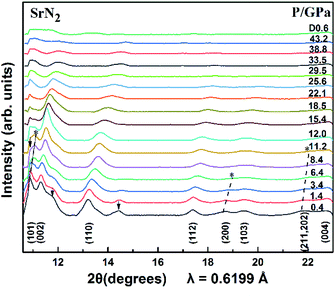
The SrN2 was compressed up to 43.2 GPa. The XRD patterns are demonstrated in Fig. 3. Nine diffraction peaks of SrN2, which belong to (101), (002), (110), (112), (200), (103), (211), (202), and (004) planes, were observed. The diffraction peaks of (200) disappeared at 6.4 GPa, and (211) and (202) disappeared at 10.0 GPa. The strongest diffraction peak of (101) finally disappeared at 12.0 GPa. The disappearance of the diffraction peaks is temporarily assigned as a possible phase transition. The high-pressure phase is stable up to 43.2 GPa in this study. The peaks of HP-SrN2 indexing results led to an orthorhombic structure. However, it is difficult to determine the structure of the phase of HP-SrN2 because the diffraction diagrams are significantly broadened and low intensity at higher pressure. It is worth noting that the detection of the changes of the diazenide anions positions is an inherent challenge for synchrotron XRD measurements owing to their greatly low scattering cross-section. Therefore, a symmetry breaking due to the changes of diazenide anions orientation cannot be observed in synchrotron X-ray diffraction. The similar phenomenon in SrO2 was observed.33 The influence of oxide atoms in SrO2 was entirely ignored on the XRD patterns owing to their low scattering cross section. We temporally ascribe the phase transition of SrN2 to the rotation of diazenide units and the rearrangement of Sr ions according to the rotation character of diazenide units in CaN2 (ref. 19) under high pressure. As pressure is released to 0.6 GPa, the tetragonal structure recovered from the high-pressure orthorhombic structure, demonstrating a reversible phase transition of SrN2. Compared to the starting conditions, the figure of the back-transformed SrN2 shows differences in intensities and is broadened, which are presumably caused by preferred orientation and grain size effects, respectively.
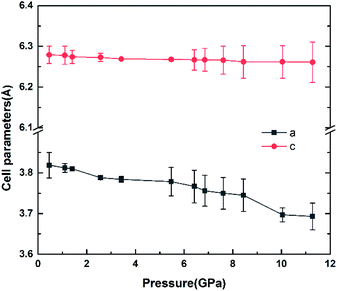
The variation of unit cell lattice parameters of the tetragonal structure with pressure is plotted in Fig. 4. SrN2 shows anisotropic compressibility with pressure coefficients of 1.16 × 10−2 Å GPa−1 for a- and b-axis, and 1.66 × 10−3 Å GPa−1 for c-axis from 0.4 GPa to 11.2 GPa, respectively, which indicates that a- and b-axis are more compressive than c-axis. Analysis of the crystal structure of SrN2 reveals that vector projections of repulsive force of diazenides ions are constrained to [001] direction, and without components in [100] and [010] directions as shown in Fig. 2. Therefore, we identify that the orientation of the diazenide anions is the dominant factor that affects the compressibility behaviour of SrN2.
The bulk modulus of SrN2 was fitted to the Birch–Murnaghan equation of state (EOS):
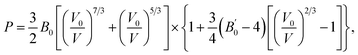 | (1) |
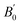 is the pressure derivative of B0. The data measured below 11.2 GPa were used to yield the bulk modulus because the phase transitions occur at 12.0 GPa. The bulk modulus of B0 = 132.4 (10.2) GPa of SrN2 is conforming to the Birch–Murnaghan EOS. The bulk modulus of SrN2 is close to that of CaN2 (113.2 GPa),21 which can be interpreted by the fact that SrN2 and CaN2 are isostructural at ambient conditions. The experimental pressure evolutions of the unit cell volume of SrN2 are plotted in Fig. 5. The bulk modulus of SrN2 was theoretically predicted to be 96.08 GPa and 65 GPa using pseudo-atomic calculations with the local density approximation (LDA) and the generalized gradient approximation Perdew–Burke–Ernzerhof (GGA-PBE), and the ab initio calculations with the GGA-PBE, respectively, by Zhang et al.20 and Wessel et al.,15 in which the pseudo-atomic calculations results are closer to the experimental results. The different calculation methods employed different empirical or theoretical approximations are suitable for different materials. Compare our experimental results with reported calculations results, the pseudo-atomic calculations with the LDA and the GGA-PBE were better fitted diazenides than the ab initio calculations with the GGA-PBE. The bulk modulus of SrN2 is two times larger than its corresponding metal azide Sr(N3)2 (123.7 GPa of SrN2 vs. 49.1 GPa of Sr(N3)2 (ref. 34)). The nitrogen bonds are formed as double bonding in both diazenides anions (N
is the pressure derivative of B0. The data measured below 11.2 GPa were used to yield the bulk modulus because the phase transitions occur at 12.0 GPa. The bulk modulus of B0 = 132.4 (10.2) GPa of SrN2 is conforming to the Birch–Murnaghan EOS. The bulk modulus of SrN2 is close to that of CaN2 (113.2 GPa),21 which can be interpreted by the fact that SrN2 and CaN2 are isostructural at ambient conditions. The experimental pressure evolutions of the unit cell volume of SrN2 are plotted in Fig. 5. The bulk modulus of SrN2 was theoretically predicted to be 96.08 GPa and 65 GPa using pseudo-atomic calculations with the local density approximation (LDA) and the generalized gradient approximation Perdew–Burke–Ernzerhof (GGA-PBE), and the ab initio calculations with the GGA-PBE, respectively, by Zhang et al.20 and Wessel et al.,15 in which the pseudo-atomic calculations results are closer to the experimental results. The different calculation methods employed different empirical or theoretical approximations are suitable for different materials. Compare our experimental results with reported calculations results, the pseudo-atomic calculations with the LDA and the GGA-PBE were better fitted diazenides than the ab initio calculations with the GGA-PBE. The bulk modulus of SrN2 is two times larger than its corresponding metal azide Sr(N3)2 (123.7 GPa of SrN2 vs. 49.1 GPa of Sr(N3)2 (ref. 34)). The nitrogen bonds are formed as double bonding in both diazenides anions (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)2− and azides anions (N
N)2− and azides anions (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)−.11 The previous studies proved that the N
N)−.11 The previous studies proved that the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N plays a crucial role in the compressibility of both Sr(N3)2 and SrN2. The N
N plays a crucial role in the compressibility of both Sr(N3)2 and SrN2. The N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond distance of 1.226 (3) Å in SrN2 is longer than that of 1.184 (2) Å in Sr(N3)2 leading to weaker N
N bond distance of 1.226 (3) Å in SrN2 is longer than that of 1.184 (2) Å in Sr(N3)2 leading to weaker N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds in SrN2. The bulk modulus of SrN2 is larger than that of Sr(N3)2, which contradict to the longer N
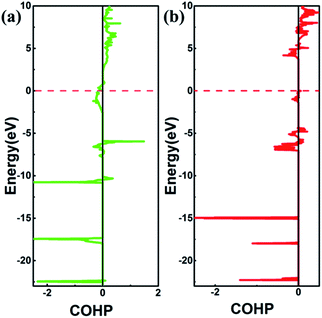
N bonds in SrN2. The bulk modulus of SrN2 is larger than that of Sr(N3)2, which contradict to the longer N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond of SrN2. We thus infer the interaction between Sr and N in SrN2 is much stronger than that in Sr(N3)2. To obtain deeper insight into the nature of chemical bonding between Sr and N in SrN2 and Sr(N3)2, we performed crystal orbital overlap population (COHP) analysis. COHP can divide the band-structure energy into the orbital pair interactions, which is used to indicate the contribution of bonding, nonbonding, and antibonding to the band-structure energy. Our analysis showed that bonding states are fully occupied and antibonding states are partially occupied in SrN2, while both bonding states and anti-bonding states are partially occupied in Sr(N3)2, as shown in Fig. 6, leading to strong covalent bonding between Sr and N atoms in SrN2 and Sr(N3)2. Furthermore, the bonding strength can be expressed by the values of integrated crystal orbital Hamilton population (ICOHP), which are in the order of −1.233 and −0.736 for SrN2 and Sr(N3)2, respectively, as shown in Fig. 6. It is confirmed that interaction between Sr1–N1 atoms is stronger than that of Sr2–N2 atoms. Hence, covalent bonding between Sr and N atoms is stronger in SrN2, which resulted in a larger bulk modulus.
N bond of SrN2. We thus infer the interaction between Sr and N in SrN2 is much stronger than that in Sr(N3)2. To obtain deeper insight into the nature of chemical bonding between Sr and N in SrN2 and Sr(N3)2, we performed crystal orbital overlap population (COHP) analysis. COHP can divide the band-structure energy into the orbital pair interactions, which is used to indicate the contribution of bonding, nonbonding, and antibonding to the band-structure energy. Our analysis showed that bonding states are fully occupied and antibonding states are partially occupied in SrN2, while both bonding states and anti-bonding states are partially occupied in Sr(N3)2, as shown in Fig. 6, leading to strong covalent bonding between Sr and N atoms in SrN2 and Sr(N3)2. Furthermore, the bonding strength can be expressed by the values of integrated crystal orbital Hamilton population (ICOHP), which are in the order of −1.233 and −0.736 for SrN2 and Sr(N3)2, respectively, as shown in Fig. 6. It is confirmed that interaction between Sr1–N1 atoms is stronger than that of Sr2–N2 atoms. Hence, covalent bonding between Sr and N atoms is stronger in SrN2, which resulted in a larger bulk modulus.
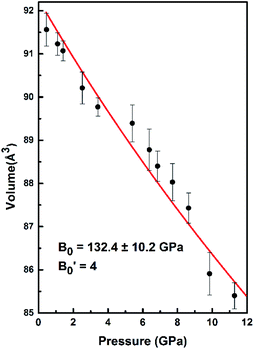 | ||
| Fig. 5 The volume changes with the pressure for SrN2. The red line exhibits the fitting of data to the Birch–Murnaghan equation of state (EOS). | ||
Conclusions
In this work, the SrN2 was synthesized by using the controlled decomposition of the Sr(N3)2 under high-pressure and high-temperature conditions. The high-pressure in situ synchrotron XRD study of the synthesized SrN2 up to 43.2 GPa revealed a pressure-induced tetragonal-to-orthorhombic phase transition at 12.0 GPa due to the rotation of diazenide units and the rearrangement of Sr ions. The compressibility of SrN2 is anisotropic due to the orientation of the diazenide anions. The bulk modulus of SrN2 is B0 = 132.4 (10.2) GPa. In order to further analyze the bulk modulus of SrN2 and Sr(N3)2, we calculated the bonding strength via computing the values of ICOHP, which shows stronger Sr–N covalent bonds in SrN2 than that in Sr(N3)2, leading the larger value of bulk modulus than that of Sr(N3)2.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (11774128, 11674144, 11604133) and the Natural Science Foundation of Shandong Province (ZR2018JL003, 2019KJJ003, JQ201602, and ZR2018MA038). The high-pressure synchrotron XRD measurements were performed at the Beijing Synchrotron Radiation Facility (BSRF).Notes and references
- C. Zhang, C. Sun, B. Hu and M. Lu, Science, 2017, 355, 374 CrossRef CAS PubMed.
- M. I. Eremets, R. J. Hemley, H. K. Mao and E. Gregoryanz, ChemInform, 2001, 32, 170–174 Search PubMed.
- E. Gregoryanz, C. Sanloup, M. Somayazulu, J. Badro, G. Fiquet, H. K. Mao and R. J. Hemley, Nat. Mater., 2004, 3, 294–297 CrossRef CAS PubMed.
- J. C. Crowhurst, A. F. Goncharov, B. Sadigh, C. L. Evans, P. G. Morrall, J. L. Ferreira and A. J. Nelson, Science, 2006, 311, 1275–1278 CrossRef CAS PubMed.
- P. Pust, V. Weiler, C. Hecht, A. Tücks, A. S. Wochnik, A. K. Henß, D. Wiechert, C. Scheu, P. J. Schmidt and W. Schnick, Nat. Mater., 2014, 13, 891–896 CrossRef CAS PubMed.
- P. Pust, P. J. Schmidt and W. Schnick, Nat. Mater., 2015, 14, 454 CrossRef CAS PubMed.
- K. O. Christe, W. W. Wilson, J. A. Sheehy and J. A. Boatz, Angew. Chem., Int. Ed., 1999, 38, 2004–2009 CrossRef CAS.
- S. B. Schneider, R. Frankovsky and W. Schnick, Angew. Chem., Int. Ed., 2012, 51, 1873–1875 CrossRef CAS PubMed.
- R. Frankovsky, G. M. Friederichs, S. B. Schneider, W. Schnick, M. Mangstl and J. Schmedt auf der Günne, Chem. Mater., 2013, 25, 4149–4155 CrossRef.
- Z. W. Chen, X. J. Guo, Z. Y. Liu, M. Z. Ma, Q. Jing, G. Li, X. Y. Zhang, L. X. Li, Q. Wang, Y. J. Tian and R. P. Liu, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 1–4 Search PubMed.
- M. Wessel and R. Dronskowski, J. Am. Chem. Soc., 2010, 132, 2421–2429 CrossRef CAS PubMed.
- J. C. Crowhurst, A. F. Goncharov, B. Sadigh, J. M. Zaug, D. Aberg, Y. Meng and V. B. Prakapenka, J. Mater. Res., 2008, 23, 1–5 CrossRef CAS.
- G. Auffermann, Y. Prots and R. Kniep, Angew. Chem., Int. Ed., 2001, 40, 547–549 CrossRef CAS.
- G. V. Vajenine, G. Auffermann, Y. Prots, W. Schnelle, R. K. Kremer, A. Simon and R. Kniep, Inorg. Chem., 2001, 32, 4866–4870 CrossRef PubMed.
- W. Michael and D. Richard, J. Comput. Chem., 2010, 31, 1613–1617 Search PubMed.
- G. Auffermann, R. Kniep and W. Bronger, Z. Anorg. Allg. Chem., 2006, 632, 565–571 CrossRef CAS.
- S. B. Schneider, R. Frankovsky and W. Schnick, Inorg. Chem., 2012, 51, 2366–2373 CrossRef CAS PubMed.
- A. Kulkarni, J. C. Schön, K. Doll and M. Jansen, Chem.–Asian J., 2013, 8, 743–754 CrossRef CAS PubMed.
- H. Wang, Y. Yao, Y. Si, Z. Wu and G. Vaitheeswaran, J. Phys. Chem. C, 2014, 118, 650–656 CrossRef CAS.
- L. Q. Zhang, Y. Cheng, Z. W. Niu, C. G. Piao and G. F. Ji, Z. Naturforsch., A: Phys. Sci., 2014, 69, 619–628 CAS.
- S. Xu, L. Zhang and Y. Cheng, J. Wuhan Univ. Technol., Mater. Sci. Ed., 2016, 32, 100–105 CrossRef.
- Y. Shen, A. R. Oganov, G. Qian, J. Zhang and H. Dong, Sci. Rep., 2015, 5, 14204 CrossRef PubMed.
- J. Zhang, X. Wang, K. Yang, Y. Cheng and Z. Zeng, Sci. Rep., 2018, 8, 13144 CrossRef PubMed.
- J. Lin, Z. Zhu, Q. Jiang, S. Guo, J. Li, H. Zhu and X. Wang, AIP Adv., 2019, 9, 055116 CrossRef.
- R. Yu, Q. Zhan and L. C. De Jonghe, Angew. Chem., Int. Ed., 2007, 46, 1136–1140 CrossRef CAS PubMed.
- M. Wessel and R. Dronskowski, Chem.–Eur. J., 2011, 17, 2598–2603 CrossRef CAS PubMed.
- H. K. Mao, J. Xu and P. M. Bell, J. Geophys. Res., 1986, 91, 4673–4676 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 391–396 CrossRef.
- H. J. Monkhorst, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035 CrossRef CAS PubMed.
- Y. Wang, S. Wang, Y. Zhang, J. Lv, Y. Chen, W. Zheng and Y. Ma, Inorg. Chem., 2017, 56, 7545–7549 CrossRef CAS PubMed.
- H. Zhu, X. Han, P. Zhu, X. Wu, Y. Chen, M. Li, X. Li and Q. Cui, J. Phys. Chem. C, 2016, 120, 12423–12428 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra00789g |
| This journal is © The Royal Society of Chemistry 2020 |