Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Cu(I) substituted wurtzite ZnO: a novel room temperature lead free ferroelectric and high-κ giant dielectric†
Neeraj Singh and
Preetam Singh *
*
Department of Ceramic Engineering, Indian Institute of Technology (Banaras Hindu University), Varanasi, Uttar Pradesh, India 221005. E-mail: preetamsingh.cer@itbhu.ac.in; preetamchem@gmail.com; Tel: +91-9473720659
First published on 20th March 2020
Abstract
Semiconducting wurtzite ZnO, with the highest incipient piezoelectricity is an attractive alternative choice with doping transition metal ions in the host lattice to develop novel binary ferroelectric materials that can be easily fabricated in any device architecture. Up to 8% Cu+ ion substitution on Zn2+ sites in the ZnO lattice was achieved by careful selection of raw material and adaptation of a low temperature sol–gel synthesis route for the preparation of bulk material. Phase purity and substitution of Cu+ ions in the ZnO lattice along with oxide-ion vacancy formation was confirmed using Powder X-ray diffraction (XRD), Scanning Electron Microscopy (SEM), and Energy Dispersive X-ray analysis (EDX), X-ray Photoelectron Spectroscopy (XPS) and Magnetic property measurement system (MPMS) studies. A giant dielectric constant (∼6300) was observed at 600 °C for Zn0.95Cu0.05O1−δ pellets at 100 kHz frequency. Bulk Zn0.95Cu0.05O1−δ also exhibits ferroelectricity at room temperature with remnant polarization Pr and Vc equal to 9.60 × 10−3 μC cm−2 and 3.83 × 102 V cm−1 respectively.
Introduction
Semiconducting ferroelectric materials have technological importance due to extensive applications in optoelectronic devices for uses in optical communication, memory, displays and coherent optical processing.1–6 The specific device applications also include capacitors, modulators, beam deflectors, light valves and holographic storage media. Further, one of the efficient ways to scavenge electrical energy through vibration based energy harvesting is by utilization of piezoelectric and ferroelectric materials. Ferroelectric bulk crystals are desired for usage in optoelectronic devices because of the combination of extraordinary optical and electronic properties originated from their non-centro symmetric crystal structure and structural anisotropy that exhibit many nonlinear optical properties. Using field effects coupled with high-κ dielectrics and ferroelectric polarizations, the electric properties of ferroelectric semiconductors have been widely tuned to facilitate the emergence of various gate-modulated devices such as transistors, logic inverters and memory storage devices, light-emitting diodes (LEDs) and photo detectors.In semiconducting materials, ferroelectricity appears mainly by the delicate balance between a long-range dipole–dipole interaction and a short-range interaction. Slight distortion of electron cloud due to structural changes in dielectrics gives a rise of dipole moments. The ferroelectric phase transitions are associated with a structural phase transition from high symmetry paraelectric phase to the low symmetry ferroelectric phase. Therefore, new materials with a simple structure are not only preferable for understanding the microscopic origin of ferroelectricity, but are also important for integrating into modern ferroelectric devices with utilization of novel ferroelectric/piezoelectric/relaxor and multiferroic materials that do not contain environmental hazards such as Pb and Bi. Also, there is an interest to bring d0 and dn (0 ≤ n ≤ 10) transition metal atoms together in a simple oxide matrix to realize multiferroic properties. Wurtzite piezoelectric ZnO, with highest piezoelectricity can be attractive alternative choice with doping transition metal ion in host lattice to develop novel ferroelectric materials.7–9 Zinc oxide (ZnO) is considered as one of the very important metal oxides due to its unique chemical and physical properties such as electrochemical coupling, good chemical and photo stability and wide range of radiation absorption capabilities.10,11 Further ZnO is a very low-toxicity semiconductor that have been implemented successfully in biomedicine and in pro-ecological systems.12,13 Although pure ZnO has the possibility to exhibit ferroelectricity, the polarization switching does not observed until its melting point (1975 °C) because of large activation energy accompanied by dipole switching process.
ZnO has also been considered for spintronic applications: if doped with 1–10% of magnetic ions (Cu, Mn, Fe, Co, V, etc.), ZnO could become ferromagnetic even at room temperature.14–17 Substitution of ZnO with different elements such as Fe, Al, Ni, Cu and Mg, can optimize the band gap of ZnO and that will give the needed flexibility for application in modern opto-electronic devices.18–20 Cu is one of promising dopants because of its high abundance and low toxicity and multiple electronic state (Cu+/Cu2+/Cu3+) formation that can have inbuilt effect of structural phase transitions. Therefore, the study was aimed to investigate the interaction of d10 cations (Zn2+ and Cu+) in tetrahedral symmetry and role of resultant oxygen vacancy generated through incorporation of Cu+ ions in host ZnO lattice on dielectric interaction/polarizations and search of a possible ferroelectric or ultra-high κ dielectric material. There is some report on ferroelectricity in Cu doped ZnO thin films that may be arises due to formation surface oxygen vacancy in ZnO thin films fabricated ultra-vacuum conditions.21,22 However, there is no report on appearance of ferroelectric phase in bulk ZnO based materials. Thus, it was important to synthesize Cu+ doped ZnO in bulk and study dielectric properties and search the ferroelectric transition in bulk material. For the first time by employing selective precursor, Cu(I)Cl and sol–gel method, we have able to synthesize Cu(I) doped ZnO that show high-κ dielectric and ferroelectricity in bulk. Synthesis, characterization and study of dielectric/ferroelectric properties of Cu(I) doped ZnO microcrystals are presented in this manuscript.
Experimental section
Synthesis and characterizations
Cu doped ZnO; (Zn1−xCuxO1−δ) ceramic sample were prepared by the modified sol–gel route in the range of x = 0.02 to 0.15. In the molar ratio, (1−x)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x
x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5 ZnO, CuCl and EDTA were taken for sample preparation. For Zn0.95Cu0.05O1−δ, 95 mmol ZnO is dissolved in dilute nitric acid on hot plat at 200 °C with continuous stirring and after obtaining clear solution, 5 mmol CuCl was added into it, the colour of solution turned into greenish blue. After this, ammonia was added drop by drop till sky blue colour was appeared. Further, 150 mmol EDTA (ethylene diamine tetra acetate) was added for chelation.
1.5 ZnO, CuCl and EDTA were taken for sample preparation. For Zn0.95Cu0.05O1−δ, 95 mmol ZnO is dissolved in dilute nitric acid on hot plat at 200 °C with continuous stirring and after obtaining clear solution, 5 mmol CuCl was added into it, the colour of solution turned into greenish blue. After this, ammonia was added drop by drop till sky blue colour was appeared. Further, 150 mmol EDTA (ethylene diamine tetra acetate) was added for chelation.
The solution is now heated at 200 °C with continuous stirring till dryness and kept in a hot air oven at 200 °C for 10 h to remove moisture. The powder was ground after that in mortar pestle and kept for calcinations in alumina crucible at 800 °C for 15 hours. Further the material was reground and further heated at 1050 °C for 12 h. The resultant powder obtained was of green colour. The schematic of synthesis procedure is presented in Fig. 1(a) of pellets were made by hydraulic press at 8 tonne in a die of ∼1 cm thickness and the green pellet was heated at 1050 °C for 15 h twice to obtain a dense pellet. Images of prepared Cu substituted ZnO powder and obtained pellet was also shown in Fig. 1(b). The density of the pellet was measured using Archimedes method was 97% of the theoretical density.
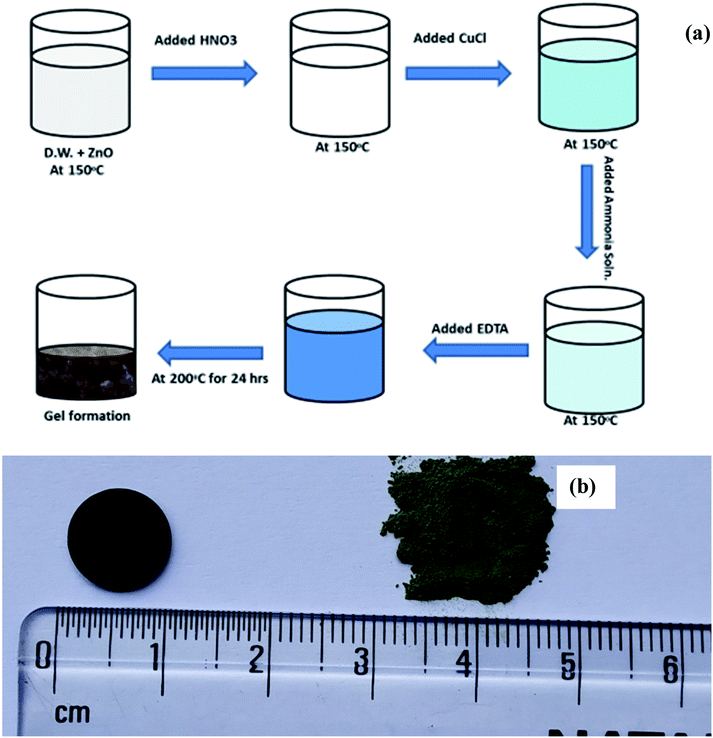 | ||
| Fig. 1 (a) Schematic of the synthesis scheme of Cu doped ZnO; Zn1−xCuxO1−δ and (b) photograph of synthesized powder and sintered pellet of Zn0.95Cu0.05O1−δ. | ||
The structure and phase purity of Cu doped ZnO samples were analysed by powder X-ray diffraction (XRD) analysis. XRD was carried out using RIGAKU diffractometer (Smart Lab 9 kW, target: Cu Kα, λ = 1.5408 Å). Structure of the samples were refined using Rietveld method taking hexagonal P63/mmc wurtzite ZnO as model structure. Microstructure of the powder as well as pellets were analysed by scanning electron microscopy. The EDX analysis was carried out by the probe connected to SEM instrument to confirm the composition of the samples. Scanning electron microscope (SEM) and Energy-dispersive X-ray spectroscopy (EDX) studied were carried out by EVO-18 Research, ZEISS. XPS studies were carried out to evaluated electronics structure of the materials. X-ray photoelectron spectra (XPS) of the sample were recorded in a Thermo Scientific Multilab 2000 instrument using Al Kα operated at 150 W. Binding energies reported here are with reference to C (1s) at 284.5 eV and they are accurate within 0.1 eV. The complex impedance spectroscopic study of Cu doped ZnO pellets were made by Metrohm Autolab (PGSTAT204) equipped with FRA32M module. Impedance measurements were analysed using NOVA software. The two-probe ac impedance measurements were made in air in the frequency range from 1 Hz to 1 MHz with applied ac amplitude of 20 mV. Two Ag blocking electrodes were made by coating Ag paste (from Heraeus) on the two faces of the pellets and baking at 400 °C for 1 h.
For the ferroelectric studies, polishing of the pellets were carried out by fine grain size emery paper followed by heat treatment at 600 °C to remove residual stresses from the pellet. After that electroding was done on the both side of pellet by silver paste. Further pellet was heated at 400 °C for 1 hour to dry the electrodes fabricated on the pellet. Ferroelectric measurement was carried out at room temperature from 100 Hz to 500 Hz frequency range using RADIANT precision premier II. For magnetic studies of our sample Zn0.95Cu0.05O1−δ, fine ground powder was subjected to magnetic property measurement system (MPMS) by Squid based magnetometer (MPMS-3, Quantum Design Inc.).
Result and discussion
The structural parameters and phase purity have been studied using the powder X-ray diffraction patterns. XRD patterns of Zn1−xCuxO1−δ (x ≤ 0.15) is shown Fig. 2(a). Sharp and intense diffraction peaks of all the samples confirm high crystallinity of samples. It also reveals a clean hexagonal phase formation (sp. gp P63mc) in wurtzite ZnO structure for full doping range along with minute impurities of CuO phase at higher Cu doping concentrations.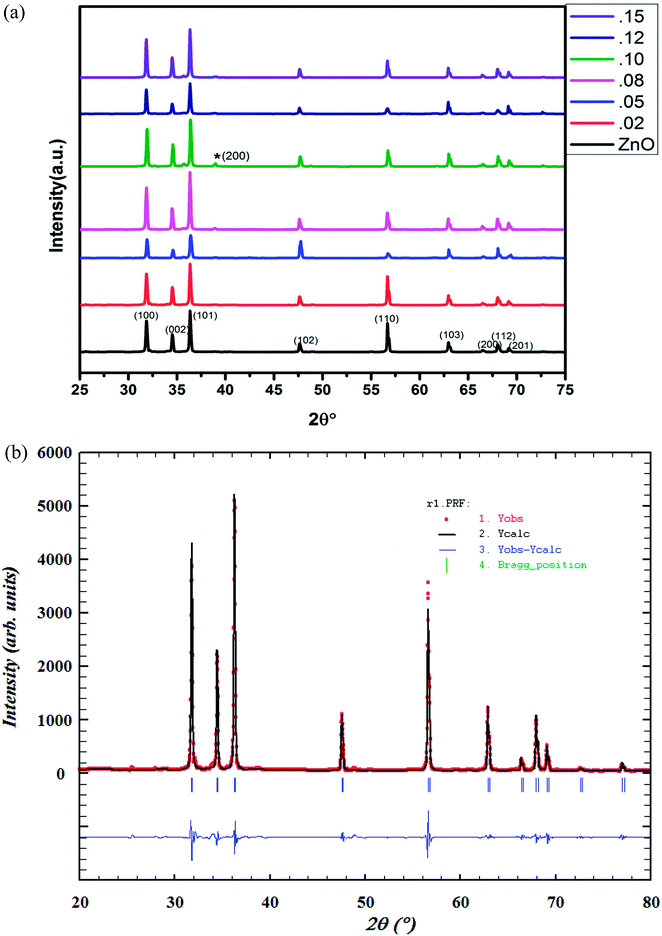 | ||
| Fig. 2 (a) Powder XRD pattern of Zn1−xCuxO1−δ (x ≤ 0.15) samples. (b) Rietveld refined powder XRD pattern of Zn0.95Cu0.05O1−δ. | ||
Cu+ is not stable in air. It radially oxidize to Cu2+, that is why Cu+ ion impurities that is not substituted in ZnO lattice appears as CuO (Cu2+ oxide). Cu+ ion is stable in air only in the form of CuX (X = Cl, Br and I). For the preparation of Zn1−xCuxO1−δ, we have heated our sample in air that is why CuO was formed as impurity phase.
Using FullProf software, structure of materials was refined by Rietveld method. The Rietveld refined XRD image of Zn0.95Cu0.05O1−δ phase is shown in Fig. 2(b). The absence or negligible amount of diffraction peaks for metallic Cu, Cu2O and CuO phases suggest the substitution of Cu in ZnO lattice without altering its wurtzite structure. Structural parameter derived from Rietveld refinement of Zn1−xCuxO1−δ (x ≤ 0.12) is given in ESI (Table S1†). The change in lattice parameter of Zn1−xCuxO1−δ is almost negligible. This may be due to the fact that in tetrahedral coordination, ionic radius of Cu+ is 0.74 Å and Cu2+ is 0.71 Å and that is almost same or close to the ionic radii of Zn2+ (0.74 Å) in tetrahedral coordination.23 That is why, during lattice formation, Cu ions easily able to occupy on Zn sites in wurtzite crystal lattice. However, with the increase in doping percentage of Cu, (x ≥ 0.08), weak diffraction peaks corresponding to CuO phase start appearing in the powder XRD pattern (Fig. 2(a)) due to segregation of cu ions. Thus, only up to 8% Cu ions can be substituted on Zn2+ sites in ZnO lattice.
SEM images of (a) powder and (b) intersection of pellet of Zn0.95Cu0.05O1−δ in ESI Fig. S1.† The SEM study reveals that the grains are of micrometre sizes it the range of 2–50 μm and hexagonal shape. The pellets are well-sintered, and the grains were in good contact with each other. The EDX image shown in ESI Fig. S1(c)† also confirms the composition and apparent homogeneity of the materials. EDX study has been carried out by the EDX probe attached in the SEM instrument (Fig. S1†) and indeed Zn and Cu were found in the ratio of 0.95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.05, which agrees well with the composition taken for the preparation. The density of the pellets was measured by the Archimedes method in water and was ∼97% of the theoretical density of the material.
0.05, which agrees well with the composition taken for the preparation. The density of the pellets was measured by the Archimedes method in water and was ∼97% of the theoretical density of the material.
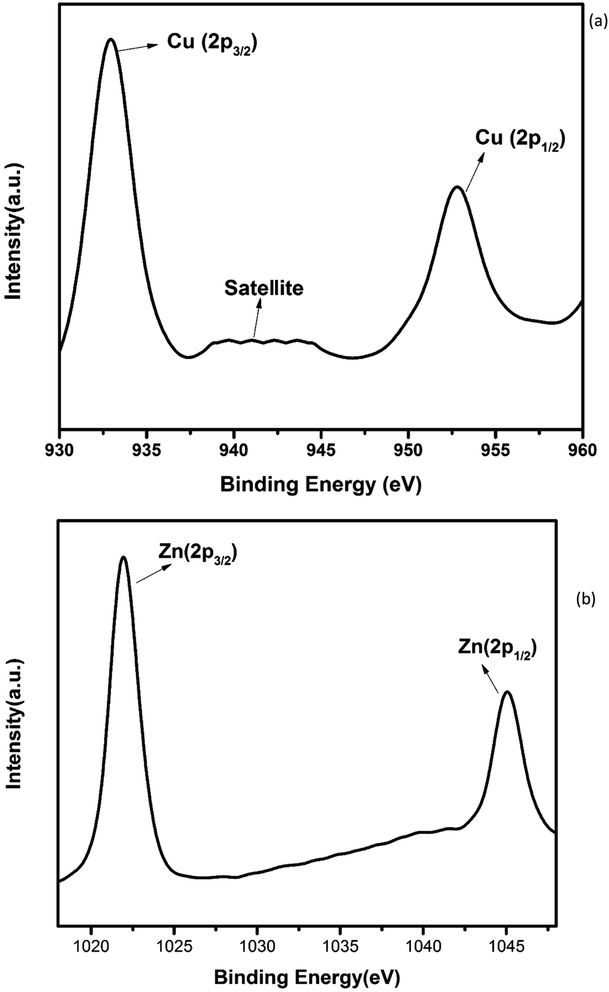
The electronic structure and oxidation states of Cu and Zn in Zn0.95Cu0.05O1−δ samples were investigated by X-ray photo-electron spectroscopy. Core level Cu (2p) spectra of Zn0.95Cu0.05O1−δ sample is shown in Fig. 3(a). Binding energy of Cu (2p3/2) is observed around 932.9 eV and a very broad and weak satellite peak was observed at 10 eV from the main peak confirms that Cu ions are mostly is in +1 oxidation state. In general, both Cu and Cu+ (2p3/2) electron have binding energy close to 933 eV with absence or very weak presence of satellite peak.24,25 For Cu2+ ions, the binding energy of 2p3/2 core electrons are 933.5 eV with appearance of very strong satellite peak around 940 eV.25 Thus it is clear for the spectra of Cu (2p) core level shown in Fig. 3(a) that Cu is exist mostly in Cu+ state in Zn0.95Cu0.05O1−δ. The Zn (2p) core level spectra is shown in Fig. 3(b). Binding energy of Zn (2p3/2) electrons was observed at 1021.5 eV. Binding energy for 2p3/2 electrons for Zn (metal) and Zn2+ ions are 1021 eV and 1021.4 eV respectively.25,26 Thus, Zn is in 2+ oxidation state in Zn0.95Cu0.05O1−δ samples. Therefore presence of Cu+ on Zn2+will generate oxygen ion vacancy Zn0.95Cu0.05O1−δ lattice. Using Kröger Vink notation, the oxygen vacancy formation is represented as
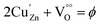 | (1) |
An estimate of relative concentrations of Zn and Cu were carried out from the intensities of Zn (2p) and Cu (2p) peaks in Zn0.95Cu0.05O1−δ.
Relative surface concentration is calculated from the formula:27
| Relative concentration CM = (IM/λMσMDM)/∑(IM/λMσMDM) | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.05 in Zn0.95Cu0.05O1−δ. Thus surface compositions of Zn0.95Cu0.05O1−δ almost same as the bulk composition.
0.05 in Zn0.95Cu0.05O1−δ. Thus surface compositions of Zn0.95Cu0.05O1−δ almost same as the bulk composition.
Further to understand the electronic structure of Zn0.95Cu0.05O1−δ samples, magnetic response of the Zn0.95Cu0.05O1−δ was also studied using magnetic property measurement system (MPMS) by Squid based magnetometer (MPMS-3, Quantum Design Inc.). Fig. 4 shows a typical magnetization vs. magnetic field (M–H) curve obtained from a Zn0.95Cu0.05O1−δ sample at 300 K, revealing a clear diamagnetic behavior under applied magnetic fields up to ±5 T.30,31 Beside that, at magnetic intensities lower than ±0.2 T, the material exhibited a residual ferromagnetic signal, evident after a subtraction of the diamagnetic signal as shown in the inset of Fig. 4.30,31 The diamagnetic behavior of Zn0.95Cu0.05O1−δ is largely due to presence of fully filled d orbital of Zn2+ and Cu+ having electronic configuration 3d104s04p0. The weak ferromagnetism in Zn0.95Cu0.05O1−δ can be originated due to the polarization of unpaired 2p electrons of O with the empty 4p orbital of Zn and Cu around oxygen vacancies in wurtzite lattice. Oxygen vacancy induced room temperature ferromagnetisms is observed within the percolation limit in various oxide system such as doped and un-doped ZnO, TiO2, CeO2, and SnO2.31–34 Thus the magnetization (M–H) study also confirm the oxygen vacancy formation due to incorporation of diamagnetic Cu+ ion on Zn2+ sites in ZnO lattice.
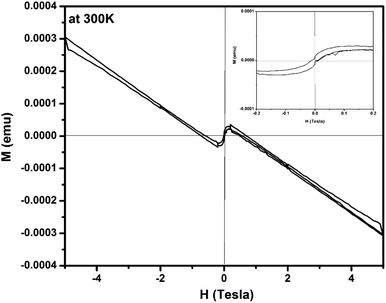 | ||
| Fig. 4 Magnetization vs. magnetic field (M–H) curve for Zn0.95Cu0.05O1−δ sample at 300 K. Inset show the ferromagnetic contribution within ±0.2 T. | ||
The absence of oxide ion or oxygen vacancy formation can introduce net dipole moment in Zn and Cu tetrahedral and can also destabilize the local structure/coordination and distort the local polyhedral structure of wurtzite ZnO lattice to result ferroelectric transitions. The impedance spectroscopy was carried at variable temperature in air to study the dielectric behaviour of the material in the frequency range of 100 kHz to 1 Hz. The dielectric constant was calculated using formula:
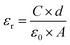 | (3) |
Capacitance (C) was calculated by using formula
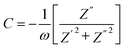 | (4) |
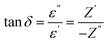 | (5) |
Fig. 5(a), show the plots of real part of dielectric constant 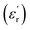 at 100 kHz frequency (f) for the Zn1−xCuxO1−x/2 (x = 0.02, 0.05, 0.08, 0.1, 12 and 0.15) pallets in the temperature range of 100–650 °C. In general, the
at 100 kHz frequency (f) for the Zn1−xCuxO1−x/2 (x = 0.02, 0.05, 0.08, 0.1, 12 and 0.15) pallets in the temperature range of 100–650 °C. In general, the 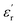 values were increasing in the range of 100 °C to 650 °C with a maxima appearing around 600 °C. The maxima for dielectric constant
values were increasing in the range of 100 °C to 650 °C with a maxima appearing around 600 °C. The maxima for dielectric constant 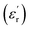 of Zn1−xCuxO1−δ were appeared for x = 0.05 and x = 0.12. The dielectric constant
of Zn1−xCuxO1−δ were appeared for x = 0.05 and x = 0.12. The dielectric constant 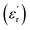 for x = 0.05 was ∼6300 and for x = 0.12 was ∼3275 respectively at 100 kHz f at 600 °C. The variation in dielectric loss
for x = 0.05 was ∼6300 and for x = 0.12 was ∼3275 respectively at 100 kHz f at 600 °C. The variation in dielectric loss 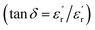 with temperature, at selected frequency, is shown in Fig. 5(b). tan
with temperature, at selected frequency, is shown in Fig. 5(b). tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ was ∼13 for x = 0.05 and ∼30 for x = 0.12 at 100 kHz frequency at 600 °C. Considering the high dielectric constant of the materials, the observed dielectric loss is quite less for Zn1−xCuxO1−δ samples. As can be seen from Fig. 5(a), that dielectric constant of Cu doped ZnO is varying with the doping of Cu and the highest dielectric constant (6300 at 600 °C) at 100 kHz frequency was obtained for Zn0.95Cu0.05O1−δ, the later studies were centralized around the dielectric and ferroelectric properties of Zn0.95Cu0.05O1−δ. Fig. 6(a and b) show the dielectric constant and dielectric loss for Zn0.95Cu0.05O1−δ samples at various temperature in the range of 100–650 °C at variable frequencies. It was found that both dielectric constant and dielectric loss were increasing continuously up to 600 °C at all frequencies. However, both dielectric constant and dielectric loss were decreasing with increasing frequencies. The increase in dielectric constant
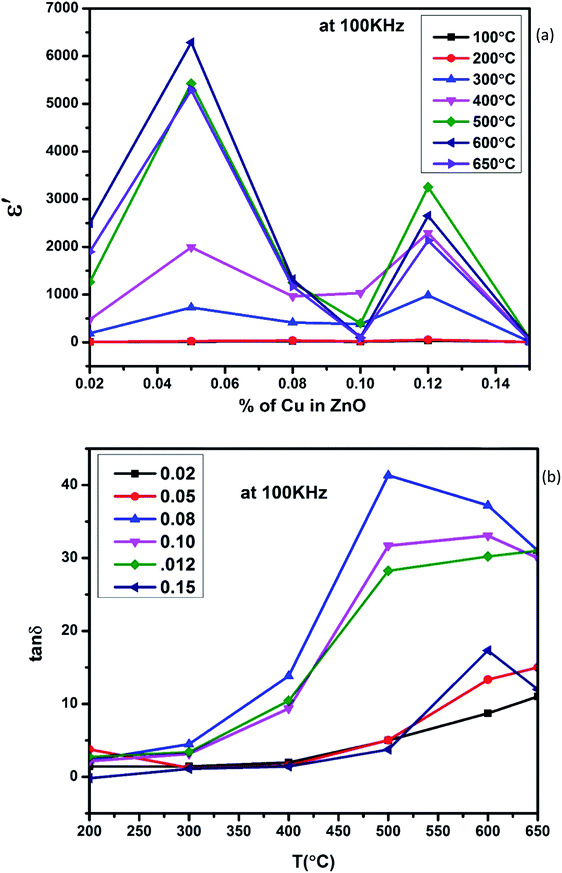
δ was ∼13 for x = 0.05 and ∼30 for x = 0.12 at 100 kHz frequency at 600 °C. Considering the high dielectric constant of the materials, the observed dielectric loss is quite less for Zn1−xCuxO1−δ samples. As can be seen from Fig. 5(a), that dielectric constant of Cu doped ZnO is varying with the doping of Cu and the highest dielectric constant (6300 at 600 °C) at 100 kHz frequency was obtained for Zn0.95Cu0.05O1−δ, the later studies were centralized around the dielectric and ferroelectric properties of Zn0.95Cu0.05O1−δ. Fig. 6(a and b) show the dielectric constant and dielectric loss for Zn0.95Cu0.05O1−δ samples at various temperature in the range of 100–650 °C at variable frequencies. It was found that both dielectric constant and dielectric loss were increasing continuously up to 600 °C at all frequencies. However, both dielectric constant and dielectric loss were decreasing with increasing frequencies. The increase in dielectric constant 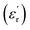 with increasing temperatures at different frequencies for Zn1−xCuxO1−δ is likely due to the localized nature of hopping charge carriers in addition to interfacial polarization due to space charge. These extrinsic contributions to
with increasing temperatures at different frequencies for Zn1−xCuxO1−δ is likely due to the localized nature of hopping charge carriers in addition to interfacial polarization due to space charge. These extrinsic contributions to 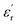 are expected to contribute significantly only at higher frequencies. Further, it was also observed that the maximum dielectric constant and maximum dielectric loss was obtained at Tm = 600 °C between frequency range of 10 kHz to 100 kHz. This suggests that the behaviour of the material is not relaxor type as Tm is not varying with applied frequencies. Therefore P–E characteristic of the material was studied at room temperature using RADIANT precision premier II. The measured polarization hysteresis loop for Cu doped ZnO; Zn0.95Cu0.05O1−δ is shown in Fig. 7. The observation of the clear hysteresis-loop behaviour, by a Sawyer–Tower circuit, with the external applied field confirms the existence of ferroelectricity in bulk Zn0.95Cu0.05O1−δ pellets at room temperature. In our knowledge, this is the first report of formation of a clear P–E hysteresis-loop for any of bulk ZnO based samples. The values of remnant polarization Pr and Vc was found 9.60 × 10−3 (μC cm−2) 3.83 × 102 (V cm−1), respectively, for Zn0.95Cu0.05O1−δ. The values of Pr and Vc are quite low, however, the formation P–E hysteresis-loop in Cu+ doped ZnO samples open new direction in making of binary nontoxic ferroelectrics and understanding the role oxygen vacancy and transition metal ion d orbital interaction with oxygen 2p orbital in binary oxides.
are expected to contribute significantly only at higher frequencies. Further, it was also observed that the maximum dielectric constant and maximum dielectric loss was obtained at Tm = 600 °C between frequency range of 10 kHz to 100 kHz. This suggests that the behaviour of the material is not relaxor type as Tm is not varying with applied frequencies. Therefore P–E characteristic of the material was studied at room temperature using RADIANT precision premier II. The measured polarization hysteresis loop for Cu doped ZnO; Zn0.95Cu0.05O1−δ is shown in Fig. 7. The observation of the clear hysteresis-loop behaviour, by a Sawyer–Tower circuit, with the external applied field confirms the existence of ferroelectricity in bulk Zn0.95Cu0.05O1−δ pellets at room temperature. In our knowledge, this is the first report of formation of a clear P–E hysteresis-loop for any of bulk ZnO based samples. The values of remnant polarization Pr and Vc was found 9.60 × 10−3 (μC cm−2) 3.83 × 102 (V cm−1), respectively, for Zn0.95Cu0.05O1−δ. The values of Pr and Vc are quite low, however, the formation P–E hysteresis-loop in Cu+ doped ZnO samples open new direction in making of binary nontoxic ferroelectrics and understanding the role oxygen vacancy and transition metal ion d orbital interaction with oxygen 2p orbital in binary oxides.
 | ||
| Fig. 5 (a) Variation of dielectric constant and (b) variation of dielectric loss with respect to Cu+ ion substitution in ZnO lattice at 100 kHz with increase in temperature. | ||
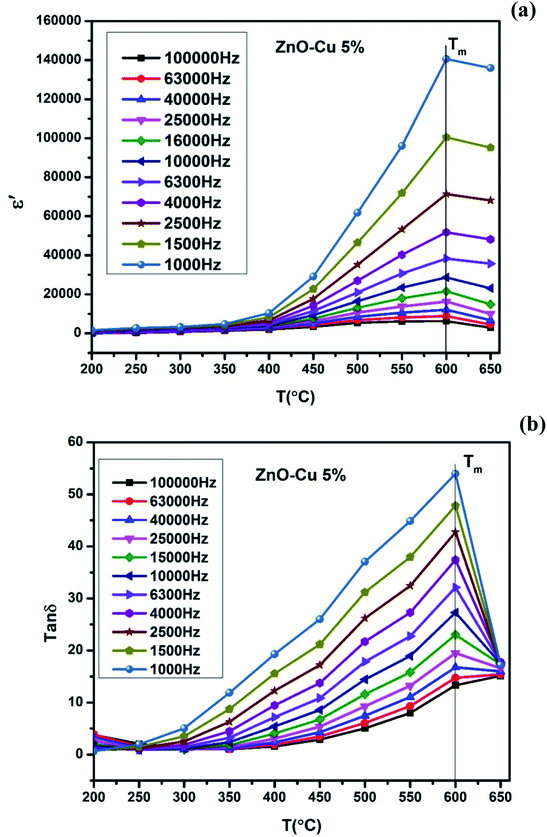 | ||
| Fig. 6 (a) Variation of dielectric constant and (b) variation of dielectric loss of Zn0.95Cu0.05O1−δ pellets at various frequencies with increase in temperature. | ||
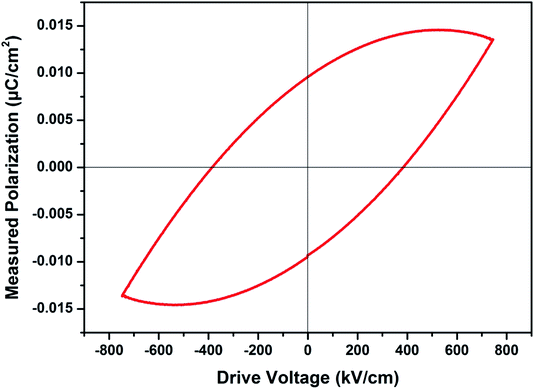 | ||
| Fig. 7 Plot of polarization (P) vs. electric field (E) for Zn0.95Cu0.05O1−δ pellets at room temperature. | ||
The materials Zn0.95Cu0.05O1−δ also exhibit ferroelectricity at room temperature with remnant polarization Pr and Vc equal to 9.60 × 10−3 μC cm−2 and 3.83 × 102 V cm−1 respectively. However the other materials of Cu and Zn systems from thin film have relative higher values for the ferroelectricity, the values of the ZnO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cu (8 at%) was investigated. As the frequency increases, the maximum polarization decreases from ≈0.78 μC cm−2 at 500 Hz to ≈0.72 μC cm−2 at 2 kHz. The shape of the P–E loops and the remanent polarization were found to exhibit little frequency dependence in the range of 0.5 to 2 kHz.21 However this is the first report of ferroelectricity in the bulk samples. We believe that if our samples can be fabricated in the form of thin film, with highly aligned grain, high remnant polarization can be achieved.
Cu (8 at%) was investigated. As the frequency increases, the maximum polarization decreases from ≈0.78 μC cm−2 at 500 Hz to ≈0.72 μC cm−2 at 2 kHz. The shape of the P–E loops and the remanent polarization were found to exhibit little frequency dependence in the range of 0.5 to 2 kHz.21 However this is the first report of ferroelectricity in the bulk samples. We believe that if our samples can be fabricated in the form of thin film, with highly aligned grain, high remnant polarization can be achieved.
Conclusions
The quest to develop or identify ferroelectric in binary oxide materials leads us investigate oxygen vacant structure in strong incipient dielectric host such as wurtzite ZnO lattice. Cu+ ion substitution on Zn2+ sites not only resulted net polarization but also open the path for strong polarization between O 2p and fully filled d10 Zn/Cu 4p orbital in tetrahedral coordination. Cu+ ion substitution on Zn2+ sites in ZnO lattice is achieved by careful selection raw material CuCl and adaptation low temperature sol–gel synthesis route for the preparation of bulk material. The magnetization (M–H) study confirm the diamagnetic behavior of Zn0.95Cu0.05O1−δ samples that is arises largely due to presence of fully filled d orbital of Zn2+ and Cu+ having electronic configuration 3d104s04p0 and also confirm the oxygen vacancy formation due to incorporation of diamagnetic Cu+ ion on Zn2+ sites in ZnO lattice. Up to 8% of Cu+ ions were substituted in ZnO lattice and highest dielectric constant (∼6300) was obtained at 600 °C for Zn0.95Cu0.05O1−δ at 100 kHz frequency. The materials Zn0.95Cu0.05O1−δ also exhibit ferroelectricity at room temperature with remnant polarization Pr and Vc equal to 9.60 × 10−3 μC cm−2 and 3.83 × 102 V cm−1 respectively.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
Authors thank Department of Ceramic Engineering, IIT(BHU) and Central Instrument Facility (CIF), IIT(BHU) for its facility and support. Dr Preetam Singh Thank SERB for the financial support (Project no.: EMR/2016/006840). Neeraj Singh thanks IIT (BHU) Varanasi for financial support as teaching assistant. Authors also thank Dr T. Maiyalagan, SRM Institute of Science and Technology Chennai, India for XPS Measurements and Dr Akhilesh Kumar Singh, School of Materials Science and Technology, IIT(BHU) Varanasi, India for P–E loop measurements.References
- C. C. Homes, T. Vogt, S. M. Shapiro, S. Wakimoto and A. P. Ramirez, Optical Response of High-Dielectric-Constant Perovskite-Related Oxide, Science, 2001, 293, 673–676 CrossRef CAS PubMed.
- Y. Li, F. Qian, J. Xiang and C. M. Lieber, Nanowire electronic and optoelectronic devices, Mater. Today, 2006, 9(10), 18–27 CrossRef CAS.
- S. Y. Yang, J. Seidel, S. J. Byrnes, P. Shafer, C.-H. Yang, M. D. Rossell, P. Yu, Y.-H. Chu, J. F. Scott, J. W. Ager III, L. W. Martin and R. Ramesh, Above-band gap voltages from ferroelectric photovoltaic devices, Nat. Nanotechnol., 2010, 5, 143–147 CrossRef CAS PubMed.
- Z. Wen, C. Li, D. Wu, A. Li and N. Ming, Ferroelectric field effect enhanced electro resistance in metal/ferroelectric/semiconductor tunnel junctions, Nat. Mater., 2013, 12, 617–621 CrossRef CAS PubMed.
- F. Wang, I. Grinberg and A. M. Rappe, Semiconducting ferroelectric photovoltaics through Zn2+ doping into KNbO3 and polarization rotation, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(1–5), 235105 CrossRef.
- W.-Q. Liao, Y. Zhang, C. Hu, J.-G. Mao, H.-Y. Ye, P. Li, S. D. Huang and R. Xiong, A lead-halide perovskite molecular ferroelectric semiconductor, Nat. Commun., 2015, 6(1–7), 7338 CrossRef PubMed.
- Z. L. Wang and J. Song, Piezoelectric nano generators based on zinc oxide nanowire arrays, Science, 2006, 312(5771), 242–246 CrossRef CAS PubMed.
- M. Choi, D. Choi, M. Jin, I. Kim, S. Kim, J. Choi, S. Y. Lee, J. M. Kim and S. W. Kim, Mechanically Powered Transparent Flexible Charge – Generating Nano devices with Piezoelectric ZnO Nanorods, Adv. Mater., 2009, 21, 2185–2189 CrossRef CAS.
- X. Wang, J. Zhou, J. Song, J. Liu, N. Xu and Z. L. Wang, Piezoelectric Field Effect Transistor and Nanoforce Sensor Based on a Single ZnO Nanowire, Nano Lett., 2006, 6(12), 2768–2772 CrossRef CAS PubMed.
- E. Bacaksiz, M. Parlak, M. Tomakin, A. Ozcelik, M. Karakız and M. Altunbas, The effects of zinc nitrate, zinc acetate and zinc chloride precursors on investigation of structural and optical properties of ZnO thin films, J. Alloys Compd., 2008, 466, 447–450 CrossRef CAS.
- D. Segets, J. Gradl, R. Klupp Taylor, V. Vassilev and W. Peukert, Analysis of Optical Absorbance Spectra for the Determination of ZnO Nanoparticle Size Distribution, Solubility, and Surface Energy, ACS Nano, 2009, 3(7), 1703–1710 CrossRef CAS PubMed.
- M. Chaari and A. Matoussi, Electrical conduction and dielectric studies of ZnO pellets, Physica B, 2012, 407, 3441–3447 CrossRef CAS.
- H. Zhang, B. Chen, H. Jiang, C. Wang, H. Wang and X. Wang, A strategy for ZnO nanorod mediated multi-mode cancer treatment, Biomaterials, 2011, 32, 1906–1914 CrossRef CAS PubMed.
- N. A. Spaldin, Search for ferromagnetism in transition-metal-doped piezoelectric ZnO, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(1–7), 125201 CrossRef.
- M. Venkatesan, C. B. Fitzgerald, J. G. Lunney and J. M. D. Coey, Anisotropic Ferromagnetism in Substituted Zinc Oxide, Phys. Rev. Lett., 2004, 93(1–4), 177206 CrossRef CAS PubMed.
- K. R. Kittilstved, N. S. Norberg and D. R. Gamelin, Chemical Manipulation of High-TC Ferromagnetism in ZnO Diluted Magnetic Semiconductors, Phys. Rev. Lett., 2005, 94(1–4), 147209 CrossRef PubMed.
- D. B. Buchholz, R. P. H. Chang, J.-Y. Song and J. B. Ketterson, Room-temperature ferromagnetism in Cu doped ZnO thin films, Appl. Phys. Lett., 2005, 87(1–3), 082504 CrossRef.
- A. B. Djurisić, A. M. C. Ng and X. Y. Chen, ZnO nanostructures for optoelectronics: Material properties and device applications, Prog. Quantum Electron., 2010, 34, 191–259 CrossRef.
- R. Elilarassi and G. Chandrasekaran, Synthesis and optical properties of Ni-doped zinc oxide nanoparticles for optoelectronic applications, Optoelectron. Lett., 2010, 6(1), 6–10 CrossRef.
- K. Omri, A. Bettaibi, K. Khirouni and L. El Mir, The optoelectronic properties and role of Cu concentration on the structural and electrical properties of Cu doped ZnO nanoparticles, Phys. B, 2018, 537, 167–175 CrossRef CAS.
- T. S. Herng, M. F. Wong, D. Qi, J. Yi, A. Kumar, A. Huang, F. C. Kartawidjaja, S. Smadici, P. Abbamonte, C. Sánchez-Hanke, S. Shannigrahi, J. M. Xue, J. Wang, Y. P. Feng, A. Rusydi, K. Zeng and J. Ding, Mutual Ferromagnetic–Ferroelectric Coupling in Multiferroic Copper-Doped ZnO, Adv. Mater., 2011, 23, 1635–1640 CrossRef CAS PubMed.
- D. P. Singh, S. K. Gupta, K. K. Pandey, S. P. Yadav, M. C. Varia and R. Manohar, Ferroelectric liquid crystal matrix dispersed with Cu doped ZnO nanoparticles, J. Non-Cryst. Solids, 2013, 363, 178–186 CrossRef CAS.
- R. D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. C. Biesinger, Advanced analysis of copper X-ray photoelectron spectra, Surf. Interface Anal., 2017, 49, 1325–1334 CrossRef CAS.
- M. C. Biesinger, L. W. M. Laua, A. R. Gerson and R. St. C. Smart, Resolving surface chemical states in XPS analysis of first row transition metals, oxides and hydroxides: Sc, Ti, V, Cu and Zn, Appl. Surf. Sci., 2010, 257, 887–898 CrossRef CAS.
- N. Pauly, F. Yubero, J. P. Espinós and S. Tougaard, XPS primary excitation spectra of Zn 2p, Fe 2p, and Ce 3d from ZnO, α-Fe2O3, and CeO2, Surf. Interface Anal., 2019, 51, 353–360 CrossRef CAS.
- C. J. Powell and P. E. Larson, Appl. Surf. Sci., 1978, 1, 186–201 CrossRef CAS.
- J. H. Scofield, J. Electron Spectrosc. Relat. Phenom., 1976, 8, 129–137 CrossRef CAS.
- D. R. Penn, J. Electron Spectrosc. Relat. Phenom., 1976, 9, 29–40 CrossRef CAS.
- G. Guzmán, R. Escudero, R. Silva and M. Herrera, Influence of Ga vacancies, Mn and O impurities on the ferromagnetic properties of GaN micro- and nanostructures, J. Appl. Phys., 2018, 123(1–9), 161578 CrossRef.
- A. S. Ganeshraja, S. Thirumurugan, K. Rajkumar, K. Zhu, Y. Wang, K. Anbalagan and J. Wang, Effects of structural, optical and ferromagnetic states on the photocatalytic activities of Sn–TiO2 nanocrystals, RSC Adv., 2016, 6, 409–421 RSC.
- M. Zhu, Z. Zhang, M. Zhong, M. Tariq, Y. Li, W. Li, H. Jin, K. Skotnicova and Y. Li, Oxygen vacancy induced ferromagnetism in Cu-doped ZnO, Ceram. Int., 2017, 43, 3166–3170 CrossRef CAS.
- G. Niu, E. Hildebrandt, M. A. Schubert, F. Boscherini, M. H. Zoellner, L. Alff, D. Walczyk, P. Zaumseil, I. Costina, H. Wilkens and T. Schroeder, Oxygen Vacancy Induced Room Temperature Ferromagnetism in Pr-Doped CeO2 Thin Films on Silicon, ACS Appl. Mater. Interfaces, 2014, 6(20), 17496–17505 CrossRef CAS PubMed.
- G. S. Chang, J. Forrest, E. Z. Kurmaev, A. N. Morozovska, M. D. Glinchuk, J. A. McLeod, A. Moewes, T. P. Surkova and N. H. Hong, Oxygen-vacancy-induced ferromagnetism in undoped SnO2 thin films, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(1–9), 165319 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra00933d |
| This journal is © The Royal Society of Chemistry 2020 |