Open Access Article
Open Access ArticleA superhydrophilic bilayer structure of a nylon 6 nanofiber/cellulose membrane and its characterization as potential water filtration media
Ahmad Fauzi,
Dian Ahmad Hapidin,
Muhammad Miftahul Munir *,
Ferry Iskandar
*,
Ferry Iskandar and
Khairurrijal Khairurrijal
and
Khairurrijal Khairurrijal
Department of Physics, Faculty of Natural Sciences and Mathematics, Institut Teknologi Bandung, Jalan Ganesa 10, Bandung 40132, Indonesia. E-mail: miftah@fi.itb.ac.id
First published on 4th May 2020
Abstract
A bilayer structure of a nylon 6 nanofibrous membrane on a cellulose membrane has been successfully developed for water filter application. The nylon 6 nanofibrous membrane was deposited on the cellulose membrane via the electrospinning technique. The bilayer membrane properties, including mechanical strength, wettability, porosity, and microfiltration performance (flux and rejection), were thoroughly investigated. The membrane properties were studied using nylon 6 nanofibrous membranes having various fiber diameters and membrane thicknesses, which were obtained by adjusting the solution concentration and spinning time. The measurement of solution parameters, i.e., viscosity, conductivity, and surface tension, showed a strong relationship between the solution concentration and these parameters, which later changed the fabricated fiber sizes. The FTIR spectra depicted complete solvent evaporation after the electrospinning process. Smaller nanofiber diameters could improve the mechanical strength of the membranes. The porosity test showed a strong relationship between the nanofiber diameter and the pore size and pore distribution of the membranes. The water contact angle measurement showed the significant influence of the cellulose membrane on increasing the hydrophilicity of the bilayer structure, which then improved the membrane flux. The particle rejection test, using PSL sizes of 308 and 450 nm, showed high rejection (above 98%) for all sample thickness variations. Overall, the bilayer structure of the nylon 6 nanofibers/cellulose membranes showed excellent and promising performance as water filter media.
1. Introduction
The declining water quality due to contamination by harmful pollutants has drawn worldwide concern because of adverse impacts on human health. It has encouraged the development of various methods of water purification such as filtration, sieving, decantation, adsorption, and distillation. Among these methods, filtration is the most used, effective, and efficient water purification method.1 Filtration usually utilizes pollutant-capturing media, such as sand, charcoal, wool, cotton, zeolites, and polymeric membranes. The polymeric membranes are the most commonly used filtration media because of their excellent mechanical strength, flexibility, and low price. Despite these advantages, conventional polymeric membranes usually have an asymmetric structure, causing low porosity and low flux.2 The flux represents the ability of the membrane to allow the water to flow through it. Membranes with higher flux will consume less energy during the filtration process. To overcome this issue, many researchers have developed filtration membranes arranged by polymeric nanofibers.3–7 Nanofiber-based membranes offer some advantages such as high porosity, low basis weight, high surface area, controllable pore size, and continuous-interconnected pores.8 These properties allow the membrane to achieve higher flux without sacrificing particle rejection.9 Nanofibrous membranes have been utilized as water filter media for microfiltration, ultrafiltration, and nanofiltration.10–15Nanofibrous membranes can be fabricated using a versatile electrospinning technique. This technique can create nonwoven structures with easy control over the nanofiber morphology and diameter by adjusting the precursor solution, processing, and environment parameters.16–20 The precursor solution can be made from various polymers, such as polyacrylonitrile (PAN),2 polyvinylpyrrolidone (PVP),21 and nylon 6.3 For water filter applications, the fabricated nanofibrous membranes are usually deposited on a strong-support, such as nonwoven PET, to enhance the filter mechanical strength.22,23 However, the hydrophobic property of the nonwoven PET substrate is undesirable for water filtration processes because it can decrease the flux and cause membrane fouling.24 On the other hand, cellulose membranes offer promising properties, such as superhydrophilic surfaces, low cost, solvent resistance, and good mechanical strength. They have also been applied as water filters to absorb metals.25–28 Our previous study reported the development of a bilayer structure consisting of nanofibrous and cellulose membranes, and its performance led to its characterization as a clarification medium for apple juice.29 The cellulose membrane was arranged on a PAN nanofibrous membrane and played the role of a prefilter; the nanofibrous membrane played the role of a separator of the primary particles or dissolved solids. The study proved that the bilayer structure could provide both high flux and good separation of particles or dissolved solids. Accordingly, the bilayer structure of the nanofibrous and cellulose membrane could potentially be applied in the design of high-performance water filter media, which is the main objective of the present study.
This paper comprehensively presents the synthesis, characterization, and evaluation of a superhydrophilic bilayer structure composed of nanofibrous and cellulose membranes for use as water filtration media. The nanofibrous membranes were made using nylon 6 polymer due to its excellent mechanical strength and its extensive use as water filtration media.3,30 To control and widen the nanofiber diameter range, we made nylon 6 solutions with varying concentrations. Accordingly, the physicochemical properties of the electrospun nylon 6 nanofibrous and cellulose membranes were fully characterized and analyzed. The characterization included functional group analysis, surface wettability, pore size, mechanical properties, and filtration performances. The filtration performances were evaluated by measuring the filter flux and rejection. The rejection was measured using polystyrene latex (PSL) as test particles.
2. Experimental
2.1 Materials
The precursor solutions were prepared by dissolving nylon 6 pellets having a density of 1.084 g mL−1 (Sigma Aldrich, Singapore) in formic acid solvent (Bratachem, Indonesia). Commercial cellulose membrane (Whatman, Fisher, Grade 91 Wet Strengthened Qualitative Filter Paper) was used as a substrate for depositing the nylon 6 nanofibers. The cellulose membrane had the pore size, thickness, and basis weight of 10 μm, 205 μm, and 65 g m−2, respectively. The arrangement of nylon 6 nanofibrous membranes on the cellulose substrate led to the formation of a bilayer-structure membrane. Polystyrene latex (PSL) particles with the geometrical mean sizes of 95, 308, and 451 nm were used for investigating the bilayer membrane rejection.312.2 Membrane preparation and characterization
Nylon 6 pellets were dissolved in formic acid and mixed using a magnetic stirrer at 60 °C until the solution became homogeneous. The solution viscosity and conductivity were measured at 25 °C using a Fenske–Oswald viscometer (Fisher Scientific, 50 A643) and conductometer (Mettler Toledo, Seveneasy Conductivity, Switzerland), respectively.An electrospinning apparatus (Nachriebe 601, Nachriebe, Center for Aerosols and Analytical Instrumentation, Department of Physics, ITB, Bandung, Indonesia) was employed for fabricating the nylon 6 nanofibrous membranes. The schematic of the electrospinning system is illustrated elsewhere.32 The nylon 6 precursor solutions were inserted into a syringe with an inner needle diameter of 0.8 mm (21 G). The precursor solution was pushed out from the syringe needle using a syringe pump having a constant flow rate of 3 μL min−1. The high voltage source of 14 kV was connected to the syringe needle and the needle tip was separated 10 cm from a drum collector. The drum collector was earth grounded, rotated, and moved left and right to distribute the collected nanofibers evenly. The drum collector was also wrapped with the cellulose membrane as the substrate for depositing the nylon 6 nanofibers. The electrospinning process was conducted at 22–24 °C and relative humidity of 70%.
The fabricated nylon 6 nanofibrous membranes were divided into two groups, i.e., membranes with fiber diameter variation (NFD) and membranes with thickness variation (NFT). The NFD membranes were obtained by varying the precursor solution concentration while slightly adjusting the spinning time so that all the samples had the same thickness of about 15.5 ± 0.2 μm. The solution concentrations of the NFD samples were 17, 20, 23, 26, and 29 wt%, coded as NFD17, NFD20, NFD23, NFD26, and NFD29, respectively, which resulted in fiber diameters ranging from 65–663 nm. The NFT membranes were obtained by varying the spinning time using the same precursor solution concentration of 20 wt% so that all samples had the same fiber diameter of about 98 ± 14 nm. The spinning time for the NFT samples were 1, 2, 3, 6, and 9 hours, coded as NFT1, NFT2, NFT3, NFT6, and NFT9, respectively, which resulted in the membrane thickness ranging from 11–97.6 μm.
Nylon 6 nanofibrous mats were also deposited on hydrophilic (cellulose membrane) and hydrophobic (PET nonwoven) substrates to investigate the effect of substrate wettability on the flux of the bilayer structure. Nylon 6 nanofibrous mats deposited on the cellulose membrane and PET nonwoven substrate were coded as NFC and NFNWS, respectively. The NFC and NFNWS samples were made using the same nylon 6 concentration of 20 wt% and the spinning time of 4 hours.
The morphologies of the cellulose membrane and nylon 6 nanofibers were characterized by scanning electron microscopy (SEM) (JEOL, 6510 LV). The thicknesses of the nylon 6 nanofibrous membranes were measured using a thickness gauge (Sylvac S228). The chemical bonds of nylon 6 pellets, nylon 6 nanofibers, cellulose membrane, formic acid, and pure water were investigated using a Fourier-transform infrared (FTIR) spectrometer (Bruker, Alpha) in the wavelength range of 500–4000 cm−1. The mechanical strength of the membranes was measured using a universal testing machine (UTM) (Tensilon RTF 1310) with a maximum load of 100 N. The bilayer membranes were cut into rectangular pieces of size 2 cm × 10 cm. All samples were tested at a head speed of 1 mm min−1 at room temperature.
The wettability of the bilayer membranes was investigated from the water contact angle (WCA) value measured by a contact angle measurement apparatus (Nachriebe 320, Nachriebe, Center for Aerosols and Analytical Instrumentation, Department of Physics, ITB, Bandung, Indonesia).32,33 The water droplet (volume of 5 μL) images on the bilayer membrane surface were taken using a camera and it was digitally processed by an image processing software to obtain the WCA values. The WCA measurements were carried out on the NFT1, NFT2, NFT6, NFT9, and NFNWS samples. Moreover, WCA values were also recorded from NFT2 samples every 0.2 seconds to investigate the decrease in the WCA over time.
The membrane pore size distribution was measured by a capillary flow porometer (Nachriebe 330, Nachriebe, Center for Aerosols and Analytical Instrumentation, Department of Physics, ITB, Bandung, Indonesia). Before the pore size measurement, the tested membranes were wet with the wetting agent of isopropyl alcohol (Bratachem, Indonesia), then, the non-reacting air pressure was gradually increased to push the wetting agent so that bubble points appeared. The relation between pressure and pore size is expressed by the Young Laplace equation as follows:
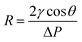 | (1) |
2.3 Filtration test
The membrane filtration performances were determined from pure water flux and particle rejection parameters. The pure water flux is defined as the volume of water passing through the tested membrane, expressed in unit time per area. The flux can reflect the energy needed for the filtration process. A good filter should have high flux so it consumes lower energy during the filtration process. Darcy's law expresses the theoretical approach of the flux (J), derived from the Navier–Stokes equation as follows:23
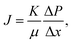 | (2) |
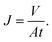 | (3) |
In this study, the flux test used the dead-end mechanism with the apparatus consisting of a filter holder (inner diameter of 25 mm) (Sartorius, Germany), an air pressure controller, a stopwatch, and an electronic balance.35 The effect of the substrate wettability on the bilayer membrane flux was investigated by conducting the flux tests on the NFNWS and NFC samples. The tests used the input pressure of 20–90 kPa with an increase of 10 kPa. The effects of the nylon 6 nanofibers diameter and membrane thickness on the bilayer membrane flux were also investigated by conducting the flux tests on the NFD samples (NFD17, NFD20, NFD23, NFD26, and NFD29) and NFT samples (NFT1, NFT2, NFT3, NFT6, and NFT9). The test used the pressure range of 0–70 kPa with an increase of 10 kPa.
The rejection parameter was measured by passing the PSL suspension through the tested membranes with the PSL particle size of 95, 308, and 450 nm. The feed solutions were made by mixing the PSL suspension with the distilled water at a concentration of 100 ppm. The feed solution was inserted into an 800 mL reservoir connected to the filter holder. The tested membranes were placed tightly inside the filter holder. The feed solutions were passed through the membranes with a constant flow rate. The filter rejection parameter (η) was calculated by comparing the PSL concentration from the feed (PSL concentration before filtration, Cf) and the permeate (PSL concentration after filtration, CP) suspension as follows:
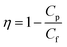 | (4) |
The PSL concentration from the feed and permeate suspension were measured using a turbidity meter (Nan-Bei, China) that was previously calibrated to obtain the relationship between the turbidity (NTU) against the PSL concentration.
3. Results and discussion
3.1 Membrane fiber size and morphology
Fig. 1(a) shows the SEM image of the cellulose membrane having the fiber diameters of tens of micrometers. Fig. 1(b) shows the cross-section view of the nylon 6 nanofibers deposited on the cellulose membrane. Randomly deposited nanofibers formed a nonwoven structure with large porosity and interconnected pores that caused higher membrane flux. | ||
| Fig. 1 (a) SEM image of the cellulose membrane, (b) cross-section SEM image of the cellulose membrane and the nylon 6 nanofibrous membrane. | ||
Fig. 2(a)–(e) shows the SEM images and the fiber size distribution of (a) NFD17, (b) NFD20, (c) NFD23, (d) NFD26, and (e) NFD29 samples. All produced membranes had the bead-free and smooth fiber morphology, with various fiber diameters ranging from nano- to micrometer size. The bead-free nylon 6 nanofibers were also obtained by Ryu et al. (2003), who used formic acid solvent with the solution concentrations of 15, 20, 25, and 30 wt%.30
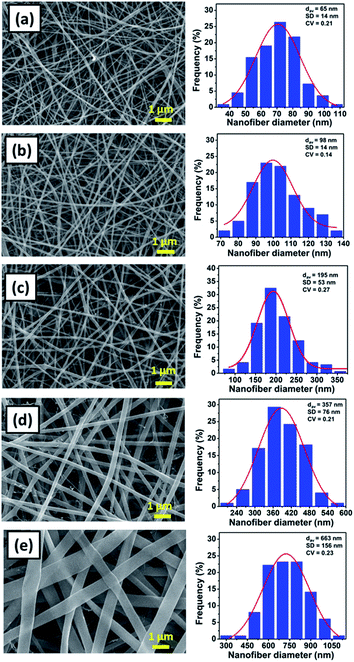 | ||
| Fig. 2 The SEM images of nylon 6 nanofibrous membranes and the fiber size distribution for (a) NFD17, (b) NFD20, (c) NFD23, (d) NFD26, and (e) NFD29 samples. | ||
The NFD17, NFD20, NFD23, NFD26, and NFD29 samples had the average fiber diameter (dav) of 65, 98, 195, 357, and 663 nm, and the standard deviation (SD) of 14, 14, 53, 76, and 156 nm, respectively. Nylon 6 nanofibrous membranes fabricated from higher solution concentrations had larger fiber diameters, in accordance with other studies.36–39 The jet from higher solution concentration would dry faster so that it experienced the stretching process in a shorter period, leading to large fiber formation. Larger fiber diameters obtained from higher solution concentrations were also related to the higher solution viscosity, which will be explained later.
Fig. 3 shows a linear relationship between the membrane thickness and spinning time. If the volume of the collected fibers (Vf) is related to the volume of the collected membrane (VT) with a packing density parameter (α), then the fiber production rate can be expressed as dVf/dt = α dVT/dt. The drum collector with radius R collects and spreads the fibers along L. If the collected fibers form a membrane with thickness D, the total collected membrane volume is VT = π(D2 + 2DR)L. Therefore, the fiber production rate can be written as follows:
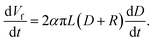 | (5) |
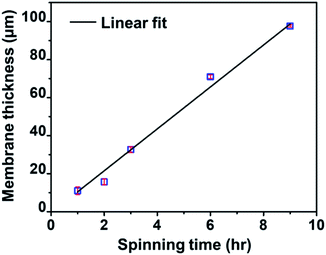 | ||
| Fig. 3 The relationship between spinning time and the thickness of the nylon 6 nanofibrous membranes for the NFT membrane samples. | ||
If the electrospinning process is run with a constant production rate, or dVf/dt = β, and D is much smaller than R, then eqn (5) becomes:
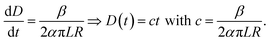 | (6) |
Eqn (6) shows a linear relationship between the collected membrane thickness (D) and spinning time (t), which was also confirmed by the experimental data in Fig. 3. The constant c relates to the nanofiber production rate, packing density, drum collector radius, and collector drum length, which were set as constant during the electrospinning process. Also, the drum collector moved horizontally to evenly distribute the collected fibers, which maintained the linear increase of the membrane thickness to the spinning time.
3.2 The influence of solution properties on nanofibers size
Table 1 shows the effect of the nylon 6 concentration on the physical properties of the solution, i.e., viscosity, surface tension, and conductivity. Briefly, the increase in the nylon 6 concentration increased the solution viscosity and surface tension. The increase in the solution viscosity of the solution with higher concentration was due to the increasing number of polymer chain entanglements.30,38 In contrast, the conductivity decreased with the solution concentration. Since the polymers generally have low conductivity, the volume and the type of solvent is usually the main parameter affecting the solution conductivity. The solvent used formic acid and, according to previous research, increasing the formic acid content could increase the conductivity of the polymeric solution.38–40| Membrane code | Nylon 6 concentration (wt%) | Viscosity (cP) | Surface tension (dyne per cm) | Conductivity (μS cm−1) | Average fiber diameter (nm) |
|---|---|---|---|---|---|
| NFD17 | 17 | 114 ± 0.62 | 46.0 ± 0.49 | 30 ± 0.78 | 65 ± 14 |
| NFD20 | 20 | 360 ± 1.87 | 47.9 ± 0.15 | 27 ± 0.67 | 98 ± 14 |
| NFD23 | 23 | 788 ± 3.27 | 49.5 ± 0.06 | 23 ± 0.72 | 195 ± 53 |
| NFD26 | 26 | 1147 ± 1.10 | 50.9 ± 0.67 | 21 ± 0.61 | 357 ± 76 |
| NFD29 | 29 | 1502 ± 3.52 | 52.9 ± 0.15 | 18 ± 0.41 | 663 ± 156 |
Table 1 also depicts the effects of the physical properties of the solution on the fabricated average fiber diameter. Higher solution viscosity caused higher intermolecular bonds among the polymer chains, which prevented the jet stretching and elongation process during the electrospinning that led to larger fiber formation.41 The solution conductivity affected the charge density in the formed jet, which also directly influenced the elongation process driven by the coulombic force. Accordingly, the solutions having lower conductivity resulted in fibers with larger diameters due to weaker stretching during the jet elongation process. On the other hand, the solution surface tension usually affects the bead formation rather than the fiber size. However, from Fig. 2, all membrane samples have bead-free fibers that indicate insufficient surface tension to form the beads for all solution variations.
Fig. 4(a) shows the fiber diameter dependencies on the solution concentration (data from Table 1). The linear regression, which was applied to the log concentration vs. log fiber diameter graph, gave the slope of 4.46. As a comparison, Mit-uppatham et al. (2004) also reported a relationship between the log concentration vs. the log diameter of nylon 6 fibers with a slope of 2.67,38 which was close to that reported by Mckee et al. (2004) with the slope of 2.6.42 The difference in the slope obtained from the present study as compared to Mit-uppatham's work was due to the difference in the nylon 6 material source. In the present study, nylon 6 pellets were used, which resulted in the solution viscosity ranging from 114–1502 cP for the concentration ranging from 17–29 wt%. Meanwhile, Mit-uppatham used nylon 6 resin, which resulted in a solution with a significantly lower viscosity for a similar concentration (738–3992 cP for the concentration 30–46 wt%). Fig. 4(b) shows the effect of the solution viscosity on the fabricated fiber diameter. The linear regression, applied to the log diameter vs. the log viscosity graph, resulted in the slope of 0.87. The graph was compared to the nylon 6 data reported by Mit-uppatham et al. (2004), which had a linear regression slope of 0.67. The slope difference between the present study and Mit-uppatham's study might be due to the difference in the molecular weight of the nylon 6 polymer used in both studies. The molecular weight relates to the relaxation of the polymer chains, so this parameter significantly affects the fabricated fiber diameter, mainly during the elongation process.40
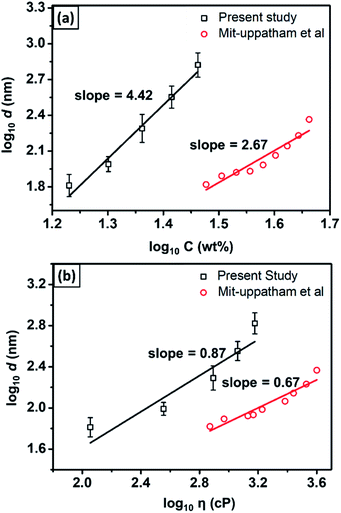 | ||
| Fig. 4 The dependence of the fiber diameter on (a) the solution concentration and (b) solution viscosity. | ||
3.3 FTIR spectra of cellulose membrane and nylon 6 nanofibers
Fig. 5 shows the FTIR spectra of the cellulose membrane, formic acid, nylon 6 pellets, and nylon 6 nanofibers, exhibiting their functional groups. The cellulose membrane spectra showed some characteristic peaks in which the peak at 3334 cm−1 is related to O–H stretching, 2896 cm−1 to C–H symmetrical stretching, 1642 cm−1 to the O–H bending of absorbed water, 1427 cm−1 to HCH and the OCH in-plane bending vibration, 1314 cm−1 to the CH2 rocking vibration at C6, and 1028 cm−1 to the C–C, C–OH, C–H ring and side ground vibration. The cellulose membrane peaks were similar to the peaks of natural fibers and cotton fibers made from natural cellulose.43–45 Nylon 6 in the nanofiber form had similar FTIR spectra to those in the pellet form, indicating that the electrospinning process did not change the functional groups of nylon 6. The most dominant peak at 1637 cm−1 indicated the C–O axial deformation and that at 1541 cm−1 indicated the C–N axial deformation. The peak at 2932 cm−1 represented the CH2α–NH axial deformation and the peak at 3298 cm−1 represented free N–H axial deformation.46,47 The formic acid also had some characteristic peaks but none of them were found in the nylon 6 nanofiber FTIR spectra, indicating complete solvent evaporation during the electrospinning process.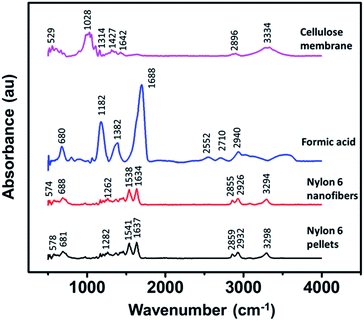 | ||
| Fig. 5 The FTIR spectra of the cellulose membrane, formic acid, nylon 6 pellets, and nylon 6 nanofibers. | ||
3.4 The mechanical properties of the membranes
Fig. 6 shows the mechanical properties of the cellulose membrane without the nylon 6 nanofibrous membrane and cellulose membranes with nylon 6 nanofibrous membranes (NFD20, NFD23, NFD26, and NFD29 samples), measured by the uniaxial tensile test method. The deposition of nylon 6 nanofibrous membrane on the cellulose membrane significantly improved the tensile strength and Young's modulus, which was a great advantage for the application of the membranes as water filter media. The tensile strengths of the cellulose membrane, NFD29, NFD26, NFD23, and NFD20 samples were 4.602, 9.071, 9.678, 9.680, and 9.824 MPa, respectively. The Young's moduli of the cellulose membrane, NFD29, NFD26, NFD23, and NFD20 were 116.63, 697.31, 701.37, 815.63, and 851.56 MPa, respectively. Both the tensile strength and Young's modulus of the NFD membranes increased with the decrease in the fiber diameter. Wong et al. (2008) explained that reducing the fiber diameter improved the molecular orientation that enhanced the membrane mechanical properties.48 Fibers with smaller diameters tend to have a more uniform molecular arrangement in the direction of the fiber axis. Arinstein et al. (2007) explained that the macromolecular orientation in the supramolecular structures of an amorphous phase significantly influences the fibers' mechanical properties.49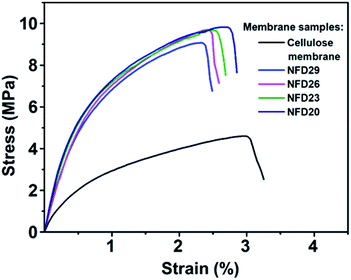 | ||
| Fig. 6 The tensile strength profile of the cellulose membrane, NFD29, NFD26, NFD23, and NFD20 membranes. | ||
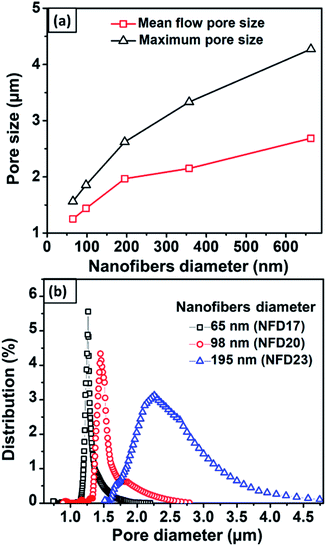
3.5 The pore characterization of the membranes
Fig. 7(a) shows the mean flow and maximum pore size against the nanofiber diameter obtained from the NFD membranes. Nanofibers with larger diameters increased the membrane mean flow and maximum pore size. Membranes with nanofiber diameter of 65–663 nm resulted in the mean flow pore size of 1.2–2.8 μm and the maximum pore size of 1.5–4.5 μm. Hussain et al. (2010) reported the relation of mean flow and maximum pore size to the nanofiber diameter.50 They found that the mean flow pore size was 5 times larger than the diameter of the nanofiber, while the maximum pore size was up to 9 times larger. Ma et al. (2011) also investigated the relationship between the pore size and fiber diameter using PAN and PES nanofibrous membranes at a thickness of about 50 μm.51 They concluded that the mean flow pore size was 3 ± 1 times larger than the nanofiber diameter, while the maximum pore size was 10 ± 1 times larger than the nanofiber diameter. In the present study, the mean flow and maximum pore size had different ratios to the nanofiber diameter, which were 10 times and 14 times larger than the nanofiber diameter. This difference might be caused by the different membrane thicknesses used in this study. The membrane thickness has a considerable influence on the pore properties in which thinner membranes tend to have pores with a larger mean flow and maximum pore to diameter ratio.Fig. 7(b) shows the pore size distribution of the NFD membranes. The figure clearly shows the significant effect of the nanofiber diameter to the pore size distribution in which membranes with larger fibers have larger modes with broader distributions. Wang et al. (2012) explained that the relationship of fiber diameter to pore size is determined by the density of the fiber crossings.2 By using planar approximation limits, fibers with smaller diameters cause closer average distances between fiber crossings, leading to a higher fiber crossing density. The higher fiber crossing density forms a smaller and more uniform pore. Li et al. (2006) reported that the pore size, as well as its size distribution, were strongly associated with the fiber diameter, length, and mass.34
Fig. 8 shows the effects of membrane thickness on the mean flow pore size, maximum pore size, and pore size distribution. Thicker nylon 6 nanofibrous membranes resulted in smaller mean flow and maximum pore size, similar to the polyvinyl alcohol nanofibrous membrane made by Liu et al. (2013).10 During the electrospinning process, the accumulated fibers on the substrate developed crossings and fragmented the pore, which led to smaller pore formation. Wang et al. (2012) reported that thicker membranes had smaller pores.2 However, the pore size reached a plateau value at high thickness due to the projection of fiber crossings, which limited the pore size to a finite range of the electrospun membrane thickness.
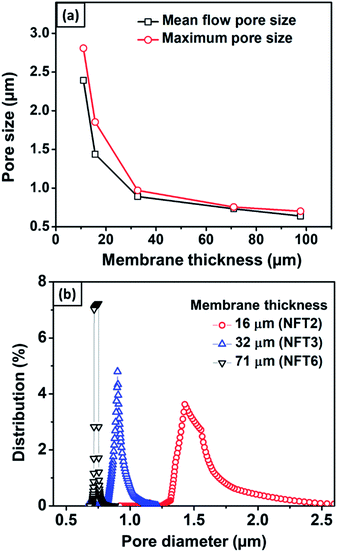 | ||
| Fig. 8 (a) The effect of membrane thickness on mean flow and maximum pore size, and (b) the pore size distribution for membranes with different thicknesses. | ||
3.6 The influence of the cellulose membrane on the bilayer membrane wettability and flux
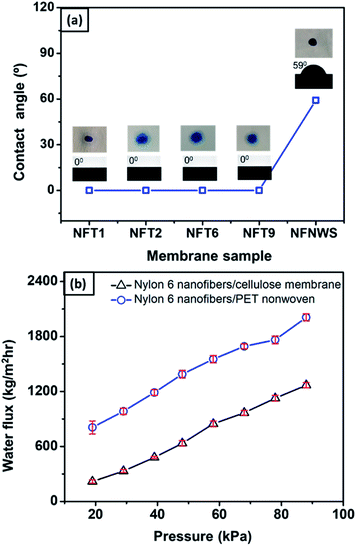
To investigate the effect of the cellulose membrane on the wettability of the bilayer structure, the nylon 6 nanofibrous membrane was also deposited on a nonwoven PET membrane as a comparison. Fig. 9(a) shows the water contact angle (WCA) of nylon 6 nanofibrous membranes deposited on the cellulose membrane (NFT1, NFT2, NFT6, and NFT9 sample) and nonwoven PET membrane (NFNWS sample). The thickness of the nylon 6 nanofibrous membrane on the cellulose membranes was varied, i.e., 11, 32, 71, and 97 μm for NFT1, NFT2, NFT6, and NFT9, respectively. The thickness of the nylon 6 nanofibrous membrane on the nonwoven PET membrane, or NFNWS sample, was 46 μm. All NFT and NFNWS samples had the same fiber diameter of 98 ± 14 nm.The membrane surface wettability can be determined from the WCA value as follows: WCA = 0° indicates superhydrophilic; WCA = 0–90° indicates hydrophilic; WCA = 90–120° indicates hydrophobic; WCA = 120–150° indicates ultra-hydrophobic; WCA > 150° indicates superhydrophobic.52–55 Nylon 6 nanofibrous membranes generally had hydrophilic to hydrophobic surfaces with the WCA ranging from 42–132°.56–58 Based on Fig. 9(a), the nylon 6 nanofibrous membrane deposited on nonwoven PET (NFNWS) had a WCA of about 59°, which was categorized as hydrophilic. However, when nylon 6 nanofibrous membranes were deposited on the cellulose membrane, it exhibited a significantly different WCA, which was about 0° or categorized as superhydrophilic. This result indicated that the cellulose membrane could significantly improve the wettability of the nylon 6 nanofibrous membrane toward being superhydrophilic. Good hydrophilicity is essential for the membrane application as a water filter to guarantee higher flux during the filtration process.
Fig. 9(b) shows the comparison of flux from the NFC (nylon 6 nanofibers/cellulose membrane) and NFNWS (nylon 6 nanofibers/PET nonwoven) samples. The nanofibrous membrane deposited on both the cellulose and PET nonwoven substrates had a similar fiber diameter of 98 ± 14 nm and the same membrane thickness of 46 μm. Nylon 6 nanofibers deposited on the cellulose membrane had a higher flux than those deposited on the PET nonwoven substrate. These results confirmed that the cellulose membrane could significantly improve the hydrophilicity of the bilayer membrane, which then increased the membrane flux. Li et al. (2013) reported the effect of membrane hydrophilicity on the flux using nanofibrous membranes made from PET and PET/PVA composite. The PET/PVA membrane showed a higher flux because it was more hydrophilic than the PET membrane.59
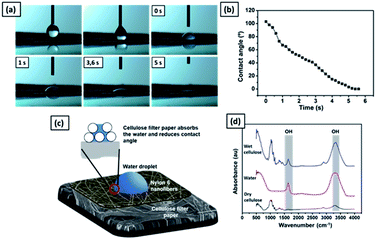
Fig. 10(a) shows the time sequence images of a water droplet on the nylon 6 nanofibers/cellulose membrane. The WCA value decreased from 105° to 0° in five seconds, as shown in Fig. 10(b). The high hydrophilicity of the cellulose membrane provided immediate absorption of the water droplet on the nylon 6 nanofibrous membrane, as illustrated in Fig. 10(c). The nylon 6 nanofiber membrane was relatively thin so the water droplets could enter its pores and touch the cellulose membrane underneath. When the water droplet was in contact with the cellulose membrane surface, due to the membrane hydrophilicity, the water droplet was absorbed immediately by the cellulose membrane, which then decreased the WCA.
Fig. 10(d) shows the FTIR spectra of dry and wet cellulose membranes. The peak at 1650 cm−1 represents the H–O–H angle vibration. The peak at 3340 cm−1 is associated with the OH stretching. The cellulose polymer contains large numbers of hydroxyl functional groups that give it a strong affinity for and make it reactive with materials containing hydroxyl groups, such as water. The reaction of water molecules with cellulose chains form hydrogen bonds.
3.7 Microfiltration performance of nylon 6 nanofibers/cellulose membranes
Fig. 11(a) shows the pure water flux vs. differential pressure of nylon 6 nanofibrous membranes having various fiber diameters (NFD samples). The cellulose membrane had a very high flux (not shown in the figure) as compared to the nanofibrous membrane flux. All tested membrane samples showed a linear increase in flux with a given differential pressure, which was in accordance with eqn (2).60 From Fig. 11(a), the increasing nanofiber diameter resulted in a higher membrane flux, which has also been reported by Sawitri et al.29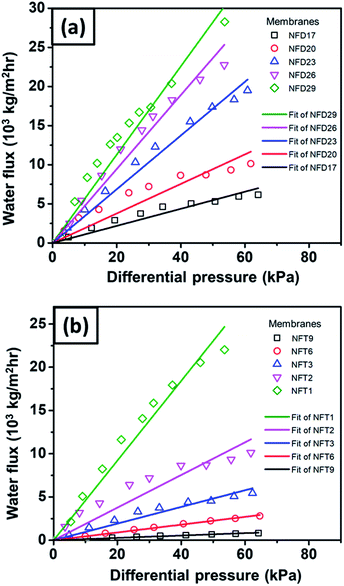 | ||
| Fig. 11 The water flux vs. differential pressure for nylon 6 nanofibers/cellulose membranes with the variation of (a) nanofiber diameter and (b) nanofibrous membrane thickness. | ||
Fig. 11(b) shows the water flux vs. differential pressure for the membrane samples with various nanofibrous membrane thicknesses (NFT samples). The experimental results show an inverse relation of the flux to membrane thickness, which is in accordance with Darcy's law in eqn (2). Liu et al. (2013) also reported similar trends of flux vs. membrane thickness for PVA nanofibrous membranes.10
Fig. 12(a) shows the SEM image of the nylon 6 nanofibrous membrane after the filtration of PSL particles of size 451 nm. It is clearly shown that the PSL particles were blocked by the nanofibrous structure. Fig. 12(b) shows the rejection of PSL particles by nylon 6 nanofibers/cellulose membrane with the variation in the nylon 6 nanofiber diameter. The test used PSL particles of 95, 308, and 451 nm in size. The cellulose membrane had a significantly smaller rejection as compared to the nanofibrous membranes, which was close to zero (not shown in the figure). This indicated that the cellulose membrane in the bilayer structure did not have a significant impact on the particle capturing performance of the filter. The particle capture was mainly done by the nanofibrous membrane in the bilayer structure. From Fig. 12(b), the rejection generally increases for PSL particles with larger size. PSL particles of size 95 nm were the most difficult to filter with the rejection as low as 23.7%. As the particle size increased to 308 nm, the rejection improved significantly to above 99%. The largest test particle, PSL 451 nm, was effectively captured by the bilayer membranes with the highest rejection. This was obvious because the water filtration was greatly affected by the pore structure of the filter membrane in which larger particles were more easily captured.
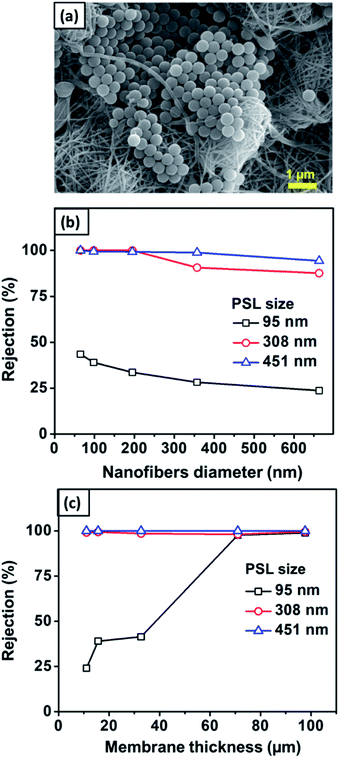 | ||
| Fig. 12 (a) SEM image of the nanofibrous membrane after filtration. (b) The effect of the nanofiber diameter on the rejection value. (c) The effect of nanofiber thickness on rejection. | ||
According to Fig. 12(b), the rejection slightly decreased with the nylon 6 nanofiber diameter. For 95 nm PSL particles, the rejection of membranes with nanofiber diameters of 65, 98, 195, 357, and 663 nm were 43.5, 39.1, 33.6, 28.2, and 23.7%, respectively. This was related to the pore size of the membranes in which larger pores allowed the particles to easily pass through the membranes. As previously discussed, the nanofiber diameter directly affected the pore size distribution in which larger nanofiber diameters formed pores with larger average diameters and broader distributions, which then decreased the membrane rejection. The membrane samples with the nanofiber diameters of 65–663 nm had the mean and maximum pore sizes of 1.2–2.8 μm and 1.4–4.5 μm, respectively. Although the membrane pore size was larger than the tested PSL particles, small PSL particles of 95 nm were still captured by the membranes with the rejection of 23.7–43.5%, as shown in Fig. 12(b). This meant that the particle capturing process was not solely influenced by the pore blocking but could also be influenced by the nanofiber structure and interconnected pores. The interconnected pores allowed the capture of particles, even if the particles were smaller than the pore size. Similar results were also reported by previous studies. Gopal et al. (2006) reported that the nanofibrous membrane with the mean pore size of 2.1 μm had a rejection of 14% for a particle size of 100 nm and 47% for a particle size of 500 nm.8 Gopal et al. (2006) also reported nanofibrous membranes with the pore sizes of 10.6–4.0 μm having the rejection of up to 98% for 1 μm test particles.61
Fig. 12(c) shows the rejection of PSL particles by nylon 6 nanofibers/cellulose membranes with the variation in the nylon 6 nanofibrous membrane thickness. The test used PSL particles with sizes of 95, 308, and 451 nm. The nylon 6 nanofibrous membrane thickness clearly affected the bilayer membrane rejection, especially for smaller particle sizes. All membrane samples showed the rejection of above 98% for PSL size of 308 nm, and above 99% for PSL size of 451 nm. For PSL size of 95 nm, the thinnest membrane samples (11 μm) gave the smallest rejection, as low as 24.3%. When the membrane thickness was increased, the rejection increased significantly, and for the thickness above 71 μm, the rejection for 95 nm PSL particles was close to that of 308 and 451 nm PSL particles.
The higher rejection on thicker membranes was related to the different pore sizes as the thicker membranes had smaller pores with narrower pore size distribution (see Fig. 8), which could improve the membrane rejection. For the membrane thickness ranging from 11–97 μm, the mean and maximum pore sizes were 2.4–0.64 μm and 2.8–0.7 μm, respectively. Since the pore size was larger than the PSL size, the membrane interconnected pore structure might also have a significant influence on the particle capture. As the membrane thickness was increased by extending the electrospinning duration, more fibers accumulated on the substrate to create the crossings that developed smaller and more interconnected pores.16 The interconnected pore structure improved the membrane rejection and also provided the pathway for the water to pass through the membrane.11 Similar results were also reported by Liu et al. (2013), who found that thickening the PVA nanofibrous membranes improved its rejection. The PVA membranes with the thickness of 10 μm had the rejection of 95% for particle size of 200 nm. The rejection improved above 98% when the PVA membrane thickness was increased to 20–100 μm.10
Wang et al. (2012) synthesized PAN nanofibrous membranes on the nonwoven PET substrate (nanofibers diameter of 100 nm and membrane thickness of 200 μm) that showed the rejection of 93%, 97%, and 99% for particle size of 200, 500, and 1000 nm, respectively.35 They also reported the rejections of a commercial membrane (GSWP-Millipore, average pore size of 240 nm and thickness of 180 μm), which were 90% for 200 nm particles and 98% for 500 nm particles. Furthermore, Aussawasathien et al. (2008) reported nylon 6 nanofibrous membranes (nanofiber diameter of 30–110 nm and membrane thickness of 150 μm) deposited on a mesh substrate having the rejection of 84.48% for 500 nm particles and 95.87% for 1 μm particles. The bilayer structure of nylon 6 nanofibers/cellulose membranes in the present study exhibited relatively higher rejection. For the nanofiber diameter of 98 nm and the membrane thickness of 97 μm, the rejections were more than 99% for the particle sizes of 95, 308, and 451 nm. These results indicated the promising application of the nylon 6 nanofibers/cellulose bilayer membranes as water filtration media.
4. Conclusions
A bilayer structure with the nylon 6 nanofibrous membrane and the cellulose membrane has been electrospun for use as water filtration media. The nylon 6 solution concentrations were varied to obtain smooth fibers with various sizes. The increasing solution concentration affected the solution viscosity, conductivity, and surface tension, which then increased the diameter of the fabricated fibers. The spinning time was also adjusted to obtain nanofibrous membranes with various thicknesses. The fiber diameter, as well as membrane thickness, affected the pore size distribution and membrane mechanical strength. A smaller fiber diameter resulted in a smaller mean flow and maximum pore size with higher membrane mechanical strength, and vice versa. The FTIR spectra depicted unchanged nylon 6 functional groups after the electrospinning process. The water contact angle measurement exhibited the significant influence of the cellulose membrane in increasing the hydrophilicity of the bilayer structure. The flux comparison of nanofibers/cellulose membrane with nanofibrous/PET nonwoven membrane proved the significant influence of the cellulose membrane in improving the flux of the bilayer structure. On the other hand, the rejection test using PSL particles sized 308 and 450 nm showed the high rejection of the bilayer structure, ranging from 87.6–99.9% for all samples. The high rejection was dominantly caused by the effective particle capture by the nylon 6 nanofibrous membrane in the bilayer structure. Overall, the bilayer structure of the nylon 6 nanofibers/cellulose membranes showed promising flux and rejection performance as water filter media.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was finally supported by Directorate of Research and Community Engagement of Ministry of Research, Technology and Higher Education, the Republic of Indonesia under the University's Excellent Research (PUPT) Grant in the fiscal year 2017–2019 and the Dissertation Research 2019–2020.Notes and references
- B. der Bruggen, C. Vandecasteele, T. Van Gestel, W. Doyen and R. Leysen, Environ. Prog. Sustainable Energy, 2003, 22, 46–56 Search PubMed
.
- R. Wang, Y. Liu, B. Li, B. S. Hsiao and B. Chu, J. Membr. Sci., 2012, 392–393, 167–174 CrossRef CAS
.
- D. Aussawasathien, C. Teerawattananon and A. Vongachariya, J. Membr. Sci., 2008, 315, 11–19 CrossRef CAS
.
- N. Daels, S. De Vrieze, I. Sampers, B. Decostere, P. Westbroek, A. Dumoulin, P. Dejans, K. De Clerck and S. W. H. Van Hulle, Desalination, 2011, 275, 285–290 CrossRef CAS
.
- F. E. Ahmed, B. S. Lalia and R. Hashaikeh, Desalination, 2015, 356, 15–30 CrossRef CAS
.
- R. S. Barhate and S. Ramakrishna, J. Membr. Sci., 2007, 296, 1–8 CrossRef CAS
.
- B. Chu and B. S. Hsiao, J. Polym. Sci., Part B: Polym. Phys., 2009, 47, 2431–2435 CrossRef CAS
.
- R. Gopal, S. Kaur, C. Y. Feng, C. Chan, S. Ramakrishna, S. Tabe and T. Matsuura, J. Membr. Sci., 2007, 289, 210–219 CrossRef CAS
.
- S. Kaur, Z. Ma, R. Gopal, G. Singh, S. Ramakrishna and T. Matsuura, Langmuir, 2007, 23, 13085–13092 CrossRef CAS PubMed
.
- Y. Liu, R. Wang, H. Ma, B. S. Hsiao and B. Chu, Polymer, 2013, 54, 548–556 CrossRef CAS
.
- K. Yoon, B. S. Hsiao and B. Chu, J. Membr. Sci., 2009, 338, 145–152 CrossRef CAS
.
- K. Yoon, B. S. Hsiao and B. Chu, J. Membr. Sci., 2009, 326, 484–492 CrossRef CAS
.
- J. Yu, Y.-G. Kim, D. Y. Kim, S. Lee, H.-I. Joh and S. M. Jo, Macromol. Res., 2015, 23, 601–606 CrossRef CAS
.
- R. Wang, S. Guan, A. Sato, X. Wang, Z. Wang, R. Yang, B. S. Hsiao and B. Chu, J. Membr. Sci., 2013, 446, 376–382 CrossRef CAS
.
- Z. Wang, H. Ma, B. S. Hsiao and B. Chu, Polymer, 2014, 55, 366–372 CrossRef CAS
.
- K. Yoon, K. Kim, X. Wang, D. Fang, B. S. Hsiao and B. Chu, Polymer, 2006, 47, 2434–2441 CrossRef CAS
.
- R. Gopal, S. Kaur, Z. Ma, C. Chan, S. Ramakrishna and T. Matsuura, J. Membr. Sci., 2006, 281, 581–586 CrossRef CAS
.
- X. Wang and B. S. Hsiao, Curr. Opin. Chem. Eng., 2016, 12, 62–81 CrossRef
.
- S. V Fridrikh, H. Y. Jian, M. P. Brenner and G. C. Rutledge, Phys. Rev. Lett., 2003, 90, 144502 CrossRef PubMed
.
- S. A. Theron, E. Zussman and A. L. Yarin, Polymer, 2004, 45, 2017–2030 CrossRef CAS
.
- M. M. Munir, A. B. Suryamas, F. Iskandar and K. Okuyama, Polymer, 2009, 50, 4935–4943 CrossRef CAS
.
- Z. Tang, C. Qiu, J. R. McCutcheon, K. Yoon, H. Ma, D. Fang, E. Lee, C. Kopp, B. S. Hsiao and B. Chu, J. Polym. Sci., Part B: Polym. Phys., 2009, 47, 2288–2300 CrossRef CAS
.
- S. S. Homaeigohar, K. Buhr and K. Ebert, J. Membr. Sci., 2010, 365, 68–77 CrossRef CAS
.
- S. Kiani, S. M. Mousavi, N. Shahtahmassebi and E. Saljoughi, Appl. Surf. Sci., 2015, 359, 252–258 CrossRef CAS
.
- S. M. Praveena, L. S. Han, L. T. L. Than and A. Z. Aris, J. Exp. Nanosci., 2016, 11, 1307–1319 CrossRef CAS
.
- Z. Weng, Y. Su, D.-W. Wang, F. Li, J. Du and H.-M. Cheng, Adv. Energy Mater., 2011, 1, 917–922 CrossRef CAS
.
- M. d'Halluin, J. Rull-Barrull, G. Bretel, C. Labrugère, E. Le Grognec and F.-X. Felpin, ACS Sustainable Chem. Eng., 2017, 5, 1965–1973 CrossRef
.
- S. M. Praveena and A. Z. Aris, Water Qual., Exposure Health, 2015, 7, 617–625 CrossRef CAS
.
- A. Sawitri, M. M. Munir, D. Edikresnha, A. Sandi, A. Fauzi, A. Rajak, D. Natalia and R. Khairurrijal, Mater. Res. Express, 2018, 5, 5 Search PubMed
.
- Y. J. Ryu, H. Y. Kim, K. H. Lee, H. C. Park and D. R. Lee, Eur. Polym. J., 2003, 39, 1883–1889 CrossRef CAS
.
- A. B. D. Nandiyanto, A. Suhendi, T. Ogi, T. Iwaki and K. Okuyama, Colloids Surf., A, 2012, 396, 96–105 CrossRef CAS
.
- A. Zulfi, D. A. Hapidin, M. M. Munir, F. Iskandar and K. Khairurrijal, RSC Adv., 2019, 9, 30741–30751 RSC
.
- A. Rajak, D. A. Hapidin, F. Iskandar, M. M. Munir and K. Khairurrijal, Nanotechnology, 2019, 30, 425602 CrossRef PubMed
.
- D. Li, M. W. Frey and Y. L. Joo, J. Membr. Sci., 2006, 286, 104–114 CrossRef CAS
.
- R. Wang, Y. Liu, B. Li, B. S. Hsiao and B. Chu, J. Membr. Sci., 2012, 392, 167–174 CrossRef
.
- C. Huang, S. Chen, C. Lai, D. H. Reneker, H. Qiu, Y. Ye and H. Hou, Nanotechnology, 2006, 17, 1558 CrossRef CAS PubMed
.
- J. Zeng, H. Haoqing, A. Schaper, J. H. Wendorff and A. Greiner, e-Polym., 2003, 3, 102–110 Search PubMed
.
- C. Mit-uppatham, M. Nithitanakul and P. Supaphol, Macromol. Chem. Phys., 2004, 205, 2327–2338 CrossRef CAS
.
- P. Supaphol, C. Mit-uppatham and M. Nithitanakul, Macromol. Mater. Eng., 2005, 290, 933–942 CrossRef CAS
.
- S. S. Ojha, M. Afshari, R. Kotek and R. E. Gorga, J. Appl. Polym. Sci., 2008, 108, 308–319 CrossRef CAS
.
- S. Ramakrishna, K. Fujihara, W.-E. Teo, T.-C. Lim and Z. Ma, An Introduction to Electrospinning and Nanofibers, World Scientific, 2005 Search PubMed
.
- M. G. McKee, G. L. Wilkes, R. H. Colby and T. E. Long, Macromolecules, 2004, 37, 1760–1767 CrossRef CAS
.
- D. Dai and M. Fan, Vib. Spectrosc., 2011, 55, 300–306 CrossRef CAS
.
- S. Y. Oh, D. Il Yoo, Y. Shin and G. Seo, Carbohydr. Res., 2005, 340, 417–428 CrossRef CAS PubMed
.
- D. Gaspar, S. N. Fernandes, A. G. De Oliveira, J. G. Fernandes, P. Grey, R. V Pontes, L. Pereira, R. Martins, M. H. Godinho and E. Fortunato, Nanotechnology, 2014, 25, 94008 CrossRef CAS PubMed
.
- A. Abbasi, M. M. Nasef, M. Takeshi and R. Faridi-Majidi, Chin. J. Polym. Sci., 2014, 32, 793–804 CrossRef CAS
.
- L. M. Guerrini, M. C. Branciforti, T. Canova and R. E. S. Bretas, Mater. Res., 2009, 12, 181–190 CrossRef CAS
.
- S.-C. Wong, A. Baji and S. Leng, Polymer, 2008, 49, 4713–4722 CrossRef CAS
.
- A. Arinstein, M. Burman, O. Gendelman and E. Zussman, Nat. Nanotechnol., 2007, 2, 59 CrossRef CAS PubMed
.
- D. Hussain, F. Loyal, A. Greiner and J. H. Wendorff, Polymer, 2010, 51, 3989–3997 CrossRef CAS
.
- H. Ma, C. Burger, B. S. Hsiao and B. Chu, J. Mater. Chem., 2011, 21, 7507–7510 RSC
.
- A. Rajak, D. A. Hapidin, F. Iskandar, M. M. Munir and K. Khairurrijal, Waste Manag., 2020, 103, 76–86 CrossRef CAS PubMed
.
- J. Drelich, E. Chibowski, D. D. Meng and K. Terpilowski, Soft Matter, 2011, 7, 9804–9828 RSC
.
- L. Zhang, N. Zhao and J. Xu, J. Adhes. Sci. Technol., 2014, 28, 769–790 CrossRef CAS
.
- T. A. Otitoju, A. L. Ahmad and B. S. Ooi, J. Ind. Eng. Chem., 2017, 47, 19–40 CrossRef CAS
.
- N. D. N. Affandi, Y. B. Truong, I. L. Kyratzis, R. Padhye and L. Arnold, in 2010 International Conference on Science and Social Research, CSSR 2010, 2010, pp. 789–794 Search PubMed
.
- A. Abdal-Hay, H. R. Pant and J. K. Lim, Eur. Polym. J., 2013, 49, 1314–1321 CrossRef CAS
.
- A. R. Jabur, L. K. Abbas and S. A. Moosa, Adv. Mater. Sci. Eng., 2016, 2016, 5810216 Search PubMed
.
- G. Li, Y. Zhao, M. Lv, Y. Shi and D. Cao, Colloids Surf., A, 2013, 436, 417–424 CrossRef CAS
.
- L. T. S. Choong, Z. Khan and G. C. Rutledge, J. Membr. Sci., 2014, 451, 111–116 CrossRef CAS
.
- R. Gopal, S. Kaur, Z. Ma, C. Chan, S. Ramakrishna and T. Matsuura, J. Membr. Sci., 2006, 281, 581–586 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2020 |