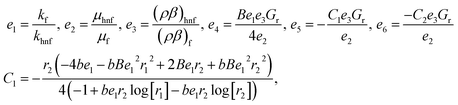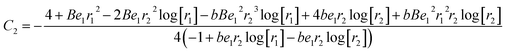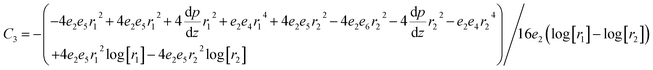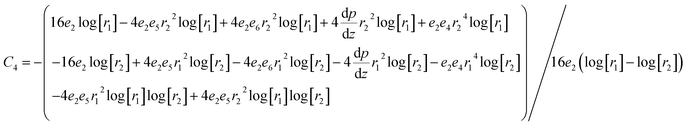DOI:
10.1039/D0RA01134G
(Paper)
RSC Adv., 2020,
10, 15035-15043
Adverse effects of a hybrid nanofluid in a wavy non-uniform annulus with convective boundary conditions
Received
5th February 2020
, Accepted 28th March 2020
First published on 17th April 2020
Abstract
The presented investigation theoretically studies the physical characteristics of a two-dimensional incompressible hybrid nanofluid in a non-uniform annulus where the boundaries are flexible. A mixed convective peristaltic mechanism is implemented to model blood-based nanofluids using two different nanoparticles (Ag + Al2O3). Convective boundary conditions are employed and different forms of nanoparticles are discussed (bricks, cylinders and platelets). The problem is shortened by engaging a lubrication method. Exact expressions for the temperature of cumulative heat source/sink standards, hemodynamic velocity, pressure gradient and streamlines of different shapes of nanoparticles are obtained. Special cases of pure blood and the Al2O3 nanofluid of our model are derived. A comparison is set between nanofluids and hybrid nanofluids from which we observed variations in heat transfer rate in different regions due to the oscillatory nature of the waves. The current model has the potential to be useful for applications related to the metabolic structures that play a vital role in heat sources inside the human body.
Introduction
The strengthening of heat energy plays a vital role in nanotechnology these days since it results in several savings in the energy and cost of treatments of various diseases.1 The structured size of nanoparticles is 100 nanometers, and this allows more diffusion into the cells to help diagnose and/or treat tumors. Nanofluids have contributed to heat transfer mechanisms in several ducts, giving rise to more applications that involve the suspension of metallic and non-metallic particles. Nanoparticle and convective boundary conditions are now a strong area of investigation for scientists and engineers owing to a wide variety of potential practices in electronic, biomedical and optical fields. Imtiaz et al.2 studied the convective mass and heat transfer through a mixed convection boundary layer flow with nanoparticles. They concluded that the flow of fluid is reduced for larger values of Hartman number. Sayed et al.3 inspected the peristaltic mechanism of a non-Newtonian nanofluid with convective boundary conditions through an inclined channel for two different nanofluids. They observed that copper and aluminum oxide nanoparticles affect the axial velocity field and heat transfer coefficients significantly. The mixed convection peristaltic motion of various types of incompressible water-based nanofluids was considered by Hayat et al.,4 where they took into consideration Hall and Joule heating effects. They concluded that the volume fraction of nanoparticles is improved by increasing the heat transfer rate.
Although different types of nanofluids showed some satisfactory results as drug carriers, scientists started to consider the suspension of various combinations of nanoparticles with physiological base fluids. And those combinations of nanofluids, namely hybrid nanofluids, exist when two or more materials are combined so that they are joined in the form of a new chemical bond. This progressive class of nanofluids displayed a greater improvement in heat transfer properties when compared to those of single nanofluids. Das et al.5 studied the nanofluid flow of Al2O3/water and Cu–Al2O3/water hybrid nanofluids in the presence of a magnetic field in the transverse direction through a porous channel where they set a comparison of the heat enhancement level due to the suspension of aluminum and copper nanoparticles in water-based nanofluids as both a unitary and a hybrid nanofluid. Xie et al.6 examined the tribological characteristics of the SiO2/MoS2 hybrid nanoparticles by studying the friction coefficient and wear volume. They concluded that the hybrid nanofluids attain a lower wear volume and friction coefficient when compared to those of pure nanofluids. The MHD hybrid nanofluids of copper and aluminum with water were analyzed by Devi and Devi7 over a permeable stretching sheet with heat transfer. They observed an enhancement in the heat transfer rate for the hybrid nanofluid over that of the pure nanofluid under the consequence of the magnetic field. The hemodynamics of the hybrid nanofluid through a stenotic artery with a tapering effect was investigated by Ijaz et al.8 They performed a comparative study for both nanofluids and hybrid nanofluids from which they deduced that the trajectory of temperature is maximum for the copper/blood case when associated to the copper-oxide/blood case for the platelet-shaped nanoparticles.
Various types of annular pathways have become important geometries for fluid transfer devices since they have numerous applications in engineering.9–11 Also, fluid flows with heat transfer taking place in gaps, such as between two concentric cylinders (annuli), for pure and hybrid nanofluids have become technically more important. Therefore, significant work has been done for circular annuli using nanofluids. Tayebi and Chamkha12 studied numerically the natural convection of a water-based Cu–Al2O3 hybrid nanofluid through two confocal elliptic cylinders. They concluded that the impact of hybrid nanoparticles is more noticeable for high values of solid volume fractions. The natural convection of hybrid nanofluids through an eccentric annulus between horizontal cylinders was also studied by Tayebi and Chamkha,13 where they deduced that the hybrid nanofluid provides a better thermal and dynamic performance when compared to the pure nanofluid. Abdellateef and Ul Haque14 investigated the peristalsis of nanofluids through an inclined annulus taking the Brownian motion and thermophoretic diffusion of nanoparticles into consideration. They concluded that an upturn in the Brownian motion results in an enhancement in the temperature and nanoparticle concentration.
In peristalsis, the waves propagate along the length of a distensible annulus conduit where the nanoparticles with the base fluid exist in the gap between the cylindrical tubes and are transported in the same direction as that of the wave propagation. The peristaltic mechanism is utilized by many organs, such as the esophagus, male and female reproductive systems, urethra and many other glandular ducts. Abdelsalam and Bhatti15 studied the peristaltic transport of non-Newtonian nanofluids with ion slip and chemical reaction under the effect of Hall currents. They concluded that the chemical reaction has a dual reaction on the concentration profile. Abdelsalam and Bhatti16 investigated the hemodynamics of peristaltic blood flow with titanium nanoparticles and a magnetic field through an annulus where they observed that the maximum velocity profile takes place near the center of the annulus. Abdelsalam and Vafai17 investigated the pulsating blood flow model with suspended particles having a peristaltic mechanism in a small artery and they concluded that the width of the enclosing streamlines of plasma is improved for the hemo concentration case. For more applications of the peristaltic mechanism through fluids, the reader is referred to ref. 18–22 and to the references therein.
Inspired by the above-mentioned debate, our objective is to study the peristaltic motion of two-dimensional incompressible hybrid nanofluids in a non-uniform annulus taking blood as a base nanofluid with Al2O3and Ag as the nanoparticles. Closed-form solutions are derived and the results are presented graphically.
Model of the problem
We made up a peristaltic stream happening for a two-dimensional incompressible viscous fluid in an annulus for the occurrence of hybrid nanoparticles (see Fig. 1). Convective boundary properties and different nano-shaped effects are, moreover, included. Besides, the equations for mass conservation, momentum and energy equations with hybrid nanoparticles are distinct as| |
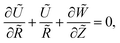 | (1) |
| |
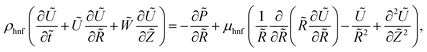 | (2) |
| |
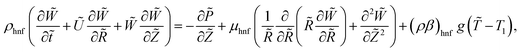 | (3) |
| |
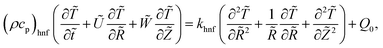 | (4) |
where 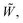
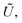
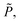 Q0, ρhnf, (ρcp)hnf, and κhnf signify the velocity mechanisms in the axial and radial track, pressure, constant of heat absorption parameter, hybrid nanofluid density, heat capacity of the hybrid nanofluid, viscosity of the hybrid nanofluid and thermal conductivity of the hybrid nanofluid demarcated as follows (8)
Q0, ρhnf, (ρcp)hnf, and κhnf signify the velocity mechanisms in the axial and radial track, pressure, constant of heat absorption parameter, hybrid nanofluid density, heat capacity of the hybrid nanofluid, viscosity of the hybrid nanofluid and thermal conductivity of the hybrid nanofluid demarcated as follows (8)| |
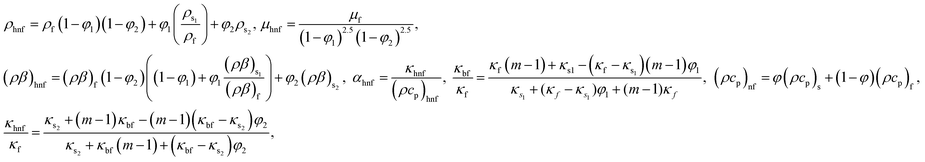 | (5) |
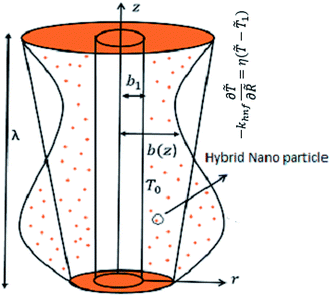 |
| | Fig. 1 Configuration of the model. | |
The particular boundary settings are varied as
| |
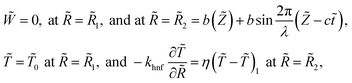 | (6) |
We introduced the following transformations in order to convert the time dependent system to a time independent system,
| |
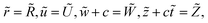 | (7) |
and introduced the subsequent dimensionless variables
| |
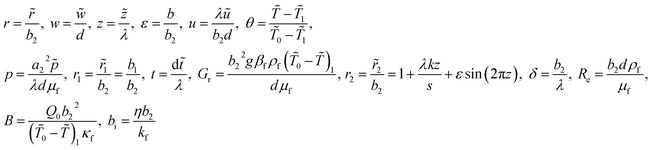 | (8) |
where
r1,
r2,
Gr,
B,
μf, and
bi signify for, radius of interior tube, radius of the exterior tube, Grashof number, heat absorption, viscosity of the fluid, wave speed and Biot number correspondingly. Plugging
eqn (7) and
(8) into the
eqn (1),
(2),
(3),
(4),
(5),
(6), covering the concords of the slight Reynolds number and a massive wavelength approximation, dropping the expressions comprising
δ,
Re and greater, we reached the subsequent equations
| |
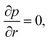 | (9) |
| |
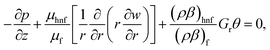 | (10) |
| |
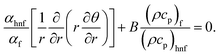 | (11) |
Eqn (9) states that p is free of r and the dimensionless boundary locates can be decorated as
| |
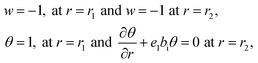 | (12) |
Exact solution and flow analysis
The exact solution of eqn (10) and (11) along with boundary conditions (12) is onward inscribed as| |
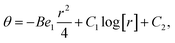 | (13) |
| |
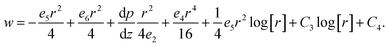 | (14) |
The expressions for the instantaneous volume flow rate F in the stationary coordinate scheme, the mean flow rate Q, pressure rise ΔP, stream function relations and heat transfer are correspondingly determined by the following expressions.
| |
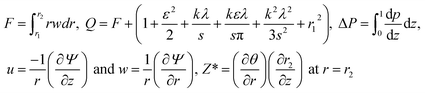 | (15) |
whereas constants are given in the appendix (
Tables 1 and
2).
Table 1 Thermo-physical properties of the fluid and nanoparticles
| Physical property |
Blood |
Solid nanoparticles |
| Ag |
Al2O3 |
| ρ (kg m−3) |
1063 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
3970 |
| κ (W mK−1) |
0.492 |
429 |
40 |
| β × 10−5 (K−1) |
0.18 |
18.9 |
8.9 |
Table 2 Shape effects of the nanoparticles
| Nanoparticles shape |
Shape factor |
| Bricks |
 |
3.7 |
| Cylinders |
 |
4.9 |
| Platelets |
 |
5.7 |
Discussion
In this section, we will offer a careful study of many significant flow bulks like the temperature curve, pressure rise, pressure gradient and streamlines by scheming graphs for diverse values of the nanoparticle shape restriction (e.g. bricks, cylinders, and platelets). Fig. 2a is dedicated to the study of the temperature sketch for cumulative standards of heat source or sink parameters. It is depicted in this figure that, by the swelling standards of the heat source parameter, the temperature profile upsurges for all the considered nanoparticle shapes. This is due to the fact that the metabolic structure plays a vital role for the heat source in the human body; additionally, the temperature curve for the platelet shape gets larger as it associates to the brick shape nanoparticle. Fig. 2b is premeditated to perceive the behavior of the temperature shape for cumulative standards of the Biot number. The temperature curve decreases when the heat transfer Biot number bi upsurges. The attained result shows that the thermal conductivity of the fluid decreases with an upsurge in bi and so a decline is observed. Here we see that the temperature curve for the platelet shape is less than that for the brick and cylinder type nanoparticles. Fig. 3a is prepared to exhibit the outcome of the Biot number on the velocity outlines. It is perceived that increasing the Biot number increases the velocity profile close to the endoscopic tube. This is due to the fact that with high convective heat transmissions to the colder fluid, the velocity shape upturns close to the endoscopic tube, but far away from the tube, the velocity profile decreases near the non-uniform peristaltic wall. Moreover, the velocity shape for the brick shape has the maximum curve as compared that of the platelet shape. The velocity shapes for diverse standards of Grashof number are revealed in Fig. 3b. It depicts that with increasing standards of the Grashof number, the velocity shape near the endoscopic tube rises; this relates to the fact that buoyancy forces play a leading role close to the endoscopic tube, while the contrary behavior is observed close to the non-uniform tube for all the considered nanoparticle shapes. The pressure rise per wavelength for diverse values of Biot and Grashof numbers is depicted in Fig. 4a and b. One can observe in Fig. 4a that with increasing values of the Biot number, the pressure rise declines due to the prominent impact of resistance to external heat flow. Fig. 4b explains that, by increasing the values of the Grashof number, the pressure rise upsurges throughout domain. This is due to the fact that buoyancy forces play a leading role, which results in upturns in the pressure rise. The influences of bi and Gr on the pressure gradient are designated in Fig. 5(a) and (b). The pressure gradient defines which track and what rate the pressure fluctuates most swiftly. It is clear that in the broader share of the tube, the pressure gradient has larger curves in the sections 0.25 ≤ z ≤ 0.75, 1.25 ≤ z ≤ 1.75, 2.25 ≤ z ≤ 3 for increasing values of the Biot number and Grashof number for all the measured nanoparticle shapes. This clearly gives a picture that the pressure gradient decreases with the Biot number due to the dominant of resistance to the external flow, while the pressure gradient increases for the Grashof number because of the dominant impact of buoyancy forces. The trapping phenomenon of the Grashof number for different nanoparticle shapes is presented in Fig. 6–8. It is witnessed in Fig. 6a that for the brick shape nanoparticle, the trapping bolus is seen near the endoscopic tube as well as near the non-uniform tube, but when we upturn the values of the Grashof number the boluses near the endoscopic tube enhance, whereas boluses near the non-uniform tube disappear. This pattern is quite similar for the cylinder and platelet shape nanoparticles (see Fig. 7 and 8). The trapping phenomenon for increasing values of the Biot number is designated in Fig. 9–11. It is depicted for the brick shape nanoparticle that trapping boluses are seen near the non-uniform peristaltic wall, but disappear when we increase the values of the Biot number. The same pattern is observed for the cylinder and platelet shape nanoparticles (see Fig. 10 and 11). Table 3 is plotted to see the performance of the heat transfer rate for the hybrid nanoparticle and the Al2O3 nanoparticle for different nanoparticle shape parameters. It is depicted in this table that for the hybrid nanoparticle, the heat transfer rate increases the maximum in the sections 0.3 ≤ z ≤ 0.7 and 1.3 ≤ z ≤ 1.7, as compare to Al2O3 for all three shapes of the nanoparticles, whereas in other regions it has opposite behavior due to the oscillating nature of the wave. Table 4 is designed to grasp the special cases for the velocity profile. It is depicted in this table that in the region near to the endoscopic wall 0.02 ≤ r ≤ 0.42, velocity profile for the hybrid nanofluid increases and the pure blood curve decreases, but owing to the parabolic nature of the tube, the velocity profile has a contradictory behavior in the rest of the section.
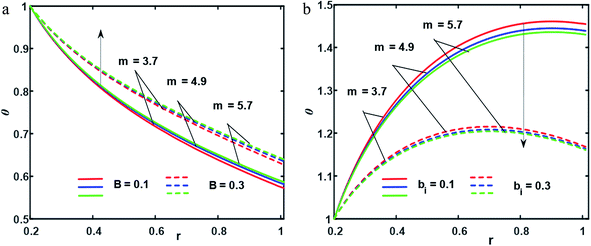 |
| | Fig. 2 (a and b) Temperature profiles ((a) for bi = 0.6, (b) for B = 1.3); ε = 0.14, λ = 0.24, k = 0.24, s = 0.6, r1 = 0.2, φ1 = 0.2, φ2 = 0.05. | |
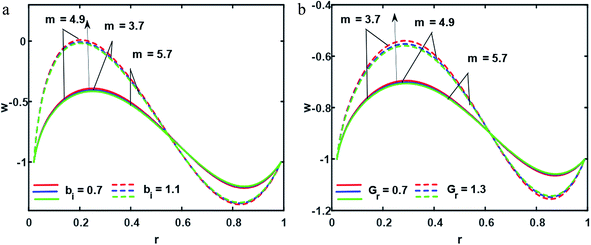 |
| | Fig. 3 (a and b) Velocity profiles ((a) for Gr = 1.6, (b) for bi = 0.7); other fixed parameters are ε = 0.04, z = 0.57, r1 = 0.02, B = 1.4, λ = 0.04, k = 0.24, s = 0.8, q = 0.56, φ1 = 0.2, φ2 = 0.05. | |
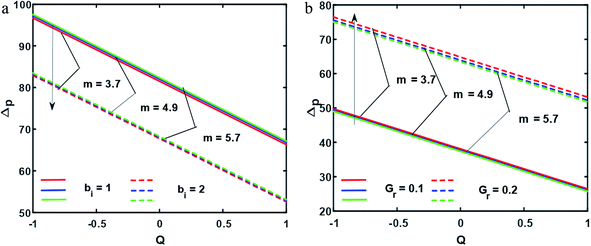 |
| | Fig. 4 (a and b), Pressure rise ((a) for Gr = 0.6, (b) for bi = 3); other fixed parameters are ε = 0.11, r = 0.32, r1 = 0.02, B = 3.2, λ = 0.36, k = 0.44, s = 0.24, φ1 = 0.2, φ2 = 0.05. | |
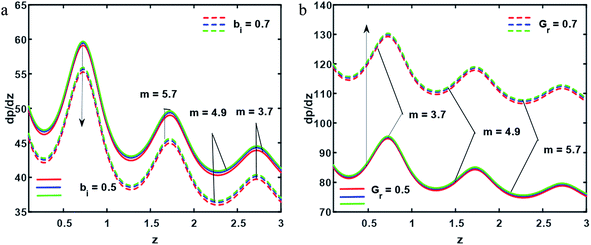 |
| | Fig. 5 (a and b) Pressure gradient ((a) for Gr = 0.32, (b) for bi = 0.3); other fixed parameters are ε = 0.11, r = 0.32, r1 = 0.22, B = 0.2, λ = 0.08, k = 0.44, s = 0.24, q = 0.5, φ1 = 0.2, φ2 = 0.05. | |
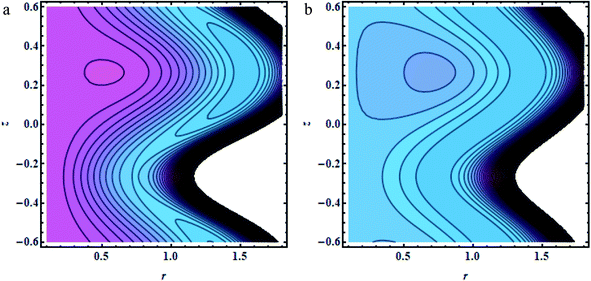 |
| | Fig. 6 (a and b) Brick shapes: (a) Gr = 0.5,(b);Gr = 1.5, other fixed parameters are ε = 0.28, r1 = 0.06, B = 1.2, λ = 0.34, k = 0.4, s = 0.8, b = 2.1, q = 0.6, φ1 = 0.2, φ2 = 0.05. | |
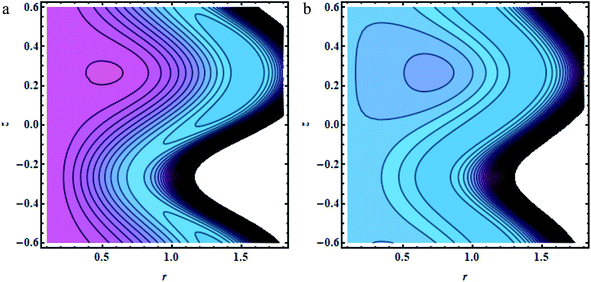 |
| | Fig. 7 (a and b) Cylinder shapes: (a) Gr = 0.5,(b) Gr = 1.5, other fixed parameters are ε = 0.28, r1 = 0.06, B = 1.2, λ = 0.34, k = 0.4, s = 0.8, b = 2.1, q = 0.6, φ1 = 0.2, φ2 = 0.05. | |
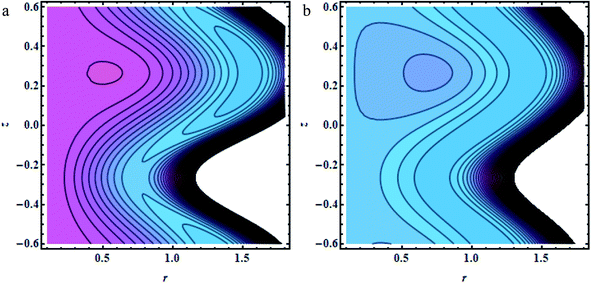 |
| | Fig. 8 (a and b) Platelet shapes: (a) Gr = 0.5,(b) Gr = 1.5, other fixed parameters are ε = 0.28, r1 = 0.06, B = 1.2, λ = 0.34, k = 0.4, s = 0.8, b = 2.1, q = 0.6, φ1 = 0.2, φ2 = 0.05. | |
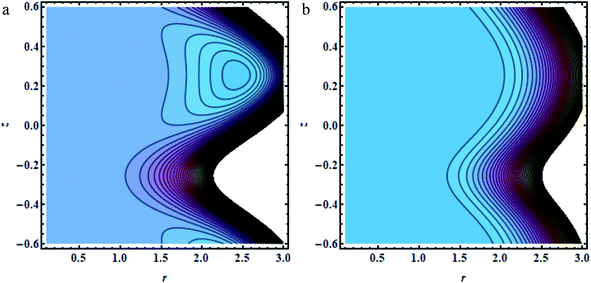 |
| | Fig. 9 (a and b) Brick shapes: (a) bi = 0.1, (b) bi = 0.5, other fixed parameters are ε = 0.28, r1 = 0.06, B = 1.2, λ = 0.34, k = 0.34, s = 0.8, G = 1.5, q = 0.36, φ1 = 0.2, φ2 = 0.05. | |
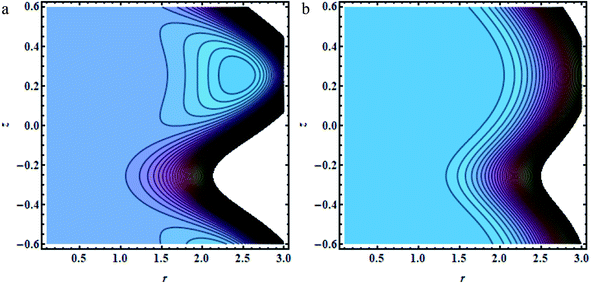 |
| | Fig. 10 (a and b) Cylinder shapes: (a) bi = 0.1, (b) bi = 0.5, other fixed parameters are ε = 0.28, r1 = 0.06, B = 1.2, λ = 0.34, k = 0.34, s = 0.8, G = 1.5, q = 0.36, φ1 = 0.2, φ2 = 0.05. | |
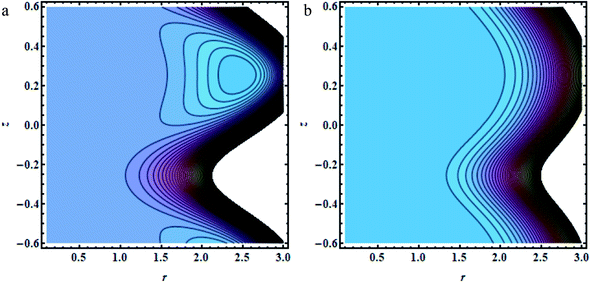 |
| | Fig. 11 (a and b) Platelet shapes (a) bi = 0.1, (b) bi = 0.5, other fixed constraints are ε = 0.28, r1 = 0.06, B = 1.2, λ = 0.34, k = 0.34, s = 0.8, G = 1.5, q = 0.36, φ1 = 0.2, φ2 = 0.05. | |
Table 3 Heat transfer rate z in contrast to Z* with the fixed parameters ε = 0.11, B = 0.1, λ = 0.08, k = 0.34, s = 0.24, φ2 = 0.1, φ2 = 0.05
| Heat transfer rate Z* |
| z |
Hybrid nanofluid |
Al2O3 nanofluid |
| m = 3.7 |
m = 4.9 |
m = 5.7 |
m = 3.7 |
m = 4.9 |
m = 5.7 |
| 0.1 |
−0.174489 |
−0.170175 |
−0.167714 |
−0.173766 |
−0.168679 |
−0.165534 |
| 0.3 |
0.0252278 |
0.0246178 |
0.0242696 |
0.0251257 |
0.0244062 |
0.023961 |
| 0.5 |
0.151389 |
0.147618 |
0.145468 |
0.150757 |
0.146311 |
0.143563 |
| 0.7 |
0.0274094 |
0.0267035 |
0.0263013 |
0.0272911 |
0.026459 |
0.0259452 |
| 0.9 |
−0.177936 |
−0.173471 |
−0.170925 |
−0.177188 |
−0.171923 |
−0.16867 |
| 1.1 |
−0.165284 |
−0.161351 |
−0.159106 |
−0.164625 |
−0.159986 |
−0.157115 |
| 1.3 |
0.0239603 |
0.0234001 |
0.0230802 |
0.0238665 |
0.0232057 |
0.0227967 |
| 1.5 |
0.143286 |
0.139856 |
0.137898 |
0.142712 |
0.138666 |
0.136163 |
| 1.7 |
0.0258547 |
0.0252183 |
0.0248553 |
0.0257481 |
0.0249977 |
0.0245336 |
| 1.9 |
−0.168276 |
−0.164223 |
−0.16191 |
−0.167598 |
−0.162817 |
−0.15986 |
Table 4 Special cases for velocity sketches with the fixed parameters ε = 0.11, B = 0.1, λ = 0.08, k = 0.34, s = 0.24, φ2 = 0.1, φ2 = 0.05
| Velocity profile |
| r |
Hybrid nanofluid (m = 3.7) |
Ag nanofluid (m = 3.7) |
Pure blood |
| 0.02 = r1 |
−1 |
−1 |
−1 |
| 0.12 |
−1.95629 |
−0.998489 |
−0.917212 |
| 0.22 |
−1.80369 |
−0.96284 |
−0.891386 |
| 0.32 |
−1.45882 |
−0.925665 |
−0.88025 |
| 0.42 |
−1.11072 |
−0.896962 |
−0.878638 |
| 0.52 |
−0.841085 |
−0.881592 |
−0.884894 |
| 0.62 |
−0.685552 |
−0.881618 |
−0.898214 |
| 0.72 |
−0.651382 |
−0.897127 |
−0.918043 |
| 0.82 |
−0.724748 |
−0.926617 |
−0.94388 |
| 0.92 |
−0.874443 |
−0.967216 |
−0.975197 |
| 0.989809 = r2 |
−1 |
−1 |
−1 |
Conclusions
The main subject of the current study is a hypothetical study of a peristaltic wavy wall with the addition of hybrid nanoparticles with different shape effects through a non-uniform outer tube. The governing problem is reduced via the postulation of a large wavelength and small Reynolds number. Some of the main suppositions of the above study can be summarized as follows:
(1) The temperature curve increases with respect to the heat source parameter but falls with respect to the Biot number.
(2) The velocities in the right and left splits of the tube have a contrary response to bi and Gr.
(3) The pressure rise and pressure gradient decrease with an increase in Biot number, unlike their behavior with Grashof number.
(4) As anticipated, the heat transfer rate Z* is oscillatory.
(5) The trapped bolus disappears for larger values of the Biot number.
(6) The trapped bolus has analogous properties for brick, platelet and cylinder shaped nanoparticles.
Appendix
Conflicts of interest
Authors declare no conflict of interest.
References
- S. I. Abdelsalam and M. M. Bhatti, New insight into AuNP applications in tumor treatment and cosmetics through wavy annuli at the nanoscale, Sci. Rep., 2019, 9(1), 1–14 CrossRef CAS PubMed.
- M. Imtiaz, T. Hayat and A. Alsaedi, Mixed convection flow of Casson nanofluid over a stretching cylinder with convective boundary consitions, Adv Powder Technol., 2016, 27, 2245–2256 CrossRef CAS.
- H. M. Sayed, E. H. Aly and K. Vajravelue, Influence of slip and convective boundary conditions on peristaltic transport of non-Newtonian nanofluids in an inclined asymmetric channel, Alexandria Eng. J., 2016, 55, 2209–2220 CrossRef.
- T. Hayat, S. Nawaz, A. Alsaedi and M. Rafiq, Mixed convective peristaltic flow of water based nanofluids with Joule Heating and convective boundary conditions, PLoS One, 2016, 11(4), 1–28 Search PubMed.
- S. Das, R. N. Jan and O. D. Makinde, MHD flow of Cu−Al2O3water hybrid nanofluid in porous channel: analysis of entropy generation, Defect Diffus. Forum, 2017, 377, 42–61 Search PubMed.
- H. Xie, B. Jiang, B. Liu, Q. Wang, J. Xu and F. Pan, An investigation on the tribological performances of the SiO2/MoS2 hybrid nanofluids for magnesium alloy-steel contacts, Nanoscale Res. Lett., 2016, 11, 329–336 CrossRef PubMed.
- S. P. A. Devi and S. S. U. Devi, Numerical investigation of hydromagnetic hybrid Cu−Al2O3 water nanofluid flow over a permeable stretching sheet with suction, Int. J. Nonlinear Sci. Numer. Simul., 2016, 17, 249–257 CAS.
- S. Ijaz, Z. Iqbal, E. N. Maraj and S. Nadeem, Investigation of Cu-CuO/blood mediated transportation in stenosed artery with unique features for theoretical outcomes of hemodynamics, J. Mol. Liq., 2018, 254, 421–432 CrossRef CAS.
- Y. Abd Elmaboud and S. I. Abdelsalam, DC/AC MHD micropump of a generalized Burgers fluid in an annulus, Phys. Scr., 2019, 94(11), 1–20 Search PubMed.
- K. S. Mekheimer, W. M. Hasona, R. E. Abo-Elkhair and A. Z. Zaher, Peristaltic blood flow with gold nanoparticles as a third grade nanofluid in catheter: application of cancer therapy, Phys. Lett. A, 2018, 382, 85–93 CrossRef CAS.
- I. M. Eldesoky, S. I. Abdelsalam, W. A. El-Askary, A. M. El-Refaey and M. M. Ahmed, Joint effect of thermal energy and magnetic field on particulate fluid suspension in a catheterized tube, Bionanoscience, 2019, 9(3), 723–739 CrossRef.
- T. Tayebi and A. J. Chamkha, Free convection enhancement in an annulus between horizontal confocal elliptical cylinders using hybrid nanofluids, Numer. Heat Transfer, Part A, 2016, 70(10), 1141–1156 CrossRef CAS.
- T. Tayebi and A. J. Chamkha, Natural convection enhancement in an eccentric horizontal cylindrical annulus using hybrid nanofluids, Numer. Heat Transfer, Part A, 2017, 71(11), 1159–1173 CrossRef CAS.
- A. I. Abdellateef and S. Z. Ul Haque, Peristaltic flow of Newtonian nanofluid through an inclined annulus cylinder, European Journal of Pure and Applied Mathematics, 2016, 9(3), 266–276 Search PubMed.
- S. I. Abdelsalam and M. M. Bhatti, The study of non-Newtonian nanofluid with Hall and ion slip effects on peristaltically induced motion in a non-uniform channel, RSC Adv., 2018, 8, 7904–7915 RSC.
- S. I. Abdelsalam and M. M. Bhatti, The impact of impinging TiO2 nanoparticles in Prandtl nanofluid along with endoscopic and variable magnetic field effects on peristaltic blood flow, Multidiscip. Model. Mater. Struct., 2018, 14(3), 530–548 CrossRef.
- S. I. Abdelsalam and K. Vafai, Particulate suspension effect on peristaltically induced unsteady pulsatile flow in a narrow artery: blood flow model, Math. Biosci., 2017, 283, 91–105 CrossRef PubMed.
- H. Sadaf, M. U. Akbar and S. Nadeem, Induced magnetic field analysis for the peristaltic transport of non-Newtonian nanofluid in an annulus, Math. Comput. Simulat., 2018, 39(9), 3413–3423 Search PubMed.
- I. M. Eldesoky, S. I. Abdelsalam, W. A. El-Askary and M. M. Ahmed, Concurrent development of thermal energy with magnetic field on a particle-fluid suspension through a porous conduit, Bionanoscience, 2019, 9(1), 186–202 CrossRef.
- Y. Abd Elmaboud, S. I. Abdelsalam and K. S. Mekheimer, Couple stress fluid flow in a rotating channel with peristalsis, J. Hydrodyn., 2018, 30(2), 307–316 CrossRef.
- S. Ijaz, H. Sadaf and Z. Iqbal, Remarkable role of nanoscale particles and viscosity variation in blood flow through overlapped atherosclerotic a channel: a useful application in drug delivery, Arabian J. Sci. Eng., 2019, 44, 6241–6252 CrossRef CAS.
- Y. Abd Elmaboud, K. S. Mekheimer and S. I. Abdelsalam, A study of nonlinear variable viscosity in finite-length tube with peristalsis, Appl. Bionics Biomechanics, 2014, 11(4), 197–206 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *b
*b
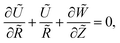
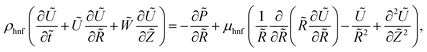
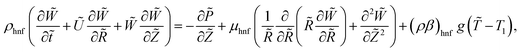
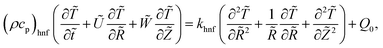
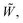
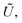
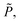 Q0, ρhnf, (ρcp)hnf, and κhnf signify the velocity mechanisms in the axial and radial track, pressure, constant of heat absorption parameter, hybrid nanofluid density, heat capacity of the hybrid nanofluid, viscosity of the hybrid nanofluid and thermal conductivity of the hybrid nanofluid demarcated as follows (8)
Q0, ρhnf, (ρcp)hnf, and κhnf signify the velocity mechanisms in the axial and radial track, pressure, constant of heat absorption parameter, hybrid nanofluid density, heat capacity of the hybrid nanofluid, viscosity of the hybrid nanofluid and thermal conductivity of the hybrid nanofluid demarcated as follows (8)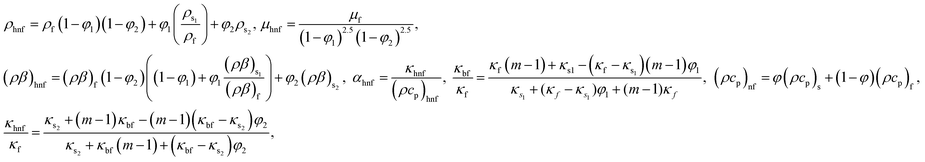
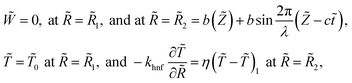
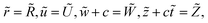
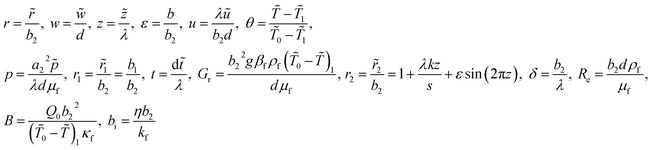
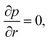
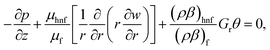
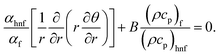
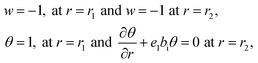
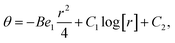
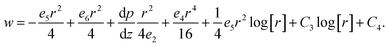
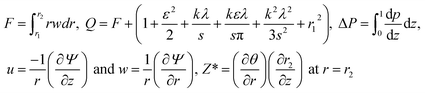
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500
500