Open Access Article
Open Access ArticleMolecular dynamics simulations of the mechanical behavior of alumina coated aluminum nanowires under tension and compression
Yudi Rosandia,
Hoang-Thien Luub,
Herbert M. Urbassek c and
Nina Gunkelmann
c and
Nina Gunkelmann *b
*b
aDepartment of Geophysics, The Nanotechnology and Graphene Research Center (PRINTG), Universitas Padjadjaran, Jatinangor, Sumedang 45363, Indonesia
bClausthal University of Technology, Institute of Applied Mechanics, Adolph-Roemer Str. 2A, Clausthal Zellerfeld 38678, Germany. E-mail: nina.gunkelmann@tu-clausthal.de
cPhysics Department and Research Center OPTIMAS, University of Kaiserslautern, Erwin-Schrödinger-Straβe, 67663 Kaiserslautern, Germany
First published on 8th April 2020
Abstract
For materials with high oxygen affinity, oxide layers will significantly change the material properties. This is of particular importance for aluminum nanowires which have many applications because of their ultrahigh strengths. Recent studies show that thin amorphous oxide shell layers on aluminum surfaces significantly change the responses of the material. However, the relations between the thickness of the oxidized layer, the strain rate and the mechanical response of nanowires to compression and tension have not been investigated intensively. In this study, we use a ReaxFF potential to analyze the influences of oxide shell layers on the material responses of the nanowires under uniaxial tension and compression at different strain rates. The Al–O interface leads to an increased defect nucleation rate at the oxide interface preventing localized deformation. During tension, we observe a reorganization of the structure of the oxide layer leading to bond healing and preventing fracture. While ductility is increasing with coating thickness during tension, the thickness of the coating is less decisive during compression.
1. Introduction
The need for high-strength but lightweight materials has become an integral part in the design of vehicles, aircrafts, buildings and wind turbines. Aluminum as a light material has many promising properties that make this material the most popular used light metal. Aluminum nanowires have low stacking-fault energies and display ultrahigh strength. They can accommodate large plastic strains by spreading mechanical twins throughout the entire volume of the nanowire.1 The mechanical properties of this material can be modified by creating various alloys fitted to the demanded mechanical and thermal characteristics. For materials with high surface-to-volume ratio and high oxygen affinity, oxide layers will significantly change the material properties. At aluminum surfaces, an oxide layer may form in seconds, even under vacuum conditions.2 However, only relatively few MD simulation studies exist on this topic focusing primarily on nanoparticles. The oxidation of aluminum nanoparticles was extensively investigated by Campbell et al.,3 Hong et al.4 and Ma et al.5 The charge transfer between the atoms was correlated with the mechanical properties. The oxidation of iron nanoparticles by X-ray diffraction and molecular dynamics was also studied, forming voids within the nanoparticles accompanied by mass diffusion of oxygen atoms into the particles.6 Zhang et al.7 investigated the chain-like nucleation and growth of oxides on aluminum nanoparticle surfaces which was shown to be highly dependent on the oxygen content, temperature, and nanoparticle size. Recently, core–shell Al/Al2O3 nanoparticles in an oxygen atmosphere under high temperature were studied by Chu et al.8 revealing four stages of preheating, melting, fast Al core, and moderate shell oxidations during the oxidation process. The thermal stability of aluminum oxide nanoparticles was recently investigated showing that partial oxidation reduces the nanoparticle melting temperature.9 Sen et al.10 showed that oxidation can lead to increased ductility in aluminum nanowires, which is a consequence of increased dislocation nucleation by an increased activation volume and an increased number of nucleation sites. Other studies on metal oxide coated nanowires support this finding by showing that the core–shell interface can provide a defect nucleation site increasing the ductility.11 Aral et al.12 analyzed the effect of oxidation on iron nanowires and found that an increase in the oxide layer thickness reduces both the yield stress and the critical strain. Generally, core–shell nanowires are of particular interest because of their great potential for various photonic and electronic applications such as piezoelectricity, chemical sensing and photo-detection.13,14 In this work, we use molecular dynamics simulations of compression and tension tests of alumina coated aluminum nanowires to show that oxidized aluminum nanowires possess significantly improved ductility without significant reduction in tensile strength. The simulations were carried out by the open-source molecular dynamics code LAMMPS.152. Methods
We construct aluminum nanowires with a diameter of 37 Å. We simulated coatings of alumina with three different shell thicknesses of 1.25 nm, 1.5 nm and 1.65 nm as well as pure Al nanowires. In the following we discuss mainly the cases with a thickness of 0, 1.25 nm and 1.5 nm (case 1–3, see Fig. 1). We found that case 4 does not strongly differ in the results from case 3, so we do not discuss the results unless differences are important. The ratio of the thickness of the core to the thickness of the total wire corresponds to 0.47 for the thickest coating which agrees with the value of 0.47 gained from experiments on core–shell Al/Al2O3 nanowires characterized by interference contrasts from TEM images.16 These nanowires were grown from core–shell nanoparticles with a core-to-wire ratio of 0.53. | ||
| Fig. 1 Cross-sectional and side views of initial configurations. The common neighbor analysis implemented in OVITO17 was used to detect the crystalline structure of the nanowire. Green: fcc, blue: Al of the coating, orange: O, white: other. | ||
The oxide shell was prepared by constructing crystalline α-Al2O3, and then removing the outer and inner concentric parts to obtain an oxide shell. After combining the Al core and the oxide shell together, we relax the samples using high-temperature annealing at 80% of the melting temperature with a Nosé/Hoover isenthalpic ensemble (NPH) during 100 ps. We employ the reactive force field ReaxFF by Zhang et al., including charge transfer between aluminum and oxygen molecules using the parameters developed by Zhang et al.7 This potential was fitted to describe Al2O3, as well as several AlxOy clusters. The lattice constants, elastic constants and surface energies agree well with first-principles calculations and experiments (see Table II in ref. 7.) The total energy of the ReaxFF potential is described by including bonding, coulombic, over-coordination, and van der Waals energies:
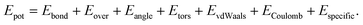 | (1) |
The simulations were carried out by performing uniaxial tension and compression tests along the z axis at a strain rate of 109 s−1 for 320 ps. To observe the mechanism of ductility enhancement in more detail, we perform tension simulations of aluminum nanowires coated by amorphous alumina layers. The nanowires are subjected to uniaxial tension tests along their wire axis with strain rates varying from 5 × 108 s−1 to 1 × 1010 s−1. The atom trajectories are followed up to 400 ps. The simulations are conducted at a temperature of 10 K using a Nosé–Hoover thermostat in order to minimize thermal noise. We use periodic boundary conditions in the axial direction and free boundary conditions along the other axes as in Aral et al.12
3. Results
We examine the crystal structure after relaxation by means of a coordination analysis implemented in OVITO.17 In Fig. 2 we plot the radial distribution function (RDF) for bulk Al and bulk Al2O3 at 10 K as well as for Al–O of the shell and Al in the core of our nanowires for the three different cases described above. The pair correlation function exhibits a sharp peak of Al–O at a small distance and a lack of peaks for larger distances which indicates that the shell is amorphous, in contrast to the sharp peaks observed for bulk Al2O3. This is in agreement with the results by Ma et al.5 The height of the primary peak decreases with the thickness of the oxide shell but this difference appears to be small. This indicates that the amorphous structure is stable due to strong bond energies of Al2O3. Note that the shell is in the compressive state and the core in the tensile state, as was also observed in the study by Campbell et al.3 A reason is the significant charge transfer leading to large negative pressure in the oxide. The peaks of Al in the core are more sharp for the samples of pure Al because of oxygen diffusion towards the interior of the cluster. The curves for Al of all cases show a multi-peak morphology pointing to the typical crystallographic state in contrast to the amorphous oxide shell. However, the peak at 4.0 Å is clearly split into two peaks for pure Al while we observe only one peak for the thickest coating. A reason could be diffusion of O atoms into the Al core during relaxation.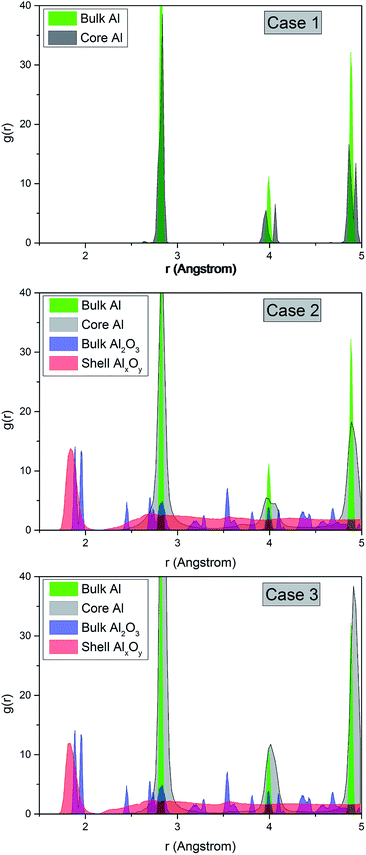 | ||
| Fig. 2 Pair distribution function for Al–O of the shell and Al in the core for three configurations. For comparison, the RDF for bulk Al and Al2O3 structures are shown. | ||
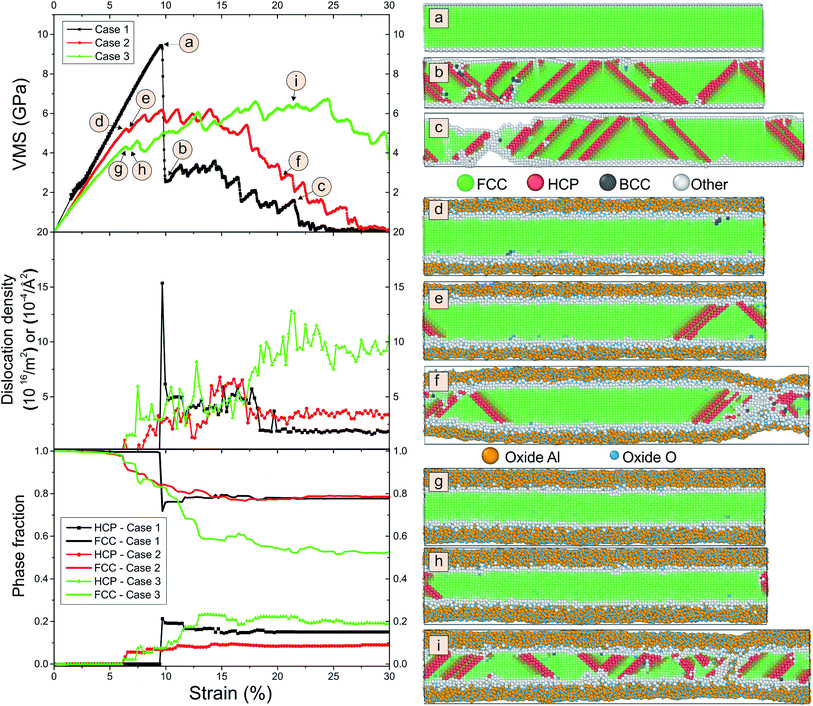
We compare the behavior of the nanowire during tension for different coating thicknesses. In Fig. 3 we plot snapshots of the samples during tension, the von Mises stress, the dislocation density and the phase fraction versus strain. The von Mises stress σVMS is used to describe the onset of plasticity.
 | (2) |
The dislocation density is detected by the dislocation extraction algorithm within OVITO.17 Surprisingly, we observe from Fig. 3 that the fracture of the nanowire is significantly delayed for the coated nanowires. While for pure Al we see clear fracture at around 22% strain, for the coated samples we observe a slight dilution of the sample at a position in the right half of the snapshot that does not occur for the thickest layer. We see many stacking faults originating at the interface for both pure and coated samples. This becomes evident from the array of diagonal “hcp stripes” seen in the fcc matrix as the hcp layers detected by the local analysis correspond to stacking faults in the fcc packing sequence. As can be seen from the subfigure of phase fraction versus strain, these stacking faults nucleate at 10% strain for pure Al and the number of stacking faults remains constant during further tension. These stacking faults are associated with dislocations and correspond to the pronounced peak in dislocation density. For the coated samples, the number of dislocations linearly increases between 10% and 15% strain and reach higher values. As shown before,10,19 the Al–O interface leads to an increased number of dislocations sites. Note that this result is consistent with experiments of Au nanowhiskers coated by Al2O3 via atomic layer deposition.20 Here, an increase in both the activation energy and the activation volume for dislocation nucleation is observed. The activation energy of dislocation nucleation depends strongly on the nature of interface structure.
The pure Al nanowire exhibits a high von Mises stress at 9.6% strain followed by fracture up to 30% strain. In contrast, the samples with coatings do not show a stress drop but the von Mises stress continuously decreases.
Our result can also be understood from the distribution of virial stresses of the sample at a strain of 10% strain, right before the formation of stacking faults. The bulk material is under pressure while tension is mainly concentrated on the coating surface. In contrast, for pure Al the stress distribution is uniform across the sample. The formation of voids at the interface between Al and the coating enables the formation of Al–O–Al atomic chains at the necking position resulting in a healed bond network. Note that several authors found that nanowires may become superplastic at room temperature and can form long atomic chains at the fracture surfaces.10,21
We observe in Fig. 3 that the dislocation density is largest for the sample with thick coating. Here, still no necking is visible at about 20% elongation. Instead, we see many stacking faults. These are detected as hcp by the common neighbor analysis.
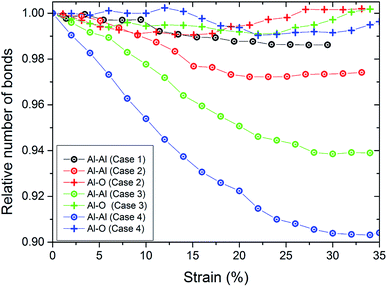
The increase of the number of Al–O bonds during the tension test demonstrates the chemical reaction driven ductility enhancement. The bond-breaking of aluminum atoms leads to immediate oxidation. Due to the stronger bonds, the ductility is gained by formations of Al–O–Al chains, especially at the necking position (see Fig. 3). In this location, the atoms are thermally active, allowing fast oxidation and diffusion of oxygen into the pure aluminum material. Hence, the mechanical properties in this region are shifted towards the properties of alumina. For quantifying this, we show in Fig. 4 the number of bonds in the wire during tension. We define the number of bonds on a distance-based criterion. The cutoff for bonds of Al–O was rcut = 0.25 nm and for Al–Al rcut = 0.35 nm. Note that we do not find O2 bonds during the tensile test. For pure Al, we observe an continuous decrease in the number of bonds during tension up to around 25% strain. Here, the nanowire fractures which stabilizes the number of bonds. This is consistent with the drop in tensile stress to zero at this strain (see Fig. 5). We observe that for the thin coating, the number of Al–O bonds is increasing and the broken Al–Al bonds are healed. This is why the fracture of the wire is considerably delayed. The number of Al–Al bonds decrease up to a strain of around 15% and are approximately constant afterwards. At this strain, the neck is formed. For the thicker coatings (cases 3 and 4), the number of Al–Al bonds are continuously decreasing and we do not observe neck formation. This decrease is strongest for the thickest coating. Again, the number of Al–O bonds increases leading to bond healing while the increase is only weak for the thickest coating.
 | ||
| Fig. 5 Comparison of the stress–strain curves for pure Al and coated Al nanowires for different thicknesses at a strain rate of 5 × 108 s−1 during tension. | ||
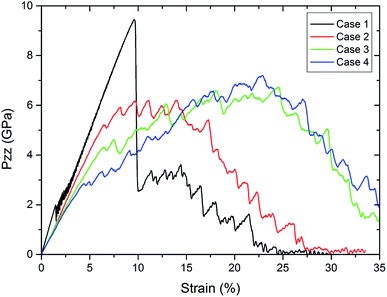
To show the dependence of the thickness, Fig. 5 displays the tensile stress versus strain for the pure Al nanowires and the nanowire coated by alumina of various thicknesses. The pure Al nanowire exhibits a high tensile strength at 9.6% strain followed by fracture up to 30% strain. This behavior was also found in experiments of gold nanowires and was correlated to the formation of extended thinned regions.22 A slip step was visible shortly before the stress dropped. Simultaneously, the onset of plastic deformation was observed manifesting itself by thinning of the wire and further extension of the thinned region. TEM investigation revealed that the deformation occurred by multiple short twins on one glide system. Further TEM studies showed that the plasticity of metallic nanowires deformed under vacuum is controlled by the nucleation and escape of dislocations from the free surfaces.23 In contrast to the crystalline nanowires, the samples with coatings do not show a stress drop. For the thickest coating, we see monotonous increase in tensile stress to 4.9% strain at 2.3 GPa and for the thinnest coating to 6.5% strain at 5.2 GPa. In particular for the thock coatings, cases 3 and 4, we observe further unsteady increase of strength after the first load drop up to 25% strain in contrast to the crystalline Al wire. The coated samples exhibit a lower strength but enhanced ductility. For the thicker coatings the tensile strength as well as the ductility are elevated in comparison to the thinner coatings. With increasing thickness of the oxide layer we observe an increase in failure strain. This increase in failure strain emphasizes the increase in ductility for increasing thickness. The elastic part of the curve also differs. While we observe elastic deformation up to 2% for the pure sample, we cannot depict the end of the linear regime for the coated samples. Note that Young's modulus slightly decreases by the coating. A reason could be that the effective diameter of the Al nanowire is smaller due to interaction of Al with the oxide layer. A drastic decrease in the Young's moduli of Al nanowires with decreasing nanowire diameters was predicted due to the formation of an amorphous oxide shell with a low modulus.24
We display the influence of the strain rate for pure Al and the coated samples in Fig. 6. The strain and stress at the first stress drop in displayed for different strain rates. The strain rate did not significantly affect the yield strain of pure Al. However, for a strain rate of 1 × 10 s−1 the tensile stress does not approach to zero up to 55% strain. For the coated samples, the ductility significantly increases with increasing strain rate. Here, a non-monotonic increase in strength is clearly visible, in particular for the thickest oxide layer. A reason could be that for higher strain rate deformation only a short time is available for void growth at the interface. The yield stress and the strength increases with increasing strain rate.
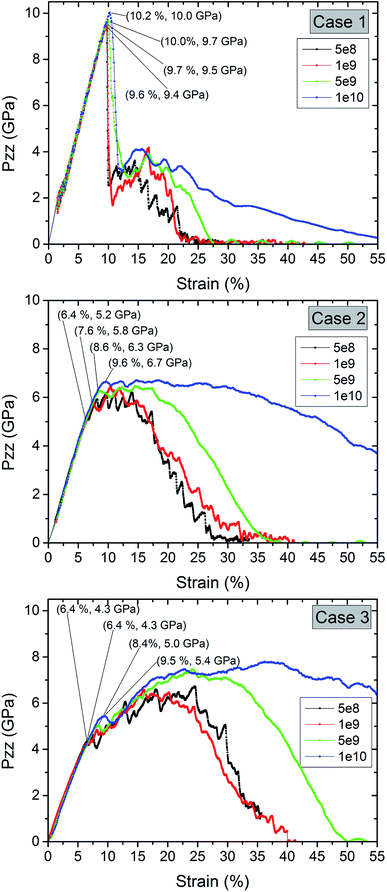 | ||
| Fig. 6 Comparison of the stress–strain curves for pure Al and coated Al nanowires at different strain rates during tension. | ||
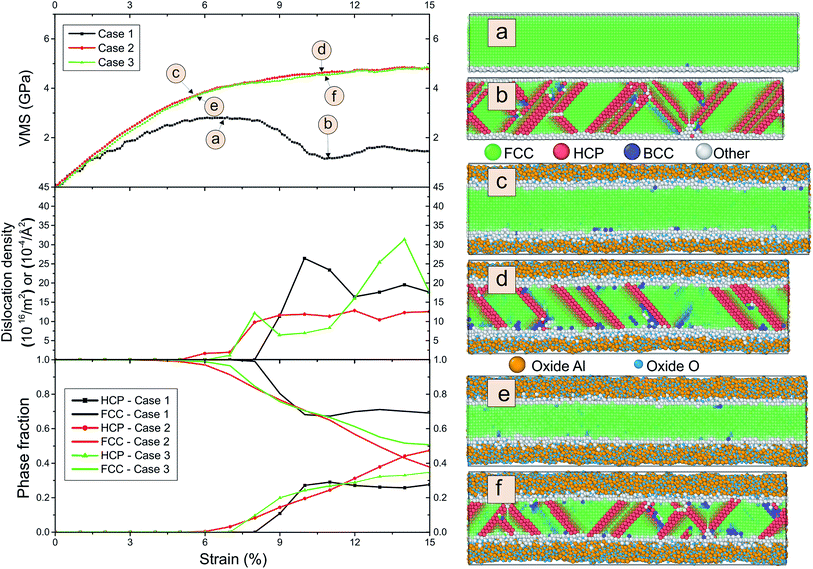
To evaluate the influence of oxygen on the tension-compression asymmetry, we studied compression using different strain rates. Fig. 7 shows the von Mises stress, the dislocation density and phase fraction during compression for three different cases.
We observe a maximum in the stress–strain curve at around 7% and subsequent plastic relaxation to nearly zero stress at 22% strain for the pure sample. In contrast, the von Mises stress reaches a plateau for the covered sample. We do not observe strong differences in dependence of the thickness of the coating. The dislocation density is large for all cases and the maximum of the dislocation density is only slightly larger for the thickest coating in comparison to the crystalline wire. Note that we detect a large amount of hcp stacking faults and some bcc clusters. The number of stacking faults is elevated for the coated samples. We observe that the thickness of the oxide shell increases during compression. This process can be explained from radial diffusion of Al and oxide.
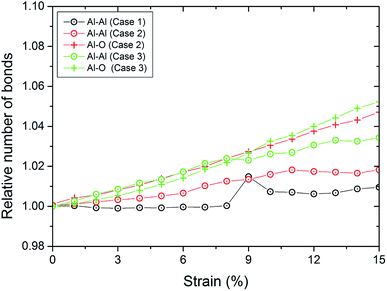
We also display in Fig. 8 the evolution of the number of bonds during compression. As expected, the number of bonds is steadily increasing. However, we observe that for both coatings, the slope of the curve for the number of Al–O bonds is above that for the number of Al–Al bonds. This means that we observe a reorganization of the structure of the oxide layer. For pure Al, we observe a kink at 9% strain. This is also reflected in the kink in the stress curve for pure Al at this strain where the first stacking faults occur as can be detected from the number of atoms which are detected as hcp (see Fig. 7).
4. Conclusion and future investigations
Our results show that oxygen helps to increase the ductility of Al nanowires. During tension, a reorganization of the Al–O layer stabilizes the nanowire and leads to delayed fracture. Ductility is increasing during tension. In the compression, we do not see any plastic relaxation of the von Mises stress with strain for the oxidized samples. The behavior does not depend significantly on the thickness of the coatings, which indicates a tension-compression asymmetry. These results are important to optimize the toughness of nanodevices affecting their long-term stability. This could contribute to more efficient manufacturing processes.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge for supports from Simulation Science Center Clausthal/Göttingen. The project was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 394563137 – SFB1368. The computations were performed with resources provided by the North-German Supercomputing Alliance (HLRN). YR is grateful for the funding from the Directorate General of Higher Education (DIKTI), Ministry of Education and Culture Republic of Indonesia, under the Fundamental Science Research scheme. This research is partially funded by the Ministry of Education and Culture under the World Class University (WCU) Program managed by Institut Teknologi Bandung. We acknowledge support by Open Access Publishing Fund of Clausthal University of Technology.Notes and references
- S.-H. Kim, H.-K. Kim, J.-H. Seo, D.-M. Whang, J.-P. Ahn and J.-C. Lee, Acta Mater., 2018, 160, 14–21 CrossRef CAS.
- F. Jona, J. Phys. Chem. Solids, 1967, 28, 2155–2160 CrossRef CAS.
- T. Campbell, R. K. Kalia, A. Nakano, P. Vashishta, S. Ogata and S. Rodgers, Phys. Rev. Lett., 1999, 82, 4866–4869 CrossRef CAS.
- S. Hong and A. C. van Duin, J. Phys. Chem. C, 2015, 119, 17876–17886 CrossRef CAS.
- B. Ma, F. Zhao, X. Cheng, F. Miao and J. Zhang, J. Appl. Phys., 2017, 121, 145108 CrossRef.
- Y. Sun, X. Zuo, S. K. R. S. Sankaranarayanan, S. Peng, B. Narayanan and G. Kamath, Science, 2017, 356, 303–307 CrossRef CAS PubMed.
- Q. Zhang, T. Çaǧın, A. van Duin, W. A. Goddard, Y. Qi and L. G. Hector, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 045423 CrossRef.
- Q. Chu, B. Shi, L. Liao, K. H. Luo, N. Wang and C. Huang, J. Phys. Chem. C, 2018, 122, 29620–29627 CrossRef CAS.
- M. Ramírez, R. I. González, S. E. Baltazar, J. Rojas-Nunez, S. Allende, J. A. Valdivia, J. Rogan, M. Kiwi and F. J. Valencia, Inorg. Chem. Front., 2019, 6, 1701–1706 RSC.
- F. G. Sen, A. T. Alpas, A. C. T. van Duin and Y. Qi, Nat. Commun., 2014, 5, 3959 CrossRef CAS PubMed.
- A. Gao, S. Mukherjee, I. Srivastava, M. Daly and C. V. Singh, Adv. Mater. Interfaces, 2017, 4, 1700920 CrossRef.
- G. Aral, Y.-J. Wang, S. Ogata and A. C. T. van Duin, J. Appl. Phys., 2016, 120, 135104 CrossRef.
- J. Li, G. Fang, C. Li, L. Yuan, L. Ai, N. Liu, D. Zhao, K. Ding, G. Li and X. Zhao, Appl. Phys. A: Mater. Sci. Process., 2008, 90, 759–763 CrossRef CAS.
- M. Veith, J. Lee, M. M. Miro, C. K. Akkan, C. Dufloux and O. C. Aktas, Chem. Soc. Rev., 2012, 41, 5117–5130 RSC.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- M. Veith, E. Sow, U. Werner, C. Petersen and O. C. Aktas, Eur. J. Inorg. Chem., 2008, 2008, 5181–5184 CrossRef.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. van Duin, npj Comput. Mater., 2016, 2, 15011 CrossRef CAS.
- N. Gunkelmann, E. M. Bringa and Y. Rosandi, J. Phys. Chem. C, 2018, 122, 26243–26250 CrossRef CAS.
- J. Shin, L. Y. Chen, U. T. Sanli, G. Richter, S. Labat, M.-I. Richard, T. Cornelius, O. Thomas and D. S. Gianola, Acta Mater., 2019, 166, 572–586 CrossRef CAS.
- N. W. Moore, J. Luo, J. Y. Huang, S. X. Mao and J. E. Houston, Nano Lett., 2009, 9, 2295–2299 CrossRef CAS PubMed.
- A. Sedlmayr, Experimental Investigations of Deformation Pathways in Nanowires, KIT Scientific Publishing, 2012 Search PubMed.
- H. Zheng, A. Cao, C. R. Weinberger, J. Y. Huang, K. Du, J. Wang, Y. Ma, Y. Xia and S. X. Mao, Nat. Commun., 2010, 1, 144 CrossRef PubMed.
- F. G. Sen, Y. Qi, A. C. T. van Duin and A. T. Alpas, Appl. Phys. Lett., 2013, 102, 051912 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |