A remarkable mixture of germanium with phosphorus and arsenic atoms making stable pentagonal hetero-prisms [M@Ge₅E₅]⁺, E = P, As and M = Fe, Ru, Os

Abstract

A pentagonal hetero-prismatic structural motif was found for singly transition metal doped M@Ge₅E₅⁺ clusters, where the transition metal atom is located at the centre of a (5/5) Ge₅E₅ prism in which Ge is mixed with either P or As atoms. Structural characterization indicates that each (5/5) Ge₅E₅ prism is established by joining of two Ge₃E₂ and Ge₂E₃ strings in a prismatic fashion rather than two Ge₅ and E₅ strings. Each string results from a remarkable mixture of Ge and E atoms and contains only one E–E connection due to the fact that Ge–E bonds are much stronger than E–E connections. From the donor–acceptor perspective, the Ge₅E₅ tube donates electrons to the M center, which behaves as an acceptor. NBO atomic charge and ELI_D analyses demonstrate such electrostatic interactions of the M dopant with a Ge₅E₅⁺ tube which likely induce thermodynamic stability for the resulting M@Ge₅E₅⁺ cluster. CMO analysis illustrates that the conventional 18 electron count is recovered in the M@Ge₅E₅⁺ cations.

---

1. Introduction

Due to a potentially important role of germanium based compounds in semiconductors and optoelectronic industries,^1–4 the geometric, electronic, thermodynamic and spectroscopic properties of small Ge clusters and their doped varieties have carefully been investigated by both theoretical and experimental methods alike.^5–15 According to numerous previous studies on doped germanium clusters, singly transition metal doped germanium clusters provide us with a wide range of geometrical features. It is known that the M@Ge₁₆ clusters with M = Ti, Zr, and Hf establish Frank–Kasper polyhedrons in which each metal dopant is encapsulated by a T_d Ge₁₆ cage.¹⁶ Similar to silicon clusters, a hexagonal prism shape has been identified for the V@Ge₁₂⁻, Mo@Ge₁₂ and W@Ge₁₂ clusters.^17–20 Of the transition metal doped MGe₁₂^−/0 clusters, the gold doped AuGe₁₂⁻ anion presents a high symmetry structure whose Au dopant is encapsulated by an I_h Ge₁₂ host.²¹ Some previous theoretical studies found that the three-dimensional star-like structure can be constructed by the ionic interactions of seven satellite alkali cations with a flat E₅⁶-pentagonal ring in which E is one of elements of group 14.^22–24 Moreover, by using DFT calculations including van der Waals effects, Li et al. has point out the small Ge₆, Ge₉, and Ge₁₀ clusters can play as the block units which can be connect together in order to form assembly materials and the van der Waals force impressively strengthens the covalent bond between different units, but plays less important role on the bonds in unit.²⁵ Remarkably, it is highly particular that the pentagonal prism shape was experimentally observed for the CoGe₁₀³⁻ and FeGe₁₀³⁻ clusters in which either the Co or the Fe atom is centered in a D_5h (5/5) Ge₁₀ pentagonal prism.^26,27 A large number of systematic investigations were carried out to elucidate the structural evolution of singly metal doped germanium clusters at various charged states.^{18–20,28–35} Accordingly, an interplay between the metal dopant and the Ge-host gives rise to the richness on geometries varying from incomplete cage through encapsulated tube to Frank–Kasper polyhedron.

Within a great effort in the search for novel geometrical motifs of germanium-based cluster, multiple doping of P and As hetero-atoms to germanium hosts produced some symmetric hetero-fullerene structures. Following introduction of As atoms the mixed [V@Ge₈As₄]³⁻ and [Nb@Ge₈As₆]₃⁻ hetero-fullerenes were generated. Structural identifications for the experimentally prepared [V@Ge₈As₄]³⁻ and [Nb@Ge₈As₆]³⁻ clusters showed that the V and Nb dopants are located at the central region of the Ge₈As₄ and Ge₈As₆ hetero-cages, respectively.^36,37 Similarly, with dopant being Cr, Mo and W atoms, high symmetry structures were also observed in which the metal dopant is covered by a D_3h Ge₈E₆ frame with E = P and As. Subsequent theoretical studies pointed out that these M@Ge₈E₆ hetero-cages share an electron shell of [1S²1P⁶1D¹⁰1F¹⁴1G¹⁸2S²2P⁶2D¹⁰] enclosing 68 electrons. The existence of Ge-cages with mixed P and As elements suggests that a doping of P or As into a germanium host emerges as a good approach to generate high symmetry hetero-structures.

Although the MGe₁₀^q prismatic structures have gained so much attentions, their hetero-derivatives with P and As have been not considered yet. Indeed, while the FeGe₁₀^q was identified as a pentagonal prism in nine charge states with q being from −5 to +3, the isovalent RuGe₁₀^q clusters are of polyhedral geometry.^34,38 Additionally, the compounds containing a P₅ or As₅ pentagon were found in the carbon-free as well as mixed M(Cp)E₅ sandwich complexes. Within these coordination compounds, each P₅ or As ring coordinates to a transition metal rather than forms any mixed-ring.^39–43 It is subsequently predicted that M@Ge₅P₅⁺ and M@Ge₅As₅⁺ could be stable in a sandwich form where the M center is coordinated by both Ge₅ and E₅ rings. In this context, it is of interest to explore the effects of the P and As hetero-atoms to geometry of Fe@Ge₁₀^q pentagonal prism. With the aim to search for novel clusters possessing a stable tubular structural motif, we set out to carry out a theoretical investigation on geometries and electronic structure of the species Ge₅E₅⁺ in mixing the five germanium atoms with five P or As counterparts, and then they are singly doped by a transition metal (TM) giving rise to the doped M@Ge₅E₅⁺ clusters. The main role of the TM dopant is to stabilize the high symmetry tubular prism motif which is usually not stable in free forms. For a systematic exploration, we consider the elements of group 8 including Fe, Ru and Os as the dopant M. It turns out that such a mixture between Ge with either P or As leads to a set of remarkably stable pentagonal prisms containing an unprecedented combination of these elements.

2. Computational methods

In order to explore the potential energy surface (PES) of each of the M@Ge₅E₅⁺ systems considered, its guess geometries are generated by using a stochastic algorithm previously implemented by us.⁴⁴ Our stochastic search method was improved based on the ‘random kick’ procedure reported by Saunders⁴⁵ for exploring the low-lying isomers of compounds. According to this procedure, each atom of an initial structure is kicked to randomly move within a sphere of radius r, then the structures, generated from that, become the inputs for subsequent geometry optimizations using electronic structure calculations, and the “moving radius” r of atoms is the only variable controlled in this procedure. In our modified stochastic searching procedure, three additional variables will be controlled to provide better structures constructed for the following geometry optimizations. We modify this algorithm by adding a permutation subroutine in which each atom exchanges its position with all the others. For each MGe₅E₅⁺ system, we generate 1000 initial isomers for geometry optimization. This algorithm has been proven to be highly efficient in the search for the energetically lower-lying isomers of the systems containing various components.^46–48 Additionally, on the basis of the well-known MGe₁₀^q structures that have already been reported in previous studies, we substitute Ge atoms by either P or As atoms, and thereby generate the initial isomers for the mixed M@Ge₅E₅⁺ systems.

All guessing structures of each series are geometrically optimized by using B3P86 functional in conjunction with small LANL2DZ basis set.⁴⁹ Subsequently, the obtained structures, which have relative energy in range 50 kcal mol⁻¹, will be selected to re-optimize using the same functional but in conjunction with a larger basis set, including the 6-311+G(d) set⁵⁰ for Ge, P and As atoms, and the aug-cc-pVTZ or aug-cc-pVTZ-PP for Fe, Ru and Os^51,52 in which PP stands for pseudo-potential. The current study utilizes the hybrid B3P86 functional due to it has previously been tested as suitable for treatment of geometrical and electronic structures of mixed clusters containing transition metals.⁵³ All geometric optimizations and electronic structure calculations are performed using the Gaussian 09 suite of program.⁵⁴ It should be noted that the cationic state is considered in order to probe the closed-shell electron configuration with a low spin state.

3. Result and discussion

3.1 Geometries

As for a convention, we label the structures considered as A.M.x in which A = P and As stand for Ge₅P₅ and Ge₅As₅ hosts, respectively, M = Fe, Ru and Os denotes the TM dopant, and finally, x = 1, 2, …, indicates the isomers with increasing relative energy. For the Ge₅E₅⁺ cations, the structures are denoted as A.x. Relative energies given here under are consistent with respect to the corresponding isomer x = 1.

To probe the effects of the metal dopant on the geometries of Ge₅P₅⁺ and Ge₅As₅⁺ cations, we first present in Fig. 1 the lower-lying isomers of both Ge₅P₅⁺ and Ge₅As₅⁺ cations obtained at the B3P86/6-311+G(d) level. No special shape is observed for both Ge–P and Ge–As mixed systems (Fig. 1). For Ge₅P₅⁺, the lowest energy structure P.1 contains four P–P connections, whereas P.2 turns out to contain a P₅ cycle connected to a Ge₅ counterpart and is only 3 kcal mol⁻¹ higher in energy than P.1. The next isomers including P.3, P.4 and P.5 are significantly less stable. Regarding the Ge₅As₅⁺ cations, As.1 contains only one As–As bond but it emerges as the lowest-energy structure. The geometric characteristic of As.1 is completely different from that of the isovalent P.1. Remarkably, As.3 possesses an As₅ pentagonal string and is 8 kcal mol⁻¹ higher. Other higher energy isomers of the Ge₅As₅⁺ cation are also shown in Fig. 1.

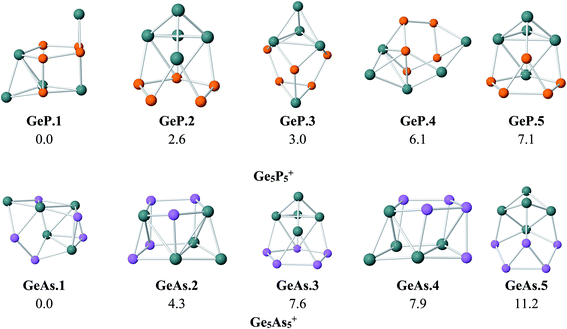Fig. 1 Shapes and relative energies (in kcal mol⁻¹) of lower-lying isomers of Ge₅P₅⁺ and Ge₅As₅⁺ clusters. Geometry optimizations and energy calculations were performed at the B3P86/6-311+G(d) level.

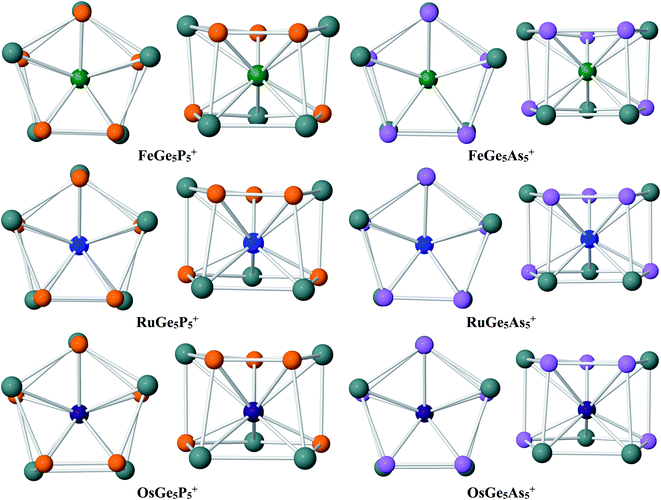
Geometry identification for M@Ge₅P₅⁺ cations with M = Fe, Ru and Os clearly points out that a metal dopant M stabilizes the Ge₅P₅⁺ host into a double ring shape. The lower-lying isomers of M@Ge₅P₅⁺ clusters are displayed in Fig. 2, and also in Fig. S1–S3 of the ESI file.† Accordingly, the M@Ge₅P₅⁺ cations mainly feature a pentagonal prism, and each metal dopant, involving Fe, Ru and Os, is found to be located in the central region of a mixed (5/5) Ge₅P₅ double ring, which actually is formed by connecting Ge₄P, Ge₃P₂, Ge₂P₃ and GeP₄ pentagons together in a prismatic fashion. Of the latter, a combination of both Ge₃P₂ and Ge₂P₃ strings establishes the global energy minimum structure for the M@Ge₅P₅⁺ cation. No isomer having a (Ge₅)M(E₅)⁺ sandwich complex has been found. The appearance of M@Ge₅P₅⁺ double ring prism emphasizes the crucial role of the metal dopant Fe, Ru and Os in stabilizing a Ge₅P₅⁺ cation in a high symmetry form.

Fig. 2 Shapes of the global energy minimum structures of M@Ge₅E₅⁺ with M = Fe, Ru and Os and E = P and As. Geometry optimizations were performed using the B3P86 functional with the 6-311+G(d) basis set for Ge and E and aug-cc-pVTZ basis set for Fe and aug-cc-pVTZ-PP basis set for Ru and Os metals.

Similar to the Fe@Ge₁₀^q cluster, a mixed Fe@Ge₅P₅⁺ cluster is thus stabilized in a pentagonal prism. Moreover, such a structural motif is consistently found for both Ru@Ge₅P₅⁺ and Os@Ge₅P₅⁺ as their ground state, whereas the Ru@Ge₁₀^q cluster does not exist. This result again demonstrates the important role of P atoms in formation of pentagonal prism, in such a way that a multiple doping of P atoms into a germanium host, or replacing of Ge by P atoms, appears to be an efficient approach to generate double ring structures for germanium-based clusters. It is interesting to note that the formation of P–P direct connections in each cluster series containing Fe, Ru and Os is in relation to the cluster stability. The most stable structure of Fe@Ge₅P₅⁺, Ru@Ge₅P₅⁺ and Os@Ge₅P₅⁺ cations contains each only one P–P bond, whereas other isomers having two or more P–P bonds are significantly less stable (Fig. S1–S3†). The isomers P.Fe.5, P.Fe.6 and P.Fe.7 contain each three P–P direct connections, and they are 10–15 kcal mol⁻¹ higher in energy. Similarly, structures containing Ru and Os exhibit three or more P–P direct bonds are calculated to be highly unstable. Overall, introduction of Fe, Ru and Os dopants into a Ge₅P₅⁺ host establishes a (5/5) hetero-prism double ring structure for M@Ge₅P₅⁺ cations, but the Ge and P atoms are mixed in such a way that formation of two or more P–P direct bonds tend to destabilize the resulting clusters.

Regarding the M@Ge₅As₅⁺ clusters, a similar behavior is again observed. DFT calculations emphasize that a hetero-prismatic shape is again dominating as displayed in Fig. S4–S6 of the ESI file.† On the structural aspect, each of the Fe, Ru and Os dopants occupies a place of the central region of a prismatic cage formed by the Ge₄As, Ge₃As₂, Ge₂As₃ and GeAs₄ pentagons. Similar to M@Ge₅P₅⁺, disposition of both Ge₃As₂ and Ge₂As₃ pentagonal strings in an anti-prism form gives rise to the most stable structure for M@Ge₅As₅⁺, as depicted in Fig. 2. The similarity on geometric characteristic of M@Ge₅As₅⁺ clusters and their P homologues (M@Ge₅P₅⁺ cations) again emphasizes the crucial stabilizing role of Fe, Ru and Os metals in turning an irregular cage to a tubular structure. In case of FeGe₅As₅⁺, there is a competition for the ground state. Actually, the triplet As.Fe.1 and As.Fe.2 isomers, which are structures containing two and three As–As connections, are only ∼1 kcal mol⁻¹ more stable than the singlet As.Fe.3, an isomer containing only one As–As bond. Additionally, the triplet ³A′′ (C_s) As.Fe.3 is only ∼1 kcal mol⁻¹ higher than its single state, so that they are competitive for ground state of the Fe@Ge₅As₅⁺ cluster. However, this result emphasizes that the existence of hetero-prism containing one As–As connection is a general tendency in M@Ge₅As₅⁺ clusters.

As in the P homologues, the thermodynamic stability of M@Ge₅As₅⁺ cations is found again in correlation with the number of direct As–As bonds. In fact, the isomer having one As–As connection is significantly more stable than those possessing two or more As–As bonds, as shown in Fig. S4–S6 of the ESI file.† In other words, formation of additional As–As bonds tends to destabilize the doped clusters.

The above structural identifications illustrate the coherent fact that the metal atoms of group 8 involving Fe, Ru and Os induce a great geometrical modification for the Ge₅E₅⁺ cations with E being an element in group of 15 (P and As). Both Ge₅P₅⁺ P.1 and Ge₅As₅⁺ As.1 cations do not exist in a special form, and more importantly, a prismatic shape is not observed at all for their lower-lying isomers. Incorporation of a metal of the group Fe, Ru and Os into such Ge₅E₅⁺ cations brings in a (5/5) pentagonal double ring prismatic shape for doped M@Ge₅E₅⁺ clusters, in which the strings are formed upon mixture of atoms. This appears to be a general tendency for this class of clusters (Fig. 3).

Fig. 3 Geometric shapes of the lowest-energy structure of M@Ge₅E₅⁺.

The geometric feature of M@Ge₅E₅⁺ clusters clearly shows that they prefer a mixed tubular shape rather than form a carbon-free sandwich complex. In fact, the existence of M@Ge₅E₅⁺ shows a different trend in which both P₅ and As₅ rings no longer exist. The sandwich structure (Ge₅ME₅)⁺ is extremely unstable, even it does not appear as a local minimum on the M@Ge₅E₅⁺ potential energy surface. It can thus be concluded that in the global minimum isomer of MGe₅E₅⁺, the metal center is coordinated by both Ge₃E₂ and Ge₂E₃ rings without any E₅ string.

For a further characterization of the electron distribution, the bond length and Wiberg bond index (WBI) of the Ge–E, Ge–Ge and E–E bonds are tabulated in Table 2. For free M–E molecules, a bond length of ∼2.1 Å is found for M–P connections with M = Fe, Ru and Os, but their WBI values vary from 2.6, 3.2 to 3.5, respectively (Table 1). According to the usual meaning of WBI, P atom forms a triple bond with Fe and Ru while a nearly quadruple bond is identified for OsP dimer. A similar result is observed in M–As and M–Ge diatomic molecules where Os establishes a nearly quadruple bond with As and Ge, and a triple bond character is found for Fe–As, Fe–Ge, Ru–As and Ru–Ge dimeric species. The strength of M–E and M–Ge dimers tends to increase in going from M = Fe to Os. The WBI values of free Ge₂, GeP and GeAs dimers are calculated to be 2.5, 2.7 and 3.1, respectively. As a consequence, they can be formally classified as a triple bond. Particularly, P₂ and As₂ have bond lengths of 1.9 and 2.2 Å, respectively, and the corresponding WBI values amount to 3.6 and 3.5.

Table 1 Geometrical parameters (distance in angstrom) and WBI (a. u.) of M@Ge₅E₅⁺ prisms

	Fe@Ge5P5^+	Ru@Ge5P5^+	Os@Ge5P5^+		Fe@Ge5As5^+	Ru@Ge5As5^+	Fe@Ge5As5^+
M–P1	2.3/1.2	2.4/1.6	2.5/1.5	M–As1	2.4/1.1	2.5/1.4	2.6/1.5
M–P2	2.3/1.2	2.4/1.4	2.4/1.6	M–As2	2.4/1.1	2.5/1.4	2.6/1.6
M–P4	2.3/1.3	2.3/1.2	2.3/1.9	M–As4	2.4/1.1	2.4/1.6	2.4/1.9
M–Ge4	2.6/1.0	2.7/1.2	2.7/1.4	M–Ge4	2.6/0.9	2.7/1.2	2.7/1.3
M–Ge1	2.5/1.1	2.6/1.3	2.6/1.5	M–Ge1	2.6/1.0	2.6/1.3	2.6/1.5
M–Ge2	2.5/1.1	2.6/1.4	2.5/1.6	M–Ge2	2.6/0.9	2.6/1.4	2.6/1.6
P2–P3	2.2/1.0	2.2/1.0	2.2/0.1	As2–As3	2.5/0.9	2.4/1.0	2.4/1.0
P1–Ge4	2.5/0.7	2.4/0.9	2.4/0.8	As1–Ge4	2.5/0.9	2.5/0.9	2.5/0.8
P2–Ge4	2.5/0.8	2.5/0.7	2.5/0.7	As2–Ge4	2.5/0.7	2.6/0.8	2.9/0.5
P1–Ge1	2.5/0.7	2.6/0.6	2.6/0.6	As1–Ge1	2.6/0.7	2.7/0.6	2.7/0.6
P2–Ge2	2.5/0.7	2.6/0.5	2.7/0.4	As2–Ge2	2.6/0.8	2.7/0.6	2.7/0.5
P4–Ge4	2.5/0.7	2.6/0.6	2.6/0.5	As4–Ge4	2.6/0.7	2.7/0.6	2.6/0.7
P4–Ge1	2.4/0.9	2.6/0.6	2.6/0.6	As4–Ge1	2.5/0.9	2.6/0.7	2.6/0.6
Ge3–Ge2	2.6/0.7	2.8/0.5	2.9/0.5	Ge3–Ge2	2.7/0.7	2.7/0.8	2.7/0.5

---

Within the M@Ge₅P₅⁺ clusters, P–P connections have bond length of ∼2.2 Å and WBI values of ∼1.0 clearly indicating a single bond character. A similar single bond character is found for Ge–Ge, which exhibits a WBI value of 0.7 in Fe@Ge₅P₅⁺, and 0.5 in both Ru@Ge₅P₅⁺ and Os@Ge₅P₅⁺. Connections of Ge with P atoms are characterized by WBI values in the range of 0.4–0.9, also implying a Ge–P single bond. Accordingly, Ge and P atoms form Ge–Ge, Ge–P and P–P single bonds in the Ge₅P₅ prismatic tube. A similar pattern is observed for the Ge₅As₅ cages in which Ge–As connections have WBI values of 0.5–0.9 for Ge–As bonds, and ∼1.0 for As–As and Ge–Ge bonds. It is important to explore the bonding between Ge₃E₂ and Ge₂E₃ rings. The connectivities associated with the superposition between both Ge₃E₂ and Ge₂E₃ strings is identified as single bond according to WBI results. Therefore, it is not possible to consider the pentagonal Ge₃E₂ and Ge₂E₃ rings of M@Ge₅E₅⁺ as two independent rings. On the other hand, the M@Ge₅E₅⁺ is a tubular cluster rather than a [(Ge₃E₂) M (Ge₂E₃)]⁺ carbon-free sandwich complex.

For connections containing the metal atom, the M–P bonds of M@Ge₅P₅⁺ are not only significantly longer than those of the corresponding M–P diatomic molecules, but their WBI values are also found to be in a range of 1.2–1.9. Similarly, M–As connections of M@Ge₅As₅⁺ prism have WBI values varying from 1.1 to 1.9. Hence, metal atoms form, in connecting with P and As atoms, stronger bonds than single bonds. In comparison to free MGe, MP and MAs dimers, formation of M@Ge₅E₅⁺ prisms significantly reduces the strength of the corresponding connection. As shown in Table 2, the M–Ge connections have WBI values of ∼1–2, whereas the WBI of free MGe species is greater than 2. In other words, the strength of a M–Ge bond is reduced when a doped M@Ge₅E₅⁺ prism is established. Overall, the WBI analysis indicates that Ge and E atoms either E = P or As, connect together by a single bond whereas a metal atom gives rise to multiple bonds in interacting with the Ge, P and As elements.

Table 2 Bond length (d, angstrom) and WBI (a.u.) of MGe, ME, E₂ and GeE diatomic molecules

Molecule	d	WBI	Molecule	d	WBI	Molecule	d	WBI
Fe–P	2.1	2.6	Ru–P	2.1	3.2	Os–P	2.1	3.5
Fe–As	2.2	2.4	Ru–As	2.2	3.3	Os–As	2.1	4.1
Fe–Ge	2.3	2.3	Ru–Ge	2.2	3.3	Os–Ge	2.1	3.5
Ge–Ge	2.4	2.5	Ge–P	2.2	2.7	Ge–As	2.4	3.1
P–P	1.9	3.6	As–As	2.1	3.5

---

Although both P₂ and As₂ dimeric molecules are highly stable, as indicated by large values of their dissociation energies and WBI, the appearance of P–P and As–As connections in a M@Ge₅E₅⁺ prismatic cluster tends to destabilize it. Within the most stable isomer of a M@Ge₅E₅⁺ cluster, both P–P and As–As connections are identified as single bonds, according to WBI results. Therefore, in order to rationalize the rather negative effect of the P–P and As–As connections on the stability of M@Ge₅E₅⁺ cluster, the dissociation energies (DE) of the E–E bonds as evaluated from the homolytic breaking H₂E–EH₂ → 2EH₂, H₃Ge–EH₂ → Ge₃H₃ + EH₂ and H₃Ge–GeH₃ → 2GeH₃ processes which describe well the dissociation of E–E, Ge–E and Ge–Ge single bonds, are calculated and given in Table 1. Accordingly, the DEs of the H₃Ge–GeH₃ bond has a value of 66 kcal mol⁻¹ whereas the DE values of H₃Ge–PH₂ and H₃Ge–AsH₂ are computed to be ∼60 kcal mol⁻¹. The H₂P–PH₂ and H₂As–AsH₂ species have DEs of ∼50 kcal mol⁻¹ which are significantly smaller than the others. This result points out both P–P and As–As single bonds are consistently weaker than the mixed Ge–P, Ge–As and the pure Ge–Ge counterparts. Therefore, formation of Ge–P, Ge–As and Ge–Ge bonds is expected to give raise more thermodynamic stability to M@Ge₅E₅⁺ prismatic structure than the P–P and As–As connections. As a result, the most stable isomer of each M@Ge₅E₅⁺ cluster contains only one P–P or As–As bond whereas eight Ge–E connections are formed (Table 3).

Table 3 Dissociation energy (DE, kcal mol⁻¹) and bond length (r, Å) of H₂E–XH₃ molecules (TPSSh/6-311++G(d,p))

	DE (E–X)	r (E–X)
H2P–PH2	50.3	2.26
H2As–AsH2	47.0	2.47
H3Ge–GeH3	66.2	2.43
H3Ge–PH2	60.7	2.34
H3Ge–AsH2	57.9	2.44

---

3.2 Chemical bonding analysis: donor–acceptor complex

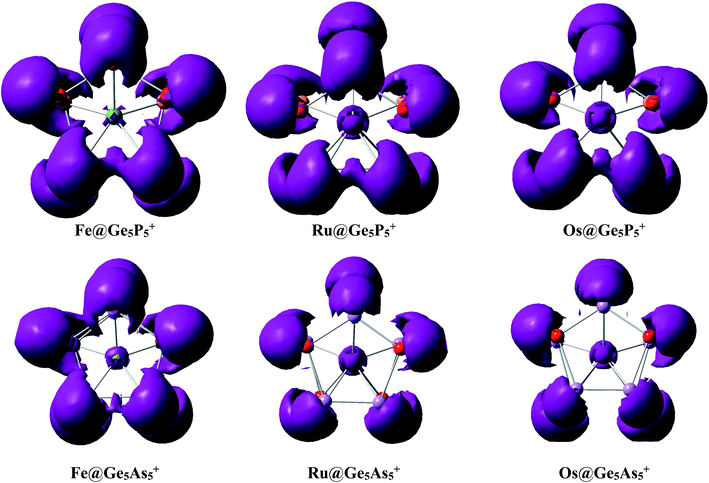
Interaction between a metal dopant M with a Ge₅E₅⁺ cage is further probed using the NBO atomic charges (Table 2) that illustrate that metal atoms bear a largely negative charge, ∼−3.5 electron. On the other hand, the Ge₅E₅⁺ prismatic double ring supplies electrons to the metal dopant, and thereby establishes a negatively charged center M^δ−. Each M@Ge₅E₅⁺ prismatic structure can thus be regarded as a [M^δ− (Ge₅E₅)^δ+]⁺ donor–acceptor complex where the metal atom M behaves as an acceptor centre and the Ge₅E₅⁺ cage plays as a donor moiety.

An analysis of the electron distribution using the electron localization indicator (ELI_D)⁵⁵ is carried out to further explore the bonding phenomena of M@Ge₅E₅⁺ clusters. As shown in Fig. 4, at the bifurcation value of 1.3, a di-synaptic basin, V(E,E), is clearly observed for E–E connections in all clusters considered. Similarly, localization domains are found for either Ge–P or Ge–As connection indicating their covalent bond character. The V(M,Ge) and V(M,E) basins with M = Fe, Ru and Os, and E = P are found at lower bifurcation values suggesting that the connections containing metal atom have an ionic character. This result is consistent with the NBO analysis given above in which Ge₅E₅⁺ is shown to transfer much electron to the M center. Both NBO and ELI_D analyses illustrate that the electrostatic interaction of a negatively charged metal dopant with a Ge₅E₅⁺ positively charged tubular moiety contributes to a thermodynamic stabilization of the resulting M@Ge₅E₅⁺ hetero-prisms.

Fig. 4 ELI_D maps plotted at the bifurcation value of 1.3 for M@Ge₅E₅⁺.

3.3 The 18 electron count

The stability of the singly metal doped tubes is often rationalized by using the classical electron count in which the metal atom receives electrons to gain a fulfilled d¹⁰ configuration. It should however be noted that the Fe, Ru and Os atoms have a general electron configuration of [ns²(n − 1)d⁶], which thus needs 4 additional electrons to fill their (n − 1)d¹⁰ shell. NBO analysis given above indicates that each Ge₅E₅⁺ cage transfers an amount of ∼3.5 electron to the metal center. In other words, each Ge₅E₅⁺ cage effectively provides 4 valence electrons to establish a closed (n − 1)d¹⁰ subshell for the metal M, and thereby stabilizes the M@Ge₅E₅⁺ tubular prism. Following this line of argument, the orbital interaction diagram between the Fe atom and a Ge₅P₅⁺ prism is constructed and displayed in Fig. 5. The result constructed for the Ge₅P₅⁺ case can certainly be generalized for the other derivatives.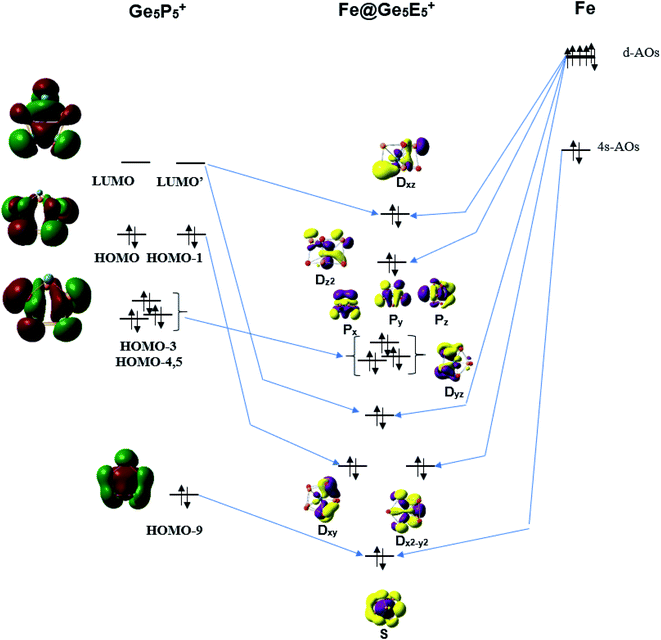

Fig. 5 A representative orbital interaction diagram of Fe with Ge₅P₅⁺ prism producing MOs containing 18 electrons.

According to Fig. 5, the 4s-AO of Fe atom involves interaction with the HOMO-9 of Ge₅P₅⁺ and produces an S level for Fe@Ge₅P₅⁺. The D_xy and D_x²–y² levels are produced upon interaction of the HOMO and HOMO-1 with 3d-AOs of Fe. Interaction of the LUMO and LUMO+1 of Ge₅P₅⁺ prism with 3d-AOs of Fe induces the D_xz and D_yz eigenstates of Fe@Ge₅P₅⁺. The 3d_z² AO of Fe becomes D_z² of Fe@Ge₅P₅⁺ prismatic cluster. The P_x, P_y and P_z levels of Fe@Ge₅P₅⁺ are mainly contributed by the HOMO-3,4,5 of Ge₅P₅⁺ cage. Finally, orbital interactions of the Fe dopant with Ge₅P₅⁺ prism produce an electron configuration of [S²P⁶D¹⁰] which in fact contains 18 valence electrons.

A similar orbital interaction is also found for other clusters including RuGe₅P₅⁺, OsGe₅P₅⁺ and MGe₅As₅⁺ as shown in Fig. S7–S11 of ESI file.† These results show that metal dopants Fe, Ru and Os gain each 4 electrons from the Ge₅E₅⁺ cage to fulfill its (n − 1)d¹⁰ level, and thereby induce an enhanced stability for the M@Ge₅E₅⁺ prismatic structures, which not only share a general structural motif but also have a same stabilizing mechanism where the metal center gains 4 electrons from Ge₅E₅⁺ prismatic cage to establish a 18 electron configuration. It is interesting that the polyanions Co@Ge₁₀³⁻ and Fe@Ge₁₀⁴⁻ pentagonal prismatic clusters, which are iso-valent with Fe@Ge₅E₅⁺, are stabilized by a similar mechanism. They are similar to Ge₅E₅⁺ prisms; the Ge₁₀ prismatic host also supplies electrons to fulfill 3d¹⁰ levels of Co and Fe centers, and subsequently establishes a 18 electron configuration.^38,56 This gives an emphasis that hetero-atoms including P and As not only replace Ge position in a prismatic framework but also provide electrons to fulfil 18 electron configuration.

4. Concluding remarks

In summary, we presented a theoretical investigation on geometry, stability and chemical bonding of the Ge₅E₅⁺ and MGe₅E₅⁺ cationic clusters with E = P, As; M = Fe, Ru and Os. Structural identifications clearly pointed out that the doping of a transition metal atom greatly influences to geometry of the Ge₅E₅⁺ cage. Structurally, the singly doped M@Ge₅E₅⁺ clusters are stabilized in pentagonal hetero-prism shape whereas the Ge₅E₅⁺ cation is not in any special form. Each hetero-prismatic structure is formed by superposition of the Ge₄E, Ge₃E₂, Ge₂E₃ and GeE₄ pentagons together in prismatic fashion, but the combination of Ge₃E₂ and Ge₂E₃ strings peculiarly establishes the global minimum structure for M@Ge₅E₅⁺ cations. Interestingly, the cluster contains only one E–E connection exhibits the lowest-energy while a structure possesses two or more E–E bonds is significantly less stable. Ge–E bonds are in fact stronger than E–E connections. Within the donor–acceptor perspective, with acceptor being the metal dopant, the GeE cage donates around 4 electrons to the M center and then stabilize M@Ge₅E₅⁺ clusters. A CMO analysis illustrates that the conventional 18 electron count is effectively recovered in the stabilized M@Ge₅E₅⁺ cations.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 103.01-2019.372 to NMT.

References

1. W. L. Brown, R. R. Freeman, K. Raghavachari and M. SchlÜTer, Science, 1987, 235, 860.
2. E. C. Honea, A. Ogura, C. A. Murray, K. Raghavachari, W. O. Sprenger, M. F. Jarrold and W. L. Brown, Nature, 1993, 366, 42–44.
3. Y. Kamata, Mater. Today, 2008, 11, 30–38.
4. R. Pillarisetty, Nature, 2011, 479, 324–328.
5. J. Wang, G. Wang and J. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 205411.
6. R. B. King, I. Silaghi-Dumitrescu and A. Lupan, Inorg. Chem., 2005, 44, 3579–3588.
7. R. B. King, I. Silaghi-Dumitrescu and M. M. Uţǎ, Inorg. Chem., 2006, 45, 4974–4981.
8. R. B. King and I. Silaghi-Dumitrescu, Inorg. Chem., 2003, 42, 6701–6708.
9. W. Qin, W.-C. Lu, Q.-J. Zang, L.-Z. Zhao, G.-J. Chen, C. Z. Wang and K. M. Ho, J. Chem. Phys., 2010, 132, 214509.
10. W. Qin, W.-C. Lu, L.-Z. Zhao, Q.-J. Zang, G.-J. Chen, C. Z. Wang and K. M. Ho, J. Chem. Phys., 2009, 131, 124507.
11. B.-x. Li and P.-l. Cao, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 15788–15796.
12. A. A. Shvartsburg, B. Liu, Z.-Y. Lu, C.-Z. Wang, M. F. Jarrold and K.-M. Ho, Phys. Rev. Lett., 1999, 83, 2167–2170.
13. L. Wang and J. Zhao, J. Chem. Phys., 2008, 128, 024302.
14. S. Bulusu, S. Yoo and X. C. Zeng, J. Chem. Phys., 2005, 122, 164305.
15. S. Yoo and X. C. Zeng, J. Chem. Phys., 2006, 124, 184309.
16. V. Kumar and Y. Kawazoe, Phys. Rev. Lett., 2002, 88, 235504.
17. N. D. Phi, N. T. Trung, E. Janssens and V. T. Ngan, Chem. Phys. Lett., 2016, 643, 103–108.
18. X.-J. Deng, X.-Y. Kong, H.-G. Xu, X.-L. Xu, G. Feng and W.-J. Zheng, J. Phys. Chem. C, 2015, 119, 11048–11055.
19. J. Wang and J.-G. Han, J. Phys. Chem. A, 2006, 110, 12670–12677.
20. R. Trivedi, K. Dhaka and D. Bandyopadhyay, RSC Adv., 2014, 4, 64825–64834.
21. S.-J. Lu, L.-R. Hu, X.-L. Xu, H.-G. Xu, H. Chen and W.-J. Zheng, Phys. Chem. Chem. Phys., 2016, 18, 20321–20329.
22. M. Contreras, E. Osorio, F. Ferraro, G. Puga, K. J. Donald, J. G. Harrison, G. Merino and W. Tiznado, Chem.–Eur. J., 2013, 19, 2305–2310.
23. W. Tiznado, N. Perez-Peralta, R. Islas, A. Toro-Labbe, J. M. Ugalde and G. Merino, J. Am. Chem. Soc., 2009, 131, 9426–9431.
24. A. Vásquez-Espinal, K. Palacio-Rodríguez, E. Ravell, M. Orozco-Ic, J. Barroso, S. Pan, W. Tiznado and G. Merino, Chem.–Asian J., 2018, 13, 1751–1755.
25. H. Li, W. Chen, X. Han, L. Li, Q. Sun, Z. Guo and Y. Jia, J. Comput. Chem., 2015, 36, 1919–1927.
26. B. Zhou, M. S. Denning, D. L. Kays and J. M. Goicoechea, J. Am. Chem. Soc., 2009, 131, 2802–2803.
27. J.-Q. Wang, S. Stegmaier and T. F. Fässler, Angew. Chem., Int. Ed., 2009, 48, 1998–2002.
28. Q. Jing, F.-y. Tian and Y.-x. Wang, J. Chem. Phys., 2008, 128, 124319.
29. X.-J. Deng, X.-Y. Kong, X.-L. Xu, H.-G. Xu and W.-J. Zheng, ChemPhysChem, 2014, 15, 3987–3993.
30. J. Wang and J.-G. Han, J. Phys. Chem. B, 2006, 110, 7820–7827.
31. C. Siouani, S. Mahtout, S. Safer and F. Rabilloud, J. Phys. Chem. A, 2017, 121, 3540–3554.
32. X.-J. Hou, G. Gopakumar, P. Lievens and M. T. Nguyen, J. Phys. Chem. A, 2007, 111, 13544–13553.
33. D. Bandyopadhyay, P. Kaur and P. Sen, J. Phys. Chem. A, 2010, 114, 12986–12991.
34. Y. Jin, Y. Tian, X. Kuang, C. Lu, J. L. Cabellos, S. Mondal and G. Merino, J. Phys. Chem. C, 2016, 120, 8399–8404.
35. S. Jaiswal and V. Kumar, Comput. Theor. Chem., 2016, 1075, 87–97.
36. S. Mitzinger, L. Broeckaert, W. Massa, F. Weigend and S. Dehnen, Chem. Commun., 2015, 51, 3866–3869.
37. R. Ababei, W. Massa, B. Weinert, P. Pollak, X. Xie, R. Clérac, F. Weigend and S. Dehnen, Chem.–Eur. J., 2015, 21, 386–394.
38. M. M. Uţă, D. Cioloboc and R. B. King, J. Phys. Chem. A, 2012, 116, 9197–9204.
39. E. Urne˙žius, W. W. Brennessel, C. J. Cramer, J. E. Ellis and P. v. R. Schleyer, Science, 2002, 295, 832–834.
40. J. Frunzke, M. Lein and G. Frenking, Organometallics, 2002, 21, 3351–3359.
41. K. Kotrle and R. Herchel, Inorg. Chem., 2019, 58, 14046–14057.
42. R. F. Winter and W. E. Geiger, Organometallics, 1999, 18, 1827–1833.
43. M. Lein, J. Frunzke and G. Frenking, Inorg. Chem., 2003, 42, 2504–2511.
44. T. B. Tai and M. T. Nguyen, J. Chem. Theory Comput., 2011, 7, 1119–1130.
45. M. Saunders, J. Comput. Chem., 2004, 25, 621–626.
46. H. T. Pham, N. T. Cuong, N. M. Tam, V. D. Lam and N. T. Tung, Chem. Phys. Lett., 2016, 643, 77–83.
47. N. M. Tam, L. V. Duong, H. T. Pham, M. T. Nguyen and M. P. Pham-Ho, Phys. Chem. Chem. Phys., 2019, 21, 8365–8375.
48. N. M. Tam, V. T. Ngan and M. T. Nguyen, Chem. Phys. Lett., 2014, 595–596, 272–276.
49. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
50. P. J. Hay, J. Chem. Phys., 1977, 66, 4377–4384.
51. K. A. Peterson, D. Figgen, M. Dolg and H. Stoll, J. Chem. Phys., 2007, 126, 124101.
52. D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, J. Chem. Phys., 2009, 130, 164108.
53. V. T. Ngan, P. Gruene, P. Claes, E. Janssens, A. Fielicke, M. T. Nguyen and P. Lievens, J. Am. Chem. Soc., 2010, 132, 15589–15602.
54. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, et al., Gaussian 09 Revision: D.01, 2009.
55. M. Kohout, F. R. Wagner and Y. Grin, Int. J. Quantum Chem., 2006, 106, 1499–1507.
56. M. M. Uţă, D. Cioloboc and R. B. King, Inorg. Chem., 2012, 51, 3498–3504.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra01316a

---