Open Access Article
Open Access ArticleElectronic structure and second-order nonlinear optical properties of lemniscular [16]cycloparaphenylene compounds†
Li-jing Gong‡
 *,
Cheng Ma‡,
Wan-feng Lin,
Jin-kai Lv and
Xiang-yu Zhang
*,
Cheng Ma‡,
Wan-feng Lin,
Jin-kai Lv and
Xiang-yu Zhang
Aviation University of Air Force, Changchun 130022, Jilin, China. E-mail: gonglijing@126.com
First published on 7th April 2020
Abstract
Chiral organic compounds are excellent second-order nonlinear optical (NLO) materials due to their inherent non-symmetric electronic structures combined with the advantages of organic compounds. At present, density functional theory (DFT) has become a powerful tool for predicting the properties of novel materials. In this paper, based on chiral lemniscular [16]cycloparaphenylene, three novel compounds are designed by introduction of donor/acceptor units and their combinations. The geometrical/electronic structure, electronic absorption, and the second-order NLO properties of these compounds have been systematically investigated by DFT/TDDFT theory. The simulated UV-Vis/CD spectra of compound 1 are in good agreement with the experimental ones, enabling us to assign their electronic transition characteristics and absolute configuration with high confidence. The investigations show that energy gaps, absorption wavelength and second-order NLO response may be effectively tuned by the introduction of the donor or acceptor units or their combinations. For instance, the second-order NLO value of compound 4 is about 207 times as large as the average second-order polarizability of the organic molecule urea. Thus, the studied compounds are expected to be potential large second-order NLO materials.
1. Introduction
The design and synthesis of materials with large nonlinear optical (NLO) performance have attracted considerable attention due to their potential applications in optical and optoelectronic devices.1–8 However, second-order NLO properties can be characterized at the molecular level with second-order polarizability, which is the most important point in practical applications. The necessary requirement for second-order NLO materials is a non-centrosymmetric electronic structure.9,10 So far, there are two main strategies to achieve this structure. One method is to insert an electron-donor and/or electron-acceptor substituted unit into organic compounds with an extended π-conjugated backbone at appropriate positions.11–17 The other method is to use chiral compounds, which have intrinsic asymmetric electronic structures.18–21 Numerous studies have shown that chiral compounds can be a valuable alternative for excellent second-order NLO materials.22–25Cyclic π-conjugated systems with different combinations of twist and local curvature have aroused particular interest of organic chemists. This is not only because of their theoretical interest, but also because of their possible applications in materials science. At present, most studies focus aromatic compounds with one or three half-twist of the π surface,26–34 and planar π-conjugated aromatic compounds with two half-twist of the π surface.27,28,35,36 However, very little research has been done on radial π-conjugated aromatic compounds with two half-twist of the π surface, which adopts figure eight (lemniscular) shape and helps maximize p orbital overlap and reduce internal strain.
Very recently, K. Senthilkumar, et al. reported a cycloparaphenylene-based molecular lemniscates (CPPL),37 named compound 1 (Fig. 1). It is composed of a 9,9′-bicarbazole unit and twelve phenylene units, which has a figure-eight (lemniscular) shape. Its electronic and optical properties combine features more characteristic of smaller cycloparaphenylenes, such as a radially conjugation, a reduced electronic bandgap and red-shifted fluorescence. The twisted nanohoop of CPPL also has strong chiroptical responses, including circularly polarized luminescence. Moreover, its unique figure-eight structure arising from chirality can meet the basic requirement of second-order NLO material. Accordingly, compound 1 may be a potential candidate for excellent second-order NLO material.
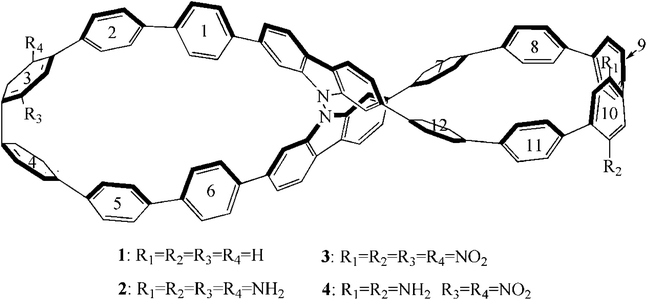
It is well known that macroscopic properties are closely related to microscopic electron structures, especially for excited electronic transition properties. In order to further improve the performance of compound 1, compounds 2–4 were designed. The introduction of donor NH2 unit or acceptor NO2 unit at R1–R4 positions was named as compound 2 and 3, respectively. For compound 4, NH2 unit is at R1 and R2 positions, and NO2 unit is at R3 and R4 positions. In order to more clearly describe the electronic structure and charge transfer properties, we numbered the benzene ring in the compounds, as shown in Fig. 1.
So far, density functional theory (DFT) calculations have become a powerful tool to rationalize the observed properties and design new materials with excellent performance. In this paper, our main goal is to clarify with the help of DFT/TDDFT calculations to (i) investigate the frontier molecular orbitals (FMOs) (ii) analyze electronic transition mechanism and (iii) study NLO properties.
2. Computational details
All of the calculations were carried out with Gaussian 09 software.38 The ground-state structures of compounds 1–4 were fully optimized with D3-B3LYP39/6-31G(d) level of theory. The B3LYP functional is a combination of Becke's three-parameter hybrid exchange functional40 and the Lee–Yang–Parr41 correlation functional. The D3-B3LYP functional considers the long-range dispersion effects and has shown excellent advantage of predicting structural parameters, harmonic frequencies and other molecular properties.42–44 Harmonic vibration frequency calculations showed that the optimized structure is the local minimum in potential energy surface. In the optimization process, there is no symmetry or internal coordination constraints.The calculated absorption wavelengths, oscillator strengths and major contributions of the studied compounds were calculated at the TD-PBE0/6-31G(d)45 level. To strengthen our calculated results, the effect of different basis sets and functionals on electron transition properties was also probed. To consider the solvent effect of dichloromethane, the integral equation formalism version of the polarized continuum model (PCM) was utilized.46–48 The electron density difference maps (EDDM) were obtained by using Multiwfn software version 3.5 (dev).
It is noted that static first hyperpolarizability is an important parameter to reflect its magnitude of second-order NLO response. In this work, the second-order NLO response of compounds 1–4 is determined by hyper-Rayleigh scattering (βHRS), as follows:49,50
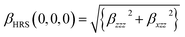 | (1) |
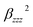 and
and 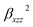 are the orientational average of the first hyperpolarizability tensor without assuming Kleinman's conditions.
are the orientational average of the first hyperpolarizability tensor without assuming Kleinman's conditions.
3. Results and discussion
3.1 Frontier molecular orbital analysis
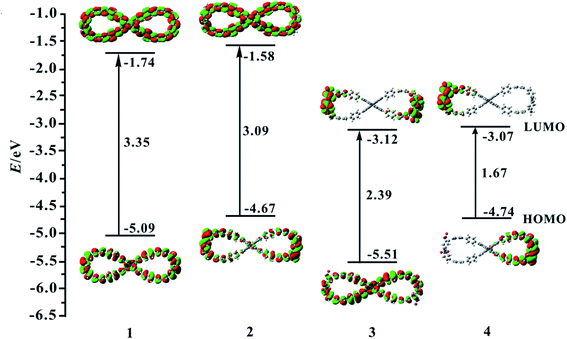
In this paper, four compounds were investigated, as shown in Fig. 1. Their ground state geometrical structures have been fully optimized at D3-B3LYP/6-31G(d) level of theory. For organic compounds, their frontier molecular orbitals (FMOs) distributions and energy gaps (HOMO–LUMO gap) are closely related to the electronic and optical properties. The sketch of the HOMO and LUMO orbitals, the calculated HOMO/LUMO energy levels, and energy gaps of compounds 1–4 are shown in Fig. 2.For compound 1, the HOMO and LUMO mainly attributes on the whole skeleton, with π and π* character. For compound 2, its LUMO orbital distribution is almost the same as that of the compound 1, but the HOMO is significantly different from that of compound 1. Its HOMO mostly localizes on benzene rings and N atoms, demonstrating that the introduction of donor NH2 groups at R1–R4 positions in compound 2 may change the HOMO distribution. For compound 3, its LUMO mainly distributes on rings 2–4, rings 9–11 and NO2 groups, while the HOMO is basically the same as that of compound 1. This indicates that the introduction of acceptor NO2 unit at R1–R4 positions has a significant influence on the LUMO distribution of compound 1. When the donor NH2 and acceptor NO2 units are simultaneously introduced into compound 1, the FMO of compound 4 is significantly different from that of compound 1. The HOMO and LUMO orbital distributions of compound 4 are clearly separated. Its HOMO distribution mainly localizes on the right benzene rings 7–12 and NH2 groups, and the LUMO distribution mostly localizes on the left benzene rings 2–4 and NO2 groups. The changes of FMO distributions, indicating that the introduction of the combination of the donor group (NO2) and acceptor group (NH2) facilitates charge separation of frontier molecular orbital, which is beneficial to realize intramolecular charge transfer from HOMO to LUMO.
Subsequently, the effect of different substituents on energy gap is also investigated. Compared with compound 1, the FMO energy levels of compound 2 all increase, and the increase in HOMO energy level is significantly higher than the increase in LUMO energy level. Therefore, its band gap is reduced by 0.26 eV compared to that of compound 1. For compound 3, its HOMO and LUMO energy levels obviously reduce. Especially the LUMO energy level, its reduction value reached 1.38 eV in comparison with compound 1. Therefore, the band gap of compound 3 evidently reduces, which attributes to the introduction of the NO2 group affects the distribution of LUMO. This signifies that the introduction of NO2 group can distinctly reduce the band gap. For compound 4, the HOMO energy level is close to that of compound 2, while the LUMO energy level is close to that of compound 3. So its band gap is the smallest of the four studied compounds, only 1.67 eV, originating from the evident separation of the electron distributions of HOMO and LUMO. This demonstrates that an effective method for reducing the band gap of compound 1 is to introduce a combination of donor NH2 and acceptor NO2 groups.
3.2 Electronic absorption of compounds 1–4
In recent years, TDDFT method can be successful in describing the nature of electronic transitions.51–55 However, choosing the effective calculation level is very important to accurately calculate electronic transition properties. Firstly, four Pople's basis sets (e.g. 6-31G(d), 6-31G(d,p), 6-31+G(d), and 6-31+G(d,p)) were chosen to discuss the influences of basis set extension on the electronic absorption wavelength by using B3LYP functional. The calculated most intense absorption bands of compound 1 at the different basis set levels were listed in Table S1.†The calculated results were all closely to the experiment value, and the difference between the absorption wavelengths of the largest basis set and the smallest basis set is about 10 nm. This signifies that the effect of the basis set size on the calculated absorption wavelength is not obvious. From the perspective of the performance and reasonable computational resource, 6-31G(d) basis set was selected in the following calculation.Subsequently, four different functionals (B3LYP,40 PBE0,56–58 CAM-B3LYP,59,60 and BH&HLYP61) were selected to test the effects on the absorption wavelengths. The calculated results are given in Table S2.† The results show the absorption wavelength which calculated by PBE0 are in excellent agreement with the experimental data. Meanwhile, the absorption wavelength in dichloromethane phase was also computed using the PBE0/6-31g(d) level (Table S2†). It is found that the absorption wavelength in the solution phase is close to that in gas phase, indicating that the influence of solvent is negligible. Thus, the PBE0 functional combined with 6-31G(d) basis set was employed in the following electronic excitation calculations in gas phase for the studied compounds.
Based on the above analytical results, the 60 lowest electronic excitation energies of the studied compounds 1–4 were calculated at the TD-PBE0/6-31G(d) level. The calculated absorption wavelengths, oscillator strengths and major contributions are summarized in Table 1. The UV-Vis and CD spectra of compound 1 along with experiment spectra are shown in Fig. 3. In order to understand the nature of electronic absorption, the molecular orbitals (MO) involved into the main transition were also shown in Fig. 4.
| Compound | λ | f | Major contribution |
|---|---|---|---|
| 1 | 362.67(357) | 3.9165 | H−2 → LUMO (48%), HOMO → L+2 (43%) |
| 2 | 354.81 | 1.5475 | H−3 → LUMO (73%), H−2 → LUMO (11%) |
| 3 | 345.88, 487.42 | 1.5146, 0.2417 | HOMO → L+6 (78%), H−1 → LUMO (83%), HOMO → LUMO (10%) |
| 4 | 350.43 | 0.8217 | H−3 → L+2 (11%), H−2 → L+2 (13%), H−1 → L+2 (29%), H−1 → L+3 (12%), H−1 → L+4 (11%) |
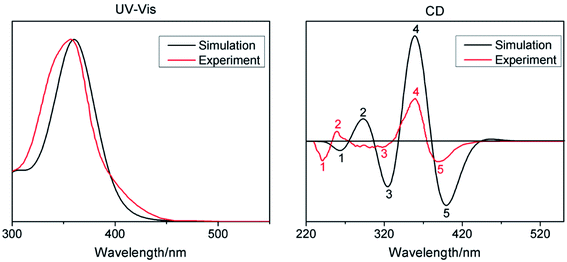 | ||
| Fig. 3 Calculated UV-Vis (left) and CD (right) spectra of compounds 1 at the TD-PBE0/6-31G(d) level of theory along with experimental spectra (red line). | ||
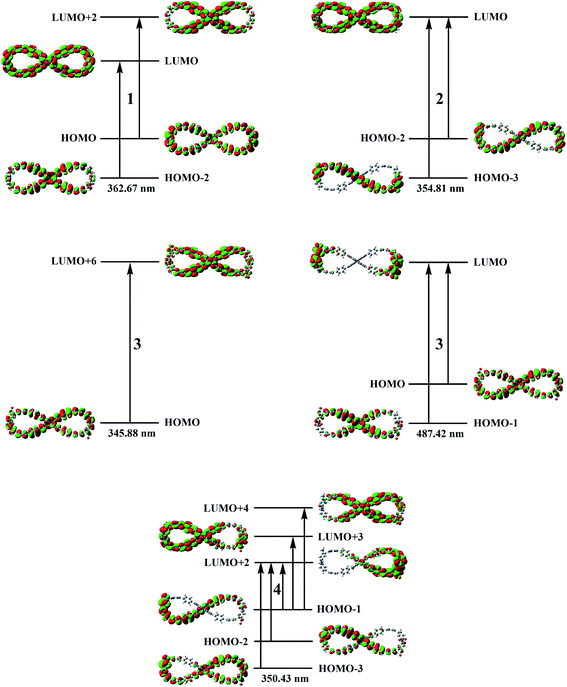 | ||
| Fig. 4 Molecular orbital isosurfaces involved in the main electron transitions of compounds 1–4 at the PBE0/6-31G(d) level of theory. | ||
For compound 1, the calculated UV-Vis spectrum reproduces the experimental one. The simulated CD spectrum reproduces the negative/positive sign (i.e., cotton bands) of the experimental ones. These allow us to assign the AC of compound 1 with high confidence. This also confirms once again that the chosen calculation level is feasible in calculating electronic transition properties. Compared with compound 1, the most intense absorption bands of compounds 2–4 are blue-shifted. Unlike compounds 1, 2 and 4, compound 3 has two electron absorption bands, and the low-energy absorption band is at 487.42 nm.
Subsequently, we explore the electronic transition properties. For compound 1, its most intense absorption band is attributed to HOMO−2 → LUMO and HOMO → LUMO+2 electronic excitation, which can be assigned as π → π* character on the entire skeleton. The electronic excitation of the most intense absorption band for compound 2 mainly results from HOMO−3 → LUMO and HOMO−2 → LUMO transitions with the upper part or the bottom part between ring 3 and ring 10 to the entire molecule backbone charge transfer (CT), respectively. For compound 3, the most intense absorption band at 345.88 nm originates from HOMO → LUMO+6 excitation and its electronic excitation feature is from the bottom part to the upper part between ring 3 and ring 10 CT. The low-energy absorption band is assigned to HOMO−1 → LUMO and HOMO → LUMO excitation, with obvious CT from 9,9′-bicarbazole units and rings 1, 2, 6, 7, 11 and 12 to rings 2–4, 9–11 and NO2 units. For HOMO−1 → LUMO excitation, there is a significant charge spatial separation. For compound 4, the electronic transition arises from HOMO−3 → LUMO+2, HOMO−2 → LUMO+2, HOMO−1 → LUMO+2, HOMO−1 → LUMO+3 and HOMO−1 → LUMO+4 excitation, with obvious CT character from left nanohoop to right nanohoop and π → π* character on the right nanohoop. Overall, the introduction of donor and acceptor units has great influence on both electronic transition character and absorption wavelength.
3.3 Second-order NLO properties
Chiral compounds are considered as a valuable alternative for finding large second-order NLO materials due to their inherent asymmetric structures. At the same time, the studied compounds show distinct intramolecular charge transfer character. These unique features may lead to the large first hyperpolarizability (βHRS). In recent years, DFT calculations have become a widely accepted method for predicting the new NLO materials.62,63 However, the βHRS is very sensitive to the selected functionals. Three popular DFT functionals (i.e., B3LYP,40 CAM-B3LYP,59,64 M06-2X65) are selected to test the reliability of our calculation results. The calculated βHRS values of compound 1–4 are given Table 2. Among the selected functionals, the βHRS value calculated by the B3LYP functional is the largest one, whereas the βHRS values calculated by the other two functionals are relatively close. Previous studies also have shown that the B3LYP functional overestimates βHRS.66,67 and the CAM-B3LYP functional combined with 6-31+G(d) basis set is a reliable method to calculate βHRS.63,68 Thus, the βHRS values obtained by CAM-B3LYP/6-31+G(d) level functional were used for further analysis.| Compound | B3LYP | CAM-B3LYP | M06-2X |
|---|---|---|---|
| 1 | 1.03 | 1.13 | 1.14 |
| 2 | 2.43 | 1.64 | 1.68 |
| 3 | 13.95 | 6.75 | 6.82 |
| 4 | 110.15 | 34.99 | 38.29 |
The βHRS values of the studied compounds range from 1.13 to 34.99 × 10−30 esu, indicating that subtle structural changes can obviously enhance the second-order NLO response. Compared with compound 1, the βHRS value of compound 2 is slightly larger than that of compound 1, which shows that the introduction of NH2 unit at R1–R4 positions has little effect on the βHRS value. In contrast, the βHRS value of compound 3 is about 4 times as large as compound 2. It demonstrates that the introduction of the NO2 unit is an effective method to increase the βHRS value. Surprisingly, the βHRS value of compound 4 is the largest of all studied compounds, which is accordance with results of the energy gaps. This magnifies that the introduction of NH2 unit at R1 and R2 positions and NO2 unit at R3 and R4 positions can effectively enhance the NLO response. The βHRS value of compound 4 is 34.99 × 10−30 esu, which is about 207 times as large as the average second-order polarizability of the organic molecule urea.11 Therefore, the studied compounds are expected to be potential large second-order NLO materials.
To explain their NLO origin, the corresponding electron density difference maps (EDDM) of compounds 1 and 4 were given in Fig. 5. It can be seen that the NLO origin of compound 1 mainly derives from the localized CT on 9,9′-bicarbazole units and rings 1, 6, 7 and 12. Obviously, the intramolecular CT is mainly responsible for the NLO origin of the compounds 4 which is transferred from the left nanoloop to the right benzene rings 10–12 and NO2 unit. Therefore, the large NLO response originates from the large charge transfer character.
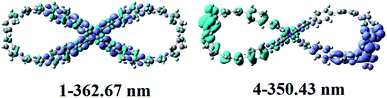 | ||
| Fig. 5 Electron density difference maps of compounds 1 and 4. Blue and purple colours indicate depletion and accumulation of electron density, respectively. | ||
4. Conclusions
In this paper, we employed the DFT/TDDFT theory to investigate the geometrical/electronic structure, electronic absorption, and the second-order NLO properties of four chiral cycloparaphenylene-based molecular lemniscate compounds. The simulated UV-Vis/CD spectra of compound 1 are consistent with the experimental results, which allow us to fully assign the electronic transition properties and absolute configuration. The introduction of the donor or acceptor units or their combinations can effectively reduce energy gaps, make absorption wavelength blue-shift and enhance second-order NLO response. Especially, compound 4 has the largest first hyperpolarizability value among the studied four compounds, indicating that the introduction of their combination is a feasible method to obtain the largest first hyperpolarizability. The charge transfer from the left nanoloop to the right benzene rings 10–12 and NO2 unit is mainly responsible for the NLO origin. Considering their large second-order NLO value and intrinsic asymmetric electronic structure, the studied compounds may become the potential candidates for excellent second-order NLO materials.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work is supported by the Education Department of Jilin Province, China, under grant number 2016511.References
- C. Wang, T. Zhang and W. Lin, Chem. Rev., 2012, 112, 1084–1104 CrossRef CAS PubMed.
- B. J. Coe, J. Fielden, S. P. Foxon, B. S. Brunschwig, I. Asselberghs, K. Clays, A. Samoc and M. Samoc, J. Am. Chem. Soc., 2010, 132, 3496–3513 CrossRef CAS PubMed.
- P. Beaujean, F. Bondu, A. Plaquet, J. Garcia-Amorós, J. Cusido, F. M. Raymo, F. Castet, V. Rodriguez and B. Champagne, J. Am. Chem. Soc., 2016, 138, 5052–5062 CrossRef CAS PubMed.
- P. Singla, N. Van Steerteghem, N. Kaur, A. Ashar, P. Kaur, K. Clays, K. Narayan and K. Singh, J. Mater. Chem. C, 2017, 5, 697–708 RSC.
- C. Hu, Z. Chen, H. Xiao, Z. Zhen, X. Liu and S. Bo, J. Mater. Chem. C, 2017, 5, 5111–5118 RSC.
- K. Tao, Z. Wu, S. Han, J. Zhang, C. Ji, Y. Wang, W. Zhang, J. Luo and Z. Sun, J. Mater. Chem. C, 2018, 6, 4150–4155 RSC.
- S. Edappadikkunnummal, S. N. Nherakkayyil, V. Kuttippurath, D. M. Chalil, N. R. Desai and C. Keloth, J. Phys. Chem. C, 2017, 121, 26976–26986 CrossRef CAS.
- A. Stathis, I. Papadakis, N. Karampitsos, S. Couris, G. Potsi, A. B. Bourlinos, M. Otyepka and R. Zboril, ChemPlusChem, 2019, 84, 1288–1298 CrossRef CAS PubMed.
- M. Gingras, Chem. Soc. Rev., 2013, 42, 1051–1095 RSC.
- E. Botek, J.-M. André, B. Champagne, T. Verbiest and A. Persoons, J. Chem. Phys., 2005, 122, 234713 CrossRef PubMed.
- D. R. Kanis, M. A. Ratner and T. J. Marks, Chem. Rev., 1994, 94, 195–242 CrossRef CAS.
- S. Y. Kim, M. Lee and B. H. Boo, J. Chem. Phys., 1998, 109, 2593–2595 CrossRef CAS.
- A. Plaquet, B. Champagne, J. Kulhánek, F. Bureš, E. Bogdan, F. Castet, L. Ducasse and V. Rodriguez, ChemPhysChem, 2011, 12, 3245–3252 CrossRef CAS PubMed.
- T. C. Zeyrek, J. Korean Chem. Soc., 2013, 57, 461–471 CrossRef CAS.
- J.-Z. Liao, D.-C. Chen, F. Li, Y. Chen, N.-F. Zhuang, M.-J. Lin and C.-C. Huang, CrystEngComm, 2013, 15, 8180–8185 RSC.
- A. A. Kalinin, S. M. Sharipova, T. I. Burganov, A. I. Levitskaya, O. D. Fominykh, T. A. Vakhonina, N. V. Ivanova, A. R. Khamatgalimov, S. A. Katsyuba and M. Y. Balakina, J. Photochem. Photobiol. Chem., 2019, 370, 58–66 CrossRef CAS.
- L. Gong, C. Liu, C. Ma, W. Lin, J. Lv and X. Zhang, RSC Adv., 2019, 9, 17382–17390 RSC.
- T. Verbiest, S. Van Elshocht, M. Kauranen, L. Hellemans, J. Snauwaert, C. Nuckolls, T. J. Katz and A. Persoons, Science, 1998, 282, 913–915 CrossRef CAS PubMed.
- S. Sergeyev, D. Didier, V. Boitsov, A. Teshome, I. Asselberghs, K. Clays, C. M. Vande Velde, A. Plaquet and B. Champagne, Chem.–Eur. J., 2010, 16, 8181–8190 CrossRef CAS PubMed.
- D. Cornelis, E. Franz, I. Asselberghs, K. Clays, T. Verbiest and G. Koeckelberghs, J. Am. Chem. Soc., 2011, 133, 1317–1327 CrossRef CAS PubMed.
- S. Suresh, A. Ramanand, D. Jayaraman and P. Mani, Rev. Adv. Mater. Sci., 2012, 30, 175–183 CAS.
- B. J. Coe, D. Rusanova, V. D. Joshi, S. Sánchez, J. Vávra, D. Khobragade, L. Severa, I. Císařová, D. Šaman and R. Pohl, J. Org. Chem., 2016, 81, 1912–1920 CrossRef CAS PubMed.
- L. E. Buckley, B. J. Coe, D. Rusanova, S. Sánchez, M. Jirásek, V. D. Joshi, J. Vávra, D. Khobragade, L. Pospíšil and Š. Ramešová, Dalton Trans., 2017, 46, 1052–1064 RSC.
- J.-T. Ye, H.-Q. Wang, Y. Zhang and Y.-Q. Qiu, J. Phys. Chem. C, 2020, 124, 921–931 CrossRef CAS.
- B. Li, P. Sathishkumar, F. L. Gu and C. Zhu, J. Phys. Chem. A, 2020, 124, 955–965 CrossRef CAS PubMed.
- Y. Tanaka, S. Saito, S. Mori, N. Aratani, H. Shinokubo, N. Shibata, Y. Higuchi, Z. S. Yoon, K. S. Kim and S. B. Noh, Angew. Chem., Int. Ed., 2008, 47, 681–684 CrossRef CAS PubMed.
- T. Tanaka and A. Osuka, Chem. Rev., 2017, 117, 2584–2640 CrossRef CAS PubMed.
- M. Stępień, N. Sprutta and L. Latos-Grażyński, Angew. Chem., Int. Ed., 2011, 50, 4288–4340 CrossRef PubMed.
- M. Stępień, L. Latos-Grażyński, N. Sprutta, P. Chwalisz and L. Szterenberg, Angew. Chem., Int. Ed., 2007, 46, 7869–7873 CrossRef PubMed.
- R. Herges, Chem. Rev., 2006, 106, 4820–4842 CrossRef CAS PubMed.
- D. Ajami, K. Hess, F. Köhler, C. Näther, O. Oeckler, A. Simon, C. Yamamoto, Y. Okamoto and R. Herges, Chem.–Eur. J., 2006, 12, 5434–5445 CrossRef CAS PubMed.
- D. Ajami, O. Oeckler, A. Simon and R. Herges, Nature, 2003, 426, 819–821 CrossRef CAS PubMed.
- G. R. Schaller, F. Topić, K. Rissanen, Y. Okamoto, J. Shen and R. Herges, Nat. Chem., 2014, 6, 608 CrossRef CAS PubMed.
- G. Naulet, L. Sturm, A. Robert, P. Dechambenoit, F. Röhricht, R. Herges, H. Bock and F. Durola, Chem. Sci., 2018, 9, 8930–8936 RSC.
- B. Thulin and O. Wennerström, Acta Chem. Scand., Ser. B, 1976, 30, 688–690 CrossRef.
- A. Robert, P. Dechambenoit, E. A. Hillard, H. Bock and F. Durola, Chem. Commun., 2017, 53, 11540–11543 RSC.
- K. Senthilkumar, M. Kondratowicz, T. Lis, P. J. Chmielewski, J. Cybińska, J. L. Zafra, J. Casado, T. Vives, J. Crassous and L. Favereau, J. Am. Chem. Soc., 2019, 141, 7421–7427 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, et al.Gaussian 09 Revision E.01, Gaussian, Inc., Wallingford, CT, 2010 Search PubMed.
- M. Elstner, P. Hobza, T. Frauenheim, S. Suhai and E. Kaxiras, J. Chem. Phys., 2001, 114, 5149–5155 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- L.-K. Xu, T.-J. Bi, M.-J. Ming, J.-B. Wang and X.-Y. Li, Chem. Phys. Lett., 2017, 679, 158–163 CrossRef CAS.
- F. Ahmad, M. J. Alam, M. Alam, S. Azaz, M. Parveen, S. Park and S. Ahmad, J. Mol. Struct., 2018, 1151, 327–342 CrossRef CAS.
- S. S. Meenakshi Sundaram, S. Karthick, K. Sailaja, R. Karkuzhali and G. Gopu, J. Photochem. Photobiol., B, 2020, 203, 111735 CrossRef PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Luque, M. Orozco, P. Bhadane and S. Gadre, J. Phys. Chem., 1993, 97, 9380–9384 CrossRef CAS.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef CAS.
- F. Mançois, L. Sanguinet, J.-L. Pozzo, M. Guillaume, B. Champagne, V. Rodriguez, F. Adamietz, L. Ducasse and F. Castet, J. Phys. Chem. B, 2007, 111, 9795–9802 CrossRef PubMed.
- A. Plaquet, M. Guillaume, B. Champagne, F. Castet, L. Ducasse, J.-L. Pozzo and V. Rodriguez, Phys. Chem. Chem. Phys., 2008, 10, 6223–6232 RSC.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107 CrossRef PubMed.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2004, 121, 12772–12773 CrossRef CAS.
- C. Liu, Y. Si, S. Shi, G. Yang and X. Pan, Dalton Trans., 2016, 45, 7285–7293 RSC.
- D. Jacquemin, B. Mennucci and C. Adamo, Phys. Chem. Chem. Phys., 2011, 13, 16987–16998 RSC.
- C. Guido, D. Jacquemin, C. Adamo and B. Mennucci, J. Chem. Theor. Comput., 2015, 11, 5782–5790 CrossRef CAS PubMed.
- S. Tomić and N. M. Harrison, AIP Conf. Proc., 2010, 1199, 65–66 CrossRef.
- R. Orlando, V. Lacivita, R. Bast and K. Ruud, J. Chem. Phys., 2010, 132, 244106 CrossRef PubMed.
- V. Barone and A. Polimeno, Chem. Soc. Rev., 2007, 36, 1724–1731 RSC.
- A. Pedone, J. Chem. Theory Comput., 2013, 9, 4087–4096 CrossRef CAS PubMed.
- A. B. Tathe, L. Rhyman, P. Ramasami and N. Sekar, J. Fluoresc., 2015, 25, 1117–1126 CrossRef CAS PubMed.
- A. Sorkin, M. A. Iron and D. G. Truhlar, J. Chem. Theory Comput., 2008, 4, 307–315 CrossRef CAS PubMed.
- Y. Zhang and B. Champagne, J. Phys. Chem. C, 2012, 116, 21973–21981 CrossRef CAS.
- M. Torrent-Sucarrat, J. Anglada and J. Luis, J. Chem. Theor. Comput., 2011, 7, 3935–3943 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- J.-L. Chen, J.-T. Hong, K.-J. Wu and W.-P. Hu, Chem. Phys. Lett., 2009, 468, 307–312 CrossRef CAS.
- H. Sun and J. Autschbach, ChemPhysChem, 2013, 14, 2450–2461 CrossRef CAS PubMed.
- S. J. A. Van Gisbergen, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1998, 109, 10657–10668 CrossRef CAS.
- M. de Wergifosse and B. Champagne, J. Chem. Phys., 2011, 134, 074113 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: The computed main absorption band (λ, nm) using the B3LYP functional at the different basis sets level for compound 1, the computed main absorption band (λ, nm) using the different functionals at 6-31G(d) basis set level for compound 1. See DOI: 10.1039/d0ra01323d |
| ‡ L. J. Gong and C. Ma: these authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2020 |