Open Access Article
Open Access ArticleCu–Ag alloy for engineering properties and applications based on the LSPR of metal nanoparticles
Chao-chao Jian,
Jianqi Zhang and
Xiangchao Ma *
*
School of Physics and Optoelectronic Engineering, Xidian University, Xi'an, 710071, China. E-mail: xcma@xidian.edu.cn
First published on 1st April 2020
Abstract
Efficient generation of high-energy hot carriers from the localized surface plasmon resonance (LSPR) of noble metal (Ag, Au and Cu) nanoparticles is fundamental to many applications based on LSPR, such as photovoltaics and photocatalysis. Theoretically, intra- and inter-band electron transitions in metal nanoparticles are two important channels for the non-radiative decay of LSPR, which determine the generation rate and energy of hot carriers. Therefore, on the basis of first-principles calculations and Drude theory, in this work we explore the potential role of alloying Ag with Cu in modulating the generation rate and energy of hot carriers by studying the intra- and inter-band electron transitions in Cu, Ag and Cu–Ag alloys. It is meaningful to find that the d-sp inter-band electron transition rates are notably increased in Cu–Ag alloys. In particular, the inter-band electron transition rates of Cu0.5Ag0.5 become larger than that of single Cu and Ag across the whole energy range between 1.5 and 3.2 eV. In contrast, intra-band electron transition rates of Cu–Ag alloys become smaller than that of single Cu and Ag. Because the intra-band electron transitions mainly contribute to the resistive loss in metals, which finally results in a thermal effect rather than high-energy hot carriers, the reduction of intra-band electron transitions in Cu–Ag alloy is beneficial for the transforming the energy absorbed by LSPR into high-energy hot carriers through other non-radiative channels. These results indicate that alloying of Ag and Cu can effectively improve the generation rates of high-energy hot carriers through the inter-band electron transition, but decrease the resistive loss through intra-band transition of electrons, which should be used as a guide in optimizing the non-radiative decay processes of LSPR.
Introduction
In 1972, Fujishima discovered the so-called “Honda–Fujishima Effect”, which uncovered the prelude of heterogeneous photocatalysis.1 Over the past decades, the technologies of photo-chemistry and photocatalysis have been widely applied in fields including pollutant degradation,2 water decomposition,3 carbon dioxide reduction,4 etc. Photocatalytic materials and photocatalytic conditions are the two main factors influencing photocatalytic efficiency, among which photocatalytic materials are paid the most attention.5–7 Semiconductors are one of the most important types of photocatalytic materials, but they generally exhibit band structure mismatch with solar energy, inefficient light absorption and high recombination rate of photo-generated carriers, which significantly limit the solar energy conversion efficiency. Therefore, expanding the spectral response range (especially the visible light) and prolonging the lifetime of photo-generated carriers are important for improving photocatalytic efficiency. In this respect, the localized surface plasmon resonance (LSPR), which is typically observed in the nanoparticles of noble metals upon certain light irradiation, is promising in improving the solar energy conversion. Plasmonic systems are promising as alternatives to semiconductors because the LSPR of metal nanoparticles can absorb solar energy more efficiently. For example, Linic et al. systematically illustrated the applications of plasmonic metal nanostructures for effective conversion of solar to chemical energy.8LSPR is the collective oscillation of conduction electrons in metallic nanoparticles when the incident photon frequency matches the intrinsic resonant frequency of the conduction electrons. Physically, all metals can have resonant polarization and the difference lies in the energy range.9 Most of the solar energy consists of ultraviolet-visible light, so we mainly focus on the noble metal (Au, Ag and Cu) nanostructures with LSPR. The solar energy absorbed by LSPR supplies the photocatalytic process through primarily two mechanisms: the generation of hot carriers and near-field enhancement.10,11 On one hand, the inevitable non-radiative decay of LSPR results in electron transitions in metal nanoparticles, thus generating electrons and holes with high energy (the so-called hot carriers).12 Some hot carriers with enough energy and proper momentum can not only directly participate in redox reactions on the surface of nanoparticles, but also be transferred to adjacent semiconductors, which then induce redox reactions on the surface of semiconductor.13 As can be inferred, the generation rates and energy distribution of hot carriers play central roles in determining the photocatalytic efficiency based on the hot carriers. On the other hand, the near-field enhancement can significantly improve the absorption efficiency of adjacent semiconductor with proper bandgap.14
Theoretically, the non-radiative decay of LSPR can take place through four channels:15 (1) inter-band electron transition; (2) surface-assisted electron transition; (3) phonon-assisted electron transition; (4) the classical resistive loss. Among them, the inter-band electron transition contributes mostly to the generation of hot carriers, and the resistive loss, which originates from the intra-band transitions of conduction electrons, mainly generates heat and competes with the other channels. Therefore, for efficient generation of hot carriers, it is important to find ways to improve the inter-band electron transition of plasmonic metals, but decrease the resistive loss. The electronic structures of metal fundamentally determine the intra- and inter-band electronic transitions,16 which can be adjusted by various methods, such as strain,17 defects18 and alloying.19 It is interesting to investigate the role of alloy in modulating the electronic structure and optical properties of metals.20,21 In order to examine whether alloying Au with another metal is beneficial for plasmonic application, Keast et al. investigated the alloys and compounds of Au with other metals by calculating the density of states (DOS), dielectric function and plasmon quality factor.22 The results showed that certain compounds of Au are suitable for plasmonic applications. For the metal alloy, the key factor is the ratio of metals in the alloy. Zhang et al. reported that atomic ratio in Pd–Cu alloy influences the catalytic performance of HCOOH oxidation.23 Wang et al. measured fast nonlinear refractive index and nonlinear absorption coefficient of Ag–Cu alloy nanocluster.24 The results show that with different Ag/Cu ratio, linear absorption and nonlinear absorption are different in near infrared (NIR) region. It is suggested that by changing the ingredient percentage of metals in alloy, different optical nonlinearities could be selectively obtained.
In this paper, Cu–Ag alloy is taken as an example to explore the potential impact of atomic ratios in modulating the generation and energy distribution of hot carriers through the non-radiative decay of LSPR. Specifically, the electronic structures and optical properties of pure Cu, Ag and Cu0.125Ag0.875, Cu0.25Ag0.75, and Cu0.5Ag0.5 are systematically investigated on the basis of first-principles calculations and Drude theory. And the effect of alloy on the near-field properties is also assessed by calculating the dimensionless quality factor. It is found that Cu–Ag alloy can significantly increase the generation rates of high-energy hot electrons by increasing the inter-band electron transitions within the energy between 1.5 and 3.2 eV, and the behavior of Cu0.5Ag0.5 alloy even surpass that of single Cu and Ag. On the other hand, Cu–Ag alloys reduce the near-field enhancement compared to both Ag and Cu. These results show that Cu–Ag is beneficial for applications based on the generation of hot carriers, but is unfavorable for applications based on the near-field enhancement.
Computational method
Our DFT calculation are conducted using VASP based on the plane wave basis function, and the generalized gradient approximation (GGA) of Perdew, Burke, and Ernzerhof (PBE) was used for the exchange–correlation potential.25 The plane wave cutoff energy is 500 eV. Firstly, all the Cu–Ag alloyunit cells with different atomic ratios are structurally relaxed, so that each atom is subjected to a force that less than 0.01 eV Å−1, and a stable alloy crystal structure is obtained. During structure optimization and self-consistent, the Brillouin zones for the alloys are sampled with (4 × 8 × 8). In the calculation of optical properties, a much denser k-points (16 × 32 × 32) are used for sampling the Brillouin zones to reach converged results.26 All the parameters above have been tested to give converged results.For Cu–Ag alloy crystals, this paper mainly focuses on the light absorption caused by the d-sp inter-band electron transitions and the sp intra-band electron transitions. The electron transition rates of the d-sp inter-band and the sp intra-band are characterized, respectively. The light absorption coefficient α(ω) of Cu–Ag related to the d-sp inter-band electronic transition27 is calculated as follows:
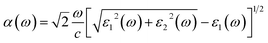 | (1) |
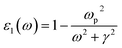 | (2) |
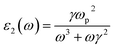 | (3) |
Then the optical absorption coefficients are evaluated according to eqn (1). As shown in eqn (2) and (3), the plasma frequency31 ωp2 and inverse electron lifetime γ must be calculated to obtain the dielectric function. The details for calculating plasma frequency are the same as our previous work.17 For the inverse electron lifetime γ, the typical experimental value for noble metals, ℏγ ∼ 0.1 eV, is used.32 On the other hand, the near-field and light absorption properties are also important factors affecting the solar energy conversion efficiency based on the LSPR, so the near-field enhancement is described by calculating the quality factor.22 This parameter provides a frequency-dependent value that is related to the near-field enhancement for a plasmon excitation.
Results and discussion
Crystal structures of Cu–Ag alloys
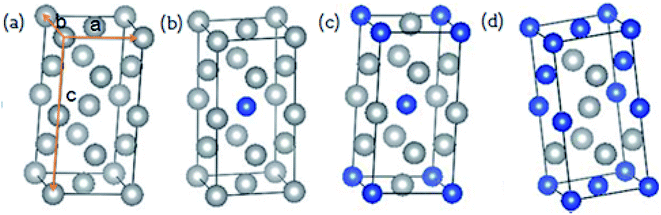
In 2016, Gong et al. experimentally prepared the Cu–Ag alloy films by mixing Cu and Ag metals in different proportions and explored the effects of metal alloy ratios on optical properties.33 It is shown that the metal ratio significantly affects the optical properties of metal alloy. Since Cu and Ag elements belong to the same family in the periodic table and have the same electronic configuration, and both are face-centered cubic crystals, the difference in their atomic radius is less than 15%, and a substitutional solid solution can be formed. Keast et al. constructed substitutional alloys,22 AuX, by setting two units of the Au conventional cell and replacing one of the eight atoms with substitutional element, X. In order to construct Cu–Ag alloys with different atomic ratios, the same method is used as shown in Fig. 1 and the substitute atoms (Cu) in Cu–Ag alloys have a random occupancy on the positions of Ag. It is noted that the Cu–Ag alloys in the composition range that was investigated are not thermodynamically stable, and they should be produced by some non-equilibrium technique such as physical vapor deposition. The calculated lattice constants of Cu–Ag alloy unit cells are listed in Table 1. From Table 1, the lattice constants of Ag and Cu are respectively 4.147 and 3.638 Å, which are very similar to the experimental values.30 For the Cu–Ag alloys, their lattice constants are between that of Ag and Cu, and the lattice constants gradually decrease as the ratio of Cu increase. On the other hand, for the same atomic ratio, the lattice constants with different alloy structures are almost the same.| Ag | Cu | Cu0.125Ag0.875 | Cu0.25Ag0.75 | Cu0.5Ag0.5 | |
|---|---|---|---|---|---|
| a | 4.147 | 3.638 | 4.094 | 4.037 | 3.948 |
| b | 4.147 | 3.638 | 4.094 | 4.037 | 3.909 |
| c | 8.295 | 7.276 | 8.188 | 8.075 | 7.782 |
Electronic structures of Cu–Ag alloys with different atomic ratios
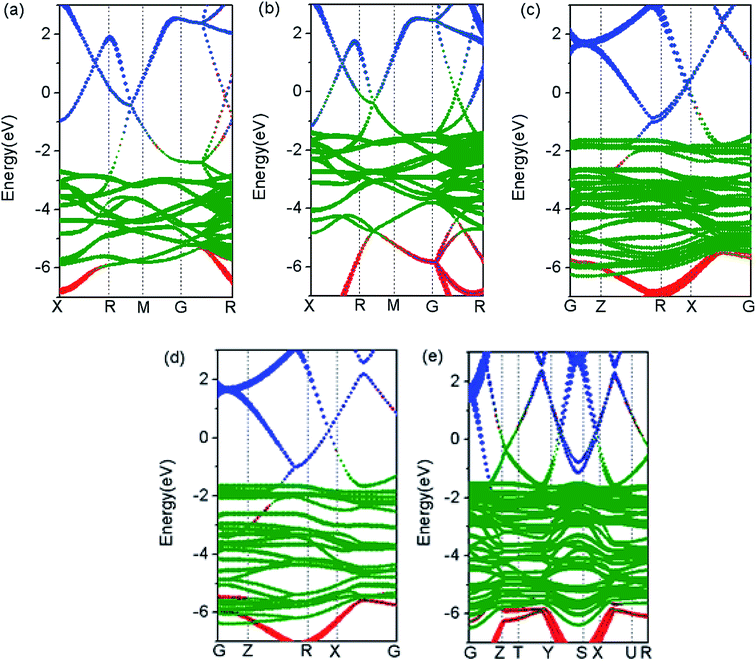
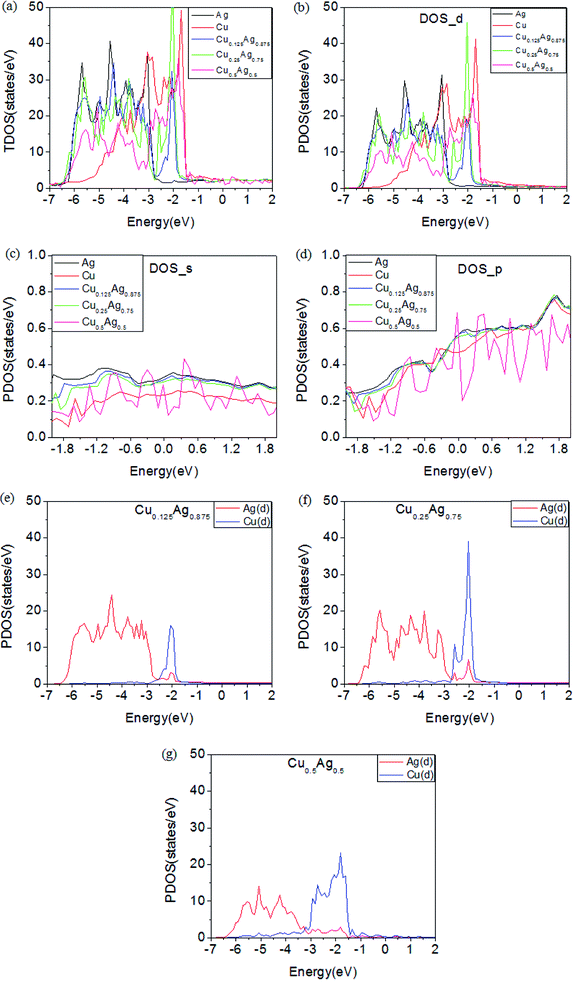
Cu–Ag alloy nanoparticles may efficiently absorb solar energy on the basis of LSPR, and the non-radiation decay of LSPR can generate large number of hot electrons and holes by exciting intra- and inter-band electron transitions. Therefore, the detailed distribution of electronic states near the Fermi level determines the energy of hot carriers in Cu–Ag alloys. In Fig. 2, we show the band structures of Cu–Ag alloys with different atomic ratios. In comparison with pure Cu and Ag, the d-bands of Cu–Ag alloys are significantly expanded, and the expansion slightly increases with the ratio of Cu. In addition, the upper edge of the d-bands in Cu–Ag alloys moves closer to the Fermi level and is located at about −1.5 eV below the Fermi level, which is similar to that of pure Cu, but higher than that of pure Ag by about 1 eV. This indicates that the energy of hot holes in Cu–Ag alloys may be very similar to that of pure Cu. Furthermore, the hybridization of d states with s and p states near the Fermi level increase as the ratio of Cu in the alloys, suggesting that the d-sp inter-band transition rates may become larger. In addition, the position of the sp hybridization band near the Fermi level varies with the ratio of Cu. From the point of view of the d-sp inter-band and sp intra-band electronic transitions, the results above indicate that alloying Ag with Cu may significantly change the energy distribution and generation rates of hot carriers from the decay of LSPR.To uncover the behavior of band structures for Cu–Ag alloys above, we further investigate the total and orbital projected density of states (TDOS and PDOS) of pure Cu, Ag and Cu–Ag alloys. As shown in Fig. 3(a), the changes in the DOS are mainly located in the energy range between −6.5 and −1.5 eV, whereas the DOS located in the energy range near the Fermi level is only slightly changed. From the results of band structures in Fig. 2, the DOS in the energy range between −6.5 and −1.5 eV are mainly contributed by the d orbitals of metals. Therefore, in Fig. 3(b) we show PDOS of d orbitals for the pure Cu, Ag and Cu–Ag alloys. As can be seen, the d-band width is progressively increased with the ratio of Cu. Moreover, the limiting values for the lower edges and upper edges of the d-band are approaching that of the Ag and Cu atoms, respectively. Detailed investigation of PDOS for the d orbitals of Ag and Cu components in the Cu–Ag alloys shows that the extension of the d-bands results from the strong hybridization of the d orbitals of Ag and Cu components. As shown in Fig. 3(e–g), in each alloy there are some resonant peaks for the d orbitals of Ag and Cu at some energy values, and the number of resonant peaks increases with the ratio of Cu. Moreover, the widths for the d orbitals of Ag and Cu components respectively increase with the ratio of Cu. The extension of the d-bands can facilitate the hybridization of them with the sp bands, thus may increase the d-sp inter-band transition range and transition rate. For the PDOS of s and p orbitals of the pure Cu, Ag and Cu–Ag alloys, as shown in Fig. 3(c) and (d), their distributions in energy are almost the same, but their specific values are different at a given energy value. In particular, the s and p PDOS of Cu0.5Ag0.5 are quite different from the others. These results indicate that the sp intra-band transition properties can also be modulated to some extent. Moreover, effects on the inter- and intra-band transition properties of electron depend strongly on the specific alloy ratio and structures.
The reason for the changes in the electronic structures of Cu–Ag alloys can be understood as two aspects: on one hand, it can be seen from Table 1 that the volume of Cu–Ag alloys with different atomic ratios is reduced to varying degrees compared to pure Ag crystal. Since the atomic radius of the Cu atom is smaller than that of the Ag atom, replacing the Ag atoms with the Cu atoms is equivalent to the lattice volume compression. According to the free-electron gas model of metal, the decrease in the volume of Cu–Ag alloys can increase the degree of delocalization of the free electron like sp band. On the other hand, the distance between the Cu and Ag atoms in Cu–Ag alloy is reduced relative to that in pure Ag. According to the tight binding model, the d-band dispersion of Cu–Ag alloys may be increased. Meanwhile, the d-sp hybridization can also become stronger.
Intra- and inter-band optical absorption properties of Cu–Ag alloys with different atomic ratios
The above band structures and DOS of Cu–Ag alloys indicate that Cu–Ag alloys can change the energy distribution of hot carriers and intra- and inter-band electron transition properties, which may affect the non-radiative decay of the LSPR based on the alloy nanoparticles. To quantify the effects of different atomic ratios on electronic transitions, the optical absorption coefficients of Cu–Ag alloys with different atomic ratios are calculated and shown in Fig. 4. For comparison, the results of pure Cu and Ag are also calculated. In this paper, the concept of metal alloying is proposed to improve the solar energy conversion efficiency on the basis of LSPR. Therefore, we mainly focus on the light absorption between 1.5 and 3.2 eV, which includes the majority of solar energy. Fig. 4(a) shows the calculated optical absorption coefficients contributed by the d-sp inter-band electron transitions. For pure Ag, the absorption coefficients in the energy between 1.5 and 2.4 eV is almost zero, and start to progressively increase in the energy range between 2.4 and 3.2 eV. In contrast, the absorption coefficients of Cu in the whole energy range between 1.5 and 3.2 eV is much larger than that of Ag, and steadily increases with energy. Therefore, it is inferred that addition of certain amount of Cu may increase the absorption coefficients of Ag and thereby increase the solar to hot carrier conversion efficiency. Indeed, as shown in Fig. 4(a), in comparison with Ag, the absorption coefficients of the Cu–Ag alloys are notably increased. In particular, the absorption coefficients of Cu0.5Ag0.5 become even larger than that of Cu across the whole energy range. In addition, for Cu0.125Ag0.875 the absorption coefficients also become larger than that of Cu in the energy range between 1.5 and 1.8 eV. All the results above indicate that Cu–Ag alloy can increase the d-sp inter-band transition rates, and the properties of alloy with proper ratio and structure can even surpass that of the single component metals.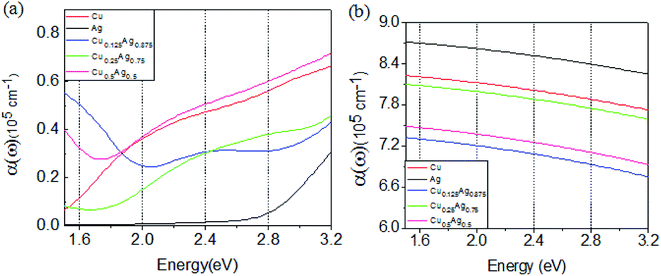 | ||
| Fig. 4 Optical absorption coefficients as a function of energy due to the inter-band (a) and intra-band (b) electron transitions for pure Cu, Ag and Cu–Ag alloys with different atomic ratios. | ||
Free electrons in a metal may jump between different electronic states within the same energy band forming hot carriers. Due to the high concentration of carriers in metal, it is necessary to analyze the contribution of intra-band electron transition rates, which is also an important channel for the non-radiative decay of LSPR. Fig. 4(b) shows the calculated absorption coefficients of pure Cu, Ag, and Cu–Ag alloys due to intra-band electron transitions. Theoretically, the onsets of sp intra-band absorption can start at 0 eV. However, in terms of solar energy conversion, as stated previously, we focus mainly on the energy range between 1.5 and 3.2 eV. Contrary to the inter-band absorption properties, Fig. 4(b) shows that the intra-band absorption coefficients of Cu–Ag alloy are reduced, and the reduction in Cu0.125Ag0.875 is the largest. As shown in the part of Computational methods, in this work the optical absorption due to the intra-band electron transition is calculated on the basis of Drude model. This means that the calculated intra-band transitions here mainly contribute to the resistive loss in metals, which finally result in thermal effect rather than high-energy hot carriers in metal. Therefore, the reduction of intra-band transitions in Cu–Ag alloy can be beneficial for the transforming the energy absorbed by LSPR into high-energy hot carriers through other non-radiative decay channels. In addition, it seems that the changes with atomic ratio in alloys for both the inter- and intra-band transition is rather random.
Near field enhancement effect
The near-field enhancement is another important effect induced by the LSPR of metallic nanoparticles, which has also shown many applications.34 In this section we further analyze the potential effect of Cu–Ag alloy on the LSPR near-field enhancement. To do this, we calculate the dimensionless quality factor Q, which is defined as:35
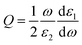 | (4) |
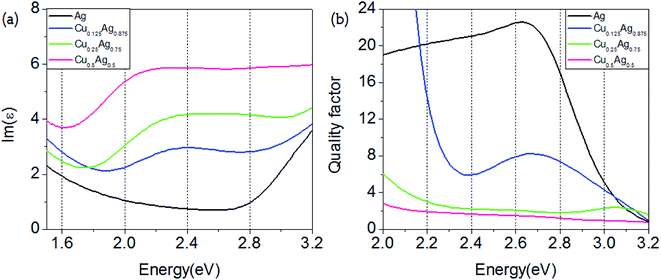 | ||
| Fig. 5 Energy-dependent imaginary parts of the dielectric function (a) and quality factor Q (b) for pure Ag and Cu–Ag alloys with different atomic ratios. | ||
Conclusion
In conclusion, to investigate the effects of Cu–Ag alloy in engineering the properties and applications based the LSPR of metal nanoparticles, we have systematically studied the electronic structures and optical properties of pure Cu, Ag and three Cu–Ag alloys with different atomic ratios and alloy structures. It is shown that the hybridization of d-bands between Ag and Cu atoms is rather strong and increases with the atomic ratio of Cu in Cu–Ag alloys, which decreases the d-sp inter-band transition energy and increases the d-sp inter-band transition rates. Therefore, the absorption coefficients resulting from the d-sp inter-band transitions are significantly increased for Cu–Ag alloys. In particular, the absorption coefficients of Cu0.5Ag0.5 become larger than that of single Cu and Ag across the whole energy range between 1.5 and 3.2 eV. In addition, for Cu0.125Ag0.875 the absorption coefficients are also larger than that of single Cu and Ag in the energy range between 1.5 and 1.8 eV. In contrast, the absorption coefficients due to sp intra-band transition become smaller than that of single Cu and Ag. Because the intra-band transitions investigated here mainly contribute to the resistive loss in metals, which finally result in thermal effect rather than high-energy hot carriers in metal. Therefore, the reduction of intra-band transitions in Cu–Ag alloy can be beneficial for the transforming the energy absorbed by LSPR into high-energy hot carriers through other non-radiative decay channels. These results indicate that alloying of Ag and Cu can effectively improve the generation rates of hot carriers through the inter-band transition, but decrease the resistive loss through intra-band transition of electrons, which should be used as a guide in optimizing the non-radiative decay processes of LSPR. On the other hand, it is found that Cu–Ag alloys reduce the near-field enhancement due to the increase in the inter-band electron transitions. Therefore, Cu–Ag alloys are not suitable for applications based on the near-field enhancement effects of LSPR.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (11704298), the 2018 Postdoctoral Innovation Talent Support Program (BX20180233), the Key Industry Innovation Chain of Shaanxi (2018JQ1054), the China Postdoctoral Science Foundation (2019M653549), and the 111 Project (B17035).References
- A. Fujishima and K. Honda, Electrochemical Photolysis of Water at a Semiconductor Electrode, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- L. Zhang, C. Yang, K. Lv, Y. Lu, Q. Li, X. Wu, Y. Li, X. Li, J. Fan and M. Li, SPR Effect of Bismuth Enhanced Visible Photoreactivity of Bi2WO6 for NO Abatement, Chin. J. Catal., 2019, 40, 755–764 CrossRef CAS.
- T. Hisatomi and K. Domen, Reaction Systems for Solar Hydrogen Production via Water Splitting with Particulate Semiconductor Photocatalysts, Nat. Catal., 2019, 2, 387–399 CrossRef CAS.
- L. Collado, A. Reynal, F. Fresno, M. Barawi, C. Escudero, V. Perez-Dieste, J. M. Coronado, D. P. Serrano, J. R. Durrant and V. A. de la Peña O’Shea, Unravelling the Effect of Charge Dynamics at the Plasmonic Metal/Semiconductor Interface for CO2 Photoreduction, Nat. Commun., 2018, 9, 4986 CrossRef PubMed.
- L. Yang, F. Wang, A. Hakki, D. E. Macphee, P. Liu and S. Hu, The Influence of Zeolites Fly Ash Bead/TiO2 Composite Material Surface Morphologies on Their Adsorption and Photocatalytic Performance, Appl. Surf. Sci., 2017, 392, 687–696 CrossRef CAS.
- A. Santinom, M. A. d. Silva, J. E. L. Villa, R. J. Poppi, I. O. Mazali and D. P. d. Santos, Surface-enhanced Raman Scattering (SERS) as Probe of Plasmonic Near-field Resonances, Vib. Spectrosc., 2018, 99, 34–43 CrossRef CAS.
- H. Qin, Q. Wei, J. Wu, F. Yang, B. Zhou, Y. Wang and S. Tian, Effects of Ag Nanoparticles on the Visible-light-driven Photocatalytic Properties of Cu2O Nanocubes, Mater. Chem. Phys., 2019, 232, 240–245 CrossRef CAS.
- S. Linic, P. Christopher and D. B. Ingram, Plasmonic-metal Nanostructures for Efficient Conversion of Solar to Chemical Energy, Nat. Mater., 2011, 10, 911–921 CrossRef CAS PubMed.
- B. Hammer and J. K. Norskov, Why Gold is the Noblest of All the Metals, Nature, 1995, 376, 238–240 CrossRef CAS.
- T. Zhang, D. Su, R. Z. Li, S. J. Wang, F. Shan, J. J. Xu and X. Y. Zhang, Plasmonic Nanostructures for Electronic Designs of Photovoltaic Devices: Plasmonic Hot-carrier Photovoltaic Architectures and Plasmonic Electrode Structures, J. Photonics Energy, 2016, 6, 1–13 CAS.
- X. C. Ma, Y. Dai, L. Yu and B. B. Huang, Energy Transfer in Plasmonic Photocatalytic Composites, Light: Sci. Appl., 2016, 5, e16017 CrossRef CAS PubMed.
- T. Barman, A. A. Hussain, B. Sharma and A. R. Pal, Plasmonic Hot Hole Generation by Interband Transition in Gold-polyaniline, Sci. Rep., 2015, 5, 18276 CrossRef CAS PubMed.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Linear Optical Properties in the Projector-augmented Wave Methodology, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- A. Manjavacas, J. G. Liu, V. Kulkarni and P. Nordlander, Plasmon-induced Hot Carriers in Metallic Nanoparticles, ACS Nano, 2014, 8, 7630 CrossRef CAS PubMed.
- A. M. Brown, R. Sundararaman, P. Narang, W. A. Goddard III and H. A. Atwater, Nonradiative Plasmon Decay and Hot Carrier Dynamics: Effects of Phonons, Surfaces, and Geometry, ACS Nano, 2016, 10, 957–966 CrossRef CAS PubMed.
- A. M. Brown, R. Sundararaman, P. Narang, A. M. Schwartzberg, W. A. Goddard III and H. A. Atwater, Experimental and Ab Initio Ultrafast Carrier Dynamics in Plasmonic Nanoparticles, Phys. Rev. Lett., 2017, 118, 087401 CrossRef PubMed.
- X. Ma, H. Sun, Y. Wang, X. Wu and J. Zhang, Electronic and Optical Properties of Strained Noble Metals: Implications for Applications Based on LSPR, Nano Energy, 2018, 53, 932–939 CrossRef CAS.
- X. Zhang, J. Li, X. Wang, Z. Chen, J. Mao, Y. Chen and Y. Pei, Vacancy Manipulation for Thermoelectric Enhancements in GeTe Alloys, J. Am. Chem. Soc., 2018, 1–5 Search PubMed.
- J. H. Dou, Z. A. Yu, J. Zhang, Y. Q. Zheng, Z. F. Yao, Z. Tu, X. Wang, S. Huang, C. Liu, J. Sun, Y. Yi, X. Cao, Y. Gao, J. Y. Wang and J. Pei, Organic Semiconducting Alloys with Tunable Energy Levels, J. Am. Chem. Soc., 2019, 141, 6561–6568 CrossRef CAS PubMed.
- X. k. Wu, W. j. Chen, Y. s. Yu and Y. l. Tang, The First Principle Study of the Electronic Structure of SixGe(1−x) Alloy Films, Phys. Lett. A, 2018, 382, 3418–3422 CrossRef CAS.
- P. Kapoora, A. Kumar, M. Sharma, J. Kumar, A. Kumar and P. K. Ahluwalia, Alloyed Monolayers of Cu, Ag, Au and Pt in Hexagonal Phase: A Comprehensive First Principles Study, Mater. Sci. Eng., B, 2018, 228, 84–90 CrossRef.
- V. J. Keast, R. L. Barnett and M. B. Cortie, First Principles Calculations of the Optical and Plasmonic Response of Au Alloys and Intermetallic Compounds, J. Phys.: Condens. Matter, 2014, 26, 305501 CrossRef CAS PubMed.
- R. Zhang, M. Yang, M. Peng, L. Ling and B. Wang, Understanding the Role of Pd:Cu Ratio, Surface and Electronic Structures in Pd-Cu Alloy Material Applied in Direct Formic Acid Fuel Cells, Appl. Surf. Sci., 2019, 465, 730–739 CrossRef CAS.
- Y. H. Wang, C. Z. Jiang, F. Ren, Q. Q. Wang, D. J. Chen and D. J. Fu, Effect of Ingredient on Optical Properties of Ag/Cu Metal Alloy Nanoclusters in Silica Glass, J. Mater. Sci., 2007, 42, 7294–7298 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-zone Integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- X. Huang, T. R. Paudel, S. Dong and E. Y. Tsymbal, Hexagonal Rare-earth Manganites as Promising Photovoltaics and Light Polarizers, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(8), 125201 CrossRef.
- N. Shahcheraghi, V. J. Keast, A. R. Gentle, M. D. Arnold and M. B. Cortie, Anomalously Strong Plasmon Resonances in Aluminium Bronze by Modification of the Electronic Density-of-states, J. Phys.: Condens. Matter, 2016, 28, 405501 CrossRef CAS PubMed.
- K. S. B. De Silva, A. Gentle, M. Arnold, V. J. Keast and M. B. Cortie, Dielectric Function and its Predicted Effect on Localized Plasmon Resonances of Equiatomic Au–Cu, J. Phys. D: Appl. Phys., 2015, 48, 215304 CrossRef.
- N. W. Ashcroft, N. D. Mermin and W. Dan, Solid State Physics Revised Edition, Cengage Leaning Asia Pte Ltd, 2016 Search PubMed.
- J. Harl, G. Kresse, L. D. Sun, M. Hohage and P. Zeppenfeld, Ab initio Reflectance Difference Spectra of the Bare and Adsorbate Covered Cu(110) Surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 35436 CrossRef.
- M. J. v. Setten, S. Er, G. Brocks, R. A. d. Groot and G. A. de Wijs, First-principles Study of the Optical Properties of MgxTi(1−x)H2, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125117 CrossRef.
- C. Gong and M. S. Leite, Noble Metal Alloys for Plasmonics, ACS Photonics, 2016, 3, 507–513 CrossRef CAS.
- M. W. Dlamini and G. T. Mola, Near-field Enhanced Performance of Organic Photovoltaic Cells, Phys. B, 2019, 552, 78–83 CrossRef CAS.
- F. Wang and Y. R. Shen, General Properties of Local Plasmons in Metal Nanostructures, Phys. Rev. Lett., 2006, 97, 206806 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2020 |