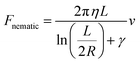Open Access Article
Open Access ArticleDifference in the interaction of nano-diameter rod and tubular particles with a disclination line in a nematic liquid crystal
Meenu Murali a,
Hakam Aghaa,
Aleš Mrzelb and
Giusy Scalia
a,
Hakam Aghaa,
Aleš Mrzelb and
Giusy Scalia *a
*a
aDepartment of Physics and Materials Science, University of Luxembourg, L-1511 Luxembourg. E-mail: giusy.scalia@uni.lu; meenu.murali@uni.lu
bJožef Stefan Institute, Jamova cesta 39, 1000 Ljubljana, Slovenia
First published on 5th June 2020
Abstract
In the presence of a disclination line, inclusions within an aligned nematic liquid crystal (LC) are first attracted and ultimately trapped in it. The kind of orientational distortion created by the inclusions is fundamental in determining the trapping. In the present work, we observe differences in the trapping behaviour, onto a ½ defect line in a nematic LC, of two types of particles both elongated but different in their actual geometry. Even if both types have cylindrical shape, aggregates of Mo6S2I8 nanowires (rod-like shape) and multiwall carbon nanotubes (tubular shape, i.e. hollow) trap differently although still due to deformations induced in the LC director field. Attractive forces are stronger on elongated bundles of nanowires than on similarly sized bundles of multi-wall carbon nanotubes. The reason is the difference in the attraction forces originating from different types of distortions of the LCs. The hollow and the full cylinders are not homotopically equivalent and this inequivalence holds also for the liquid crystal around them. The nanowires induce defects in the LC close-by their surfaces as shown for microrods, topologically equivalent to spheres. In contrast, multi-wall carbon nanotubes, being hollow, do not form defects close to their ends. However, the tubes are strongly bent and the strong planar anchoring of LC at the surface induces deformation in the LC enabling attraction forces with the defect line. HiPco single wall carbon nanotubes could not be trapped because their bundles looked much straighter and smaller than the ones of MWCNTs and thus neither defects nor standard strong deformations are expected. In conclusion, even if the shape of both types of particles is cylindrical, the topological difference between rods and tubes has profound consequences on the physical behaviour and on the presence and type of defect-mediated nematic attraction forces.
1. Introduction
Liquid crystal (LC) molecules have anisotropic shape and in the phase with the lowest order, the nematic phase, they tend to orient along a common direction identified by a unit vector, the director![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) .1 Generally, topological defects2 occur where there is no average molecular orientation and thus, where the director is undefined. Topological defects can exist as points, lines or walls. This study is concerned with the controlled generation of line defects, also known as disclination lines, and in particular the one with a specific defect strength of ½.
.1 Generally, topological defects2 occur where there is no average molecular orientation and thus, where the director is undefined. Topological defects can exist as points, lines or walls. This study is concerned with the controlled generation of line defects, also known as disclination lines, and in particular the one with a specific defect strength of ½.
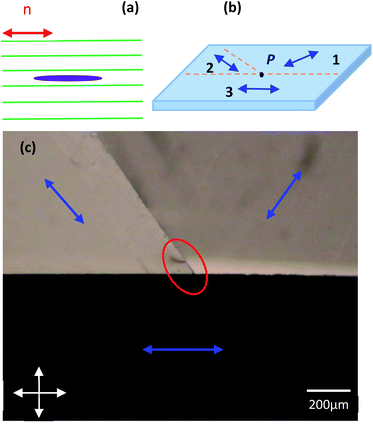
In 2009, the team of Galerne showed that defect lines can be tailor-made and thus, created in chosen locations by designed surface treatments of cells for LCs.3 Surface treatments are well-established techniques to create large-scale monodomains with LC uniformly aligned unidirectionally, but as it has been shown, even defects in the alignment can be externally produced by modifying the surface treatment conditions and they are also stable. This was done by treating the surfaces in a way that the LC molecules orient planarly but along different directions in three regions and in the point where the different orientations meet, a point defect is formed. When a cell uses two such identical surfaces, a defect line is formed that connects the two-point defects located at each LC interface with the substrate.
When particles whose surface induces uniform LC alignment are introduced into a uniformly aligned nematic LC, long range forces are induced between the particles as a result of elastic distortions of the director field around their surface.4 The boundary conditions, given by the surface anchoring conditions, impose topological constraints which must be satisfied by the director field of the liquid crystal; this will lead to the formation of topological defects which cannot be removed.5 The LC will form defects around the particles to compensate the defects formed by the presence of the particle. Thus, spherical inclusions themselves constitute permanent defects of strength +1. These topological defects play a crucial role in determining the elastic interactions between suspended particles and the disclination line in the nematic liquid crystal. Depending on the characteristic surface extrapolation length lw = K/Wa, where K is the bulk elastic constant and Wa the anchoring energy of the nematic molecules at the particle surface, and on the preferred type of anchoring conditions, different director field structures can develop around a single nanoparticle.6,7 In fact if the diameter D of the particle is small and D ≪ lw, the anchoring is not expected to be able to produce large orientational in the surrounding nematic matrix. Thus, the elastic energy of the bulk prevails and can impose a uniform orientation all over the surface of the particle, thereby preventing the formation of particle-coupled defects such as a disclination ring or point defects, as shown for an elongated particle in Fig. 1a. On the other hand, when D ≫ lw, and the anchoring is strong, topological singularities result from this. It has been reported earlier8 that spherical particles with uniform homeotropic alignment, typically induced with a homeotropic aligning agent, in aligned nematic LC film produce large orientational distortions around them that result in the formation of defects causing nematic interactions. In order to minimize the total energy of the system and to have a net topological charge equal to zero; topological defects form in the vicinity of the particles either on one side, creating a dipolar colloidal particle or on two opposite sides, due to the formation of line around an equator (Saturn ring), which gives a quadrupolar particle.5 This is also valid for spherical particles giving planar alignment for the LC molecules. All described cases are considered under strong anchoring conditions for the alignment at the particle surface. Similar observations have also been made in the case of microrods as inclusions since cylinders are topologically equivalent to spheres and thus similar defect formations are expected.9 The coupled particle-induced defect gives rise to a strong interaction between the dispersed particles and the defect line. Since the director field around the particles can be of dipolar or quadrupolar symmetry, the long-range interactions can be of dipolar or quadrupolar type, respectively. While in many previous works5,9–11 the interaction forces considered are between the particles, in the Galerne and co-workers research, the attraction force is between the particles and the defect line. The authors4 showed that spherical beads with suitable surface treatment could be attracted and trapped by the disclination line leading the way to create 3-dimensional conductive microwires by means of self-assembly.3 This was achieved due to the attractive forces arising from the LC director distortions around the colloidal particles and from the defect line.
In this work, we also realize defect lines by specific surface treatments to generate vertical interconnects in the LC for trapping untreated nanotubes and nanorods into the defect line, still relying on the ease of LC to form macroscopically oriented monodomains, enabling a control in the creation of defects. The purpose of this paper is to study the interaction between a ½ strength defect line and two types of cylindrically shaped nanodiameter particles but with the fundamental difference of being rod shaped and tube shaped, respectively. For this, we have used aggregates of Mo6S2I8 nanowires as rod shaped particles and carbon nanotubes (CNT) of two types, single wall carbon nanotubes (SWCNT) and multi wall carbon nanotubes (MWCNT), as tubular shapes. CNTs due to their high van der Waals attractive interaction tend to form bundles and agglomerates, which limits their applicability as films or in composites. Thus, in most of the preparations using post-nanotube-growth approaches the debundling and stabilization of liquid suspensions of CNTs are very important steps. The CNTs align with their long axis following the LC director and on their surface the LC aromatic molecules align planarly. Since the aspect ratio of CNTs is extremely large, effects induced by the ends has usually been disregarded. However, CNTs are hollow and usually with open ends and their geometry is different from the rod shape which has ends made of the same material as that of the walls. This difference also has topological consequences since a tube is not homotopically equivalent to a rod thus not the same defect formation as for spheres is expected. In this work, we analyze the trapping mechansim of these two types of nano-diameter cylinders in light of their topological difference.
2. Experimental section
2.1 Creation of localized defect in LCs
Disclination lines are generated by the control of the LC boundary conditions via the realization of patterns on substrates to induce planar LC alignment with three regions having different director orientations as sketched in Fig. 1b. The surface treatment is performed by unidirectional smearing of a suitably shaped polytetrafluoroethylene (PTFE) bar on cleaned glass substrate placed on a hot plate heated to roughly 200 °C, according to a process initiated by Haller12 and later developed by Wittmann and Smith.13 The three regions are created around a point as indicated in the sketch of Fig. 1a with the letter P. At this point, the LC molecules cannot orient along any specific direction which results in a defect. Two such glass substrates are placed on top of each other with appropriate spacing (∼150 μm) so that the inner surfaces have the smeared PTFE film facing. Nematic LC is then filled in by capillarity. The LC aligns along the different directions as visible in the polarizing optical microscopy (POM) image with crossed polarizers, reported in Fig. 1c. The director orientations have been indicated in blue to help the visualization of the three different orientationally ordered monodomains. In correspondence to the meeting of the three monodomains, a line defect is created from the top to the bottom substrate, seen within the red oval, Fig. 1c. Our target is to trap bare particles with cylindrical shape, that are not homotopically equivalent, more specifically nanorods and nanotubes, in the disclination line and to investigate their trapping behaviour. At this end nanotube-LC and nanowire-LC dispersions need to be prepared.2.2 Dispersion of the nanotubes and nanowires and sample preparation
The liquid crystal that was used in this study is a room temperature nematic liquid crystal 5CB (4-cyano-4′-pentylbiphenyl), purchased from Synthon Co. The nematic to isotropic transition temperature of 5CB is 35.5 °C. When inserted into the tailor-made cell, the LC formed a defect line as expected, as shown in Fig. 1c. The Mo6S2I8 nanowires were synthesized directly from the elements in their final composition as described in ref. 14. The resulting product was a powder formed of bundles of Mo6S2I8 nanowires of 50–80 nm diameter and several microns in length. The single nanowires have sub-nanometre diameter and they can be described as inorganic polymers. The bundles of nanowires are rigid and straight particles that can be described as nanorods. The nanowires were introduced directly in the nematic LC (0.01% by weight) and dispersed using pulsed ultrasound waves emitted by a Hielscher UP200St tip probe ultrasonicator (36 W) for 2–3 minutes.Two types of CNTs were used, as purchased: high-pressure carbon monoxide disproportionation (HiPco) type single wall carbon nanotubes of diameter ∼0.8–1.2 nm purchased from Unidym Inc. (Lot# P2772) and multiwall carbon nanotubes of length 5–15 μm and 60–100 nm outer diameter, purchased from SES Research Inc. (Lot US - 0551). CNTs (0.1% by weight) were dispersed in dichloromethane (DCM) using the probe ultrasonicator for 70 minutes. The CNT + DCM mixture was then introduced in the nematic 5CB and then the solvent was evaporated by heating the mixture up to 80 °C for about 10 minutes obtaining a concentration of 0.01% by weight in LC. The nematic dispersion was then introduced by capillarity action into a cell of thickness ∼150 μm, made as described above. The optical investigations were carried out with a polarizing optical microscope Nikon Eclipse LV100ND.
3. Results and discussion
3.1 Interaction of nanotubes and nanorods with the disclination line
In order to investigate the trapping mechanism of the two different types of cylindrically shaped nano-diameter particles, i.e. nanorods and nanotubes, onto the defect line, we have used bundles of Mo6S2I8 nanowires and CNTs of two different kinds: MWCNTs and SWCNTs. The surfaces of the nanowires and of both the CNTs are untreated in order to study the influence in the trapping behaviour of the different shapes considering that the alignment of the LC at the edges or ends is uniquely determined by the particles surface and shape and not by aligning molecules that might screen shape effects.A scanning electron microscope (SEM) image of both types of CNTs and bundles of Mo6S2I8 nanowires, deposited on silicon wafer and after solvent evaporation, is shown in Fig. 2. Both images (Fig. 2b and c) show a good CNT dispersion and lack of large bundles or entangled aggregates. However, the MWCNTs appear with kinks, sign of defects formed in the walls causing local bending. The SWCNTs look much straighter than the MWCNTs, whereas the bundles of Mo6S2I8 nanowires, Fig. 2a are straight rigid rods. When the suspension of 0.01 weight% of nanorods fills the cell, particles inducing close-by defects in the LC produce an interaction in the vicinity of the defect line and the resulting force attracts the particles towards the defect.
The type of anchoring on the particle surface defines the nature of interaction and the magnitude of the nematic force is proportionally related to the particle size.15
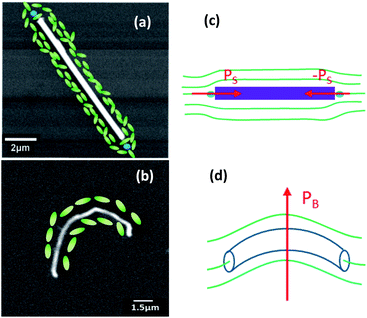
Let us consider a simplified scenario first, with uniformly aligned nematic LC colloid in which we presume that the Mo6S2I8 nanowires and the CNTs nanotubes are single and well dispersed in. Here, in both the cases, LC molecules align tangentially to the surface and along the long axis as observed on various types of elongated particles.16–18 This is where the director is least distorted and is thus energetically more favourable. Cylindrical, rod-like particles induce elastic distortions in the surrounding medium, therefore the boundary conditions impose topological constrains that must be satisfied by the director, leading to the formation of topological defects. Most commonly, two antipodal surface point defects of strength −½ known as boojums appear on both the ends to maintain the topological neutrality, Fig. 3a. The nanowire with its companion defects produces two splay moments Ps of a dipolar nature, Fig. 3c. As described in the literature, the two moments together produce a quadrupole moment Qs that will couple with the splay field n(∇ · n), produced by the disclination line. Thus, they interact with the disclination line via quadrupolar interaction. A resulting nematic force F = −∇U is produced from this interaction, where U is the elastic interaction potential exerted by the disclination onto the particles19 and is given by,
| U = −KQsn · ∇(∇ · n) | (1) |
Instead the MWCNTs are rather curved bundles as seen in Fig. 2c. Therefore, the CNTs can produce a distortion of bend type, Fig. 3d.
In the case of spherical particles with planar alignment producing defects in asymmetric configuration20 there is bend distortion and the coupling interaction U in this case can be expressed as the scalar product of the bend moment PB and the bend field19 n × (∇ × n) produced by the disclination line,
| U = −KPB · (n × (∇ × n)) | (2) |
In this case, we should expect a stronger nematic force Fd ∼ 1/r2 from a dipolar interaction potential than the quadrupolar case. We might argue that this configuration could have similarities with the bent MWCNTs case even if there are no defects, thus no large local director distortions. However, continuing the analogy, the expected force goes differently as in the case of a quadrupolar interaction Fq ∼ 1/r3, expected for the straight nanowires. Here r is the distance of the particle from the disclination line.
Now, when the particles are in the vicinity of the disclination line and present in the central part of the cell, far away from the top and bottom glass plates, where they might experience screening effects, they may advance slowly towards the disclination line. This translational force exerted by the disclination line on the particles is an orientation distortion mediated force resulting from the interaction we discussed above. Neglecting the vertical fall due to weight and assuming a laminar flow around the nanoparticles, we may project the motion of the particles strictly on x and y-axis, defined in the plane parallel to the substrates, and considering a stationary uniform motion of the particle. The attraction force can be derived by the equation of balance of the forces in which the attractive nematic force now exactly balances the viscous drag force. Therefore, at any given time, the nematic force can be calculated by determining the Stokes drag force acting on the particles given by the Stokes equation adapted for a cylinder advancing in a viscous fluid:
3.2 Trapping of nanotubes and nanorods onto the disclination line
Experimentally, in order to investigate the interaction between the nanoparticles and the disclination line, a mixture of nano-diameter particles in 5CB LC is prepared as described in the Section 2.2, and introduced into a cell having its surfaces prepared to host a disclination line in a prefixed location. The motion of elongated aggregates of similar dimensions approaching the defect line was monitored by optical microscopy. Fig. 4 shows a sequence of images of aggregates of both MWCNTs (a–c) and nanowires (d–f) (1 and 2 rows, respectively) approaching a disclination line of strength ½ and finally getting trapped on it. In Fig. 4d–f, the defect line is quite long as the glass plates are shifted well apart for better visualisation.But for the measurements of locations, we always used samples having a straight short defect line. This sequence of images was taken with a digital camera. The figure depicts the variation of the relative separation between the particles and the disclination line with time. Each position of the particle during its trajectory towards the disclination line has been tracked assigning (x, y) coordinates. The measurements confirm that the interaction between the disclination line and the particles, except for SWCNTs, is a function of distance and the velocity will increase as the particle approaches the disclination line.
In our work we observe no trapping in the case of SWCNTs, Fig. 4g–i, even after leaving the cell for several hours. Additionally, the sample is heated to isotropic phase for further verification. Once in the isotropic phase, the disclination line disappears and if the SWCNTs would have been attracted into the defect line, traces of big aggregates or bundles would have been visible. The SWCNTs seem to be too straight and small to produce sufficient distortion in the nematic matrix around it, and even in case of very distorted nanotubes, the Brownian motion introduces large fluctuations dominating over the motion of the SWCNTs towards the defect line. Also, theoretically, for a particle to be definitely trapped onto a defect line, the minimal particle radius should be ∼30 nm.19 The nanometer size of the diameter of isolated SWCNTs can be indeed an issue since it is definitely smaller than the value reported above. Thus, the interaction of the SWCNTs with the defect line can be expected not existing or minimal compared to thermal fluctuations resulting in dispersing the SWCNTs rather than attracting them to the defect line. Furthermore, CNTs being hollow tubes, the alignment of LC on their ends is different than what is expected in the straight rod approximation model in which the same alignment of LC is present all over the surface including the ends where, if planar, the LC director is perpendicular to the rod axis resulting in conflicting LC orientations in a surrounding LC uniform alignment.22 Therefore, we exclude the existence of any defect formation on the SWCNT ends, leading to defect-mediated interaction with the defect line. Also, SWCNTs are usually in bundles and aggregates and, even if these can be quite small in good dispersions, the diameter dimension can be larger than the size reported for not causing director distortions. Thus the fact that no trapping was observed (Fig. 4g–i) is consistent with the absence of attraction forces due to absence of defects as well as of simple strong distortions in the LC.
In contrast, as seen in the second row of Fig. 4, we have obtained the trapping of many aggregates of Mo6S2I8 nanowires and, in the first row of the same figure and in Fig. 5, of MWCNTs, which appear as dark threads making the disclination lines more visible, judging from the optical microscopy images. The images of the tubes were taken hours after introducing the LC with dispersed nanotubes in the cell.
The trapping of aggregates of nanowires, Fig. 4d–f, was generally more successful than of MWCNTs. In Fig. 4a–c we notice some of the MWCNTs were not attracted to the defect line. At large distances the elastic interaction energy between the MWCNTs and the defect line is weaker compared to that of a nanowire. This is evident from the plot in Fig. 6, where it is clear that the aggregates of MWCNTs are taking roughly double the time to reach the defect line compared to a nanowire following similar trajectory. Nevertheless, the aggregates of MWCNTs are eventually trapped onto the defect line. This result shows that although the MWCNTs are structurally similar to SWCNTs, there are substantial differences for the LC alignment. The larger diameters of MWCNTs result in higher number of benzene rings of carbon per unit length in a MWCNT than in SWCNTs offering to the LC molecules more surface to interact with and thus to anchor. The result is a stronger overall London interaction energy per unit length of nanotubes for MWCNTs with the LC molecules. Considering that 5CB LC has shown strong anchoring on SWCNTs23 we expect to be in the strong anchoring regime also for the MWCNTs. Therefore, a MWCNT should promote a stronger planar anchoring on a nanotube compared to a SWCNT and if the CNTs induce a director deformation this is more extended for MWCNTs. In order to get a more precise understanding of the mechanism, numerical simulations would be necessary.
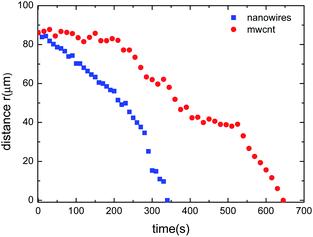 | ||
| Fig. 6 Displacement of the dispersed aggregates of nanowires and MWCNTs attracted towards the disclination line as a function of time. Here the region of approach of the particles in the LC cell is the number 3, as marked in Fig. 1b. | ||
Fig. 7a and b plots the attractive force as a function of the relative separation. For the calculation of the attractive force, Fnematic, we used the following values, measured from optical microscopy images, for the tracked particle: for the particles approaching the defect line from zone 1 R = 2206 μm and L = 23.32 μm for MWCNTs, R = 2.89 μm and L = 23.64 μm for the nanords and for particles approaching from zone 3 R = 2.39 μm and L = 20.38 μm for MWCNTs and R = 3.05 μm and L = 19.95 μm for the nanorods. Both the aggregates of MWCNTs and nanowires considered in these plots are chosen such that they have approximately the same size as judged by the optical microscope, and approach the defect line from similar, equivalent locations. In these two cases it is clear that the nematic force exerted on the nanowires is almost double the force acting on the MWCNTs. Due to the uncertainty in the exact location of the particle closer to the defect line because of the distortion around it, we take into account the force up to couple of micrometres before the defect line. At a distance of 10 μm from the defect line, the nematic force acting on the aggregate of nanowires is about 4 and 5 pN while the value for the two aggregates of MWCNTs is about 1.5 and 2.5 pN respectively. This trend is consistent with all the measurements that we performed and can be explained by considering the difference in the particles structural morphology. Although we consider both the particles as rigid rods; only the bundles of nanowires are in fact rods. It should be pointed out that the measurements reported here are for aggregates of similar dimensions but the easier trapping observed for nanowires compared to carbon nanotubes has been observed for aggregates nanowires of different dimensions. This means that the general trapping efficiency of the bundled Mo6S2I8 nanowires does not seem dependent on the specific dimensional range reported here but it is a rather general behaviour.
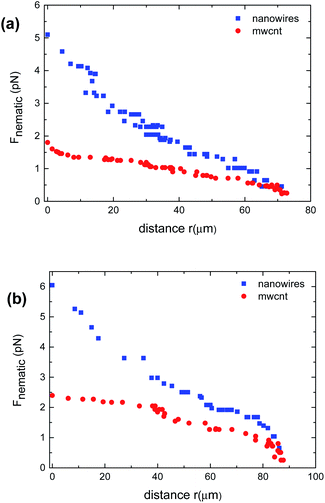 | ||
| Fig. 7 Interaction between a disclination line and the nanowires and MWCNTs, plotted as a function of relative separation. Here the regions of approach of the particles in the LC are the ones: (a) marked as 1 and (b) marked as 3, in Fig. 1b. | ||
The ends of the bundles of nanowires are closed and made of the same material and structure as the lateral surfaces, thus the same alignment would occur at the ends as described for microrods or spheres, inducing defects in the LC and nematic forces. In contrast, the CNTs are hollow structures and since they are hollow, we do not have the same planar alignment at the ends as on the wall surfaces thus no boundary conditions inducing strong distortions of the director and formation of defects. Liquid crystal molecules or air can be present in the inner part of the tubes and in both cases the LC on the ends is expected to follow the alignment of the molecules planarly aligned along the sides, which corresponds to a perpendicular orientation on the contour of the ends of the tube seen as cylinder. Therefore, on one hand for the nanowires, the attractive potential results from the interaction between the defect line and the particle-induced defects system, i.e. from the free energy minimization of the disclination-particle system. Whereas, on the other hand, the elastic interaction between the MWCNTs and the defect line can be explained based on the observation that the MWCNTs that were inserted in the LC are very curved bundles with visible kinks, Fig. 2c. The planar anchoring of the LC molecules along these curved surfaces together with the strong bending deformations of the nanotubes induces strong enough overall elastic distortions to allow the CNTs to be attracted by the defect line, and ultimately to be trapped onto it for the minimization of the free energy of the LC.
4. Conclusions
The nematic interaction of LC with nanotubes and nanowires is profoundly different in nature and the origin lies in the topological difference of the two shapes. Even if the hollow nature has been disregarded so far, due to the extremely high anisotropic ratio of CNTs, its effect is dramatically manifested when the space-time curve and the derived attractive forces before the trapping are studied. We have conducted the study of the attraction forces between the defects and nano-diameter particles in aggregates using tailor-made defect lines, formed in a precise location and with a defined strength using PTFE surface treatments on glass substrates assembled into cells and filled with 5CB nematic LC. When rod-shaped inclusions with surfaces inducing planar anchoring in the LC are introduced in a well aligned nematic LC, these inclusions minimize the total free energy of elastically distorted nematic liquid crystals by generating defects of opposite sign. Two defects of strength −½, or, less commonly, one of strength −1, compensating the +1 formed by the rod particle for the LC are formed near the interfacial region of the particle. Approaching the defect line with strength ½, attraction forces are generated to compensate the distortion. The trapping of the aggregates of MWCNTs were comparatively slower than that of the aggregates of Mo6S2I8 nanowires. The attraction forces as from the experimental observations are clearly stronger and longer range for Mo6S2I8 nanowires than for MWCNTs. The tubular shape implies that the planar alignment is not present at the ends of the tubes, compatible with alignment parallel to the tube axis, thus no defects are produced by the LC as compensation. Director deformation nematic forces can be created to align the nanotubes inducing their alignment along the director or, as here for MWCNTs, from the strongly deformed shape. In the latter case, the deformed director field couples with the distortions induced by the line defect resulting in attraction forces which enable the trapping of the MWCNTs. In these disclination lines, SWCNTs could not be trapped and even if isolated tubes have size of about 1 nm, thus smaller than the size regarded effective for the generation of nematic forces, their effective size is larger due to their bundling and aggregation. In any case, the tubular structure would not promote defect formation close to the ends but also no other deformations since they are straighter or with bending on smaller scale than the MWCNTs, explaining why trapping could not be achieved.Disclination lines in LCs can be attractive systems for studying LC deformations induced by nanoparticles by monitoring the attraction forces. Also, the confinement into defects is interesting for applications as pressure sensitive vertical conductive interconnects in soft dielectric matrix since it can be used to promote the formation of the networks of nanowires but also of nanotubes, due to the local particle density increase from the entrapment into a restricted space.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research was financially supported by the Luxembourg National Research Fund (FNR) within the projects MASSENA-Pride/15/ 10935404 and Milicana-COREC15/MS/10465407.References
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Oxford University Press Inc., New York, 1993 Search PubMed.
- S. Chandrasekhar and G. S. Ranganath, Adv. Phys., 1986, 35, 507–596 CrossRef CAS.
- J. B. Fleury, D. Pires and Y. Galerne, Phys. Rev. Lett., 2009, 103, 1–4 CrossRef PubMed.
- P. Poulin, H. Stark, T. C. Lubensky and D. A. Weitz, Science, 1997, 275, 1770–1773 CrossRef CAS PubMed.
- P. Poulin and D. A. Weitz, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 626–637 CrossRef CAS.
- S. V. Burylov and Y. L. Raikher, Phys. Lett. A, 1990, 149, 279–283 CrossRef CAS.
- S. V. Burylov and Y. L. Raikher, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 358 CrossRef CAS PubMed.
- J. C. Loudet, P. Barols and P. Poulin, Nature, 2000, 407, 611–613 CrossRef CAS PubMed.
- U. Tkalec, M. Škarabot and I. Muševi, Soft Matter, 2008, 4, 2402–2409 RSC.
- I. Muševič, M. Škarabot, U. Tkalec, M. Ravnik and S. Žumer, Science, 2006, 313, 954–958 CrossRef PubMed.
- T. C. Lubensky, D. Pettey, N. Currier and H. Stark, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 610–625 CrossRef CAS.
- I. Haller, Appl. Phys. Lett., 1974, 24, 349–351 CrossRef CAS.
- J. C. Wittmann and P. Smith, Nature, 1991, 352, 414–417 CrossRef CAS.
- M. Remškar, A. Mrzel, M. Viršek and A. Jesih, Adv. Mater., 2007, 19, 4276–4278 CrossRef.
- H. Stark, Phys. Rep., 2001, 351, 387–474 CrossRef CAS.
- D. Rajh, S. Shelestiuk, A. Mertelj, A. Mrzel, P. Umek, S. Irusta, A. Zak and I. Drevenšek-Olenik, Phys. Status Solidi A, 2013, 210, 2328–2334 CrossRef CAS.
- C. Lapointe, A. Hultgren, D. M. Silevitch, E. J. Felton, D. H. Reich and R. L. Leheny, Science, 2004, 303, 652–655 CrossRef CAS PubMed.
- I. Dierking, G. Scalia, P. Morales and D. LeClere, Adv. Mater., 2004, 16, 865–869 CrossRef CAS.
- H. Agha, J. B. Fleury and Y. Galerne, Eur. Phys. J. E, 2012, 35, 1–12 CrossRef PubMed.
- G. K. Batchelor, J. Fluid Mech., 1970, 44, 419–440 CrossRef.
- H. Stark and D. Ventzki, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2001, 64, 9 CrossRef PubMed.
- Y. Galerne, Phys. Rev. E, 2016, 93, 042702 CrossRef PubMed.
- G. Scalia, M. Haluska, J. P. F. Lagerwall, U. Dettlaff-Weglikowska, F. Giesselmann and S. Roth, Phys. Status Solidi B, 2006, 246, 3238 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |