Carbon monoxide formation from trimethylamine-boranecarboxylate: DFT studies of S_Ni and chelotropic mechanisms

Abstract

Trimethylamine-boranecarboxylic acid (CH₃)₃N-BH₂COOH and other amine carboxyboranes have been observed to undergo slow decarbonylation in neutral aqueous solution. This reaction, when it occurs in vivo, may have a therapeutic effect by delivering low concentrations of carbon monoxide over an extended period. In order to identify a possible mechanistic pathway for decarbonylation, the smallest tertiary amine derivative and its corresponding carboxylate ion were studied using CCSD(T)/PCM/6-311++G(2d,p)//M06-2X/PCM/6-311++G(2d,p) model chemistry. The proposed mechanistic pathway begins with a trimethylamine boranecarboxylate ion, which first undergoes an internal substitution reaction (S_Ni) to give free amine and the carboxyborane anion BH₂COO⁻. The latter cyclic ion then releases CO via a rapid chelotropic fragmentation. The role of water solvent in these reactions was explored by structural and energetic analysis of hydrogen-bonded complexes. It was found that complexation with water inhibits dissociation of trimethylamine by stabilizing the trimethylamine carboxyborane anion, whereas water accelerates CO loss by stabilizing the polar chelotropic transition state.

---

Introduction

Boron is ubiquitous in plants, where it is considered to play an important role in maintaining cell wall structure and membrane integrity.^1,2 In animals, boron is acquired through the diet and is essential for embryonic development.^3,4 While the majority of natural boron occurs as boric acid, a number of synthetic organoboron compounds, the amine carboxyboranes, have been under study for several years for their potential medicinal effects. One such compound is trimethylamine boranecarboxylic acid (TMA-BH₂COOH), which has been shown to have anti-inflammatory, anti-neoplastic, and anti-osteoporotic activities.^5,6 The fundamental structural unit of amine carboxyboranes is an amine–boron coordinate covalent bond. This type of bond allows structural modification by exchange of the amine group,^7,8 and as described herein, it has a strong effect on the attached carboxyl moiety.

The main physiological effect of amine carboxyboranes is thought to result from carbon monoxide released during a fragmentation reaction that also forms the free amine and, eventually, borate ion.⁷ Hence the designation as a carbon monoxide releasing molecule, or CORM. Despite the obvious toxic effects of CO at high levels, CO at low concentrations has been shown to be a transmitter molecule that performs critical physiological functions.^9–11 Although a product and kinetic study has been reported,⁷ the mechanism of CO formation is not known. The present computational study provides a simple molecular model for trimethylamine boranecarboxylate fragmentation that provides insight into the kinetics of the reaction. This information may be useful in the design of new CORM pro-drugs.

Compounds containing the B–N dative bond have been the subject of a number of theoretical studies.^12–17 The studies have shown that accurate prediction of geometry and energy in this class of compounds requires the use of correlated ab initio theory such as MP2 or a recent density functional theory using an augmented and polarized basis set. Fisher et al. studied several amine carboxyboranes, including TMA-BH₂COOH, in an attempt to correlate the computed B–N dissociation energies with various physiological effects.¹⁵ In several cases there was a negative correlation suggesting that a more facile B–N dissociation is associated with a greater physiological effect. The carboxylate forms of amine carboxyboranes were not studied.

Several organic decarbonylation reactions are known. Formic¹⁸ and lactic acids¹⁹ decarbonylate with strong acid catalysis, which probably involve acylium ion intermediates. In the gas phase, lactic acid undergoes thermal dehydration to a ketooxirane intermediate, which loses CO in a chelotropic reaction, that is, a concerted fragmentation reaction where both bonds to the carbonyl C are breaking in the transition state.²⁰ Extrusion of CO from medium-sized cyclic ketones leads to aromatic rings^21,22 or non-aromatic alkenes.^23,24 CO loss from the three-membered ring precursors α-acetolactone²⁵ and 2,3-di-t-butylcyclopropanone^26,27 has been observed in the gas phase.

In contrast to the forcing conditions employed in most decarbonylations, amine carboxyborane decarbonylation occurs, albeit slowly, in neutral or alkaline aqueous solution at room temperature.⁷ The rate of decarbonylation of a given CORM pro-drug under physiological conditions is a crucial pharmacological feature: too fast, and a toxic dose of CO will be delivered all at once; too slow, and the CORM will be excreted before delivering the CO payload. The impetus for the present study was a report that aqueous titration of TMA-BH₂COOH must be carried out at high speed “owing to a tendency for the compounds to undergo hydrolysis as evidenced by formation of gas bubbles”.²⁸ The gases produced during titration were not identified, but they are likely to be CO and H₂. CO has been identified as a hydrolysis product of TMA-BH₂COOH⁷ and other CORMs.²⁹ The goal of this study is to rationalize the relatively facile hydrolysis and decarbonylation reactions of TMA-BH₂COOH, as well as assess the role of solvent water on reactivity.

We focus here on the decomposition chemistry of the carboxylate form, TMA-BH₂COO⁻. A two-step dissociation-chelotropic elimination mechanism is proposed that accounts for the observed rate of decomposition of trimethylamine carboxyborane when explicit waters are included in the calculation.

Computational methods

Calculations used Gaussian 09 (ref. 30) software. Geometry optimization and frequency calculations used the M06-2X functional, which has been shown to give low mean unsigned errors when tested against several reaction barrier databases,^31,32 along with the polarizable continuum model (water, epsilon = 78.35).³³ Four different basis sets were used: 6-311++G(2d,p), and jun-, jul-, and aug-cc-pVTZ.³⁴ Single point energy calculations (CCSD(T)/PCM/6-311++G(2d,p)) used the M06-2X/PCM/6-311++G(2d,p) geometry; unscaled thermal corrections (298.15 K, 1 atm) were applied from frequency calculations at the same level. Vibrational analysis of energy minima showed all real frequencies. Transition structures exhibited one imaginary vibration corresponding to the reaction coordinate, with smooth conversion of transition states to reactants and products in IRC calculations. Imaginary frequencies were in the range of 180–490i cm⁻¹ (Table S1 in the ESI†). Quantum theory of atoms in molecules was carried out with the AIMAll program;³⁵ electron localization function (ELF) surfaces were calculated and plotted with Multiwfn program (version 3.6).³⁶ Both programs using a formatted checkpoint file from a Gaussian population calculation as input. The NBO 7.0 program was used for calculating natural bond orbitals, donor–acceptor orbital interactions, and Wiberg bond orders.³⁷ Gibbs free energies of bi- and ter-molecular reactions were adjusted as follows: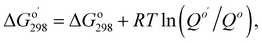 where 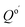is the reaction quotient under standard condensed-phase conditions, i.e., all concentrations = 1.0 M, and Q^o is the reaction quotient with all species at 1.0 atm pressure and 298.15 K, where the concentration of an ideal gas = 1/24.45 M = 0.04090 M.

Results and discussion

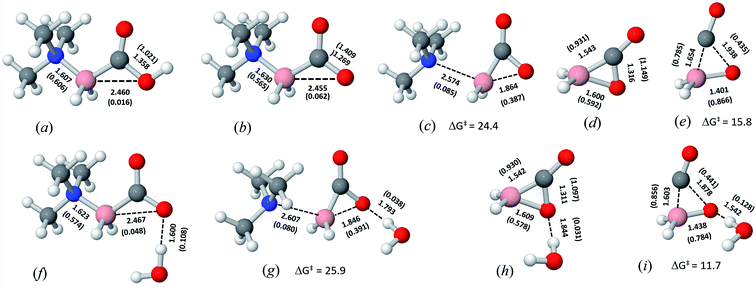
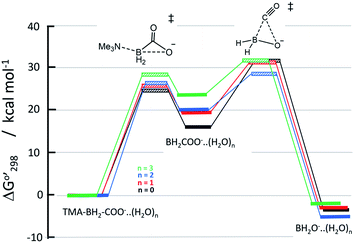
This study is focused on the geometry and energy of trimethylamine carboxyborane and its corresponding carboxylate, and the intermediates and transition states leading to decarbonylation in aqueous solution. In acidic solution, where presumably the neutral form predominates, trimethylamine carboxyborane is rather stable, surviving, for example, 8 h in boiling 0.3 M aqueous HCl.³⁸ Trimethylamine carboxyborane has a pK_a of 8.3 (ref. 28) due to the borate atom bonded directly to the carboxyl group. Nevertheless, at physiological pH a certain fraction will exist in the carboxylate form. For this reason, and in order to explain the alkaline sensitivity observed by Scheller,²⁸ the carboxylate form was investigated. The results, summarized in the Scheme 1 below, identified a two-step decomposition pathway that begins with intramolecular nucleophilic attack of the carboxylate 1′ to give the amine and a cyclic carboxyborane anion 2, which then undergoes concerted CO loss leaving the borinate ion 3. The conjugate acid of 3, borinic acid BH₂OH, is known to be unstable in water, where it is rapidly converted to boric acid or borate, the observed final boron-containing product.³⁹ The reactions of borinic acid were not studied. A van der Waals complex of trimethylamine and cyclic carboxyborane anion forms immediately after N–B bond breakage (Fig. S1†). The van der Waals complex energetics do not affect the rate of the forward S_Ni reaction.

Scheme 1 Two step mechanism for formation of carbon monoxide and trimethylamine from trimethylamine carboxyborane.

All reactants, products, and transition states were optimized using various basis sets up to aug-cc-pVTZ. Energies are given in Table S2;† cartesian coordinates are in Tables S3 and S4 in the ESI.† Fig. S2† compares 33 bond distances, including N–B, B–O and hydrogen bond O–H, for eleven molecules and transition states for the four model chemistries. Very small differences (±1 mÅ) were seen among the jun-, jul-, and aug-cc-pVTZ values. For the 33 distances in the table, the mean unsigned difference between the 6-311++G(2d,p) distance and the average jun/jul/aug-cc-pVTZ distance, was 4.8 mÅ.

TMA carboxyboranes

The optimized geometries of TMA carboxyborane and carboxylate ion are similar: both contain coplanar C–O and N–B bonds; however, the carboxylate form contains a significant interaction between the carboxylate O and B atoms (Fig. 1a and b). The coplanar conformations place the distal O in both forms near the backside of the N–B bond, where a donor–acceptor interaction can occur between O and the N–B σ* orbital (Fig. S3 in ESI†). In the carboxylate, the second-order perturbative stabilization energy E(2) is much greater, 2.45 vs. 0.96 kcal mol⁻¹, due to the carboxylate's higher negative charge and p-type lone pair orbital that points more directly at B. The main consequence of donation into the N–B σ* orbital is to lengthen and weaken the N–B bond, where the bond order is decreased about 7% (0.565 vs. 0.606) compared to trimethylamine carboxyborane. Thus, TMA carboxylate anion is poised for nucleophilic attack on B by the carboxylate O.

Fig. 1 Optimized geometries of (a) trimethylamine carboxyborane, (b) trimethylamine boranecarboxylate, (c) trimethylamine boranecarboxylate S_Ni transition state, (d) carboxyborane anion, (e) carboxyborane anion chelotropic CO loss transition state, (f) water–trimethylamine boranecarboxylate complex, (g) water–S_Ni transition state complex, (h) water–carboxyborane anion complex, and (i) water–carboxyborane anion chelotropic transition state. Distance, Å; Wiberg bond order in parentheses. M06-2X/6-311++G(2d,p)/PCM-H₂O.

S_Ni substitution

In the S_Ni transition state, intramolecular attack of the carboxylate's distal O begins to form an O–B bond on the backside of B, as the tertiary amine is being detached from the front side (Fig. 1c). The three reacting atoms (O, B, and N) adopt a nonlinear arrangement in the transition state due to the formation of a three-member ring on the backside, while maintaining good overlap of the B–N bond orbitals.

Carboxyborane anion

In the proposed mechanism, trimethylamine is released with simultaneous formation of the cyclic carboxyborane anion (Fig. 1d). This ion is isosteric and isoelectronic with α-acetolactone (Fig. S4†). The B–O bond of the former is longer and weaker compared to the analogous bond in α-acetolactone. On the other hand, the ring C–O bond of carboxyborane anion is slightly shorter and stronger compared to α-acetolactone, which is likely due to greater resonance interaction between the ring O and C=O in carboxyborane anion.

Bonding in carboxyborane anion and α-acetolactone was analyzed with the quantum theory of atoms in molecules (QTAIM)^40,41 using the PCM/M06-2X/6-311++G(2d,p) electron density (Fig. S4†). When the electron density was plotted in the plane of the ring, a region was identified between B and O in BH₂COO⁻ that has a rather flat topography at the 0.2 e bohr⁻³ level: this region lacks the curvature necessary for detection of a bond critical path and point. In contrast, α-acetolactone contains sufficient curvature in the C–O region to allow identification of bond and ring critical paths and points.

The weak B–O bond in carboxyborane anion makes possible an O-interchange motion that involves either twisting around the B–C bond, or rebonding the carbonyl O on the opposite face of B. The BH₂COO⁻ PES contains two C_2v-symmetric transition states for these interconversions: one with the BH₂ and COO groups coplanar (for the twisting motion), and the other with these groups perpendicular (for the re-bonding motion) (Fig. S5†). These transition states are respectively 13.5 and 5.8 kcal mol⁻¹ above the cyclic structure. The analogous (C–O) bond in α-acetolactone is stronger, and the barriers to twisting and inversion are correspondingly higher: 43.9 and 25.4 kcal mol⁻¹ respectively.

Chelotropic CO loss

In the DFT optimized model for the decarbonylation transition state, CO is formed by concerted extrusion from the cyclic carboxyborane anion (Fig. 1e). The transition state is planar, with the carbonyl group angled more acutely relative to the B–O bond (OCO angle of 115°), compared to carboxyborane anion (OCO angle of 128°). In non-symmetric decarbonylation precursors, the carbonyl group in the reactant is typically bent in the same direction as the leaving CO molecule in the transition state.⁴² The extrusion is asymmetric, with the ring σ_O,C bond elongating and weakening more at the transition state than σ_B,C. This is due in part to electron donation by the in-plane carbonyl lone pair into because the latter is aligned with the acutely angled carbonyl bond. The 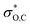orbital also accepts electrons from σ_B,C, and at the same time the 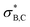orbital accepts electrons from σ_O,C (Fig. S6†). These two interactions are complementary and synergistic: they comprise a closed charge-transfer delocalization pattern that is characteristic of thermally allowed cycloaddition reactions.⁴³ Decarbonylation of three-membered-ring carbonyl compounds has been classified as a pseudopericyclic reaction.^44,45 In the case of amine carboxyboranes this step must be fast with a relatively low activation barrier because spectroscopic studies of CO release from TMA-BH₂COOH did not identify any B-containing precursor for CO release.⁷

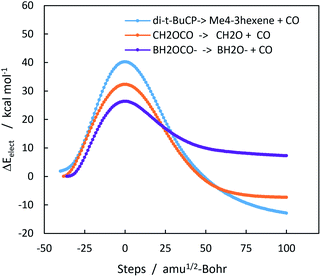
Chelotropic decarbonylation can in theory occur from any three-membered ring containing a carbonyl group. Experimentally, two such compounds have been reported to undergo decarbonylation, α-acetolactone and trans-2,3-di-t-butylcyclopropanone. α-Acetolactone decarbonylation was observed during collision induced mass spectroscopy of chloroacetate ion.²⁵ This experiment also allowed the authors to calculate the heat of formation of α-acetolactone, which was −47.3 ± 4.7 kcal mol⁻¹. When combined with the heats of formation of CO (−26.42 kcal mol⁻¹), and formaldehyde (−27.70 kcal mol⁻¹),^46,47 a ΔH^o_rxn of −6.8 kcal mol⁻¹ for α-acetolactone decarbonylation can be derived. The M06-2X/6-311++G(2d,p) value for the gas phase reaction is −9.3 kcal mol⁻¹. Fig. 2 shows the complete IRC trajectories for these three decarbonylation reactions. Geometries and energies (Fig. S9 and Tables S5–S7) are in the ESI.†

Fig. 2 Intrinsic reaction coordinate (IRC) trajectories for gas phase decarbonylation of trans-2,3-di-t-butylcyclopropanone, α-acetolactone, and carboxyborane anion. M06-2X/6-311++G(2d,p). ΔE^‡ values: 40.4, 32.3, 26.4 kcal mol⁻¹ respectively. ΔE_rxn values: −13.6, −6.7, 12.4 kcal mol⁻¹ respectively. BH₂COO⁻ decarbonylation is endothermic in the gas phase, but exothermic in a polar solvent or when complexed with water.

Kinetic data for trans-di-t-butylcyclopropanone decarbonylation was obtained by Greene et al. who reported a half-life of 9.5 h at 150 °C;^26,27 this rate corresponds to a free energy barrier ΔG^‡ of 34.2 kcal mol⁻¹. Applying thermodynamic data from an M06-2X/6-311++G(2d,p) frequency calculation at 423 K to CCSD(T) energies of the reactant and transition state gives a ΔG^‡₄₂₃ value of 35.1 kcal mol⁻¹.

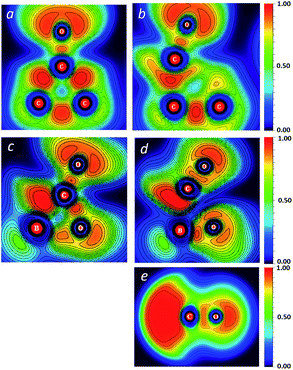
The difference in the activation barriers between carboxyborane anion and trans-di-t-butylcyclopropanone in Fig. 2 may be ascribed to greater CO-like bonding in the former transition state and starting anion: these can be seen in electron localization function (ELF) cross-sections through the plane of the three-membered ring (Fig. 3). The ELF measures the extent of spacial localization of an electron on a zero-to-one scale.^48,49 The carboxyborane anion transition state shows the departing CO molecule with localized lone pair electrons similar to CO itself, and the C–O bond almost completely retracted onto O. The di-t-butylcyclopropane transition state, in contrast, is much closer to the reactant structure: the short-side C–C bond and mid-ring minimum are nearly intact, and the carbonyl lone pairs have the p-type character of a ketone.

Fig. 3 Electron localization function (ELF) plots of reactants and transition states for CO loss from trans-2,3-di-t-butylcyclopropane (a and b) and carboxyborane anion (c and d). ELF of carbon monoxide (e). For (a–d), cross-section is through the plane of the ring. M06-2X/6-311++G(2d,p), gas phase.

Aqueous solvation

The effects of water solvent on the structure and reactivity of carboxyborane anions were assessed in two ways: by (1) comparing structure and reactivity in the gas phase with that if the aqueous polarizable continuum model (PCM),³³ and (2) including explicit water molecules in reacting structures and transition states. Energy changes for all reactions including hydration equilibria are shown in Table 1.

Table 1 Energy changes of trimethylamine boranecarboxylate S_Ni and carboxyborane chelotropic reactions, and reaction barriers for transition state (t.s.) formation (kcal mol⁻¹)

	M06-2X/6-311++G(2d,p)^a					CCSD(T)^b
	Gas phase	PCM-H2O				PCM-H2O
	ΔG^o298	ΔEelect	ΔH^o298	ΔS^o/e.u.	ΔG^o298	ΔG^o298	^c
a H298 = Eelect + ZPVE + thermal-correction-to-298 + RT, where T is temperature in K, and R = gas constant. Thermal correction = Etr + Evib + Erot + Eelec, where Etr = 3RT/2, Erot = 3RT/2, Eelec ≈ 0.000, Evib = RΣθi[0.5 + (exp(θi/T) − 1)] with θi = vibrational temperature of the ith vibration; G298 = H298 − TStot.b H298,CCSD(T) = Eelect,CCSD(t) + (ZPVE + thermal-correction)M06-2X + RT; and G298,CCSD(t) = H298,CCSD(T) − TStot,M06-2X.c Corrected to 1 M standard state.d T = TMA, trimethylamine.
T-BH2COO^− → T + BH2COO^−^d	−2.79	28.01	24.93	42.77	12.18	14.42	16.31
T-BH2COO^− → T + CO + BH2O^−	−3.99	31.17	25.35	1.87	1.87	−5.50	−3.61
T-BH2COO^− + H2O → T-BH2COO(H2O)^−	−9.60	−11.00	−9.76	−30.92	−0.53	0.63	−1.27
T-BH2COO^− + 2H2O → T-BH2COO(H2O)2^−	−16.22	−18.67	−15.88	−58.23	1.49	3.01	−0.78
T-BH2COO^− + 3H2O → T-BH2COO(H2O)3^−	−23.61	−27.97	−23.60	−85.74	1.93	4.13	−1.56
T-BH2COO^− → T⋯BH2COO^− (t.s.)	11.16	29.66	27.25	9.14	24.52	24.40
T-BH2COO(H2O)^− → T⋯BH2COO(H2O)^− (t.s.)	14.68	34.08	31.58	16.56	26.64	25.87
T-BH2COO(H2O)2^− → T⋯BH2COO(H2O)2^− (t.s.)	17.92	36.35	34.03	19.29	30.51	26.25
T-BH2COO(H2O)3^− → T⋯BH2COO(H2O)3^− (t.s.)	19.74	37.95	35.28	19.86	29.36	28.25
T-BH2COO(H2O)^− → T + BH2COO(H2O)^−	4.98	33.10	30.01	48.99	15.95	17.27	19.17
T-BH2COO(H2O)2^− → T + BH2COO(H2O)2^−	6.58	36.17	33.06	51.78	17.62	18.35	20.25
T-BH2COO(H2O)3^− → T + BH2COO(H2O)3^−	11.01	39.25	36.44	43.99	22.14	22.52	23.75
T-BH2COO(H2O)^− → T + CO + BH2O(H2O)^−	−6.57	30.94	25.11	83.75	0.14	−6.88	−3.10
BH2COO^− → CO⋯BH2O^− (t.s.)	23.48	23.15	21.24	1.55	20.78	15.82
BH2COO(H2O)^− → CO⋯BH2O(H2O)^− (t.s.)	17.79	17.11	15.04	−0.78	15.27	11.74
BH2COO(H2O)2^− → CO⋯BH2O(H2O)2^− (t.s.)	13.68	12.38	10.35	−3.12	11.28	8.44
BH2COO(H2O)3^− → CO⋯BH2O(H2O)3^− (t.s.)	10.67	11.19	9.07	−4.48	10.40	7.89
BH2COO^− + H2O → BH2COO(H2O)^−	−3.99	−5.39	−4.05	−24.70	3.32	3.48	1.59
BH2COO^− + 2H2O → BH2COO(H2O)2^−	−6.85	−10.51	−7.75	−49.22	6.94	6.94	3.16
BH2COO^− + 3H2O → BH2COO(H2O)3^−	−9.06	−19.01	−14.27	−84.34	10.89	11.56	5.88
BH2COO^− → BH2O^− + CO	−1.20	3.16	0.42	−10.31	−10.31	−19.92	−18.03
BH2COO(H2O)^− → BH2O(H2O)^− + CO	−9.39	−2.68	−5.52	34.76	−15.89	−24.16	−22.26
BH2COO(H2O)2^− → BH2O(H2O)2^− + CO	−15.14	−7.26	−10.07	33.11	−19.94	−27.32	−25.43
BH2COO(H2O)3^− → BH2O(H2O)3^− + CO	−17.03	−6.26	−9.17	38.88	−20.76	−27.90	−26.00
BH2O^− + H2O → BH2O(H2O)^−	−12.18	−11.23	−10.00	−25.93	−2.26	−0.76	−2.65
BH2O^− + 2H2O → BH2O(H2O)2^−	−20.78	−20.93	−18.24	−52.11	−2.69	−0.46	−4.24
BH2O^− + 3H2O → BH2O(H2O)3^−	−24.89	−28.44	−23.85	−81.46	0.45	3.59	−2.10

---

Solvation energies for most of the anions and transition states were in the range of 55–60 kcal mol⁻¹ with the exception of TMA-BH₂COO⁻ (dipole moment = 17.4 D), where the calculated solvation energy was 73.9 kcal mol⁻¹ (Table S2†). In contrast, the calculated solvation energy for the S_Ni transition state (dipole moment = 12.3 D) was only 60.6 kcal mol⁻¹. This difference largely explains the increase in the S_Ni activation barrier going from gas to aqueous phase, i.e., from 11.2 to 24.4 kcal mol⁻¹ (Table 1, line 6). Therefore, aqueous solvation slows the S_Ni reaction by selective, strong solvation of the polar reactant. Aqueous solvation has the opposite effect on chelotropic decarbonylation. In this case, the solvation energy of the transition state is about 3 kcal mol⁻¹ greater than for BH₂COO⁻, while the activation barrier for this reaction decreases about the same amount going from gas to aqueous phase (Table 1, line 14).

The geometries of gas- and aqueous-phase transition states of the two steps (Fig. S2 in ESI†) are consistent with the reactivity differences described above; as outlined here, they also follow the Hammond Postulate.⁵⁰ In the gas-phase S_Ni transition state, the forming O–B bond is 0.14 Å longer and the breaking B–N bond is 0.14 Å shorter than those bonds in the aqueous transition state. That is, the S_Ni transition state of the faster (gas phase) reaction is more reactant-like. In the gas-phase CO-loss transition state, the forming O–B double bond is 0.04 Å shorter and the breaking B–C bond is 0.13 Å longer than those bonds in the aqueous transition state. That is, the CO-loss transition state of the slower (gas phase) reaction is more product-like.

Explicit solvent interactions were studied using complexes of one, two, and three waters with reactants and transition states. Single water complexes are shown in Fig. 1; two and three water complexes are shown in Fig. S2 and S7.† The optimized water complexes provide an approximation of the actual solvation shell, which is likely to contain even more water. For example, a recent molecular dynamics study of BH₄⁻ hydrolysis showed that BH₄⁻ is solvated by an average of six water molecules.³⁹ Nevertheless, the DFT-optimized complexes exemplify the structural effects of hydrogen bonding. In case of TMA-BH₂COO⁻ + H₂O complex (Fig. 1f), the O-to-B donor–acceptor interaction is weaker and the B–N bond is shorter and stronger compared to the uncomplexed ion (Fig. 1b). In the S_Ni transition state that follows (Fig. 1g), the hydrogen bonds become longer and weaker than in the starting complex. Taken together, these waters increase the S_Ni activation barrier by several kcal mol⁻¹. In contrast, the hydrogen bonded waters decrease the chelotropic activation barrier (compare Fig. 1h, i and Table 1, lines 14, 15). In this step the transition state is more polar than the starting carboxyborane anion, and thus the hydrogen bond become stronger and shorter.

Use of larger basis sets than 6-311++G(2d,p) has little effect on the calculated geometry or reactivity in these hydrogen bonded systems. Energy changes for S_Ni and chelotropic CO-loss reactions are nearly identical—to within about 1 kcal mol⁻¹—whether calculations were carried out using M06-2X/PCM-H₂O/6-311++G(2d,p), or M06-2X/PCM-H₂O/jun-, jul-, or aug-cc-pVTZ (Fig. S8 in ESI†).

Reaction energy profile and associated rate constants

Relative Gibbs free energies of the reactants, transition states, and products are plotted in Fig. 4. The relative free energies of starting trimethylamine carboxyborane anion and the various anion–water complexes are set to zero, which is reasonable given that the waters serve merely to solvate the reacting ions, and do not participate directly in bond formation. In general, we see that trimethylamine carboxyborane anion dissociates in an endothermic reaction to form trimethylamine and carboxyborane anion BH₂COO⁻, followed by exothermic chelotropic CO extrusion to borinate ion. The free energy profiles in Fig. 4 were constructed assuming all species are at the standard state of 1.0 M, and suggest that the second step is rate limiting. However, if the reactant concentration is milli- or micomolar, as expected under experimental or physiological conditions, the relative free energies of the carboxyborane intermediate and the subsequent unimolecular CO-loss transition state is lowered by 3 to 5 kcal mol⁻¹. In other words, a low concentration of reactant leads, after dissociation, to a corresponding low concentration of free amine, vastly increasing the thermodynamic barrier for reversal of the first step. Finally, if one assumes a realistic water concentration of 55.4 M, trimethylamine carboxyborane anion trihydrate will comprise more than 99.5% of the reactant species. This results in approximately 86% of the flux of the first step traversing the trihydrate barrier (green in Fig. 4).

Fig. 4 Energy changes for CO production via S_Ni displacement of trimethylamine from TMA-BH₂COO⁻, followed by chelotropic loss of CO, with all species bound to 0, 1, 2 or 3 waters. Crosshatched lines are transition states; solid lines are energy minima. Energy levels after dissociation include G^o₂₉₈(TMA).

The rate constant for amine dissociation from trihydrated TMA-BH₂COO⁻ anion, calculated from transition state theory (k = (k_BT/h)[exp(−ΔG^‡/RT)]) and the 28.25 kcal mol⁻¹ barrier, is 4.39 × 10⁻⁵ h⁻¹ at 298 K, or 2.89 × 10⁻⁴ h⁻¹ at 310 K. Ayudhya et al. used NMR to measure the rate of hydrolysis of TMA-BH₂COOH at 310 K and physiological pH,⁷ observing 0.74% reaction after 12.0 days, yielding a first-order rate constant of 2.6 × 10⁻⁵ h⁻¹. If the reaction occurred via the TMA-BH₂COO⁻ ion (in any hydrated form), and if 9.1% of the trimethylamine carboxyborane were present in the anion form (pH = 7.3 with a pK_a of 8.38 (ref. 28)), then the corrected rate constant would be 2.8 × 10⁻⁴ h⁻¹. This corresponds to an activation barrier of 28.2 kcal mol⁻¹.

Conclusions

The close correspondence here of calculated and experimental activation barriers is fortuitous, since the trimethylamine carboxyborane anion trihydrate approximates a larger multi-water cluster that probably exists in solution. Nevertheless, the fact that the numbers are close suggests that much of the physical environment of TMA-BH₂COO⁻ in water solution has been captured by the DFT and ab initio calculations. In addition, these results highlight the important role of the hydration shell in controlling the rate of fragmentation of amine carboxyboranes and CO loss from the intermediate carboxyborane anion. Importantly, obtaining the most accurate activation barrier required using a water cluster and polarizable continuum. It is likely that variations in solvation play a major role in determining the reactivity of this class of compounds. Although trimethylamine carboxyborane decarbonylates exceedingly slowly, other related compounds that have fewer waters of hydration may react faster. Finally, noting that in the gas phase, activation barriers for S_Ni substitution are 10–12 kcal mol⁻¹ less than in water (Table 1, column 1), these calculations suggest that faster reactions may occur in less polar environments such as non-polar solvents, protein complexes, or membranes.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by grants of computing time from the Department of Chemistry and Biochemistry and the Geophysical Institute of the University of Alaska Fairbanks. Also, this work used an allocation of computer time (TG-CHE180010) from the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562.⁵¹

References

1. E. P. Miller, Y. Wuband and C. J. Carrano, Metallomics, 2016, 8, 161–169.
2. H. Hu and P. H. Brown, Plant Physiol., 1994, 105, 681.
3. R. I. Rowe and C. D. Eckhert, J. Exp. Biol., 1999, 202, 1649–1654.
4. J. W. Spears, Biol. Trace Elem. Res., 2019, 188, 35–44.
5. I. H. Hall, K. G. Rajendran, S. Y. Chen, O. T. Wong, A. Sood and B. F. Spielvogel, Arch. Pharm., 1995, 328, 39–44.
6. I. H. Hall, B. F. Spielvogel and A. Sood, Anti-Cancer Drug, 1990, 1, 133–142.
7. T. I. Ayudhya, P. J. Pellechia and N. N. Dingra, Dalton Trans., 2018, 47, 538–543.
8. T. I. Ayudhya, A. L. Rheingold and N. N. Dingra, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2019, 75, 543–546.
9. X. Ji, K. Damera, Y. Zheng, B. Yu, L. E. Otterbein and B. Wang, J. Pharm. Sci., 2016, 105, 406–416.
10. D.-S. Kim, S.-W. Chae, H.-R. Kim and H.-J. Chae, Immunopharm. Immunot., 2009, 31, 64–70.
11. S. W. Ryter and A. M. K. Choi, Transl. Res., 2016, 167, 7–34.
12. K. M. Dreux, L. E. McNamara, J. T. Kelly, A. M. Wright, N. I. Hammer and G. S. Tschumper, J. Phys. Chem. A, 2017, 121, 5884–5893.
13. T. M. Gilbert, J. Phys. Chem. A, 2004, 108, 2550–2554.
14. H. A. LeTourneau, R. E. Birsch, G. Korbeck and J. L. Radkiewicz-Poutsma, J. Phys. Chem. A, 2005, 109, 12014–12019.
15. L. S. Fisher, K. McNeil, J. Butzen and T. A. Holme, J. Phys. Chem. B, 2000, 104, 3744–3751.
16. C. F. Pupim, A. J. L. Catão and A. López-Castillo, J. Mol. Model., 2018, 24, 283.
17. C. C. De Silva and T. A. Holme, Comp. Theoret. Chem., 2013, 1019, 78–84.
18. H. Koch and W. Haaf, Org. Syn., 1973, 5, 20.
19. M. Zielinski, A. Zielinska, H. Papiernik-Zielinska, G. Czarnota, G. Kasprzyk, W. Staedter and L. Gumolka, Isotopenpraxis, 1994, 30, 333–347.
20. L. R. Domingo, J. Andrés, V. Moliner and V. S. Safont, J. Am. Chem. Soc., 1997, 119, 6415–6422.
21. L. F. Feiser, Org. Syn., 1966, 46, 44.
22. R. Neidlein, M. Kohl and W. Kramer, Helv. Chim. Acta, 1989, 72, 1311–1318.
23. J. P. Buxton and C. J. S. M. Simpson, Chem. Phys., 1986, 105, 307–316.
24. D. M. Birney, S. Ham and G. R. Unruh, J. Am. Chem. Soc., 1997, 119, 4509–4517.
25. D. Schröder, N. Goldberg, W. Zummack, H. Schwarz, J. C. Poutsma and R. R. Squires, Int. J. Mass Spectrom., 1997, 165/166, 71–82.
26. F. D. Greene, D. B. Sclove, J. F. Pazos and R. L. Camp, J. Am. Chem. Soc., 1970, 92, 7488.
27. J. F. Pazos, J. G. Pacifici, G. O. Pierson, D. B. Sclove and F. D. Greene, J. Org. Chem., 1974, 39, 1990–1995.
28. K. H. Scheller, R. B. Martin, B. F. Spielvogel and A. T. McPhail, Inorg. Chim. Acta, 1982, 57, 227–228.
29. M. Klein, U. Neugebauer, M. Schmitt and J. Popp, ChemPhysChem, 2016, 17, 985–993.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Rev. D.01, Wallingford CT, 2009.
31. Y. Zhao and D. G. Truhlar, Theoret. Chem. Accts., 2008, 120, 215–241.
32. A. J. C. Varandas, M. Martínez González, L. A. Montero-Cabrera and J. M. Garcia de la Vega, Chem. - Eur. J., 2017, 23, 9122–9129.
33. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
34. E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034.
35. T. A. Keith, AIMAll, v 17.11.14, TK Gristmill Software, Overland Park KS, USA, 2019.
36. T. Lu and F.-W. Chen, J. Comput. Chem., 2012, 33, 580–592.
37. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7, Theoretical Chemistry Institute, University of Wisconsin, Madison, Madison, WI, 2018.
38. B. F. Spielvogel, L. Wojnowich, M. K. Das, A. T. McPhail and K. D. Hargrave, J. Am. Chem. Soc., 1976, 98, 5702–5703.
39. P. Li, G. Henkelman, J. A. Keith and J. K. Johnson, J. Phys. Chem. C, 2014, 118, 21385–21399.
40. R. F. W. Bader, Atoms in molecules. A quantum theory, Clarendon, Oxford, Great Britain, 1990.
41. C. F. Matta and R. J. Boyd, The quantum theory of atoms in molecules: from solid state to DNA and drug design, Wiley-VCH, Weinheim, 2007.
42. H.-X. Wei, C. Zhou, S. Ham, J. M. White and D. M. Birney, Org. Lett., 2004, 6, 4289–4292.
43. F. Weinhold and C. Landis, Valency and Bonding, Cambridge University Press, Cambridge, UK, 2005.
44. E. Chamorro, J. Chem. Phys., 2003, 118, 8687–8698.
45. J. Rodriguez-Otero, E. Cabaleiro-Lago, J. Hermida-Ramón and A. Peña-Gallego, J. Org. Chem., 2003, 68, 8823–8830.
46. M. W. Chase Jr, NIST-JANAF Themochemical Tables, Fourth Edition, J. Phys. Chem. Ref. Data, Monogr. 9, 1998, 1–1951.
47. R. A. Fletcher and G. M. Pilcher, Trans. Faraday Soc., 1970, 66, 794–799.
48. T. Lu and F.-W. Chen, Acta Phys.-Chim. Sin., 2011, 27, 2786–2792.
49. P. Fuentealba, E. Chamorro and J. C. Santos, in Theoretical Aspects of Chemical Reactivity, ed. A. Toro-Labbé, Elsevier, 2006, vol. 19, ch. 5, pp. 57–85.
50. G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338.
51. J. Towns, T. Cockerill, M. Dahan, I. Foster, K. Gaither, A. Grimshaw, V. Hazlewood, S. Lathrop, D. Lifka, G. D. Peterson, R. Roskies, J. R. Scott and N. Wilkins-Diehr, Comput. Sci. Eng., 2014, 16, 62–74.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S10; Tables S1–S7. See DOI: 10.1039/d0ra01572e

---