DOI:
10.1039/D0RA01641A
(Paper)
RSC Adv., 2020,
10, 18124-18130
Calculation of magnetic response properties of tetrazines†
Received
20th February 2020
, Accepted 1st May 2020
First published on 12th May 2020
Abstract
Magnetic response properties of 1,2,3,5-tetrazine derivatives including the newly synthesized 4,6-diphenyl-1,2,3,5-tetrazine have been studied computationally at the density functional theory (DFT) level. Calculations of magnetically induced current densities and induced magnetic fields show that the unsubstituted 1,2,3,5-tetrazine is almost as aromatic as benzene. Separating the magnetic shielding functions into molecular orbital components provided additional insights into the magnetic response. The aromatic character estimated from magnetically induced current densities and induced magnetic fields shows that NICSπzz(0) values and ring-current strengths yield about the same degree of aromaticity, whereas NICSzz(0) and NICSzz(1) values are contaminated by σ electron contributions. The studied 1,2,3,5-tetrazine derivatives are less aromatic than the unsubstituted one. Calculations of magnetic response properties of 4,6-diphenyl-1,2,3,5-tetrazine showed that it is the least aromatic among the studied molecules according to the ring-current criterion, while 4,6-[1,2,3,5]-ditetrazinyl-1,2,3,5-tetrazine is as aromatic as 4,6-dimethyl-1,2,3,5-tetrazine and slightly less aromatic than the unsubstituted 1,2,3,5-tetrazine.
Introduction
Novel methods for synthesizing heterocyclic aromatic molecules such as di-, tri- and tetrazines have recently been developed.1–8 1,3-Diazine (pyrimidine) is one of the more important azines, because its derivatives are of biological relevance as building blocks in the nucleobases of deoxyribonucleic acid (DNA).9,10 Triazines have been widely studied because of their use in biological and industrial applications.11–13 The molecular structures of the three possible tetrazine isomers (1,2,3,4-tetrazine, 1,2,3,5-tetrazine, and 1,2,4,5-tetrazine) differ by the relative positions of the nitrogen atoms in the six-membered ring,13–15 of which 1,2,4,5-tetrazine is the easiest one to synthesize, because it has only two nitrogens next to each other. Tetrazine derivatives are recognized as high-energy density materials (HEDMs) due to their high nitrogen content, strong N–N and N–C bonds, large heat of formation, high thermal stability and suitable structural properties.15–22 The aromatic properties of tetrazine have been previously studied by Wang et al.,23 who based on nucleus independent chemical shift (NICS)24,25 calculations and by using energy criteria concluded that the aromatic character is about the same for all azines they studied. In their NICS(0) studies, they found that the three tetrazine isomers are non-aromatic, while NICSπzz(0) calculations suggested that 1,2,3,5-tetrazine is the least aromatic among the three isomers.23 Yang et al. found that the NICS(0) value decreases with increasing number of nitrogens in the ring suggesting that tetrazines are less aromatic than triazines and so on.26 Sanchez-Sanz obtained the similar trend for the NICS(0) values of the azines, whereas the NICS(1) and NICS(2) values were found to be almost independent of the number of nitrogens in the ring.27 Wu and Boger recently synthesized 4,6-diphenyl-1,2,3,5-tetrazine and found that is aromatic.8
In this work, we investigate the aromatic properties of tetrazines by calculating magnetically induced current densities and induced magnetic fields of unsubstituted and substituted 1,2,3,5-tetrazines. The calculations yield qualitative and quantitative information about electron delocalization and the degree of aromaticity of the tetrazine ring.28–33 The studied molecules comprise 1,2,3,5-tetrazine, 4,6-dimethyl-1,2,3,5-tetrazine, 4,6-bis(1-methylethenyl)-1,2,3,5-tetrazine, 4,6-diphenyl-1,2,3,5-tetrazine, and 4,6-[1,2,3,5]-ditetrazinyl-1,2,3,5-tetrazine, which are shown in Fig. 1. Magnetic response properties of the two others unsubstituted tetrazine isomers are given as ESI.†
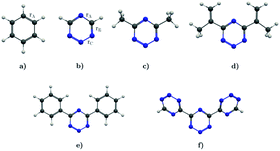 |
| | Fig. 1 The molecular structure of (a) benzene, (b) 1,2,3,5-tetrazine, (c) 4,6-dimethyl-1,2,3,5-tetrazine, (d) 4,6-bis(1-methylethenyl)-1,2,3,5-tetrazine, (e) 4,6-diphenyl-1,2,3,5-tetrazine, and (f) 4,6-[1,2,3,5]-ditetrazinyl-1,2,3,5-tetrazine. | |
Computational details
The molecular structures were fully optimized at the density functional theory (DFT) level using the PBE0 hybrid functional and triple-zeta valence basis set augmented with polarization functions (def2-TZVP).34–36 Grimme's semi-empirical dispersion correction (D3) was used for considering van der Waals interactions.37 Bond lengths and HOMO–LUMO gaps are given in Table S1 of the ESI.† External magnetic fields induce current densities (Jind) in molecules, which gives rise to a secondary induced magnetic field (Bind)28–33,38–42 that is proportional to the magnetic shielding tensor.42 In aromatic ring-shaped molecules, the magnetic response is diamagnetic, i.e., a net diatropic ring current is sustained by the aromatic ring, whereas antiaromatic rings sustain a net paratropic ring current.28–33 Nuclear magnetic resonance (NMR) shielding and current-density calculations were performed at the PBE0 level using split-valence basis sets augmented with polarization functions (def2-SVP).43 Gauge-including atomic orbitals (GIAOs) were used in the NMR shielding and current-density calculations.44,45 The electronic structure calculations were performed with the Gaussian 16 software.46 Current densities were calculated using the gauge-including magnetically induced current (GIMIC) method,28–30 which is freely available and interfaced to Gaussian 16.47 The current densities are visualized with ParaView.48 The Bind was calculated using the Aromagnetic code,49 which is also interfaced to Gaussian 16 and visualized with VisIt.50 The external magnetic field was aligned along the highest symmetry axis of the molecular ring. Thus, the z component of the induced magnetic field (Bindz) is the most important one providing information about the aromatic character of the molecular ring.31–33 Bindz (in ppm) is numerically equivalent to NICSzz values.31–33 The calculated Bind was separated into its molecular orbitals (MOs) contributions32,51 using the NBO6 code52 via the Natural Chemical Shielding (NCS) analysis.53 Ring-current strength susceptibilities, (Jind in nA T−1) were obtained with the GIMIC program by performing numerical integration of the current density flowing through a plane from the center of the ring to a very far distance outside the ring, where the current density vanishes.28–30 The height of the plane is 8 bohr above and below the ring plane. Ring-current strength susceptibilities are called ring-current strengths in the rest of the paper. The same ring-current strength is obtained for all bonds of the ring, when the basis-set is complete.28 Ring-current strengths reported for different bonds in Table S2 of the ESI† show very small discrepancies, even though the rather small SVP basis set was used. The lower symmetry of the tetrazine ring as compared to benzene may lead to nonvertical current-density vortices that also affect the accuracy of the numerical integration, because some ring-current strength contributions may fall outside the integration plane.
Results and discussion
Benzene and 1,2,3,5-tetrazine
Benzene is the archetypal aromatic molecule with 6π electrons fulfills Hückel's rule for aromaticity.54,55 The molecular structure belongs to the D6h point group. The length of the conjugated bonds is 1.39 Å and it has a large HOMO–LUMO gap of 7.11 eV at the PBE0 level, so, this is a very stable molecule. An external magnetic field perpendicular to the molecular ring induces a diatropic ring current in aromatic molecules, which is visualized as the clockwise direction in Fig. 2.38–41 A weaker paratropic (counterclockwise) ring current involving mainly the σ orbitals flows in the molecular plane inside the ring.56–58 It has been shown that at a distance of 1 bohr from the molecular plane the π electrons dominates in ring current density.58–60 Numerical integration yields a net diatropic ring-current strength (Jind) of 12.05 nA T−1. The Jind of the studied molecules are summarized in Table 1. The ring current of benzene induces a secondary field (Bind) in the opposite direction to the applied one, which leads to negative Bindz values.31–33 The MO partitions of the shielding tensor obtained with the NCS-GIAO method53 lead to large core contributions, which have been found to increase with the number of atoms in the ring.61 Core contributions to the magnetic shielding determined from orbital current densities that are calculated using the ipsocentric approach60,62 are much smaller, because it avoids rotations of occupied orbitals that cause gauge-origin problems.60,62–64 The two approaches yield the same shielding contributions from σ and π orbitals of planar molecules that cannot mix through orbital rotations.60,62 Therefore, we do not calculate orbital contributions from individual orbitals but divide the magnetic shieldings into contributions from σ (core + σ) and π orbitals. Bindz has shielding cones (shown in blue) above and below the ring, while the σ electrons are responsible for the positive deshielding regions (shown in red) outside the ring as shown in Fig. 3.31–33,51 The Bindz calculated along the symmetry axis (z axis) shown in Fig. 4 also provides qualitative and quantitative information about the degree of aromaticity.25,65–67 The total Bindz declines asymptotically as z−3 for large z.65 The π contribution (Bindz,π), which has a similar mathematical shape at large distances,68,69 has a minimum of −36.41 ppm in the center of the ring and large negative values along the z axis. These are about −13 ppm even at 2 Å from the ring center. Orbital contributions to the negative Bindz values calculated in the ring center (NICSzz(0) values)24,25 are given in Table 2. The core + σ contribution is 23.21 ppm at the ring center representing the maximum value of the profile. It almost cancels the π contribution near the ring, but it declines rapidly with increasing z.63,64,66,67 Although the maximum and minimum values vary from one system to another, the magnetic behavior is largely the same for the studied molecules. Thus, the NICSzz(0), NICSzz(1) and even the NICSzz(2) indexes are contaminated with core + σ contributions affecting the estimated degree of aromaticity in the systems from NICSzz values. The Bindz,π(0) value, which is equivalent to the NICSπzz(0), is therefore a better aromaticity index for the studied molecules.
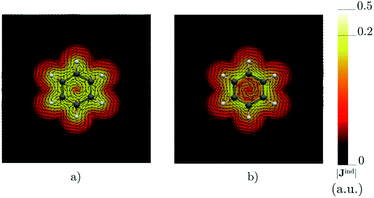 |
| | Fig. 2 The current density (Jind) plotted at (a) 0 bohr and (b) 1 bohr from the molecular plane of benzene. |Jind| values are given in atomic units (1 a.u. = 100.63 nA T−1 Å−2). The figure was made with ParaView.48 | |
Table 1 Integrated strengths (in nA T−1) of the diatropic, paratropic and net ring current of the studied molecules. The current densities were calculated at the PBE0/def2-SVP level
| Molecule |
Core + σ |
π |
Total |
| Benzene |
23.21 |
−36.41 |
−13.20 |
| 1,2,3,5-Tetrazine |
29.58 |
−35.94 |
−6.36 |
| 4,6-Dimethyl-1,2,3,5-tetrazine |
27.88 |
−31.15 |
−3.27 |
| 4,6-Bis(1-methylethenyl)-1,2,3,5-tetrazine |
29.42 |
−26.30 |
3.12 |
| 4,6-Diphenyl-1,2,3,5-tetrazine |
30.31 |
−20.65 |
9.66 |
| 4,6-[1,2,3,5]-Ditetrazinyl-1,2,3,5-tetrazine |
22.17 |
−26.83 |
−4.66 |
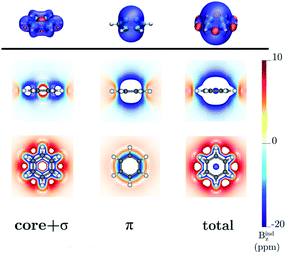 |
| | Fig. 3 The isosurfaces of the Bindz of benzene are shown in the upper panel. The shielding and deshielding cones at −10 ppm and 10 ppm are in blue and red, respectively. The Bindz isolines calculated in the transverse and molecular planes are shown in the lower panel. The figure was made with VisIt.50 | |
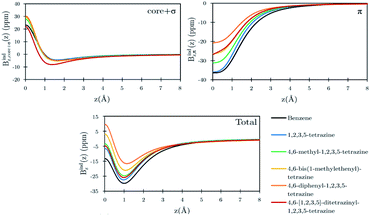 |
| | Fig. 4 Orbital contributions to the Bindz profiles along the z-axis for benzene and the tetrazines calculated at the PBE0/def2-SVP level. The z axis of the profile calculation passes through the center of the benzene/tetrazine ring. | |
Table 2 Orbital contributions to the Bindz values (in ppm) computed in the center of the studied molecules (NICSzz(0)) calculated at the PBE0/def2-SVP level
| Molecule |
Diatropic |
Paratropic |
Net |
| Benzene |
17.32 |
−5.27 |
12.05 |
| 1,2,3,5-Tetrazine |
15.39 |
−5.31 |
10.08 |
| 4,6-Dimethyl-1,2,3,5-tetrazine |
14.82 |
−5.50 |
9.32 |
| 4,6-Bis(1-methylethenyl)-1,2,3,5-tetrazine |
13.87 |
−5.84 |
8.03 |
| 4,6-Diphenyl-1,2,3,5-tetrazine |
12.81 |
−6.14 |
6.66 |
| 4,6-[1,2,3,5]-Ditetrazinyl-1,2,3,5-tetrazine |
14.64 |
−5.17 |
9.46 |
Calculations on 1,2,3,5-tetrazine, whose molecular structure belongs to the C2v point group with 6π electrons is expected to be aromatic according to the Hückel rule. The addition of the functional groups to the 1,2,3,5-tetrazine ring does not significantly affect the HOMO–LUMO gap (see Table S1†). The average HOMO–LUMO gap of 4.52 eV of the studied 1,2,3,5-tetrazines is much smaller than for benzene. However, the 1,2,3,5-tetrazine has a HOMO–LUMO gap of 4.85 eV, which is much smaller than for benzene. The current-density plot in Fig. 5 shows that 1,2,3,5-tetrazine sustains a diatropic ring current above, below and outside the ring, whereas it sustains a paratropic ring current inside the ring as benzene. The integrated ring-current strengths in Table 1 show that 1,2,3,5-tetrazine sustains a net ring current of 10.08 nA T−1, which is only 2 nA T−1 weaker than for benzene. The calculated Bindz,π(0) value of −35.94 ppm also suggest that 1,2,3,5-tetrazine is almost as aromatic as benzene. The orbital contributions to Bindz shown in profiles and plots of Fig. 4 and 6, respectively, look qualitatively like those obtained for benzene. The π contribution to the magnetic shielding of the tetrazines are practically the same as for benzene, whereas the core + σ contribution is about 7 ppm larger in the ring center than for benzene. Thus, according to the magnetic criteria 1,2,3,5-tetrazine is less aromatic than benzene. The two other tetrazine isomers (1,2,3,4-tetrazine and 1,2,4,5-tetrazine) have a similar magnetic response as 1,2,3,5-tetrazine. Their ring-current strengths and Bindz(0) values are reported in Tables S2 and S3 of the ESI.† The magnetic response properties of 1,2,3,4-tetrazine and 1,2,4,5-tetrazine are not discussed further in this work.
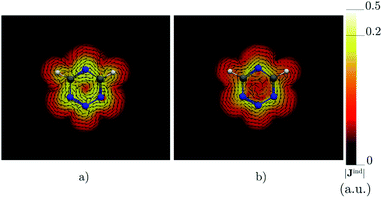 |
| | Fig. 5 The current density (Jind) plotted at (a) 0 bohr and (b) 1 bohr from the molecular plane of 1,2,3,5-tetrazine. |Jind| values are given in atomic units (1 a.u. = 100.63 nA T−1 Å−2). The figure was made with ParaView.48 | |
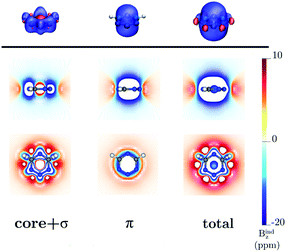 |
| | Fig. 6 The isosurfaces of the Bindz of 1,2,3,5-tetrazine are shown in the upper panel. The shielding and deshielding cones at −10 ppm and 10 ppm are in blue and red, respectively. The Bindz isolines calculated in the transverse and molecular planes are shown in the lower panel. The figure was made with VisIt.50 | |
4,6-Dimethyl- and 4,6-bis(1-methylethenyl)-1,2,3,5-tetrazine
We studied 4,6-dimethyl-1,2,3,5-tetrazine and 4,6-bis(1-methylethenyl)-1,2,3,5-tetrazine in order to understand how alkyl substituents affect the aromatic character of the tetrazine ring. The geometry and HOMO–LUMO gap of the tetrazine ring are not significantly affected by the methyl or methylethenyl substitution. The calculated ring-current strengths show that 4,6-dimethyl-1,2,3,5-tetrazine and 4,6-bis(1-methylethenyl)-1,2,3,5-tetrazine are aromatic sustaining ring currents of 9.32 nA T−1 and 8.03 nA T−1, respectively. Thus, the alkyl substitution leads to 1–2 nA T−1 weaker ring currents. A current strength of 6.93 nA T−1 flows along the C–C bond between the methyl substituents and the tetrazine ring, whereas only 2.4 nA T−1 continues along the ring. The corresponding current strengths for 4,6-bis(1-methylethenyl)-1,2,3,5-tetrazine are 6.41 nA T−1 and 1.6 nA T−1 for the outer and inner pathway, respectively. The current densities of 4,6-dimethyl-1,2,3,5-tetrazine and 4,6-bis(1-methylethenyl)-1,2,3,5-tetrazine are given in Fig. S1 and S3 of the ESI† and the orbital contributions to Bindz are shown in Fig. S2 and S4 of the ESI.† The ring-current pathway is on the outside of the alkyl substituents as shown in the streamline representation of Jind in Fig. S5 of the ESI.† Calculations of the magnetic response show that the alkyl substituted tetrazines are aromatic but slightly less than the unsubstituted tetrazine ring.
4,6-Diphenyl- and 4,6-[1,2,3,5]-ditetrazinyl-1,2,3,5-tetrazine
The ring-current strength of 4,6-diphenyl-1,2,3,5-tetrazine is 6.66 nA T−1, which is 3.42 nA T−1 weaker than the ring-current for the unsubstituted tetrazine. NMR signals were detected.8 Calculations yielded a rotational barrier of 31 kJ mol−1 implying that the phenyl groups rotate at room temperature. The interaction between the phenyl hydrogens in the ortho position and the nitrogens of the tetrazine ring as well as the common ring current stabilize the planar structure. The pictures of the current density maps and streamlines in Fig. 7 and 8 show a global ring current around the three rings. Calculations of the Bind also suggest that the phenyl-substituted is the least aromatic of the studied molecules because the shielding cone of the tetrazine ring is smaller than for the unsubstituted ring (Fig. 9). This can also be seen in the Bindz,π profile (Fig. 4), because for this system the minimum is the least pronounced. The Bindz,π(0) value of −20.65 ppm is in absolute value about 15 ppm smaller than for the unsubstituted tetrazine ring, which correlates well with the calculated ring-current strengths. The trend of the Bindz,π(0) values of the studied tetrazines is largely the same as the one obtained for the ring-current strengths. On the other hand, the central ring of 4,6-[1,2,3,5]-ditetrazinyl-1,2,3,5-tetrazine is planar, whereas the tetrazine substituents are slightly tilted with respect to the ring in the middle. The strength of the ring current that flows along the C–C bond between two tetrazine rings is 4.81 nA T−1, which is half the total ring-current strength of 9.46 nA T−1 for the tetrazine ring in the middle. Thus, the ring current splits into local and global pathways at the tetrazine substituents as shown in Fig. 7. The current density in Fig. S6 of the ESI† shows that 4,6-[1,2,3,5]-ditetrazinyl-1,2,3,5-tetrazine sustains a similar diatropic ring current in the central ring of tetrazine as dimethyl-substituted tetrazine, which have almost the same Bindz,π(0) values, as seen in Table 2. The Bindz,π(0) value for 4,6-[1,2,3,5]-ditetrazinyl-1,2,3,5-tetrazine of −26.83 ppm is in absolute value 4.32 ppm smaller than for the unsubstituted tetrazine showing that the degree of aromaticity is in qualitative agreement with the one deduced from ring-current strengths. The same can be concluded from the Bindz plots in Fig. S7 of the ESI.†
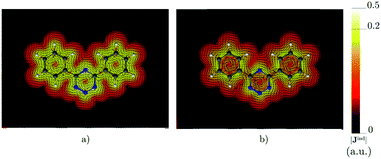 |
| | Fig. 7 The current density (Jind) plotted at (a) 0 bohr and (b) 1 bohr from the molecular plane of 4,6-diphenyl-1,2,3,5-tetrazine. |Jind| values are given in atomic units (1 a.u. = 100.63 nA T−1 Å−2). The figure was made with ParaView.48 | |
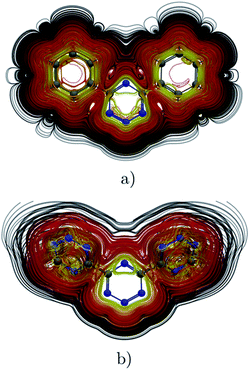 |
| | Fig. 8 Streamlines representation of Jind for (a) 4,6-diphenyl-1,2,3,5-tetrazine showing the global ring current pathways, and the local and global ones for (b) 4,6-[1,2,3,5]-ditetrazinyl-1,2,3,5-tetrazine. The figure was made with ParaView.48 | |
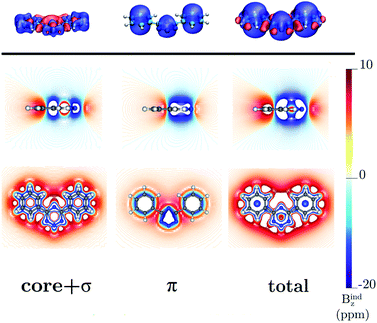 |
| | Fig. 9 The isosurfaces of the Bindz of 4,6-diphenyl-1,2,3,5-tetrazine are shown in the upper panel. The shielding and deshielding cones at −10 ppm and 10 ppm are in blue and red, respectively. The Bindz plots calculated in the transverse and molecular planes are shown in the lower panel. The figure was made with VisIt.50 | |
Conclusions
Calculations of magnetically induced current densities and induced magnetic fields show that unsubstituted 1,2,3,5-tetrazine is aromatic sustaining a net diatropic ring current when it is exposed to an external magnetic field perpendicular to the ring. The behavior of the magnetic responses is like that of benzene. The calculations show that there is a correlation between ring-current strengths and Bindz,π(0) values, whereas NICSzz(0), NICSzz(1) and NICSzz(2) values are contaminated by core and σ contributions leading to uncertainties in the degree of aromaticity based on them. Calculations of the magnetic response of the substituted 1,2,3,5-tetrazines shows that the substituents are an integrated part of the aromatic system. In the case of 4,6-diphenyl-1,2,3,5-tetrazine, the tetrazine ring does not only sustains a ring current of its own but there is also a global ring current flowing along the C–C single bond between the tetrazine and phenyl rings and continues outside of the phenyl rings. The global aromaticity and the interaction between the hydrogens in the ortho position of the phenyls and the nitrogens of the tetrazine ring stabilize 4,6-diphenyl-1,2,3,5-tetrazine. Calculations of the aromatic character of 4,6-[1,2,3,5]-ditetrazinyl-1,2,3,5-tetrazine showed that it has an aromatic tetrazine ring in the middle. The calculations also showed that a global ring-current flows around the three tetrazine rings. The ring current splits almost equally into a local ring current around the tetrazine ring in the middle and the global ring current.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research has been supported by the Academy of Finland through project 314821. CSC – the Finnish IT Center for Science and the Finnish Grid and Cloud Infrastructure (persistent identifier urn:nbn:fi:research-infras-2016072533) are acknowledged for computer time. We thank Magnus Ehrnrooth foundation and the Swedish Cultural Foundation in Finland for financial support. M. O.-I. and C. A. C. also thank Conacyt for their PhD fellowships. The authors thank the anonymous reviewers who helped to improve our article with important suggestions.
References
- M. H. V. Huynh, M. A. Hiskey, D. E. Chavez, D. L. Naud and R. D. Gilardi, J. Am. Chem. Soc., 2005, 127, 12537–12543 CrossRef CAS PubMed.
- M. Savastano, C. García-Gallarín, M. D. L. de la Torre, C. Bazzicalupi, A. Bianchi and M. Melguizo, Coord. Chem. Rev., 2019, 397, 112–137 CrossRef CAS.
- A. P. Brucks, 1,2,4,5-Tetrazine, Encycl. Reagents Org. Synth., 2015, 1–2 CAS.
- H. M. M. Dalloul, Heterocycl. Commun., 2003, 9, 307–312 CAS.
- X.-F. Wu and Z. Wang, Synthesis of Triazine. Transition Metal Catalyzed Pyrimidine, Pyrazine, Pyridazine and Triazine Synthesis, Synthesis of Triazine, 2017, ch. 5, pp. 79–93 Search PubMed.
- X.-F. Wu and Z. Wang, Synthesis of Triazine. Transition Metal Catalyzed Pyrimidine, Pyrazine, Pyridazine and Triazine Synthesis, Synthesis of Triazine, 2017, ch. 4, pp. 73–77 Search PubMed.
- A. A. Konnov, M. S. Klenov, A. M. Churakov, Y. A. Strelenko, A. O. Dmitrienko, L. N. Puntus, K. A. Lyssenko and V. A. Tartakovsky, Asian J. Org. Chem., 2018, 7, 2534–2543 CrossRef CAS.
- Z.-C. Wu and D. L. Boger, J. Am. Chem. Soc., 2019, 141, 16388–16397 CrossRef CAS PubMed.
- A. R. Aroor, Chemistry of Nucleic Acids. Medical Biochemistry, 2011, ch. 8, pp. 543–555 Search PubMed.
- E. Rosenberg, Chemistry of DNA, It's in Your DNA, 2017, ch. 2, pp. 9–16 Search PubMed.
- R. Patel and A. Malhotra, Triazines: Synthesis, Applications, and Toxicity, Nova Science Pub Incorporated, 1st edn, 2012, pp. 1–209 Search PubMed.
- O. Bekircan, M. Küxük, B. Kahveci and S. Kolayli, Arch. Pharm., 2005, 338, 365–372 CrossRef CAS PubMed.
- H. Neunhoeffer and P. F. Wiley, Chemistry of 1,2,3-Triazines and 1,2,4-Triazines, Tetrazines, and Pentazin, John Wiley & Sons, 2009, vol. 33, pp. 1–1335 Search PubMed.
- A. M. Prokhorov and P. E. Progr, Heterocycl. Chem., 2015, 27, 451–464 CAS.
- N. Saracoglu, Tetrahedron, 2007, 63, 4199–4236 CrossRef CAS.
- Y. Zhou, X. Long and Y. Shu, J. Mol. Model., 2010, 16, 1021–1027 CrossRef CAS PubMed.
- J. Tu, D. Svatunek, S. Parvez, A. C. Liu, B. J. Levandowski, H. J. Eckvahl, R. T. Peterson, K. N. Houk and R. M. Franzini, Angew. Chem., Int. Ed. Engl., 2019, 58, 9043–9048 CrossRef CAS PubMed.
- C. Yongjin and B. Shuhong, Johnson Matthey Technol. Rev., 2019, 63, 51–72 CrossRef.
- G. Wang, Z. Fu, H. Yin and F. Chen, Propellants, Explos., Pyrotech., 2019, 44, 1010–1014 CrossRef CAS.
- D. M. Badgujar, M. B. Talawar, S. N. Asthana and P. P. Mahulikar, J. Hazard. Mater., 2008, 151, 289–305 CrossRef CAS PubMed.
- T. M. Klapötke, Chemistry of High-Energy Materials, Walter de Gruyter, 2nd edn, 2012, Berlin Search PubMed.
- A. E. Baydar, G. V. Boyd, P. F. Lindley and A. R. Walton, J. Chem. Soc., Perkin Trans. 2, 1985, 1, 415–418 RSC.
- Y. Wang, J. I.-C. Wu, Q. Li and P. v. R. Schleyer, Org. Lett., 2010, 12, 4824–4827 CrossRef CAS PubMed.
- P. von R. Schleyer, C. Maerker, C. A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef CAS PubMed.
- H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von R. Schleyer, Org. Lett., 2006, 8, 863–866 CrossRef CAS PubMed.
- Y.-F. Yang, Y. Liang, F. Liu and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 1660–1667 CrossRef CAS PubMed.
- G. Sánchez-Sanz, Tetrahedron, 2015, 71, 826–839 CrossRef.
- J. Jusélius, D. Sundholm and J. Gauss, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Wiley Interdiscip. Rev. Comput. Mol. Sci, 2016, 6, 639–678 CrossRef CAS.
- G. Merino, T. Heine and G. Seifert, Chem.–Eur. J., 2004, 10, 4367–4371 CrossRef CAS PubMed.
- T. Heine, R. Islas and G. Merino, J. Comput. Chem., 2007, 28, 302–309 CrossRef CAS PubMed.
- R. Islas, T. Heine and G. Merino, Acc. Chem. Res., 2012, 45, 215–228 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- N. F. Ramsey, Phys. Rev., 1950, 78, 699–703 CrossRef CAS.
- J. A. Pople, Mol. Phys., 1958, 1, 175–180 CrossRef CAS.
- R. McWeeny, Mol. Phys., 1958, 1, 311–321 CrossRef CAS.
- J. A. Gomes and R. B. Mallion, Chem. Rev., 2001, 101, 1349–1383 CrossRef CAS PubMed.
- T. Heine, C. Corminboeuf and G. Seifert, Chem. Rev., 2005, 105, 3889–3910 CrossRef CAS PubMed.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- R. Ditchfield, Mol. Phys., 1974, 27, 789–807 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 16, 2016 Search PubMed.
- GIMIC, Version 2.0, a current density program, 2019, can be freely downloaded from https://github.com/qmcurrents/gimic Search PubMed.
- J. Ahrens, B. Geveci and C. Law, ParaView: An End-User Tool for Large Data Visualization, Visualization Handbook, Elsevier, 2005, see also: http://www.paraview.org Search PubMed.
- M. Orozco-Ic, J. L. Cabellos and G. Merino, Aromagnetic, a magnetic shielding program, Cinvestav-Mérida, Mexico, 2016 Search PubMed.
- H. Childs, E. Brugger, B. Whitlock, J. Meredith, S. Ahern, D. Pugmire, K. Biagas, M. Miller, C. Harrison, G. H. Weber, H. Krishnan, T. Fogal, A. Sanderson, C. Garth, E. W. Bethel, D. Camp, O. Rübel, M. Durant, J. M. Favre and P. Navrátil, Visit: An End-User Tool For Visualizing and Analyzing Very Large Data, 2012, see also: https://wci.llnl.gov/simulation/computer-codes/visit Search PubMed.
- N. D. Charistos, A. G. Papadopoulos and M. P. Sigalas, J. Phys. Chem. A, 2014, 118(6), 1113–1122 CrossRef CAS PubMed.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- J. A. Bohmann, F. Weinhold and T. C. Farrar, J. Chem. Phys., 1997, 107, 1173–1184 CrossRef CAS.
- E. Hückel, Z. Phys., 1931, 70, 204–286 CrossRef.
- E. Hückel, Z. Phys., 1931, 72, 310–337 CrossRef.
- P. Lazzeretti, E. Rossi and R. Zanasi, J. Chem. Phys., 1982, 72, 3129–3139 CrossRef.
- R. W. A. Havenith and P. W. Fowler, Chem. Phys. Lett., 2007, 449, 347–353 CrossRef CAS.
- H. Fliegl, D. Sundholm, S. Taubert, J. Jusélius and W. Klopper, J. Phys. Chem. A, 2009, 113, 8668–8676 CrossRef CAS PubMed.
- E. Steiner and P. W. Fowler, Chem. Commun., 2001, 21, 2220–2221 RSC.
- E. Steiner and P. W. Fowler, J. Phys. Chem. A, 2001, 105, 9553–9562 CrossRef CAS.
- M. Orozco-Ic, J. Barroso, N. D. Charistos, A. Muñoz-Castro and G. Merino, Chem.–Eur. J., 2020, 26, 326–330 CrossRef CAS PubMed.
- E. Steiner and P. W. Fowler, Phys. Chem. Chem. Phys., 2004, 6, 261–272 RSC.
- G. Acke, S. Van Damme, R. W. A. Havenith and P. Bultinck, Phys. Chem. Chem. Phys., 2019, 21, 3145–3153 RSC.
- G. Acke, S. Van Damme, R. W. A. Havenith and P. Bultinck, J. Comput. Chem., 2017, 39, 511–519 CrossRef PubMed.
- J. Jusélius and D. Sundholm, Phys. Chem. Chem. Phys., 1999, 1, 3429–3435 RSC.
- A. Stanger, J. Org. Chem., 2006, 71(3), 883–893 CrossRef CAS PubMed.
- R. Báez-Grez, L. Ruiz, R. Pino-Rios and W. Tiznado, RSC Adv., 2018, 8, 13446–13453 RSC.
- G. Monaco and R. Zanasi, J. Phys. Chem. A, 2014, 118, 1673–1683 CrossRef CAS PubMed.
- S. Pelloni, G. Monaco, P. Lazzeretti and R. Zanasi, Phys. Chem. Chem. Phys., 2011, 13, 20666–20672 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Tables S1–S3, Fig. S1–S7 and Cartesian coordinates of the molecular structures. See DOI: 10.1039/d0ra01641a |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Christian A. Celaya
a,
Christian A. Celaya ab and
Dage Sundholm
ab and
Dage Sundholm *a
*a









