Open Access Article
Open Access ArticleThe role of interaction between low molecular weight neutral organic compounds and a polyamide RO membrane in the rejection mechanism†
Muxue Zhanga,
Lauren Breitnerb,
Kerry J. Howeb and
Daisuke Minakata *a
*a
aDepartment of Civil and Environmental Engineering, Michigan Technological University, 1400 Townsend Drive, Houghton, Michigan 49931, USA. E-mail: dminakat@mtu.edu; Tel: +1 906-487-1830
bDepartment of Civil, Construction and Environmental Engineering, University of New Mexico, MSC01 1070, Albuquerque, New Mexico 87131-1070, USA
First published on 21st April 2020
Abstract
Reverse osmosis (RO) is a membrane technology that separates dissolved species from water. RO has been applied for the removal of chemical contaminants from water and is employed in wastewater reclamation to provide an additional barrier to improve the removal of trace organic contaminants. The presence of a wide variety of influent chemical contaminants and the insufficient rejection of low molecular weight neutral chemicals by RO calls for the need to develop a comprehensive model that predicts the rejection of various chemicals in RO. Yet the role of the interaction between neutral organic compounds and a RO membrane, and how the functional groups of organic compounds affect the interaction have not been fully elucidated. In this study, we first constructed a molecular model for a reference polyamide (PA) membrane. We then investigated the impact of explicit water molecules and PA membrane functionality on the membrane structure using quantum mechanical calculations. We examined solvent–membrane interactions and then solvent–membrane–solute interactions using two neutral test solutes, arsenic and boron, by comparing the theoretically calculated aqueous-phase free energies of interaction with their experimental values. Finally, the validated PA membrane model was used to calculate the free energies of interaction for a wide variety of organic compounds such as haloalkanes, haloalkenes, alkylbenzenes and halobenzenes, which correlated with the experimentally obtained mass transfer coefficients. The correlation indicates that the interaction between organic compounds and PA membranes plays a critical role in the rejection mechanism.
Introduction
The presence of a wide variety of trace chemicals called chemicals of emerging concern (CECs) in effluents of wastewater1–4 presents challenges to the practice of direct potable reuse, in which reclaimed wastewater is introduced directly to the potable water supply distribution system, or indirect potable reuse, in which reclaimed wastewater is introduced to the potable water supply system after passing through an environmental buffer.5Reverse osmosis (RO) is an attractive and promising membrane-based treatment process that can be applied for the removal of CECs and employed after microfiltration (MF)/ultrafiltration (UF) processes in typical wastewater reclamation schemes.6–9 While RO rejects a wide variety of CECs with greater than 99% rejection efficiency, neutral compounds with a molecular weight (MW) less than 200 g mol−1 have poor rejection efficiencies.7
The rejection of organic compounds by non-porous dense RO membranes is explained by two major factors: (1) solute–membrane interactions and (2) the diffusion of solute through the membrane active layer.10 The former interaction refers to the thermodynamic properties of solute–membrane interactions, i.e., the coefficient describing the partitioning of solute between membrane and water. The latter factor, diffusion, refers to the kinetics of solute movement in membranes. In general, strong interactions between organic compounds and membranes are dominant for the mass transfer of small molecules from water to membranes11 and increase the concentration of the solute within the membrane, which decreases the rejection efficiency.12,13 Three major solute–solvent–membrane interactions that have been distinguished are (1) steric exclusion, (2) electrostatic interactions, and (3) an affinity between the solute and membrane.12,14,15 The affinity component includes hydrophobic attraction, hydrogen bonding, and the dielectric effect of water molecules and is described by the free energy of interaction between the solute and the membrane in the aqueous phase.14 In the non-porous solid RO membrane, the diffusion of an organic compound occurs mainly through polyamide rich domains than through the water-filled voids of membrane11 and is also affected by the membrane–solute interaction. In general, an independent measurement of each parameter in very thin-film composite materials used for RO is technically challenging.11
Molecular mechanics- and quantum mechanics (QM)-based computational chemistry tools are robust techniques that can be used to characterize membrane properties and provide mechanistic insights into solute–solvent–membrane interactions. Classical molecular modeling and dynamics (MM/MD) have been used to construct RO membrane structures and characterize the membrane properties to engineer the design of membrane materials and simulate the rejection of solute.15–20 Studies using MD techniques have been very successful at simulating cross-linked polyamide (PA) membranes and related polymer materials. Xiang et al. (2013) found the critical role of carboxylate group of a polyamide membrane surface for binding with a foulant, alginate, through their MD study.21 Ghoufi et al. (2017) has recently used MD simulation to qualitatively show the significant contributions from solute–membrane (−4 to −3 kJ mol−1 of interaction energy) and solute–water (−5 to −2 kJ mol−1) interactions to the experimentally determined partition coefficients (e.g., 0.09 for 4 aminopiperidine, 0.15 for pinacolone, and 0.81 for methylisobutyl ketone) based on the FTIR spectroscopy measurement with SWC4+ RO membrane at 21.0 °C and 11–17 bar of transmembrane pressure differences.22 Among compounds that have the same MW, a compound that strongly interacts with membranes has the largest partition coefficient (i.e., lowest rejection by the membrane). However, energies determined by MM/MD only provide qualitative measures and those energies may not be used for the prediction of organic compounds' rejections. In contrast, ab initio and density functional theory (DFT) QM calculations provide reliable thermodynamic properties based on statistical thermodynamics.23 If a membrane segment is properly assigned and simulations of solute–solvent–membrane interactions are performed with a reasonable computational demand, this approach can be used to systematically calculate interaction energies between the membrane and a wide variety of CECs, which are then fed into a predictive model.
In this study, we use QM calculations to construct various segments of a PA membrane by cross-linking 1,3-diaminobenzene (MPD) and 1,3,5-benzenetricarbonyl trichloride (TMC) and examining the impacts of hydrogen bonds on the functional groups of the PA molecular model membrane. We use arsenous acid (H3AsO3) as a test neutral chemical to study the membrane–solute–solvent interaction because of the availability of its experimental parameters and use a similar compound of boron (H3BO3) to enhance the findings. We also calculate the aqueous-phase free energies of interactions for the membrane–water–solute interaction for a wide variety of organic compounds and compare the resultant thermodynamic properties with the mass transfer coefficients obtained from our previous experiments.
Materials and methods
Mass transfer coefficients of solutes
The rejection of organic compounds, Rej, by RO can be quantified using the ratio of organic compound concentrations in permeate, Cp, and feed solution, CF, as shown in eqn (1)24
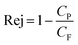 | (1) |
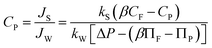 | (2) |
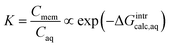 | (3) |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ks ∝ ΔGintraq ks ∝ ΔGintraq
| (4) |
The aqueous-phase free energy of interaction, ΔGintraq (kcal mol−1), is the free energy difference associated with the differences in the interactions of the solute in the aqueous phase and in the membrane matrix
| ΔGintraq = Gsolute–membrane–nH2Oaq − (Gmembrane–nH2Oaq + Gsoluteaq) | (5) |
For the detailed calculation procedure see the ESI, Text S1.† We use the subscripts ‘calc’ and ‘exp’ to indicate the theoretically calculated and experimentally obtained aqueous-phase free energies of interaction, respectively. The experimentally determined ks values for various organic compounds were determined from a bench-top laboratory scale experiment and reported in our other publications.28,29 Briefly, the experiments were done with a bench-top system containing multiple flat sheet membranes at three operational pressures, constant solution temperature (20 °C), and a constant pH of 6.5. The concentrations of feed and permeate after the steady-state condition were measured for organic compounds and the rejection efficiencies were determined. Using eqn (1) and (2), the ks values were determined for various RO membrane products. In this study, we only used the ks values obtained through a ESPA2-LD PA brackish water RO membrane (Hydranautics) because this was used as a reference membrane. The detailed descriptions of ks values about the organic compounds will be given below.
Conformer search and geometry optimization
The energetically stable conformers of our PA membrane model structure and their interactions with solute and water were first searched with molecular mechanics using the Merck Molecular Force Field (MMFF)30 employed in the Spartan’16 Parallel Suite (Wavefunction Inc.),31 which has been widely used for various conformer searches including our previous study,32–35 and the global minimum energies of the conformers were then calculated. Second, the structures of the top five conformers were further optimized at the B3LYP36,37 level with the 6–31*G basis set using Spartan’16. Third, each optimized conformer structure was used as the input gaseous-phase geometry for optimization and frequency calculations at the M06-2X/cc-pVDZ level38 using Gaussian 09, revision D.1.39 Finally, using the optimized gaseous-phase structure as a starting point, the aqueous-phase structure was optimized, and the frequencies were calculated at the same level (i.e., M06-2X/cc-pVDZ)40 using an implicit universal solvation model (SMD)41 at 20 °C (293.15 K). The detailed procedures for the structural optimization and frequency calculations are given in ESI Text S2.†Results and discussions
Membrane structures
Based on previous research, we built the base molecular models for the PA membrane active layer by connecting TMC and MPD monomers in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to generate cross-linked ring and linear structures with four-units.15,16,42 Models consisting of two- and six-unit TMC and MPD cross-linked monomers, elemental composition of the membrane model, and the impact of side chains resulting from larger PA membrane structures were also investigated (ESI Text S3†). To maintain acceptable computational time consumption for the subsequent QM calculations and focus on the effects of the solute–membrane interactions on the critical membrane structure, we used the four-unit model for the following study. The four-unit PA membrane model contained two TMC and two MPD molecules with two carboxylic functional groups, which can dissociate depending on the solution pH.43–45 The charge of the carboxylic functional groups of the PA membrane model affects the membrane structure. To evaluate the impact of the dissociation of carboxylic functional group(s) on the PA membrane structure, we thus built three models: (1) a PA membrane containing two non-dissociated carboxylic functional groups (PA-0), (2) a PA membrane containing one dissociated and one non-dissociated carboxylic functional group (PA-1), and (3) a PA membrane containing two dissociated carboxylic functional groups (PA-2).
1 to generate cross-linked ring and linear structures with four-units.15,16,42 Models consisting of two- and six-unit TMC and MPD cross-linked monomers, elemental composition of the membrane model, and the impact of side chains resulting from larger PA membrane structures were also investigated (ESI Text S3†). To maintain acceptable computational time consumption for the subsequent QM calculations and focus on the effects of the solute–membrane interactions on the critical membrane structure, we used the four-unit model for the following study. The four-unit PA membrane model contained two TMC and two MPD molecules with two carboxylic functional groups, which can dissociate depending on the solution pH.43–45 The charge of the carboxylic functional groups of the PA membrane model affects the membrane structure. To evaluate the impact of the dissociation of carboxylic functional group(s) on the PA membrane structure, we thus built three models: (1) a PA membrane containing two non-dissociated carboxylic functional groups (PA-0), (2) a PA membrane containing one dissociated and one non-dissociated carboxylic functional group (PA-1), and (3) a PA membrane containing two dissociated carboxylic functional groups (PA-2).
Water–membrane interactions and the free energy of interaction
To investigate the water–membrane interaction, we added several explicit water molecule(s) that interact with the PA membrane in addition to the implicit solvation model. In general, the implicit solvation model does not account for long-range dispersion interactions in the outer solvation shell and the addition of explicit water molecule(s) is therefore recommended to explicitly account for H-bonds.46 A detailed discussion on the impact of water molecules on the three PA membrane structures is provided in the ESI Text S4.† Fig. S8 in ESI† plots the calculated gaseous- and aqueous-phase free energies of interaction (ΔGmembrane–nH2Ogas,calc and ΔGmembrane–nH2Oaq,calc) against the number, n, of explicit water molecule(s) for the PA-0, PA-1, and PA-2 membrane models. We found that as more explicit water molecules were added, both the gaseous- and aqueous-phase free energies of interaction for PA-1 and PA-2 decreased. For example, the aqueous-phase free energy of interaction per mole of 4-unit membrane model with/without explicit water molecules decreased from −0.41 kcal mol−1 for PA-1 with 1 explicit water molecule to −3.52 kcal mol−1 with 6 explicit water molecules. In contrast, the free energy of interaction for PA-0 increased as a greater number of explicit water molecules were added. A similar trend was observed for the gaseous-phase free energy of interaction. Since greater negative values of free energy of interaction indicate greater stability, these results suggest that dissociated carboxylic functional groups were stabilized with the addition of explicit water molecules by forming additional hydrogen bonds. An increase in the ΔGmembrane–nH2Oaq,calc value when n = 6 for PA-0 (both carboxylic functional groups are non-dissociated) because the addition of extra explicit water molecules created a cluster and decreased the resultant GnH2Oaq,calc, which increases the ΔGmembrane–nH2Oaq,calc for PA-0 based on the eqn (5).To validate the theoretically calculated aqueous-phase free energy of interaction for the membrane–water system, we calculated the free energy of interaction using eqn (6) based on the literature-reported, experimentally obtained partition coefficient of water in a PA membrane.16
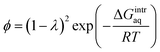 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to simulate PA membrane hydration. The experimental partition coefficient was reported as 0.29.49 Using these data described above, we obtained a value of −0.47 kcal mol−1, which is very close to the values obtained from our theoretical calculations with various membrane structures in the presence of explicit water molecules. For example, we obtained −0.41 kcal mol−1 for the aqueous-phase free energy of interaction for the PA membrane PA-1 in the presence of one explicit water molecule. Based on 1.39 g cm−3 of a total mass density of waters reported by Suzuki et al. (2015),16 we calculated the number of water molecules in the membrane interior as 474 within the total width 48.7 Å of the slab membrane model. The observed number of amide bonds in the bulk membrane was measured as 479 ± 10 at a 1
1 to simulate PA membrane hydration. The experimental partition coefficient was reported as 0.29.49 Using these data described above, we obtained a value of −0.47 kcal mol−1, which is very close to the values obtained from our theoretical calculations with various membrane structures in the presence of explicit water molecules. For example, we obtained −0.41 kcal mol−1 for the aqueous-phase free energy of interaction for the PA membrane PA-1 in the presence of one explicit water molecule. Based on 1.39 g cm−3 of a total mass density of waters reported by Suzuki et al. (2015),16 we calculated the number of water molecules in the membrane interior as 474 within the total width 48.7 Å of the slab membrane model. The observed number of amide bonds in the bulk membrane was measured as 479 ± 10 at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of MPD and TMC. Given that the number of carboxylate functional groups equals the number of amide functional groups in a 1
1 ratio of MPD and TMC. Given that the number of carboxylate functional groups equals the number of amide functional groups in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 TMC–MPD unit, approximately one water molecule is present around the carboxylate functional group. Our PA membrane molecular model in the presence of one explicit water molecule therefore reproduces the properties of a bulk membrane system simulated by the molecular model, and the theoretically calculated free energy of interaction validates the use of this model.
1 TMC–MPD unit, approximately one water molecule is present around the carboxylate functional group. Our PA membrane molecular model in the presence of one explicit water molecule therefore reproduces the properties of a bulk membrane system simulated by the molecular model, and the theoretically calculated free energy of interaction validates the use of this model.
Solute–membrane–water interaction and the free energy of interaction
The validation of the PA1 membrane model for the solute–membrane–water interaction is given in Text S5 in ESI.†Correlation of mass transfer coefficients with free energy of interaction for organic compounds
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ks =−0.381ΔGintraq,calc + 3.611 for 9 haloalkanes (r2 = 0.739) and ln
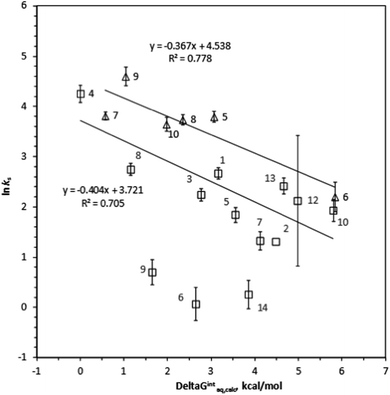
ks =−0.381ΔGintraq,calc + 3.611 for 9 haloalkanes (r2 = 0.739) and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ks =−0.367ΔGintraq,calc + 4.538 for 6 haloalkenes (r2 = 0.778). Fig. 2 shows the correlation: ln
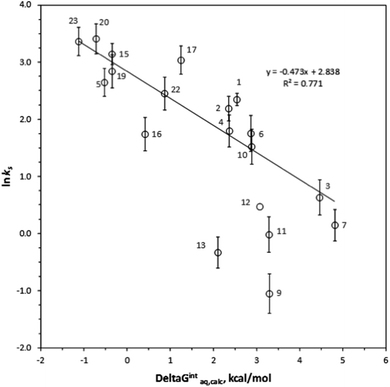
ks =−0.367ΔGintraq,calc + 4.538 for 6 haloalkenes (r2 = 0.778). Fig. 2 shows the correlation: ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ks =−0.410ΔGintraq,calc + 4.035 for 23 alkylbenzenes and halobenzenes (r2 = 0.774). Overall the reasonable linear correlation was observed. In general, ±2.0 kcal mol−1 of accuracy in calculating the energy was reported with the M06-2X/cc-pVDZ and the SMD solvation model.40,41 However, the accuracy in calculating the free energy of interaction may be tradeoff because the value was the difference between a complex and two independent systems as shown in eqn (5). Using the estimated ±2.0 kcal mol−1 of accuracy in calculating the ΔGintraq,calc value, the accuracy in calculating the ks value using the correlation for haloalkane would be within ±2.0 L m−2 h of the ks value and this corresponds to less than 4% of rejection efficiency. Given that the estimated experimental accuracy in obtaining the rejection efficiency within ±10%, our observed correlation is accurate enough to estimate the rejection within the experimental error. Tables S8 and S9 in ESI† summarize the experimentally determined ks values and theoretically calculated ΔGintraq,calc values for all compounds. Three data points (1,1,2,2-tetracholorethane for data point no. 6, 1,2,3-trichloropropane for no. 9, and 1,2-dibromo-3-chloropropane for no. 14) were not included in the correlation for haloalkanes because of two potential reasons: (1) experimental error and (2) contribution of molecular size to diffusion. When the ks values were close to 2.0 L m−2 h, which correlated to more than 95% rejection and may be affected by the analytical measurements (see ESI Text S6†). Also, these three molecules are relatively larger molecules compared to others so that they could exceed the size at which they could diffuse through the PA membrane. Consequently, the small ks values may have result from the low diffusion. The effect of molecular diffusion alone in the RO is currently under investigation using different approach. For the same reason, three data points (1,3,5-trimethylbenzene for data point no. 9, sec-butylbenzene for no. 11, and 4-isopropyltoluene for no. 13) were not included in the correlation analysis for halobenzenes because their ks values were <1.0 L m−2 h. We observed reasonable linear correlations overall. Stronger interactions between an organic compound and the membrane (i.e., more negative ΔGintraq,calc) generally led to a higher partitioning of the organic compound into the membrane matrix because of the relationship in eqn (3). Furthermore, the higher partitioning of an organic compound into the membrane matrix led to a lower rejection of the organic compound,12,13 and larger ks values were thus observed. Accordingly, the negative slopes observed in Fig. 1 and 2 are consistent with the general observation above and previous findings in the literature.22
ks =−0.410ΔGintraq,calc + 4.035 for 23 alkylbenzenes and halobenzenes (r2 = 0.774). Overall the reasonable linear correlation was observed. In general, ±2.0 kcal mol−1 of accuracy in calculating the energy was reported with the M06-2X/cc-pVDZ and the SMD solvation model.40,41 However, the accuracy in calculating the free energy of interaction may be tradeoff because the value was the difference between a complex and two independent systems as shown in eqn (5). Using the estimated ±2.0 kcal mol−1 of accuracy in calculating the ΔGintraq,calc value, the accuracy in calculating the ks value using the correlation for haloalkane would be within ±2.0 L m−2 h of the ks value and this corresponds to less than 4% of rejection efficiency. Given that the estimated experimental accuracy in obtaining the rejection efficiency within ±10%, our observed correlation is accurate enough to estimate the rejection within the experimental error. Tables S8 and S9 in ESI† summarize the experimentally determined ks values and theoretically calculated ΔGintraq,calc values for all compounds. Three data points (1,1,2,2-tetracholorethane for data point no. 6, 1,2,3-trichloropropane for no. 9, and 1,2-dibromo-3-chloropropane for no. 14) were not included in the correlation for haloalkanes because of two potential reasons: (1) experimental error and (2) contribution of molecular size to diffusion. When the ks values were close to 2.0 L m−2 h, which correlated to more than 95% rejection and may be affected by the analytical measurements (see ESI Text S6†). Also, these three molecules are relatively larger molecules compared to others so that they could exceed the size at which they could diffuse through the PA membrane. Consequently, the small ks values may have result from the low diffusion. The effect of molecular diffusion alone in the RO is currently under investigation using different approach. For the same reason, three data points (1,3,5-trimethylbenzene for data point no. 9, sec-butylbenzene for no. 11, and 4-isopropyltoluene for no. 13) were not included in the correlation analysis for halobenzenes because their ks values were <1.0 L m−2 h. We observed reasonable linear correlations overall. Stronger interactions between an organic compound and the membrane (i.e., more negative ΔGintraq,calc) generally led to a higher partitioning of the organic compound into the membrane matrix because of the relationship in eqn (3). Furthermore, the higher partitioning of an organic compound into the membrane matrix led to a lower rejection of the organic compound,12,13 and larger ks values were thus observed. Accordingly, the negative slopes observed in Fig. 1 and 2 are consistent with the general observation above and previous findings in the literature.22
Haloalkanes and haloalkenes
In the following section, we will investigate the relationships between the structures of haloalkanes and haloalkenes, their free energies of interaction, and the ks values in more detail. This approach will provide more insight into the impact of a single functional group on a compound with the same base structure. A comparison of chloroform (compound no. 1) and tetrachloromethane (no. 2) revealed that the substitution of a H atom by a chlorine atom decreased the ks value (i.e., increased the rejection) due to the decreased interaction with the membrane. The ΔGintraq,calc values of chloroform and tetrachloromethane are 3.16 kcal mol−1 and 4.48 kcal mol−1, indicating that the interaction corresponds to the rejection trend. A comparison of 1,2-dichloropropane (no. 7) and 1,3-dichloropropane (no. 8) revealed that a chlorine functional group adjacent to a terminal carbon resulted in a lower ks value than a chlorine atom at a medial carbon, as shown by the ks values for 1,2-dichloropropane (3.79 L m−2 h) and 1,3-dichloropropane (15.6 L m−2 h), which indicate decreased rejection of the latter compound. Because these two compounds have identical MWs and very similar sizes, the 4.12 kcal mol−1 ΔGintraq,calc value for 1,2-dichloropropane and 1.16 kcal mol−1 ΔGintraq,calc value for 1,3-dichloropropane indicate the critical role of the interaction with membrane. Replacing a chlorine atom with a bromine atom in aliphatic haloalkanes increased the ks value from 8.38 L m−2 h for bromodichloromethane (no. 12) to 11.2 L m−2 h for chlorodibromomethane (no. 13) (i.e., decreased rejection) due to the greater hydrophobicity resulting from the bromine atom. Although this trend does not follow the expected trend of ks values (i.e., chloroform > bromodichloromethane > chlorodibromomethane > bromoform), the ΔGintraq,calc value of 4.98 L m−2 h for bromodichloromethane and 4.66 L m−2 h ΔGintraq,calc value for chlorodibromomethane showed that the trend in the interaction corresponds to the rejection.Overall, the ks values for haloalkenes were slightly larger than those for haloalkanes (i.e., less rejection of haloalkenes). This trend is because of the well-known favorable interaction of the π-bond of an unsaturated C–C double bond with the benzene ring structure of TMC.50 Both linear and ring structures of a PA membrane model with 4 chains were used for haloalkenes and halobenzenes to account for all possible interactions of a C–C double bond of an organic compound with TMC. A chlorine functional group on an alkene base structure decreased the ks values (i.e., increased the rejection). The ks value for trichloroethene (no. 5) was 44.4 L m−2 h and much larger than the 9.05 L m−2 h ks value for tetrachloroethene (no. 6). The hydrophobic nature of the chlorine functional group increases the ΔGintraq,calc value from 3.06 kcal mol−1 for trichloroethene to 5.84 kcal mol−1 for tetrachloroethene. This result indicates that the interaction trend corresponds to the rejection. Being a cis- or trans-isomer significantly affected rejection. The ks values were 41.9 L m−2 h for cis-1,3-dichloropropene (no. 8) and 99.5 L m−2 h for trans-1,3-dichloropropene (no. 9). The ΔGintraq,calc value was 2.35 kcal mol−1 for cis-1,3-dichloropropane and 1.04 kcal mol−1 for trans-1,3-dichloropropane. While these two isomers have almost identical MWs and molar volumes, the location of the functional group affected the ability of these isomers to permeate the PA membrane, and the free energy of interaction corresponds to the rejection trend.
Alkylbenzenes and halobenzenes
The type of functional groups and their positions on a benzene ring significantly affect the rejection of alkylbenzenes and halobenzenes, and we found the interaction between an organic compound and the PA membrane plays a critical role for the rejection of these compounds. Longer mono-alkyl functional groups decreased the ks values (i.e., increased the rejection), probably due to greater interactions between the alkyl side chain and the PA membrane. For example, the ks value decreased from 8.94 L m−2 h for toluene (compound no. 1 in benzene group) to 6.05 L m−2 h for ethylbenzene (no. 4), 5.80 L m−2 h for propylbenzene (no. 6), and 4.60 L m−2 h for n-butylbenzene (no. 10). In comparison, the ΔGintraq,calc values increased from 2.34 kcal mol−1 for toluene to 2.47 kcal mol−1 for ethylbenzene, 2.86 kcal mol−1 for propylbenzene, and 3.14 kcal mol−1 for n-butylbenzene. The chlorine functional group on a benzene ring increased the ks value from its value in the presence of an alkyl functional group due to hydrophobic interactions with PA membrane (i.e., decreased rejection). For example, the ks value was 8.94 L m−2 h for toluene, 23.26 L m−2 h for chlorobenzene (no. 15), and 29.02 L m−2 h for bromobenzene (no. 23). The ΔGintraq,calc value was 2.34 kcal mol−1 for toluene, −0.36 kcal mol−1 for chlorobenzene, and −1.13 kcal mol−1 for bromobenzene. Thus, even though the base benzene ring structure interacts with membrane ring structures such as benzene, the functional group significantly affects the rejection and the interaction of the functional group with the PA membrane. Noteworthy that the role of a chlorine functional group is complex: while the chlorine functional group on alkanes decreased the ks value, the chlorine functional group adjacent to an unsaturated carbon of alkenes and benzenes increased the ks values. For isomers of molecules with benzene base structures, the interaction is also the key mechanism controlling rejection. The ks values were 5.72 L m−2 h for 2-chlorotoluene (no. 16) and 20.88 L m−2 h for 4-chlorotoluene (no. 17). A compound that has di-functional groups at the 1- and 4- positions was thus rejected less than a compound with functional groups at the 1- and 2-positions. This trend is consistent with the values of ΔGintraq,calc, which were 0.41 kcal mol−1 for 2-chlorotoluene and 1.24 kcal mol−1 for 4-chlorotoluene.Conclusion
This study highlights the novel approach to using ab initio QM-based computational chemistry calculations to investigate the interaction between a wide variety of neutral organic compounds and polyamide RO membrane for water treatment application. Our molecular model constructed in this study was validated with the experimentally determined water–membrane and solute–water–membrane interactions. We determined linear correlations between the theoretically calculated free energies of interaction for a wide variety of organic compounds and the experimentally obtained mass transfer coefficients. The correlation indicates that the interaction between organic compounds and RO membranes plays a critical role in the rejection mechanism.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was supported by “Reuse-14-19/4769” from the Water Research Foundation. We gratefully acknowledge the Water Research Foundation's financial, technical, and administrative assistance in funding and managing the project through which this information was discovered, developed, and presented. M. Z. and D. M. appreciate the support from the Michigan Tech High Performance Computing Initiative “Superior” cluster for the QM calculations.References
- P. Westerhoff, H. Moon, D. Minakata and J. Crittenden, Oxidation of organics in retentates from reverse osmosis wastewater reuse facilities, Water Res., 2009, 43(16), 3992–3998 CrossRef CAS PubMed.
- M. J. Benotti, R. A. Trenholm, B. J. Vanderford, J. C. Holady, B. D. Stanford and S. A. Snyder, Pharmaceuticals and Endocrine Disrupting Compounds in US Drinking Water, Environ. Sci. Technol., 2009, 43(3), 597–603 CrossRef CAS PubMed.
- S. D. Richardson and S. Y. Kimura, Water Analysis: Emerging Contaminants and Current Issues, Anal. Chem., 2016, 88(1), 546–582 CrossRef CAS PubMed.
- D. W. Kolpin, E. T. Furlong, M. T. Meyer, E. M. Thurman, S. D. Zaugg, L. B. Barber and H. T. Buxton, Pharmaceuticals, hormones, and other organic wastewater contaminants in US streams, 1999-2000: a national reconnaissance, Environ. Sci. Technol., 2002, 36(6), 1202–1211 CrossRef CAS PubMed.
- NRC, Water Reuse: Potential for expanding the nation's water supply through reuse of municipal wastewater, National Academy Press, Washington, D.C., 2012 Search PubMed.
- K. Kimura, G. Amy, J. Drewes and Y. Watanabe, Adsorption of hydrophobic compounds onto NF/RO membranes: an artifact leading to overestimation of rejection, J. Membr. Sci., 2003, 221(1–2), 89–101 CrossRef CAS.
- P. Xu, J. E. Drewes, C. Bellona, G. Amy, T. U. Kim, M. Adam and T. Heberer, Rejection of emerging organic micropollutants in nanofiltration-reverse osmosis membrane applications, Water Environ. Res., 2005, 77(1), 40–48 CrossRef CAS PubMed.
- A. Giwa, N. Akther, V. Dufour and S. W. Hasan, A critical review on recent polymeric and nano-enhanced membranes for reverse osmosis, RSC Adv., 2016, 6, 8134–8163 RSC.
- M. G. Buonomenna, Membrane processes for a sustainable industrial growth, RSC Adv., 2013, 3, 5694–5740 RSC.
- W. J. Kuros, G. K. Fleming, S. M. Jordan, T. H. Kim and H. H. Hoehn, Polymeric membrane materials for solution-diffusion based permeation separations, Prog. Polym. Sci., 1988, 13, 339–401 CrossRef.
- E. Dražević, K. Kosutic, M. Svalina and J. Catalano, Permeability of uncharged organic molecules in reverse osmosis desalination membranes, Water Res., 2017, 116, 13–22 CrossRef PubMed.
- A. I. Schafer, I. Akanyeti and A. J. C. Semiao, Micropollutant sorption to membrane polymers: a review of mechanisms for estrogens, Adv. Colloid Interface Sci., 2011, 164(1–2), 100–117 CrossRef PubMed.
- D. Dolar, N. Drasinac, K. Kosutic, I. Skoric and D. Asperger, Adsorption of hydrophilic and hydrophobic pharmaceuticals on RO/NF membranes: identification of interactions using FTIR, J. Appl. Polym. Sci., 2017, 134(5), 44426 CrossRef.
- A. R. D. Verliefde, E. R. Cornelissen, S. G. J. Heijman, E. M. V. Hoek, G. L. Amy, B. Van Der Bruggen and J. C. Van Dijk, Influence of Solute-Membrane Affinity on Rejection of Uncharged Organic Solutes by Nanofiltration Membranes, Environ. Sci. Technol., 2009, 43(7), 2400–2406 CrossRef CAS PubMed.
- X. Tian, J. Wang, H. Zhang, Z. Cao, M. Zhao, Y. Guan and Y. Zhang, Establishment of transport channels with carriers for water in reverse osmosis membrane by incorporating hydrotalcite into the polyamide layer, RSC Adv., 2018, 8, 12439–12448 RSC.
- T. Araki, R. Cruz-Silva, S. Tejima, K. Takeuchi, T. Hayashi, S. Inukai, T. Noguchi, A. Tanioka, T. Kawaguchi, M. Terrones and M. Endo, Molecular Dynamics Study of Carbon Nanotubes/Polyamide Reverse Osmosis Membranes: Polymerization, Structure, and Hydration, ACS Appl. Mater. Interfaces, 2015, 7(44), 24566–24575 CrossRef CAS PubMed.
- Y. Suzuki, Y. Koyano and M. Nagaoka, Influence of Monomer Mixing Ratio on Membrane Nanostructure in Interfacial Polycondensation: Application of Hybrid MC/MD Reaction Method with Minimum Bond Convention, J. Phys. Chem. B, 2015, 119(22), 6776–6785 CrossRef CAS PubMed.
- V. Kolev and V. Freger, Hydration, porosity and water dynamics in the polyamide layer of reverse osmosis membranes: A molecular dynamics study, Polymer, 2014, 55(6), 1420–1426 CrossRef CAS.
- M. Ding, A. Szymczyk, F. Goujon, A. Soldera and A. Ghoufi, Structure and dynamics of water confined in a polyamide reverse-osmosis membrane: a molecular-simulation study, J. Membr. Sci., 2014, 458, 236–244 CrossRef CAS.
- M. J. Kotelyanskii, N. Wagner and M. Paulaitis, Atomistic simulation of water and salt transport in the reverse osmosis membrane FT-30, J. Membr. Sci., 1998, 139, 1 CrossRef CAS.
- Y. Xiang, Y. Liu, B. Mi and Y. Leng, Hydrated polyamide membrane and its interaction with alginate: a molecular dynamics study, Langmuir, 2013, 29, 11600–11608 CrossRef CAS PubMed.
- A. Ghoufi, E. Dražević and A. Szymczyk, Interactions of organics within hydrated selective layer of reverse osmosis desalination membrane: a combined experimental and computational study, Environ. Sci. Technol., 2017, 51, 2714–2719 CrossRef CAS PubMed.
- J. W. Gibbs, Elementary Principles in Statistical Mechanics, 1902, Charles Scribner’s Sons, New York Search PubMed.
- K. J. Howe, D. W. Hand, J. C. Crittenden, R. R. Trussell and G. Tchobanoglous, Principles of Water Treatment, MWH Wiley John Wiley & Sons, Inc., 2012 Search PubMed.
- A. Ben-David, Y. Oren and V. Freger, Thermodynamic factors in partitioning and rejection of organic compounds by polyamide composite membranes, Environ. Sci. Technol., 2006, 40, 7023–7028 CrossRef CAS PubMed.
- Perry's Chemical Engineer's Handbook, ed. Perry R. H., Green D.W., McGraw-Hill, New York, NY, 1997 Search PubMed.
- V. S. Bryantsev, S. M. Diallo and A. W. Goddard III, Calculation of solvation free energies of charged solutes using mixed cluster/continuum models, J. Phys. Chem. B, 2008, 112, 9709–9719 CrossRef CAS PubMed.
- J. K. Howe, D. Minakata, N. L. Breitner and M. Zhang Predicting Reverse Osmosis Removal of Unique Organics. Water Environment & Reuse Foundation final report, WRRF 14-19. 2018 Search PubMed.
- L. Breitner, K. Howe and D. Minakata, Effects of functional chemistry on the rejection of low-MW neutral organics through reverse osmosis membranes for potable reuse, Environ. Sci. Technol., 2019, 53(19), 11401–11409 CrossRef CAS PubMed.
- T. A. Halgren and R. B. Nachbar, Merck molecular force field. IV. Conformational energies and geometries for MMFF94, J. Comput. Chem., 1996, 17(5–6), 587–615 CAS.
- Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O’Neill, R. A. DiStasio Jr, R. C. Lochan, T. Wang, G. J. O. Beran, N. A. Besley, J. M. Herbert, C. Y. Lin, T. Van Voorhis, S. H. Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Z. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. M. Rhee, J. Ritchie, E. Rosta, C. D. Sherrill, A. C. Simmonett, J. E. Subotnik, H. L. Woodcock III, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Advances in methods and algorithms in a modern quantum chemistry program package, Phys. Chem. Chem. Phys., 2006, 8(27), 3172–3191 RSC.
- M. Zhang, K. J. Howe and D. Minakata, Predicting the partitioning of organic compounds through polymer materials: quantum mechanical applications, J. Environ. Eng., 2018, 144(4), 04018019 CrossRef.
- Y. Cai, M. C. Concha, J. S. Murray and R. B. Cole, Evaluation of the role of multiple hydrogen bonding in offering stability to negative ion adducts in electrospray mass spectrometry, J. Am. Soc. Mass Spectrom., 2002, 13(12), 1360–1369 CrossRef CAS PubMed.
- C. P. Butts, C. R. Jones and J. N. Harvey, High precision NOEs as a probe for low level conformers–a second conformation of strychnine, Chem. Commun., 2011, 47(4), 1193–1195 RSC.
- E. C. Sherer, G. M. Turner and G. C. Shields, Investigation of the potential energy surface for the first step in the alkaline hydrolysis of methyl acetate, Int. J. Quantum Chem., 1995, 56(S22), 83–93 CrossRef.
- A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Phys. Chem., 1993, 98(2), 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B, 1988, 37(2), 785–789 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, Density functionals with broad applicability in chemistry, Acc. Chem. Res., 2008, 41(2), 157–167 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li; H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09 Revision A. 2, Gaussian. Inc., Wallingford, CT, 2009, 139 Search PubMed.
- Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396 CrossRef CAS PubMed.
- H. F. Ridgway, J. D. Gale, Z. E. Hughes, M. B. Stewart, J. D. Orbell and S. R. Gray, Molecular scale modeling of membrane water treatment processes, Functional Nanostructured Materials and Membranes for Water Treatment, 2013, pp. 249–299 Search PubMed.
- O. Coronell, B. J. Mariñas, X. J. Zhang and D. G. Cahill, Quantification of functional groups and modeling of their ionization behavior in the active layer of FT30 reverse osmosis membrane, Environ. Sci. Technol., 2008, 42(14), 5260–5266 CrossRef CAS PubMed.
- O. Coronell, B. J. Mariñas and D. G. Cahill, Accessibility and Ion Exchange Stoichiometry of Ionized Carboxylic Groups in the Active Layer of FT30 Reverse Osmosis Membrane, Environ. Sci. Technol., 2009, 43(13), 5042–5048 CrossRef CAS PubMed.
- O. Coronell, M. I. Gonzalez, B. J. Mariñas and D. G. Cahill, Ionization behavior, stoichiometry of association, and accessibility of functional groups in the active layers of reverse osmosis and nanofiltration membranes, Environ. Sci. Technol., 2010, 44(17), 6808–6814 CrossRef CAS PubMed.
- K. R. Adam, New density functional and atoms in molecules method of computing relative pKa values in solution, J. Phys. Chem. A, 2002, 106(49), 11963–11972 CrossRef CAS.
- LeBas, The Molecular Volumes of Liquid Chemical Compounds, Longmans, London, 1915 Search PubMed.
- E. Harder, D. Eric Walters, Y. D. Bodnar, R. S. Faibish and B. Roux, Molecular dynamics study of a polymeric reverse osmosis membrane, J. Phys. Chem. B, 2009, 113(30), 10177–10182 CrossRef CAS PubMed.
- B. Mi, D. G. Cahill and B. J. Mariñas, Physico-chemical integrity of nanofiltration/reverse osmosis membranes during characterization by Rutherford backscattering spectrometry, J. Membr. Sci., 2007, 291, 77–85 CrossRef CAS.
- M. Zou, J. Zhang, Z. Chen and X. Li, Simulating adsorption of organic pollutants on finite (8.0) single-walled carbon nanotubes in water, Environ. Sci. Technol., 2012, 46(16), 8887–8894 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra01966f |
| This journal is © The Royal Society of Chemistry 2020 |