Open Access Article
Open Access ArticleAb initio theory study of laser cooling of barium monohalides
Rong Yang *a,
Bin Tangb and
XiangYu Hanac
*a,
Bin Tangb and
XiangYu Hanac
aSchool of Mathematics and Physics, Chongqing Jiaotong University, Chongqing 400074, PR China. E-mail: cqyr88@126.com
bInstitute of Finance & Trade, Chongqing City Management College, Chongqing 401331, PR China
cInstitute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, PR China
First published on 2nd June 2020
Abstract
The feasibility of laser cooling barium monohalides BaX (X = F, Cl, Br, I) is investigated using ab initio methods with the inclusion of spin–orbit coupling (SOC) effects. Calculated spectroscopic constants for BaF, BaCl, BaBr and BaI are in very good agreement with the available experimental measurements. The results demonstrate that the calculated electronic structure is accurate and can be used to establish the optical scheme of laser cooling. The highly diagonal Franck–Condon factors (FCFs) (BaF: f00 = 0.980, f11 = 0.939, f22 = 0.894; BaCl: f00 = 0.998, f11 = 0.995, f22 = 0.992) between the X2Σ+1/2 and A2Π1/2 states are determined, which are found to be in good agreement with previous theoretical results. The radiative lifetimes (BaF: 39.13–41.20 ns; BaCl: 117.99–110.23 ns) of the A2Π1/2–X2Σ+1/2 transition for the first five vibrational levels show that the A2Π1/2 is a rather short lifetime state. The current study indicates that BaF and BaCl are two good choices of molecules for laser cooling. Therefore, BaI and BaBr are not promising laser-cooling candidates because the FCFs of the A2Π1/2–X2Σ+1/2 transition are off-diagonal. We further propose the three-laser cooling schemes based on the A2Π1/2–X2Σ+1/2 transition for BaF and BaCl.
1. Introduction
The transverse laser cooling of SrF1,2 and YO3 has overthrown the notion that laser-cooling molecules is impracticable. The criteria to be considered candidates for laser cooling are a strong transition with highly-diagonal Franck–Condon factors (FCFs) in a wavelength region accessible to tabletop lasers and strong optical forces resulting from the short radiative lifetime. Diagonal FCFs minimize the number of lasers required to keep the molecule in a closed-loop cooling cycle. Naturally, the experimental demonstrations have initiated the search for other molecules which are appropriate for laser cooling. In 2004, Di Rosa4 conducted a brief survey of promising candidates for laser cooling. SrF and YO did not occur on his study and there clearly could be others that have not been investigated by theoretical and experimental studies. In this paper, thus, we focus on the theoretical studies of the laser cooling of barium monohalides, though neither have yet been cooled.In recent years, the interest in laser cooling of diatomic polar molecules has grown owing to a variety of prospective applications.5 Laser cooling of SrF,1,2 KRb,6 YO3 and CaF7 has been experimentally performed, and polar molecules (such as RaF,8 AlH,9 AlF9) have been investigated in previous theoretical research. Alkaline-earth metal atoms and molecules are of persistent interest in the investigation of cold atoms and molecules. These molecules like monohydrides MH (M = Be, Mg, Ca, Sr, and Ba)10 and some monohalides (such as BeF,11 MgF12) have been identified as the promising candidates for laser cooling theoretically. However, the study on laser cooling of barium monohalides BaX (X = F, Cl, Br, I) is very limited. In addition to being nominated as laser cooling candidates, BaX (X = F, Cl, Br, I) play an important role in stellar spectroscopy.13 Considering that the A2Π → X2Σ+ transition of barium monohalides has been suggested by Di Rosa4 and experiments have been made for SrF,1,2 YO3 and CaF,7 we believe it is possible to cool barium monohalides with a similar experimental method.
In the current study, we focus on investigating the feasibility of direct laser cooling of BaX (X = F, Cl, Br, I), then proposing the scheme to perform laser cooling of BaX (X = F, Cl, Br, I). Karthikeyan et al.14 have evaluated the FCFs for electronic transitions A–X of BaF molecule by employing a reliable numerical integration procedure. The calculated FCF (f00) of BaF is 0.951, and the laser excitation wavelength is about 857 nm. For BaF, Kang et al.15 also reported results about FCFs by ab initio. The radiative lifetime obtained for the A2Π state of the BaF molecule is 56.0 ± 0.9 ns using laser spectroscopy.16 The first seven electronic states of the BaCl molecule have been studied by laser induced fluorescence, combined with high resolution Fourier spectroscopy.17 The zero pressure radiative lifetime of BaCl has been measured by laser-induced fluorescence in the near-infrared wavelength region.18 Husain et al.19 have determined the spectroscopic parameters of the X-state and low lying excited states of BaBr, and calculated the FCFs using a simplified Morse oscillator model following Tuckett20 (A–X: f00 = 0.6903). The A2Π state of BaBr has been analyzed by Ernst et al.21 Miliordos et al.22 have been examined the electronic structure of BaI by ab initio multi-reference configuration interaction (MRCI) and coupled cluster (RCCSD(T)) methods. As mentioned above, BaX (X = F, Cl, Br, I) has been investigated extensively in the past. However, there is a lack of systematic studies of laser cooling of BaX (X = F, Cl, Br, I) up to now.
The paper is organized as follows. The theoretical methods and the basis sets used in the ab initio calculations for the included electronic states of BaX (X = F, Cl, Br, I) are briefly described in Section 2. We present the results and data discussions, and propose the laser cooling schemes for BaX (X = F, Cl, Br, I) in Section 3. In Section 4, the conclusions of this work are given.
2. Computational details
To investigate the feasibility of direct laser cooling of barium monohalides, we first calculate the electronic structure for the two lowest doublet electronic states (A2Π and X2Σ+), then determine the radiative properties including radiative lifetimes, FCFs and diode laser excitation wavelengths of the A2Π → X2Σ+ transitions. All the present ab initio calculations are carried out in the C2ν point group using the MOLPRO23 package. The spectroscopic constants, including equilibrium bond distance (Re), harmonic frequency (we), anharmonic vibrational frequency (weχe), rotational constant (Be) and electronic transition energy (Te) for the A2Π and X2Σ+ states of BaX (X = F, Cl, Br, I) are evaluated by solving the nuclear Schrödinger equation by Le Roy's LEVEL 8.0 program.24 With the potential energy curves (PECs) and transition dipole moments of different electronic states, this program can also obtain the FCFs and radiative lifetimes of the various vibrational levels. The FC factor is one of the parameters which controls the intensity distribution in the emission of molecular bands. The square of the overlap integral is termed as FC factor (fν′ν),25
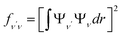 | (1) |
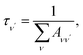 | (2) |
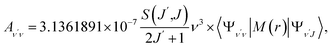 | (3) |
The complete active space self-consistent field (CASSCF)28,29 and MRCI plus Davidson correction (MRCI + Q)30–32 methods have been performed for the ab initio electronic structure calculations of BaX (X = F, Cl, Br, I). Scalar relativistic effects are accounted for using the Douglas–Kroll–Hess (DHK)33,34 transformation of the relativistic Hamiltonian. For the heavier Ba atom, the spin–orbit coupling (SOC) effects are important for the electronic structure. In this work, SOC effects are evaluated with one- and two-electrons Breit–Pauli operators35 at the MRCI level of theory. It is worth noting, we can neglect the rotational degrees of freedom in the first approximation, since we focus on investigating the vibrational cooling.
To improve the accuracy of potential energy curve calculations, the effects of the core–valence correction and the relativistic correlation are taken into account. This was done by adopting the small-core scalar relativistic effective core potential (ECP) ECP10MWB,36 ECP10MDF,37 ECP28MDF,38 and ECP46MDF39 together with the corresponding valence basis sets for Cl, Br, I and Ba, respectively, and, the AVQZ40 all-electron basis sets for the F atom. Within the C2ν point group symmetry, all molecular orbitals were labeled by their symmetry (a1, b1, b2, a2). In our calculations of BaF molecule, eight molecular orbitals are selected as active spaces, which correspond to the 2s2p shells of the F atom and 5p6s shells of the Ba atom. That is to say, ten electrons are distributed in a (4, 2, 2, 0) active space for BaF molecule. For BaCl, BaBr and BaI, these active spaces are also (4, 2, 2, 0). The 3s3p shells of the Cl atom, 4s4p shells of the Br atom and 5s5p shells of the Br atom are put in the active space, respectively.
3. Results and discussions
3.1 Potential energy curves (PECs) and spectroscopic constants
Because the A2Π → X2Σ+ transition has been suggested by experiments for SrF, YO and CaF, we only carry out ab initio calculations to the two states (A2Π and X2Σ+). The PECs of A2Π and X2Σ+ states of BaX (X = F, Cl, Br, I) are presented in Fig. 1(a) and (b). Fig. 1 shows that the PECs of A2Π and X2Σ+ states look surprisingly similar. It implies that highly diagonal FCFs for the A2Π → X2Σ+ transition are possible.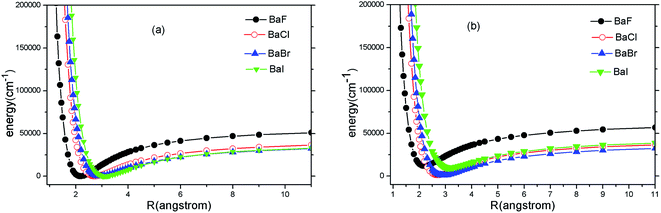 | ||
| Fig. 1 (Color online) Potential energy curves of X2Σ+ (a) and A2Π (b) of BaX (X = F, Cl, Br, I) at MRCI + Q/ECP46MDF(Ba), AVQZ(F), ECP10MWB(Cl), ECP10MDF(Br), ECP28MDF(I). | ||
For the heavier Ba atom, SOC effects are important for the electronic structure. Concerning the effects of SOC on the electronic structure of BaX (X = F, Cl, Br, I), the A2Π state splits into A2Π1/2 and A2Π3/2. Our present calculated spectroscopic constants of A2Π1/2 and X2Σ+1/2 with available experimental values are tabulated in Table 1. The reasons why we focus on A2Π1/2 and X2Σ+1/2 are explained as follows. Many experimental studies provided some accurate and important spectroscopic data for A2Π1/2 and X2Σ+1/2 states. Earlier theoretical researches14,15 reported BaF has highly diagonal FCFs between A2Π1/2 and X2Σ+1/2.
| Molecule | States | Te (cm−1) | Re (Å) | we (cm−1) | weχe (cm−1) | Be (cm−1) | Ref. |
|---|---|---|---|---|---|---|---|
| BaF | X2Σ+1/2 | 0 | 2.186 | 460.72 | 1.79 | 0.2114 | This work |
| 0 | 2.161b | 469.41a | 1.84a | — | Expt. (aRef. 41; bRef. 42) | ||
| A2Π1/2 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 893 893 |
2.199 | 436.58 | 1.72 | 0.2089 | This work | |
| 11647a | 2.183c | 435.50a | 1.68a | — | Expt. (aRef. 41; cRef. 43) | ||
| BaCl | X2Σ+1/2 | 0 | 2.728 | 267.38 | 0.79 | 0.0814 | This work |
| 0 | — | 279.89 | 0.81 | 0.0840 | Expt. (Ref. 17) | ||
| A2Π1/2 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657 657 |
2.683 | 261.33 | 0.80 | 0.0810 | This work | |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 679 679 |
— | 257.30 | 0.81 | 0.0811 | Expt. (Ref. 17) | ||
| BaBr | X2Σ+1/2 | 0 | 2.927 | 175.14 | 0.39 | 0.0390 | This work |
| 0 | 2.847 | 192.30 | 0.41 | — | Expt. (Ref. 19) | ||
| A2Π1/2 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 171 171 |
2.911 | 169.98 | 0.40 | — | This work | |
| — | 2.899 | 177.13 | 0.40 | — | Expt. (Ref. 19) | ||
| BaI | X2Σ+1/2 | 0 | 3.126 | 149.92 | 0.27 | 0.0262 | This work |
| 0 | 3.088 | 152.16 | 0.27 | — | Expt. (Ref. 44–46) | ||
| A2Π1/2 | 9753 | 3.167 | 140.47 | 0.27 | 0.0255 | This work | |
| 9605 | 3.139 | 141.75 | 0.28 | — | Expt. (Ref. 45 and 46) |
For the X2Σ+1/2 state of BaF, the corresponding percentage errors in Re, we and weχe are 1.16%, 1.85% and 2.72% with respect to experiment,41,42 respectively. It is also encouraging to see that our calculated Te, Re, we and weχe of the A2Π1/2 state are in good agreement with experiment41,43 and the relative errors are only 2.11%, 0.73%, 0.25% and 2.38%, respectively. In the case of the X2Σ+1/2 state of BaCl, our present results compare very well with the experimental data17 (we ∼12.51 cm−1, weχe ∼0.02 cm−1, Be ∼0.0026 cm−1). And for the A2Π1/2 of BaCl, our spectroscopic constants calculated at MRCI level are also in reasonable agreement with experiment17 (Te ∼22 cm−1, we ∼4.03 cm−1, weχe ∼0.01 cm−1, Be ∼0.0001 cm−1). Concerning the X2Σ+1/2 of BaBr, the difference of Re, we and weχe values in the experiment19 and present work is not signficant, and the relative errors are 2.81%, 8.92% and 4.88%, respectively. While for the A2Π1/2 of BaBr, Table 1 shows that our present results accord with experiment19 (Re ∼0.012 Å, we ∼7.15 cm−1, weχe ∼0.00 cm−1). For BaI, present values of Re, we and weχe for the X2Σ+1/2 state are 3.126 Å, 140.47 cm−1 and 0.27 cm−1, which are very close to the experimental data.44–46 Miliordos et al.22 provided a even larger Re (3.251 Å) and a even smaller weχe (0.24 cm−1) compared to the experimental data44–46 by MRCI method. As for the A2Π1/2 of BaI, the calculated Re and Te results are only 0.028 Å and 148 cm−1 larger, while the we and weχe results are only 1.28 cm−1 and 0.01 cm−1 smaller than the observed experimental data.45,46 The differences between the previous theoretical value21 and experimental data45,46 are bigger (Te ∼1536 cm−1, Re ∼0.194 Å, we ∼12.75 cm−1, weχe ∼0.31 cm−1). In summary, the results demonstrate that the electronic structure of BaX (X = F, Cl, Br, I) calculated at MRCI + Q/ECP46MDF(Ba), AVQZ(F), ECP10MWB(Cl), ECP10MDF(Br), ECP28MDF(I) level is accurate and can be used to establish the optical scheme of laser cooling.
3.2 FCFs
The first criterion to be nominated as candidates for laser cooling is highly diagonal FCFs. As listed in the literature, most FCFs f00 of experimental cooling molecules are greater than 0.9. For example, the FCF f00 of SrF reaches 0.98. A larger FCF has significant benefits for limiting the number of lasers required to keep the molecule in a closed-loop cooling cycle. Of course, some cooling schemes for molecules with smaller FCFs have also been proposed.47 The FCF values for the A–X transitions of BaX are tabulated in Table 2 and 3. Our computed FCF values of BaF are in good agreement with the recent results.14,15 For BaBr, the present results at the MRCI level are a little bigger than the values reported by Husain et al.19 Husain et al.19 calculated the FCFs using a simplified Morse oscillator model following Tuckett. From Table 2, it could be clearly seen that the Δν = 0 bands of BaX have the strongest transition probability. That is to say, the highly diagonal FCFs f00 (BaF: 0.980 and BaCl: 0.998) for the A–X transition are determined. To visually demonstrate the overlap of the vibrational wave functions for A–X transition, we have plotted the FCFs of spontaneous radiative transitions in Fig. 2. Fig. 2 also shows that BaF and BaCl have large diagonal FCFs.| Molecules | ν′ = 0 | 1 | 2 | 3 | |
|---|---|---|---|---|---|
| BaF | ν = 0 | 0.9802 | 0.0197 | 0.7824(−4) | 0.9904(−6) |
| Ref. 14 (aRef. 15) | 0.9510, 0.9810a | 0.0490, 0.0189a | 0.0000, 0.3960(−3)a | 0.0000a | |
| 1 | 0.0194 | 0.9389 | 0.0414 | 0.0030(−1) | |
| Ref. 14 (aRef. 15) | 0.0480 | 0.8540, 0.9400a | 0.0960 | 0.0030 | |
| 2 | 0.0041(−1) | 0.0401 | 0.8937 | 0.0650 | |
| Ref. 14 (aRef. 15) | 0.0020 | 0.0930 | 0.7580, 0.8960a | 0.1410 | |
| 3 | 0.3362(−5) | 0.0013 | 0.0620 | 0.8452 | |
| Ref. 14 | 0.0000 | 0.0050 | 0.1350 | 0.6660 | |
| BaCl | ν = 0 | 0.9982 | 0.0017 | 0.4883(−4) | 0.1043(−6) |
| 1 | 0.0023 | 0.9949 | 0.0032 | 0.1440(−3) | |
| 2 | 0.8568(−4) | 0.0031 | 0.9920 | 0.0045 | |
| 3 | 0.2042(−5) | 0.2423(−3) | 0.0042 | 0.9894 |
| Molecules | f00 f01 f02 f03 |
|---|---|
| f10 f11 f12 f13 | |
| BaI | 0.779 0.197 0.023 0.002 |
| 0.192 0.436 0.307 0.059 | |
| BaBr | 0.791(0.690)a 0.189(0.216)a 0.020 0.001 |
| 0.188(0.260)a 0.440(0.272)a 0.302 0.061 |
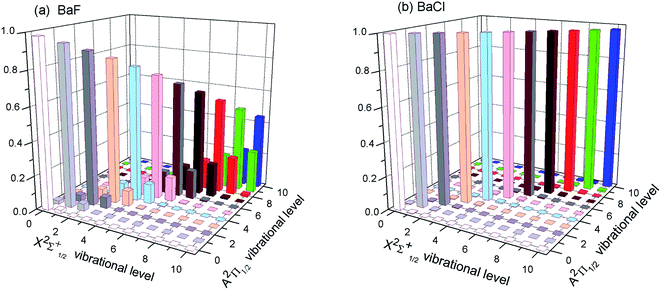 | ||
| Fig. 2 (Color online) The calculated FCFs of (a) BaF and (b) BaCl for the lowest vibrational levels of the cooling transition A2Π1/2 → X2Σ+1/2 at MRCI + Q/ECP46MDF(Ba), AVQZ(F), ECP10MWB(Cl). | ||
However for the A–X transition of BaI, the diagonal term f11(0.436) is calculated, and the off-diagonal term f10(0.192), f12(0.307), f13(0.059) are also obtained (see Table 3). These results show that the A–X transition of BaI does not have highly diagonal FCFs. The calculated f00 of 0.779 for BaI is not large enough to be potentially viable for direct laser cooling. The relative probabilities from A2Π1/2(ν′ = 0) to X2Σ+1/2(ν) are governed by the FCFs which are about 78% for ν = 0, 20% for ν = 1, 2.3% for ν = 2, 0.2% for ν = 3, 0.007% for ν = 4, and negligibly small for all ν > 4. Five cooling lasers are required for limiting the inefficiency or loss of BaI molecule in the cooling cycle. Cycling transitions requiring one or two repump lasers are common in atomic systems, experimentally. For the A–X transition of BaI, the number of lasers required is not practical. The case of BaBr is similar to the case of BaI (see Table 3). So BaI and BaBr are not good candidate molecules for direct laser cooling. Thus we do not need to discuss BaI and BaBr molecules in the following section.
3.3 Spontaneous radiative lifetime and radiative width
Aside from the large diagonal FCFs, sufficiently short lifetime is desirable for rapid laser cooling. A shorter lifetime of the transition could produce a strong Doppler force, which will produce a significant rate of optical cycling. To produce larger spontaneous scattering forces, the rate of optical cycling (105–108 s−1) is suitable. From eqn (1), the radiative lifetime of vibrational level ν′ for a given state is given by the inverse of the total Einstein coefficient. The radiative width (Γ) is related to the lifetime of the state by Γ = 1/(2πcτ). The computed radiative lifetimes and radiative width of BaF and BaCl are listed in Table 4 for the first five vibrational levels (ν′ = 0–5). As shown in Table 4, radiative lifetimes increase with increasing ν′, and radiative widths decrease with increasing ν′. We found that our radiative lifetimes for ν′ = 0 agree well with the experimental results (BaF: (56.0 ± 0.9) ns;16 BaCl: (107 ± 4) ns18). The radiative lifetimes (BaF: 39.13–41.20 ns; BaCl: 117.99–110.23 ns) of the A–X transition for the first five vibrational levels show that the A2Π1/2 is a rather short lifetime state. Thus, BaF and BaCl meet the second criterion for direct laser cooling.| Molecule | State | ν′ = 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|---|
| BaF | A2Π1/2 | 49.13 | 49.63 | 50.15 | 50.66 | 51.20 |
| 1.08(−4) | 1.07(−4) | 1.06(−4) | 1.05(−4) | 1.04(−4) | ||
| BaCl | A2Π1/2 | 117.99 | 115.95 | 113.99 | 112.09 | 110.23 |
| 4.49(−5) | 4.57(−5) | 4.64(−5) | 4.73(−5) | 4.81(−5) |
3.4 Laser cooling scheme
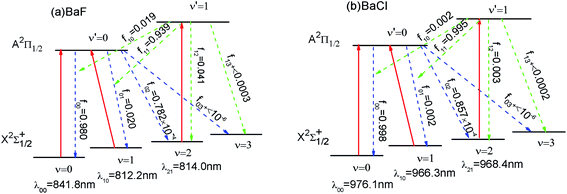
As shown in Fig. 3 (a), we have suggested a three-laser cooling scheme for the BaF molecule. The main cycling laser can drive the X2Σ+1/2(ν = 0) → A2Π1/2(ν′ = 0) transition at wavelength λ00 = 841.8 nm. Our computed wavelength λ00 agrees well with the result (822.0 nm) given by Kang et al.15 However, the decays to the X2Σ+1/2(ν = 1) state, to the X2Σ+1/2(ν = 2) state, and the X2Σ+1/2(ν ≥ 3) state from the A2Π1/2 state occur with probability f01 (= 2%), f02 (≈ 0.008%) and f+03(<10−6), respectively. To enhance the cooling effect, using the X2Σ+1/2(ν = 1) → A2Π1/2 (ν′ = 0) transition as the first vibrational pump and the X2Σ+1/2(ν = 2) → A2Π1/2(ν′ = 1) transition for the second pump are required. With this scheme, a BaF molecule can scatter about Nscat = 1/f+03 > 106 photons before decaying into the higher vibrational levels (ν ≥ 3) in X2Σ+1/2. Therefore, two repumping lasers with λ10 = 812.2 nm and λ21 = 814.0 nm are needed. The required cooling wavelengths of λ00 = 841.8 nm, λ10 = 812.2 nm and λ21 = 814.0 nm are located in the near-infrared range, where the continuous wavelength laser radiation can be easily generated. One problem with the above laser cooling scheme is the presence of a metastable state A′2Δ between the X2Σ+1/2 and A2Π1/2.41 It is notable that the decay rate γ ∝ d2w3. Here the transition dipole moment of A–X (dAX) is much larger than that of the A–A′ (dAA′): dAX/dAA′ ≈ 68;15 the frequency of A–X (wAX) is much larger than that of the A–A′ (wAA′): wAX/wAA′ ≈ 12.41 Thus γAX/γAA′ ≈ 106. So the presence of the intervening A′2Δ state leak is unlikely to limit the laser cooling transition A–X significantly. The laser cooling of BaCl is similar to that of BaF. In order to avoid or reduce cumbersome problems, here we only show the proposed laser–driven transitions (solid red) and spontaneous decay (dotted line) with calculated fν′ν for BaCl in Fig. 3(b).4. Conclusions
In the present work, accurate ab initio calculations including the SOC effects are performed on barium monohalides at the MRCI + Q level of theory. The AVQZ basis set (F), pseudopotentials ECPnMDF (n = 46, 10, 28) (Ba, Br, I), ECP10MWB(Cl) and corresponding basis sets are used in the present calculations. The PECs for the A2Π and X2Σ+ states of BaX (X = F, Cl, Br, I) are presented and analyzed. Our calculated spectroscopic constants (Re, we, weχe, Be, Te) of the X2Σ+1/2 and A2Π1/2 states are in good agreement with available experimental data. Using the PECs and transition dipole moments, we also obtain the FCFs and radiative lifetimes for the X2Σ+1/2 → A2Π1/2 transition. The results indicate that BaF and BaCl both have highly-diagonal FCFs and short radiative lifetime. Thus BaF and BaCl are promising candidates. The three-laser cooling schemes that drive the A2Π1/2 → X2Σ+1/2 transitions have been proposed for BaF and BaCl. However for BaI and BaBr, the A–X transitions do not have highly diagonal FCFs, and the calculated f00 (BaI: 0.779; BaBr: 0.791) is not large enough to be potentially viable for direct laser cooling. BaI and BaBr are not identified as very promising laser-cooling candidates.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11704052).References
- E. S. Shuman, J. F. Barry and D. DeMille, Nature, 2010, 467, 820 CrossRef CAS PubMed.
- J. F. Barry, D. J. McCarron, E. B. Norrgard, M. H. Steinecker and D. DeMille, Nature, 2014, 512, 286 CrossRef CAS PubMed.
- M. T. Hummon, M. Yeo, B. K. Stuhl, A. L. Collopy, Y. Xia and J. Ye, Phys. Rev. Lett., 2013, 110, 143001 CrossRef PubMed.
- M. D. Di Rosa, Eur. Phys. J. D, 2004, 31, 395 CrossRef.
- L. D. Carr, D. DeMille, R. V. Krems and J. Ye, New J. Phys., 2009, 11, 055049 CrossRef.
- J. Kobayashi, K. Aikawa, K. Oasa and S. Inouye, Phys. Rev. A, 2014, 89, 021401(R) CrossRef.
- V. Zhelyazkova, A. Cournol, T. E. Wall, A. Matsushima, J. J. Hudson, E. A. Hinds, M. R. Tarbutt and B. E. Sauer, Phys. Rev. A, 2014, 89, 053416 CrossRef.
- T. A. Isaev, S. Hoekstra and R. Berger, Phys. Rev. A, 2010, 82, 052521 CrossRef.
- N. Wells and I. C. Lane, Phys. Chem. Chem. Phys., 2011, 13, 19018 RSC.
- Y. F. Gao and T. Gao, Phys. Rev. A, 2014, 90, 052506 CrossRef.
- I. C. Lane, Phys. Chem. Chem. Phys., 2012, 14, 15078 RSC.
- S. Y. Kang, Y. F. Gao, F. G. Kuang, T. Gao, J. G. Du and G. Jiang, Phys. Rev. A, 2015, 91, 042511 CrossRef.
- H. Holweger and E. A. Mueller, Sol. Phys., 1974, 39, 19 CrossRef CAS.
- B. Karthikeyan, K. Balachandrakumar, V. Raja and N. Rajamanickamc, J. Appl. Spectrosc., 2013, 80, 5 CrossRef.
- S. Y. Kang, F. G. Kuang, G. Jiang and J. G. Du, Mol. Phys., 2016, 114, 810 CrossRef CAS.
- L. E. Berg, N. Gador, D. Husain, H. Ludwigs and P. Royen, Chem. Phys. Lett., 1998, 287, 89 CrossRef CAS.
- C. Amiot, M. Hafid and J. Verges, J. Mol. Spectrosc., 1996, 180, 121 CrossRef CAS.
- A. Derkatch, C. Lundevall, L.-E. Berg and P. Royen, Chem. Phys. Lett., 2000, 332, 278 CrossRef CAS.
- D. Husain, J. Lei, F. Castano and M. N. Sánchez Rayo, J. Photochem. Photobiol. Chem., 1997, 107, 1 CrossRef CAS.
- R. P. Tuckett, personal communication, 1992.
- W. E. Ernst, G. Weller and T. Torring, Chem. Phys. Lett., 1985, 121, 6 CrossRef.
- E. Miliordos, A. Papakondylis, A. A. Tsekouras and A. Mavridis, J. Phys. Chem. A, 2007, 111, 10002 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, R. Lindh, F. R. Manby and M. Schütz, et al., MOLPRO, is a package of ab initio programs, version 2009.1, http://www.molpro.net Search PubMed.
- R. J. Le Roy, LEVEL 8.0, A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels, CPRR-663, University of Waterloo, Waterloo, ON, 2007 Search PubMed.
- D. R. Bates, Mon. Not. Roy. Astron. Soc., 1952, 112, 614 CrossRef CAS.
- G. Herzberg, Spectra of Diatomic Molecules, Van Nostrand, New York, 1950 Search PubMed.
- P. F. Bernath, Spectra of Atoms and Molecules, Oxford University Press, New York, 2nd ed, 2005 Search PubMed.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82, 5053 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259 CrossRef CAS.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1988, 145, 514 CrossRef CAS.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61 CrossRef CAS.
- N. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89 Search PubMed.
- B. A. Hess, Phys. Rev. A, 1986, 33, 3742 CrossRef CAS PubMed.
- A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823 CrossRef CAS.
- A. Bergner, M. Dolg, W. Kuechle, H. Stoll and H. Preuss, Mol. Phys., 1993, 80, 1431 CrossRef CAS.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113 CrossRef CAS.
- K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877 CrossRef CAS PubMed.
- I. S. Lim, H. Stoll and P. Schwerdtfeger, J. Chem. Phys., 2006, 124, 034107 CrossRef PubMed.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning Jr, J. Chem. Phys., 1999, 110, 7667 CrossRef CAS.
- R. F. Barrow, A. Bernard, C. Effantin, J. D'incan, G. Fabre, A. E. Hachimi, R. Stringat and J. Verges, Chem. Phys. Lett., 1988, 147, 535 CrossRef CAS.
- C. Ryzlewicz and T. Torring, Chem. Phys., 1980, 51, 329 CrossRef CAS.
- K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure IV: Constants of Diatomic Molecules, Van Nostrand-Reinhold, 2005 Search PubMed.
- R. F. Gutterres, J. Vergěs and C. Amiot, J. Mol. Spectrosc., 1999, 196, 29 CrossRef CAS PubMed.
- R. F. Gutterres, J. Vergěs and C. Amiot, J. Mol. Spectrosc., 2000, 200, 253 CrossRef CAS PubMed.
- R. F. Gutterres, J. Vergěs and C. Amiot, J. Mol. Spectrosc., 2001, 206, 62 CrossRef CAS.
- R. Yang, Y. F. Gao, B. Tang and T. Gao, Phys. Chem. Chem. Phys., 2015, 17, 1900 RSC.
| This journal is © The Royal Society of Chemistry 2020 |