Room temperature ferromagnetism in D–D neutron irradiated rutile TiO₂ single crystals

Abstract

Room temperature ferromagnetism (RTFM) was observed in unirradiated rutile TiO₂ single crystals prepared by the floating zone method due to oxygen vacancy (V_O) defects. D–D neutrons mainly collide elastically with TiO₂, producing V_O, titanium vacancies (V_Ti) and other point defects; the density and kind of defect is related to the neutron irradiation fluence. D–D neutron irradiation is used to regulate the concentration and type of defect, avoiding impurity elements. As the irradiation fluence increases, the saturation magnetization (M_s) first increases, then decreases and then increases. To verify the origin of RTFM, the CASTEP module was used to calculate the magnetic and structural properties of point defects in TiO₂. V_O induces a 2.39 μ_B magnetic moment, Ti³⁺ and F⁺ induce 1.28 μ_B and 1.70 μ_B magnetic moments, respectively, while V_Ti induces a magnetic moment of ∼4 μ_B. Combining experimental and theoretical results, increases in V_O concentration lead to M_s increases; more V_O combine with electrons to form F⁺, inducing a smaller magnetic moment. V_O and V_Ti play a key role and M_s changes accordingly with larger fluence. V_O, F⁺ and V_Ti are the most likely origins of RTFM.

---

1 Introduction

TiO₂ is a versatile functional material that has important applications^1–3 in the fabrication of spintronics, optical coatings and solar cells. TiO₂ doped with different ions has been synthesized^4–6 to modify its ferromagnetic and optical properties. TiO₂ also has outstanding magnetic properties, showing RTFM in both ion-doped and undoped states. However, there is no consensus on the origin of magnetism of TiO₂, and some experimental results contradict each other. Kaspar et al.⁷ pointed out that extended structural defects appear to be necessary to promote ferromagnetic ordering in Cr:TiO₂. Saadaoui et al.⁸ found that the ferromagnetism is intrinsic and controlled by oxygen vacancies. Zheng et al.⁹ reported that oxygen defects can be the dominating factor for increasing the saturation moment of Cu-doped TiO₂ film. Zhou et al.¹⁰ found that ferromagnetism was related to a lower level of V_O defects. Parras et al.¹¹ pointed out that the magnetic moment is indeed due to the Ti³⁺ ions induced by reduction. Wang et al.¹² reported that V_Ti could be the origin of RTFM.

Defects play an important role in the structural, magnetic and optical properties of semiconductor materials; in particular, the intrinsic defects of TiO₂ have the potential to induce spintronic properties at room temperature. Magnetic semiconductors with high Curie temperatures are expected to be used in spintronic materials with great potential applications because they can utilize both charge and spin degrees of freedom in a single component. Venhatesan and Coey et al.¹³ reported that HfO₂ films have high-temperature ferromagnetism and first proposed the concept of d⁰ magnetism. They avoided the interference of the second phase of magnetic elements in dilute magnetic semiconductors (DMS) and only studied the effect of intrinsic defects. Since then, many research groups have studied defects causing RTFM in TiO₂-based DMS materials.

In our previous work, the magnetic properties of Cu-doped TiO₂ were investigated^14,15 by theoretical and experimental studies. RTFM may be induced by V_O or Cu²⁺–V_O; the effects of intrinsic defects and Cu-doping are ambiguous. The effects of γ-ray and D–D neutron irradiation^16,17 on the RTFM of TiO₂ single crystals were initially explored. RTFM was observed, and V_O was the main origin of room temperature ferromagnetism. D–D neutrons mainly scatter with TiO₂ single crystals; they have the right energy to cause vacancy defects, but not to produce a nuclear reaction at a higher energy or capture neutrons at a lower energy. Furthermore, because D–D neutron fluence could regulate the concentration and kind of defect, it is beneficial to explore the effect of intrinsic defects on RTFM properties. The effects of different defect concentrations and types on ferromagnetism can be obtained by adjusting the neutron fluence. Using D–D neutron irradiation has significant advantages over doping with other magnetic elements to clarify the origin of RTFM.

In this study, to illustrate the effect of intrinsic defects on magnetic and structural properties and optical band gap, D–D neutron irradiation was carried out to verify the effect of intrinsic defects in rutile TiO₂ single crystals. In addition, we use the CASTEP module based on a density functional theory (DFT) method to calculate the magnetic properties of intrinsic vacancy defects. This lays a foundation for the application of TiO₂ in photocatalysis and spintronics.

2 Materials and methods

Pure TiO₂ single crystals from MaTeck prepared by the floating zone method with one side polished were cut to 5 × 10 × 0.5 mm³. D–D neutron irradiation with fluences of 0 n cm⁻², 2 × 10⁹ n cm⁻², 5 × 10⁹ n cm⁻², 1 × 10¹⁰ n cm⁻², and 2.5 × 10¹⁰ n cm⁻² was used.

X-ray diffraction (XRD, D/Max-2400) with Cu K_α radiation (λ = 0.15406 nm) was used to characterize the structure of TiO₂. The working voltage is 40 kV, the working current is 60 mA, the step length is 0.02°, the scanning speed is 20° min⁻¹, and the scanning range is 20–80°. The excitation wavelength of the Raman spectrum is 532 nm, the laser power of the backscattering mode is 10 mW, and the spot size is 2 μm. The Raman displacement range is 100–1000 cm⁻¹ and the integral time is 10 s. Three points were selected from each sample for testing. A superconducting quantum interferometer (SQUID) was used to measure the M–H curves under an external magnetic field parallel to the surface of the sample. X-ray photoelectron spectroscopy (XPS) was conducted using a PHI-5702 multi-functional electronic spectrometer. A conductive adhesive was used to stick the sample to the sample rack, with the polished surface facing out. The wide spectra (0–1000 eV), Ti (450–468 eV) and O (525–537 eV), and C (274–296 eV) fine spectra were tested, respectively. The photon energy of the X-ray source with Al as the anode material is 1486.6 eV. The photoluminescence (PL) source is a xenon lamp with an excitation source wavelength of 415 nm and a spectral range of 450–750 nm. Electron spin resonance (ESR) spectra were tested on a Bruker EMX plus at 2 K at the Steady High Magnetic Field Facilities, High Magnetic Field Laboratory, CAS. The samples were cut to 2 mm × 2 mm for testing. The magnetic field range is 2900–3900 G and the microwave frequency is 9.4 GHz. The ultraviolet visible (UV-vis) spectra were obtained in reflection mode with the measurement range of 300–700 nm.

3 Results and discussion

Fig. 1 represents the XRD patterns after neutron irradiation. There are TiO₂ (002) and Cu K_α peaks in the spectra. The full width at half maximum (FWHM) of the (002) peak is very small, indicating that the single crystals have high crystallinity. The (002) peak shows a small shift toward a small angle, which means that the lattice expands a little due to the repulsion force between the oxygen vacancies. Fig. 1(b) shows two small peaks at 56.4° and 60.7°, corresponding to Ti₂O₃ and Ti₃O₅, which indicates that TiO₂ is non-stoichiometric.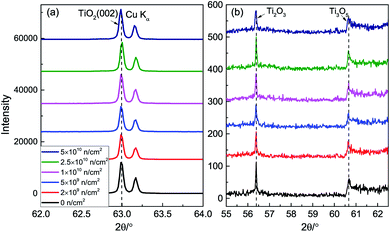

Fig. 1 XRD patterns; (a) (002) peak and (b) drawing of partial enlargement of TiO₂ before and after neutron irradiation.

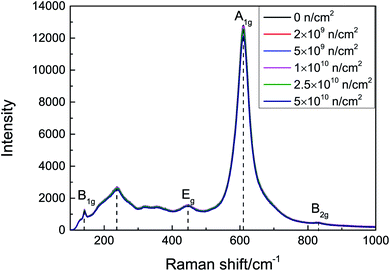
The space group¹⁸ of rutile TiO₂ is D_4h¹⁴, and the Raman-active vibrational energy levels are B_1g (143 cm⁻¹), E_g (447 cm⁻¹), A_1g (611 cm⁻¹), and B_2g (828 cm⁻¹). The scattering intensity is proportional to the number of corresponding molecules and is related to the smoothness of the surface and diffuse reflection. The Raman spectra of the samples before and after irradiation are presented in Fig. 2. There is an asymmetrical broad peak at 235 cm⁻¹, corresponding to the second-order scattering of phonons or internal disorder. The damage can be described by the FWHM of the A_1g peaks; as the irradiation fluence increases, the A_1g peak still maintains a good FWHM. No peak shift or new vibration level was observed, which indicates that no obvious lattice damage was caused by neutron irradiation.

Fig. 2 Raman spectra of TiO₂ before and after neutron irradiation.

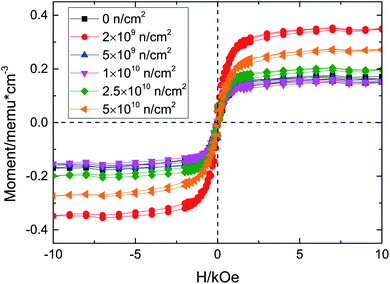
Fig. 3 illustrates the M–H curves before and after D–D neutron irradiation. All the samples exhibit RTFM, including the unirradiated sample, which agrees with the experimental results¹⁹ and our preliminary work.¹⁷ Oxygen deficiencies are inevitably introduced in the preparation by the floating zone method;^20,21 V_O would induce a magnetic moment. Santara et al.¹⁹ reported that V_O induced strong ferromagnetism at and above room temperature in undoped TiO₂ nanoporous nanoribbons. Furthermore, Kim et al.²² pointed out that oxygen vacancy defects play an important role in the ferromagnetism of undoped rutile TiO₂. Moreover, our previous work,¹⁷ using γ-ray irradiated TiO₂, also found that the origin of RTFM of unirradiated TiO₂ single crystals was V_O; thus the RTFM of unirradiated TiO₂ is due to V_O. D–D neutron irradiation has advantages in regulating the concentrations and kinds of defect; because of its energy it only collides with atoms in elastic scattering and the nuclear reaction cross section is 0, so no nuclear reaction occurs. Therefore, D–D neutron irradiation has been used to regulate defect concentration and type to study changes of RTFM.

Fig. 3 M–H curves of TiO₂ before and after neutron irradiation.

The maximum saturation magnetization (M_s) is in the 2 × 10⁹ n cm⁻² sample, while the M_s of the 5 × 10⁹ n cm⁻² and 1 × 10¹⁰ n cm⁻² samples are almost equal to that of the unirradiated sample. Then, the M_s increased with the irradiation fluence, which means that there is an optimal value for V_O defect concentration. D–D neutron irradiation mainly causes point vacancy defects. Considering the XRD and Raman results and the physical process of D–D neutron irradiation of TiO₂, the ferromagnetism may due to vacancy defects, such as V_O, V_Ti, and so on. In our previous work, we found that V_O could induce ∼2 μ_B magnetic moment, while V_Ti could introduce ∼4 μ_B magnetic moment, which we will verify below. After D–D neutron irradiation, V_O and V_Ti are induced due to the elastic collisions between neutrons and Ti and O atoms; these defects increase M_s. For the 5 × 10⁹ n cm⁻² and 1 × 10¹⁰ n cm⁻² samples, M_s decreases on account of the compound defects that V_O make up with other defects,¹⁰ e.g., F⁺, V_O–Ti³⁺; these defects provide a smaller magnetic moment, so the total magnetic moment of the system is decreased. We preliminarily studied the Doppler broadening and positron annihilation spectroscopy^16,23,24 of Cu-doped and D–D neutron irradiated TiO₂, and V_Ti was found after spectral analysis. V_Ti would certainly be generated after D–D neutron irradiation of TiO₂ single crystals. Below, we will further investigate the increase due to the V_Ti and V_O defects produced when the fluence increased for the 2.5 × 10¹⁰ n cm⁻² and 5 × 10¹⁰ n cm⁻² samples.

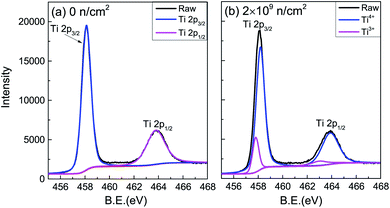
The valence of Ti after irradiation was characterized by XPS spectra.^25–27 Only Ti, O and C could be detected. Using C 1 s (284.6 eV) for charge correction, the Ti 2p core electron spectra of the unirradiated and 2 × 10⁹ n cm⁻² samples are shown in Fig. 4. The peak separation fitting of the Ti 2p spectra was performed by the Gauss–Lorentz function. The Ti⁴⁺ 2p_3/2 and 2p_1/2 binding energies were 458.5 eV and 464.2 eV, respectively, and the energy level spacing^28,29 was 5.7 eV for Ti⁴⁺ and 5.2 eV for Ti³⁺. After peak-differentiation and imitation, the unirradiated sample still showed +4 valence. Ti³⁺ was produced in irradiated TiO₂, proving that V_O was indirectly generated after irradiation. Ti³⁺ contributes a paramagnetic signal,³⁰ and the Ti³⁺ peak area shows no obvious change with the increased irradiation dose, which is inconsistent with the change of M_s.

Fig. 4 XPS spectra of (a) raw and (b) 2 × 10⁹ n cm⁻² TiO₂ samples.

To investigate the defect type after neutron irradiation, PL spectra are displayed in Fig. 5(a). After peak separation, the three main peaks are centered at 473 nm (2.62 eV), 600 nm (2.07 eV) and 820 nm (1.51 eV), as shown in Fig. 5(b). As the PL spectra are similar, we choose the 2 × 10⁹ n cm⁻² sample for detailed analysis. In TiO₂, the electron trap state caused by V_O is about 0.5–1 eV below the bottom of the conduction band.³¹ Therefore, the band peak at 473 nm is assigned to V_O and the deep level emission^32,33 of V_O, which is consistent with the first principles calculation below. The 600 nm luminescence peak is attributed to the consequence of polarization of the lattice ions surrounding the vacancy.³⁴ The peak at 818 nm might be a consequence of Ti³⁺ or F⁺ defects. Table 1 shows the area of the peaks after normalization. The area of the 473 nm peak is found to vary according to the change of M_s; this is direct evidence that V_O causes RTFM. With the increase of neutron injection, V_O gradually forms an extinction center; more and more V_O combine with electrons to form F⁺.³⁵ F⁺ induce a smaller magnetic moment, leading to a decrease in M_s. In a word, V_O was produced after neutron irradiation of TiO₂.

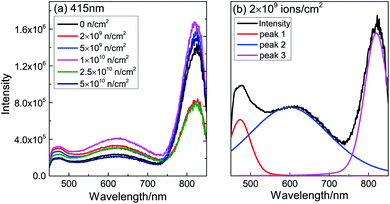Fig. 5 (a) Raw PL spectra of TiO₂ before and after neutron irradiation and (b) normalized PL spectra for 2 × 10⁹ n cm⁻².

Table 1 Peak area of PL spectra after peak fitting

Sample (n cm^−2)	473 nm	600 nm	820 nm
0	0.0777	0.3424	0.5798
2 × 10^9	0.1195	0.5308	0.3496
5 × 10^9	0.0889	0.3729	0.5382
1 × 10^10	0.0871	0.4241	0.4888
2.5 × 10^10	0.0970	0.5195	0.3835
5 × 10^10	0.0751	0.2944	0.6305

---

The CASTEP module was used to calculate the density of states (DOS) of TiO₂, which is based on a plane wave pseudo-potential method and DFT. The electron exchange correlation function is treated using a generalized gradient approximation (GGA) exchange-correlation functional in the form of Perdew–Bruke–Ernzerhof (PBE). GGA+U methods^36,37 were considered to give a proper description of the strong correlation effects. The Hubbard U was employed as U_Ti,d = 6.47 eV, U_O,p = 4.3 eV. The Monkhorst–Pack scheme k-point mesh was 2 × 2 × 3 for the 2 × 2 × 2 supercell. The calculation ensured an energy convergence of 1 × 10⁻⁶ eV per atom and the cut-off energy was 340 eV.

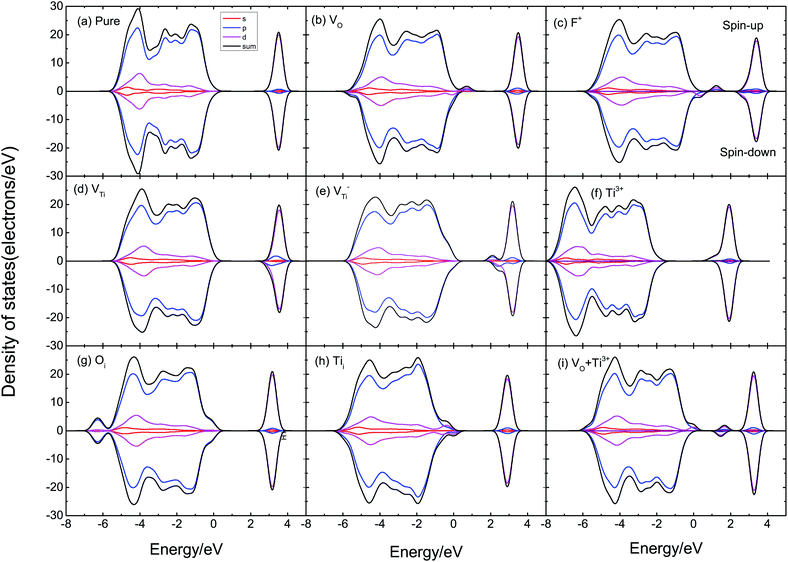
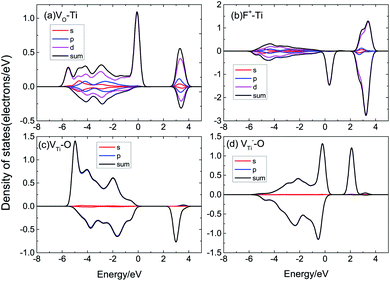
According to Fig. 6, we can find that the DOS of supercells with V_O, V_Ti, and F⁺ defects are asymmetric, indicating that supercells with these defects have a magnetic moment. As displayed in Fig. 6(a), pure TiO₂ has symmetric DOS and spin-zero ground states; it does not show magnetism. V_O defects could induce a magnetic moment in TiO₂, as shown in Fig. 6(b). We also calculated F⁺, V_Ti, V⁻_Ti, Ti³⁺, O_i, Ti_i, V_O–Ti³⁺, as shown in Fig. 6(c)–(i). The supercells with F⁺ and Ti³⁺ are found to have lower magnetic moments of 1.28 μ_B and 1.70 μ_B, respectively, while the supercell with O_i could not induce a magnetic moment. When there is V_Ti or Ti_i, its DOS is spin-polarized and the system has a magnetic moment of ∼4 μ_B. The supercell with V_O–Ti³⁺ induces a magnetic moment about the same as that of V_O.

Fig. 6 Spin-polarized total and partial DOS of (a) pure TiO₂, (b) the TiO₂ supercell with one V_O, (c) the TiO₂ supercell with F⁺, (d) the TiO₂ supercell with V_Ti, (e) the TiO₂ supercell with V⁻_Ti, (f) the TiO₂ supercell with Ti³⁺, (g) the TiO₂ supercell with O_i, (h) the TiO₂ supercell with Ti_i, (i) the TiO₂ supercell with V_O–Ti³⁺.

The magnetic moment of the V_O system is 2.39 μ_B. The partial densities of states (PDOS) of Ti with V_O are shown in Fig. 7(a); the magnetic moment arises from the 3d orbital electrons of the Ti atoms around V_O. When there is V_O, the Ti atoms around V_O are repelled by the V_O, then the electron population of the Ti 3d orbital varies, causing spin-polarization in the system. It can be seen that F⁺ induces a 1.28 μ_B magnetic moment. F⁺ provides a lower magnetic moment than V_O, as shown in Fig. 7(b); its magnetic moment is also due to the asymmetric PDOS of the Ti 3d orbital. V_Ti can induce a 4.53 μ_B magnetic moment due to the O 2p orbital hybridization, as shown in Fig. 7(c). Fig. 7(d) shows the PDOS of O 2p of V⁻_Ti. For Ti vacancies with various valence states, the titanium vacancy with negatively monovalent charge (V⁻_Ti) is more stable under different conditions.³⁸ According to our calculations, V⁻_Ti induces ∼4 μ_B magnetic moment, which is almost consistent with the magnetic moment introduced by the neutral V_Ti.

Fig. 7 The PDOS of (a) Ti of V_O, (b) Ti of F⁺, (c) O of V_Ti, (d) O of V⁻_Ti.

Combining the above experimental and theoretical calculation results, we infer that the magnetism in TiO₂ after D–D neutron irradiation is caused by V_O, V_Ti and F⁺. Besides, we also calculated the defect formation energies of these kinds of point and compound defects, as shown in Table 2. We used the following formula to calculate defect formation energy (E_f):^39–41

E_f = E_(D) − E_(TiO2) + n₁μ_(O) + n₂μ_(Ti) + qE_F (1)

E_(TiO2) = μ_(Ti) + 2μ_(O) (2)

E_(D) is the total energy of the supercell with defects (V_O, or V_Ti, …), E_(TiO2) is the total energy of pure rutile TiO₂, n₁ and n₂ are the number of removed O (or Ti) atoms, and μ is the chemical potential energy. In the O-rich case, μ_(O) is half of μ(O₂), μ_(O) = −430 eV; μ_(Ti) can be calculated from formula (2), μ_(Ti) = −1612.04 eV. In the O-poor case, μ_(Ti) is equal to the metal Ti, and μ^metal_(Ti) = −1602.85 eV; μ_(O) can be calculated from formula (2), μ_(O) = −434.58 eV. q is the charge of the defects, and the Fermi level E_F is the energy of the electron reservoir, referenced to the valence-band maximum (VBM).

Table 2 Formation energy of TiO₂ with neutral intrinsic defects

Ef/eV	VO	VTi	Oi	Tii
O-rich	7.00	0.57	0.58	11.89
O-poor	2.41	8.62	5.17	2.71

---

The results were different in the O-rich and O-poor cases. V_O is more easily formed than V_Ti in terms of the energy of dislocation threshold and defect formation. Therefore, it is easier to form V_O, V_Ti, F⁺, Ti³⁺ and V_O–Ti³⁺ than Ti_i defects in the atmosphere, and the most likely origin of magnetism in TiO₂ is V_O, V_Ti, F⁺ and Ti³⁺. For unirradiated TiO₂, native V_O defects induced RTFM. After D–D neutron irradiation, the defect concentration increases with the irradiation fluence, and the defect type also changes. More and more V_O and V_Ti provide conditions for the formation of other defects; Ti³⁺, F⁺ and other compound defects (V_O + Ti³⁺ and so on) are produced, and the density of these defects becomes higher and higher with the increase of neutron irradiation fluence. We also found that V_O can induce a 2.39 μ_B magnetic moment. Ti³⁺ and F⁺ defects introduce smaller magnetic moments that cause the RTFM of the 5× 10⁹ n cm⁻² and 1 × 10¹⁰ n cm⁻² samples to decrease. Bao et al.⁴² proposed that the RTFM may be due to the formation of V_Ti from the substitution of Ga for Ti, and V_Ti was verified by positron annihilation spectroscopy. Qin et al.⁴³ reported that the RTFM is attributed to V_Ti and N_O defects in the rutile structure. Then, more V_Ti and V_O play a key role in increasing the RTFM of the 2.5 × 10¹⁰ n cm⁻² and 5 × 10¹⁰ n cm⁻² samples.

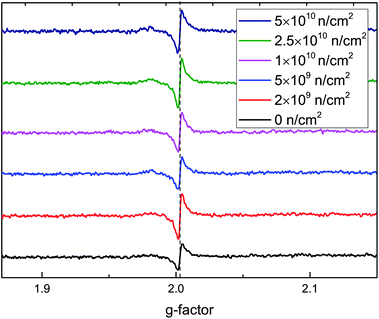
To further verify that the RTFM is caused by V_O defects, ESR spectra at 2 K are shown in Fig. 8. A peak was found around a g-factor of 2.003, which was assigned to an oxygen vacancy binding a single electron⁴⁴ in rutile TiO₂. The signal intensity first increases and then decreases, then increases with the increase in irradiation fluence, which is in accordance with the M–H curves. From the above analysis, the highest concentration of V_O is induced by 2 × 10⁹ n cm⁻²; it also causes the greatest changes in magnetism.

Fig. 8 ESR spectra of TiO₂ before and after neutron irradiation.

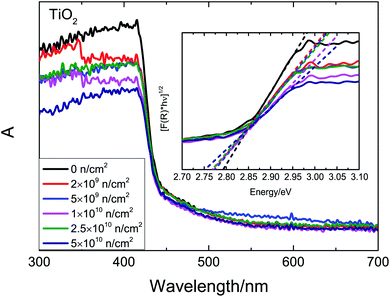
The UV-Vis absorption spectra after irradiation are shown in Fig. 9. According to first-principles calculations, a strong absorption at 420 nm is inherent. The optical band gap (E_g) is estimated by the K–M function. The E_g decreases gradually with the increase in fluence. Based on our previous analysis and theoretical research,^14,45 V_O, V_Ti and V_O–Ti³⁺ defects introduce unpaired states in the band gap, which could narrow the band gap. As the fluence increases, ever larger concentrations of defects and ever thicker defect states imply an ever narrower band gap. With the increase in irradiation fluence, the total defect concentration increases, and the change of defect types causes the M_s to change.

Fig. 9 UV-Vis spectra of TiO₂ before and after neutron irradiation.

4 Conclusion

In summary, we found that the origin of RTFM of unirradiated TiO₂ is V_O. D–D neutron irradiation was used to engineer the defect concentration and type. After D–D neutron irradiation, the M_s increases with the increasing concentration of V_O and V_Ti. As the neutron irradiation fluence increases, more and more V_O combine electrons to form F⁺. F⁺ induce a smaller magnetic moment, leading to a decrease in M_s. With further increases of the irradiation fluence, V_Ti and V_O play an important role in increasing the magnetic moment. Therefore, RTFM is caused by V_O, F⁺, and V_Ti. The optimal fluence of D–D neutron irradiation remains to be further explored.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (11575074, 11975006, 11905089), the Key Laboratory of Special Function Materials and Structure Design, Ministry of Education, Lanzhou University (lzujbky-2018-kb06), the Fundamental Research Funds for the Central Universities of Ministry of Education of China (lzujbky-2017-it39, lzujbky-2018-it38), the DSTI Foundation of Gansu (2018ZX-07). A portion of this work was performed at the Steady High Magnetic Field Facilities, High Magnetic Field Laboratory, CAS.

Notes and references

1. U. Bach, D. Lupo, P. Comte, J. E. Moser, F. Weissörtel, J. Salbeck, H. Spreitzer and M. Grätzel, Nature, 1998, 395, 583–585.
2. R. Asahi, T. Morikawa, T. Ohwaki, K. Aoki and Y. Taga, Science, 2001, 293, 269–271.
3. H. Yaghoubi, N. Taghavinia and E. K. Alamdari, Surf. Coat. Technol., 2010, 204, 1562–1568.
4. V. R. Singh, K. Ishigami, V. K. Verma, G. Shibata, Y. Yamazaki, T. Kataoka, A. Fujimori, F. H. Chang, D. J. Huang and H. J. Lin, Appl. Phys. Lett., 2012, 100, 242404.
5. S. K. S. Patel, S. Kurian and N. S. Gajbhiye, AIP Adv., 2012, 2, 012107.
6. A. R. Barman, A. Annadi, K. Gopinadhan, W. M. Lu and T. Venkatesan, AIP Adv., 2012, 2, 1883.
7. T. C. Kaspar, T. C. Droubay, V. Shutthanandan, S. M. Heald and S. A. Chambers, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155327.
8. H. Saadaoui, X. Luo, Z. Salman, X. Y. Cui, N. N. Bao, P. Bao, R. K. Zheng, L. Tseng, Y. H. Du and T. Prokscha, Phys. Rev. Lett., 2016, 117, 227202.
9. J. Y. Zheng, S. H. Bao, Y. H. Lv and P. Jin, ACS Appl. Mater. Interfaces, 2014, 6, 22243–22249.
10. Z. Zhou, H. Wang, Z. Zou, D. Meng, J. Guo and Z. Yang, Mater. Res. Bull., 2017, 86, 287–297.
11. M. Parras, A. Varela, R. Cortes-Gil, K. Boulahya, A. Hernando and J. M. Gonzalez-Calbet, J. Phys. Chem. Lett., 2013, 4, 2171–2176.
12. W. Songbo, P. Lun, S. Jia-Jia, M. Wenbo, Z. Ji-Jun, W. Li and Z. Xiangwen, J. Am. Chem. Soc., 2015, 137, 2975–2983.
13. M. Venkatesan, C. B. Fitzgerald and J. M. D. Coey, Nature, 2004, 430, 630.
14. Q. L. Lin, G. P. Li, N. N. Xu, H. Liu and C. L. Wang, Acta Phys. Sin., 2017, 66, 302–315.
15. H. Liu, G. P. Li, N. N. Xu, Q. L. Lin, L. Yang and C. L. Wang, Acta Phys. Sin., 2016, 65, 185–193.
16. N. N. Xu, G. P. Li, X. D. Pan and L. M. Bao, Chin. Phys. B, 2014, 23, 10610.
17. H. Liu, G. P. Li, Q. L. Lin, D. J. E, X. D. Gao, X. B. Wei, X. D. Pan, S. X. Zhang, J. J. Ding and W. Lan, J. Supercond. Novel Magn., 2019, 32, 3557–3562.
18. S. P. S. Porto, P. A. Fleury and T. C. Damen, Phys. Rev., 1967, 154, 522–526.
19. S. Batakrushna, P. K. Giri, I. Kenji and F. Minoru, Nanoscale, 2013, 5, 5476–5488.
20. M. Higuchi, T. Hosokawa and S. Kimura, J. Cryst. Growth, 1991, 112, 354–358.
21. J. Rodrigues, M. Peres, A. J. S. Fernandes, M. P. F. Graca, N. A. Sobolev, F. M. Costa and T. Monteiro, Appl. Surf. Sci., 2012, 258, 9143–9147.
22. D. Kim, J. Hong, Y. R. Park and K. J. Kim, J. Phys.: Condens. Matter, 2009, 21, 195405.
23. N. N. Xu, G. P. Li, Q. L. Lin, H. Liu and L. M. Bao, J. Supercond. Novel Magn., 2017, 30, 1–6.
24. N. N. Xu, G. P. Li, Q. L. Lin, H. Liu and L. M. Bao, Chin. Phys. B, 2016, 25, 106101.
25. X. Wang, Y. Song, L. L. Tao, J. F. Feng, Y. Sui, J. Tang, B. Song, Y. Wang, Y. Wang and Y. Zhang, Appl. Phys. Lett., 2014, 105, 262402.
26. B. Anitha and M. A. Khadar, J. Nanopart. Res., 2016, 18, 1–14.
27. J. Li, F. Li, Y. Zhuang, L. Jin, L. Wang, X. Wei, Z. Xu and S. Zhang, J. Appl. Phys., 2014, 116, 074105.
28. F. Wang, H. Li, Q. Wu, J. Fang, Y. Huang, C. Yin, Y. Xu and Z. Luo, Electrochim. Acta, 2016, 202, 1–7.
29. Z. Zhao, X. Zhang, G. Zhang, Z. Liu, D. Qu, X. Miao, P. Feng and Z. C. Sun, Nano Res., 2015, 8, 1–11.
30. E. C. Buck, Radiat. Eff. Defects Solids, 1995, 133, 141–152.
31. M. A. Henderson, W. S. Epling, C. H. F. Peden and C. L. Perkins, J. Phys. Chem. B, 2003, 107, 534–545.
32. X. Q. Cheng, C. Y. Ma, X. Y. Yi, F. Yuan, Y. Xie, J. M. Hu, B. C. Hu and Q. Y. Zhang, Thin Solid Films, 2016, 615, 13–18.
33. M. Memesa, S. Lenz, S. G. J. Emmerling, S. Nett, J. Perlich, P. Muller-Buschbaum and J. S. Gutmann, Colloid Polym. Sci., 2011, 289, 943–953.
34. D. Li, H. Haneda, N. K. Labhsetwar, S. Hishita and N. Ohashi, Chem. Phys. Lett., 2005, 401, 579–584.
35. L. Kernazhitsky, V. Shymanovska, V. Naumov, L. Fedorenko, V. Kshnyakin, N. Shcherban, S. Filonenko and J. Baran, J. Lumin., 2017, 187, 521–527.
36. B. J. Morgan and G. W. Watson, J. Phys. Chem. C, 2010, 114, 2321.
37. M. Wang, M. Feng and X. Zuo, Appl. Surf. Sci., 2014, 292, 475–479.
38. Y. Zhang, N. Ma, M. Zhou, E. Cao, S. Li, W. Hao and Z. Yang, J. Phys. Chem. Solids, 2018, 121, 276–284.
39. S. Naphattalung, M. F. Smith, K. Kim, M. H. Du, S. H. Wei, S. B. Zhang and S. Limpijumnong, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 125205.
40. A. Janotti, J. B. Varley, P. Rinke, N. Umezawa, G. Kresse and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085212.
41. G. Mattioli, P. Alippi, F. Filippone, R. Caminiti and A. Amore Bonapasta, J. Phys. Chem. C, 2010, 114, 21694–21704.
42. N. N. Bao, J. B. Yi, H. M. Fan, X. B. Qin, P. Zhang, B. Y. Wang, J. Ding and S. Li, Scr. Mater., 2012, 66, 821–824.
43. X. B. Qin, D. X. Li, R. Q. Li, P. Zhang, Y. X. Li and B. Y. Wang, Chin. Phys. B, 2014, 23, 067502.
44. Q. Jin, Y. Shen, S. Zhu, X. Li and M. Hu, Chin. J. Catal., 2016, 37, 1521–1528.
45. J. Li, S. Meng, L. Qin and H. Lu, Chin. Phys. B, 2017, 26, 370–375.

---