Open Access Article
Open Access ArticleFerroelectric performance of nylons 6-12, 10-12, 11-12, and 12-12
Ayumi Yanakaa,
Wataru Sakai b,
Kenji Kinashi
b,
Kenji Kinashi b and
Naoto Tsutsumi
b and
Naoto Tsutsumi *b
*b
aDoctor's Program of Materials Chemistry, Graduate School of Science and Technology, Kyoto Institute of Technology, Sakyo, Kyoto 606-8585, Japan
bFaculty of Materials Science and Engineering, Kyoto Institute of Technology, Sakyo, Kyoto 606-8585, Japan. E-mail: tsutsumi@kit.ac.jp
First published on 21st April 2020
Abstract
Nylons have great potential for electrical applications requiring high polarizability and low dielectric loss. Recently, the narrow single hysteresis loop with relaxor ferroelectricity and the double hysteresis loop due to antiferroelectricity have been reported in nylon random copolymers, terpolymers, and common even-numbered nylons. Although several studies of ferroelectric nylons have been reported, even–even-numbered and odd–even-numbered nylons have not been sufficiently explored. Here, the ferroelectricity of spin-coated even–even-numbered and odd–even-numbered nylons was investigated. A series of even–even-numbered nylons, including nylons 6-12, 10-12, and 12-12, and an odd–even-numbered nylon, nylon 11-12, were polymerized with 1,10-dodecanedicarboxylic acid (12) and four aliphatic diamines with various methylene units, 1,6-hexanediamine (6), 1,10-decanediamine (10), 1,11-undecanediamine (11), and 1,12-dodecanediamine (12). The obtained nylon polymers were spin coated and then subjected to melt-quenching or thermal annealing followed by quenching. From the X-ray diffraction and the electrical hysteresis loop data, the correlation between the ferroelectricity and the crystal parameters of crystallinity and crystallite size of the γ crystal phase was investigated. Furthermore, the free volume of the nylon samples was estimated to correlate with the ferroelectricity. Temperature-dependent ferroelectricity was investigated for nylon 10-12. At a high temperature, the nylon samples showed a narrow polarization–electric field hysteresis loop and a rhombus-shaped polarization current–electric field hysteresis loop due to the relaxor ferroelectricity. This behaviour was caused by electrically rotating the nanodomains with weakened hydrogen bonds at higher temperatures.
Introduction
Polymers with ferroelectric properties are attractive for a wide range of electroactive applications, such as electromechanical actuators,1 nonvolatile memory (ferroelectric random access memory: FeRAM),2 and electric energy storage,3,4 because of their easy processing, and flexible, lightweight, and environmentally friendly properties. Many ferroelectric polymers have been discovered and widely investigated, including poly(vinylidene fluoride) (PVDF), polyurea, vinylidene cyanide polymers, poly(lactic acid), and odd-numbered nylons.5–11 Among them, PVDF and its copolymers with trifluoroethylene [P(VDF–TrFE)] are well known ferroelectric polymers and have been applied to a variety of practical devices due to their large polarizability of 2.1 D from the VDF repeat units.12–14 However, these PVDF-based polymers require special production facilities and are high-cost polymers due to the complex synthesis process.Nylon polymers are well known as designable high performance polymers and can be inexpensively and simply prepared. Furthermore, the amide group (NH–CO) in nylon has a dipole moment of 3.7 D.15 Therefore, in addition to PVDF-based polymers, nylons are attractive as ferroelectric polymers. Odd-numbered nylons, nylons with the odd number of carbon atoms in each segment, is ferroelectric because of their polar crystalline structures with parallel hydrogen bonds.16 However, the α crystal form of nylon 11 with strong hydrogen packing does not exhibit ferroelectricity.10,17 The δ′ crystal form of nylon 11 shows ferroelectric behaviour because the δ′ crystal form has weak hydrogen bonds in the molecular chains due to the twisted chain conformation.18,19 For the same reason, it has been known that odd–odd-numbered nylons with γ crystal forms show ferroelectric behavior.20–23 On the other hand, even-numbered nylons, such as nylon 12 and nylon 6, have nonpolar crystalline structures with antiparallel hydrogen bonds and are thus expected to be nonferroelectric. However, in recent studies of nylon 12 and nylon 6, the melt-quenched and stretched, melt-quenched, annealed, and stretched samples showed electric-field-induced ferroelectric switching behaviors.24–26 It is considered that the ferroelectricity of even-numbered nylons was caused by weak hydrogen bonds originating from multiple twisted chain conformations in pseudohexagonal γ crystal structures. From the above discussion, it is clear that the polar crystalline structure is not a prerequisite for ferroelectric performance in nylon samples. Narrow single hysteresis loops with relaxor ferroelectricity and double hysteresis loops due to antiferroelectricity have also been observed in nylon random copolymers, terpolymers, and common even-numbered nylons.25,27 Therefore, nylons exhibit great potential for electrical applications requiring high polarizability and low dielectric loss.28 Solution processed transparent ferroelectric nylon has been recently reported.29,30
Although the ferroelectric properties of various nylon polymers have been investigated, the ferroelectricity of even–even-numbered and odd–even-numbered nylons have not been sufficiently confirmed. In this study, we investigated the ferroelectric performances of spin-coated even–even-numbered nylons, nylon 6-12, 10-12, and 12-12, and the odd–even-numbered nylon 11-12. Spin-coated thin films are advantageous regarding both scientific aspects and commercial applications in the production of microelectronic devices requiring relatively low operating voltages. We explored the correlation between ferroelectric properties and methylene chain length using even–even-numbered nylons with different numbers of carbon atoms in each segment. Crystallographic measurements were also performed using a wide-angle X-ray diffraction (WAXD) method. The obtained results for crystalline structures were also correlated to the ferroelectric properties. Furthermore, temperature-dependent ferroelectric performances were also discussed.
Experimental section
Materials
Melt polymerization method was used to prepare even–even-numbered and odd–even-numbered nylons. One dicarboxylic acid, namely, 1,10-dodecanedicarboxylic acid (12) (Tokyo Chem. Ind., Japan), and four diamines, namely, 1,6-hexanediamine (6) (FUJIFILM Wako Pure Chemical Corp., Japan), 1,10-decanediamine (10) (FUJIFILM Wako Pure Chemical Corp.), 1,11-undecanediamine (11) (Tokyo Chem. Ind.), and 1,12-dodecanediamine (12) (FUJIFILM Wako Pure Chemical Corp.), were used.Synthesis of nylons 6-12, 10-12, 11-12, and 12-12
The nylon polymers were prepared with the corresponding nylon salts using the same synthetic procedures described in a previous report.23 The detailed preparation procedures are shown in a previous report.23Ethanol solution (15 mL) of 7.52 × 10−3 mol 1,10-dodecanedicarboxylic acid (12) was slowly added to ethanol solution (15 mL) of 7.5 × 10−3 mol 1,6-hexanediamine (6) at 40 °C with stirring vigorously, and the nylon 6-12 salt was obtained. The obtained nylon 6-12 salt was dried. The dried nylon 6-12 salt was heated at 200 °C for 15 min and then at 230 °C for 3 h under a nitrogen atmosphere and further heated for 3 h in vacuo. Finally nylon 6-12 polymer was obtained. The obtained polymer was reprecipitated with a mixture of hexafluoro-iso-propanol (HFIP) and acetone and dried at 100 °C for 24 h. The melting point of nylon 6-12 was 213 °C.
For synthesizing nylon 12-12, similar procedures as did for the synthesis of nylon 6-12 were employed with 1,12-dodecanediamine (12) instead of (6). Nylon 12-12 salt was prepared using 1,10-dodecanedicarboxylic acid (12) and 1,12-dodecanediamine (12) in ethanol at 40 °C. The obtained polymer was reprecipitated with a mixture of HFIP and acetone and dried at 100 °C for 24 h. The melting point of nylon 12-12 was 187 °C.
For synthesizing nylon 10-12, similar procedures as did for nylon 6-12 were employed with 1,10-decanediamine (10) instead of (6) and lower temperatures condition of 190 °C and 210 °C instead of 200 °C and 230 °C, respectively. Nylon 10-12 salt was prepared using 1,10-dodecanedicarboxylic acid (12) and 1,10-decanediamine (10) in ethanol at 40 °C. The obtained polymer was reprecipitated with a mixture of HFIP and tetrahydrofuran (THF) and dried at 100 °C for 24 h. The melting point of nylon 10-12 was 190 °C.
For synthesizing nylon 11-12, similar procedures as did for nylon 10-12 were employed with 1,11-undecanediamine (11) instead of (10). Nylon 11-12 salt was prepared using 1,10-dodecanedicarboxylic acid (12) and 1,11-undecanediamine (11) in ethanol at 40 °C. The obtained polymer was reprecipitated with a mixture of HFIP and acetone and dried at 100 °C for 24 h. The melting point of nylon 11-12 was 189 °C.
Sample preparation
Nylons 6-12, 10-12, 11-12, and 12-12 were dissolved in HFIP to prepare 0.5 wt% nylon HFIP solutions for the ferroelectric measurements. The nylon HFIP solutions were spin-coated at 4000 rpm for 30 s onto 3 × 3 cm2 glass substrates deposited with 5 mm φ aluminium bottom electrodes. The obtained spin-coated sample film was then dried at 100 °C for 24 h in vacuo. Nylons 6-12, 10-12, 11-12, and 12-12 were dissolved in HFIP to prepare 1 wt% nylon HFIP solutions for X-ray diffraction measurements. The nylon solutions were cast on 3 × 3 cm2 silicon wafers substrate. The obtained cast film was dried at 100 °C for 24 h in vacuo.The dried samples were melted at 250 °C to obtain the melted and quenched (MQ) nylon samples; after keeping at melted state for 10 min, these samples were immediately quenched in ice water. Annealed samples were obtained by annealing MQ samples at 175 °C for 2 h. After annealing, these samples were quenched in ice water (denoted as AQ). Finally, a 5 mm φ aluminium top electrode was deposited on the four obtained types of nylon samples to measure the ferroelectric response. The photograph of the sample device is shown in Fig. 1.
Instrumentation and characterization
A ferroelectric measurement system (FCE-1/1A, Toyo Corporation, Japan) was used to measure the polarization current–electric field (I–E) and the polarization–electric field (P–E) hysteresis loops. The applied voltage and frequency ranges were 8–18 V and 100 Hz–10 kHz, respectively. At high temperature measurements, the nylon samples were immersed in fluorinert FC-43 (3M Japan Ltd., Japan) to avoid dielectric breakdown.The poling current J(t) obtained by hysteresis measurement was expressed by the equation of
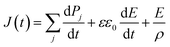 | (1) |
A differential scanning calorimetry (DSC) (Q2000, TA instruments, USA) was used to record the glass-transition temperature (Tg) and the melting temperature (Tm) of nylons at a scanning rate of 10 °C min−1 and a scanning range from 25 to 300 °C.
A MiniFlex600 (Rigaku, Japan) was used to perform the θ–2θ scan of WAXD. The X-ray diffractometer was also used as a Cu Kα radiation source of 0.154 nm operating at 40 kV and 50 mA.
The thickness of the thin film was determined using an atomic force microscope (AFM) (Nano-R, Pacific Technology, USA). All measurements were performed in ambient condition.
Results and discussion
Characterization
The obtained nylons were investigated by ATR-IR and differential scanning calorimetry (DSC). Fig. 2(a) shows the ATR-IR spectra for the polymerized nylons 6-12, 10-12, 11-12, and 12-12. All samples exhibited the identified absorption bands of the amide groups and methylene segments, and there were no obvious differences compared with various nylon samples.25,31,32 The absorption bands at approximately 1630 cm−1 and 1530 cm−1 originate from the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch (amide I) and the N–H stretch (amide II), respectively. The C–CO stretch (amide IV), the N–H out-of-plane bend (amide V), and the C
O stretch (amide I) and the N–H stretch (amide II), respectively. The C–CO stretch (amide IV), the N–H out-of-plane bend (amide V), and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O out-of-plane bend (amide VI) are also observed at approximately 940 cm−1, 690 cm−1, and 580 cm−1, respectively. The methylene segment bands that contributed to the CH2 bending band and the CH2 wagging band were measured at approximately 1460 cm−1, 1420 cm−1, and 720 cm−1, respectively. The temperature Tm of the polymerized nylon samples is shown in Fig. 2(b). The Tm gradually decreased as the methylene segments increased, and these obtained Tm values corresponded to the data in previous reports.33–36 From these characterization results, it was clear that the objective even–even-numbered and odd–even-numbered nylon were synthesized successfully.
O out-of-plane bend (amide VI) are also observed at approximately 940 cm−1, 690 cm−1, and 580 cm−1, respectively. The methylene segment bands that contributed to the CH2 bending band and the CH2 wagging band were measured at approximately 1460 cm−1, 1420 cm−1, and 720 cm−1, respectively. The temperature Tm of the polymerized nylon samples is shown in Fig. 2(b). The Tm gradually decreased as the methylene segments increased, and these obtained Tm values corresponded to the data in previous reports.33–36 From these characterization results, it was clear that the objective even–even-numbered and odd–even-numbered nylon were synthesized successfully.
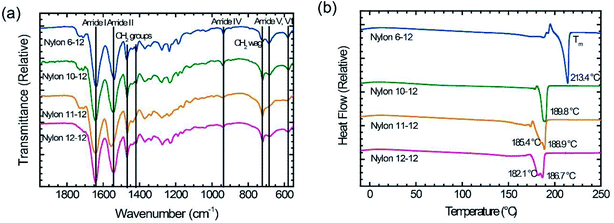 | ||
| Fig. 2 (a) ATR-IR spectra and (b) DSC thermograms for nylon 6-12, nylon 10-12, nylon 11-12, and nylon 12-12 sample films. | ||
Thermal properties
Fig. 3 displays DSC thermogram of MQ and AQ samples. For all samples, the glass transition temperature Tg is clearly observed in the vicinity of 40 °C, and the melting temperature Tm is also clearly measured between 180 and 215 °C. It was observed that the Tm decreases as the number of methylene units in the diamine group increases.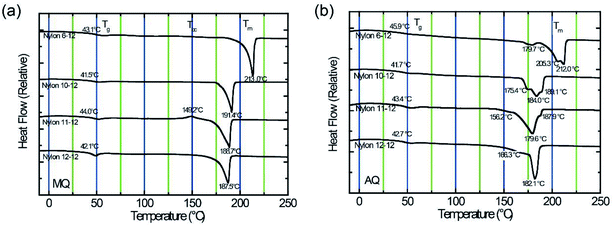 | ||
| Fig. 3 DSC thermograms for nylon 6-12, nylon 10-12, nylon 11-12, and nylon 12-12 sample films. (a) Thermograms for MQ samples. (b) Thermograms for AQ samples. | ||
The MQ samples show a single peak, as shown in Fig. 3(a), whereas the AQ samples exhibit multiple melting peaks, as shown in Fig. 3(b). These peaks can be ascribed to the melting of unstable crystals at lower temperatures, followed by the melting of stable crystals at higher temperatures.37–39
Crystal structures
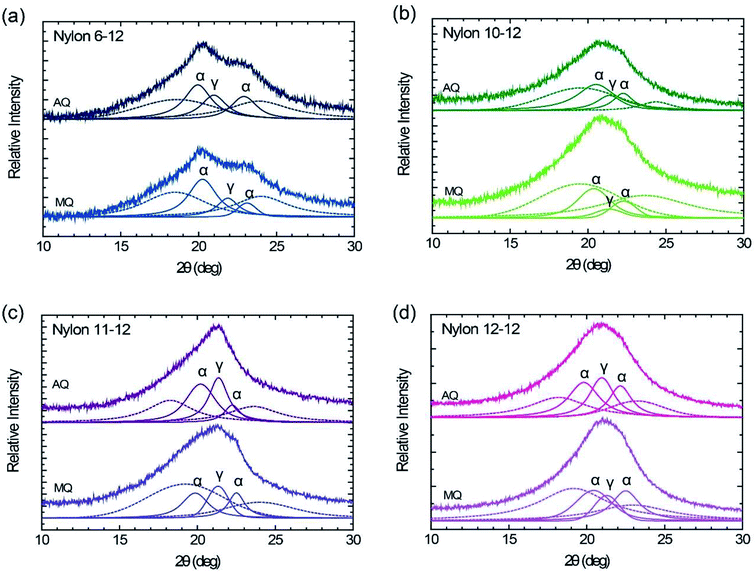
WAXD patterns of the MQ and AQ samples for nylons 6-12, 10-12, 11-12, and 12-12 are shown in Fig. 4. The cast film with thickness of ca. 20 μm was used for the WAXD measurements. The MQ sample of nylon 6-12 exhibits two peaks at 2θ = 20.3° and 2θ = 23.1°, assigned to the reflection of (100) and (010, 110) planes based on the triclinic α crystal form, which represent the inter chain sheet and the hydrogen bonded sheet, respectively.40 Additionally, the pseudohexagonal γ crystal form peak also appears at 2θ = 21.9°.40,41 In the other MQ samples, nylons 10-12, 11-12, and 12-12, the α crystal form peaks, at 2θ = 19.9–20.4°and 2θ = 22.3–22.5°, and the pseudohexagonal γ crystal form peak, at 2θ = 21.3–21.4°, were measured.35,38,42–44 The diffraction angle, the lattice spacing, the crystallite size, and the crystallinity (degree of crystallization) are summarized in Table 1. As shown in Table 1, larger crystallite size was grown by annealing in nylons 10-12, 11-12, and 12-12, but not in nylon 6-12. We fixed the annealing temperature at 175 °C for 2 h for all samples. Melting point is 213 °C for nylon 6-12, 191.4 °C for nylon 10-12, 188.7 °C for nylon 11-12, and 187.5 °C for nylon 12-12 as shown in Fig. 3(a). The difference between melting point and annealing temperature is 38 °C for nylon 6-12, 16.4 °C for nylon 10-12, 13.7 °C for nylon 11-12, and 12.5 °C for nylon 12-12. Crystallite size depends on the annealing temperature how it closes to the melting point and thus the molecular motion of polymer chains. This is the reason why crystallite size for nylon 6-12 AQ sample is smaller than that for MQ sample.| Sample | Crystal form | Peak (°) | Lattice spacing (nm) | Crystallite size (nm) | Crystallinity (%) | ||||
|---|---|---|---|---|---|---|---|---|---|
| MQ | Nylon 6-12 | α | 20.3 | 23.1 | 0.44 | 0.38 | 3.90 | 5.91 | 30.0 |
| γ | 21.9 | 0.41 | 5.04 | 10.2 | |||||
| Nylon 10-12 | α | 20.4 | 22.3 | 0.44 | 0.40 | 3.32 | 4.37 | 22.5 | |
| γ | 21.4 | 0.42 | 3.98 | 4.0 | |||||
| Nylon 11-12 | α | 19.9 | 22.5 | 0.45 | 0.40 | 4.23 | 6.68 | 24.5 | |
| γ | 21.3 | 0.42 | 5.31 | 11.4 | |||||
| Nylon 12-12 | α | 20.4 | 22.5 | 0.43 | 0.40 | 3.06 | 4.00 | 30.7 | |
| γ | 21.3 | 0.42 | 4.49 | 7.6 | |||||
| AQ | Nylon 6-12 | α | 19.9 | 22.9 | 0.45 | 0.39 | 3.97 | 4.33 | 34.2 |
| γ | 21.0 | 0.42 | 4.26 | 14.2 | |||||
| Nylon 10-12 | α | 20.5 | 22.3 | 0.43 | 0.40 | 2.85 | 5.37 | 41.1 | |
| γ | 21.4 | 0.42 | 4.26 | 14.0 | |||||
| Nylon 11-12 | α | 20.2 | 22.2 | 0.44 | 0.40 | 3.76 | 6.86 | 32.6 | |
| γ | 21.4 | 0.42 | 5.72 | 21.3 | |||||
| Nylon 12-12 | α | 19.8 | 22.2 | 0.45 | 0.40 | 3.56 | 4.87 | 38.7 | |
| γ | 21.0 | 0.42 | 4.54 | 20.0 | |||||
In all AQ samples, similar to those of the MQ samples, the two peaks assigned to the reflection of (100) and (010, 110) planes based on the triclinic α crystal form and the broad peak based on the pseudohexagonal γ crystal form are apparent. On the one hand, the crystallinity of the AQ samples is larger than that of the MQ samples, but on the other hand, the crystallite size of the AQ sample does not grow much larger than that of the MQ sample. It is speculated that this phenomena caused by growing unstable crystal and the slow crystal growth close to the melting point. In fact, melting peaks due to the unstable crystal were confirmed as shown in Fig. 3(b), and the annealing treatment was performed at a temperature close to the melting point as shown in Fig. 2(b).
Ferroelectric responses
The thickness of the spin-coated thin film ranges from 47 to 68 nm, as listed in Table 2. The I–E and P–E hysteresis loops were measured by applying a sinusoidal electric field with voltage ranging from 8 to 18 V with a frequency of 1 kHz. The ferroelectric switching of the MQ and the AQ samples are shown in Fig. 5 and 6, respectively, and the Pr and Ec of all nylon samples are summarized in Table 2. As shown in Fig. 5, Pr and Ec increase with increasing applied voltage. Additionally, it is clearly shown that Pr = 4.3 mC m−2 for the nylon 11-12 MQ sample, which is larger than those of the even–even-numbered nylons. The degree of crystallization of the nylon 11-12 MQ sample originated from the γ crystal form was 11.4%, which is larger than that of nylons 6-12, 10-12, or 12-12 as shown in Table 1. As a result, the nylon 11-12 MQ sample shows the largest Pr value of all MQ samples. Odd–even nylons such as the nylon 11-12 have repeated parallel dipole moment and antiparallel dipole moment derived from amide groups unlike even–even nylons. Therefore, the crystallization of the nylon 11-12 MQ samples was highest. Furthermore, it is noted that the P–E hysteresis loops of the nylon 12-12 MQ sample in Fig. 5(h), the nylon 6-12 AQ sample at lower voltage of 8, 10 and 12 V in Fig. 6(b), and the nylon 12-12 AQ sample at voltage of 14 V in Fig. 6(h) are asymmetric with respect to the E-axis. This may be related to the charge injection from the electrode which will cause the localized space charge field in the bulk. The polar crystal and the noncentrosymmetrically assembled polar crystal are commonly understood as the key to the appearance of ferroelectricity. Namely, the parallel packing of the polar crystal is believed to be essential for ferroelectricity. Thus, a large number of studies on ferroelectric nylons have focused on odd-numbered nylons, such as nylons 5, 7, 9, and 11, and on odd–odd-numbered nylons, such as nylon 11-11, because the preferential parallel alignment of the polar amide group along the molecular chains in odd-numbered and odd–odd-numbered nylons contributes to the ferroelectricity. However, recent ferroelectric studies of nylon 12 (ref. 24–26) give the straight question whether the odd number of methylene chains in the nylon polymer is essential for ferroelectricity or not. Even-numbered, even–even-numbered, and odd–even-numbered nylons possess anti-parallel packing of the polar amide groups along the molecular chains in the crystals, which causes a cancellation of the net polarization. Thus, these even-numbered nylons have been expected to be nonferroelectric.16 In the even-numbered nylons, the triclinic α crystal form is a stable crystalline phase with strongly anti-parallel hydrogen bonding sheets; therefore, no ferroelectricity could be observed for the α crystal form. However, in recent studies, the pseudohexagonal γ crystal form is a metastable crystalline phase with a twisted chain conformation and weakened hydrogen bonds, which enables electric-field-induced ferroelectricity.24–26 From this discussion, the observed ferroelectric switching of the MQ even–even-numbered and odd–even-numbered nylon samples seemed to be caused by the polarization of the γ crystal form.| Sample | MQ | AQ | ||||
|---|---|---|---|---|---|---|
| Film thickness (nm) | Pr (mC m−2) | Ec (mV m−1) | Film thickness (nm) | Pr (mC m−2) | Ec (mV m−1) | |
| Nylon 6-12 | 51 | 3.7 | 74 | 54 | 3.0 | 141 |
| Nylon 10-12 | 55 | 1.3 | 101 | 47 | 2.6 | 140 |
| Nylon 11-12 | 58 | 4.3 | 132 | 68 | 4.8 | 112 |
| Nylon 12-12 | 59 | 3.0 | 100 | 48 | 3.9 | 128 |
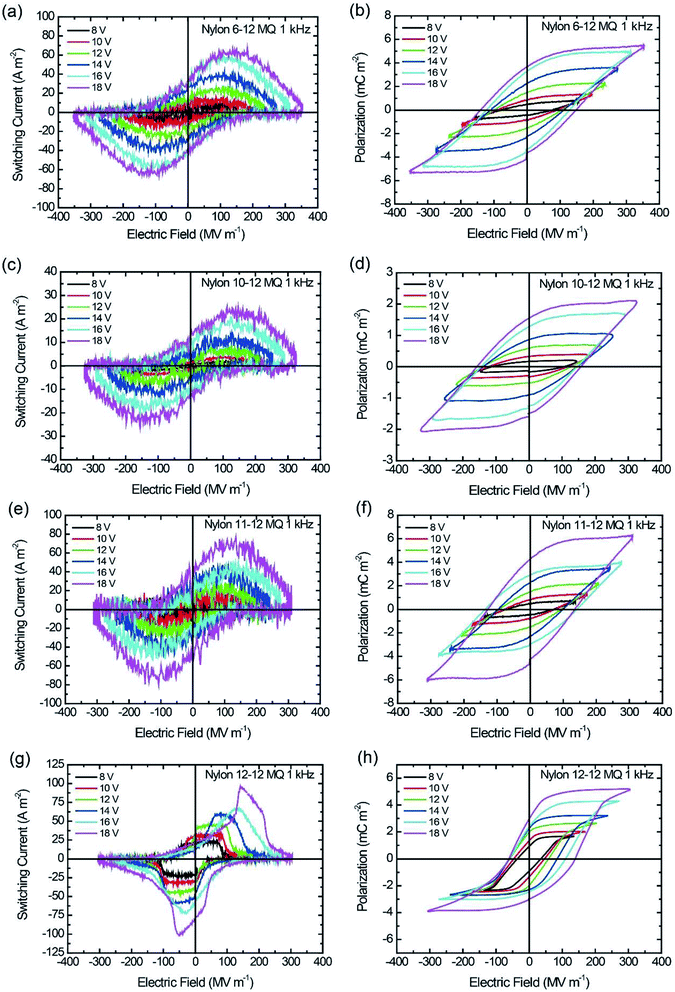 | ||
| Fig. 5 I–E and P–E hysteresis loop for MQ samples at 1 kHz switching. (a and b) Nylon 6-12, (c and d) nylon 10-12, (e and f) nylon 11-12, and (g and h) nylon 12-12. | ||
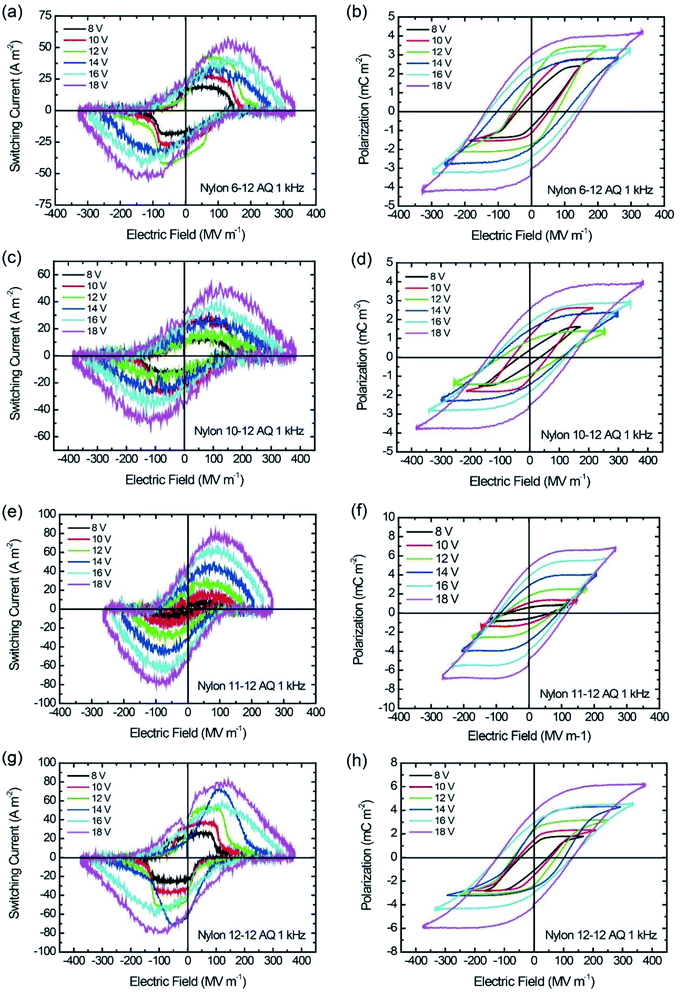 | ||
| Fig. 6 I–E and P–E hysteresis loop for AQ samples at 1 kHz switching. (a and b) Nylon 6-12, (c and d) nylon 10-12, (e and f) nylon 11-12, and (g and h) nylon 12-12. | ||
Similar to the MQ samples, the Pr and Ec for the AQ samples increase as the applied electric field increases in the P–E hysteresis loops, as shown in Fig. 6. The nylon 11-12 AQ sample also exhibited the largest Pr value of 4.8 mC m−2 because it had the highest crystallinity in the γ crystal form.
Fig. 7(a) gave the plots of Pr value with increasing the crystallinity of the γ crystal for the MQ and AQ samples. For both the MQ and AQ samples, a positive correlation is shown between the crystallinity and Pr value. Higher crystallinity is related to larger Pr values. However, the Pr values for the AQ samples are slightly higher than those for the MQ samples, even though the crystallinity of the AQ samples is considerably higher than that of the MQ samples. The crystallite size dependence of the Pr values were also shown with increasing the γ crystal for the MQ and AQ samples in Fig. 7(b). For both the MQ and AQ samples, a positive correlation is shown between the crystallite size and Pr value. A larger crystallite size is related to a larger Pr value. Although the crystallite size of the AQ samples is not much different from the size of the MQ samples, the Pr values of the AQ samples are higher than those of the MQ samples for nylons 10-12, 11-12, and 12-12 but not for nylon 6-12. This is because of the higher crystallinity of the AQ samples than that of the MQ samples.
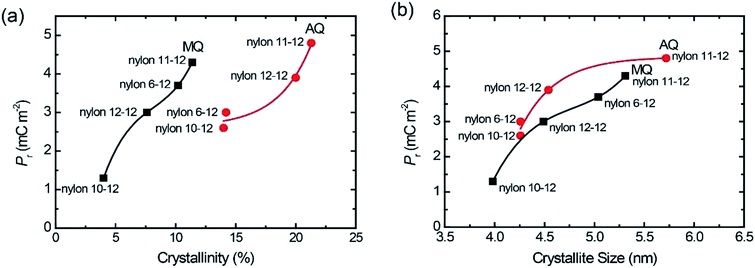 | ||
| Fig. 7 Pr plots with increasing crystallinity (a) and crystallite size (b) for both AQ and MQ samples. | ||
The theoretical Pr value, when all of the amide group dipole moments freely contribute to the net polarization reversal, is calculated with the following equation,
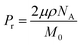 | (2) |
| Sample | M0 (g mol−1) | ρ (g cm−3) | Pr (mC m−2) |
|---|---|---|---|
| Nylon 6-12 | 310.5 | 1.14 | 53.1 |
| Nylon 10-12 | 366.6 | 1.11 | 43.6 |
| Nylon 11-12 | 380.6 | 1.10 | 41.8 |
| Nylon 12-12 | 394.6 | 1.10 | 40.1 |
The Pr values measured for both the MQ and AQ samples are considerably smaller than the theoretical values shown in Table 3. This is because of the lower crystallinity and smaller crystallite size of the γ crystal for the MQ and AQ samples. Furthermore, the intermolecular hydrogen bond and the free volume in the samples are also significantly related to the measured Pr values. Strong hydrogen bonds significantly restrict the ferroelectric switching of polar dipoles. The Pr values measured for the AQ samples are comparable to or slightly higher than those for the MQ samples, even though the crystallinity of the γ crystals for the AQ samples is much higher than that for the MQ samples. This is because of the suppression of dipole rotation due to the tight intermolecular hydrogen bonds between crystallites. Another parameter is the free volume in each sample. Here, we estimate the free volume for both the MQ and AQ samples. The free volume Vf of the nylon samples was derived from the obtained semicrystalline molar volume Vsc and the zero point molar volume V0. The Vf values were estimated from the following relationship,
| Vf = Vsc − V0 | (3) |
| Vsc = xcVc + (1 − xc)Va | (4) |
| V0 = 1.3Vw | (5) |
| Sample | V0 (cm3 mol−1) | MQ | AQ | ||
|---|---|---|---|---|---|
| Vsc (cm3 mol−1) | Vf (cm3 mol−1) | Vsc (cm3 mol−1) | Vf (cm3 mol−1) | ||
| Nylon 6-12 | 246.6 | 291.2 | 44.6 | 288.6 | 42.0 |
| Nylon 10-12 | 299.8 | 359.2 | 59.4 | 348.2 | 48.5 |
| Nylon 11-12 | 313.1 | 371.4 | 58.3 | 364.2 | 51.1 |
| Nylon 12-12 | 326.4 | 386.2 | 59.8 | 377.6 | 51.2 |
The temperature-dependent ferroelectric performance was also investigated. Fig. 8 shows the ferroelectric hysteresis loops of the MQ and the AQ samples of nylon 10-12 measured at 90 °C. Both P–E hysteresis loops are relatively narrow with a very small coercive field compared with those of the P–E hysteresis loops measured at room temperature, which are shown in Fig. 5(d) and 6(d). The corresponding loop responses in the I–E hysteresis loops are shown in Fig. 8(a) and (c). At a high temperature, rhombus-shaped loops were observed, whereas the I–E hysteresis loops at room temperature showed a simple reversal response, as shown in Fig. 5(c) and 6(c). These narrow P–E hysteresis loops and the rhombus-shaped I–E hysteresis loops prove the relaxor ferroelectricity-like behaviour of the nylon polymers. The relaxor ferroelectric phenomenon was caused by electrical rotation of the electric-field-induced nanodomains with weakened hydrogen bonds at a high temperature. The high-temperature treatment state and high electric field poling induced a more twisted chain in the nylon samples, weakening the hydrogen bonds.25
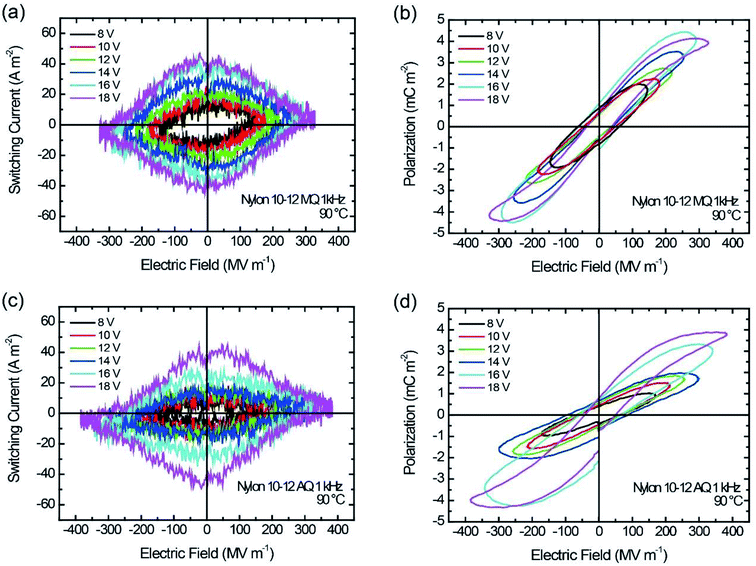 | ||
| Fig. 8 I–E and P–E hysteresis for nylon 10-12 samples at 90 °C. (a and b) MQ and (c and d) AQ. The sinusoidal frequency is 1 kHz. | ||
Conclusions
The ferroelectricity of spin-coated films of even–even-numbered nylons, including nylon 6-12, 10-12, and 12-12, and the odd–even-numbered nylon 11-12 was investigated. Nylon 11-12 exhibited a larger Pr value than that of the even–even-numbered nylons. Larger crystallinity and crystallite size corresponded to larger Pr values. However, the Pr values measured for both the MQ and AQ samples are considerably smaller than the theoretically expected values. Furthermore, the Pr values of the AQ samples are comparable to or slightly higher than those for the MQ samples, even though the crystallinity of the γ crystal of the AQ samples is much higher than that of the MQ samples. We considered that these behaviours correlate to the intermolecular hydrogen bonds and the free volume. Higher crystallinity enhances the ferroelectric properties, but simultaneously it introduces tight intermolecular hydrogen bonds which supresses the dipole rotation. Furthermore smaller free volume estimated for the AQ samples would induce less electrical rotation of the ferroelectric domains. Relaxor ferroelectric behaviours were also observed due to the electrical rotation of nanodomains with weakened hydrogen bonds at high temperature measurements. These ferroelectric even–even-numbered nylons and odd–even-numbered nylons show promise for use in electric energy storage applications.Conflicts of interest
The authors declare no competing financial interests.References
- Q. M. Zhang, V. Bharti and X. Zhao, Giant electrostriction and relaxor ferroelectric behavior in electron-irradiated poly(vinylidene fluoride-trifluoroethylene) copolymer, Science, 1998, 280, 2101–2104 CrossRef CAS PubMed.
- S. Das and J. Appenzeller, On the scaling behavior of organic ferroelectric copolymer PVDF-TrFE for memory application, Org. Electron., 2012, 13, 3326–3332 CrossRef CAS.
- L. Zhu, Exploring strategies for high dielectric constant and low loss polymer dielectrics, J. Phys. Chem. Lett., 2014, 5, 3677–3687 CrossRef CAS PubMed.
- Q. Chen, Y. Shen, S. Zhang and Q. M. Zhang, Polymer-based dielectrics with high energy storage density, Annu. Rev. Mater. Res., 2015, 45, 433–458 CrossRef CAS.
- T. Furukawa, M. Date and E. Fukuda, Hysteresis phenomena in polyvinylidene fluoride under high electric field, J. Appl. Phys., 1980, 51, 1135–1141 CrossRef CAS.
- S. Tasaka, T. Shouko and N. Inagaki, Ferroelectric polarization reversal in polyureas with odd number of CH2 groups, Jpn. J. Appl. Phys., 1992, 31, L1086–L1088 CrossRef CAS.
- T. Hattori, Y. Takahashi, M. Iijima and E. Fukada, Piezoelectric and ferroelectric properties of polyurea-5 thin films prepared by vapor deposition polymerization, J. Appl. Phys., 1996, 79, 1713–1721 CrossRef CAS.
- M. Poulsen, S. Ducharme, A. V. Sorokin, S. Reddy, J. M. Takacs, Y. Wen and J. Kim, Investigation of ferroelectricity in poly(methyl vinylidene cyanide), Ferroelectr., Lett. Sect., 2005, 32, 91–97 CrossRef CAS.
- Q. Y. Pan, S. Tasaka and N. Inagaki, Ferroelectric behavior in poly-L-lactic acid, Jpn. J. Appl. Phys., 1996, 35, L1442–L1445 CrossRef CAS.
- D. Katz and V. Gelfandbein, Ferroelectric behavior of α-nylon 11, J. Phys. D: Appl. Phys., 1982, 15, L115–L117 CrossRef CAS.
- H. S. Nalwa, Ferroelectric polymers, in Ferroelectric Polymers: Chemistry, Physics, and Applications, ed. H. S. Nalwa, Marcel Dekker, New York, 1995, Part 1, pp. 1–392 Search PubMed.
- R. Aljishi and P. L. Taylor, Equilibrium polarization and piezoelectric and pyroelectric coefficients in poly(vinylidene fluoride), J. Appl. Phys., 1985, 57, 902–905 CrossRef CAS.
- K. Tashiro, Crystal structure and phase transition of PVDF and related copolymers, in Ferroelectric Polymers: Chemistry, Physics, and Applications, ed. H. S. Nalwa, Marcel Dekker, New York, 1995, ch. 2, pp. 63–182 Search PubMed.
- L. Yang, B. A. Tyburski, F. Domingues Dos Santos, M. K. Endoh, T. Koga, D. Huang, Y. J. Wang and L. Zhu, Relaxor ferroelectric behavior from strong physical pinning in a poly(vinylidene fluoride-co-trifluoroethylene-co-chlorotrifluoroethylene) random terpolymer, Macromolecules, 2014, 47, 8119–8125 CrossRef CAS.
- C. R. Cantor and P. R. Schimmel, Biophysical Chemistry: 1. The Conformation of Biological Macromolecules, W.H. Freeman, San Francisco, 1980 Search PubMed.
- H. S. Nalwa, Ferroelectric nylons, in Ferroelectric Polymers: Chemistry, Physics, and Applications, ed. H. S. Nalwa, Marcel Dekker, New York, 1995, ch. 6, pp. 281–323 Search PubMed.
- E. W. Jacobs and J. C. Hicks, Electric-field induced morphological changes in nylon-11, Appl. Phys. Lett., 1984, 44, 402–403 CrossRef CAS.
- N. Tsutsumi and T. Yamaoka, Ferroelectric properties of ultrathin films of Nylon 11, Thin Solid Films, 2009, 518, 814–818 CrossRef CAS.
- J. I. Scheinbeim, J. W. Lee and B. A. Newman, Ferroelectric Polarization Mechanisms in Nylon 11, Macromolecules, 1992, 25, 3729–3732 CrossRef CAS.
- Y. Masuda, O. Achiwa, M. Inagaki, H. Hirosawa and S. Tasaka, Unique ferroelectricity and structure of nylon 39 induced by an electric field, Sen'i Gakkaishi, 2013, 69(3), 60–63 CrossRef.
- S. Liu, Z. Cui, P. Fu, M. Liu, L. Zhang, Z. Li and Q. Zhao, Ferroelectric behavior and polarization mechanism in odd-odd polyamide 11, 11, J. Polym. Sci., Part B: Polym. Phys., 2014, 52, 1094–1099 CrossRef CAS.
- S. Liu, Z. Cui, P. Fu, M. Liu, Y. Zhang, R. Jia and Q. Zhao, Piezoelectricity and ferroelectricity in odd-odd nylons with long alkane segments, Appl. Phys. Lett., 2014, 104, 172906–172909 CrossRef.
- N. Tsutsumi, N. Kajimoto, K. Kinashi and W. Sakai, Understanding ferroelectric performances of spin-coated odd-odd nylon thin films, J. Appl. Polym. Sci., 2019, 136, 47595 CrossRef.
- Z. Zhang, M. H. Litt and L. Zhu, Unified understanding of ferroelectricity in n-nylons: Is the polar crystalline structure a prerequisite?, Macromolecules, 2016, 49, 3070–3082 CrossRef CAS.
- Z. Zhang, M. H. Litt and L. Zhu, Understanding the paraelectric double hysteresis loop behavior in mesomorphic even-numbered nylons at high temperatures, Macromolecules, 2017, 50, 5816–5829 CrossRef CAS.
- A. Yanaka, W. Sakai, K. Kinashi and N. Tsutsumi, Ferroelectric switching in spin-coated nylons 11 and 12, J. Appl. Polym. Sci., 2020, 137, 48438 CrossRef CAS.
- Z. Zhang, M. H. Litt and L. Zhu, Achieving Relaxor Ferroelectric-like Behavior in Nylon Random Copolymers and Terpolymers, Macromolecules, 2017, 50, 9360–9372 CrossRef CAS.
- S. Anwar, B. Jeong, M. M. Abolhasani, W. Zajaczkowski, M. H. Amiri and K. Asadi, Polymer field-effect transistor memory based on a ferroelectric nylon gate insulator, J. Mater. Chem. C, 2020 10.1039/c9tc06868f.
- S. Anwar, D. Pinkal, W. Zajaczkowski, P. V. Tiedemann, H. S. Dehsari, M. Kumar, T. Lenz, U. Kemmer-Jonas, W. Pisula, M. Wagner, R. Graf, H. Frey and K. Asadi, Solution-processed transparent ferroelectric nylon thin films, Sci. Adv., 2019, 5, eaav3489 CrossRef PubMed.
- P. V. Tiedemann, S. Anwar, U. Kemmer-Jonas, K. Asadi and H. Frey, Synthesis and Solution Processing of Nylon-5 Ferroelectric Thin Films: The Renaissance of Odd-Nylons?, Macromol. Chem. Phys., 2020, 221, 1900468 CrossRef.
- Y. Huang, W. Li and D. Yan, Preparation and characterization of a series of polyamides with long alkylene segments: Nylons 12-20, 10-20, 8-20, 6-20, 4-20 and 2-20, Polym. Bull., 2002, 49, 111–118 CrossRef CAS.
- X. Cui, Z. Liu and D. Yan, Synthesis and characterization of novel even–odd nylons based on undecanedioic acid, Eur. Polym. J., 2004, 40, 1111–1118 CrossRef CAS.
- N. A. Jones, E. D. T. Atkins, M. J. Hill, S. J. Cooper and L. Franco, Chain-folded lamellar crystals of aliphatic polyamides. Investigation of nylons 4-8, 4-10, 4-12, 6-10, 6-12, 6-18 and 8-12, Polymer, 1997, 38, 2689–2699 CrossRef CAS.
- N. A. Jones, E. D. T. Atkins, M. J. Hill, S. J. Cooper and L. Franco, Polyamides with a Choice of Structure and Crystal Surface Chemistry. Studies of Chain-Folded Lamellae of Nylons 8-10 and 10-12 and Comparison with the Other 2N 2(N + 1) Nylons 4-6 and 6-8, Macromolecules, 1997, 30, 3569–3578 CrossRef CAS.
- X. Cui and D. Yan, Preparation, characterization and crystalline transitions of odd–even polyamides 11, 12 and 11, 10, Eur. Polym. J., 2005, 41, 863–870 CrossRef CAS.
- N. A. Jones, E. D. T. Atkins and M. J. Hill, Investigation of Solution-Grown, Chain-Folded Lamellar Crystals of the Even-Even Nylons: 6-6, 8-6, 8-8, 10-6, 10-8, 10-10, 12-6, 12-8, 12-10, and 12-12, J. Polym. Sci., Part B: Polym. Phys., 2000, 38, 1209–1221 CrossRef CAS.
- M. Liu, Q. Zhao, Y. Wang, C. Zhang, Z. Mo and S. Cao, Melting behaviors, isothermal and non-isothermal crystallization kinetics of nylon 12-12, Polymer, 2003, 44, 2537–2545 CrossRef CAS.
- Y. Li, X. Zhu, G. Tian, D. Yan and E. Zhou, Multiple melting endotherms in melt-crystallized nylon 10, 12, Polym. Int., 2001, 50, 677–682 CrossRef CAS.
- L. Franco and J. Puiggali, Structural data and thermal studies on nylon-12, 10, J. Polym. Sci., Part B: Polym. Phys., 1995, 33, 2065–2073 CrossRef CAS.
- C. Ramesh, New crystalline transitions in Nylons 4-6, 6-10, and 6-12 using high temperature X-ray diffraction studies, Macromolecules, 1999, 32, 3721–3726 CrossRef CAS.
- H.-J. Biangardi, Brill transition of polyamide 6-12, J. Macromol. Sci., Part B: Phys., 1990, 29, 139–153 CrossRef.
- D. Yan, Y. Li and X. Zhu, Brill transition in Nylon 10-12 investigated by variable temperature XRD and real time FT-IR, Macromol. Rapid Commun., 2000, 21, 1040–1043 CrossRef CAS.
- Y. Li, D. Yan and E. Zhou, In situ Fourier transform IR spectroscopy and variable-temperature wide-angle X-ray diffraction studies on the crystalline transformation of melt-crystallized nylon 12-12, Colloid Polym. Sci., 2002, 280, 124–129 CrossRef CAS.
- Y. Li, D. Yan and X. Zhu, Crystal forms of nylon 10-12 crystallized from melt and after solution casting, Eur. Polym. J., 2001, 37, 1849–1853 CrossRef CAS.
- D. W. van Krevelen, in Property of Polymers, Elsevier, Amsterdam, 1990, ch. 4, pp. 71–88 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |