Open Access Article
Open Access ArticleHexahydrofarnesyl as an original bio-sourced alkyl chain for the preparation of glycosides surfactants with enhanced physicochemical properties†
Guillaume Lemahieua,
Julie Aguilhon*b,
Henri Strubb,
Valérie Molinier*c,
Jesús F. Ontiverosa and
Jean-Marie Aubry *a
*a
aUniv. Lille, CNRS, Centrale Lille, ENSCL, Univ. Artois, UCCS – Unité de Catalyse et Chimie du Solide, UMR 8181, F-59000 Lille, France. E-mail: jean-marie.aubry@univ-lille.fr
bTotal Raffinage Chimie, Biofuels Division, Tour Coupole, 2 Place Jean Millier, 92400 Courbevoie, France. E-mail: julie.aguilhon@total.com
cTotal Exploration Production, Pôle d’Etudes et de Recherche de Lacq, B. P. 47, 64170 Lacq, France. E-mail: valerie.molinier@total.com
First published on 24th April 2020
Abstract
Five new bio-based surfactants have been synthetized by coupling hexahydrofarnesol with mono and di-saccharides. Hexahydrofarnesol (3,7,11-trimethyl-dodecan-1-ol) is a by-product of the industrial production of farnesane, a sustainable aviation fuel obtained by a fermentation process from sugar feedstocks. Using hexahydrofarnesol as the lipophilic starting material allows obtaining 100% bio-based surfactants while valorizing an industrial by-product. Moreover, the C15-branched alkyl chain brings unique properties to the surfactants. This paper presents a physicochemical characterization of these new surfactants including their behaviors in water (water solubility, critical micellar concentration and surface tension) and in oil/water systems (interfacial tension against model oil and ternary phase behavior). Their hydrophilicities have been determined thanks to the PIT-slope method and compared to the ones of standard surfactants with linear alkyl chains, in order to distinguish the contributions of the sugar polar heads and of the branched hexahydrofarnesyl lipophilic chain. This novel class of surfactants combines the properties of sugar-based surfactants (low sensitivity to temperature and salinity, ability to form Winsor III microemulsion systems over a wide range of salinity), along with specificities linked to the branched alkyl chain (lower Krafft temperature, low surface tension).
1 Introduction
Alkyl-polyglucosides (APG) were the first surfactants derived from sugars synthetized as early as in 1933.1–3 The first application of these surfactants came 40 years later in the field of detergency and was given up due to the relative high production cost compared to the existing polyethoxylated non-ionic surfactants. In the middle of the 80s, valorization strategies for agricultural resources and the awareness of the environmental footprint of chemicals led to a renewed interest in this class of surfactants.4 Since the beginning of the 90s, several companies have produced and used their own APG such as Kao Corp.,5 Hüls6 and Henkel.7 Nowadays, APG are used not only in detergency but also in various applications fields such as pharmaceutical production or agricultural formulations due to their high compatibility with human skin and body as well as their low impact on the environment.8 Their higher foaming and dispersing properties9,10 are also assets that motivate the replacement of polyethoxylated non-ionic surfactants classically used.11 Indeed, due to regulation evolution regarding polyethoxylated surfactants and their replacement in some markets, lots of academic and industrial researches are focused on the development of APG and other sugar-based surfactants as alternatives.Sugar-based surfactants have also proved to be effective dispersing agents in case of oil spills.12 They can also be used as non-ionic co-surfactants in association with anionic surfactants, to achieve WIII microemulsion systems by decreasing the interfacial tension between oil and water to ultralow values (around 10−3 mN m−1).13 This is of particular interest for Enhanced Oil Recovery (EOR) applications. Interestingly, APG are able to form WIII microemulsion systems in high salinity and high temperature conditions14,15 and can be used to generate low interfacial tension systems that are largely independent of both salinity and temperature, contrarily to polyethoxylated surfactants classically used.16
The structure of the sugar-based surfactant itself is an important parameter to play with for adjusting the affinity for both oil and water phases. In that way, QSPR models can be useful tools to design tailored surfactants.17 The diversity of available sugars and the multiplicity of the substitution positions make it possible to adjust the polarity of the head.18 Regarding the lipophilic tail, bio-based hydrophobic components generally come from acids or alcohols derived from vegetable or fat oils. They are usually obtained as mixtures of linear chains with an even number of carbons. Petro-based alcohols generally have medium to highly branched alkyl chains, obtained through oligomerization of alkenes (“oxo”-type) or by Guerbet reaction. Both the length and the ramification of the chain play an important role on the physicochemical properties of the final surfactant.19 For instance, it is known that the ramification of the chain promotes the formation of WIII microemulsion systems by bringing more disorder in the interfacial film.20,21 Having in hands a well-defined bio-based branched alcohol is valuable for studying structure–properties relationship and envisaging innovative and 100% bio-based surfactants.
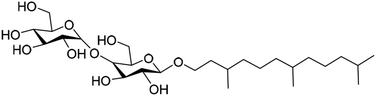
In this context, five well-defined starting sugars have been combined with hexahydrofarnesol (HHF, 3,7,11-trimethyl-dodecan-1-ol) (Table 1). HHF is a by-product of the industrial production of farnesane (2,6,10-trimethyldodecane), a sustainable aviation fuel that can be used as a “drop-in” product blended with traditional petroleum-derived jet.22 Farnesane is itself obtained by hydrogenation of farnesene, a sesquiterpene obtained from sugar feedstocks by biotechnological processes. During this fermentation, farnesol is obtained as a side product, and converted into HHF in the hydrogenation process. As HHF is recovered in the heavy fraction during the distillation of farnesane, it can be considered as a by-product. Coupling HHF with sugars is a smart way to valorize this by-product into potentially efficient and innovative 100% bio-sourced sugar surfactants.
2 Material and methods
2.1. Chemicals
Hexahydrofarnesol was isolated during the distillation of farnesane, which was prepared by hydrogenation of farnesene.23,24 Farnesene was obtained from Amyris.The hexahydrofarnesyl glycoside samples were prepared externally by coupling hexahydrofarnesol with arabinose, xylose, glucose, mannose and maltose.
Alkyl monoglycosides HHFA, HHFX, HHFG and HHFMan were prepared by direct Fisher glycosylation starting from the corresponding commercial anhydrous sugars. The sugars were dispersed in a large excess of HHF (100 mL/10 g sugar) under acidic catalysis (H2SO4 – 2% mol) and under vacuum (10 mbar) at 105 °C. At the end of the reaction, the samples obtained have been purified by silica gel chromatography with an elution of 100% dichloromethane followed by 100% ethyl acetate. The chemical pathway is exemplified in Scheme 1 for HHFA.
 | ||
| Scheme 1 Synthetic pathway and purification procedure for the preparation of hexahydrofarnesyl monoglycosides HHFA, HHFX, HHFG and HHFMan (exemplified with HHFA). | ||
HHFMalt was synthetized from the commercial peracetylated maltose. Glycosylation proceeded by activation of the anomeric position thanks to BF3EtO2, followed by deprotection in a methanolic solution, as displayed in Scheme 2. HHFMalt has been purified by silica gel chromatography with an elution of ethyl acetate and methanol.
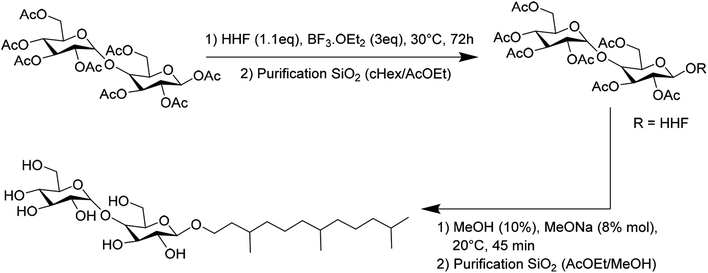 | ||
| Scheme 2 Synthetic pathway and purification for the preparation of hexahydrofarnesyl maltoside HHFMalt. | ||
Each purified sample was dried under vacuum (0.5 mbar) in the presence of P2O5 to remove all solvent contaminants. The final samples have been characterized by HPLC-MS, 1H and 13C NMR (Fig. 1–20 in ESI†) and exhibit a purity higher than 95%, as determined by 1H NMR. Table 2 recaps the isolated yields and purities of the samples. For HHFA (Fig. 1 and 2 in ESI†), two peaks with the same mass have been detected by HPLC-MS and correspond to the mixture of pyranose and furanose forms in the ratio 23/77.
| Surfactant | Isolated yield (%) | Retention time (min) | Purity (%) determined by 1H NMR |
|---|---|---|---|
| HHFA | 22 | 4.4 (23%) and 4.9 (77%) | >95 |
| HHFX | 46 | 4.7 | >95 |
| HHFG | 33 | 3.1 | >95 |
| HHFMan | 37 | 3.7 | >95 |
| HHFMalt | 25 | 2.2 | >95 |
The samples were used as received without further purification. At room temperature, they are either viscous liquids (HHFX), gelatinous solids (HHFG, HHFMan) or sticky powders (HHFA, HHFMalt).
For comparison, an APG surfactant from Seppic (Simulsol SL26C) was used. It is a C10–16-polyglucoside, with a polymerisation degree of 1.3 and an active content of 50.7 % wt. The pure n-alkyl-β-D-glucosides (C8, C10 and C12) and n-alkyl-β-D-maltosides (C10, C12, C14 and C16) used to characterize the HHF lipophilic tail with the PIT-slope method were provided by Sigma Aldrich with a high degree of purity (≥99%). The C10E4 reference surfactant used in the PIT-slope method was synthetized and distilled in the lab to obtain an ultra-pure sample.25
2.2. Aqueous solubilization
For estimating the aqueous solubility of the samples, 1% wt, 0.1% wt and 0.01% wt solutions were prepared in deionized or salted aqueous media. For homogenization, the samples were vigorously stirred with a magnetic stirrer in a water bath at 50 °C for approximately 3 hours, and then left at 50 °C during 15 hours in an oven.For the 1% wt and 0.1% wt samples, the solubility was visually inspected at 50 °C, and then after 15 hours at room temperature and at 83 °C. For the 0.01% wt samples, the solubility was visually inspected at room temperature, and after 15 hours at 65.5 °C and 83 °C.
For determining aqueous solubility limits of HHFA, HHFX, HHFG and HHFMan samples, the 0.01% wt solutions were filtered on 0.2 μm pore size syringe filter (Pall Corporation, Acrodisc PF syringe filters, diameter 0.8 cm/0.2 μm) two consecutive times at room temperature. The filtrate was dosed by HPLC/MS, thanks to a calibration line established beforehand on a 5–100 ppm scale.
2.3. Superficial and interfacial tension
Superficial and interfacial tensions were measured along time by drop shape analysis in the rising drop mode on a Tracker instrument from Teclis®. Measurements were performed at room temperature (20 ± 2) °C. The bubble/drop volume was maintained constant during the measurement and was set between 5 and 8 μL. Superficial tensions were measured at various concentrations for each sample. The surface tension at equilibrium recorded for each solution allowed plotting γ = f(C) to workout CMC values. For HHFMalt, 0.01% wt, 0.005% wt and 0.0025% wt stock solutions were prepared. First, the surface tension of deionized water was measured, and then the concentration of the solution was gradually increased by dilution with stock solutions. For HHFA, HHFX, HHFG and HHFMan, the same procedure was followed. The stock solutions were filtered on 0.2 μm filter. For these samples, fewer points were measured because of long equilibration times and of some instability during measurements. Therefore, only CMC ranges are given.Interfacial tensions were measured at solubility limit for HHFA, HHFX, HHFG, and HHFMan, and at 0.01% wt for HHFMalt against n-octane (Acros Organics, >95%).
The superficial and interfacial tensions are given with an error of ±0.5 mN m−1.
2.4. PIT-slope characterization
The amphiphilicity of the different sugar-based surfactants was determined according to the PIT-slope method already published.26,27The Phase Inversion Temperature (PIT) can be precisely determined and expresses the amphiphilicity of the surfactant in its environment, including the contributions of oil hydrophobicity and water salinity. However, the PIT cannot always be determined directly, that is why, in order to characterize all types of surfactants, it is more convenient to measure the PIT variation induced by adding increasing amounts of the surfactant under study to a well-defined SOW reference system. The reference system used is 3%C10E4/n-octane/10−2 M NaClaq because it shows a reproducible PIT close to room temperature (23.9 °C).28
To clearly identify the amphiphilicity of the surfactant under study, the variation of the PIT must be represented as a function of its molar fraction compared to the C10E4 reference surfactant as detailed below. The error on PIT-slope characterization is less than 10% in average.27
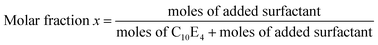 | (1) |
2.5. Ternary phase diagram behavior
Alternatively, a qualitative tool to estimate the surfactant affinity for oil or water in any Surfactant–Oil–Water (SOW) system was proposed by Winsor29 with the so-called R-ratio. R > 1 (respectively R < 1) indicates a surfactant affinity for oil (respectively water), R = 1 when the surfactant affinity is the same for oil and water. The different values of R correspond to different equilibrium behaviors for the SOW systems, named Winsor I (O/W microemulsion in equilibrium with excess oil), Winsor II (W/O microemulsion in equilibrium with excess water) and WIII (bicontinuous microemulsion with excess oil and water). The R-ratio was later extended to take into account all interactions occurring at the O/W interface20 that drive the affinity towards water or oil.The so-called “Optimum Formulation” is when the surfactant affinities for oil and water are the same (R = 1), corresponding to a Winsor III system in which the same amounts of oil and water are solubilized in the middle-phase microemulsion. In practice, the optimum formulation is located by performing salinity scans which varying the salinity and keeping all other parameters constant. To compare the hydrophilic/lipophilic balances of surfactants, one way is to determine their optimal salinities in a given O/W system. The higher the optimal salinity is, the more hydrophilic the surfactant is.
In this study, n-octane was chosen as oil to perform a salinity scan by varying the NaCl concentration with various systems composed of 1.8% surfactant and 2.7% 1-BuOH as co-surfactant at 50 °C and water–oil ratio (WOR) equal to 1. The surfactants were dissolved in 1-BuOH and diluted in deionized water. Once all components were introduced into the pipette, they were sealed under a nitrogen flow and placed at 50 °C for 10 minutes. They were then mixed three times at first and again after 1 h, 2 h and one night of equilibration at 50 °C. Observations of phase behavior were made after complete stabilization.
3 Results and discussion
3.1. Amphiphilic properties in aqueous systems
The diglycoside HHFMalt is soluble in water at 0.1% wt, from room temperature to 83 °C. This means that no clouding phenomenon occurs in this temperature range. On the other hand, a 0.1% wt solution left during 3 days at 4 °C does not precipitate, which means that no Krafft temperature exists down to 4 °C due to an increased hydrogen bonding between water and disaccharide headgroups.31 However, this is also a direct effect of the branched HHF chain which brings disorder into crystalline phases of surfactants and allows it to be soluble even at low temperatures. This property is a real advantage of the branched surfactants compared to their linear counterparts. In comparison, β-C10Malt has a Krafft point of 26 °C and β-C14Malt of 32 °C.32–34 Both surfactants are not soluble at room temperature whereas HHFMalt is. At 1% wt, a phase separation between a viscous phase (liquid crystal) and a clear aqueous phase (L1) is observed.
The volume of the liquid crystalline phase does not seem to vary when the temperature changes from room temperature to 83 °C, which tends to indicate a very low temperature-sensitivity of the aqueous phase behavior. This observation is in accordance with previous studies on this class of surfactants.35–37
The solubility limits of the monoglycosides at room temperature are given in Table 3 and were determined by HPLC/MS. There are approximately 2 orders of magnitude difference in solubility between the maltoside derivative and the other glycosides. The solubility limits of all the monoglycosides are in the same range and depend on conformation and hydrogen bonding effects. The mannose derivative seems to be the least soluble sample.
The solubility has also been investigated in 25 wt% NaCl solution. No sample is soluble, down to 0.01% wt, from room temperature to 83 °C. The results obtained are in agreement with the salting-out effect of NaCl already highlighted in case of octyl-glucoside38–40 and dodecyl-maltoside.41
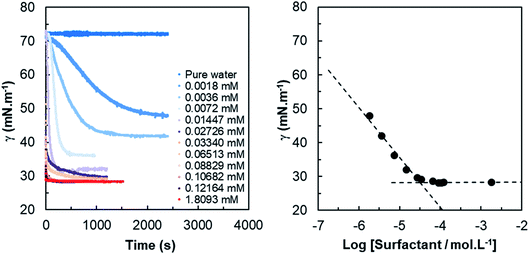 | ||
| Fig. 1 (Left) Dynamic surface tension measurements as function of time for various concentrations of HHFMalt in aqueous media; (right) CMC determination for HHFMalt surfactant. | ||
| Surfactant | Polar head | CMC | γCMC, mN m−1 | |
|---|---|---|---|---|
| mmol L−1 | ppm | |||
| HHFA | Arabinose (C5) | 0.0037–0.0060 | 1.34–2.15 | 27.3 |
| HHFX | Xylose (C5) | 0.0101–0.0304 | 3.65–10.98 | 28.6 |
| HHFG | Glucose (C6) | 0.0092–0.0336 | 3.58–13.11 | 27.1 |
| HHFMan | Mannose (C6) | 0.0041–0.0196 | 1.61–7.68 | 27.2 |
| HHFMalt | Maltose (C6–C6) | 0.0298 | 16.49 | 28.3 |
All samples reduce significantly the water surface tension. This means that all surfactants form micelles at concentrations below the solubility limit. It is difficult to discuss differences in hydrophilicity for the various polar heads, because of the very low solubilities and uncertainties in CMC determination, except for HHFMalt which is the most hydrophilic surfactant in this series. Nevertheless, the results show that its CMC is close to some of the monoglycosides. This is consistent with the fact that within a homogeneous series, the CMC value is most impacted by the lipophilic chain length, which is the same for all surfactants under study.42 Some literature data on other sugar-based surfactants are collected in Table 5 for comparison. For these surfactants, the hydrophobic chains are linear and reliable CMC values are usually given for alkyl chains up to C12 because of insolubility issues afterwards.31 The data marked with a footnote should be taken with caution because of non-soluble samples. It is interesting to notice the important anomeric effect for dodecylglucoside α and β, which does not occur for dodecylmaltoside. Overall, the CMC value found for HHFMalt (branched C15) lies within the ones reported for the C14 and C16 derivatives. It is important to stress that the surface tension γCMC (mN m−1) is lower for the farnesylglycosides compared to long chain linear n-alkyl-glucosides, which should indicate a better wetting ability.
| Polar head | Surfactant | Chain length | CMC (mmol L−1) | γCMC (mN m−1) | Reference |
|---|---|---|---|---|---|
| a Turbid solutions close and above CMC. | |||||
| Xylose (C5) | 5-O-Xylose monoester (α, β isomers) | C12 | 0.041 | 28.9 | 43 |
| C14a | 0.015 | 36.0 | 43 | ||
| C16a | 0.022 | 41.0 | 43 | ||
| Glucose (C6) | β-D-Glucoside | C8 | 25.0 | 30.1 | 44 |
| C10 | 2.2 | 27.7 | 44 | ||
| C12 | 0.19 | 39.4 | 44 | ||
| C12 | 0.13 | 33.1 | 43 | ||
| α-D-Glucoside | C12a | 0.042 | 41.2 | 43 | |
| Maltose (C6–C6) | β-D-Maltoside | C8 | 23.2 | — | 34 |
| C9 | 6.50 | — | 34 | ||
| C10 | 1.95 | 36.7 | 45 | ||
| C10 | 2.19 | — | 34 | ||
| C12 | 0.19 | — | 34 | ||
| C12 | 0.15 | 35.3 | 45 | ||
| C12 | 0.13 | 33.1 | 43 | ||
| C14 | 0.0167 | — | 34 | ||
| C16 | 0.00145 | — | 34 | ||
| α-D-Maltoside | C12 | 0.12 | 35.9 | 43 | |
In order to quantify the lipophilic contribution of the HHF carbon chain on the CMC, a linear correlation between the logarithm of the CMC with the linear alkyl chain length of n-alkyl-β-D-maltosides was made following the empirical equation of Klevens:46,47
| log(CMC) = A − BN | (2) |
Using this equation and the CMC of HHFMalt (0.0298 mmol L−1), the value of a linear equivalent chain length of 13.5 carbons can be estimated for hexahydrofarnesyl (Fig. 2). Branching tends to increase the CMC due to unfavorable packing of branched alkyl chains into spherical or cylindrical micelles, which was shown by experimental measurements48,49 and model predictions.50 This effect on surfactant packing was found to be effective even for branching on the first carbons of the alkyl chains near the sugar polar head, which is in accordance with our results.51–53
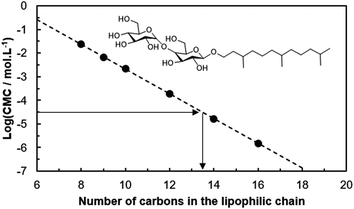 | ||
| Fig. 2 Correlation between the logarithm of the CMC and the alkyl chain length for n-alkyl-β-D-maltosides. | ||
The dynamic tension profiles on Fig. 1-left show an expected evolution with the concentration of surfactant. For the most diluted solutions (0.0018 mM to 0.0145 mM), the induction time is quite high and it decreases when the concentration increases. For concentrations close to or larger than the CMC, the surface tension at 0.06s is already considerably lower than the initial value (γ0) of 72.8 mN m−1. The dynamic surface tension decay can be also exploited to approximate the self-diffusion coefficient of surfactants in water. Indeed, the diffusion controlled adsorption Γ(t) of surface active species at air/liquid interface is described by the Ward and Tordai equation.54 For non-ionic surfactants, the decrease of the surface tension as a function of time γ(t) has been evaluated from the classical Gibbs absorption equation48,55,56 by two different asymptotic models for short and long times.57–59
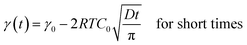 | (3) |
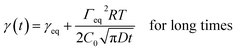 | (4) |
The values obtained are comparable to the ones found in literature for the same class of monomeric surfactant62 and logically higher than corresponding micelles for which a value of 7 × 10−11 m2 s−1 has been calculated from NMR experiments with n-dodecyl-β-D-maltoside in D2O solutions.63,64
Dynamic surface tension can be also fitted by an empirical equation according to Rosen model.65–71 Rosen et al. divided the dynamic surface tension curves into four different regions: induction, rapid fall, meso-equilibrium and equilibrium toward surface tension. The model fits the experimental data well for the most common dynamic surface tension curves. Considering the surface tension of the solvent γ0 and at equilibrium γeq obtained from experimental data, the surface tension at each time γ(t) can be deduced from the following equation:
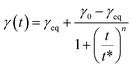 | (5) |
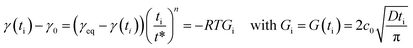 | (6) |
The results obtained highlight a good fitting of the Rosen model with experimental dynamic surface tension curves for various HHFMalt concentrations (Fig. 3 and 22 in ESI†) as well as exhibiting diffusion coefficients in the same range as the one determined from short and long times approximation models (Table 6).
| C0 (mmol L−1) | ti (s) | t* (s) | n | γeq (mN m−1) | γ(ti) (mN m−1) | Γi (106 mol m−2) | D (1010 m2 s−1) |
|---|---|---|---|---|---|---|---|
| 0.0145 | 25.6 | 43.8 | 2.45 | 32.1 | 63.2 | 1.08 | 1.7 |
| 0.0072 | 120.4 | 167.0 | 4.02 | 36.3 | 64.3 | 0.96 | 1.2 |
| 0.0036 | 180.5 | 335.3 | 2.13 | 41.4 | 65.5 | 0.83 | 2.3 |
| 0.0018 | 433.0 | 752.6 | 2.38 | 47.0 | 66.4 | 0.73 | 3.0 |
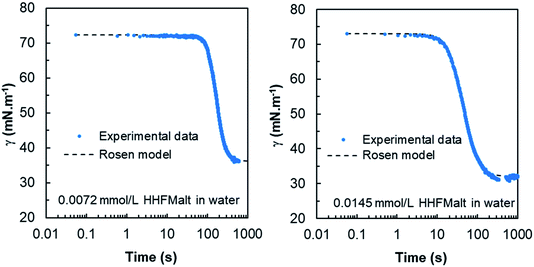 | ||
| Fig. 3 Experimental dynamic surface tension curves versus Rosen model for 0.0072 and 0.0145 mmol L−1 HHFMalt concentrations below the CMC. t* and n are obtained by minimizing the global error between experimental data with the Rosen model. The results for 0.0018 and 0.0036 mmol L−1 HHFMalt concentrations are displayed in Fig. 22 in ESI.† | ||
3.2. Amphiphilic behavior in surfactant oil water (SOW) systems
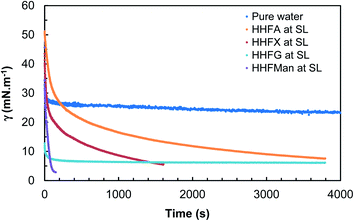 | ||
| Fig. 4 Dynamic interfacial tensions vs. n-octane for the different surfactants under study except HHFMalt (drops come off before equilibrium for HHFX and HHFMan at solubility limit). | ||
For HHFX and HHFMan, the drop comes off naturally before reaching equilibrium, indicating that interfacial tensions are lower than 1 mN m−1 which is the limit of the instrument. For HHFMalt at 0.01% wt, no measurement was possible because of drop coming off right from the beginning of the experiment. Table 7 recaps the values of interfacial tensions vs. n-octane. To compare all the glycosides derivatives, a value at 100 s is given, as an indication of the individual diffusion of surfactants at the interface.
| Surfactant | Polar head | Concentration | γow (mN m−1) | |
|---|---|---|---|---|
| at 100 s | at tmax | |||
| a Non stabilized values. | ||||
| HHFA | Arabinose (C5) | Solubility limit | 21.9 | 7.6a (4000 s) |
| HHFX | Xylose (C5) | Solubility limit | 21.2 | 5.6a (1500 s) |
| HHFG | Glucose (C6) | Solubility limit | 7.3 | 6.1 (4000 s) |
| HHFMan | Mannose (C6) | Solubility limit | 4.2 | 2.9a (170 s) |
| HHFMalt | Maltose (C6–C6) | 0.01% wt | <1 | <1 |
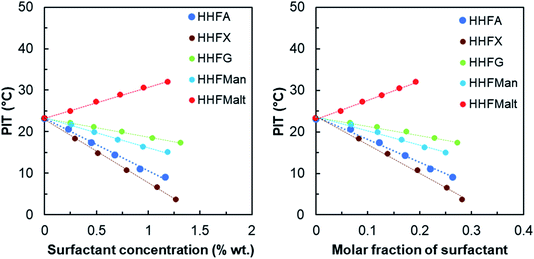
| Surfactant | Polar head | dPIT/dC (°C/wt%) | dPIT/dx (°C) |
|---|---|---|---|
| HHFA | Arabinose (C5) | −12.6 | −55.4 |
| HHFX | Xylose (C5) | −15.3 | −68.8 |
| HHFG | Glucose (C6) | −4.5 | −21.8 |
| HHFMan | Mannose (C6) | −7.2 | −34.1 |
| HHFMalt | Maltose (C6–C6) | 7.5 | 46.2 |
HHFMalt is the most hydrophilic surfactant because of its disaccharide head. This result confirms previous CMC and solubility experiments for which the HHFMalt surfactant has been defined as the most hydrophilic. Among the monosaccharide derivatives, the ones derived from hexoses (HHFG and HHFMan) are more hydrophilic than the ones derived from pentoses (HHFA and HHFX). Glucose appears to be more hydrophilic than mannose and arabinose more hydrophilic than xylose, which shows again that the sugar conformation has a great influence on its polarity. Indeed, the more isolated hydroxyl groups are, the higher the hydrophilicity of the surfactant is, due to favorable hydrogen bonding with water.78 It is the case for HHFA, which is more hydrophilic than HHFX due to hydroxyl groups 3 and 4 in equatorial and axial positions, compared to two equatorial positions for xylose. The same considerations hold for HHFG, which is more hydrophilic than HHFMan due to hydroxyl group 2 in equatorial position.
In order to compare the HHF surfactants with linear surfactants and to establish the effect of branching, the PIT-slope values of well-defined n-alkyl-β-D-glucosides and n-alkyl-β-D-maltosides were quantified. Fig. 6 shows the PIT-slope of n-alkyl-glucosides and n-alkyl-maltosides.
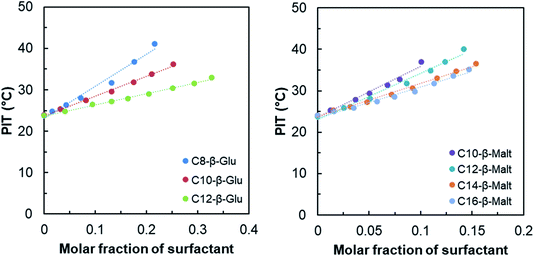 | ||
| Fig. 6 PIT variation of the reference system as function of the n-alkyl-β-D-glucoside (left) and the n-alkyl-β-D-maltoside (right) surfactants molar fraction. | ||
As expected, the PIT-slope values obtained for n-alkyl-glucoside and maltoside surfactants are in accordance with their linear carbon tail lengths. The increase of the length of alkyl chain from 8 to 12 diminishes the hydrophilicity of the surfactants and the PIT-slope decreases linearly, as shown in Fig. 7.
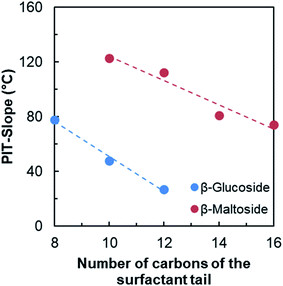 | ||
| Fig. 7 Evolution of the PIT-slope values with the number of carbons of the surfactant tail for n-alkyl-β-D-glucoside and n-alkyl-β-D-maltoside surfactants. | ||
Linear fit from Fig. 7 can be used to estimate the “equivalent linear chain length” of the HHF tail. In both cases, the PIT-slope values of the HHF surfactants are lower than those measured for the linear corresponding surfactants and the data was extrapolated. Using n-alkyl-glucosides correlation, the approximate value is 15.7 carbons, whereas it is 18.8 when the n-alkyl-maltosides results are used.
These values should not be compared to the one obtained from CMC experiments, because in the PIT-slope experiments, the alkyl chain interacts with the oil phase. In the same vein, previous studies have highlighted the hydrophobic influence of the ramification of the surfactant tail, which decreases the optimum salinity of SOW system.79 The fact that the PIT-slope correlation gives different values of equivalent surfactant chain length in case of glucosides and maltosides can be linked to possible differences of partition coefficients.
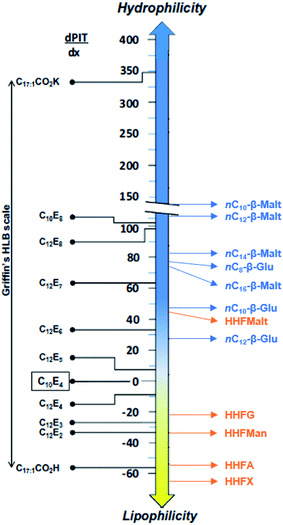
Determining the PIT-slope values of these surfactants allows classifying them among other conventional surfactants already characterized by the method and especially the CiEj surfactants.26,27,80,81 Results displayed in Fig. 8 highlight that HHFMalt has a hydrophilicity between C12E6 and C12E7, whereas the HHFG is between the C12E3 and C12E4. This figure stresses again that the type of sugar used as polar head has a huge influence on the hydrophilicity. Indeed, the HHFMan is found to be equivalent to the C12E2.
In the same way, it is possible to determine the equivalent number of ethoxylated group to one glucoside or maltoside unit by comparison of the linear alkyl β-glucosides and maltosides to the CiEj surfactants. The trend of the PIT-slope values of C12Ej with the number of ethoxylated groups can be described by a second degree polynomial relation (Fig. 9). Using this correlation with nC12-β-glucoside and maltoside, the hydrophilicity contribution of one glucoside unit is equivalent to 5.9 ethoxylated groups, whereas a maltoside unit is equivalent to 8.3 ethoxylated groups.
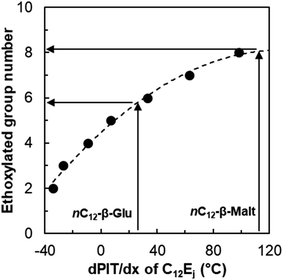 | ||
| Fig. 9 Evolution of the PIT-slope values of C12Ej with the number of ethoxylated groups of the surfactant. | ||
The different PIT-slope values of sugar-based surfactants can be also useful to determine their Preferred Alkane Carbon Number (PACN), which is the linear alkane that gives a WIII microemulsion system with the surfactant at 25 °C without salt or alcohol. The PACN is also a parameter of the normalized HLD equation, defined by Salager et al., which describes the phase behavior of SOW systems to reach the optimum formulation.82–84 As described in the literature,85 the PIT-slope can be linked to the HLD equation, and so to the PACN, by the relation below:
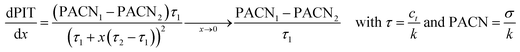 | (7) |
As the parameters of the reference surfactant PACN1 and τ1 are known (PACN1 = 8.2 and τ1 = 0.31 °C−1),85 the different PACN of sugar-based surfactants can be calculated (Table 9). Values of PACN are inversely proportional to the PIT-slope values. The negative values of PACN for a surfactant indicate that a polar oil is needed to get a three phase behavior at 25 °C without salt and alcohol. The high values of PACN indicate a lipophilic surfactant that needs very long alkanes to get a WIII behavior. Liquid alkanes at 25 °C range from pentane to hexadecane, and only HHFG reaches theoretically the optimum formulation with an alkane (pentadecane) at 25 °C without salt.
| Surfactant name | dPIT/dx (°C) | PACN |
|---|---|---|
| HHFA | −55.4 | 25.4 |
| HHFX | −68.8 | 29.5 |
| HHFG | −21.8 | 15.0 |
| HHFMan | −34.1 | 18.8 |
| HHFMalt | 46.2 | −6.1 |
| nC8-β-Glu | 77.8 | −15.9 |
| nC10-β-Glu | 47.8 | −6.6 |
| nC12-β-Glu | 27.0 | −0.8 |
| nC10-β-Malt | 123.0 | −29.9 |
| nC12-β-Malt | 112.2 | −26.6 |
| nC14-β-Malt | 80.7 | −16.8 |
| nC16-β-Malt | 74.3 | −14.8 |
All monosaccharide surfactants form Winsor II systems at 50 °C, whatever the salinity, which means that the affinity of these surfactants is higher for the oil phase, even if the aqueous phase does not contain electrolyte. For instance, the most lipophilic compound, HHFX, is soluble neither in water nor in oil, and oil droplets are observed on the pipette wall (Fig. 23 in ESI†). This is consistent with the negative PIT-slope values and the very low water solubility of these compounds.
HHFMalt, a hydrophilic surfactant following the PIT-slope criteria, changes from a Winsor I system at 0% wt NaCl to a Winsor III system from 5 to 15% wt NaCl. Equal amounts of oil and water are solubilized in the middle-phase microemulsion at a salinity around 12% wt NaCl, which can be identified as the “optimal salinity”. The APG SL26 (commercial C12–16Glu1.3) exhibits the same behavior using the same co-surfactant (Fig. 28 in ESI†). These results prove that sugar-based surfactant are really interesting for formulating WIII microemulsion systems along a wide range of salinity, which can be a real benefit for enhanced oil recovery applications for example. This ternary phase behavior confirms also the PIT-slope, CMC and solubility measurements exposed previously by identifying HHFMalt as the most hydrophilic surfactant.
4 Conclusions
Five novel sugar surfactants prepared from bio-based hexahydrofarnesol have been evaluated as regards to their water solubility, surface and interfacial tension, amphiphilicity and ternary phase behavior in n-octane/water systems. Only the disaccharide (maltose) derivative is significantly soluble (>0.1 wt%) in deionized water whereas the water solubility of monosaccharide derivatives is lower than 50 ppm which might be a limitation for certain industrial applications. This study reveals that the hexahydrofarnesyl chain must be coupled with di- or poly-saccharides to achieve a high water solubility and to provide surfactants with well-balanced amphiphilicity.Despite their poor water-solubility, all sugar-based surfactants strongly reduce the surface tension of water even at very low concentrations (<20 ppm). In addition, the PIT-slope measurements allowed assessing their true amphiphilicities which are consistent with the known hydrophilicity of the sugar heads. As expected, the HHFMalt surfactant was found to be the most hydrophilic in this series. The PIT-slope of this surfactant is in agreement with its phase behavior in the HHFMalt/n-octane/water ternary system. The equivalent linear carbon chain of the HHF tail, as well as the equivalent ethoxylated group number of sugar head, have also been approximated by this method.
In n-octane/water with 1-butanol as co-surfactant, HHFMalt forms Winsor III-type systems over a wide salinity range, whereas the monosaccharides form only Winsor II-type systems whatever the salinity. Thanks to this particular behavior, HHFMalt can be well suited for some enhanced oil recovery processes.
In the same way, to valorize monosaccharide derivatives, it would also be worthwhile to combine them with more water soluble surfactants (ionic ones or shorter alkyl chains for instance) to investigate possible synergistic formulations.
Conflicts of interest
The authors declare that they have no conflict of interest.Acknowledgements
The authors would like to thank TOTAL for financing this work and for allowing its publication. Chevreul Institute (FR 2638), Ministère de l’Enseignement Supérieur et de la Recherche, Région Nord-Pas de Calais and FEDER are also acknowledged for supporting this work. We are deeply grateful to M. Christian Dur who performed the solubility, phase behavior, surface and interfacial tension experiments, and to Ms. Leoni Koller who performed some of the PIT-slope experiments during her Master internship.References
- H. T. Boehme AG, A process for the production of sulphuric acid esters of glucosides, Patent GB, 384230, 1932.
- H. T. Boehme AG, Improvements in or relating to liquids or plastic preparations for the treatment of fibrous materials, Patent GB, 393769, 1933.
- D. Balzer and H. Luders, Nonionic surfactants: alkyl polyglucosides, Taylor & Francis, 2000 Search PubMed.
- C. Baron and T. E. Thompson, Biochim. Biophys. Acta, Biomembr., 1975, 382, 276–285 CrossRef CAS.
- A. Kiyoshi, F. Tadaaki, H. Kunizo, O. Hiroshi and T. Shinji, Process for producing alkyl glycoside, JP Pat., 04308599, 1992.
- H. Luders, Process for the preparation of alkyloligoglycosides, US Pat., 4866165A, 1989.
- M. Biermann, K. Hill, W. Wuest, R. Eskuchen, J. Wollmann, A. Bruns, G. Hellmann, K.-H. Ott, W. Winkle and K. Wollmann, Process for the production of surface active alkyl glycosides, US Pat., 5374716A, 1990.
- H.-D. Doerfler, Angew. Chem., Int. Ed., 1997, 36, 2527 Search PubMed.
- O. J. Rojas, C. Stubenrauch, L. A. Lucia and Y. Habibi, Interfacial properties of sugar-based surfactants, AOCS Press, 2009, pp. 457–480 Search PubMed.
- M. K. Matsson, B. Kronberg and P. M. Claesson, Langmuir, 2004, 20, 4051–4058 CrossRef CAS PubMed.
- G. Bognolo, Techniques de l’ingénieur, 2013, 2, J2265 Search PubMed.
- G. Dass, R. Tyagi and N. Kumar, J. Surf. Sci. Technol., 2015, 31, 156–163 CAS.
- W. von Rybinski and K. Hill, Angew. Chem., Int. Ed., 1998, 37, 1328–1345 CrossRef CAS PubMed.
- Z. Jeirani, B. Mohamed Jan, B. Si Ali, I. M. Noor, C. H. See and W. Saphanuchart, Ind. Crops Prod., 2013, 43, 6–14 CrossRef CAS.
- M. Santa, G. Alvarez-Jürgenson, S. Busch, P. Birnbrich, C. Spindler and G. Brodt, in SPE Enhanced Oil Recovery Conference, Society of Petroleum Engineers, Kuala Lumpur, Malaysia, 2011 Search PubMed.
- S. Iglauer, Y. Wu, P. Shuler, Y. Tang and W. A. Goddard, Colloids Surf., A, 2009, 339, 48–59 CrossRef CAS.
- T. Gaudin, H. Lu, G. Fayet, A. Berthauld-Drelich, P. Rotureau, G. Pourceau, A. Wadouachi, E. Van Hecke, A. Nesterenko and I. Pezron, Adv. Colloid Interface Sci., 2019, 270, 87–100 CrossRef CAS PubMed.
- Y. Queneau, S. Chambert, C. Besset and R. Cheaib, Carbohydr. Res., 2008, 343, 1999–2009 CrossRef CAS PubMed.
- Q. Zhang, Y. Li, Y. Song, J. Li and Z. Wang, Colloids Surf., A, 2018, 538, 361–370 CrossRef CAS.
- M. Bourrel and C. Chambu, Soc. Pet. Eng. J., 1983, 23, 327–338 CrossRef CAS.
- R. S. Schechter and M. Bourrel, Microemulsions and related systems: formulation, solvency, and physical properties, ed. M. Dekker, 1988 Search PubMed.
- International Renewable Energy Agency, Renewable Energy Statistics, 2017, 52 Search PubMed.
- N. S. Renninger and D. J. Mcphee, Fuel compositions comprising farnesane and farnesane derivatives and method of making and using same, US pat., US7399323B2, 2008.
- P. P. Peralta-Yahya, F. Zhang, S. B. del Cardayre and J. D. Keasling, Nature, 2012, 488, 320–328 CrossRef CAS PubMed.
- S. Queste, J. L. Salager, R. Strey and J. M. Aubry, J. Colloid Interface Sci., 2007, 312, 98–107 CrossRef CAS PubMed.
- J. F. Ontiveros, C. Pierlot, M. Catté, V. Molinier, J.-L. Salager and J.-M. Aubry, Colloids Surf., A, 2014, 458, 32–39 CrossRef CAS.
- J. F. Ontiveros, C. Pierlot, M. Catté, V. Molinier, J.-L. Salager and J.-M. Aubry, J. Colloid Interface Sci., 2015, 448, 222–230 CrossRef CAS PubMed.
- A. Pizzino, V. Molinier, M. Catté, J. F. Ontiveros, J.-L. Salager and J.-M. Aubry, Ind. Eng. Chem. Res., 2013, 52, 4527–4538 CrossRef CAS.
- P. A. Winsor, Trans. Faraday Soc., 1948, 44, 376 RSC.
- R. G. Laughlin, The Aqueous Phase Behaviour of Surfactants, Academic Press, San Diego, 1994 Search PubMed.
- C. Stubenrauch, Curr. Opin. Colloid Interface Sci., 2001, 6, 160–170 CrossRef CAS.
- C. A. Ericsson, O. Söderman and S. Ulvenlund, Colloid Polym. Sci., 2005, 283, 1313–1320 CrossRef CAS.
- R. A. Salkar, H. Minamikawa and M. Hato, Chem. Phys. Lipids, 2004, 127, 65–75 CrossRef CAS PubMed.
- W. J. De Grip and P. H. M. Bovee-Geurts, Chem. Phys. Lipids, 1979, 23, 321–335 CrossRef CAS.
- B. J. Boyd, C. J. Drummond, I. Krodkiewska and F. Grieser, Langmuir, 2000, 16, 7359–7367 CrossRef CAS.
- V. Vill, H. M. von Minden, M. H. J. Koch, U. Seydel and K. Brandenburg, Chem. Phys. Lipids, 2000, 104, 75–91 CrossRef CAS PubMed.
- H. M. von Minden, K. Brandenburg, U. Seydel, M. H. J. Koch, V. Garamus, R. Willumeit and V. Vill, Chem. Phys. Lipids, 2000, 106, 157–179 CrossRef CAS PubMed.
- P. Mukerjee, J. Phys. Chem., 1965, 69, 4038–4040 CrossRef CAS.
- P. Mukerjee, J. Phys. Chem., 1970, 74, 3824–3826 CrossRef CAS.
- P. Mukerjee and C. C. Chan, Langmuir, 2002, 18, 5375–5381 CrossRef CAS.
- L. Zhang, P. Somasundaran and C. Maltesh, Langmuir, 1996, 12, 2371–2373 CrossRef CAS.
- Sugar-Based Surfactants: Fundamentals and Applications, ed. C. Carnero Ruiz, CRC Press, 2008 Search PubMed.
- G. Garofalakis, B. S. Murray and D. B. Sarney, J. Colloid Interface Sci., 2000, 229, 391–398 CrossRef CAS PubMed.
- K. Shinoda, T. Yamaguchi and R. Hori, Bull. Chem. Soc. Jpn., 1961, 34, 237–241 CrossRef CAS.
- M. J. Rosen and S. B. Sulthana, J. Colloid Interface Sci., 2001, 239, 528–534 CrossRef CAS PubMed.
- H. B. Klevens, J. Phys. Colloid Chem., 1948, 52, 130–148 CrossRef CAS PubMed.
- H. B. Klevens, J. Am. Oil Chem. Soc., 1953, 30, 74–80 CrossRef CAS.
- M. J. Rosen and J. T. Kunjappu, Surfactants and interfacial phenomena, Wiley, Hoboken, N.J., 4th edn, 2012 Search PubMed.
- J. A. Molina-Bolívar and C. C. Ruiz, in Sugar-Based Surfactants, CRC Press, 2008, pp. 80–123 Search PubMed.
- T. Gaudin, P. Rotureau, I. Pezron and G. Fayet, Ind. Eng. Chem. Res., 2016, 55, 11716–11726 CrossRef CAS.
- H. Minamikawa and M. Hato, Chem. Phys. Lipids, 2005, 134, 151–160 CrossRef CAS PubMed.
- F. Nilsson, O. Söderman and I. Johansson, J. Colloid Interface Sci., 1998, 203, 131–139 CrossRef CAS.
- S. Matsumura, K. Imai, S. Yoshikawa, K. Kawada and T. Uchibori, J. Jpn. Oil Chem. Soc., 1991, 40, 709–714 CrossRef CAS.
- A. Ward and L. Tordai, J. Chem. Phys., 1946, 14, 453–461 CrossRef CAS.
- P. C. Hiemenz and P. C. Hiemenz, Principles of colloid and surface chemistry, ed. M. Dekker, New York, 1986, vol. 188 Search PubMed.
- J. T. Davies and E. K. Rideal, Interfacial Phenomena, Academic Press, New York, 1st edn, 1961, pp. 343–450 Search PubMed.
- J. Eastoe, J. S. Dalton, P. G. A. Rogueda, E. R. Crooks, A. R. Pitt and E. A. Simister, J. Colloid Interface Sci., 1997, 188, 423–430 CrossRef CAS.
- V. B. Fainerman, A. V. Makievski and R. Miller, Colloids Surf., A, 1994, 87, 61–75 CrossRef CAS.
- C.-H. Chang and E. I. Franses, Colloids Surf., A, 1995, 100, 1–45 CrossRef CAS.
- C. J. Drummond, G. G. Warr, F. Grieser, B. W. Ninham and D. F. Evans, J. Phys. Chem., 1985, 89, 2103–2109 CrossRef CAS.
- F. Nilsson, O. Söderman and I. Johansson, Langmuir, 1996, 12, 902–908 CrossRef CAS.
- A. J. M. Valente, M. Nilsson and O. Söderman, J. Colloid Interface Sci., 2005, 281, 218–224 CrossRef CAS PubMed.
- Q. Yang, Q. Zhou and P. Somasundaran, Colloids Surf., A, 2007, 305, 22–28 CrossRef CAS.
- Q.-Q. Yang, Q. Zhou and P. Somasundaran, J. Mol. Liq., 2009, 146, 105–111 CrossRef CAS.
- Xi Yuan and M. J. Rosen, J. Colloid Interface Sci., 1988, 124, 652–659 CrossRef.
- M. J. Rosen and X. Y. Hua, J. Colloid Interface Sci., 1990, 139, 397–407 CrossRef CAS.
- X. Y. Hua and M. J. Rosen, J. Colloid Interface Sci., 1991, 141, 180–190 CrossRef CAS.
- M. J. Rosen, Z. H. Zhu and X. Y. Hua, J. Am. Oil Chem. Soc., 1992, 69, 30–33 CrossRef CAS.
- T. Gao and M. J. Rosen, J. Am. Oil Chem. Soc., 1994, 71, 771–776 CrossRef CAS.
- T. Gao and M. J. Rosen, J. Colloid Interface Sci., 1995, 172, 242–248 CrossRef CAS.
- M. J. Rosen and L. D. Song, J. Colloid Interface Sci., 1996, 179, 261–268 CrossRef CAS.
- L. K. Filippov, J. Colloid Interface Sci., 1994, 163, 49–60 CrossRef CAS.
- L. K. Filippov, J. Colloid Interface Sci., 1994, 164, 471–482 CrossRef CAS.
- L. K. Filippov and N. L. Filippova, J. Colloid Interface Sci., 1996, 178, 571–580 CrossRef CAS.
- L. K. Filippov, J. Colloid Interface Sci., 1996, 182, 330–347 CrossRef CAS.
- B.-Y. Cai, J.-T. Yang and T.-M. Guo, J. Chem. Eng. Data, 1996, 41, 493–496 CrossRef CAS.
- T. Al-Sahhaf, A. Elkamel, A. Suttar Ahmed and A. R. Khan, Chem. Eng. Commun., 2005, 192, 667–684 CrossRef CAS.
- Z. Mosapour Kotena, R. Behjatmanesh-Ardakani and R. Hashim, Liq. Cryst., 2014, 41, 784–792 CrossRef CAS.
- C. E. Hammond and E. J. Acosta, J. Surfactants Deterg., 2012, 15, 157–165 CrossRef CAS.
- G. Lemahieu, J. F. Ontiveros, V. Molinier and J. Aubry, IOR 2019 – 20th European Symposium on Improved Oil Recovery, Pau, France, 2019 Search PubMed.
- G. Lemahieu, J. F. Ontiveros, V. Molinier and J.-M. Aubry, J. Colloid Interface Sci., 2019, 557, 746–756 CrossRef CAS PubMed.
- J. L. Salager, J. C. Morgan, R. S. Schechter, W. H. Wade and E. Vasquez, Soc. Pet. Eng. J., 1979, 19, 107–115 CrossRef.
- J.-L. Salager, A. M. Forgiarini and J. Bullón, J. Surfactants Deterg., 2013, 16, 449–472 CrossRef CAS.
- J.-L. Salager, A. M. Forgiarini, L. Márquez, L. Manchego and J. Bullón, J. Surfactants Deterg., 2013, 16, 631–663 CrossRef CAS PubMed.
- J. F. Ontiveros, C. Pierlot, M. Catté, J.-L. Salager and J.-M. Aubry, Colloids Surf., A, 2018, 536, 30–37 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02326d |
| This journal is © The Royal Society of Chemistry 2020 |