X-ray absorption spectroscopy of archetypal chromium porphyrin and corrole derivatives

Abstract

A combination of Cr K-edge XAS and DFT calculations have been performed on archetypal chromium porphyrinoid complexes Cr^IV[TMP]O (2) and Cr^V[TPC]O (3), and the results have been compared to the reference compound Cr^III[TPP]Cl (1), where TPP²⁻, TMP²⁻, and TPC³⁻ are the anions of meso-tetraphenylporphyrin, meso-tetramesitylporphyrin, and meso-triphenylcorrole, respectively. The intensity-weighted average energy position in 1 (5990.9 eV), 2 (5992.0 eV) and 3 (5992.6 eV) are consistent with increasing the metal oxidation state along the series. EXAFS and theoretical analysis of 2 and 3 reveal that the Cr–O bond is longer and weaker in 3 relative to 2, despite the structural similarity and increase in oxidation state in 3. This is also reflected in a comparison of the Cr K-pre-edge transitions. The roughly twenty-fold increase in intensity in the two oxo complexes is unsurprising and well-precedented for other first-row transition metals. However, although 3 had greater overall intensity, the intensity of transitions along the Cr–O bond is greater. EXAFS, DFT and TDDFT analyses show that the more contracted N₄ core of the corrole results in a greater out-of-plane displacement of the Cr in 3 relative to 2, which in turn accentuates the lower local symmetry of the Cr in 3 relative to 2. This difference helps us to appreciate the TDDFT result that whereas two 1s→ 3d_z² transitions make up the majority of the intensity in the pre-edge of 2, the pre-edge of 3 also includes fairly intense transitions to molecular orbitals with 3d_xz, 3d_yz and 3d_z² character, thus accounting for the somewhat higher overall intensity for 3.

---

Introduction

The importance of X-ray absorption spectroscopy (XAS) as an analytical method for chromium stems from two broad reasons. One, chromium analysis is important for an unusually wide range of substances, including catalysts and reagents, alloys and ceramics, and soil and environmental samples, in the last of which Cr(VI) acts as a major toxin. Two, chromium exhibits a variety of oxidation states, from 0 to +VI, which should be readily distinguishable with XAS. Until now, XAS studies have largely probed Cr(III) and Cr(VI), and paid little attention to the Cr(IV) and Cr(V) states. In an attempt to bridge this knowledge gap, we present here a Cr K-edge XAS study of three archetypal chromium porphyrinoid complexes, including Cr^III[TPP]Cl (1), Cr^IV[TMP]O (2), and Cr^V[TPC]O (3), where TPP²⁻, TMP²⁻, and TPC³⁻ are the anions of meso-tetraphenylporphyrin, meso-tetramesitylporphyrin, and meso-triphenylcorrole (Scheme 1). The sterically hindered TMP ligands was chosen to improve the stability of the Cr(IV) complex, but the differences in peripheral substitution are not expected to result in any significant difference in the relative XAS data among the three complexes. Somewhat surprisingly, in spite of their obvious sensitivity to transition metal d electron counts, XAS has only been infrequently applied to Cr porphyrins and indeed to metalloporphyrin-type complexes in general, except for those involving Mn and Fe.^1–8 Indeed, only one directly relevant study has been reported in the literature, focusing on Cr^IV[TTP]O and Cr^V[TTP]N, where TTP²⁻ is the dianion of meso-tetra(p-tolyl)porphyrin.⁹ Understandably, we have used substantially improved theoretical methods in the present study to model the Cr K-edge XAS data on the high-valent compounds 2 and 3, and where appropriate, we will point out similarities and differences relative to the earlier study. Importantly, we will probe the nature of the Cr–O bond in the 2 and 3 and discuss factors that are responsible for tuning the bond strength.

Scheme 1 Chromium porphyrin and corrole derivatives investigated in this study.

Results and discussion

Cr K-edge XAS

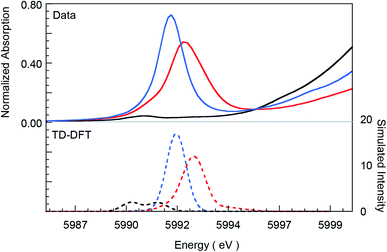
Fig. 1 presents Cr K-edge XAS data for 1, 2 and 3. The inset shows the expanded pre-edge region, which results from Cr 1s-to-3d transitions. The weak intensity of the pre-edge indicates its electric dipole-forbidden (but quadrupole-allowed) nature.^10–14 The pre-edge energy position and intensity distribution are strongly influenced by changes in the oxidation state and ligand field at the absorbing Cr center and can be quantitatively compared across related systems to gain information about these parameters. The pre-edge energy position shifts to higher energy with an increase in ligand field strength (which destabilizes the valence 3d levels) and with localized oxidation at the Cr center. The total intensity and the intensity pattern are modulated by the overall metal–ligand interaction, increase in the number of valence 3d holes, and an increase in the metal 3d–4p mixing (associated with a decrease in centrosymmetry). The three Cr complexes studied here correspond to an almost ideal square-pyramidal geometry with the porphyrin (1 and 2) or corrole (3) occupying the equatorial plane and a Cl (1) or O (2 and 3) occupying the axial position. The structural similarity of the three complexes greatly facilitates a comparison of the pre-edge energy position and intensity patterns.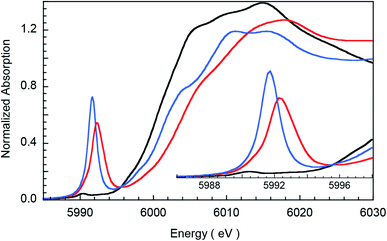

Fig. 1 Normalized Cr K-edge XAS for 1 (black), 2 (blue), and 3 (red). The inset shows the expanded pre-edge region.

A comparison of the intensity-weighted average energy position for the S = 3/2 Cr(III) reference complex 1 (5990.9 eV) and 2 (5992.0 eV) shows a blue-shift of 1.1 eV for the latter. This large shift is consistent with an increase in oxidation at the Cr center in 2 to Cr(IV). The total intensity of the pre-edge also increases ∼20 fold (from 0.2 to 3.9) on going from 1 to 2. The latter effect results from the short axial Cr–O bond in 2, which pulls the Cr atom out of the TMP plane, thereby increasing Cr 3d_z²–4p_z orbital mixing, which is responsible for the significant increase in intensity of the relevant transition(s) within the Cr pre-edge manifold. Indeed, intense pre-edge features are ubiquitous for Mn^15–17 and Fe^18–21 complexes with short M–O bonds for which the energy position and intensities have been quantitatively studied with a combination of X-ray absorption and TDDFT methods. A comparison of 2 and 3 shows a further blue-shift in the pre-edge energy position of 3 by 0.6 eV (5992.0 eV to 5992.6 eV). Interestingly, although the pre-edge of 2 appears to be more intense than that of 3, the total intensity of the pre-edge increases by 13% from 3.9 to 4.5 units on going from 2 to 3. This difference reflects the fact that the transitions contributing to the Cr K-pre-edge of 3 are more spread-out, making the pre-edge envelope of 3 broader than that of 2. The significant blue-shift and increase in intensity of the pre-edge position of 3 suggests that the Cr center in 3 is more oxidized than that in 2.

The blue-shift and increased intensity of the Cr K-pre-edge of 3 are consistent with the previous polarized Cr K-edge XAS study on high-valent Cr^IV[TTP]O and Cr^V[TTP]N, which showed a nearly 1 eV shift on going from the Cr(IV) to the Cr(V) complex.⁸ The study also showed that the pre-edge feature observed at ∼5990 eV is almost completely z-polarized, consistent with the fact that the pre-edge transitions are extremely weak, electric quadrupole-allowed transitions that gain intensity through 3d_z²–4p_z mixing. Accordingly, the Cr center in 3 may be assigned as Cr(V). Below, these experimental results are compared with DFT calculations to obtain a comprehensive picture of the bonding differences in 2 and 3.

Cr K-edge EXAFS

The non-phase-shift-corrected Fourier transforms and corresponding Cr K-edge EXAFS data (inset) are presented in Fig. 2 for 2 and 3. The EXAFS best fits are shown in Fig. 3 and Table 1. The best fit for 2 reveals 1 Cr–O and 4 Cr–N distances of 1.56 Å and 2.03 Å, respectively, while 3 is best fit with 1 Cr–O and 4 Cr–N distances of 1.60 Å and 1.95 Å, respectively. The second and third shell of the EXAFS data were fit using single and multiple scattering contributions from the porphyrin and corrole rings in the equatorial plane. The presence of the short Cr–O distances in both compounds confirm the structural integrity of the samples used for the XAS measurements. These results were used as structural calibration for the level of theory used for the DFT calculations (see below).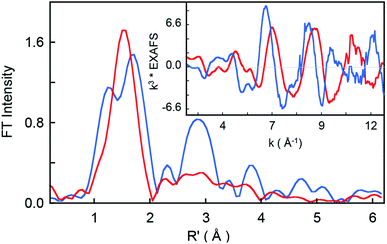

Fig. 2 Non-phase-shift-corrected Fourier transform data for 2 (blue) and 3 (red). The inset shows the Cr K-edge EXAFS comparison.

Fig. 3 Comparison of Cr K-pre-edge XAS data (top panel, solid lines) for 1 (black), 2 (blue), and 3 (red) with TDDFT calculated spectra (dashed lines). The calculated spectra have been energy-shifted by 154 eV and the calculated intensities have been scaled for graphical representation.

Table 1 EXAFS least squares fitting results

Complex	Coordination/path	R^a (Å)	σ^2^b (Å^2)	E0 (eV)	F^c
a The estimated standard deviations for the distances are on the order of ±0.02 Å.b The σ^2 values have been multiplied by 10^5.c The error is given by 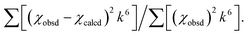The S0^2 factor was set at 1.
2	1 Cr–O	1.56	128	−3.87	0.56
	4 Cr–N	2.03	121
	2 Cr–C	2.46	398
	6 Cr–C	3.04	153
	8 Cr–C–N	3.40	462
	16 Cr–C–N	4.38	554
3	1 Cr–O	1.60	22	6.29	0.33
	4 Cr–N	1.95	424
	6 Cr–C	2.99	638
	12 Cr–C–N	3.15	712
	4 Cr–C	4.22	152

---

DFT and TDDFT calculations

Spin-unrestricted DFT calculations were performed on the three complexes studied and selected calculated results are presented in Table 2. The optimized bond distances (Table 1) are in good agreement with those observed from the Cr K-edge EXAFS results presented in Table 1. The calculated Löwdin spin populations clearly underscore the electronic-structural differences among the three compounds. Thus, 1 is a typical S = 3/2 Cr(III) complex, 2 is a low-spin d² species, and 3 is an S = 1/2 d¹ species. These descriptions are consistent with electronic-structural assignments based on energy shifts and intensity distributions observed in the Cr K-pre-edge data.

Table 2 Select DFT results for 1, 2 and 3

	Bond distance (Å)		Löwdin spin population			Mayer bond order
	Cr–O/Cl	Cr–Nav	Cr	O/Cl	porphyrin/corrole	Cr–O/Cl	Cr–Nav
1	2.24	2.04	2.91	0.05	0.04	1.15	0.56
2	1.56	2.06	0	0	0	2.31	0.60
3	1.58	1.95	1.20	−0.13	−0.03	2.12	0.78

---

Chromium 1s → 3d TDDFT calculations were performed to theoretically simulate the Cr K-pre-edge region. As shown in Fig. 3, the experimental data are reasonably well reproduced, indicating that the calculations are correctly capturing details of the metal–ligand bonding in the three compounds. Gratifyingly, the calculations reproduce the intense transitions in 2 and 3, and somewhat less well, also the increase in total pre-edge intensity (6%) in 3 relative to 2. As mentioned before, the pre-edge intensity increases with an increase in the number of 3d holes, an increase in 3d–4p mixing, or a combination thereof. A direct comparison of these factors between 2 and 3 is possible because they are geometrically similar (both are square-pyramidal) and have the same set of ligands (a short axial Cr–O bond and four equatorial Cr–N bonds). Geometry optimizations revealed that the Cr–O distance is slightly longer for 3 than for 2 (1.58 versus 1.56 Å). The Cr–O Mayer bond order is also greater for 2 relative to 3 (Table 2). These factors both indicate a greater Cr 3d_z²–4p_z orbital mixing in 2, which leads to more intense 1s→ 3d_z² transitions in 2 relative to 3 and the appearance of greater intensity.

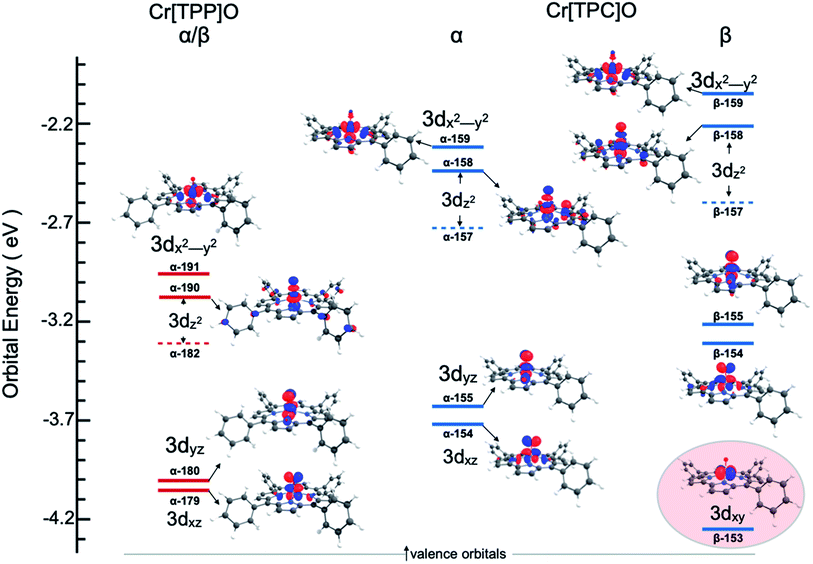
One explanation for the increase in total pre-edge intensity in 3 is the increase in number of holes (3d¹ relative to 3d² in 2). To check this possibility, the valence Kohn–Sham molecular orbitals with substantial Cr 3d character were visualized and analyzed. Fig. 4 shows that the extra hole on 3 resides predominantly in a 3d_xy orbital. Since 1s → 3d_xy transitions are dipole-forbidden and do not significantly contribute to the pre-edge intensity (<1% of total intensity), the increase in total pre-edge intensity relative to 2 does not reflect the number of 3d holes in the two complexes.

Fig. 4 Valence unoccupied MO energy level and Mulliken population contour plots for 2 and 3. The energy level diagram for the β MO's are identical to the α MO's for Cr[TPP]O and are not included. Only the Cr 3d-based MOs are shown and ligand-based MOs have been omitted for clarity. The 3d_z² atomic orbital contributes to two MO's (a minority component is in the MO represented by a dashed line). The highlighted MO for Cr[TPC]O emphasizes the extra hole and the Cr(V) state of 3.

To understand the greater total pre-edge intensity in 3, individual contributions to the TDDFT transition manifold were mapped to the Cr 3d-based molecular orbitals. The results are summarized in Fig. 5, where both the dipole (dominant) and quadrupole (minor) contributions are included, even though the latter are not discernible at the magnification of the figure. Fig. 5 reveals that whereas only two 1s → 3d_z² transitions make up the majority of the intensity in the pre-edge of 2, the pre-edge of 3 is composed of transitions to molecular orbitals with 3d_xz, 3d_yz and 3d_z² character, indicating that 3 has somewhat lower molecular symmetry than 2. This can be explained by the difference in bonding between Cr and the equatorial porphyrin and corrole ligands. A decrease in molecular symmetry can result both from a stronger ‘pull’ from the short Cr–O distance and a ‘push’ from the equatorial plane due to short equatorial metal–ligand bonds. Table 1 shows that the Cr–N equatorial bond distances are >0.1 Å shorter in 3 (corrole) relative to 2 (porphyrin). Furthermore, the cavity size of corroles is known to be smaller than porphyrins, in agreement with the theoretical results presented here, which show that the calculated distance between two N atoms trans with respect to the Cr is 4.0 Å and 3.7 Å in 2 and 3, respectively. The 0.3 Å shortening and the larger size of Cr (relative to Mn and Fe) heightens the ‘push’ effect in 3. Consistent with this explanation, the NNNCr dihedral angle in 3 is ∼24° compared to ∼19° in 2. This larger displacement of the Cr out of the N₄ equatorial plane results in greater 3d_xz- and 3d_yz–4p mixing in 3 relative to 2, increasing the total Cr K-pre-edge intensity of 3, in spite of the fact that 2 has a shorter Cr–O bond and more intense 1s → 3d_z² transitions. Fig. 5 shows that the short Cr-equatorial bonds not only lead to a larger distortion of the Cr from the corrole plane, but also to increased bonding interaction involving the Cr 3d_z² orbital. Chromium 3d_z²-based valence orbitals have ∼5% and 20% N character in the case of 2 (orbital numbers 182, 190) and 3 (orbital numbers 157, 158), respectively. This increase in Cr–N interaction effectively creates a pseudo-trans-effect, which slightly weakens the Cr–O bond. The weakening is evidenced by an increase in the Mayer bond order of the Cr–O bond in the lower-valent 2 (Cr(IV)) relative to 3 (Cr(V)). This finding is an interesting deviation from the typical scenario in high-valent compounds of Fe and Mn in which the short metal–axial ligand distance shortens with increase in oxidation state. This result may also be contrasted with those of multiple-scattered-wave X_α (MSW X_α) calculations on Cr^IV[TTP]O, which indicated that the displacement of the Cr atom from the equatorial plane had no impact on the calculated spectra. This difference presumably reflects the fact that the MSW X_a study only included z-polarization and did not include xz and yz polarization, which is the dominant contributor to enhanced intensity in 3 relative to 2.

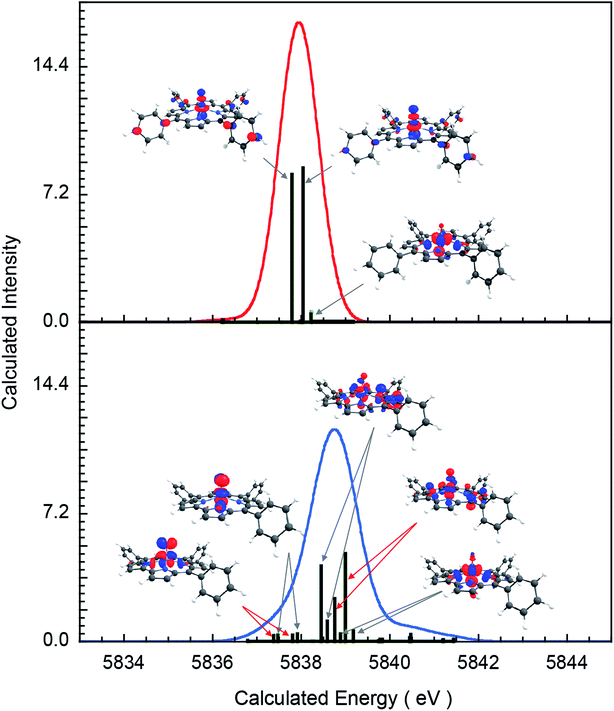Fig. 5 Individual transition contributing to the TDDFT calculated 1s →3d spectra: complex (top) 2, (bottom) 3.

Conclusion

A combined XAS and DFT/TDDFT study of three archetypal chromium porphyrinoid complexes – Cr^III[TPP]Cl (1), Cr^IV[TMP]-O (2), and Cr^V[TPC]O (3) – has provided detailed insights into the nature of the Cr K-pre-edge transitions of these compounds. The intensity-weighted average energy position of 1 (5990.9 eV), 2 (5992.0 eV), and 3 (5992.6 eV) are consistent with increasing metal oxidation state along the series. The total intensities of the pre-edge features, which were 0.2, 3.9, and 4.5 units for the three compounds, are also instructive. The roughly twenty-fold increase in intensity in the two oxo complexes is unsurprising and well-precedented for other first-row transition metals. The increased pre-edge intensity of 3 relative to 2, on the other hand, proved worthy of investigation. According to EXAFS and DFT analyses, the more contracted N₄ core of the corrole results in a greater out-of-plane displacement of the Cr in 3 relative to 2, which in turn accentuates the lower local symmetry of the Cr in 3 relative to 2. This difference helps us appreciate the TDDFT result that whereas two 1s → 3d_z² transitions make up the majority of the intensity in the pre-edge of 2, the pre-edge of 3 also includes fairly intense transitions to molecular orbitals with 3d_xz, 3d_yz and 3d_z² character, thus accounting for the somewhat higher overall intensity for 3. Finally, the increased overlap of the Cr 3d_z² orbital with the equatorial N atoms results in a pseudo-trans-effect that weakens the Cr–O bond in 3 relative to 2, in spite of the fact that 3 is more oxidized than 2.

Experimental section

Synthetic methods

meso-Tetramesitylporphyrin was purchased from Mid-Century Chemicals. Chromium(II) chloride (CrCl₂), chromium hexacarbonyl, and m-chloroperoxybenzoic acid (mCPBA) were purchased from Sigma-Aldrich. Chloroform was distilled from P₄O₁₀, deacidified by passing through a two-layered column of dry K₂CO₃ and dry basic alumina (Activity I), and stored over activated 4 Å molecular sieves. meso-Tetraphenylporphyrin²² and meso-triphenylcorrole²³ were prepared according to literature procedures. Chromium(III) meso-tetramesitylporphyrin chloride,²⁴ Cr^III[TMP]Cl, and chromium(III) meso-tetraphenylporphyrin chloride,²⁵ Cr^III[TPP]Cl (1), were prepared under aerobic conditions using protocols due to Adler et al.²⁶ Chromium(IV)-oxo meso-tetramesitylporphyrin, Cr^IV[TMP]O (2), was prepared as previously described,⁴⁴ with the following modifications: Cr^III[TMP]Cl and mCPBA (4 equiv.) were stirred in dry, deacidified CHCl₃ under argon for 15 min. Dry K₂CO₃ was added to the solution and after stirring for 3 min, the suspension was placed on a basic alumina (Activity I) column and flash-chromatographed with dry, deacidified CHCl₃ under argon, whereupon Cr^IV[TMP]O eluted as the first red band. Chromium(V)-oxo meso-triphenylcorrole was prepared as previously described using a method similar to that used for the tris(pentafluorophenyl)corrole analogue.²⁷

Cr K-edge XANES and EXAFS measurements

The Cr K-edge X-ray absorption spectra were measured at the Stanford Synchrotron Radiation Lightsource (SSRL). Complexes 1 and 3 were analyzed on the wiggler BL9-3 under standard ring conditions of 3 GeV and ∼500 mA. A Si(220) double crystal monochromator was used for energy selection. A harmonic rejection mirror was used and the monochromator detuned by 10% to reject components of higher harmonics. Complex 2 was analyzed on the wiggler BL7-3. The noM0 configuration was selected and the monochromator was detuned by 50%. For all measurements, the samples were maintained at a constant temperature of ∼10 K using an Oxford liquid He cryostat. Chromium K-edge XAS data were measured in both transmission mode using ion chambers and in total fluorescent yield mode using a PIPS detector. For the fluorescence measurements, background signal was suppressed by using soller slits equipped with a V filter. The solid samples were ground to a homogenous powder in a BN matrix. The homogeneous mixture was then placed in Al spacers and wrapped in Kapton tape. Internal energy calibration was accomplished by simultaneous measurement of the absorption of a Cr-foil placed between two ionization chambers located after the sample. The first inflection point of the foil spectrum was set at 5989 eV. At least two sweeps were collected on each spot to ensure that no radiation damage was observed. The data presented here are 6-, 8-, and 4-scan average spectra for 1, 2 and 3, respectively. Energy calibration, background correction, data averaging, and normalization were accomplished with the EXAFSPAK package. The data were processed by fitting a second-order polynomial to the pre-edge region and subtracting this from the entire spectrum as background in PySpline^27,28 and Athena which is part of the Demeter software package version 0.9.24.²⁹ A four-region spline of orders 2, 3, 3 and 3 was used to model the smoothly decaying post-edge region. Theoretical EXAFS signals χ(k) were calculated by using FEFF^30–32 (Macintosh version 7) on structures obtained from a reported crystal structure.²⁶ Theoretical models were fit to the data using EXAFSPAK.³³ The structural parameters varied during the fitting process were the bond distance (R) and bond-variance σ², which is related to the Debye–Waller factor resulting from thermal motion and static disorder of the absorbing and scattering atoms. The non-structural parameter ΔE₀ (the energy at which k = 0) was also allowed to vary but was restricted to a common value for every component in a given fit. Coordination numbers were systematically varied in the course of the fit but were fixed within a given fit.

DFT calculations

DFT geometry optimizations were carried out with the BP86 ^34–36 functional and a spin-unrestricted formalism (flipspin), allowing for broken-symmetry solutions, using the ORCA 3.0.3 program system.³⁷ The Ahlrichs all-electron triple-ζ-triple polarization basis set TZVPP^38–40 was used for Cr and TZVP was used for all other atoms. Tight SCF convergence criteria were employed throughout. The SlowConv criterion was employed. An SCF grid of 4 with no finalgrid was used. A higher grid (grid7) was used on the Cr atom. The geometry-optimized structures were used for TDDFT calculations to simulate the Cr K-pre-edge XAS region (as implemented in the ORCA package).^20,41,42 Löwdin spin populations^43,44 and Mayer bond orders⁴⁵ were calculated. The number of roots was set at 30, MaxDim was set at 300, “doQuad True” was selected and triplets were not calculated. The TDDFT calculations were performed (also with BP86) over the entire valence manifold and for both the spin-up (OrbWin = 0) and spin-down (OrbWin = 1) transitions. The calculated energies and intensities were broadened using the line-broadening script within ORCA to achieve half-widths of 1.5 eV to account for core-hole lifetime and instrument broadening. The calculated pre-edge energies were linearly upshifted by 154 eV for comparison with experimental spectra. Molecular orbital contour plots were generated with ChemCraft (https://www.chemcraftprog.com) and individual atomic orbital contributions to the molecular orbitals were obtained using QMForge.⁴⁶

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported in part by grant no. 262229 to AG from the Research Council of Norway. The Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. In particular, Rui Cao was supported by the same Department of Energy contract. The SSRL Structural Molecular Biology Program is supported by the DOE Office of Biological and Environmental Research, and by the National Institutes of Health, National Institute of General Medical Sciences (including P41GM103393). The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of NIGMS or NIH.

References

1. S. Ganguly, L. J. McCormick, J. Conradie, K. J. Gagnon, R. Sarangi and A. Ghosh, Inorg. Chem., 2018, 57, 9656–9669.
2. R. K. Hocking, S. DeBeer George, Z. Gross, F. A. Walker, K. O. Hodgson, B. Hedman and E. I. Solomon, Inorg. Chem., 2009, 48, 1678–1688.
3. S. Ganguly, J. Conradie, J. Bendix, K. J. Gagnon, L. J. McCormick and A. Ghosh, J. Phys. Chem. A, 2017, 121, 9589–9598.
4. S. Ganguly, L. J. Giles, K. E. Thomas, R. Sarangi and A. Ghosh, Chem.–Eur. J., 2017, 23, 15098–15106.
5. J. H. Palmer and K. M. Lancaster, Inorg. Chem., 2012, 51, 12473–12482.
6. H. Lim, K. E. Thomas, B. Hedman, K. O. Hodgson, A. Ghosh and E. I. Solomon, Inorg. Chem., 2019, 58, 6722–6730.
7. R. Sarangi, L. J. Giles, K. E. Thomas and A. Ghosh, Eur. J. Inorg. Chem., 2016, 3225–3227.
8. S. Ganguly and A. Ghosh, Acc. Chem. Res., 2019, 52, 2003–2014.
9. J. E. Penner-Hahn, M. Benfatto, B. Hedman, T. Takahashi, S. Doniach, J. T. Groves and K. O. Hodgson, Inorg. Chem., 1986, 25, 2255–2259.
10. R. G. Shulman, Y. Yafet, P. Eisenberger and W. E. Blumberg, Proc. Natl. Acad. Sci. U. S. A., 1976, 73, 1384–1388.
11. R. Sarangi, Coord. Chem. Rev., 2013, 257, 459–472.
12. T. E. Westre, P. Kennepohl, J. G. DeWitt, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., 1997, 119, 6297–6314.
13. J. E. Penner-Hahn, R. A. Scott, K. O. Hodgson, S. Doniach, S. R. Desjardins and E. I. Solomon, Chem. Phys. Lett., 1982, 88, 595–598.
14. C. R. Randall, L. J. Shu, Y. M. Chiou, K. S. Hagen, M. Ito, N. Kitajima, R. J. Lachicotte, Y. Zang and L. Que, Inorg. Chem., 1995, 34, 1036–1039.
15. D. F. Leto and T. A. Jackson, Inorg. Chem., 2014, 53, 6179–6194.
16. T. C. Weng, W. Y. Hsieh, E. S. Uffelman, S. W. Gordon-Wylie, T. J. Collins, V. L. Pecoraro and J. E. Penner-Hahn, J. Am. Chem. Soc., 2004, 126, 8070–8071.
17. J. Yano, J. Robblee, Y. Pushkar, M. A. Marcus, J. Bendix, J. M. Workman, T. J. Collins, E. I. Solomon, S. D. George and V. K. Yachandra, J. Am. Chem. Soc., 2007, 129, 12989–13000.
18. J. F. Berry, E. Bill, E. Bothe, S. D. George, B. Mienert, F. Neese and K. Wieghardt, Science, 2006, 312, 1937–1941.
19. T. A. Jackson, J. U. Rohde, M. S. Seo, C. V. Sastri, R. DeHont, A. Stubna, T. Ohta, T. Kitagawa, E. Munck, W. Nam and L. Que Jr, J. Am. Chem. Soc., 2008, 130, 12394–12407.
20. F. Tiago de Oliveira, A. Chanda, D. Banerjee, X. Shan, S. Mondal, L. Que Jr, E. L. Bominaar, E. Munck and T. J. Collins, Science, 2007, 315, 835–838.
21. P. Chandrasekaran, S. C. Stieber, T. J. Collins, L. Que Jr, F. Neese and S. DeBeer, Dalton Trans., 2011, 40, 11070–11079.
22. A. D. Adler, F. R. Longo, J. D. Finarelli, J. Goldmacher, J. Assour and L. Korsakoff, J. Org. Chem., 1967, 32, 476.
23. B. Koszarna and D. T. Gryko, J. Org. Chem., 2006, 71, 3707–3717.
24. J. T. Groves, W. J. Kruper, R. C. Haushalter and W. M. Butler, Inorg. Chem., 1982, 21, 1363–1368.
25. D. A. Summerville, R. D. Jones, B. M. Hoffman and F. Basolo, J. Am. Chem. Soc., 1977, 99, 8195–8202.
26. A. D. Adler, F. R. Longo, F. Kampas and J. Kim, J. Inorg. Nucl. Chem., 1970, 32, 2443–2445.
27. A. E. Meier-Callahan, H. B. Gray and Z. Gross, Inorg. Chem., 2000, 39, 3605–3607.
28. A. Tenderholt, B. Hedman and K. O. Hodgson, PySpline: A Modern, Cross-Platform Program for the Processing of Raw Averaged XAS Edge and EXAFS Data, X-ray Absorption Fine Structure - XAFS13, Stanford University, ed. B. Hedman and P. Pianetta, American Institute of Physics Stanford University, 2007, pp. 105–107.
29. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
30. J. Mustre de Leon, J. J. Rehr, S. I. Zabinsky and R. C. Albers, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 4146–4156.
31. J. J. Rehr, J. Mustre de Leon, S. I. Zabinsky and R. C. Albers, J. Am. Chem. Soc., 1991, 113, 5135–5140.
32. S. I. Zabinsky, J. J. Rehr, A. Ankudinov, R. C. Albers and M. J. Eller, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 2995–3009.
33. G. N. George, EXAFSPAK and EDG-FIT, Stanford Synchrotron Radiation Laboratory, Stanford Linear Accelerator Center, Stanford, CA, 2000.
34. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
35. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
36. J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539.
37. F. Neese, ORCA: An ab initio, DFT and semiempirical SCF-MO package; Version 3.0.1, University of Bonn, Germany, 2013.
38. A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577.
39. A. Schaefer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
40. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
41. S. DeBeer George, T. Petrenko and F. Neese, Inorg. Chim. Acta, 2008, 361, 965–972.
42. S. DeBeer George, T. Petrenko and F. Neese, J. Phys. Chem., 2008, 112, 12936–12943.
43. P.-O. Löwdin, J. Chem. Phys., 1950, 18, 365–375.
44. P.-O. Löwdin, Adv. Chem. Phys., 1970, 5, 185–199.
45. I. Mayer, Chem. Phys. Lett., 1983, 97, 270–274.
46. A. Tenderholt, QMForge, Stanford University, 2007.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02335c

---