Open Access Article
Open Access ArticleThe effects of Stone–Wales defects on the thermal properties of bilayer armchair graphene nanoribbons
Xingli Zhang *ac,
Jinglan Zhanga and
Ming Yang*bc
*ac,
Jinglan Zhanga and
Ming Yang*bc
aCollege of Mechanical and Electrical Engineering, Northeast Forestry University, Harbin 150040, China. E-mail: zhang-xingli@nefu.edu.cn
bInstitute of Engineering Thermophysics, Chinese Academy of Sciences, Beijing 100190, China. E-mail: yangming@iet.cn
cDepartment of Mechanical Engineering, University of Colorado, Boulder, CO 80309, USA
First published on 20th May 2020
Abstract
We investigate the influence of Stone–Wales (S–W) defects on the thermal properties of bilayer graphene nanoribbons (BGNRs) with armchair edges by nonequilibrium molecular dynamics simulations (NEMD). It is shown that an increasing number of S–W defects leads to a significant decrease of the thermal conductivity of BGNRs at room temperature. Moreover, the AA-stacked BGNRs have significantly higher thermal conductivity than that of the AB-stacked BGNRs for all S–W defect numbers. In the temperature range of 300–700 K, the S–W defects always have a weaker effect on heat transfer of AB-stacked BGNRs than AA-stacked BGNRs, which is closely related to their weaker anharmonic effects induced by structure defects. In addition, the simulation results are further explained by performing an analysis of phonon spectrum properties and phonon vibrational modes.
Introduction
Graphene nanoribbons have outstanding thermal transport properties due to their honeycomb lattice structure consisting of sp2 bonds, and have attracted immense interest in high performance electronic applications.1–3 Compared with monolayer graphene nanoribbons, bilayer graphene nanoribbons (BGNRs) have a relatively lower thermal conductivity because of the grain boundaries in each layer and weak coupling between layers. However, experimentally, the thermal conductivity of BGNRs still reaches 2800 W m−1 K−1, much larger than that of most other thermally conductive materials.4,5 In addition, BGNRs are more advantageous in their sensitivity to external perturbation and tunability with a perpendicular electric field. These factors raise the exciting prospect of using BGNRs as promising materials in nanotechnology.6,7 It is well known that synthesis, processing and integration of BGNRs could result in various defects, such as point vacancies, Stone–Wales and impurities.8 These structure defects strongly influence the heat transfer performance of BGNRs inevitably. The effects caused by defects are not only disadvantages, on the contrary, they provide a route to manipulate the thermal conductivity of BGNRs to achieve new functionalities by intentionally introducing these defects.Stone–Wales (S–W) defects are the class of topological defects in nature, consisting of two pairs of pentagons and heptagons rings, which are the result of a rotation of the C–C bond by 90°. The S–W defects are one of the most common defects in graphene, which can be observed and characterized in graphene by high resolution transmission electron microscopy.9,10 Some investigations about the effect of S–W defects on thermal transport properties of graphene have also been reported. Krasavin et al.11 used the phonon Boltzmann transport equation (BTE) to calculate the thermal conductivity of graphene nanoribbons (GNRs) with the S–W defects scatterings taken into account, and a pronounced decrease of the thermal conductivity due to S–W defects is found at low temperatures; Yeo et al.12 found that the presence of SW defects can decrease the thermal conductivity of GNRs in the temperature range 100–600 K by more than 80% as defect densities are increased to 10% coverage; Ebrahimi et al.13 using molecular dynamics (MD) simulations, explored the influence of the concentrations of the S–W defects on the thermal conductivity of zigzag and armchair GNRs. However, almost the previous studies have been devoted to exploring effects of S–W defects on thermal properties of monolayer graphene, and the investigations on BGNRs are relatively lacking.
In this paper we study and compare the effect of S–W defects on the thermal transport properties of BGNRs with two stacking orders, AB-stacked and AA-stacked. Furthermore, using MD simulations, the modulations on defects number and temperature dependence of thermal conductivity are investigated. By analyzing of the phonon properties of the atoms, we reveal the underlying physical mechanism of thermal transport in the BGNRs.
Model and methodology
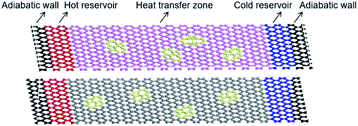
We perform the non-equilibrium molecular dynamics simulation (NEMD) with the LAMMPS code. The AIREBO potential is used to describe the interactions of the carbon atoms within same layers, and the Lennard-Jones potential is used to describe the van der Waals interactions for carbon atoms between different layers. This study used samples consisting of 1600 atoms and the S–W defects are randomly introduced by a 90° rotation of two adjacent atoms, as shown in Fig. 1, thus the increasing number of S–W defects in each layer are achieved by the rotation of 1, 2, 3 and 4 pairs of atoms. The S–W defects number of two layers are same and the defects must not be connected with each other in the same layer.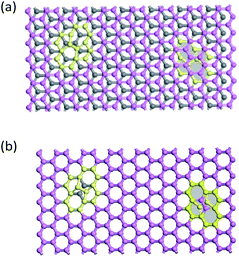 | ||
| Fig. 1 Illustration of BGNRs containing S–W defects configuration (a) AB stacking type; (b) AA stacking type. | ||
Fig. 2 shows the simulation model used in the present study. The adiabatic wall is fixed at each end of BGNRs to prevent atoms escaping from the system, and the fixed boundary condition is applied. The hot and cold reservoirs regions are used to create a temperature gradient in the system by controlling the energy given or taken from these regions. We divide the simulation system (excluding the adiabatic zones at the two ends) along the heat flux direction into 42 equal segments. The instantaneous local temperature in each segment is evaluated from the kinetic energy of the atoms within it using the formula KE = (3/2) × KB × T, where KB is Boltzmann constant. While the simulation temperature is below the Debye temperature (322 K), quantum corrections are conducted to calculate the temperatures.
The time step for the simulation is set as 0.5 fs. The simulations consist of two stages: the first stage is to ensure the whole system reach a steady state in a constant-temperature ensemble (NVT) with a coupling time of 106 MD steps; the second stage is to keep the energy conserved in a constant-energy ensemble (NVE) with a coupling time of 2 × 106 MD steps. Based on the Fourier law of conduction, the thermal conductivity is given as:
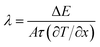 | (1) |
Results and discussion
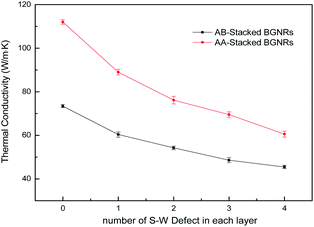
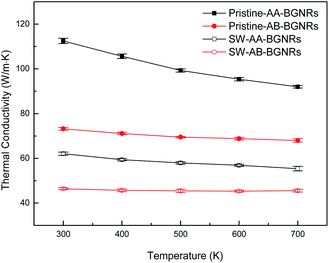
Fig. 3 shows the thermal conductivities of AB-stacked and AA-stacked BGNRs with different numbers of S–W defects. As it can be seen, the increasing defect number from 0 to 4 induces remarkable changes to the thermal transport properties of BGNRs. For example, containing four S–W defect in each layer leads to 38% and 46% reduction of thermal conductivity, corresponding to AB and AA-stacked BGNRs, respectively. Such result expresses the same changing trend compared with the results in ref. 14 and 15 which measured the thermal conductivity of monolayer GNRs doping S–W defects by computational method. It should be noted that the thermal conductivities obtained in this study are clearly smaller than these of previous works due to the different potentials used and size effects.16–18 Additionally, as can be observed, the thermal conductivity of AA-stacked BGNRs is much greater than the AB-stacked BGNRs for samples of the same number of S–W defects. The theoretical calculations from Berber et al.19 suggested that the thermal conductivity of multilayer graphene was reduced comparing to monolayer graphene because of the presence of interlayer coupling, so the difference of thermal conductivity between two type of BGNRs may be attributed to this factor. It has been also reported that the top layer of AB-stacked BGNRs has more wrinkles than its bottom layer, which could result in a strong suppression of thermal transport between two layers due to the significant phonon mismatch.15 Therefore, the thermal conductivity of AB-stacked BGNRs is much lower than that of AA-stacked case.Fig. 4 presents the thermal conductivity of BGNRs with S–W defects as a function of the temperature from 300 to 700 K. The thermal property of BGNRs with S–W defects has less dependency on temperature compared with the pristine system, which shows obvious reduction of thermal conductivity with the increasing temperature due to the effect of phonon umklapp scattering.20 Moreover, the thermal conductivity of AB-stacked BGNRs is more insensitive to the temperature changes than that of AA-stacked style. The structural disorder effects of thermal conductivity for low dimensional materials were studied in ref. 21 and 22 based on modal localization analysis and Allen-Feldman approach, and it was confirmed that the suppression of thermal conductivity due to structure defects was shown to be mild. This originates from the presence of low frequency vibrational modes, which could maintain a well-defined polarization and help preserve the thermal conductivity in the presence of disorder. Additionally, the AB-stacked BGNRs have more stable structure than AA-stacked BGNRs under natural condition, which may reduce more sensitivity of the phonon coupling and phonon umklapp scattering due to the increased temperature. The tendency of the variation of thermal conductivities in our simulation is in good agreement with the temperature dependence on the thermal conductivity of the monolayer graphene nanoribbons with S–W defect.23
In order to find the thermal transport mechanism of this simulation, the phonon frequency spectrum of BGNRs that represents vibrational energy of carbon atoms per unit frequency is investigated as shown in Fig. 5. The phonon spectrum function G(ω) is determined by calculating the Fourier transform of the velocity autocorrelation function.24 Fig. 5 indicates that the peaks of G(ω) at frequencies around 50 THz are damped out and shift towards low frequency when the AA-stacked and AB-stacked BGNRs contain 4 S–W defects, suggesting that the S–W defects might decrease the phonon mean free path due to high collision of the low energy phonons. It is also revealed that the phonon scattering is the main factor in reducing thermal conductivity in multilayer graphene structures.25 Comparing Fig. 5(a) and (b), it can be seen that the peaks of AA-stacked BGNRs decrease more largely than the AB-stacked case, which is consistent with the reduction results of thermal conductivity. It means that S–W defects lead to a greater impact on AA-stacked BGNRs under same condition.
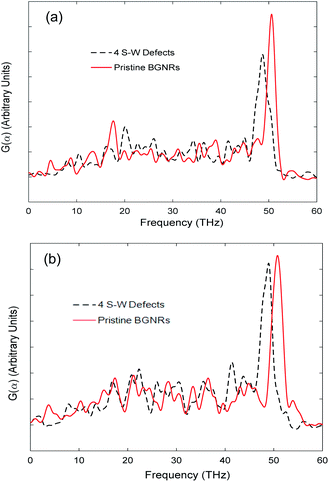 | ||
| Fig. 5 The phonon spectra of BGNRs with different number of S–W defects at 300 K (a) AA-stacked; (b) AB-stacked. | ||
We also analyze the phonon vibrational modes through the calculation of phonon participation ratio to reveal the thermal transport essence of BGNRs doping S–W defects. The participation ratio is used to describe the fraction of atoms participating in a particular phonon mode, which is defined as:26,27
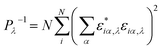 | (2) |
We plot the phonon participation ratio of AA-stacked and AB-stacked BGNRs in Fig. 6. It is clear that the S–W defects make a large reduction in the participation ratio of BGNRs compared with the pristine case, indicating the existence of more localized modes due to structure defects. For S–W defects structure, the numerous localizations induce inelastic phonon scatterings, which could increase the total number of possible scattering outcomes. Consequently, this reduces the effective capability of the BGNRs to transmit thermal energy across the S–W defects.28 Additionally, it can be observed that the overall phonon participation ratio of AB-stacked BGNRs is less than that of AA-stacked BGNRs, which indicates that the AB-stacked ordering may enhance phonon localizations in BGNRs compared with AA-stacked case.
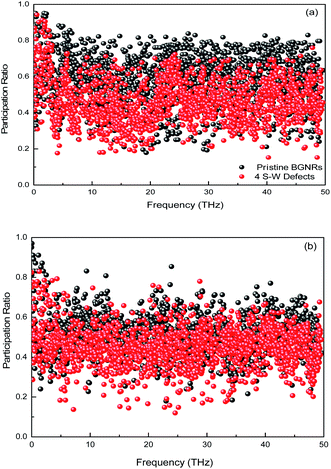 | ||
| Fig. 6 The phonon participation ratio of BGNRs with different number of S–W defects at 300 K (a) AA-stacked; (b) AB-stacked. | ||
Conclusions
In summary, we have performed NEMD method to study the effect of S–W defects on thermal transport properties of BGNRs. It is found that the S–W defects could effectively influence the thermal conductivity of the AB-stacked and AA-stacked BGNRs. For difference numbers of S–W defects and temperatures, the thermal conductivity of AA-stacked BGNs is much higher than that of AB-stacked one due to the weaker interlayer coupling. In addition, the thermal conductivity of AB-stacked BGNRs has less of a dependence on temperature. The phonon frequency spectrum results suggest that the S–W defects might decrease the phonon mean free path due to high collision of the low energy phonons in BGNRs. Moreover, the phonon vibrational modes analysis reveals that the S–W defects also cause the increase of phonon localizations in BGNRs, which lead to the reduction of thermal conductivity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work has been supported by the National Natural Science Foundation of China (grant no. 51706039 and 51606192).Notes and references
- J. Hu, X. Ruan and Y. P. Chen, Nano Lett., 2015, 9, 2730–2735 CrossRef PubMed.
- A. A. Balandin, S. Ghosh, W. Z. Bao, I. Calizo, D. Teweldebrhan and F. Miao, Nano Lett., 2208, 8, 902–907 CrossRef PubMed.
- S. J. Mahdizadeh and E. K. Goharshadi, J. Nanopart. Res., 2014, 16, 2553 CrossRef.
- Y. Tang, J. Li, Xi. Wu, Q. Liu and Y. Liu, Appl. Surf. Sci., 2016, 362, 86–92 CrossRef CAS.
- W. R. Zhong, M. P. Zhang and B. Q. Ai, Appl. Phys. Lett., 2011, 98, 113107 CrossRef.
- S. Q. Hu, J. Chen, N. Yang and B. W. Li, Carbon, 2017, 116, 139–144 CrossRef CAS.
- T. Lehmann, D. A. Ryndyk and G. Cuniberti, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 125420 CrossRef.
- J. Kotakoski, F. R. Eder and J. C. Meyer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 201406 CrossRef.
- S. P. Wang, J. G. Guo and L. J. Zhou, Phys. E, 2013, 48, 29–35 CrossRef CAS.
- H. Malekpour, P. Ramnani, S. Srinivasan, G. Balasubramanian, D. L. Nika, A. Mulchandani, R. K. Lakee and A. A. Balandin, Nanoscale, 2016, 8, 14608–14616 RSC.
- S. E. Krasavin and V. A. Osipov, J. Phys.: Condens. Matter, 2015, 27, 425302 CrossRef CAS PubMed.
- Y. J. Jie, L. Zishun and N. T. Yong, Nanotechnology, 2012, 23, 385702 CrossRef.
- S. Ebrahimi and M. Azizi, Mol. Simulat., 2017, 1366654 Search PubMed.
- D. L. Feng, Y. H. Feng, Y. Chen, W. Li and X. X. Zhang, Chin. Phys. B, 2013, 22, 016501 CrossRef.
- Y. Liu, H. Yang, N. Liao and P. Yang, RSC Adv., 2014, 4, 54474 RSC.
- Z. X. Guo, D. Zhang and X. G. Gong, Appl. Phys. Lett., 2009, 95, 163130 Search PubMed.
- W. W. Cai, A. L. Moore, Y. W. Zhu, X. S. Li, S. S. Chen and L. Shi, Nano Lett., 2010, 10, 1645–1651 CrossRef CAS PubMed.
- X. Nie, L. Zhao, S. Deng, Y. Zhang and Z. Du, Int. J. Heat Mass Tran., 2019, 137, 161–173 CrossRef CAS.
- S. Berber, Y. K. Kwon and D. Tomanek, Phys. Rev. Lett., 2000, 84, 46130–46136 CrossRef PubMed.
- H. Zhan, Y. Zhang, J. M. Bell and Y. Gu, J. Phys. Chem. C, 2015, 119, 1748–1752 CrossRef CAS.
- T. Zhu and E. Ertekin, Nano Lett., 2016, 16, 4763–4772 CrossRef CAS PubMed.
- T. Zhu and E. Ertekin, Phys. Rev. B, 2016, 93, 155414 CrossRef.
- T. Y. Ng, J. J. Yeo and Z. S. Liu, Carbon, 2012, 50, 4887–4893 CrossRef CAS.
- S. K. Chien, Y. T. Yang and C. K. Chens, Phys. Lett. A, 2010, 374, 4885 CrossRef CAS.
- S. Ghosh, W. Bao, D. L. Nika, S. Subrina, E. P. Pokatilov and C. N. Lau, Nat. Mater., 2010, 9, 555–558 CrossRef CAS PubMed.
- X. Zhang, M. Hu, K. P. Giapis and D. Poulikakos, J. Heat Tran., 2012, 134, 102402 CrossRef.
- Y. Wang, A. K. Vallabhaneni, B. Qiu and X. Ruan, Nanoscale Microscale Thermophys. Eng., 2014, 18, 155–182 CrossRef.
- C. Shao, Q. Rong, N. Li and H. Bao, Phys. Rev. B, 2018, 98, 155418 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |