Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Strain engineering and lattice vibration manipulation of atomically thin TaS2 films†
Xing Wu‡
 *a,
Yongqing Cai‡b,
Jihong Bian‡c,
Guohui Sua,
Chen Luoa,
Yaodong Yangc and
Gang Zhang
*a,
Yongqing Cai‡b,
Jihong Bian‡c,
Guohui Sua,
Chen Luoa,
Yaodong Yangc and
Gang Zhang *b
*b
aShanghai Key Laboratory of Multidimensional Information Processing, School of Communication and Electronic Engineering, 500 Dongchuan Road, Shanghai 200241, China. E-mail: xwu@ee.ecnu.eud.cn
bInstitute of High Performance Computing (IHPC), A*STAR, 138632, Singapore. E-mail: zhangg@ihpc.a-star.edu.sg
cFrontier Institute of Science and Technology, State Key Laboratory for Mechanical Behavior of Materials, Xi'an Jiaotong University, Xi'an 710054, China
First published on 28th April 2020
Abstract
Beside the extraordinary structural, mechanical and physical properties of two-dimensional (2D) materials, the capability to tune properties via strain engineering has shown great potential for nano-electromechanical systems. External strain, in a controlled manner, can manipulate the optical and electronic properties of the 2D materials. We observed the lattice vibration modulation in strained mono- and few-layer tantalum sulfide (TaS2). Two Raman modes, E1g and E12g, exhibit sensitive strain dependence, with the frequency of the former intensity increasing and the latter decreasing under a compressive strain. The opposite direction of the intensity shifts, which cannot be explained solely by van der Waals interlayer coupling, is attributed to strain-induced competition between the electron–phonon interlayer coupling and possible stacking-induced changes of the intralayer transport. Our results enrich the understanding of the lattice vibration of TaS2 and point to strain engineering as a powerful tool for tuning the electron–phonon coupling of 2D materials.
Introduction
The two-dimensional (2D) transition metal dichalcogenide (TMD) materials including MX2 (M = Mo, W, Ta; X = S, Se, Te),1–11 are most important van der Waals materials that exhibit many interesting phenomena, such as charge density waves (CDWs), hidden phases and superconductivity.12–15 For the atomically thin tantalum sulfide (TaS2), the interaction between electron and phonon for a strong coupling enhanced superconductivity has attracted lots of research interest.16,17 The thickness dependent superconductivity feature has been reported in such types of layered materials, and the transition temperature Tc is found experimentally to be enhanced with decreasing the film thickness due to the interlayer interaction.18–20 The interlayer interactions in 2D materials are related to not only the thickness but also the layer stacking order. In this respect, the crystallographic structure of TaS2 crystals is generally different from the common structures of MoS2, MoSe2, WS2 and WSe2.21,22 According to the convention theory of Wilson and Yoffe,21 the position of the atoms in each TMD atomic plane can be specified by three points in a triangular lattice (A, B, C). The upper (lower) case denotes the chalcogenide (metal) atoms. 1 L TaS2 has the same trigonal prismatic (H) structure as 1 L MoS2 (denoted as ABA or equivalently ACA). As the layer number increases, however, the stacking order of TaS2 layers differs subtly from that of MoS2. Multilayer MoS2 exhibits the so called 2HC structure, which can be represented as (ABA or BAB). In contrast, TaS2 exhibits the 2HA structure (ACA BCB), in which the Ta atoms in all the layers are aligned vertically, but the sub-lattice is rotated by 60° with respect to that of the neighboring layer. It would be interesting to examine how this subtle stacking difference and the metallic nature of TaS2 may influence the interlayer interactions, especially under the compressive strain.The nature of lattice vibration of material is fundamental in understanding its various physical properties, placing great demands on a comprehensive and complete determination of its elastic, electronic, phonon and electron–phonon properties. Moreover, it plays key role in various technological applications, including mobility in field-effect transistor,23 transition temperature of superconductor,24 performance of nano-electromechanical systems,25 and figure of merit of thermoelectric device.26 Raman spectroscopy is a powerful and non-destructive technique to investigate the lattice vibrational modes and interlayer interactions in 2D materials.27 In particular, recent research using ultralow-frequency Raman spectroscopy has revealed a set of interlayer phonon modes in few-layer graphene,28–32 phosphorene13,15,33–35 and MoS2, WS2, MoSe2 and WSe2.27,36–40 The shear (S) modes involves the lateral displacement of individual rigid layers. As these interlayer modes are created entirely from the interlayer coupling, they are highly sensitive to the detailed layer characteristics, including the layer number, interlayer coupling strength and stacking order, as well as surface and interface quality. Moreover, in application of 2D materials, strain can be introduced either intentionally or unintentionally. The difference in lattice constant and thermal expansion coefficient between 2D material and its supporting substrate can generate strain.41–43 And tensile strain also can be introduced in a controllable manner such as a tip of atomic force microscopes.44 Strain engineering, understood as the field that study how the physical properties of materials can be tuned by controlling the elastic strain fields applied to it,45 provides a perfect platform to manipulate the lattice vibration mode and electron–phonon coupling. More fascinating phenomena have been theoretically predicted for strained TaS2,46 but yet to be realized experimentally. Thus, strain controllable electron–phonon coupling measurements are critical for in-depth understanding and further applications of 2D TaS2.47–49 Comparing with other well studied TMDs such as MoS2, MoSe2, WS2 and WSe2, the phonon properties, interlayer interaction and strain dependences in monolayer and few-layer TaS2 are much less explored.
In this article, we present the first report of Raman scattering studies of mono- and few-layer 2H-TaS2 with and without strain. The compressive strain has been applied locally on the TaS2, while the lattice vibration has been detected by the dedicated designed ultrasensitive Raman spectroscopy and verified by the first-principle calculation.
Experimental section
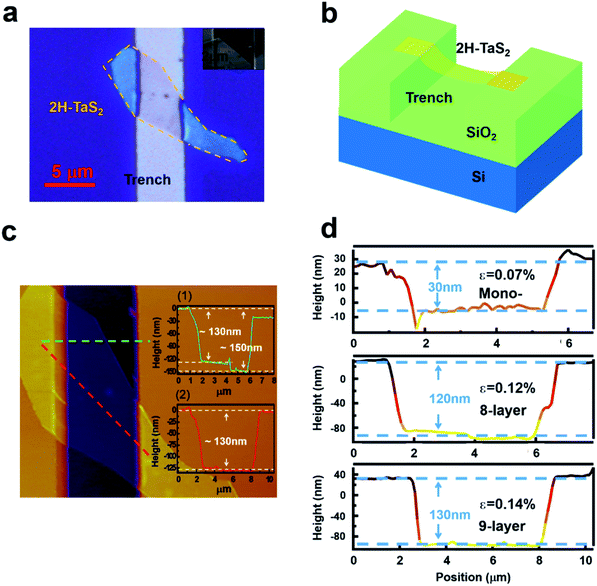
To prepare the suspended 2H-TaS2. High-quality 2H-TaS2 single crystal were grown Ta metal wires (99.95 purity) and S pellets (99.99% purity) by iodine (99.8%) vapour transport in a gradient of 730–770 °C in sealed quartz tubes for 21 days. The atomically thin suspended 2H-TaS2 membranes are obtained by using mechanical exfoliation method on the pre-defined trenches on 90 nm thick SiO2 wafers. The exfoliation process is carried out in the glove box with N2 atmosphere to avoid sample oxidation. The trenches are defined by standard photolithography method, followed by dry etching in an inductively coupled plasma (ICP) system, where CH4 and CHF3 are used as etching gases. The typical width of the trenches is 5 μm and the depth is ∼150 nm.TaS2 flakes are imaged by atomic force microscopy (AFM) (Cypher S, Oxford Instruments Asylum Research, Inc., USA) to determine the sample thickness. The tapping mode of measurement (in the repulsive force regime) was chosen. For TaS2 samples exhibiting lateral thickness variation, we observed step heights of individual layers of 0.6–0.7 nm. This value is compatible with the 0.62 nm interlayer spacing of a single layer of the S–Ta–S building block of the TaS2 crystal. The measurements show that exfoliation produces layers with a discrete number of these units. We consequently designate the thickness of our films in terms of the number of these TaS2 layers (nL). From extensive AFM scanning of freshly deposited samples, we found no evidence of structural irregularity on the nanometer length scale.
Terahertz Raman spectroscopy was performed under normal incidence with a HeNe laser centered at 488 nm. The laser beam was focused to a diameter of ∼2 μm on the samples by a ×50 objective. The reflected radiation was collected by the same objective and analyzed with a grating spectrometer equipped with a liquid-nitrogen-cooled charge coupled device (CCD). A combination of one reflective Bragg grating and two Bragg notch filters removed the majority of the laser side bands and allowed measurements of the Raman shift down to ∼8 cm−1. The typical spectral resolution was 0.5 cm−1. To avoid significant laser heating of the samples, excitation powers of 1 mW (on the sample) were used. The heating effect was estimated to be <0.5 K under the excitation conditions for all samples.
First-principles calculations were performed to investigate the strain induced frequency shift of zone-centered phonons by using the Quantum-Espresso code.54 We used the norm-conserving pseudopotential and the local density approximation (LDA) of Perdew–Wang together with an energy cutoff up to 70 Ry. A 15 × 15 × 1 Monkhorst–Pack grid was adopted to sample the first Brillouin zone for the electronic densities. The relaxed in-plane lattice constants (a = b) for monolayer and bulk TaS2 are 3.254 and 3.252 Å respectively. The c lattice constant of bulk TaS2 is 11.598 Å. To avoid the spurious interaction between images, a vacuum region with thickness of 15 Å was used. The evolution of the frequencies of zone-centered phonons with strain was calculated within the scheme of density functional perturbation theory (DFPT).
Results and discussion
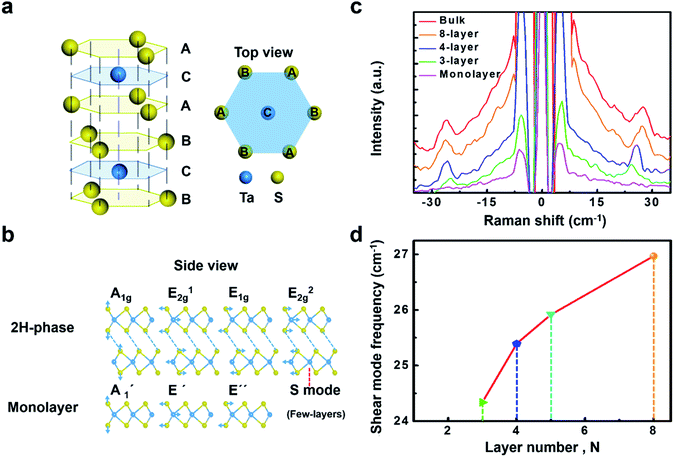
It is challenging in experimental studying monolayer and few-layer TaS2, partially due to the difficulty in exfoliating and also particularly susceptible to oxidation in atmospheric conditions,50 which hinder the manipulation of atomic thin TaS2 flakes in air. Although complex encapsulation techniques help preserving samples from oxidation, we find that a rapid integration of freshly exfoliated flakes into final devices and their immediate transfer to vacuum conditions for measurement also permits retaining the pristine properties of most TaS2 samples (details see the method section). Benefitted from the appropriate transfer, clear Raman spectrum is observed in the present work.Monolayer TaS2 consists of an atomic layer of Ta sandwiched between two layers of S in a trigonal prismatic structure (Fig. 1a). Bulk 2H-TaS2 is formed by stacking monolayer TaS2 with adjacent layers rotated by 180° with respect to one another. We summarize the characters of the phonon modes for both the bulk (2H phase) and monolayer TaS2 in Fig. 1b with respect to the symmetry assignment, frequency, optical character, and eigenvectors. The primitive cell of 2H-TaS2 and monolayer TaS2 contains six atoms. The Raman active modes are A1g, E12g and E1g. Out-of-plane A1g Raman mode in 2H-TaS2, matches with the homopolar 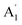 mode in the monolayer counterpart, where the top and bottom sulfur layers vibrate out of phase with direction normal to the basal plane while the Ta layer remains stationary. In-plane vibration mode E12g involves displacement of Mo and S atom, associated with the in-plane vibration of two S atoms in opposite directions, and this mode is forbidden in backscattering measurements on a surface perpendicular to the c axis. Fortunately, this mode can be observed under the compressive strain although it disappears in strain-free samples (as discussed later). The low ωS = 20–30 cm−1, which is strongly dependent on layer number N and is absent in monolayers (Fig. 1c), originates from interlayer shearing. With decreasing N, the shear mode frequency ωS decreases quickly due to the reduced effective interlayer spring constant. It can be quantitatively described as ωS = ωS,Bulk
mode in the monolayer counterpart, where the top and bottom sulfur layers vibrate out of phase with direction normal to the basal plane while the Ta layer remains stationary. In-plane vibration mode E12g involves displacement of Mo and S atom, associated with the in-plane vibration of two S atoms in opposite directions, and this mode is forbidden in backscattering measurements on a surface perpendicular to the c axis. Fortunately, this mode can be observed under the compressive strain although it disappears in strain-free samples (as discussed later). The low ωS = 20–30 cm−1, which is strongly dependent on layer number N and is absent in monolayers (Fig. 1c), originates from interlayer shearing. With decreasing N, the shear mode frequency ωS decreases quickly due to the reduced effective interlayer spring constant. It can be quantitatively described as ωS = ωS,Bulk![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(π/2N) with a bulk shear mode frequency ωS,Bulk = 26.7 cm−1 (solid line, Fig. 1d), and has been used to accurately determine the layer number N of few-layer TaS2. Although TaS2 has different stacking order from MoS2, MoSe2, WS2 and WSe2, they share the same crystal symmetry groups and exhibit similar Raman selection rules for interlayer phonons. The sensitivity of the frequencies of these modes on the thickness suggests an additional method capable of determining the number of layer by Raman spectrum.
cos(π/2N) with a bulk shear mode frequency ωS,Bulk = 26.7 cm−1 (solid line, Fig. 1d), and has been used to accurately determine the layer number N of few-layer TaS2. Although TaS2 has different stacking order from MoS2, MoSe2, WS2 and WSe2, they share the same crystal symmetry groups and exhibit similar Raman selection rules for interlayer phonons. The sensitivity of the frequencies of these modes on the thickness suggests an additional method capable of determining the number of layer by Raman spectrum.
To generate strain in a controllable manner, a tip of atomic force microscopes was adopted to load stress on suspended graphene.44 The other method is to transfer 2D material onto a flexible substrate, then strain can be generated by directly applying mechanical loading, for example, by bending, stretching or twisting the system.51 However, in both of these two strategies, only tensile strain can be loaded on 2D materials. To study the effect of compressive strain on lattice dynamics of atomically thin TaS2, a new strategy is developed in the present work. To study the strain effect of atomically thin TaS2, a special experimental setup is designed. Here in this work, by using advanced nano-fabrication process, local compression strain with a few micro meter has been applied to the 2H-TaS2 flake. The TaS2 is transferred on a trench to introduce the local compressive strain. The width of the trench is 5 μm. The advantage of this strategy is to use suspended atomically thin TaS2 sheets, suppressing the possible influence due to the substrate scattering. In our experiment, the compressive strain is fully applied on the TaS2 flake and is the intrinsic strain. Optical image shows dramatic contrast on the suspended area with the compressive strain and the one without the strain (Fig. 2a). It can be seen that the contrast of the suspended area is much lower than the one on the substrate. The schematic of the experiment platform is shown in Fig. 2b. It is noted that when a strain is applied to TaS2 materials, mechanical failure may occur either in the TaS2 materials or at the interface between TaS2 material and its supporting substrate. The Raman signals on the silicon dioxide substrate are consistent with the signals on other substrates, indicating no detachment failure at the interface between TaS2 and substrate. This is the same as the previous reports on the graphene system.51 Atomic force microscopy (AFM) has been used to verify the thickness and the depth of the TaS2 flake. Then, according to the geometry of our flakes, the compressive strain can be calculated by the equation:
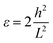 | (1) |
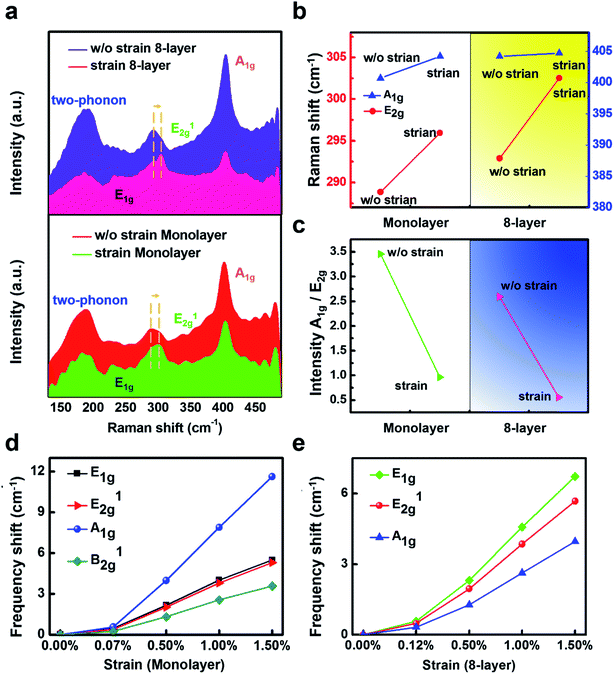
Representative Raman spectra for mono- and 8-layer TaS2 at room temperature are shown in Fig. 3a. Among the four Raman-active modes of the bulk TaS2 crystal, the prominent features observed below 500 cm−1 include two-phonon peak at ∼185, E12g ∼ 290, and A1g ∼ 404 cm−1. It is found that mono- and few-layer TaS2 flakes under compressive strain exhibit a strong in-plane vibrational mode at ∼230 cm−1, corresponding to the E1g mode. In contrast, this mode was not observed in earlier studies of mono and few-layer TaS2 without strain.18 In strain-free TaS2, E1g mode is absent attributed to the existence of trigonal prismatic coordination, which renders the vibration Raman inactive. This Raman behavior of TaS2 still resemble of MoS2. Although the detailed atomic configurations of TaS2 and MoS2 are different, the two 2H polytypes share the same symmetry point groups — D3d group with inversion symmetry for even layer number, and D3h group with mirror symmetry for odd layer number.52 Obvious stiffen (blueshift) of E12g signal could be observed, from 289 cm−1 to 296 cm−1 in monolayer and from 293 cm−1 to 303 cm−1 in 8-layer samples, while the other peaks remain unchanged with the compressive strain. The peak width is broaden as well, and this is different from the previous prediction that the compression would introduce enhancement of the intensity of the E12g mode.
We further confirm the mode assignment by calculating the phonon frequencies in mono- and bulk TaS2 using density functional perturbation theory (DFPT). It is interesting to find that all the modes show a positive value of γ, indicative of a normal behavior of stiffen frequencies with shrinking the lattice host. The variation of the frequencies for modes at the Γ point with compressive and tensile strains is plotted in Fig. 3(d) and (e), where the frequency shift (δ) with strain (ε) is defined as δ = ω(ε) − ω(0). The different slopes of the δ–ε curves reflect the different stiffening or softening behavior of each phonon mode under strain. For the 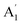 mode, the slope is the largest among all the modes for the monolayer, while the smallest for the bulk. For the bulk case, the calculation results are consistent with the experiments. But the monolayer result is different from the experiment results. This paradox could be due to the strong electron–phonon coupling in the monolayer TaS2, while the calculation only considers the vdW coupling. Generally speaking, the eigenvector of this mode shows that the S atoms vibrate in counterphase in direction normal to the plane (Fig. 1) and the Ta plane remains stationary. Thus the frequency is sensitive to the in-plane strain, but relatively insensitive to the disturbance normal to the plane such as the compressive strain, electronic doping, or chemical doping above the planes. In contrast, the E′ mode involves the in-plane vibration, and thus is more sensitive to the in-plane strain. Note here that the trends for these two modes are reversed in the case of doping on the layer, where the
mode, the slope is the largest among all the modes for the monolayer, while the smallest for the bulk. For the bulk case, the calculation results are consistent with the experiments. But the monolayer result is different from the experiment results. This paradox could be due to the strong electron–phonon coupling in the monolayer TaS2, while the calculation only considers the vdW coupling. Generally speaking, the eigenvector of this mode shows that the S atoms vibrate in counterphase in direction normal to the plane (Fig. 1) and the Ta plane remains stationary. Thus the frequency is sensitive to the in-plane strain, but relatively insensitive to the disturbance normal to the plane such as the compressive strain, electronic doping, or chemical doping above the planes. In contrast, the E′ mode involves the in-plane vibration, and thus is more sensitive to the in-plane strain. Note here that the trends for these two modes are reversed in the case of doping on the layer, where the 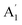 mode shows significant softening behavior, whereas the E′′ mode remains nearly constant. In comparison to 2H-MoS2, our study of the larger slope of the
mode shows significant softening behavior, whereas the E′′ mode remains nearly constant. In comparison to 2H-MoS2, our study of the larger slope of the 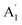 mode (E12g for bulk) than the E′ mode (A1g for bulk) with strain is different from previous measurements. This is probably due to the ABA and ABC stacked 2D materials show that the Raman activity of the interlayer modes is highly sensitive to the stacking-induced changes of the intralayer bonding. The opposite direction of the intensity, which cannot be explained solely by van der Waals interlayer coupling, is attributed to strong electron–phonon interactions.
mode (E12g for bulk) than the E′ mode (A1g for bulk) with strain is different from previous measurements. This is probably due to the ABA and ABC stacked 2D materials show that the Raman activity of the interlayer modes is highly sensitive to the stacking-induced changes of the intralayer bonding. The opposite direction of the intensity, which cannot be explained solely by van der Waals interlayer coupling, is attributed to strong electron–phonon interactions.
For all the flake thickness, with and without the compressive strain, the out-of-plane A1g vibration remained unchanged. This is unusual compared with other 2D TMDs such as MoS2, which A1g increases with the thickness. Within a classical model for coupled harmonic oscillators, the E12g and A1g modes are expected to stiffen as additional layers are added to form the bulk material from individual layers, since the interlayer vdW interactions increase the effective restoring forces acting on the atoms. While the unchanged A1g mode observed in our measurements with the compressive strain disagrees with this prediction. The failure of the model could reflect the presence of additional interlayer interactions; it could also indicate that the implicit assumption that stacking order affects intralayer bonding is incorrect. In addition, as the compressive strain increases, the A1g mode does not change shows that even the nominally interlayer interaction in TaS2 cannot affect intralayer bonding and lattice dynamics. To further study the changes of the Raman peaks-dependent strain effect, we extract the data from the Fig. 3a to show the detailed results (the frequency shift of E12g and A1g mode for mono- and 8-layer 2H-TaS2 flake with and without the strain) in Fig. 3b. In addition, Raman intensity ratio between the A1g peak and E12g peak is plotted in Fig. 3c to demonstrate the repeatability of the strain effect.
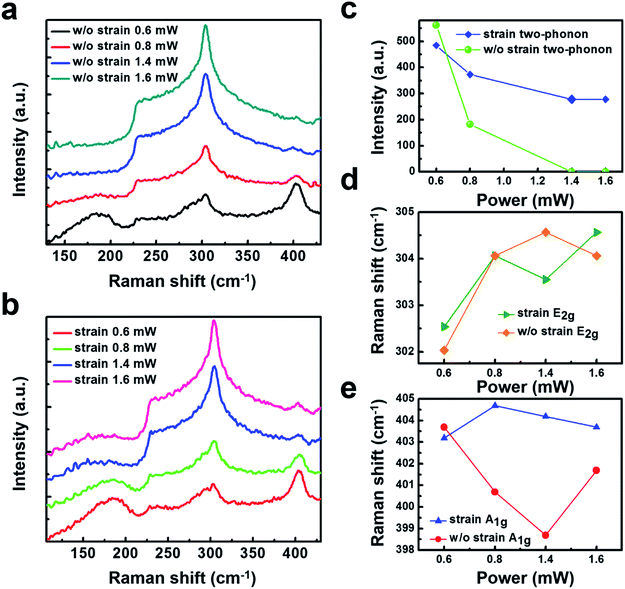
It is important to highlight that as for some TMDs are sensitivity to the Raman laser beam. To understand the influence of the irradiation power impacts on the sample, low irradiation power of 0.6 mW, 0.8 mW, and the high irradiation power of 1.4 mW, 1.6 mW are selected. The Raman spectra are tested on a normal and suspended 2H-TaS2 flake. Under the high irradiation power, the Raman spectra of the two-phonon peak fades away, as shown in Fig. 4a. It is interesting to find that the two-phonon peak in Fig. 4a disappears in the suspended 2H-TaS2 while still exists in Fig. 4b when the compressive strain is on. Our measurement gives further physical insights that the strain can impede the phenomenon that the two-phonon peak fade away under a high irradiation power. To examine more carefully of the two-phonon peak shape, Raman intensity of the two-phonon peak under the selected irradiation power is shown in Fig. 4c. It can be clearly observed that when the irradiation power is up to 1.4 mW, the sample with strain has a strong decrease that the two-phonon intensity becomes to almost zero. By contrast, the appearance of a strong relative intensity suggested that the suspended 2H-TaS2 flake still has a two-phonon peak. Fig. 4c shows that the blue-shift of E12g under the strain. Analysis the A1g mode with different irradiation powers has also been done, and it is found that a slight fluctuation in the two samples. These results have been tested repeatedly as shown in ESI Fig. S1–S3.† As the increase of the laser beam power, the intensity of E12g mode increases, while the one in A1g mode deceases. Similar suppression of the A1g mode has been observed in few-layer graphene due to the damping caused by surface adsorbates under high temperature.53
Conclusions
In summary, we have reported the important Raman signature variety of atomically thin 2H-TaS2 layers under various conditions, such as different stress-deformation and irradiation power. In contrast to the regular 2H-TaS2 sample, we find that the Raman signature for 2H-TaS2 sample with a stress-deformation can generate blue-shift of E12g mode peak, enhance the E1g mode and impede the two-phonon peak fade away under a higher irradiation power. Our results enrich the understanding of electronic structure of atomically thin 2H-TaS2, demonstrated the possibility to adjust the vibration modes of atoms via strain engineering, which extend their potential applications on nano-electromechanical systems (NEMS) and flexible electronics.Author contributions
X. W. and G. Z. conceived and designed the experiments, fabricated the suspended samples and carried out the Raman experiments. G. Z. and Y. Q. C. carried out numerical simulations and interpretation. G. H. S., Y. D. Y. and J. H. B. carried out AFM measurements. All authors contributed to the discussion and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Projects of Science and Technology Commission of Shanghai Municipality Grant Nos. (19ZR1473800, 14DZ2260800), Shanghai Rising-Star Program (17QA1401400), Young Elite Scientists Sponsorship Program by CAST (YESS), and the Fundamental Research Funds for the Central Universities.References
- C. Wan, Y. Kodama, M. Kondo, R. Sasai, X. Qian, X. Gu, K. Koga, K. Yabuki, R. Yang and K. Koumoto, Dielectric Mismatch Mediates Carrier Mobility in Organic-Intercalated Layered TiS2, Nano Lett., 2015, 15, 6302–6308 CrossRef CAS PubMed.
- M. J. Hollander, Y. Liu, W.-J. Lu, L.-J. Li, Y.-P. Sun, J. A. Robinson and S. Datta, Electrically Driven Reversible Insulator–Metal Phase Transition in 1T-TaS2, Nano Lett., 2015, 15, 1861–1866 CrossRef CAS PubMed.
- G. A. Muller, J. B. Cook, H.-S. Kim, S. H. Tolbert and B. Dunn, High Performance Pseudocapacitor Based on 2D Layered Metal Chalcogenide Nanocrystals, Nano Lett., 2015, 15, 1911–1917 CrossRef CAS PubMed.
- J. Shen, Y. He, J. Wu, C. Gao, K. Keyshar, X. Zhang, Y. Yang, M. Ye, R. Vajtai, J. Lou and P. M. Ajayan, Liquid Phase Exfoliation of Two-Dimensional Materials by Directly Probing and Matching Surface Tension Components, Nano Lett., 2015, 15, 5449–5454 CrossRef CAS PubMed.
- R. Samnakay, D. Wickramaratne, T. R. Pope, R. K. Lake, T. T. Salguero and A. A. Balandin, Zone-Folded Phonons and the Commensurate–Incommensurate Charge-Density-Wave Transition in 1T-TaSe2 Thin Films, Nano Lett., 2015, 15, 2965–2973 CrossRef CAS PubMed.
- M. Pandey, F. A. Rasmussen, K. Kuhar, T. Olsen, K. W. Jacobsen and K. S. Thygesen, Defect-Tolerant Monolayer Transition Metal Dichalcogenides, Nano Lett., 2016, 16, 2234–2239 CrossRef CAS PubMed.
- E. Zhang, R. Chen, C. Huang, J. Yu, K. Zhang, W. Wang, S. Liu, J. Ling, X. Wan, H.-Z. Lu and F. Xiu, Tunable Positive to Negative Magnetoresistance in Atomically Thin WTe2, Nano Lett., 2017, 17, 878–885 CrossRef CAS PubMed.
- P. Wang, S. Liu, W. Luo, H. Fang, F. Gong, N. Guo, Z.-G. Chen, J. Zou, Y. Huang, X. Zhou, J. Wang, X. Chen, W. Lu, F. Xiu and W. Hu, Arrayed Van Der Waals Broadband Detectors for Dual-Band Detection, Adv. Mater., 2017, 29, 1604439 CrossRef PubMed.
- F. Gong, W. Luo, J. Wang, P. Wang, H. Fang, D. Zheng, N. Guo, J. Wang, M. Luo, J. C. Ho, X. Chen, W. Lu, L. Liao and W. Hu, High-Sensitivity Floating-Gate Phototransistors Based on WS2 and MoS2, Adv. Funct. Mater., 2016, 26, 6084–6090 CrossRef CAS.
- X. Wang, P. Wang, J. Wang, W. Hu, X. Zhou, N. Guo, H. Huang, S. Sun, H. Shen, T. Lin, M. Tang, L. Liao, A. Jiang, J. Sun, X. Meng, X. Chen, W. Lu and J. Chu, Ultrasensitive and Broadband MoS2 Photodetector Driven by Ferroelectrics, Adv. Mater., 2015, 27, 6575–6581 CrossRef CAS PubMed.
- J. Wang, H. Fang, X. Wang, X. Chen, W. Lu and W. Hu, Recent Progress on Localized Field Enhanced Two-Dimensional Material Photodetectors from Ultraviolet, Small, 2017, 13, 1700894 CrossRef PubMed.
- R. Ang, Z. C. Wang, C. L. Chen, J. Tang, N. Liu, Y. Liu, W. J. Lu, Y. P. Sun, T. Mori and Y. Ikuhara, Atomistic Origin of an Ordered Superstructure Induced Superconductivity in Layered Chalcogenides, Nat. Commun., 6, 6091 CrossRef CAS PubMed.
- Y. Cai, Q. Ke, G. Zhang, Y. P. Feng, V. B. Shenoy and Y. W. Zhang, Giant Phononic Anisotropy and Unusual Anharmonicity of Phosphorene: Interlayer Coupling and Strain Engineering, Adv. Funct. Mater., 2015, 25, 2230–2236 CrossRef CAS.
- Y. Yu, F. Yang, X. F. Lu, Y. J. Yan, H. ChoYong, L. Ma, X. Niu, S. Kim, Y.-W. Son, D. Feng, S. Li, S.-W. Cheong, X. H. Chen and Y. Zhang, Gate-Tunable Phase Transitions in Thin Flakes of 1T-TaS2, Nat. Nanotechnol., 2015, 10, 270–276 CrossRef CAS PubMed.
- S. Dong, A. Zhang, K. Liu, J. Ji, Y. Ye, X. Luo, X. Chen, X. Ma, Y. Jie and C. Chen, Ultralow-Frequency Collective Compression Mode and Strong Interlayer Coupling in Multilayer Black Phosphorus, Phys. Rev. Lett., 2016, 116, 087401 CrossRef PubMed.
- D. Cho, S. Cheon, K.-S. Kim, S.-H. Lee, Y.-H. Cho, S.-W. Cheong and H. W. Yeom, Nanoscale Manipulation of the Mott Insulating State Coupled to Charge Order in 1T-TaS2, Nat. Commun., 2016, 7, 10453 CrossRef CAS PubMed.
- S. Song, D. H. Keum, S. Cho, D. Perello, Y. Kim and Y. H. Lee, Room Temperature Semiconductor–Metal Transition of MoTe2 Thin Films Engineered by Strain, Nano Lett., 2016, 16, 188–193 CrossRef CAS PubMed.
- E. Navarro-Moratalla, J. O. Island, S. Mañas-Valero, E. Pinilla-Cienfuegos, A. Castellanos-Gomez, J. Quereda, G. Rubio-Bollinger, L. Chirolli, J. A. Silva-Guillén, N. Agraït, G. A. Steele, F. Guinea, H. S. J. van der Zant and E. Coronado, Enhanced Superconductivity in Atomically Thin TaS2, Nat. Commun., 2016, 7, 11043 CrossRef CAS PubMed.
- K. S. Novoselov, A. Mishchenko, A. Carvalho and A. H. Castro Neto, 2d Materials and van Der Waals Heterostructures, Science, 2016, 353 Search PubMed.
- O. Lopez-Sanchez, D. Lembke, M. Kayci, A. Radenovic and A. Kis, Ultrasensitive Photodetectors Based on Monolayer MoS2, Nat. Nanotechnol., 2013, 8, 497–501 CrossRef CAS PubMed.
- J. Wilson and A. Yoffe, The Transition Metal Dichalcogenides Discussion and Interpretation of the Observed Optical, Electrical and Structural Properties, Adv. Phys., 1969, 18, 193–335 CrossRef CAS.
- J. Ribeiro-Soares, R. Almeida, E. Barros, P. Araujo, M. Dresselhaus, L. Cançado and A. Jorio, Group Theory Analysis of Phonons in Two-Dimensional Transition Metal Dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115438 CrossRef.
- Y. Cai, G. Zhang and Y.-W. Zhang, Polarity-Reversed Robust Carrier Mobility in Monolayer MoS2 Nanoribbons, J. Am. Chem. Soc., 2014, 136, 6269–6275 CrossRef CAS PubMed.
- G. Huang, Z. Xing and D. Xing, Prediction of Superconductivity in Li-Intercalated Bilayer Phosphorene, Appl. Phys. Lett., 2015, 106, 113107 CrossRef.
- H. Tian, T.-L. Ren, D. Xie, Y.-F. Wang, C.-J. Zhou, T.-T. Feng, D. Fu, Y. Yang, P.-G. Peng, L.-G. Wang and L.-T. Liu, Graphene-on-Paper Sound Source Devices, ACS Nano, 2011, 5, 4878–4885 CrossRef CAS PubMed.
- L. Shi, D. Yao, G. Zhang and B. Li, Large Thermoelectric Figure of Merit in Si1−xGex Nanowires, Appl. Phys. Lett., 2010, 96, 173108 CrossRef.
- X. Zhang, Q.-H. Tan, J.-B. Wu, W. Shi and P.-H. Tan, Review on the Raman Spectroscopy of Different Types of Layered Materials, Nanoscale, 2016, 8, 6435–6450 RSC.
- P. Tan, W. Han, W. Zhao, Z. Wu, K. Chang, H. Wang, Y. Wang, N. Bonini, N. Marzari and N. Pugno, The Shear Mode of Multilayer Graphene, Nat. Mater., 2012, 11, 294–300 CrossRef CAS PubMed.
- C. H. Lui, Z. Ye, C. Keiser, E. B. Barros and R. He, Stacking-Dependent Shear Modes in Trilayer Graphene, Appl. Phys. Lett., 2015, 106, 041904 CrossRef.
- D. Boschetto, L. Malard, C. H. Lui, K. F. Mak, Z. Li, H. Yan and T. F. Heinz, Real-Time Observation of Interlayer Vibrations in Bilayer and Few-Layer Graphene, Nano Lett., 2013, 13, 4620–4623 CrossRef CAS PubMed.
- C. Cong and T. Yu, Enhanced Ultra-Low-Frequency Interlayer Shear Modes in Folded Graphene Layers, Nat. Commun., 2014, 5, 4709 CrossRef CAS PubMed.
- J.-B. Wu, X. Zhang, M. Ijäs, W.-P. Han, X.-F. Qiao, X.-L. Li, D.-S. Jiang, A. C. Ferrari and P.-H. Tan, Resonant Raman Spectroscopy of Twisted Multilayer Graphene, Nat. Commun., 2014, 5, 5309 CrossRef CAS PubMed.
- X. Ling, L. Liang, S. Huang, A. A. Puretzky, D. B. Geohegan, B. G. Sumpter, J. Kong, V. Meunier and M. S. Dresselhaus, Low-Frequency Interlayer Breathing Modes in Few-Layer Black Phosphorus, Nano Lett., 2015, 15, 4080–4088 CrossRef CAS PubMed.
- A. Carvalho, M. Wang, X. Zhu, A. S. Rodin, H. Su and A. H. C. Neto, Phosphorene: From Theory to Applications, Nat. Rev. Mater., 2016, 1, 16061 CrossRef CAS.
- Y. Cai, Q. Ke, G. Zhang, Y. P. Feng, V. B. Shenoy and Y.-W. Zhang, Giant Phononic Anisotropy and Unusual Anharmonicity of Phosphorene: Interlayer Coupling and Strain Engineering, Adv. Funct. Mater., 2015, 25, 2230–2236 CrossRef CAS.
- G. Plechinger, S. Heydrich, J. Eroms, D. Weiss, C. Schüller and T. Korn, Raman Spectroscopy of the Interlayer Shear Mode in Few-Layer MoS2 Flakes, Appl. Phys. Lett., 2012, 101, 1906 CrossRef.
- M. Boukhicha, M. Calandra, M.-A. Measson, O. Lancry and A. Shukla, Anharmonic Phonons in Few-Layer MoS2: Raman Spectroscopy of Ultralow Energy Compression and Shear Modes, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195316 CrossRef.
- G. Froehlicher, E. Lorchat, F. Fernique, C. Joshi, A. Molina-Sánchez, L. Wirtz and S. Berciaud, Unified Description of the Optical Phonon Modes in N-Layer Mote2, Nano Lett., 2015, 15, 6481–6489 CrossRef CAS PubMed.
- C. H. Lui, Z. Ye, C. Ji, K.-C. Chiu, C.-T. Chou, T. I. Andersen, C. Means-Shively, H. Anderson, J.-M. Wu and T. Kidd, Observation of Interlayer Phonon Modes in van Der Waals Heterostructures, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165403 CrossRef.
- Y. Cai, J. Lan, G. Zhang and Y.-W. Zhang, Lattice Vibrational Modes and Phonon Thermal Conductivity of Monolayer MoS2, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035438 CrossRef.
- N. Ferralis, R. Maboudian and C. Carraro, Evidence of Structural Strain in Epitaxial Graphene Layers on 6H-SiC(0001), Phys. Rev. Lett., 2008, 101, 156801 CrossRef PubMed.
- M. L. Teague, A. P. Lai, J. Velasco, C. R. Hughes, A. D. Beyer, M. W. Bockrath, C. N. Lau and N. C. Yeh, Evidence for Strain-Induced Local Conductance Modulations in Single-Layer Graphene on SiO2, Nano Lett., 2009, 9, 2542–2546 CrossRef CAS PubMed.
- W. Pan, J. Xiao, J. Zhu, C. Yu, G. Zhang, Z. Ni, K. Watanabe, T. Taniguchi, Y. Shi and X. Wang, Biaxial Compressive Strain Engineering in Graphene/Boron Nitride Heterostructures, Sci. Rep., 2012, 2, 893 CrossRef PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene, Science, 2008, 321, 385 CrossRef CAS PubMed.
- G. Zhang and Y.-W. Zhang, Strain Effects on Thermoelectric Properties of Two-Dimensional Materials, Mech. Mater., 2015, 91, 382–398 CrossRef.
- K. Law and P. A. Lee, 1T-TaS2 as a quantum spin liquid, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 6996–7000 CrossRef CAS PubMed.
- C. Si, Z. Liu, W. Duan and F. Liu, First-Principles Calculations on the Effect of Doping and Biaxial Tensile Strain on Electron-Phonon Coupling in Graphene, Phys. Rev. Lett., 2013, 111, 196802 CrossRef PubMed.
- J. L. Mañes, Symmetry-Based Approach to Electron-Phonon Interactions in Graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 045430 CrossRef.
- A. C. Ferrari and D. M. Basko, Raman Spectroscopy as a Versatile Tool for Studying the Properties of Graphene, Nat. Nanotechnol., 2013, 8, 235–246 CrossRef CAS PubMed.
- N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, Elsevier, 1997 Search PubMed.
- T. M. G. Mohiuddin, A. Lombardo, R. R. Nair, A. Bonetti, G. Savini, R. Jalil, N. Bonini, D. M. Basko, C. Galiotis, N. Marzari, K. S. Novoselov, A. K. Geim and A. C. Ferrari, Uniaxial Strain in Graphene by Raman Spectroscopy: G Peak Splitting, Gruneisen Parameters, and Sample Orientation, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205433 CrossRef.
- J. Ribeiro-Soares, R. M. Almeida, E. B. Barros, P. T. Araujo, M. S. Dresselhaus, L. G. Cançado and A. Jorio, Group Theory Analysis of Phonons in Two-Dimensional Transition Metal Dichalcogenides, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 115438 CrossRef.
- C. H. Lui, Z. Ye, C. Keiser, X. Xiao and R. He, Temperature-Activated Layer-Breathing Vibrations in Few-Layer Graphene, Nano Lett., 2014, 14, 4615–4621 CrossRef CAS PubMed.
- G. Paolo, B. Stefano, B. Nicola, C. Matteo, C. Roberto, C. Carlo, C. Davide, L. C. Guido, C. Matteo, D. Ismaila, C. Andrea Dal, G. Stefano de, F. Stefano, F. Guido, G. Ralph, G. Uwe, G. Christos, K. Anton, L. Michele, M.-S. Layla, M. Nicola, M. Francesco, M. Riccardo, P. Stefano, P. Alfredo, P. Lorenzo, S. Carlo, S. Sandro, S. Gabriele, P. S. Ari, S. Alexander, U. Paolo and M. W. Renata, Quantum Espresso: A Modular and Open-Source Software Project for Quantum Simulations of Materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02499f |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2020 |