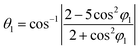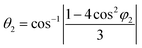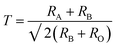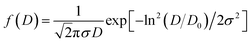Open Access Article
Open Access ArticleSynergistic effect of trivalent (Gd3+, Sm3+) and high-valent (Ti4+) co-doping on antiferromagnetic YFeO3
P. S. J. Bharadwaj a,
Swarup Kundu
a,
Swarup Kundu a,
Vijay Sai Kollipara
a,
Vijay Sai Kollipara *a and
Kalidindi B. R. Varma
*a and
Kalidindi B. R. Varma ab
ab
aDepartment of Physics, Sri Sathya Sai Institute of Higher Learning, Prasanthi Nilayam, Andhra Pradesh, India. E-mail: kvijaysai@sssihl.edu.in
bMaterials Research Centre, Indian Institute of Science, Bengaluru, India
First published on 9th June 2020
Abstract
Monophasic polycrystalline powders of Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) were successfully synthesized via a low temperature solid-state synthesis route. The X-ray diffraction and Raman spectroscopy studies indicate that all the calcined powders with R3+ (Gd3+, Sm3+) at Y3+ and Ti4+ at Fe3+ sites were crystallized in an orthorhombic phase associated with a change in lattice parameters. The Williamson–Hall method employed to calculate the strain revealed that the strain increased with the increased concentration of dopants ((Gd3+, Sm3+) at Y3+) compared to an increase in the size of crystallites, corroborating the findings of SEM. Analysis of diffuse reflectance spectra indicated a drop in bandgap from 1.93 eV to 1.86 eV and 1.96 eV to 1.91 eV for Gd, Ti co-doping and Sm, Ti co-doping respectively, demonstrating the capacity of the synthesized powders to absorb visible light. Absorbance spectra also revealed the existence of mixed states of Fe3+ and Fe4+ which was corroborated by XPS studies. The magnetic hysteresis loop analysis at room temperature illustrated that with co-doping, there is a strong enhancement in magnetization as well as coercivity, suggesting a strong transition from anti-ferromagnetic behaviour to ferromagnetic behaviour. Pertaining to the greatly improved optical and magnetic properties with the addition of (Gd3+, Sm3+) at Y3+ and Ti4+ at Fe3+ sites, these materials are anticipated to be of potential use in various applications.
Introduction
The existence of various physical properties associated with a single phase material has resulted in the study of and technological interest in multiferroic materials.1 These multiferroic materials could be employed for several applications that include temperature induced spin switching,2 magnetic field induced spin switching,3,4 solid oxide fuel cells, photo-catalysis, magneto-optical devices, capacitors, magneto-electric sensors in transducers, microwave electronics, and spintronics, owing to their magnetic and electric polarization effects.5–7 RFeO3 has a distorted perovskite structure that crystallizes in the orthorhombic Pmna space group.8 The crystallographic unit cell contains 4 equivalent iron (Fe) ions. Although RFeO3 has a distorted structure, FeO6 remains essentially an octahedron with six oxygen anions surrounding the Fe-ion, leading to crystal field splitting. The typical rare-earth orthoferrite YFeO3 falls into this category. There have been several reports on the dielectric and magnetic properties of YFeO3, even though it did not exhibit conventional ferroelectric effects at room temperature due to its low Curie temperature (−256 °C). Nevertheless, the narrow energy bandgap (1.8–2.6 eV) makes YFeO3 a viable material for magneto-optical applications.9 The weak ferromagnetic behaviour of YFeO3 is due to the canting of Fe3+ ions in an orthorhombic structure. However, it was demonstrated that the magnetic properties of YFeO3 can be enhanced by means of doping. For instance, the non-magnetic Y3+ is doped by divalent10 and trivalent ions11,12 and Fe3+ by trivalent13 and high valency ions.14 Doping at Y3+ resulted in the improvement of magnetization while the Fe3+ doping enhanced the coercivity. To the best of our knowledge, there exist no reports in the literature on co-doping of rare-earth (Gd3+, Sm3+) at Y3+ and Ti4+ at Fe3+. Therefore the objective of the current report is to investigate into the effect of co-doping of rare-earth (Gd3+, Sm3+) and Ti4+ on the structural, magnetic and optical properties of YFeO3.There are several synthesis routes that are known15–19 to obtain the polycrystalline powders of Y1−xRxFe1−(4/3)yTiyO3 where R = Gd, Sm. These multiple synthesis routes include the most popular solid-state and sol–gel routes. However, there are certain disadvantages associated with the solid-state synthesis route. First being the formation of secondary phases such as Y2O3 and Y3Fe5O12. Secondly, the existence of a hexagonal phase at low temperatures, which at higher temperatures becomes an orthorhombic phase. Our previous research identified the effective preparation of polycrystalline YFeO3 by sol–gel synthesis route in detail.12 Sol–gel approach is beneficial relative to the solid-state system because it allows for homogeneous mixing of the precursor ions at a molecular level. However, other drawbacks associated with this process are (i) the creation of pores due to the generation and trapping of gases, (ii) the coexistence of hexagonal and orthorhombic phases which could be solved by precisely regulating the calcination temperatures and (iii) usage of certain toxic complexing agents.
In view of the aforementioned disadvantages, an easy and efficient method that is slightly different from the above method has been developed. It is a low temperature solid-state route for the synthesis of Y1−xRxFe1−(4/3)yTiyO3 which has the advantage over other methods in phase purity, precision in phase control, low-cost and ultrafine particle size. This synthetic method was effectively employed to obtain pristine YFeO3.13
Materials and methods
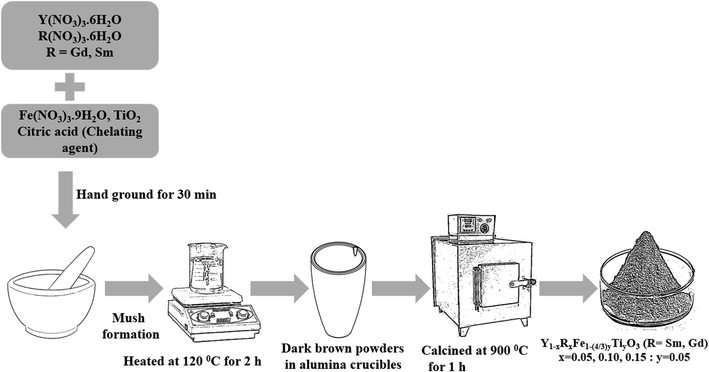
The polycrystalline powders of Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) have been successfully obtained using low temperature solid-state synthesis method. The precursors used were Y(NO3)3·6H2O (AR grade, purity > 98%), Fe(NO3)3·9H2O (AR grade, purity > 98%), Sm(NO3)3·6H2O (Sigma-Aldrich, purity > 99%), Gd(NO3)3·6H2O (Sigma-Aldrich, purity > 99%), TiO2 (Sigma-Aldrich, purity > 99%) and citric acid (AR grade, purity > 99%). Initially, the relevant precursors were weighed according to the stoichiometric ratios and were ground in an agate mortar for 30 min. This initial grinding resulted in the formation of light brown mush implicating the complex formation. This mush was then heated at 120 °C for 2 h which facilitated the removal of free water and yielded dark brown powder. These powders were then heated at 350 °C for 6 h to aid the complete decomposition of nitrates. Subsequently, these were finely ground and subjected to heating at 900 °C for 1 h resulting in the formation of monophasic polycrystalline powders. The schematic is given in Fig. 1.Mechanism of low temperature solid-state synthesis
Solid-state reaction involves four stages (i) diffusion, (ii) reaction, (iii) nucleation and (iv) growth. Diffusion takes place when the reactant or precursor molecules are in contact, followed by chemical reaction yielding the product. The nucleation is completely achieved until the product molecules aggregate to a certain scale. Once the product forms an independent crystal phase, crystal nuclei expand to a certain size. In the low temperature solid-state reaction, the reactants are brought into full contact as they reach a micron-level mixture. This is achieved by grinding the reactants which reduces their size aiding the surface energy to increase. As some of the reactants are hygroscopic, several micron liquid baths are created during the grinding process. This liquid environment helps the surface molecules of the reactants to aggregate and then react rapidly with one another. This results in the reaction to occur faster. The citric acid apart from acting as a chelating or complexing agent, provides the energy in the form of heat during calcination helping Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) to form at low temperatures.Characterization
The polycrystalline powders were characterized using X-ray powder diffractometer (X'Pert Pro, Panalytical) with Cu Kα = 1.5408 Å. The average crystallite size and lattice strain of these samples have been determined using Williamson–Hall plots. The structural analysis was further strengthened by recording Raman spectra using Raman microscope, (Thermo Scientific, laser excitation, λ = 780 nm). Microstructural and elemental analyses were performed using Jeol IT300 scanning electron microscope (SEM). Magnetic hysteresis loops at room temperature were obtained using vibrating sample magnetometer (Model EZ9, MicroSense, USA). The bandgap of the polycrystalline powders of the different formulations were measured using diffuse reflectance spectroscopy (DRS) in the range 200–800 nm employing UV-Vis spectrophotometer (Perkin Elmer LS 55). The X-ray photoelectron spectroscopic studies for all the samples were pursued by Fison Instruments S-probe TM2803.Results and discussion
The room temperature X-ray powder diffraction (XRD) patterns of Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) are represented in Fig. 2. XRD studies confirmed the formation of monophasic crystalline orthorhombic phase for all the samples under investigation with no detectable impurity peaks. This outcome from XRD studies indicate that the reaction is complete and the products formed are of required purity. The partial substitution of Gd3+ (x = 0.05, 0.10, 0.15), Sm3+ (x = 0.05, 0.10, 0.15) at Y3+ sites and Ti4+ (y = 0.05) at Fe3+ sites could be evidenced from the downward shift in the peak positions with the increase in dopant concentration, as shown in the insets of Fig. 2. The downward shift in the peak positions with an increase in dopant concentration implies that there is an increase in lattice parameters. For orthorhombic system, the peak positions and lattice parameters are related by (h/a)2 + (k/b)2 + (l/c)2 = 4 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ2, where h, k, l are Miller indices; a, b, c are lattice parameters; θ is the peak position; λ is the wavelength of the X-rays used. Further, as we are doping Gd3+ (x = 0.05, 0.10, 0.15), Sm3+ (x = 0.05, 0.10, 0.15) at Y3+ sites whose ionic radii (Gd3+ = 1.24 Å, Sm3+ = 1.10 Å) are relatively higher than that of Y3+ (1.06 Å), such shifts are expected. Moreover, if the partial substitution of Gd3+, Sm3+ and Ti4+ deviates from Y3+ and Fe3+ respectively, then the secondary phases/impurities must be formed which will reflect as extra peaks in XRD pattern. The absence of detectable X-ray peaks which are unaccounted for in these patterns confirm the effective doping at appropriate sites.
θ/λ2, where h, k, l are Miller indices; a, b, c are lattice parameters; θ is the peak position; λ is the wavelength of the X-rays used. Further, as we are doping Gd3+ (x = 0.05, 0.10, 0.15), Sm3+ (x = 0.05, 0.10, 0.15) at Y3+ sites whose ionic radii (Gd3+ = 1.24 Å, Sm3+ = 1.10 Å) are relatively higher than that of Y3+ (1.06 Å), such shifts are expected. Moreover, if the partial substitution of Gd3+, Sm3+ and Ti4+ deviates from Y3+ and Fe3+ respectively, then the secondary phases/impurities must be formed which will reflect as extra peaks in XRD pattern. The absence of detectable X-ray peaks which are unaccounted for in these patterns confirm the effective doping at appropriate sites.
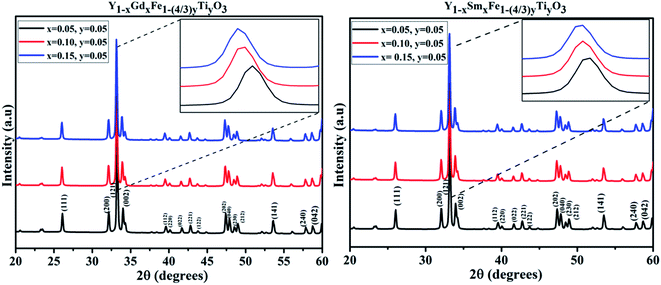 | ||
| Fig. 2 XRD patterns obtained for Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05). | ||
The computed lattice parameters based on XRD data are depicted in Table 1. The values increased with the increase in the rare earth (Gd, Sm) doping concentration at Y3+ and decreased with Ti4+ doping at Fe3+ suggesting the effectiveness of doping of Gd3+, Sm3+ which results in the increase in YFeO3 (rSm3+ (1.24 Å) > rGd3+ (1.10 Å) > rY3+ (1.06 Å)) lattice volume, whereas the substitution of Ti4+ at Fe3+ results in the reduction of YFeO3 (rFe3+ (0.645 Å) > rTi4+ (0.605 Å)) lattice volume.20 This incessant evolution of lattice parameters also indicate the successful doping of Gd3+, Sm3+ of different concentrations at Y3+ sites and Ti4+ (0.05) at Fe3+ sites in YFeO3.
| Name of the compound | Dopant concentration | Lattice parameters | Agreement factors | ||||
|---|---|---|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | Rwp (%) | Rp (%) | GOF (%) | ||
| YSFTO | x = 0.05, y = 0.05 | 5.589 | 7.603 | 5.283 | 2.73 | 1.96 | 1.37 |
| x = 0.10, y = 0.05 | 5.593 | 7.619 | 5.291 | 3.07 | 2.24 | 1.58 | |
| x = 0.15, y = 0.05 | 5.597 | 7.626 | 5.307 | 3.27 | 2.35 | 1.61 | |
| YGFTO | x = 0.05, y = 0.05 | 5.591 | 7.613 | 5.287 | 3.03 | 2.15 | 1.57 |
| x = 0.10, y = 0.05 | 5.594 | 7.618 | 5.294 | 2.88 | 2.08 | 1.64 | |
| x = 0.15, y = 0.05 | 5.601 | 7.622 | 5.301 | 3.26 | 2.13 | 1.94 | |
The X-ray diffraction peaks for Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) powders were indexed to YFeO3 orthorhombic crystal structure (ISCD 98-008-0866) associated with ‘Pmna’ space group of ‘mmm’ point group. The perovskite (ABO3) structure incorporating different elements in the periodic table as structural distortion, though ideally it is cubic. These distortions are essentially of three types, tilting of BO6 octahedra, polar cationic displacement and Jahn–Teller distortions. Out of these three, tilting of BO6 octahedra is most commonly found in Pmna space group to which YFeO3 belongs. The increase in lattice parameters with an increase in dopant concentration leads to an increase in structural distortion. The structural distortion could be calculated using O'Keefe geometric approximation.21
where θ1, θ2 and φ1, φ2 are bond angles and octahedral tilt angles respectively.
The sharing of O2− ions between two FeO6 octahedral structures leads to the formation of two kinds of Fe–O–Fe superexchange bonds, θ1 and θ2. These bond angles and tilt angles obtained using crystallographic information data acquired from Reitveld analysis were represented in VESTA software (ver. 3.5.2). The extent of distortion with respect to doping concentration i.e., the change in tilt angles and bond lengths are given in Table 2.
| Name of the compound | Bond angles | Tilt angles | Bond length (Å) | ||
|---|---|---|---|---|---|
| θ1 | θ2 | φ1 | φ2 | (Fe/Ti–O) | |
| Y1−xSmxFe1−(4/3)yTiyO3 | |||||
| x = 0.05, y = 0.05 | 144.615 | 143.59 | 21.35 | 22.49 | 2.032 |
| x = 0.10, y = 0.05 | 144.613 | 143.582 | 21.343 | 22.50 | 2.035 |
| x = 0.15, y = 0.05 | 144.607 | 143.570 | 20.863 | 22.51 | 2.037 |
| Y1−xGdxFe1−(4/3)yTiyO3 | |||||
| x = 0.05, y = 0.05 | 144.831 | 143.712 | 21.22 | 22.42 | 2.03 |
| x = 0.10, y = 0.05 | 144.829 | 143.689 | 21.21 | 22.44 | 2.034 |
| x = 0.15, y = 0.05 | 144.597 | 143.560 | 21.42 | 22.51 | 2.044 |
With the doping at Y3+ and Fe3+ sites the structure should remain as orthorhombic. The phase stability is measured using Goldschmidt tolerance factor which is given by
Crystallite size and strain analysis
The crystallite size could be calculated using Scherrer formula associated with the full width at half maximum of the peaks as given in eqn (1).
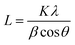 | (1) |
The Bragg peak width of the obtained XRD patterns also consists of instrument broadening effects. To circumvent such aberrations, the diffraction pattern obtained from the standard silicon sample was used to ascertain the instrument broadening. The relation given in eqn (2) is used to obtain the instrument broadening corresponding to the diffraction peaks of the samples under investigation.
| βL2 = [βsample2 − βinstrumental2] | (2) |
Further, in doped samples of the present kind, the peak broadening owing to the strain is not completely ruled out. The strain and strain-induced peak broadening are related as given in the following eqn (3).
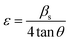 | (3) |
Scherrer equation is reliant on diffraction angle θ as 1/cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ but not as tan
θ but not as tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ as in Williamson–Hall (W–H) method. It implies that Scherrer formula considers only the instrumental broadening but not the strain-induced broadening.
θ as in Williamson–Hall (W–H) method. It implies that Scherrer formula considers only the instrumental broadening but not the strain-induced broadening.
The Williamson–Hall (W–H) equation assumes that the contribution of strain and crystallite size to peak broadening are independent to each other. Therefore the W–H equation is a simple sum of eqn (1) and (3) which is given by
| βhkl = βs + βL | (4) |
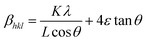 | (5) |
The above equation can be rearranged in the form given below
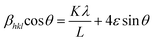 | (6) |
We have employed W–H method (eqn (6)) to perform both crystallite size and strain analysis depending on different θ positions. The W–H plots are depicted in Fig. 3 for all Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) samples that are drawn with 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ along x-axis and βhkl
θ along x-axis and βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ along y-axis. The crystallite size was calculated from the y-intercept and the strain was derived from the slope of the linear fit to the data, respectively. The W–H method assumes the strain to be isotropic and identical along all crystallographic directions. The crystallite size and strain for different compositions of Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) are illustrated in Table 3.
θ along y-axis. The crystallite size was calculated from the y-intercept and the strain was derived from the slope of the linear fit to the data, respectively. The W–H method assumes the strain to be isotropic and identical along all crystallographic directions. The crystallite size and strain for different compositions of Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) are illustrated in Table 3.
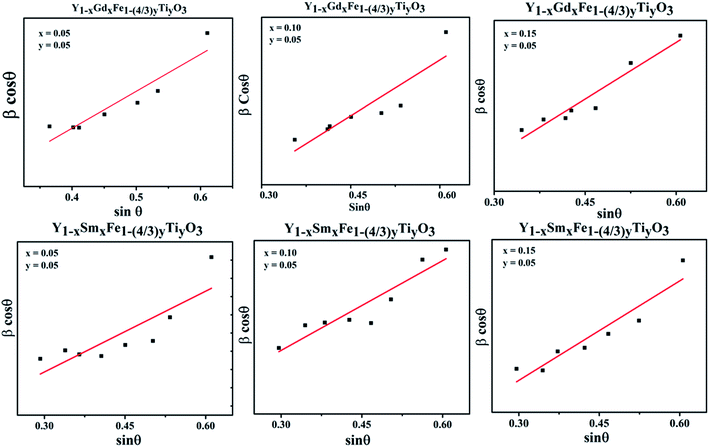 | ||
| Fig. 3 Williamson–Hall plots for Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05). | ||
| Name of the compound | Dopant concentration | Crystallite size (nm) | Strain | Tolerance factor |
|---|---|---|---|---|
| YSFTO | x = 0.05, y = 0.05 | 112.3 | 0.273 | 0.863 |
| x = 0.10, y = 0.05 | 119.6 | 0.284 | 0.865 | |
| x = 0.15, y = 0.05 | 124.2 | 0.317 | 0.868 | |
| YGFTO | x = 0.05, y = 0.05 | 104.3 | 0.254 | 0.859 |
| x = 0.10, y = 0.05 | 115.8 | 0.281 | 0.861 | |
| x = 0.15, y = 0.05 | 121.7 | 0.307 | 0.859 |
Analysis of crystal structure is considered to be incomplete until it is substantiated by fitting with various crystallographic parameters and multiple pattern variables with a chosen structural model from database. Rietveld proposed a method wherein the individual intensities at each step of powder diffraction data was fit. In this method, a least square technique was incorporated till the best fit is attained between observed powder diffraction data and calculated pattern from the selected model in the database. Rietveld refinement was incorporated to ascertain the validity of orthorhombic structural model and to precisely calculate the lattice parameters. The Rietveld refined plots are depicted in Fig. 4. The Rietveld refinement was done using High score plus software. The experimental data are depicted as transparent rings, while the calculated intensities are depicted as solid lines. The Bragg positions for ‘Pmna’ space group are depicted by the vertical lines at the bottom. The disparity between observed and measured intensities are seen in the form of solid lines in all the figures. The background is corrected using pseudo-voigt function. Parameters like scale factors, shape parameters, isothermal parameters, occupancies and lattice constants were taken to be fixed during the refinement process. We considered oxygen positions to be free parameters whereas other atomic positions were taken to be fixed. The Rwp, weighted profile residual factor which accounts for the background, the Rp, profile residual factor that only takes peaks into account without accounting the background and the goodness of fit (GOF) which describes how well it fits into a set of observations, were found to be low, suggesting the goodness of refinement. The refined lattice parameters and agreement factors are given Table 1.
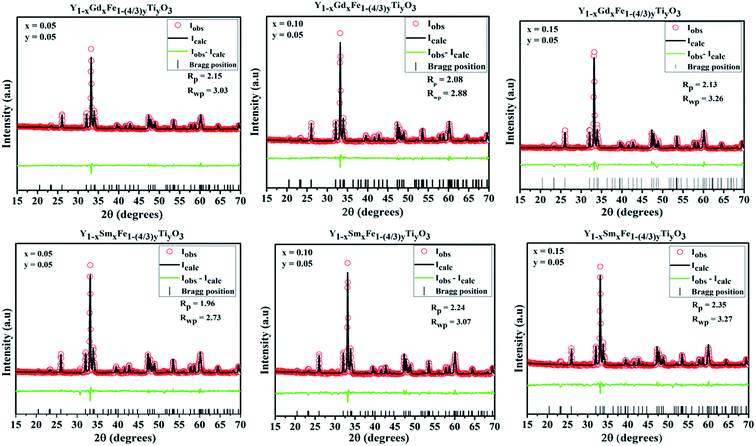 | ||
| Fig. 4 Rietveld refined plots for Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05). | ||
Raman studies
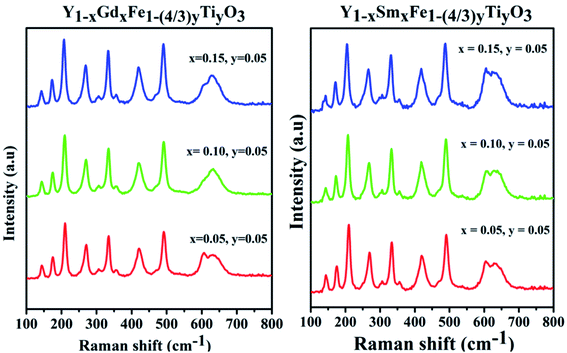
Generally, ABO3 perovskite has a cubic structure with corner-linked BO6 octahedra with B cations at the centre and A cations in the space between the octahedral, respectively. Raman scattering is forbidden due to symmetry in cubic perovskite structure. From the XRD studies, it is evidenced that samples with different configurations under study are typical example of perovskite structure (ABO3) and crystallize in orthorhombic structure with Pmna space group. The antiphase tilt of FeO6 octahedra gives rise to the distorted orthorhombic structure. This tilting of FeO6 octahedra necessarily introduces a distortion in the RO12 icosahedron (polyhedron).As per group theory, the orthorhombic Pmna structure has 24 Raman active modes 7Ag + 5B1g + 7B2g + 5B3g. Out of these modes 12 are first order Raman modes.22 The Raman spectra for the system Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) is presented in the Fig. 5.
The structural analysis could be done by analyzing the Raman bands in the four different spectral regions.
(i) Region 1: 120–200 cm−1, with two peaks 149 cm−1 and 177 cm−1 which are attributed to the vibrations of yttrium ion. According to harmonic oscillator approximation ω ∼ (k/M)1/2, where ω is the frequency, k is the spring constant and M is atomic mass, the heaviest atom is predicted to vibrate in low wavenumber region and this justifies the shift in the peaks with different dopants and different doping concentrations.
(ii) Region 2: 200–380 cm−1, characterized by 3 different bands. The band at 220 cm−1 is attributed to Fe3+ ion vibration and the bands around 270 cm−1 and 340 cm−1 are attributed to Fe3+ magnetic ions excitation.
(iii) Region 3: 380–550 cm−1, with two bands of different intensities at 430 cm−1 and 481 cm−1 which are attributed to the excitation of Fe3+ magnetic ions.
(iv) Region 4: 550–800 cm−1, characterized by two partially overlapping bands around 600 cm−1, one band is a characteristic of Fe–O bond. The appearance of a second band which is not observed in pristine YFeO3 might be due to the doping of Ti4+ at Fe3+ sites.
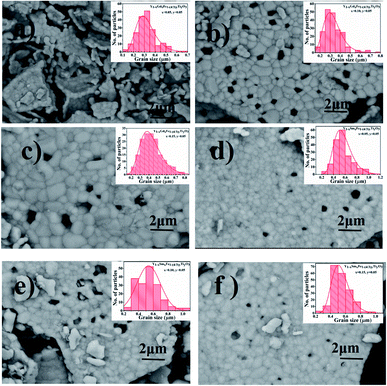
The surface morphology of all the synthesized powdered samples was depicted using backscattered electron micrographs as shown in Fig. 6. All the powder samples were sputtered by platinum to avoid surface charging and were mounted using carbon tape. The samples under study exhibit only one region with uniform colour tonality which is associated with the electron density, proving that all the synthesized samples are monophasic without any impurity phases. The crystallite size distributions are depicted in each micrograph as the insets. The log normal function was used to fit the obtained data.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(σ2/2)
exp(σ2/2)
And the mean particle size is given by
| σD = 〈D〉[exp(σ2) − 1]1/2 |
It is observed that the crystallite size increased from 0.28 μm to 0.44 μm for Y1−xSmxFe1−(4/3)yTiyO3 (x = 0.05, 0.10, 0.15; y = 0.05) with an error bar of 0.0173 to 0.0241 (Fig. 6a–c) and from 0.49 μm to 0.60 μm for Y1−xGdxFe1−(4/3)yTiyO3 (x = 0.05, 0.10, 0.15; y = 0.05) with an error bar of 0.0156 to 0.0210. The reason for such an increase in crystallite size with an increase in dopant concentration could also be due to the reduction of oxygen vacancies. The heterovalent doping of Ti4+ at Fe3+ results in the charge compensation by impregnating such vacancies. This is evidenced by the reduction of pores which can be observed in Fig. 6. Moreover, the partial replacement of Ti4+ whose ionic radii and atomic weight lower than that of Fe3+ enhances the grain growth.22 The crystallite size calculated from XRD analysis varies significantly from that obtained by the SEM analysis. This is ascribed to the agglomeration effects owing to their smaller size and innate magnetism.23
The energy dispersive X-ray spectra (EDS) of all the synthesized show the peaks associated with Y, Sm, Gd, Fe, Ti and O atoms. The peaks associated with 2.07 keV and 0.27 keV were attributed to Pt and carbon tape (used for sample preparation) respectively. Apart from proving the existence of all the elements associated with the samples under investigation, the EDS spectrum quantifies their relative proportions reasonably well. The lack of elemental impurities in the synthesized samples could be evidenced by the absence of unaccounted peaks (Table 4).
| Name of the Compound | Dopant concentration | Atomic% | |||||
|---|---|---|---|---|---|---|---|
| Y L | Sm L | Gd L | Fe K | Ti K | O K | ||
| YSFTO | x = 0.05, y = 0.05 | 17.45 | 2.21 | — | 27.04 | 2.54 | 50.76 |
| x = 0.10, y = 0.05 | 16.81 | 3.15 | — | 28.12 | 2.63 | 49.29 | |
| x = 0.15, y = 0.05 | 15.92 | 4.23 | — | 28.97 | 2.74 | 51.86 | |
| YGFTO | x = 0.05, y = 0.05 | 17.77 | — | 2.66 | 26.7 | 2.69 | 50.18 |
| x = 0.10, y = 0.05 | 16.37 | — | 3.25 | 27.4 | 2.7 | 50.28 | |
| x = 0.15, y = 0.05 | 15.99 | — | 4.1 | 28.5 | 2.61 | 48.8 | |
Optical properties
The optical properties unravel the changes that take place in the noticeable Fe d–d transitions which appear in the visible region and uncover the changes that are likely to occur in the bandgap of the material. Diffuse reflectance spectroscopy (DRS) was invoked to study the absorption characteristics and variation in the bandgap with a change in doping concentration. Scattered radiation excluding the specular reflected radiation is collected which matches closely with the Kubelka–Munk function which is given by F(R) = (1 − R)2/2R, where R is the diffuse reflectance.24The absorbance vs. wavelength plots for all the samples under study are shown in Fig. 7. The Kubelka–Munk function was used to formulate the [F(R)hν]2 vs. hν, where h is Planck's constant and ν is the frequency of the source of illumination. The optical band gap energy, Eg, is derived from the intersection of the tangent line at [F(R)hν]2 = 0. These plots are shown as the insets in Fig. 7 and the band gap values are given in Table 5.
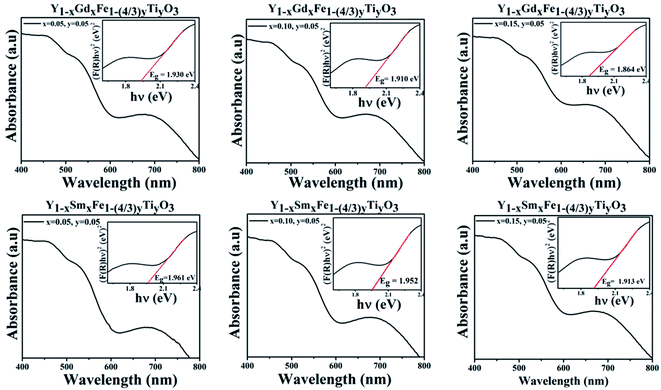 | ||
| Fig. 7 Absorption spectra and corresponding Tauc plots for Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05). | ||
| Name of the compound | Dopant concentration | Eg (eV) | Error |
|---|---|---|---|
| YGFTO | x = 0.05, y = 0.05 | 1.96178 | 0.03021 |
| x = 0.10, y = 0.05 | 1.95268 | 0.02892 | |
| x = 0.15, y = 0.05 | 1.913224 | 0.02756 | |
| YSFTO | x = 0.05, y = 0.05 | 1.930412 | 0.02791 |
| x = 0.10, y = 0.05 | 1.910113 | 0.03219 | |
| x = 0.15, y = 0.05 | 1.86448 | 0.03428 |
In the absorbance plots, there is a strong transition in the range 500–600 nm which corresponds to the electronic transitions implying the charge transfer from valence band of oxygen (O) 2p states to conduction band of iron (Fe) 3d states. These are the allowed p–d transitions.25,26 The octahedral crystal field splitting of BO6 octahedra in ABO3 type perovskite gives rise to splitting of d-orbital into the sub-orbitals of t2g (dxy, dyz, dxz) and eg (dx2−y2, dz2). The intensities of the d–d transitions that occur from t2g to eg orbitals were observed to be 103 times lower than the dipole allowed p–d transitions (O 2p–Fe 3d).27 In the present study, Fe occupies 3+ oxidation state that is to say it is a d5 system. The d–d transitions in d5 system are forbidden by electric dipole selection rule (Δl = ±1) and spin selection rule (ΔS = 0).27 Even though RFeO3 samples were dominated by exchange interactions of p–d transitions, we observed the d–d transitions for all the samples under investigation. It is evident from the appearance of intense bands around 1.7 eV in the Tauc plots (Fig. 8).
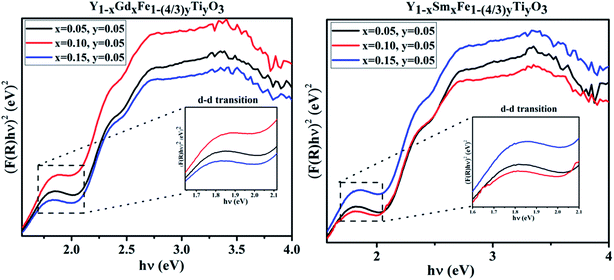 | ||
| Fig. 8 d–d transitions from the Tauc plots of Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05). | ||
Tanabe–Sugano (T–S) diagrams were reported to be used to determine the energies of Fe2+ (3d6), Fe3+ (3d5), Fe4+ (3d6) systems.28 T–S diagrams envisage the zero spin allowed d–d transitions for Fe3+, while they project the spin allowed d–d transitions for Fe2+ which is from t42ge2g–t32ge3g at 1.277 eV and Fe4+ which is from t32ge1g–t22ge2g at 1.72 eV.28 In the present study, the bands around 1.7 eV are attributed to the spin allowed d–d transitions, which comply with the T–S diagrams of spin allowed d–d transitions of Fe4+. It should be noted from these observations in the absorption spectra of Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05), that Fe essentially exists in the mixed states of Fe3+ and Fe4+. This can be further supported by XPS studies. The existence of mixed states of iron can be attributed to the doping effect.
XPS analysis
X-ray photon spectroscopy that provides with a comprehensive estimate of the chemical states of the elements present in the Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) was performed. The deconvolution of Fe 2P3/2 peak has been done using Shirley background and Gaussian–Lorentzian fitting. The deconvolution gives rise to two different peaks with binding energies around 709.64 eV and 710.72 eV corresponding to Fe3+ and Fe4+ respectively.29 It is observed that Fe4+ content increased with an increase in dopant concentration at Y3+. There is a significant shift in Fe 2P3/2 peaks towards higher binding energies as depicted in Fig. 9, implying a gradual increase of charge at Fe site.30 This shift is related to the increase of relative amounts of Fe4+ ions with an increase in dopant concentration. This proves that the Fe exists in mixed oxidation states of Fe3+ and Fe4+. The emergence of Fe4+ in the synthesized samples is ascribed to the doping of Ti4+ at Fe3+; Sm3+ and Gd3+ at Y3+ sites and presence of oxygen vacancies.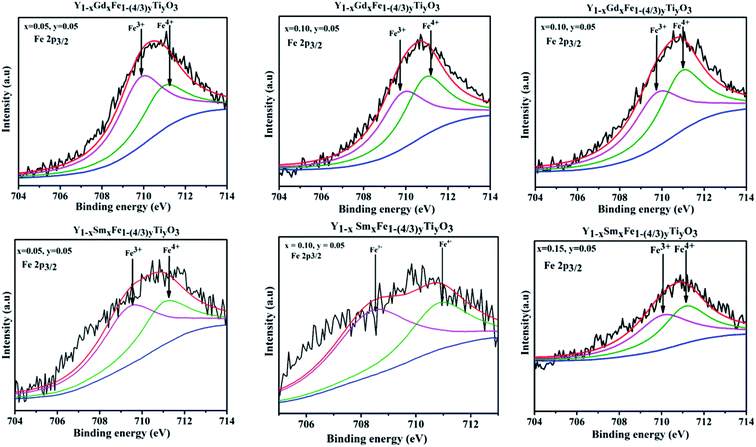 | ||
| Fig. 9 XPS spectra obtained for Fe 2p3/2 for Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05). | ||
Two peaks are shown for O 1s XPS pattern. The peak around 528 eV is attributed to lattice oxygen and peak at 532 eV is attributed to the surface adsorbed oxygen.31 In case of Sm3+ and Gd3+ doping with x = 0.05, the peak at 528 eV is not so visible. The reason might be the loss of electron making it O− from O2− ion and giving rise to prominent 532 eV peak, suggesting the higher concentrations of oxygen vacancies. With the increase in dopant concentration at Y3+ the height and area of the peak at 528 eV (lattice oxygen peak) gradually increases and becomes more evident. A detailed quantitative analysis was used to evaluate the content of oxygen deficiencies. The oxygen content was separated into lattice oxygen (O2−) and surface adsorbed oxygen (O−) using deconvolution. We have calculated the atomic ratio of O2−/O− which gives an estimate of the concentration of oxygen deficiencies. For Y1−xSmxFe1−(4/3)yTiyO3 (x = 0.05, 0.10, 0.15; y = 0.05) the atomic ratio of O2−/O− increased from 2.19 to 10.134 whereas for Y1−xGdxFe1−(4/3)yTiyO3 (x = 0.05, 0.10, 0.15; y = 0.05) O2−/O− ratio increased from 2.52 to 10.70. This increase in atomic ratio of O2−/O− with an increase in dopant concentration implies the reduction of concentration of oxygen deficiencies (Fig. 10).
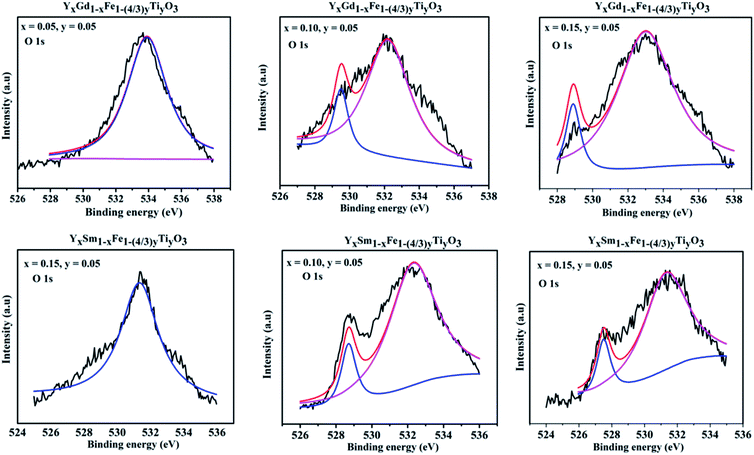 | ||
| Fig. 10 XPS spectra obtained for O 1s for Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05). | ||
Magnetic properties
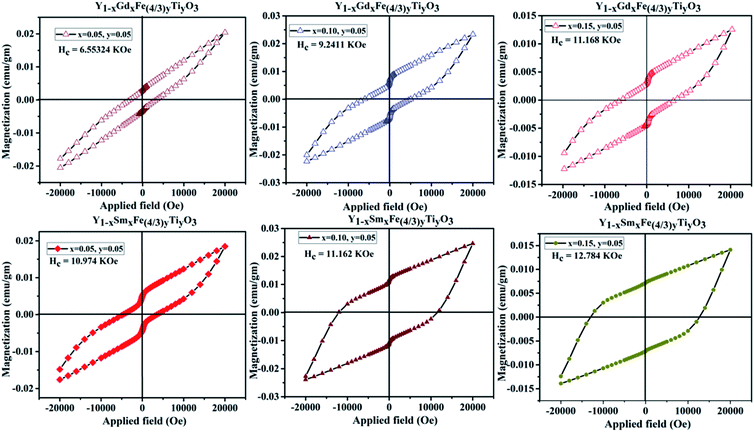
The magnetic properties in rare-earth orthoferrites originate from the super-exchange interaction of Fe3+–Fe3+, R3+–R3+, R3+–O2−–Fe3+.32 The room temperature magnetization versus applied magnetic field (M–H) loop of YFeO3 suggests that it is an antiferromagnetic material.12 The GKA (Goodenough, Kanamori and Anderson) rules predict the antiferromagnetic behaviour of YFeO3 through oxygen mediated super-exchange interaction of pristine YFeO3.33 As mentioned earlier, the d5 orbitals of Fe3+ split into triply degenerate t2g (dxy, dyz, dxz) and doubly degenerate eg (dx2−y2, dz2) orbitals. The eg orbitals of Fe3+ which are along the crystal axes overlap with 2p orbitals of O2− which give rise to the super-exchange of Fe3+–O2−–Fe3+ at 180°. However, the magnetic moment alignment of Fe3+ ions is not precisely antiparallel giving rise to the canting of the spins. This results in a small magnetization effect and weak ferromagnetism in YFeO3. Literature reports show that there is an obvious effect on magnetic properties with magnetic and diamagnetic partial substitution/doping.11,12,34 Fig. 11 gives the M–H hysteresis loops for different compositions of Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) at room temperature. There is an increase in magnetization with an increase in dopant concentration at Y3+. However, even at the highest applied magnetic field of 2 T, the magnetization doesn't seem to saturate. The pinching or linear behaviour of pristine YFeO3 is a typical anti-ferromagnetic behaviour. The hysteresis behaviour is attributed to the significantly improved canting of spins. The enhancement in magnetization is due to larger spin canting associated with the presence of Ti4+ dopant ions and Fe3+ vacancies that are required for restoration of charge balance in the lattice. Also, the uncompensated surface spins of Fe3+ ions can enhance the magnetization. Yet another reason might be the formation of Y3+–O2−–R3+ instead of R3+–O2−–R3+ chain due to large magnetic moment of the dopant ions Gd3+, Sm3+. It is also observed that there a significant enhancement in coercivity. The possible reasons for this might be the formation of frustrated spin systems arising as a result of non-collinear magnetic ordering originating from the presence of uncompensated spins due to partial substitution of Ti4+ dopant ions at Fe3+ sites and balancing of Fe3+ vacancies.Lattice defects could be introduced by the doping of different radii ions at Y3+ site. Host lattice defects that are intrinsic can also be activated when different ions partially occupy Y3+ or Fe3+ sites which is evident from the increase in lattice constants. The increase in lattice constants with the increase in dopant concentration results in the increase in exchange interaction leading to the enhancement in magnetization. In the scenario of Ti4+ doping at Fe3+, the ionic radius of Ti4+ is almost similar to that of Fe3+, a strong surface anisotropy plays the major role in the significant increase of coercive field. The enhancement in Hc (coercivity) also suggests the possible existence of ferromagnetic (FM) exchange interaction.
It should be noted here that Fe–O–Fe super-exchange coupling is a predominant factor in the determination of magnetic ordering. This super-exchange interaction could be influenced by valence states of magnetic ions. Hence, it becomes necessary to have information about valence states of Fe to understand the origin of magnetic behaviour comprehensively. XPS analysis revealed that Fe exists in Fe3+ and Fe4+ mixed states. The XPS studies revealed that the relative amount Fe4+ increases with an increase in dopant concentration. It can also be speculated that the amount of Fe4+ increases with a decrease in oxygen deficiencies. This view is supported by our analysis of O 1s XPS pattern in the earlier section. Previous studies have shown that the 180° super-exchange coupling of Fe4+–O2−–Fe4+ is ferromagnetic.35 Therefore, the enhancement in ferromagnetic ordering can be due to Fe4+–O2−–Fe4+ super-exchange coupling. However, the presence of Fe3+ ions and oxygen deficiencies can induce a different kind of magnetic order which contributes to a small magnetization.36 It is well known that even a minute structural change/distortion such as tilting of FeO6 octahedra impact magnetic properties largely. In particular, parameters such as bond angle and bond length which determine orbital overlap, charge transfer and exchange interaction will have a potential effect on magnetic properties. The XPS and VSM analyses carried out on the samples under investigation prompted us to propose two types of exchange coupling interactions i.e., antiferromagnetic super-exchange coupling from Fe3+–O2−–Fe3+ and Fe4+–O2−–Fe4+ and double exchange coupling from Fe3+–O2−–Fe4+. Also the magnetic properties are affected by oxygen vacancies which interrupt the bridges between O and Fe/Ti and are undesirable from the point of hopping. The detailed quantitative information on the crystallographic changes obtained by XRD and oxygen vacancies allows us to comprehend the magnetic properties correlated by exchange coupling mechanism. We have observed an increase in Fe/Ti–O distance with an increase in dopant (Sm/Gd) concentration, resulting in a decrease in O 2p bandwidth. This decreases the orbital overlap between Fe (3d) and O (2p).
In Fe3+–O2−–Fe3+ super-exchange coupling interaction, the charge transfer mainly depends on overlap between Fe (3d) and O (2p) and is maximum when the distortion angle is zero. Such kind of super-exchange leads to anti-ferromagnetism. Since all the prepared samples are in orthorhombic symmetry which is evidenced from Goldschmidt tolerance factor, have the largest deviation from the ideal cubic structure. As the distortion increases with an increase in dopant (Sm3+/Gd3+) concentration listed in the Table 2, the behavior of the samples deviates from antiferromagnetic to ferromagnetic.
In Fe3+–O2−–Fe4+, the conducting electrons hop from Fe3+ towards Fe4+ via O2− bridge is a double exchange coupling interaction. As mentioned earlier, the increase in dopant (Sm3+/Gd3+) concentration at Y3+ sites resulted in the increase in Fe/Ti–O distance which consequently reduces the mobility of double exchange electrons which decrease the ferromagnetic property of the prepared samples. However, the reduction in oxygen vacancies evidenced from XPS studies paves the way for the exchange coupling mechanism to take place effectively thus resulting in the improved ferromagnetic behavior of the prepared samples. At this juncture, it is worth mentioning that we did not consider Ti4+–O2−–Ti4+ exchange interaction since Ti4+ as such is non-magnetic, the doping is comparatively minute and the probability of Ti atoms next to each other is negligibly small considering the random distribution of ions in Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05). Table 6 elucidates the maximum magnetization (Mm), remanent magnetization (Mr) and coercivity (Hc) of Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05).
| Name of the compound | Dopant concentration | Mm (10−3) emu g−1 | Mr (10−3) emu g−1 | Hc (coercive field) kOe |
|---|---|---|---|---|
| YSFTO | x = 0.05, y = 0.05 | 14.02 | 4.62 | 10.973 |
| x = 0.10, y = 0.05 | 18.06 | 7.15 | 11.162 | |
| x = 0.15, y = 0.05 | 24.27 | 11.14 | 12.784 | |
| YGFTO | x = 0.05, y = 0.05 | 12.39 | 3.76 | 6.551 |
| x = 0.10, y = 0.05 | 20.47 | 4.28 | 9.24 | |
| x = 0.15, y = 0.05 | 22.84 | 6.26 | 11.168 |
Conclusions
Phase-pure Y1−xRxFe1−(4/3)yTiyO3 (R = Sm, Gd; x = 0.05, 0.10, 0.15; y = 0.05) were synthesized via low-temperature solid-state synthesis route. Thus prepared powders were found to be orthorhombic matching to that of parent compound YFeO3. The optical bandgap for all the samples under investigation was observed to decrease with the increase in dopant concentration. The enhancement in magnetization and coercivity suggests a transition from antiferromagnetic to ferromagnetic behaviour. The improved magnetic properties are attributed to the existence of Fe4+ along with Fe3+ and the reduction of oxygen deficiencies.Funding
This research work did not obtain any particular grants from state, private or non-profit funding agencies.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors devote the research to the founder chancellor Bhagawan Sri Sathya Sai Baba and thank the Sri Sathya Sai Central Trust for providing synthesis and characterization facilities at Central Research Instruments Facility (SSSIHL-CRIF). The authors also thank Japan Advanced Institute of Science and Technology, Japan for providing with XPS characterization facility.References
- N. A. Spaldin, MRS Bull., 2017, 42, 385–389 CrossRef.
- S. Cao, H. Zhao, B. Kang, J. Zhang and W. Ren, Sci. Rep., 2015, 4, 5960 CrossRef PubMed.
- S. M. Yusuf, A. Kumar and J. V. Yakhmi, Appl. Phys. Lett., 2009, 95, 11–14 CrossRef.
- J. Mao, Y. Sui, X. Zhang, Y. Su, X. Wang, Z. Liu, Y. Wang, R. Zhu, Y. Wang, W. Liu and J. Tang, Appl. Phys. Lett., 2011, 98, 2009–2012 Search PubMed.
- C. W. Nan, M. I. Bichurin, S. Dong, D. Viehland and G. Srinivasan, J. Appl. Phys., 2008, 103, 031101 CrossRef.
- L. Mitoseriu, Bol. Soc. Esp. Ceram. Vidrio, 2005, 44, 177–184 CrossRef CAS.
- H. Schmid, J. Phys.: Condens. Matter, 2008, 20, 434201 CrossRef.
- G. King and P. M. Woodward, J. Mater. Chem., 2010, 20, 5785–5796 RSC.
- N. Singh, J. Y. Rhee and S. Auluck, J. Korean Phys. Soc., 2008, 53, 806–811 CrossRef CAS.
- D. Van Tac, V. O. Mittova and I. Y. Mittova, Inorg. Mater., 2011, 47, 521–526 CrossRef.
- X. Yuan, Y. Sun and M. Xu, J. Solid State Chem., 2012, 196, 362–366 CrossRef CAS.
- P. S. J. Bharadwaj, S. Kundu, K. Vijay Sai and K. B. R. Varma, J. Phys.: Condens. Matter, 2020, 32, 035810 CrossRef CAS PubMed.
- M. Wang and T. Wang, Materials, 2019, 12, 1–11 Search PubMed.
- N. O. Khalifa, H. M. Widatallah, A. M. Gismelseed, F. N. Al-Mabsali, R. G. S. Sofin and M. Pekala, Hyperfine Interact., 2016, 237, 46 CrossRef.
- M. C. Carotta, G. Martinelli, Y. Sadaoka, P. Nunziante and E. Traversa, Sens. Actuators, B, 2002, 48, 270–276 CrossRef.
- J. Ding, X. Lü, H. Shu, J. Xie and H. Zhang, Mater. Sci. Eng. B Solid State Mater. Adv. Technol., 2010, 171, 31–34 CrossRef CAS.
- R. L. Zhang, C. Le Chen, K. X. Jin, L. W. Niu, H. Xing and B. C. Luo, J. Electroceram., 2014, 32, 187–191 CrossRef CAS.
- M. Siemons, T. Weirich, J. Mayer and U. Simon, Z. Anorg. Allg. Chem., 2004, 630, 2083–2089 CrossRef CAS.
- Z. Zhou, L. Guo, H. Yang, Q. Liu and F. Ye, J. Alloys Compd., 2014, 583, 21–31 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- M. O'Keeffe and B. G. Hyde, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 3802–3813 CrossRef.
- E. VenkataRamana, F. Figueiras, A. Mahajan, D. M. Tobaldi, B. F. O. Costa, M. P. F. Graca and M. A. Valente, J. Mater. Chem. C, 2016, 4, 1066–1079 RSC.
- A. Shokri, S. Farjami and K. Boustani, Ceram. Int., 2018, 44, 22092–22101 CrossRef CAS.
- P. Kubelka, J. Opt. Soc. Am., 1948, 38, 448–457 CrossRef CAS PubMed.
- V. Gopalan, S. W. Cheong, J. L. Musfeldt, N. High and M. Field, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 4–7 Search PubMed.
- J. H. Jung, M. Matsubara, T. Arima, J. P. He, Y. Kaneko and Y. Tokura, Phys. Rev. Lett., 2004, 93, 1–4 CrossRef PubMed.
- A. S. Moskvin, A. A. Makhnev, L. V. Nomerovannaya, N. N. Loshkareva and A. M. Balbashov, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035106 CrossRef.
- Y. Tanabe, J. Phys. Soc. Jpn., 1956, 11, 864–877 CrossRef CAS.
- T. Matsui, E. Taketani, R. Sato and K. Morii, J. Phys. D: Appl. Phys., 2007, 40, 6066–6070 CrossRef CAS.
- M. Asim Farid, H. Zhang, X. Lin, A. Yang, S. Yand, G. Li, F. Liao and J. Lin, RSC Adv., 2015, 5, 12866–12871 RSC.
- H. Aono, M. Sato, E. Traversa and M. Sakamoto, J. Am. Ceram. Soc., 2001, 47, 341–347 Search PubMed.
- A. Jaiswal, R. Das, S. Adyanthaya and P. Poddar, J. Phys. Chem. C, 2011, 115, 2954–2960 CrossRef CAS.
- P. W. Anderson, Phys. Rev., 1959, 115, 2–13 CrossRef CAS.
- K. T. Jacob, G. Rajitha and N. Dasgupta, Indian J. Eng. Mater. Sci., 2012, 19, 47–53 CAS.
- S. Mori, J. Phys. Soc. Jpn., 1970, 28, 44–50 CrossRef CAS.
- T. Matsui, H. Tanaka, N. Fujimura, T. Ito, H. Mabuchi and K. Morii, Appl. Phys. Lett., 2002, 81, 2764–2766 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |