DOI:
10.1039/D0RA02817G
(Paper)
RSC Adv., 2020,
10, 26277-26287
Systematic investigation of the magneto-electronic structure and optical properties of new halide double perovskites Cs2NaMCl6 (M = Mn, Co and Ni) by spin polarized calculations†
Received
27th March 2020
, Accepted 23rd June 2020
First published on 13th July 2020
Abstract
A cohesive study using density functional theory simulations is performed to reveal and understand the structural stability, optoelectronic and magnetic properties of Cs2NaMCl6 (M = Mn, Co and Ni) halide double perovskites. The exchange-correlation potential, which is the only unknown parameter in the state-of-the-art formulism is determined through the well-known generalized gradient approximation and integration of the mBJ potential to it. The structural optimization, mechanical stability criteria and tolerance factor confirmed the stability of the double perovskites in a cubic structure with Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry. The elastic constants endorsed the mechanical stability and justify the brittle character of these double perovskites. The spin polarized electronic band profile and behaviour of the dielectric constant and absorption coefficient in the spin up and down channels revealed the presence of half-metallic nature in these materials. Moreover, herein, we have discussed the origin of the half-metallic gap and magnetism. The unpaired electrons in the crystal field splitted d-orbitals of the M-sited constituents are responsible for the half-metallic and magnetic character. The total magnetic moment was determined to be 4μB, 4μB and 1μB for the Mn-, Co- and Ni-based double perovskites, respectively, with main contributions solely coming from the transition metal atoms. The perfect spin polarization at the Fermi level suggests the application of double perovskites in spintronic technology.
m symmetry. The elastic constants endorsed the mechanical stability and justify the brittle character of these double perovskites. The spin polarized electronic band profile and behaviour of the dielectric constant and absorption coefficient in the spin up and down channels revealed the presence of half-metallic nature in these materials. Moreover, herein, we have discussed the origin of the half-metallic gap and magnetism. The unpaired electrons in the crystal field splitted d-orbitals of the M-sited constituents are responsible for the half-metallic and magnetic character. The total magnetic moment was determined to be 4μB, 4μB and 1μB for the Mn-, Co- and Ni-based double perovskites, respectively, with main contributions solely coming from the transition metal atoms. The perfect spin polarization at the Fermi level suggests the application of double perovskites in spintronic technology.
Introduction
Spintronic technology has become the subject of growing interest since it allows the utilization of both spin degree of freedom and charge of electrons simultaneously.1–3 Therefore, spintronics is beneficial for developing devices with new functionality having multiple applications. It offers potential advantages over conventional electronic devices, such as marginal reduction in power consumption, increase in processing speed and non-volatility data storage.4,5 Materials demonstrating high spin polarization (SP) character are suitable candidates for this technology. The ratio of the density of states (DOS) in the spin-up and down orientations at the Fermi level quantifies the magnitude of spin polarization,6 SP = (DOS↑ − DOS↓)/(DOS↑ + DOS↓). Diamagnetic and paramagnetic materials have symmetric DOS in the spin-up and down channels, and thus do not exhibit the spin polarization effect. However, ferromagnetic materials demonstrate asymmetric DOS, and thus their SP is always greater than zero but less than unity. In the case of a half-metallic materials: band structure in one spin channel is metallic showing the presence of states at the Fermi level, whereas exhibit semiconducting/insulting nature in the other spin channel. Therefore, these materials demonstrate 100% spin polarization at the Fermi level and are thought to be suitable candidates for spintronic technology.7–9 Pioneer work in field of half-metallicity was carried out by de Groot et al. in 1983.7 Since then, numerous compounds from different families have been reported to demonstrate half-metallic character. Among the variously reported half-metallic materials, the growing demand is for those materials that demonstrate high magnetic moment and high Curie temperature.
Perovskites exhibit a stoichiometric formula of ABX3 with A as s/p element, B is mostly a transition/inner-transition element or even can belong to the s/p block, while X can be either oxygen (oxide perovskites) or halogen member (halide perovskites).10,11 The perovskite family is probably the most studied family because they can be synthesized and exhibit diverse physical properties, such as radioactive waste encapsulation, high-temperature superconductivity, and multiferroicity, which make these ceramics an imperative tool for various fascinating technologies, including solid-oxygen fuel cells, spintronics, and shape memory devices.12–14 Furthermore, the flexibility of the structure of perovskites allows easy tailoring/modification of their stoichiometry to optimize their electronic, magnetic and thermoelectric properties. Over the past few decades, there has been particular interest in doubling the constituents of perovskites, while replacing exactly half of the B-site cations by another cation (B′), forming the so-called double-perovskite A2BB′X6.15 Due to the interplay between the B- and B′-sited cations, double perovskites show half-metallicity and other feasible properties. Oxide double perovskites have been reported to depict fascinating properties. Sr2FeReO6, Sr2FeMoO6, Sr2CrWO6 and their related double perovskites are half-metals with a fairly high magnetic transition temperature, making them suitable candidates for future spintronics applications.16,17 Ba2FeMoO6 has a figure of merit (ZT) nearly equal to unity, and thus is suitable for thermoelectric technology.18 On the other hand, halide perovskites (X belonging to the halogen family) have been used to produce optoelectronic devices with impressive quality.19 These materials have revolutionized solar cell technology by achieving an efficiency of about 22%.19,20 However, recently Cai et al. investigated some lead-free Cs2GeB′X6-type halide perovskites and reported that these materials exhibit ferromagnetic character with a high Curie temperature.21 Moreover, E. Haque and M.A. Hossain investigated Cs2BiAgX6 (X = Cl, Br) materials and found the presence of ultralow thermal conductivity in these materials, giving rise to ZT ≈ 0.8.22 Therefore, these materials are expected to show a good thermoelectric response.
In the current study, we present a detailed report of new possible half-metallic halide double perovskites. The motive of the present study is to explore the structural stability and understand the origin of half-metallicity in these materials. The electron filling in the d-states of transition atoms plays a vital role in opening the semi-conducting gap in one of the spin directions. Numerous alkali metal halide Cs2NaB′Cl6-type double perovskites have been reported since the 1970s.23–26 The focus of the investigations was mostly to understand the structural stability of those compounds. Among them, most of the materials such as Cs2NaScCl6, Cs2NaTiCl6, Cs2NaVCl6, Cs2NaFeCl6, Cs2NaAmCl6, and Cs2NaBkCl6 were found to be crystalline in cubic structures following symmetric operations of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Within the crystalline structure, cesium is enclosed by a cage of 12-Cl atoms, while an Na/B′ atom lies within the octahedron environment of Cl. However, to date, their electronic band profile, magnetic character and transport properties still remain unexplored. Thus, based on DFT calculations, herein, we present the structural, mechanical, electronic, optical and magnetic properties of Cs2NaMCl6 (M = Mn, Co and Ni) double perovskites.
m space group. Within the crystalline structure, cesium is enclosed by a cage of 12-Cl atoms, while an Na/B′ atom lies within the octahedron environment of Cl. However, to date, their electronic band profile, magnetic character and transport properties still remain unexplored. Thus, based on DFT calculations, herein, we present the structural, mechanical, electronic, optical and magnetic properties of Cs2NaMCl6 (M = Mn, Co and Ni) double perovskites.
Computational details
Density functional theory (DFT) and post-DFT simulations have proven to be one of the most accurate methods for the computation of the structural magneto-electronic structure of crystalline materials.27,28 The ground state structural parameters of the titled double perovskites are predicted by optimization and relaxation of their unit cell structure. The optimized structure parameters are used to predict the electronic and optical profile of the double perovskites. All the calculations are performed with the help of first principle methods, wherein we have solved the Kohn–Sham equation through an iterative scheme with the help of the Wein2k code and simulation packages integrated to it. The presence of d-electrons of Mn/Co/Ni may increase the exchange correlation effects in the Cs2NaMCl6 double perovskites. Thus, the generalized gradient approximation (GGA) without and with the modified Becke–Johnson potential (GGA + mBJ) is used.29,30 Muffin tin spheres are framed around atomic constituents. The LAPW basis set is incorporated for the wave expansion, which ensured that the waves within the sphere are atomic-like and outside it has plane wave character. The parameters lmax = 10 and RMTKmax = 7 are used for the atomic and plane wave cutoff, respectively. A reduced Brillouin zone (BZ) scheme that could simulate the crystal under periodic boundary conditions is used. For the integration over the BZ, a compact mesh of 1000 k-points is incorporated. The iterations stopped self consistently when the convergence conditions 0.0001e for charge and 0.0001 Ry for energy are satisfied. The elastic constants and optical properties, which can help in understanding the mechanical stability and exploration of electronic structure are determined by incorporating the elastic and optic package implemented with the Wein2k simulation code.
Structural stability
Structural stability is crucial for any material, which affects almost all its physical properties. The titled double perovskites have not been synthesized experimentally to date; however, Cs2NaB′Cl6 (B′ = Sc, Ti, V and Fe) has been prepared, exhibiting a cubic structure having symmetry of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group.25,26 By employing simulation, the stability and ground state structure of any material can be explored by minimizing its crystal energy with respect to volume. Sequentially, to establish the ground state structure of the Cs2NaMCl6 (M = Mn, Co and Ni) double perovskites we optimized their structures with spin polarized calculations. The optimization curves are represented in Fig. 1, which disclose the stability of these double perovskites. The minimum in the E–V curve corresponds to the ground state energy. The equilibrium lattice parameters are evaluated at the optimized volume corresponding to the minimum energy and are tabulated in Table 1. On comparing the unit cell volume, it is evident that the lattice constant decreases in the order of Mn > Co > Ni-based double perovskites. This is because atomic size decreases across the period. The unit cell structures are shown in Fig. S1 (ESI),† where it can be seen the Na/M-atoms are within octahedra of Cl-atoms, while Cs is coordinated by 12 Cl-atoms.
m space group.25,26 By employing simulation, the stability and ground state structure of any material can be explored by minimizing its crystal energy with respect to volume. Sequentially, to establish the ground state structure of the Cs2NaMCl6 (M = Mn, Co and Ni) double perovskites we optimized their structures with spin polarized calculations. The optimization curves are represented in Fig. 1, which disclose the stability of these double perovskites. The minimum in the E–V curve corresponds to the ground state energy. The equilibrium lattice parameters are evaluated at the optimized volume corresponding to the minimum energy and are tabulated in Table 1. On comparing the unit cell volume, it is evident that the lattice constant decreases in the order of Mn > Co > Ni-based double perovskites. This is because atomic size decreases across the period. The unit cell structures are shown in Fig. S1 (ESI),† where it can be seen the Na/M-atoms are within octahedra of Cl-atoms, while Cs is coordinated by 12 Cl-atoms.
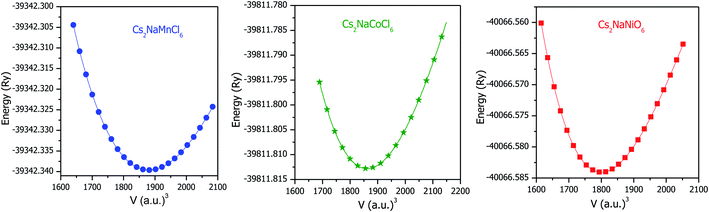 |
| | Fig. 1 Optimization curves of Cs2NaM(Mn, Co, Ni)Cl6 double perovskites by spin polarized calculations. | |
Table 1 Ground state parameters of volume V (a.u.)3, crystal energy, E0 (Ry), cohesive energy Ecoh (Ry), bond Length (a.u.), bond angle and tolerance factor (τ)
| Double perovskite |
V |
E0 |
Ecoh |
Bond length |
Bond angle |
τ |
| Cs–Cl |
Na–Cl |
M–Cl |
Cl–Cs–Cl |
Na–Cl–M |
| Cs2NaMnCl6 |
1880.86 |
−39342.3396 |
2.05 |
6.93 |
4.89 |
4.89 |
90° |
180° |
0.99 |
| Cs2NaCoCl6 |
1861.74 |
−39811.8128 |
2.01 |
6.86 |
4.85 |
4.85 |
90° |
180° |
0.99 |
| Cs2NaNiCl6 |
1800.25 |
−40066.5840 |
2.09 |
6.88 |
4.86 |
4.86 |
90° |
180° |
0.99 |
The stability of the cubic structure is further confirmed by computing the tolerance factor (τ) as:31 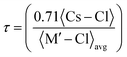 , where 〈Cs–Cl〉 represents the inter-atomic distance between Cs and Cl atoms 〈M′–Cl〉avg is the average of the 〈Na–Cl〉 and 〈M–Cl〉 bond distances. The condition τ equals unity corresponds to an ideal double perovskite structure exhibiting the symmetry of the Fm
, where 〈Cs–Cl〉 represents the inter-atomic distance between Cs and Cl atoms 〈M′–Cl〉avg is the average of the 〈Na–Cl〉 and 〈M–Cl〉 bond distances. The condition τ equals unity corresponds to an ideal double perovskite structure exhibiting the symmetry of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. The ideal structure is free from any internal stress and the Na–Cl–M bond angle is 180°. However, the cubic phase is stable over the range of 0.9–1. When the tolerance factor is smaller than the lower limit, the Na–Cl and M–Cl bonds remain compressed, while the Cs–Cl bonds are under tension. The structure relaxes and overcomes stress via the cooperative rotation of the octahedrons, which lowers the symmetry of the double perovskite. These rotations are meant to bend the Na–Cl–M bond angles from 180° to 180°–θ and the stability of the cubic phase decreases compared to lower symmetric phases. When τ > 1, the Na–Cl and M–Cl bonds come under tension, whereas the Cs–Cl bonds are under compression, and under this condition the Na–Cl–M bond angle remains 180°; however, the structure overcomes the tensile stress by allowing hexagonal stacking. The bond length and bond angle of the optimized structure are reported in Table 1. The evaluated value of the tolerance factor from the bond lengths reveals the stability of double perovskites in the cubic structure.
m space group. The ideal structure is free from any internal stress and the Na–Cl–M bond angle is 180°. However, the cubic phase is stable over the range of 0.9–1. When the tolerance factor is smaller than the lower limit, the Na–Cl and M–Cl bonds remain compressed, while the Cs–Cl bonds are under tension. The structure relaxes and overcomes stress via the cooperative rotation of the octahedrons, which lowers the symmetry of the double perovskite. These rotations are meant to bend the Na–Cl–M bond angles from 180° to 180°–θ and the stability of the cubic phase decreases compared to lower symmetric phases. When τ > 1, the Na–Cl and M–Cl bonds come under tension, whereas the Cs–Cl bonds are under compression, and under this condition the Na–Cl–M bond angle remains 180°; however, the structure overcomes the tensile stress by allowing hexagonal stacking. The bond length and bond angle of the optimized structure are reported in Table 1. The evaluated value of the tolerance factor from the bond lengths reveals the stability of double perovskites in the cubic structure.
Mechanical stability and properties
The mechanical stability and strength of materials can be explored by determining their elastic constants. The sufficient number of elastic constants necessary to survey the mechanical behaviour depends on the structural symmetry exhibited by a system. Since the double perovskites under investigation stabilize in cubic symmetry, therefore only three elastic constants, C11, C12 and C44, are required to analyse their mechanical behaviour. Born formulated the necessary condition for the mechanical stability, which are given by C11 > 0; C11 − C12 > 0; C44 > 0; C11 + 2C12 > 0.32,33 The determined elastic constants in Table 2 follow Born's stability criteria, thereby authenticating the mechanical stability of the double perovskites. Furthermore, the elastic constants can provide insight to mechanical behaviour through the computation of the elastic moduli and other parameters. The Reuss and Voigt values of the bulk (B) and shear (G) moduli represent the extreme ends of the bulk and shear moduli.34 Hill's scheme is a practical way for estimating these moduli by averaging of the extreme values, i.e., B = (BV + BR)/2 and G = (GV + GR)/2, where BV and GV are the Voigt bulk and shear moduli, respectively, which can be calculated directly from the elastic constants using the relation BV = (C11 + C12)/3; GV = (C11 − C12 + 3G44)/5. BR and GR are the Reuss values of the bulk and shear moduli, which can be obtained using the following relations: 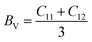 and GR = {5C44(C11 − C12)}/{4C44 + 3(C11 − C12)}, respectively. Directly from the B and G values, one can deduce the Young's modulus (Y) and Poisson's ratio (σ) using the relations Y = 9BG/(3B + G) and σ = (3B − Y)/6B, respectively. The calculated values are listed in Table 2. Generally, the elastic modulus is the resistance offered by any material towards deformation, the bulk modulus is for volumetric deformation and the shear modulus for shape deformation, whereas Y characterizes the resistance to uniaxial deformation and can be used to estimate the stiffness of a material. The moduli decreased in the order of Y > B > G, signifying that these double perovskites allow shape deformation more easily compared to volumetric deformation. The mechanical behaviour of brittleness or ductility can be directly described from the elastic parameters. The different empirical parameters that are often used to signify mechanical behaviour are the Pugh ratio (B/G) and Poisson's ratio.3,34 The index values separating the extreme behaviours are 1.75 and 0.26 for B/G and σ, respectively. Values above these decisive numerals for any material demonstrate the ductile character, otherwise brittle in nature. Accordingly, the calculated values reveal the brittle nature of the titled double perovskites. Additionally, the Zener anisotropic A factor is determined using the elastic constants and is given in Table 2. It used to characterize the deviation from isotropic behaviour. The calculated values suggest the presence of anisotropy since the magnitude of A deviates from unity. We also computed the micro-hardness (H) to examine the mechanical strength of the double perovskites. The hardness of a material can be directly linked to its bulk or shear modulus. The calculated values of H given in Table 2 suggest that all three Cs-based double perovskites have good mechanical strength.
and GR = {5C44(C11 − C12)}/{4C44 + 3(C11 − C12)}, respectively. Directly from the B and G values, one can deduce the Young's modulus (Y) and Poisson's ratio (σ) using the relations Y = 9BG/(3B + G) and σ = (3B − Y)/6B, respectively. The calculated values are listed in Table 2. Generally, the elastic modulus is the resistance offered by any material towards deformation, the bulk modulus is for volumetric deformation and the shear modulus for shape deformation, whereas Y characterizes the resistance to uniaxial deformation and can be used to estimate the stiffness of a material. The moduli decreased in the order of Y > B > G, signifying that these double perovskites allow shape deformation more easily compared to volumetric deformation. The mechanical behaviour of brittleness or ductility can be directly described from the elastic parameters. The different empirical parameters that are often used to signify mechanical behaviour are the Pugh ratio (B/G) and Poisson's ratio.3,34 The index values separating the extreme behaviours are 1.75 and 0.26 for B/G and σ, respectively. Values above these decisive numerals for any material demonstrate the ductile character, otherwise brittle in nature. Accordingly, the calculated values reveal the brittle nature of the titled double perovskites. Additionally, the Zener anisotropic A factor is determined using the elastic constants and is given in Table 2. It used to characterize the deviation from isotropic behaviour. The calculated values suggest the presence of anisotropy since the magnitude of A deviates from unity. We also computed the micro-hardness (H) to examine the mechanical strength of the double perovskites. The hardness of a material can be directly linked to its bulk or shear modulus. The calculated values of H given in Table 2 suggest that all three Cs-based double perovskites have good mechanical strength.
Table 2 Calculated elastic parameters at 0 GPa and 0 K
| Parameter (GPa) |
Cs2NaMnCl6 |
Cs2NaCoCl6 |
Cs2NaNiCl6 |
| C11 |
49.22 |
39.78 |
36.80 |
| C12 |
18.11 |
16.24 |
15.52 |
| C44 |
17.23 |
15.51 |
14.98 |
| B = BV = BR = (C11 + 2C12)/3 |
28.48 |
24.08 |
22.25 |
| GV = (C11 − C12 + 3C44)/5 |
16.56 |
14.41 |
13.65 |
| GR = 5C44(C11 − C12)/{4C44 + 3(C11 − C12)} |
16.51 |
14.28 |
13.44 |
| G = (GV + GR)/2 |
16.54 |
14.34 |
13.54 |
| Y = 9BG/(3B + G) |
41.57 |
36.07 |
34.04 |
| B/G |
1.72 |
1.72 |
1.71 |
| σ = (3B − Y)/6B |
0.25 |
0.25 |
0.25 |
| A = 4C44/(C11 − C12) |
1.10 |
1.21 |
1.28 |
| H = 0.92(B/G)1.3137G0.708 |
20.12 |
18.56 |
17.44 |
Electronic and magnetic properties
Materials with smart electronic and magnetic profiles are enormously demanded in various scientific fields. These materials are not merely interesting for increasing fundamental knowledge, but also have implications for important industrial applications. Therefore, understanding the electronic and magnetic nature of materials is essential. Herein, we plotted the variation in the density of states with energy and also the band structures (E–k diagrams) with a reduced Brillouin zone scheme to outline the electronic character of the materials. The energy state distribution is greatly affected by the exchange and correlation potential. The presence of d-state electrons may make the GGA inefficient for these double perovskites. Thus, we also incorporated the mBJ potential to define a more precise band structure. The band structure of the double perovskites via GGA is demonstrated in Fig. 2 and the magnified view of the band structures is presented in Fig. S2 (ESI).† The behaviour of the E–k dispersion curves in the vicinity of the Fermi level designates the electronic properties of any material. The overlap of the partially filled energy bands with the Fermi level gives rise to metallic character. However, completely filled bands can be found beneath the Fermi level are responsible for opening the semiconducting band gap. From the band structure, it can be observed that Cs2NaMnCl6 and Cs2NaNiCl6 show metallic character in the spin-up channel and semiconducting nature in the opposite spin direction. However, Cs2NaCoCl6 demonstrates a semiconducting band structure in the spin-up direction and metallic character in the spin-down direction. The closeness of the Fermi level to the valance band in the semiconducting channel indicates the presence of p-type semiconducting behaviour. The existence of metallic character in one spin channel and semiconducting in the other induces half-metallicity. Moreover, pseudo-gaps can be observed from the band profile of the double perovskites. In the metallic channel of Cs2NaMnCl6 and Cs2NaNiCl6, a forbidden gap originates from 0.17 eV to 4.2 eV and 0.15 eV to 5.2 eV, respectively. In contrast, in the spin-down channel of the Co-based halide perovskite, the forbidden gaps are in the region of 0.25 eV to 0.8 eV and 1.12 eV to 5.05 eV. The half-metallic character is maintained even when we incorporated the mBJ potential to GGA, as shown in Fig. 3. However, the range of the semiconducting gap is affected, as presented in Table 3.
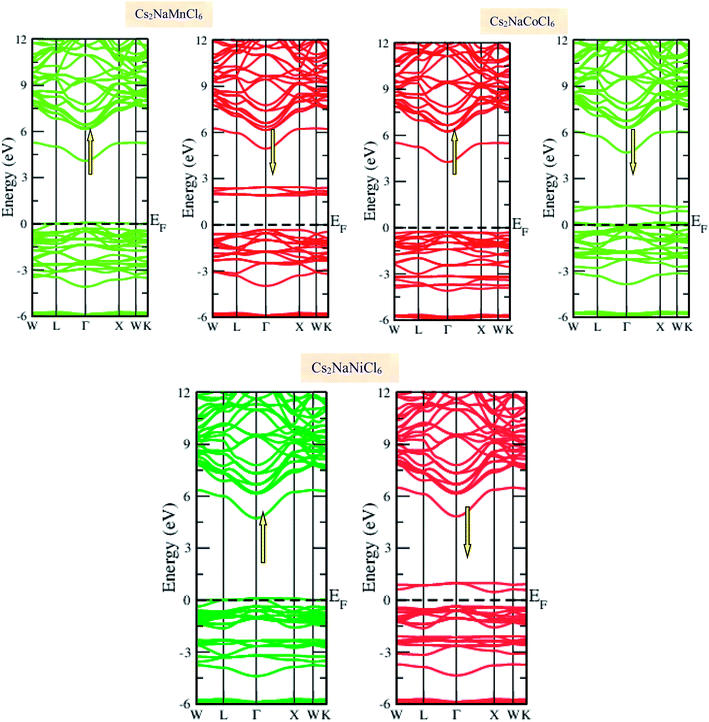 |
| | Fig. 2 Spin polarized band structures of Cs2NaMCl6 double perovskites via GGA approximation. Red lines are used for semiconducting channels and green for metallic channels. | |
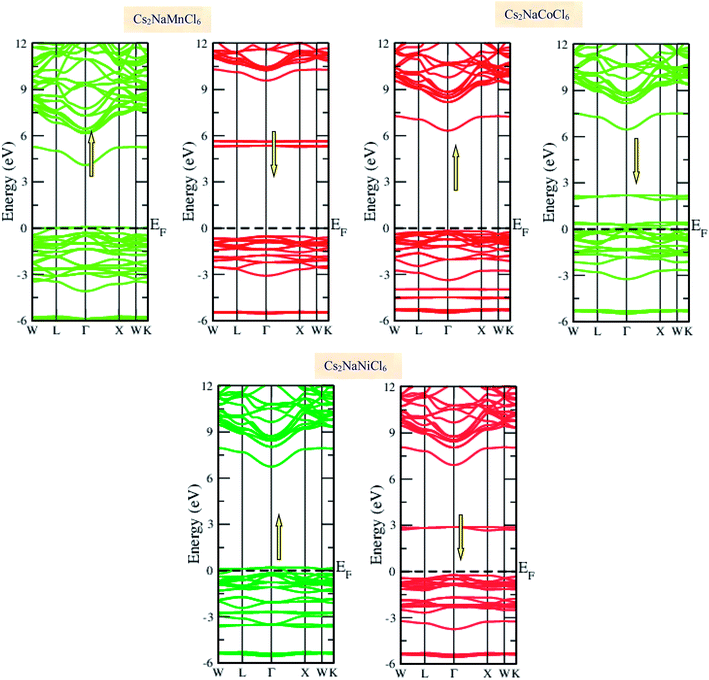 |
| | Fig. 3 GGA + mBJ band profiles of Cs2NaMCl6 double perovskites. | |
Table 3 Observed band gap (Eg in eV) in semi-conducting channel and total magnetic moment (MT in μB) of Cs2NaMCl6 double perovskites through the GGA and GGA + mBJ approximations
| Approximation |
Cs2NaMnCl6 |
Cs2NaCoCl6 |
Cs2NaNiCl6 |
| Eg |
MT |
Eg |
MT |
Eg |
MT |
| GGA |
2.06 |
4.0 |
4.25 |
4.0 |
0.96 |
1.0 |
| GGA + mBJ |
5.03 |
4.0 |
6.07 |
4.0 |
2.9 |
1.0 |
The total DOS plots shown in Fig. 4 reveal the comparative effect of the mBJ potential on the electronic properties of the Cs2NaMCl6 double perovskites. The electron states are shifted away from the Fermi level, thereby widening of band gap can be observed in the semiconducting channel. To further illustrate the band structure and clarify the energy states associated with the valance and the conduction bands, we plotted the partial density of states. The Cl-atom contributes the most towards the valance band formation, as shown in Fig. 5. In contrast, the belonging of the Cs and Na states are mostly away from the valance band, and thereby do not play any significant role in shaping the electronic structure. The d-states of the transition atom play a peculiar role, and thereby dominate the electronic properties. On comparing the pDOS of the three double perovskites, it is evident that the d-states of the transition atoms are placed differently across the Fermi level are responsible for their half-metallic character. The p–d hybridization occurs among the dt2g states of Mn and Cl in the valance band of the spin-up channel. The Mn-deg states at the Fermi level give rise to the metallic character in the spin-up channel of the Mn-based double perovskite. In contrast, in the spin-down channel, all the d-states of Mn are above the Fermi level form the conduction band minima. In the Co-based double perovskite, both the dt2g and deg states of the spin-up channel below the Fermi lever take part in p–d hybridization. On the other hand, the dt2g states are at the Fermi level in the spin-down channel and the deg states are empty lie above the Fermi level. However, in the Ni-based double perovskite, the dt2g states are completely filled for both spin channels and lie in the valance band. The deg states in the spin-up channel at the Fermi level give rise to metallic character, while in the spin-down state they form the conduction band minima. The p-states of the Cl-ligands are completely filled, and mainly contribute to the formation of the valance band. The valance states of Cs-s and Na-s are empty, and thus are located at higher energies above the Fermi level. The inner valance p-states of Cs give rise to the DOS peak at around −5 eV for both spin directions in these materials. Moreover, it can be analysed from the DOS plots that Cs, Na and Cl have equal amounts of electrons in the up- and down-states, having almost symmetric DOS across the reference level. The d-states of the transition atom are asymmetrically distributed, and therefore give rise to the magnetic character in the double perovskites.
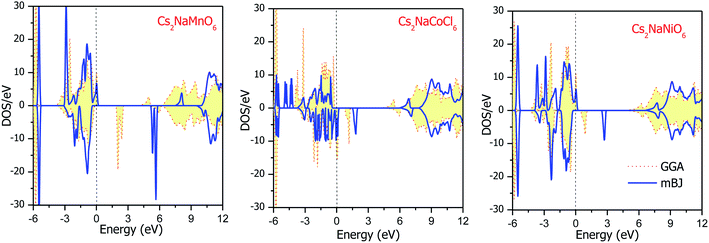 |
| | Fig. 4 Energy state distribution over the energy range of −6 to 12 eV by GGA and mBJ approximations. | |
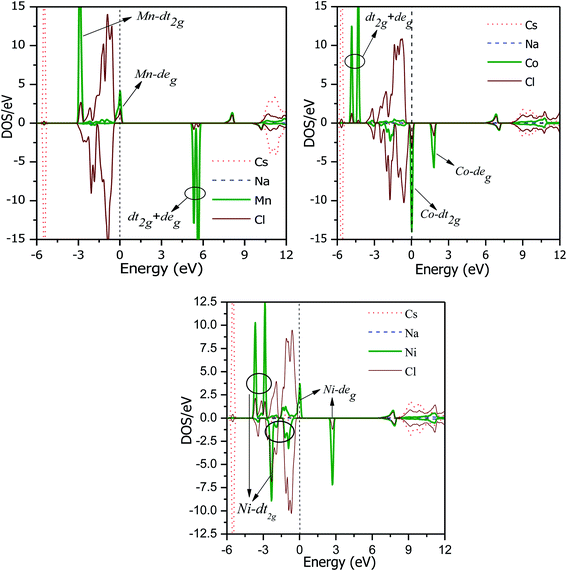 |
| | Fig. 5 PDOS of Cs2NaMCl6 double perovskites in the energy range of −6 to 12 eV. | |
Origin of half-metallicity and ferromagnetic character
As mentioned in the structural properties, the M-site atoms are located in the octahedral environment of the Cl-atoms. The crystal field due to M–Cl Coulomb interactions decrease the degeneracy of the Mn/Co/Ni d(dxy, dyz, dzx, dx2−y2, dz2) orbitals, which are splitted into dt2g (dxy, dyz, dzx) and deg (dx2−y2, dz2) sets. The dt2g state has an intake capacity of 6 electrons (3↑ + 3↓), while the deg state can accommodate a maximum of 4 electron (2↑ + 2↓) following Hund's rules. After half filling dt2g orbitals, the electrons can choose to either form a high-spin state, i.e., fill higher energy deg before pairing occurs in the dt2g orbitals or to form a low-spin state i.e., deg states are filled only after the dt2g states are completely filled. The choice of forming a high-spin state or low-spin state depends on the crystal field splitting energy (CFS) and pairing energies. The high-spin state is formed only if the splitting energy is less than the pairing energy. The CFS is affected by the number of electrons and size of the central atom.35 The type of ligand affects the splitting, strong field ligands can do large splitting. However, in the presence of weak field ligands such as Cl, the CFS is small and therefore the formation of the high-spin state depends on the oxidation number, electron number and size of the transition anion. The expected oxidation states in these double perovskites are Cs21+Na1+M3+Cl61−. Mn3+, Co3+ and Ni3+ have 4, 6 and 7 valance electrons, respectively, in their d states. The electron occupancy in the Mn3+ d state is 3t2g(↑), 1eg(↑), 0t2g(↓), and 0eg(↓), forming a high-spin state with S = 2. The d states in the spin-down state are empty and form the conduction band minima. The deg state in the spin-up channel is partially filled and resides at the Fermi level, as is evident in Fig. 5. According to the DOS plots of the Co-based double perovskite, it is obvious that the d states in the spin-up channel are completely occupied. The dt2g states in the spin-down channel are at the Fermi level. The electron filling in the valance states of the Co3+ states therefore is 3t2g(↑), 2eg(↑), 1t2g(↓), and 0eg(↓), thereby leaving four electrons unpaired with S = 2. The occupancy clearly confirms that the d-orbitals in the spin-up channel that are completely filled form the valance band. While, the dt2g states in the anti-parallel spin channel that are partially filled give the metallic character in the respective spin channel. Upon going from Mn to Ni, the number of electrons at the central atom increases, while size decreases. Ni3+ has the electronic configuration of 3t2g(↑), 3t2g(↓), 1eg(↑), and 0eg(↓), leaving one unpaired electron, and thus S = 1/2. Thereby, the spin state changes from high to low when Ni is the central atom. Each unpaired electron gives a magnetic moment of ≈1μB, and thus the total magnetic moment becomes 4μB, 4μB and 1μB for the Mn-, Co- and Ni-based double perovskites, respectively. The integral magnetic moment also signifies the presence of half-metallicity.
Nature of bonding from charge density
The characteristic of bonding can be determined from the charge density and its spatial distribution. The ionic bond is characterised by a charge-free inter-atomic distance, whereas metallic and covalent bonds have charge sharing among constituents.31 However, in the covalent bond, charge sharing is directional, whereas the metallic bond has a uniform charge distribution throughout. The spatial charge configuration along the body diagonal plane for the Mn-based double perovskite is depicted in Fig. 6. The maximum charge resides at the atomic positions. The Cs and Na atoms have a completely spherical charge distribution and there is no overlapping of charge contours with the neighbouring Cl atom. This signifies that the Cs and Na atoms have ionic bonding character with the Cl atom. Conversely, Mn displays covalent bonding character with the Cl atom since the charge distribution deviates from prefect spherical to deformed (dumb-bell type). The overlapping of the contours signifies the hybridization among the M–Cl orbitals. The p–d hybridization is also confirmed by the PDOS distribution.
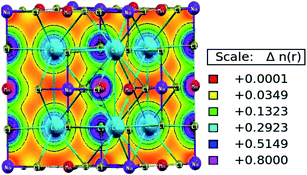 |
| | Fig. 6 Spatial charge distribution of Cs2NaMnCl6 double perovskites along the body diagonal. | |
Optical properties
The optical parameters of the Cs2NaMCl6 double perovskites are calculated in order to analyze their possible optoelectronic applications and to gain deeper insight into their electronic band profile. Since the band structures and DOS plots shown in Fig. 2 to 5 reveal metallic character in one spin channel and semiconducting in the other channel, it is obvious that the optical response will be different in these channels. Thus, we have determined the spin polarized optical behaviour of the Cs2NaMCl6 double perovskites. The complex dielectric function ε(ω) is often used to completely portray the response of a material to disturbances due to electromagnetic radiation. ε(ω) has two components, ε(ω) = ε1(ω) + iε2(ω), where the real part ε1(ω) defines the scattering power of a material.36–38 Meanwhile, the imaginary part has a direct relation with the band structure and reflects the absorptive behaviour, which is quite helpful in material selection for solar cell technology. The dielectric constant components are interrelated through the Kramer–Kronig relationships.37 The variation of ε1(ω) and ε2(ω) with photon energy is shown in Fig. 7(A and B), where it is clear that in the spin channels of Mn-up, Co-dn and Ni-up, the high value becomes negative between 0–1.2 eV for the Mn- and Ni-based double perovskites. Thereafter, they do not exhibit sharp variations with energy. In the negative range of ε1(ω), incident electromagnetic radiation (photon) is completely attenuated by the double perovskites, revealing their perfect metallic nature. The points at ε1(ω) drop below unity and have a positive slope, which are known as plasmon excitation points. However, in the spin channels of Mn-dn, Co-up and Ni-dn, ε1(ω) increases from a static value limit (zero frequency). The static values increase in the order of 1.84, 2.17, and 3.01 for Co-up, Mn-dn, and Ni-dn, respectively. The variation in the static value from one spin channel to another and by changing magnetic ions is expected due to the inverse relation of ε1(0) with the band 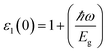 . The imaginary part of the dielectric constant ε2(ω) is very important in signifying the efficiency of optoelectronic devices, representing the photons that can be absorbed by perovskites. The optical edge observed at 0 eV for Mn-up, Co-dn and Ni-up signifies the metallic character in the respective spin channel. The presence of peaks away from zero energy signifies the absence of energy states at the Fermi level, thereby indicating a semiconducting nature in the Mn-dn, Co-up and Ni-dn spin channels. The variation in the refractive index (n) and extinction coefficients (k) with photon energy replicates the character of the real and imaginary dielectric constants, as shown in Fig. S3 (ESI).† The static refractive index values are 1.47, 1.36 and 1.74 for Mn-up, Co-dn and Ni-up, respectively. The variation in absorption coefficient (α) with photon energy is depicted in Fig. 8(A). The critical values of ‘α’, beyond which the absorption capabilities of a material increase, illustrate the threshold energies required for electrons to transition from the valance band maxima to the conduction band minima. The transitions mostly from the Cl-p sates of the valance band to the d-states of the M-site in the conduction band give rise to the optical absorption edge. The presence of pseudo gaps in the band structure also gives rise to absorption peaks. It can be seen from the figure that these double perovskites have a wide absorption region. This region is composed of different absorption peaks resulting from various electronic transitions, indicating absorption in the UV-visible region. Moreover, the absorption of photons generates electron–hole pairs, resulting in optical conductivity. The variation in optical conductivity with photon energy is similar to the absorption behaviour. This is due to the fact that absorbed photons generate conduction carriers, and thereby increase conductivity, as shown in Fig. 8(B). The peaks of optical conductivity at the static limit of Mn-up, Co-dn and Ni-up reveal their metallic character in the respective channel. In contrast, in the other spin channel, Mn-dn, Co-up and Ni-dn conduct only after the absorption edge, signifying the semiconducting channel. Hence, there results give overall support for the half-metallic character of double perovskites. The total absorption and conductivity of a spin polarized system is the sum of individual channels plus the peaks contributed by inter-channel transitions. We presented the total absorption power and conductivity without considering the inter-channel transitions of the double perovskites in Fig. S4 (ESI).† The peaks in the energy range of 0–6 eV strongly support the capability of these materials to absorb photons in the UV-visible region, confirming their suitability to be employed in various optoelectronic devices.
. The imaginary part of the dielectric constant ε2(ω) is very important in signifying the efficiency of optoelectronic devices, representing the photons that can be absorbed by perovskites. The optical edge observed at 0 eV for Mn-up, Co-dn and Ni-up signifies the metallic character in the respective spin channel. The presence of peaks away from zero energy signifies the absence of energy states at the Fermi level, thereby indicating a semiconducting nature in the Mn-dn, Co-up and Ni-dn spin channels. The variation in the refractive index (n) and extinction coefficients (k) with photon energy replicates the character of the real and imaginary dielectric constants, as shown in Fig. S3 (ESI).† The static refractive index values are 1.47, 1.36 and 1.74 for Mn-up, Co-dn and Ni-up, respectively. The variation in absorption coefficient (α) with photon energy is depicted in Fig. 8(A). The critical values of ‘α’, beyond which the absorption capabilities of a material increase, illustrate the threshold energies required for electrons to transition from the valance band maxima to the conduction band minima. The transitions mostly from the Cl-p sates of the valance band to the d-states of the M-site in the conduction band give rise to the optical absorption edge. The presence of pseudo gaps in the band structure also gives rise to absorption peaks. It can be seen from the figure that these double perovskites have a wide absorption region. This region is composed of different absorption peaks resulting from various electronic transitions, indicating absorption in the UV-visible region. Moreover, the absorption of photons generates electron–hole pairs, resulting in optical conductivity. The variation in optical conductivity with photon energy is similar to the absorption behaviour. This is due to the fact that absorbed photons generate conduction carriers, and thereby increase conductivity, as shown in Fig. 8(B). The peaks of optical conductivity at the static limit of Mn-up, Co-dn and Ni-up reveal their metallic character in the respective channel. In contrast, in the other spin channel, Mn-dn, Co-up and Ni-dn conduct only after the absorption edge, signifying the semiconducting channel. Hence, there results give overall support for the half-metallic character of double perovskites. The total absorption and conductivity of a spin polarized system is the sum of individual channels plus the peaks contributed by inter-channel transitions. We presented the total absorption power and conductivity without considering the inter-channel transitions of the double perovskites in Fig. S4 (ESI).† The peaks in the energy range of 0–6 eV strongly support the capability of these materials to absorb photons in the UV-visible region, confirming their suitability to be employed in various optoelectronic devices.
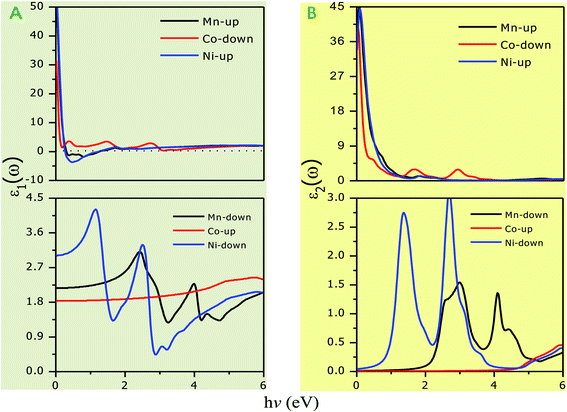 |
| | Fig. 7 Variation in dielectric constant with photon energy. (A) Real part (ε1) with gray background and (B) imaginary part (ε1) with yellowish background. | |
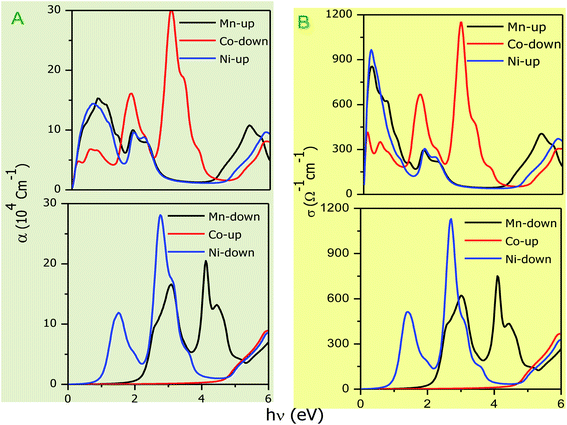 |
| | Fig. 8 (A) Variation in absorption coefficient (α) with photon energy with grey background and (B) optical conductivity with photon energy. | |
Conclusion
We have successfully established the structural and mechanical stability of halide double perovskites Cs2NaMCl6 (M = Mn, Co and Ni): the results would attract the attention of experimentalists to synthesize these novel materials. Their spin polarized electronic band structure indicates the half-metallic character for these materials. The total magnetic moment and distribution of energy levels signify that Mn3+ and Co3+ form a high-spin state, while Ni3+ is in a low-spin state. The formation of the low-spin state is probably due to the increase in the number of electrons at the central atom. The presence of the integral magnetic moment of 4μB, 4μB and 1μB for the Mn-, Co- and Ni-based double perovskites, respectively, supports the presence of half-metallic character. The variation in dielectric constant, absorption coefficient and optical conductivity with energy indicates the absorption of photons in the visible-UV region and also supports the presence of half-metallic character.
Authors contribution
All the calculations have been carried out by Mr Shabir Ahmad Mir. The manuscript was checked and hence modified by Dr Dinesh C. Gupta.
Data availability statement
The datasets generated during and/or analyzed during the current study would be available from Mr Shabir Ahmad Mir on reasonable request.
Conflicts of interest
The authors have no conflict of interest.
Acknowledgements
The authors are greatly thankful to Jiwaji University for providing facilities to carry out the research work.
References
- S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnár, M. L. Roukes, A. Y. Chtchelkanova and D. M. Trege, Spintronics: A Spin-Based Electronics Vision for the Future, Science, 2001, 294, 1488–1495 CrossRef CAS PubMed.
- V. K. Joshi, Spintronics: a contemporary review of emerging electronics devices, Int. J. Eng. Sci. Technol., 2016, 19, 1503–1513 Search PubMed.
- A. Q. Seh and D. C. Gupta, Exploration of highly correlated Co-based quaternary Heusler alloys for spintronics and thermoelectric applications, Int. J. Energy Res., 2019, 43, 8864–8877 CAS.
- C.-Y. You and S. D. Bader, Voltage controlled spintronic devices for logic applications, J. Appl. Phys., 2000, 87, 5215–5217 CrossRef CAS.
- T. Endoh and H. Honjo, A Recent Progress of Spintronics Devices for Integrated Circuit Applications, J. low power electron. appl., 2018, 8, 1–17 CrossRef.
- S. Kokado, Y. Sakuraba and M. Tsunoda, Spin polarization ratios of resistivity and density of states estimated from anisotropic magnetoresistance ratio for nearly half-metallic ferromagnets, Jpn. J. Appl. Phys., 2016, 55, 1–3 CrossRef.
- R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, New Class of Materials: Half-Metallic Ferromagnets, Phys. Rev. Lett., 1983, 50, 2024–2027 CrossRef CAS.
- T. M. Bhat and D. C. Gupta, Transport, Structural and Mechanical Properties of Quaternary FeVTiAl Alloy, J. Electron. Mater., 2016, 45, 6012–6018 CrossRef CAS.
- S. Yousuf and D. C. Gupta, Insight into half-metallicity, spin-polarization and mechanical properties of L21 structured MnY2Z (Z= Al, Si, Ga, Ge, Sn, Sb) Heusler alloys, J. Alloys Compd., 2018, 735, 1245–1252 CrossRef CAS.
- A. Kumar, A. S. Verma and S. R. Bhardwaj, Prediction of Formability in Perovskite-Type Oxides, Open Appl. Phys. J., 2008, 1, 11–19 CrossRef CAS.
- X. Mao, T. Wu, T. Chu, W. Deng and K. Han, First-Principles Screening of All-Inorganic Lead-Free ABX3 Perovskites, J. Phys. Chem. C, 2018, 122, 7670–7675 CrossRef CAS.
- Y. Moritomo, A. Asamitsu, H. Kuwahara and Y. Tokura, Giant magnetoresistance of manganese oxides with a layered perovskite structure, Nature, 1996, 380, 141–144 CrossRef CAS.
- N. A. Spaldin and M. Fiebig, Materials Science. The Renaissance of Magnetoelectric Multiferroics, Science, 2005, 309, 391–392 CrossRef CAS PubMed.
- J. M. De Teresa, M. R. Ibarra, P. A. Algarabel, C. Ritter, C. Marquina, J. Blasco, J. Garcia, A. D. Moral and Z. Arnold, Evidence for magnetic polarons in the magnetoresistive perovskites, Nature, 1997, 386, 256–259 CrossRef.
- S. Vasala and M. Karppinen, A2B′B′′O6 perovskites: a review, Prog. Solid State Chem., 2015, 43, 1–36 CrossRef CAS.
- K.-I. Kobayashi, T. Kimura, Y. Tomioka, H. Sawada and K. Terakura, Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure, Nature, 1998, 395, 677–680 CrossRef CAS.
- H.-T. Jeng and G. Y. Guo, First-principles investigations of orbital magnetic moments and electronic structures of the double perovskites Sr2FeMoO6, Sr2FeReO6, and Sr2CrWO6, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 1–7 CrossRef.
- O. Sahnoun, H. B. Benziane, M. Sahnoun and M. Driz, Magnetic and thermoelectric properties of ordered double perovskite Ba2FeMoO6, J. Alloys Compd., 2017, 714, 704–708 CrossRef CAS.
- Z. Xiao, Z. Song and Y. Yan, From Lead Halide Perovskites to Lead-Free Metal Halide Perovskites and Perovskite Derivatives, Adv. Mater., 2019, 31, 1803792 CrossRef CAS PubMed.
- Y. Shao, Y. Yuan and J. Huang, Correlation of energy disorder and open-circuit voltage in hybrid perovskite solar cells, Nat. Energy, 2016, 1, 15001 CrossRef CAS.
- B. Cai, X. Chen, M. Xie, S. Zhang, X. Liu, J. Yang, W. Zhou, S. Guo and H. Zeng, A class of Pb-free double perovskite halide semiconductors with intrinsic ferromagnetism, large spin splitting and high Curie temperature, Mater. Horiz., 2018, 5, 961–968 RSC.
- E. Haque and M. A. Hossain, Origin of ultra-low lattice thermal conductivity in Cs2BiAgX6 (X=Cl, Br) and its impact on thermoelectric performance, J. Alloys Compd., 2018, 748, 63–72 CrossRef CAS.
- M. L. Marsh and T. E. A. Schmitt, Directed evolution of the periodic table: probing the electronic structure of late actinides, Dalton Trans., 2017, 46, 9316–9333 RSC.
- K. W. Bagnall, J. B. Laidler and M. A. A. Stewart, Americium chloro-complexes, J. Chem. Soc. A, 1968, 133–136 RSC.
- L. R. Morss, M. Siegal, L. Stenger and N. Edelstei, Preparation of cubic chloro complex compounds of trivalent metals: Cs2NaMCl6, Inorg. Chem., 1970, 9, 1771–1775 CrossRef CAS.
- X. Cao, L. Kang, S. Guo, M. Zhang, Z. Lin and J. Gao, Cs2NaVCl6: A Pb-Free Halide Double Perovskite with Strong Visible and Near-Infrared Light Absorption, ACS Appl. Mater. Interfaces, 2019, 11, 38648–38653 CrossRef CAS PubMed.
- S. A. Mir and D. C. Gupta, Understanding the origin of half- metallicity and thermophysical properties of ductile La2CuMnO6 double perovskite, Int. J. Energy Res., 2019, 43, 4783–4796 CrossRef CAS.
- A. H. Reshak, Spin-polarized Second Harmonic Generation from the Antiferromagnetic CaCoSO Single Crystal, Sci. Rep., 2017, 7, 1–8 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. Koller, F. Tran and P. Blaha, Merits and limits of the modified Becke-Johnson exchange potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–10 CrossRef.
- S. A. Mir and D. C. Gupta, Exploration of uranium double perovskites Ba2MUO6 (M = Co, Ni) for magnetism, spintronic and thermoelectric applications, J. Magn. Magn. Mater., 2020, 493, 1–12 CrossRef.
- M. Born, On the stability of crystal lattices. I, Mathematical Proceedings of the Cambridge Philosophical Society, 1940, 36, 160–172, DOI:10.1017/S0305004100017138.
- S. A. Mir, S. Yousuf, T. M. Bhat, S. Singh, Ab Q. Seh, S. A. Khandy, S. A. Sofi, Z. Saleem and D. C. Gupta, Structural and elasto-mechanical properties of ordered double perovskite Ba2LuSbO6, AIP Conf. Proc., 2019, 2115, 030337 CrossRef.
- S. A. Sofi, S. Yousuf and D. C. Gupta, Prediction of robustness of electronic, magnetic and thermoelectric properties under pressure and temperature variation in Co2MnAs alloy, Comput. Condens. Matter, 2019, 16, e00375 CrossRef.
- J. E. House, Ligand Fields and Molecular Orbitals, Inorg. Chem., 2013, 591–616, DOI:10.1016/b978-0-12-385110-9.00017-0.
- Q. Mahmood, M. Hassan and M. A. Faridi, Study of magnetic and optical properties of Zn1-xTMxTe (TM = Mn, Fe, Co, Ni) diluted magnetic semiconductors: first principle approach, Chin. Phys. B, 2017, 26, 1–9 Search PubMed.
- B. Amin, R. Khenata, A. Bouhemadou, I. Ahmad and M. Maqbool, Opto-electronic response of spinels MgAl2O4 and MgGa2O4 through modified Becke-Johnson exchange potential, Phys. B, 2012, 407, 2588–2892 CrossRef CAS.
- T. Ahmed, A. Chen, D. A. Yarotski, S. A. Trugman, Q. Jia and J.-X. Zhu, Magnetic, electronic, and optical properties of double perovskite Bi2FeMnO6, APL Mater., 2017, 5, 1–8 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02817g |
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Dinesh C. Gupta
and
Dinesh C. Gupta *
*
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry. The elastic constants endorsed the mechanical stability and justify the brittle character of these double perovskites. The spin polarized electronic band profile and behaviour of the dielectric constant and absorption coefficient in the spin up and down channels revealed the presence of half-metallic nature in these materials. Moreover, herein, we have discussed the origin of the half-metallic gap and magnetism. The unpaired electrons in the crystal field splitted d-orbitals of the M-sited constituents are responsible for the half-metallic and magnetic character. The total magnetic moment was determined to be 4μB, 4μB and 1μB for the Mn-, Co- and Ni-based double perovskites, respectively, with main contributions solely coming from the transition metal atoms. The perfect spin polarization at the Fermi level suggests the application of double perovskites in spintronic technology.
m symmetry. The elastic constants endorsed the mechanical stability and justify the brittle character of these double perovskites. The spin polarized electronic band profile and behaviour of the dielectric constant and absorption coefficient in the spin up and down channels revealed the presence of half-metallic nature in these materials. Moreover, herein, we have discussed the origin of the half-metallic gap and magnetism. The unpaired electrons in the crystal field splitted d-orbitals of the M-sited constituents are responsible for the half-metallic and magnetic character. The total magnetic moment was determined to be 4μB, 4μB and 1μB for the Mn-, Co- and Ni-based double perovskites, respectively, with main contributions solely coming from the transition metal atoms. The perfect spin polarization at the Fermi level suggests the application of double perovskites in spintronic technology.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Within the crystalline structure, cesium is enclosed by a cage of 12-Cl atoms, while an Na/B′ atom lies within the octahedron environment of Cl. However, to date, their electronic band profile, magnetic character and transport properties still remain unexplored. Thus, based on DFT calculations, herein, we present the structural, mechanical, electronic, optical and magnetic properties of Cs2NaMCl6 (M = Mn, Co and Ni) double perovskites.
m space group. Within the crystalline structure, cesium is enclosed by a cage of 12-Cl atoms, while an Na/B′ atom lies within the octahedron environment of Cl. However, to date, their electronic band profile, magnetic character and transport properties still remain unexplored. Thus, based on DFT calculations, herein, we present the structural, mechanical, electronic, optical and magnetic properties of Cs2NaMCl6 (M = Mn, Co and Ni) double perovskites.![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group.25,26 By employing simulation, the stability and ground state structure of any material can be explored by minimizing its crystal energy with respect to volume. Sequentially, to establish the ground state structure of the Cs2NaMCl6 (M = Mn, Co and Ni) double perovskites we optimized their structures with spin polarized calculations. The optimization curves are represented in Fig. 1, which disclose the stability of these double perovskites. The minimum in the E–V curve corresponds to the ground state energy. The equilibrium lattice parameters are evaluated at the optimized volume corresponding to the minimum energy and are tabulated in Table 1. On comparing the unit cell volume, it is evident that the lattice constant decreases in the order of Mn > Co > Ni-based double perovskites. This is because atomic size decreases across the period. The unit cell structures are shown in Fig. S1 (ESI),† where it can be seen the Na/M-atoms are within octahedra of Cl-atoms, while Cs is coordinated by 12 Cl-atoms.
m space group.25,26 By employing simulation, the stability and ground state structure of any material can be explored by minimizing its crystal energy with respect to volume. Sequentially, to establish the ground state structure of the Cs2NaMCl6 (M = Mn, Co and Ni) double perovskites we optimized their structures with spin polarized calculations. The optimization curves are represented in Fig. 1, which disclose the stability of these double perovskites. The minimum in the E–V curve corresponds to the ground state energy. The equilibrium lattice parameters are evaluated at the optimized volume corresponding to the minimum energy and are tabulated in Table 1. On comparing the unit cell volume, it is evident that the lattice constant decreases in the order of Mn > Co > Ni-based double perovskites. This is because atomic size decreases across the period. The unit cell structures are shown in Fig. S1 (ESI),† where it can be seen the Na/M-atoms are within octahedra of Cl-atoms, while Cs is coordinated by 12 Cl-atoms.

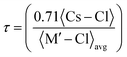 , where 〈Cs–Cl〉 represents the inter-atomic distance between Cs and Cl atoms 〈M′–Cl〉avg is the average of the 〈Na–Cl〉 and 〈M–Cl〉 bond distances. The condition τ equals unity corresponds to an ideal double perovskite structure exhibiting the symmetry of the Fm
, where 〈Cs–Cl〉 represents the inter-atomic distance between Cs and Cl atoms 〈M′–Cl〉avg is the average of the 〈Na–Cl〉 and 〈M–Cl〉 bond distances. The condition τ equals unity corresponds to an ideal double perovskite structure exhibiting the symmetry of the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. The ideal structure is free from any internal stress and the Na–Cl–M bond angle is 180°. However, the cubic phase is stable over the range of 0.9–1. When the tolerance factor is smaller than the lower limit, the Na–Cl and M–Cl bonds remain compressed, while the Cs–Cl bonds are under tension. The structure relaxes and overcomes stress via the cooperative rotation of the octahedrons, which lowers the symmetry of the double perovskite. These rotations are meant to bend the Na–Cl–M bond angles from 180° to 180°–θ and the stability of the cubic phase decreases compared to lower symmetric phases. When τ > 1, the Na–Cl and M–Cl bonds come under tension, whereas the Cs–Cl bonds are under compression, and under this condition the Na–Cl–M bond angle remains 180°; however, the structure overcomes the tensile stress by allowing hexagonal stacking. The bond length and bond angle of the optimized structure are reported in Table 1. The evaluated value of the tolerance factor from the bond lengths reveals the stability of double perovskites in the cubic structure.
m space group. The ideal structure is free from any internal stress and the Na–Cl–M bond angle is 180°. However, the cubic phase is stable over the range of 0.9–1. When the tolerance factor is smaller than the lower limit, the Na–Cl and M–Cl bonds remain compressed, while the Cs–Cl bonds are under tension. The structure relaxes and overcomes stress via the cooperative rotation of the octahedrons, which lowers the symmetry of the double perovskite. These rotations are meant to bend the Na–Cl–M bond angles from 180° to 180°–θ and the stability of the cubic phase decreases compared to lower symmetric phases. When τ > 1, the Na–Cl and M–Cl bonds come under tension, whereas the Cs–Cl bonds are under compression, and under this condition the Na–Cl–M bond angle remains 180°; however, the structure overcomes the tensile stress by allowing hexagonal stacking. The bond length and bond angle of the optimized structure are reported in Table 1. The evaluated value of the tolerance factor from the bond lengths reveals the stability of double perovskites in the cubic structure.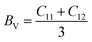 and GR = {5C44(C11 − C12)}/{4C44 + 3(C11 − C12)}, respectively. Directly from the B and G values, one can deduce the Young's modulus (Y) and Poisson's ratio (σ) using the relations Y = 9BG/(3B + G) and σ = (3B − Y)/6B, respectively. The calculated values are listed in Table 2. Generally, the elastic modulus is the resistance offered by any material towards deformation, the bulk modulus is for volumetric deformation and the shear modulus for shape deformation, whereas Y characterizes the resistance to uniaxial deformation and can be used to estimate the stiffness of a material. The moduli decreased in the order of Y > B > G, signifying that these double perovskites allow shape deformation more easily compared to volumetric deformation. The mechanical behaviour of brittleness or ductility can be directly described from the elastic parameters. The different empirical parameters that are often used to signify mechanical behaviour are the Pugh ratio (B/G) and Poisson's ratio.3,34 The index values separating the extreme behaviours are 1.75 and 0.26 for B/G and σ, respectively. Values above these decisive numerals for any material demonstrate the ductile character, otherwise brittle in nature. Accordingly, the calculated values reveal the brittle nature of the titled double perovskites. Additionally, the Zener anisotropic A factor is determined using the elastic constants and is given in Table 2. It used to characterize the deviation from isotropic behaviour. The calculated values suggest the presence of anisotropy since the magnitude of A deviates from unity. We also computed the micro-hardness (H) to examine the mechanical strength of the double perovskites. The hardness of a material can be directly linked to its bulk or shear modulus. The calculated values of H given in Table 2 suggest that all three Cs-based double perovskites have good mechanical strength.
and GR = {5C44(C11 − C12)}/{4C44 + 3(C11 − C12)}, respectively. Directly from the B and G values, one can deduce the Young's modulus (Y) and Poisson's ratio (σ) using the relations Y = 9BG/(3B + G) and σ = (3B − Y)/6B, respectively. The calculated values are listed in Table 2. Generally, the elastic modulus is the resistance offered by any material towards deformation, the bulk modulus is for volumetric deformation and the shear modulus for shape deformation, whereas Y characterizes the resistance to uniaxial deformation and can be used to estimate the stiffness of a material. The moduli decreased in the order of Y > B > G, signifying that these double perovskites allow shape deformation more easily compared to volumetric deformation. The mechanical behaviour of brittleness or ductility can be directly described from the elastic parameters. The different empirical parameters that are often used to signify mechanical behaviour are the Pugh ratio (B/G) and Poisson's ratio.3,34 The index values separating the extreme behaviours are 1.75 and 0.26 for B/G and σ, respectively. Values above these decisive numerals for any material demonstrate the ductile character, otherwise brittle in nature. Accordingly, the calculated values reveal the brittle nature of the titled double perovskites. Additionally, the Zener anisotropic A factor is determined using the elastic constants and is given in Table 2. It used to characterize the deviation from isotropic behaviour. The calculated values suggest the presence of anisotropy since the magnitude of A deviates from unity. We also computed the micro-hardness (H) to examine the mechanical strength of the double perovskites. The hardness of a material can be directly linked to its bulk or shear modulus. The calculated values of H given in Table 2 suggest that all three Cs-based double perovskites have good mechanical strength.


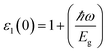 . The imaginary part of the dielectric constant ε2(ω) is very important in signifying the efficiency of optoelectronic devices, representing the photons that can be absorbed by perovskites. The optical edge observed at 0 eV for Mn-up, Co-dn and Ni-up signifies the metallic character in the respective spin channel. The presence of peaks away from zero energy signifies the absence of energy states at the Fermi level, thereby indicating a semiconducting nature in the Mn-dn, Co-up and Ni-dn spin channels. The variation in the refractive index (n) and extinction coefficients (k) with photon energy replicates the character of the real and imaginary dielectric constants, as shown in Fig. S3 (ESI).† The static refractive index values are 1.47, 1.36 and 1.74 for Mn-up, Co-dn and Ni-up, respectively. The variation in absorption coefficient (α) with photon energy is depicted in Fig. 8(A). The critical values of ‘α’, beyond which the absorption capabilities of a material increase, illustrate the threshold energies required for electrons to transition from the valance band maxima to the conduction band minima. The transitions mostly from the Cl-p sates of the valance band to the d-states of the M-site in the conduction band give rise to the optical absorption edge. The presence of pseudo gaps in the band structure also gives rise to absorption peaks. It can be seen from the figure that these double perovskites have a wide absorption region. This region is composed of different absorption peaks resulting from various electronic transitions, indicating absorption in the UV-visible region. Moreover, the absorption of photons generates electron–hole pairs, resulting in optical conductivity. The variation in optical conductivity with photon energy is similar to the absorption behaviour. This is due to the fact that absorbed photons generate conduction carriers, and thereby increase conductivity, as shown in Fig. 8(B). The peaks of optical conductivity at the static limit of Mn-up, Co-dn and Ni-up reveal their metallic character in the respective channel. In contrast, in the other spin channel, Mn-dn, Co-up and Ni-dn conduct only after the absorption edge, signifying the semiconducting channel. Hence, there results give overall support for the half-metallic character of double perovskites. The total absorption and conductivity of a spin polarized system is the sum of individual channels plus the peaks contributed by inter-channel transitions. We presented the total absorption power and conductivity without considering the inter-channel transitions of the double perovskites in Fig. S4 (ESI).† The peaks in the energy range of 0–6 eV strongly support the capability of these materials to absorb photons in the UV-visible region, confirming their suitability to be employed in various optoelectronic devices.
. The imaginary part of the dielectric constant ε2(ω) is very important in signifying the efficiency of optoelectronic devices, representing the photons that can be absorbed by perovskites. The optical edge observed at 0 eV for Mn-up, Co-dn and Ni-up signifies the metallic character in the respective spin channel. The presence of peaks away from zero energy signifies the absence of energy states at the Fermi level, thereby indicating a semiconducting nature in the Mn-dn, Co-up and Ni-dn spin channels. The variation in the refractive index (n) and extinction coefficients (k) with photon energy replicates the character of the real and imaginary dielectric constants, as shown in Fig. S3 (ESI).† The static refractive index values are 1.47, 1.36 and 1.74 for Mn-up, Co-dn and Ni-up, respectively. The variation in absorption coefficient (α) with photon energy is depicted in Fig. 8(A). The critical values of ‘α’, beyond which the absorption capabilities of a material increase, illustrate the threshold energies required for electrons to transition from the valance band maxima to the conduction band minima. The transitions mostly from the Cl-p sates of the valance band to the d-states of the M-site in the conduction band give rise to the optical absorption edge. The presence of pseudo gaps in the band structure also gives rise to absorption peaks. It can be seen from the figure that these double perovskites have a wide absorption region. This region is composed of different absorption peaks resulting from various electronic transitions, indicating absorption in the UV-visible region. Moreover, the absorption of photons generates electron–hole pairs, resulting in optical conductivity. The variation in optical conductivity with photon energy is similar to the absorption behaviour. This is due to the fact that absorbed photons generate conduction carriers, and thereby increase conductivity, as shown in Fig. 8(B). The peaks of optical conductivity at the static limit of Mn-up, Co-dn and Ni-up reveal their metallic character in the respective channel. In contrast, in the other spin channel, Mn-dn, Co-up and Ni-dn conduct only after the absorption edge, signifying the semiconducting channel. Hence, there results give overall support for the half-metallic character of double perovskites. The total absorption and conductivity of a spin polarized system is the sum of individual channels plus the peaks contributed by inter-channel transitions. We presented the total absorption power and conductivity without considering the inter-channel transitions of the double perovskites in Fig. S4 (ESI).† The peaks in the energy range of 0–6 eV strongly support the capability of these materials to absorb photons in the UV-visible region, confirming their suitability to be employed in various optoelectronic devices.





