Open Access Article
Open Access ArticleDrying-induced back flow of colloidal suspensions confined in thin unidirectional drying cells†
Kai Inoue a and
Susumu Inasawa
a and
Susumu Inasawa *ab
*ab
aGraduate School of Bio-Applications and Systems Engineering, Tokyo University of Agriculture and Technology, 2-24-16 Nakacho, Koganei, Tokyo 184-8588, Japan. E-mail: inasawa@cc.tuat.ac.jp; Fax: +81-42-388-7798; Tel: +81-42-388-7105
bDepartment of Chemical Engineering, Tokyo University of Agriculture and Technology, 2-24-16 Nakacho, Koganei, Tokyo 184-8588, Japan
First published on 21st April 2020
Abstract
A clear back flow was observed in the thin unidirectional drying cell of a colloidal suspension. Flow around the colloidal-particle packing front was more complex than expected, even though a colloidal suspension was confined in a narrow space with a submillimeter-scale or shorter gap height. We propose that an increase in particle concentration around the packing front induces downward flow, which is the origin for back flow inside the cell. A mathematical model, which considered both a drying induced horizontal flow and a circulation flow caused by a concentration gradient of particles, showed a reasonable agreement with experimental data for the width of the back-flow region. The concentration gradient of particles was not negligible and it generated a rather complicated flow even in a thin drying liquid film.
Introduction
Colloidal-suspension drying is a common industrial process and is used extensively to manufacture products, such as paints,1 optical films,2–5 ceramics6 and electrodes.7,8 During drying, solvent evaporates and the concentration of suspended particles increases, in which they eventually form particulate films. Many papers have reported drying kinetics of colloidal suspensions, and directional drying is used frequently in those studies.9–11 A suspension is introduced into a narrow space between parallel glass plates. By using this drying cell, quantitative measurements on drying-induced phenomena, such as film formation,12 crack formation13 and shear-band formation,14 have been demonstrated. Horizontal solvent flow is essential for structural anisotropy of particulate films,15 the formation of shear bands16 and for the packing ordering of weakly Brownian particles.17 A packed layer forms at the drying interface and evaporation of water from the air–water interface between the packed particles induces horizontal solvent flow to the packed layer during drying. Because of the thin geometry, it has been assumed that suspension flow is almost ideal. However, recent studies have revealed that vertical flows are induced spontaneously, even in a thin liquid layer owing to drying-induced increase in the solute concentration18–21 and in the concentration of suspended particles.22 These examples suggest that flow is complex, even in a drying thin liquid layer between parallel plates. In this paper, we present complex flow generation in the unidirectional drying of colloidal suspensions.Experimental
We used a unidirectional drying cell to dry silica colloidal suspensions as shown in Fig. S1 in the ESI.† The cell width (L) was approximately 5 mm. The cell gap height (H) was set to 50 μm, 100 μm or 200 μm using silicon rubber spacers. Colloidal silica dispersions with diameters (d) of 110 nm (Seahoster KE-W10, Nippon Shokubai Co. Ltd., Tokyo, Japan), 60 nm and 45 nm (Snowtex-OYL and Snowtex-OL, Nissan Chemical Industries Inc., Tokyo, Japan) were used. The initial fraction of colloidal silica (φw) was typically 15 wt% to 20 wt% in all suspensions. Zeta potentials of the silica particles were −46 mV (110 nm), −22 mV (60 nm), and −21 mV (45 nm). To trace flow inside the drying cells, 500 nm-diameter fluorescent silica particles were added (Sicaster-greenF, Micromod Partikeltechnologie GmbH, Rostock, Germany). The excitation wavelength was 485 nm and we used a 510 nm fluorescent light. The mass ratio of added fluorescent particles to silica particles was approximately 2 × 10−3. We used a transparent temperature-controlled substrate (ST-91, Blast Co., Ltd., Kanagawa, Japan) to maintain a constant drying temperature. We observed drying suspensions by using an optical microscope (Eclipse Ti2-E, Nikon, Tokyo, Japan). Transmission and fluorescent images were recorded simultaneously.Results and discussion
Generation of back-flow region
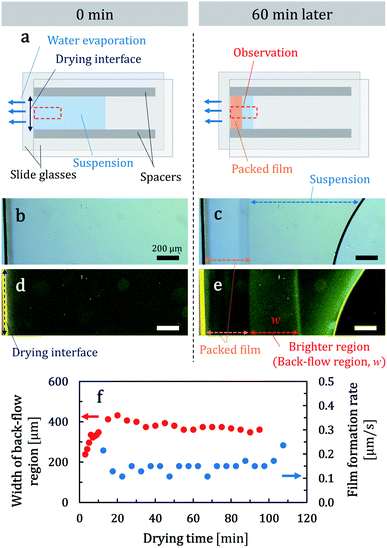
A schematic illustration of the top view of a unidirectional cell is shown in Fig. 1a. As drying proceeded, a packed layer formed at the drying interface (Fig. 1a right). Drying occurred predominantly from the left drying interface in Fig. 1a. There was the other water–air meniscus on the right side as well. But it was inside the cell and air around the right meniscus was soon saturated with water vapor. Thus drying from the right meniscus was severely restricted and water mainly evaporated from the left interface. Because of this, a packed layer formed on the left meniscus and the suspension spontaneously flowed to the left meniscus.Corresponding photographs of a part of a cell, as indicated schematically by the red dashed squares in Fig. 1a, are shown in Fig. 1b and c. We used a 45 nm-diameter colloidal suspension. The corresponding movie is available in the ESI (Movie 1†). In Fig. 1c, a clear boundary exists between the packed layer and a suspension. The particulate film thickened from the drying interface as drying proceeded, which suggests that suspended particles were transported to the drying interface by a spontaneous suspension flow. Corresponding fluorescent photographs are shown in Fig. 1d and e. The movie file is available in the ESI (Movie 2†). We observed a bright region between the packed layer and the suspension. This region shifted to the suspension side as the packed layer grew. In both fluorescent images, the left edge of the cell appeared as yellow and this would be a reflection or scattering of light by the drying interface of water and air. We also note that the right meniscus observed in Fig. 1c and e curved, which was different from the illustration in Fig, 1a right. This was caused by pinning of the right meniscus on one of the spacers.
We observed the bright region at a higher resolution at two different height positions. Particle transport toward the packing front was observed at 40 μm above the bottom of the cell (Movie 3 in the ESI†). Conversely, fluorescent particles in the bright region were transported to the opposite direction at the bottom (Movie 4 in the ESI†). We concluded that a back flow formed spontaneously in the bright region as shown in Fig. 2. After this observation, we intentionally inverted the drying cell. If the flow pattern is conserved, we would observe back flow at the top side of the inverted cell. However, back flow was observed around the bottom side of the inverted cell and the suspension flowed to the packing front at a middle height position. We measured a width of the back-flow region from recorded images which was defined as in Fig. 1e. The width of the back-flow region (back-flow width, w) was mostly constant during drying as shown in Fig. 1f.
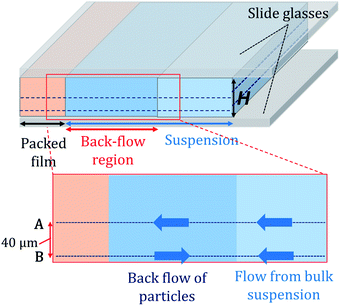 | ||
| Fig. 2 Schematic illustration of flow inside a unidirectional drying cell. Movies 3 and 4 in the ESI† were observed 40 μm from the bottom (denoted A) and around the bottom of the cell (denoted B). | ||
In our previous study, suspended-particle condensation near the packing front caused a downward flow when a drying cell was tilted intentionally.22 Particles were transported and concentrated by a drying-induced flow and finally packed into a particulate film at the packing front. However, because not all particles are packed into the film, some concentrated particles remained suspended. As a result, a slight increase in density of the concentrated suspension near the packing front induces gravity-driven downward flow. Pradhan et al. demonstrated experimentally and numerically internal convection of an aqueous NaCl solution inside a microcapillary during drying.23 A solution with a higher density formed near the drying interface and it sunk down by gravity.
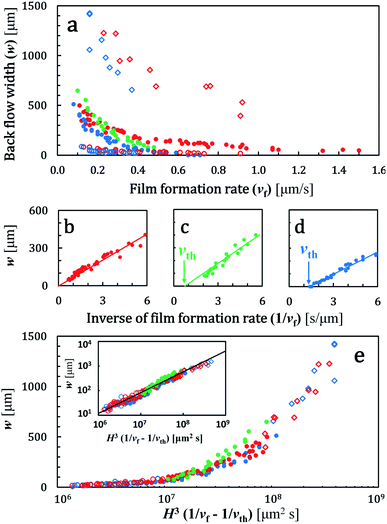
We propose that a similar scenario is applicable to understand the spontaneous formation of back flow in our experiments. Suspended particles were transported by flow to the packing front. But only water penetrated through the packed layer and transported particles were accumulated around the packing front. This increased the concentration of suspended particles around the packing front. Because of the difference in velocities of solvent and particles, particles felt a drag force.1 Suspended particles were packed when the drag force by the fluid flow through the packed layer compressed the suspended particles onto the packed layer sufficiently. Thus, a larger suspension flow or a faster film growth rate would decrease the number of particles that were not packed into the film. Therefore, less downward flow and a small back-flow width would be observed. In Fig. 3a, we summarized the back-flow width in terms of particulate-film growth rate. We changed film growth rate by changing drying temperature. As expected, the back-flow width decreased when the film growth rate was large. Fig. 3b–d shows some extracted data in Fig. 3a, which is summarized by the inverse of the film-formation rate. A threshold growth rate of film formation exists above which back flow disappears. A large back-flow width was observed in a cell with a large gap height as in Fig. 3a.
Mathematical model to explain width of the back-flow region
In this section, we consider a mathematical model to understand important factors that dominantly determine a width of the back-flow region w. Before starting mathematical modeling, we refer a very recent study on buoyancy-driven circulation flow on solutal mass transport by Salmon and Doumenc.21They studied drying of dilute binary solution of a volatile solvent and involatile solute analytically. They summarized four different regimes for solutal mass transport, two diffusive regimes and two dispersive regimes. These regimes were categorized by a product of Peclet number (Pe) and Rayleigh number (Ra). When PeRa » α0.5, solutal mass transport is in the dispersive regimes, in which α is a characteristic constant equal to 362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880.21 According to the definition in ref. 21, Pe = VevapH/D and Ra = ρ′φsus_0gH3/(μD), in which Vevap is an evaporation rate, H is a gap height of a drying cell, D is a diffusion constant for suspended particles, ρ′ is a density difference between silica particles and water, g is the gravitational acceleration and μ is a viscosity of water, respectively. In our study, Pe = 12.5 and Ra = 2.9 × 105. Used values are Vevap = 0.5 × 10−6 m s−1, H = 100 × 10−6 m, D = 4.0 × 10−12 m2 s−1 for particles with a diameter of 110 nm, ρ′ = 1.2 × 103 kg m−3, φsus_0 = 0.1, g = 9.8 m s−2 and μ = 10−3 Pa s. Value of D was calculated by Stokes–Einstein equation. We obtain PeRa = 3.7 × 106, much larger than (362
880.21 According to the definition in ref. 21, Pe = VevapH/D and Ra = ρ′φsus_0gH3/(μD), in which Vevap is an evaporation rate, H is a gap height of a drying cell, D is a diffusion constant for suspended particles, ρ′ is a density difference between silica particles and water, g is the gravitational acceleration and μ is a viscosity of water, respectively. In our study, Pe = 12.5 and Ra = 2.9 × 105. Used values are Vevap = 0.5 × 10−6 m s−1, H = 100 × 10−6 m, D = 4.0 × 10−12 m2 s−1 for particles with a diameter of 110 nm, ρ′ = 1.2 × 103 kg m−3, φsus_0 = 0.1, g = 9.8 m s−2 and μ = 10−3 Pa s. Value of D was calculated by Stokes–Einstein equation. We obtain PeRa = 3.7 × 106, much larger than (362![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880)0.5 ∼ 6 × 102. Thus we consider that solutal mass transport is dominated by a buoyancy-driven flow in our study. We note that they also analyzed a width of diffusive layer in which there was a concentration gradient of solute.21 This diffusive layer would correspond to the back-flow region in this study. However, the diffusive layer was predicted to grow as drying proceeded and a width of the layer was proportional to t2/5, in which t is drying time. Conversely, a width of the back-flow region in our study was almost constant in terms of drying time as in Fig. 1f. One important difference in our study from ref. 21 is packing of particles. Particles were condensed due to drying but they were treated as suspended and transported by flow in the analysis because the drying suspension was very dilute.21 Conversely, some particles clearly packed and fixed at the drying front in our study. Packing of particles decreases the number of suspended particles in a drying cell and this would cause such different result.
880)0.5 ∼ 6 × 102. Thus we consider that solutal mass transport is dominated by a buoyancy-driven flow in our study. We note that they also analyzed a width of diffusive layer in which there was a concentration gradient of solute.21 This diffusive layer would correspond to the back-flow region in this study. However, the diffusive layer was predicted to grow as drying proceeded and a width of the layer was proportional to t2/5, in which t is drying time. Conversely, a width of the back-flow region in our study was almost constant in terms of drying time as in Fig. 1f. One important difference in our study from ref. 21 is packing of particles. Particles were condensed due to drying but they were treated as suspended and transported by flow in the analysis because the drying suspension was very dilute.21 Conversely, some particles clearly packed and fixed at the drying front in our study. Packing of particles decreases the number of suspended particles in a drying cell and this would cause such different result.
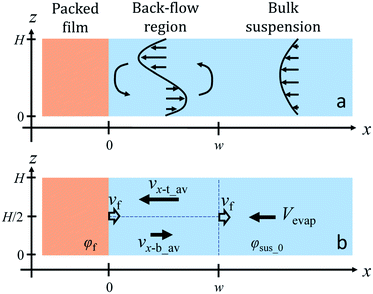
A schematic illustration of the model is shown in Fig. 4a. We set x = 0 at the advancing packing front. The boundary between the back-flow region and the bulk suspension is x = w. We assumed that a concentration of particles φ(x = 0) was φf and that at x = w was φsus_0, in which φf is a volume fraction of particles in the packed layer. Concentration of particles in the bulk suspension (x > w) was uniform with a value of φsus_0.
Within a framework of the lubrication approximation and a small Reynolds number, a steady state horizontal flow velocity ux in a gravity-driven circulation flow between parallel plates satisfies the following equations as19
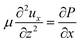 | (1) |
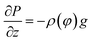 | (2) |
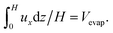 In addition, non-slip boundary conditions are imposed and ux(0) = ux(H) = 0. Analytical solution ux in eqn (1) combined with eqn (2) is
In addition, non-slip boundary conditions are imposed and ux(0) = ux(H) = 0. Analytical solution ux in eqn (1) combined with eqn (2) is
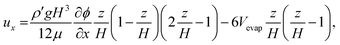 | (3) |
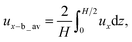 | (4) |
From eqn (4), we obtained ux-b_av = −ρ′gH3(∂φ/∂x)/(192μ) + Vevap. The average velocity ux-t_av over the top half of the cell (H/2 ≤ z ≤ H) in the back-flow region is simply obtained as ux-t_av = ρ′gH3(∂φ/∂x)/(192μ) + Vevap.
Flow pattern in a drying cell is schematically illustrated in Fig. 4b. We consider three different regions, a top and bottom half of volume in the back-flow region and the bulk suspension away from the packing front. Strictly speaking, ∂φ/∂x would vary depending on a position x in the back-flow region and ux-b_av and ux-t_av are not constant. Non-zero velocity of suspension in z-direction uz is obtained from the continuity equation when ∂φ/∂x is not constant. However we do not discuss uz because our main concern is not a full description of a flow profile but a width of the back-flow region.
In Fig. 1f, a width of the back-flow region was constant during drying. The region was in between the packing front and the bulk suspension. Packed layer of particles grew at a velocity of vf and this means that the boundary between the back-flow region and the bulk suspension also moved at vf. From the viewpoint of the advancing packing front, the velocity of the bottom part in the back-flow region almost vanished at x = w. Therefore we set ux-b_av(w) ∼ vf and we obtain −ρ′gH3μ−1(∂φ/∂x)w ∼ vf − Vevap, where (∂φ/∂x)w denotes a concentration gradient of particles at x = w.
We need to know a concentration gradient (∂φ/∂x)w. In unidirectional drying of colloidal suspension without a circulation flow, one dimensional advection-diffusion model of colloidal particles well describes a concentration profile of particles φ. Ratio of diffusion constant to the advection velocity is proposed as a scaling length for ∂φ/∂x.1 In a similar drying system with a buoyancy-driven circulation flow, an approximate analytical solution for the concentration profile of particles along x-axis is also reported.21 However as we have already stated, packing of particles at the drying interface was not considered in the latter study. Thus we consider that application of the approximate analytical solution into our present work would not be suitable. We used another approach to estimate (∂φ/∂x)w. The simplest approximation is to use an averaged concentration gradient for (∂φ/∂x)w. This means 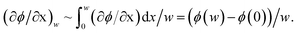 From the boundary conditions, φ(w) = φsus_0 and φ(0) = φf. Thus (∂φ/∂x)w ∼ (φsus_0 − φf)/w. Besides, macroscopic conservation of particles requires (φf − φsus_0)vf = −φsus_0Vevap. We note that direction of Vevap is opposite to vf as in Fig. 4 and thus Vevap < 0 in this study.
From the boundary conditions, φ(w) = φsus_0 and φ(0) = φf. Thus (∂φ/∂x)w ∼ (φsus_0 − φf)/w. Besides, macroscopic conservation of particles requires (φf − φsus_0)vf = −φsus_0Vevap. We note that direction of Vevap is opposite to vf as in Fig. 4 and thus Vevap < 0 in this study.
Substituting these relations, we finally obtain w ∼ ρ′gφsus_0(φf − φsus_0)H3/(μφfvf). Our mode predicts that a width of the back-flow region is proportional to H3/vf. In Fig. 3b–d, we plotted w in terms of the inverse of vf. There is a threshold velocity of film formation above which no back flow generates. Our model does not predict this threshold. But these data strongly suggest that if all condensed particles near the packing front immediately pack into the film, the gravity-driven downward flow does not occur. Thus we introduce a threshold term in the model semi-empirically as
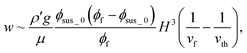 | (5) |
The velocity vth is a threshold rate of film formation. Our model predicts that w is a function of H3(1/vf − 1/vth). All data in Fig. 3a are replotted in Fig. 3e. They collapsed in a single master curve. In this replotting, values of vth were determined experimentally as 0.7 μm s−1 (110 nm particles) and 1.1 μm s−1 (60 nm particles) as in Fig. 3c and d. For 45 nm particles, we set 1/vth ∼ 0 as shown in Fig. 3b. The inset in Fig. 3e shows a log–log plot of the same data in Fig. 3e. All data were on a linear line with a slope of 0.85, which is smaller than the expected value of unity. Small difference of 0.15 between 0.85 and unity would originate from assumptions in our model. For example, we assumed that there was no concentration gradient in z-axis. In addition, we treated the viscosity as constant although a concentration of suspended particles would affect viscosity. However, in spite of such approximations, the essence of the back flow is described well. The thickness of the back flow as in Fig. 2 is also explained using this model. We did not see the back flow at a height of 40 μm as already explained. Linear velocity profile of gravity-driven flow in eqn (3) predicted that the sign of the flow changed at a height of 50 μm when the gap height was 100 μm. However this gravity-driven flow was superimposed with drying-induced horizontal flow as in eqn (3). Because of the summation of both flows, thickness of the back flow was smaller than 50 μm.
One important point is that although diffusion constant of suspended particles is not included in eqn (5), experimental data was collapsed well on a master curve as shown in Fig. 3e. In mass balance of particles in a drying suspension, advection and diffusion play key roles in particle transport and they determine a concentration profile of particles.1,21 Therefore absence of diffusion constant in eqn (5) might be contradictory to these studies. However we also consider that empirically-introduced vth could include diffusion process of particles. The threshold velocity vth depends on diameter of particles, 0.7 μm s−1 for 110 nm particles, 1.1 μm s−1 for 60 nm particles and practically infinite for 45 nm particles as shown in Fig. 3. As diffusion constant D is inversely proportional to diameter of particles, contribution of diffusion is more dominant for 45 nm particles. Therefore it is reasonable to consider that not all transported particles pack into a packed layer for 45 nm particles and we observed the back-flow region even at a large growth rate of packed film. Theoretical approach between D and vth could explain the physical meaning of vth.
Finally we discuss diffusiophoresis of large colloidal particles dispersed in a suspension of small colloidal particles. Drying of a suspension of binary colloidal particles is one of the hot topics in this field. While staggered packing of large and small particles is reported,24–26 spontaneous stratification is also observed. In this stratification, diffusiophoresis plays a key role. Large particles are ejected owing to the concentration gradient of small particles.27,28 Condensation of small particles at the drying interface sometimes induces diffusiophoretic motion of large particles. We used large colloidal particles of 500 nm to observe the flow of drying colloidal suspension in this study. In drying colloidal suspension with a free drying interface, auto-stratification are frequently observed at the top of the receding drying interface.29–32 As drying proceeds, the liquid–air interface descends. Suspended particles are accumulated by the descending interface and a concentration gradient of small particles spontaneously forms. Because of this, diffusiophoresis of large particles can occur depending on drying conditions. In our study, the drying water–air interface was fixed at one end of the drying cell and particles were transported by drying-induced advection to the interface. But there is a concentration gradient of small particles ∂φ/∂x in the back-flow region and we are not able to omit the possibility of diffusiophoresis. However, packed layer also showed a fluorescence as in Fig. 1e. This suggests that some large particles were carried with small particles and packed. Thus we consider that flow of small particles was visualized by large fluorescent particles.
Conclusions
We demonstrated a spontaneous back-flow generation in a unidirectional drying cell. Suspension flow in a thin unidirectional drying cell was not simple as had been expected. Suspended particles tend to be transported by flow. Conversely, condensation and packing of suspended particles affect suspension flow, which in turn affects particle transport.Conflicts of interest
The authors declare no conflicts of interest associated with this manuscript.Acknowledgements
This work was supported partially by JSPS KAKENHI Grant Number JP16H02413. We thank Prof. H. Kamiya for his permission to access the dynamic light scattering equipment. We thank Laura Kuhar, PhD, from Edanz Group (www.edanzediting.com/ac) for editing a draft of this manuscript.References
- L. Goehring, J. Li and P. Kiatkirakajorn, Philos. Trans. R. Soc., A, 2016, 375 Search PubMed.
- S. Portal-Marco, M. A. Vallve, O. Artega, J. Ignes-Mullol, C. Corbella and E. Bertran, Colloids Surf., A, 2012, 401, 38–47 CrossRef CAS.
- J. Yamanaka, Y. Suzuki, J. Nozawa and T. Sawada, Prog. Cryst. Growth Charact. Mater., 2016, 62, 413–416 CrossRef CAS.
- S. Inasawa and Y. Yamaguchi, Langmuir, 2009, 25(18), 11197–11201 CrossRef CAS PubMed.
- K. Yamaguchi, S. Inasawa and Y. Yamaguchi, Phys. Chem. Chem. Phys., 2013, 15, 2897–2902 RSC.
- H. Luo, C. M. Cardinal, L. E. Scriven and L. F. Francis, Langmuir, 2008, 24(10), 5552–5561 CrossRef CAS PubMed.
- S. Lim, K. H. Ahn and M. Yamamura, Langmuir, 2013, 29(26), 8233–8244 CrossRef CAS PubMed.
- S. Lim, S. Kim, K. H. Ahn and S. J. Lee, Ind. Eng. Chem. Res., 2015, 54(23), 6146–6155 CrossRef CAS.
- P. Lidon and J. B. Salmon, Soft Matter, 2014, 10, 4151–4161 RSC.
- K. Abe and S. Inasawa, Phys. Chem. Chem. Phys., 2018, 20, 8935–8942 RSC.
- S. Inasawa and Y. Yamaguchi, Soft Matter, 2012, 8, 2416–2422 RSC.
- S. Inasawa, Y. Oshimi and H. Kamiya, Soft Matter, 2016, 12, 6851–6857 RSC.
- E. R. Dufresne, D. J. Stark, N. A. Greenblatt, J. X. Cheng, J. W. Hutchinson, L. Mahadevan and D. A. Weitz, Langmuir, 2006, 22, 7144–7147 CrossRef CAS PubMed.
- P. Kiatkirakajorn and L. Goehring, Phys. Rev. Lett., 2015, 115, 088302 CrossRef PubMed.
- F. Boulogne, L. Pauchard, F. Giorgiutti-Dauphine, R. Botet, R. Schweins, M. Sztucki, J. Li, B. Cabane and L. Goehring, Europhys. Lett., 2013, 105, 3 Search PubMed.
- L. Goehring, W. J. Clegg and A. F. Routh, Langmuir, 2010, 26(12), 9269–9275 CrossRef CAS PubMed.
- C. Noirjean, M. Marcellini and S. Deville, Phys. Rev. Mater., 2017, 1, 065601 CrossRef.
- S. J. Lee, J. Hong and Y. K. Choi, Langmuir, 2014, 30(26), 7710–7715 CrossRef CAS PubMed.
- B. Selva, L. Daubersies and J. B. Salmon, Phys. Rev. Lett., 2012, 108, 198303 CrossRef CAS PubMed.
- C. Loussert, A. Bouchaudy and J. B. Salmon, Phys. Rev. Fluids, 2016, 1, 084201 CrossRef.
- J.-B. Salmon and F. Doumenc, Phys. Rev. Fluids, 2020, 5, 024201 CrossRef.
- T. Mizuguchi and S. Inasawa, Soft Matter, 2019, 15, 4019–4025 RSC.
- T. K. Pradhan and P. K. Panigrahi, Microfluid. Nanofluid., 2016, 20, 8 CrossRef.
- V. Lotito and T. Zambelli, Langmuir, 2018, 34, 7827–7843 CrossRef CAS PubMed.
- Z. Cai, Y. Li, G. Duan, L. Jia and W. Cai, ACS Nano, 2012, 6, 6706–6716 CrossRef PubMed.
- K. Inoue and S. Inasawa, RSC Adv., 2020, 10, 2566–2574 RSC.
- R. P. Sear and P. B. Warren, Phys. Rev. E, 2017, 96, 062602 CrossRef PubMed.
- R. P. Sear, J. Chem. Phys., 2018, 148, 1349909 CrossRef PubMed.
- M. Schulsz and J. L. Keddie, Soft Matter, 2018, 14, 6181–6197 RSC.
- D. K. Makepeace, A. Fortini, A. Markov, P. Locatelli, C. Lindsay, S. Moorhouse, R. Lind, R. P. Sehar and J. L. Keddie, Soft Matter, 2017, 13, 6969–6980 RSC.
- X. Liu, W. Liu, A. J. Carr, D. S. Vazquez, D. Nykypanchuk, P. W. Majewski, A. F. Routh and S. R. Bhatia, J. Colloid Interface Sci., 2018, 515, 70–77 CrossRef CAS PubMed.
- M. P. Howard, A. Nikoubashman and A. Z. Panagiotopoulos, Langmuir, 2017, 33, 3685–3693 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02837a |
| This journal is © The Royal Society of Chemistry 2020 |