Open Access Article
Open Access ArticleFirst principles study of electronic and nonlinear optical properties of A–D–π–A and D–A–D–π–A configured compounds containing novel quinoline–carbazole derivatives†
Muhammad Khalid *a,
Akbar Alib,
Rifat Jawariaa,
Muhammad Adnan Asgharc,
Sumreen Asima,
Muhammad Usman Khan
*a,
Akbar Alib,
Rifat Jawariaa,
Muhammad Adnan Asgharc,
Sumreen Asima,
Muhammad Usman Khan d,
Riaz Hussain
d,
Riaz Hussain d,
Muhammad Fayyaz ur Rehman
d,
Muhammad Fayyaz ur Rehman b,
Christopher J. Ennis
b,
Christopher J. Ennis e and
Muhammad Safwan Akram
e and
Muhammad Safwan Akram *ef
*ef
aDepartment of Chemistry, Khawaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan. E-mail: khalid@iq.usp.br
bDepartment of Chemistry, University of Sargodha, Sargodha 40100, Pakistan
cA Division of Science and Technology, University of Education Lahore, Pakistan
dDepartment of Chemistry, University of Okara, Okara-56300, Pakistan
eSchool of Health and Life Sciences, Teesside University, Middlesbrough, TS1 3BA, UK. E-mail: safwan.akram@tees.ac.uk
fNational Horizons Centre, Teesside University, Darlington, DL1 1HG, UK
First published on 10th June 2020
Abstract
Materials with nonlinear optical (NLO) properties have significant applications in different fields, including nuclear science, biophysics, medicine, chemical dynamics, solid physics, materials science and surface interface applications. Quinoline and carbazole, owing to their electron-deficient and electron-rich character respectively, play a role in charge transfer applications in optoelectronics. Therefore, an attempt has been made herein to explore quinoline–carbazole based novel materials with highly nonlinear optical properties. Structural tailoring has been made at the donor and acceptor units of two recently synthesized quinoline–carbazole molecules (Q1, Q2) and acceptor–donor–π–acceptor (A–D–π–A) and donor–acceptor–donor–π–acceptor (D–A–D–π–A) type novel molecules Q1D1–Q1D3 and Q2D2–Q2D3 have been quantum chemically designed, respectively. Density functional theory (DFT) and time-dependent density functional theory (TDDFT) computations are performed to process the impact of acceptor and donor units on photophysical, electronic and NLO properties of selected molecules. The λmax values (321 and 319 nm) for Q1 and Q2 in DSMO were in good agreement with the experimental values (326 and 323 nm). The largest shift in absorption maximum is displayed by Q1D2 (436 nm). The designed compounds (Q1D3–Q2D3) express absorption spectra with an increased border and with a reduced band gap compared to the parent compounds (Q1 and Q2). Natural bond orbital (NBO) investigations showed that the extended hyper conjugation and strong intramolecular interaction play significant roles in stabilising these systems. All molecules expressed significant NLO responses. A large value of βtot was elevated in Q1D2 (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885.90 a.u.). This theoretical framework reveals the NLO response properties of novel quinoline–carbazole derivatives that can be significant for their use in advanced applications.
885.90 a.u.). This theoretical framework reveals the NLO response properties of novel quinoline–carbazole derivatives that can be significant for their use in advanced applications.
Introduction
The development of nonlinear optical (NLO) materials has attracted significant interest in fundamental and applied research.1 Both theoretical and experimental communities2–4 have largely been investigating NLO materials due to their promising applications in different fields, including nuclear science, medicine, chemical dynamics, solid-state physics, materials science, surface interface studies and biophysics.5 Moreover, NLO materials have also gained notable significance in different technologies, such as optical computing, dynamic image processing and optical communication.6–8 Therefore, different attempts are being made to model various materials which show NLO properties, such as natural and fabricated nanomaterials, organic and inorganic semiconductors, polymer frameworks and molecular dyes.9–13 Organic NLO materials can offer low production costs, low dielectric constants, high photoelectric coefficients and design flexibility. Usually, macroscopic NLO material properties originate from the hyperpolarizability of the NLO chromophore. Therefore, NLO molecules consist of donor (D)–acceptor (A) pairs which are linked to each other through π-conjugated electron bridges (D–π–A). To develop D–π–A chromophores, the nature of the donor and acceptor moieties and conjugated length have been considered.14–19 Usually, electronic charge is delocalized in the π-bond framework of NLO organic materials. The first hyperpolarizability (βtot) is associated with intramolecular charge transfer from the electron-donating moiety (D) via the π-conjugated spacers towards the electron-accepting moiety (A).20,21Several framework types have been reported in the literature, including D–A, D–π–A, D–π–π–A, D–A–π–A, D–D–π–A, D–π–A–π–D and A–π–D–π–A.22–25 The nature of both D and A moieties plays a critical role in developing a good NLO response and the literature is replete with a huge variety of π-linkers. Through assimilation of suitable D, π-conjugation spacers and A, a push–pull architecture has been built for designing A–D–π–π–A and D–A–D–π–π–A organic compounds. These push–pull arrangements decrease the recombination of charges, influence charge detachment, deepen the penetration range within higher wavelengths, magnify the asymmetric electronic distribution and decrease the HOMO–LUMO band gap, hence elevating the NLO response.26–32
Quinoline and its derivatives have been widely studied in various areas, exhibiting a variety of practical applications: e.g. such compounds are used in optoelectronics due to their chemical and thermal stability, fluorescence and electron transporting capabilities and the possibility of their chemical modification.33 Quinoline has the ability to attract electrons and is a good candidate for an organic acceptor moiety. Carbazole derivatives are electron-rich systems (D) making them suitable for organic donor moieties and are frequently used in optoelectronics, especially in solar cell technologies, and as hole-transporter materials in organic light emitting diode (OLED) devices.34 In addition, the carbazole moiety can easily be modified by substitution at the 9-position, modifying the overall solubility and photophysical properties of the NLO molecule.35 In view of the acceptor and donor properties of these moieties, we have taken frameworks from two quinoline–carbazole based compounds (Q1 and Q2) recently synthesized by Slodek et al.36 and have built upon them to develop new compounds (Q1D1, Q1D2, Q1D3, Q2D1, Q2D2 and Q2D3) to study and explore the NLO response properties of quinoline–carbazole systems. We hope that this study will serve as a springboard for experimental chemists and physicists for the synthesis of compounds with excellent NLO response properties.
Computational procedure
In the present analysis, the absorption spectra, natural bond orbital (NBO) analysis, electronic properties and β results of Q1, Q2 and their derivatives were obtained by performing time-dependent density functional theory (TDDFT) and density functional theory (DFT) calculations. All computations were done using the Gaussian 09 program.37 Geometric optimization was performed in gas and dimethylsulfoxide (DSMO) as a solvent and without symmetry restriction at the 6-311G(d,p) basis set in combination with the CAM-B3LYP38 level of theory.39,40 For the confirmation of stable geometries and a stationary nature at the minimum energy, vibrational frequency analyses were carried out by applying identical functionals.41,42 Frontier molecular orbital (FMO) examination was performed with the CAM-B3LYP/6-311G(d,p) functional to calculate the energies of HOMO and LUMO and the energy difference between them. The natural bond orbital (NBO) investigation was performed using the same functionals for the approximation of charge transfer interactions between investigated compounds. In optimised geometries, TDDFT computations were implemented for the determination of the electronic transitions. UV-visible absorption spectra of the studied molecules were elucidated by performing TDDFT computations with the CAM-B3LYP/6-311G(d,p) basis set combination.38 To determine the solvent (DMSO) effect, a conductor-like polarizable continuum model (CPCM) was used.43 The Gaussian output file gave ten hyperpolarizability tensors (βxxx, βxyy, βxzz, βyyy, βxxy, βyzz, βzzz, βxxz, βyyz, βxyz) and six linear polarizability tensors (αxx, αyy, αzz, αxy, αxz, αyz) along the x, y and z directions, respectively. Eqn (1) and (2) are used to calculate the volume of first hyperpolarizability (βtot) and average polarizability 〈α〉.44| 〈α〉 = 1/3(αxx + αyy + αzz) | (1) |
| βtot = [(βxxx + βxyy + βxzz)2 + (βyyy + βxxy + βyzz)2 + (βzzz + βxxz + βyyz)2]1/2 | (2) |
Results and discussion
Design of A–D–π–A and D–A–D–π–A molecular models
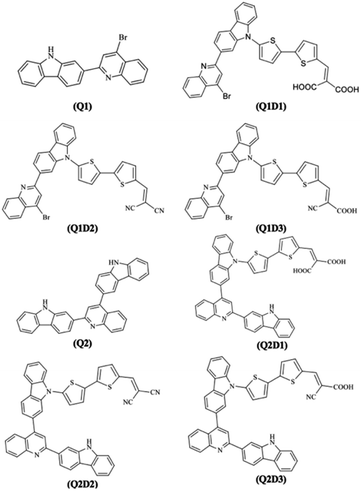
DFT calculations in this work were performed on molecules designed from the Q1 and Q2 parent structures to have good NLO properties. Compound Q1 is of the D–A type and Q2 is of D–A–D type. In these structures, the highly electron-rich carbazole moiety acts as an electron donor and the quinolone moiety as an electron acceptor. In all the designed molecules, these parent structures were modified by connection of a further acceptor moiety via a π spacer. This design strategy is set out in Fig. 1. In all cases, this π spacer was 2-(thiophen-2-yl)thiophene. Three different terminal acceptor moieties, shown in Fig. 2, were introduced to produce three designed compounds based on each of the two parent compounds Q1 and Q2.14,17,18,45 | ||
| Fig. 1 A sketch map of two families of compounds. The first is designed from Q1 (donor–acceptor) and the second is designed from Q2 (donor–acceptor–donor) configurations. | ||
Hence, the three compounds with A–D–π–A architecture designed from Q1 are Q1D1 (2-((5′-(2-(4-bromoquinolin-2-yl)-9H-carbazol-9-yl)-[2,2′-bithiophen]-5-yl)methylene)-malonic acid); Q1D2 (2-((5′-(2-(4-bromoquinolin-2-yl)-9H-carbazol-9-yl)-[2,2′-bithiophen]-5-yl)methylene)malononitrile); Q1D3 ((Z)-3-(5′-(2-(4-bromoquinolin-2-yl)-9H-carbazol-9-yl)-[2,2′-bithiophen]-5-yl)-2-cyanoacrylic acid).
Similarly, three compounds with D–A–D–π–A architecture were designed from Q2: Q2D1 (2-((5′-(2-(2-(9H-carbazol-2-yl)quinolin-4-yl)-9H-carbazol-9-yl)-[2,2′-bithiophen]-5-yl)methylene)malonic acid); Q2D2 (2-((5′-(2-(2-(9H-carbazol-2-yl)quinolin-4-yl)-9H-carbazol-9-yl)-[2,2′-bithiophen]-5-yl)methylene)malononitrile); Q2D3 ((E)-3-(5′-(2-(2-(9H-carbazol-2-yl)quinolin-4-yl)-9H-carbazol-9-yl)-[2,2′-bithiophen]-5-yl)-2-cyanoacrylic acid).
With the exception of the terminal acceptor shown in Fig. 2 and which is modulated in all compounds designed from Q1 and Q2, the D–A part is preserved throughout the designs. The structures of the investigated compounds (Q1, Q1D1–Q1D3, Q2, Q2D1–Q2D3) are portrayed in Fig. 3. DFT and TDDFT calculations were performed to investigate how π-conjugated spacers and various acceptors established with quinoline and carbazole units influence the NLO properties: (i) hyperpolarizability (β), (ii) polarizability (α) and (iii) absorption wavelength.
Electronic structure
FMO analysis is an excellent model to explain the chemical stability and the electronic and optical properties of molecules.46 In conjugated systems, the lowest unoccupied molecular orbital (LUMO) and the highest occupied molecular orbital (HOMO) determine numerous interactions between molecules, types of reaction, the UV-visible spectrum and fluorescence.47–49 The HOMO energy (EHOMO), LUMO energy (ELUMO) and HOMO–LUMO energy gap (ELUMO − EHOMO) are significant factors in understanding the chemical softness, hardness, dynamic stability and chemical reactivity of the compounds under investigation. Materials with a large HOMO–LUMO energy gap (Egap) are considered to be hard molecules with high kinetic strength and low chemical reactivity.50 Conversely, compounds with a lower HOMO–LUMO energy gap are smooth molecules with lower stability and higher reactivity.50 These compounds are highly polarizable and show excellent NLO properties.51,52 Calculations of the energies of EHOMO, ELUMO and their energy gap for the parent (Q1 and Q2) and designed (Q1D1–Q1D3 and Q2D1–Q2D3) molecules have been carried out using TDDFT computations and the results are shown in Table 1.| Compounds | E(HOMO) | E(LUMO) | Band gap |
|---|---|---|---|
| Q1 | −7.232 | −1.072 | 6.160 |
| Q1D1 | −7.226 | −1.793 | 5.433 |
| Q1D2 | −7.189 | −2.142 | 5.047 |
| Q1D3 | −7.362 | −2.030 | 5.332 |
| Q2 | −7.196 | −0.969 | 6.227 |
| Q2D1 | −7.171 | −1.699 | 5.472 |
| Q2D2 | −7.203 | −2.151 | 5.052 |
| Q2D3 | −7.137 | −1.934 | 5.203 |
The data in Table 1 show that of the parent molecules, Q1 has the lower HOMO–LUMO energy gap (6.160 eV). Furthermore, the band gap is observed to be smaller in the designed molecules. For the Q1 family, Q1 has the highest Egap value (6.160 eV) and the HOMO–LUMO energy gap decreases in the order Q1 > Q1D1 > Q1D3 > Q1D2 to 5.047 eV. A similar effect on Egap is seen in the Q2 family, with the energy gap being highest in Q2 (6.227 eV) and falling in the order Q2 > Q2D1 > Q2D3 > Q2D2 to 5.052 eV. Overall, the value of the Egap of all the investigated molecules increases in the order: Q1D2 < Q2D2 < Q2D3 < Q1D3 < Q1D1 < Q2D1 < Q1 < Q2. Thus, the introduction of a planar spacer linker to join different suitable acceptor units is an effective way to lower Egap and thus to enhance and influence the NLO properties. Of the terminal acceptors studied, 2-ethylidenemalononitrile (EMN) exhibits the greatest capacity to reduce the Egap of quinoline–carbazole based compounds. Overall, the band gap is found to be low in Q1 and its derivatives relative to the Q2 family.
In addition to the magnitude of the HOMO–LUMO energy gap, the ability of compounds to undergo intramolecular charge transfer from donor to acceptor moieties, mediated by π-linkers, is an important aspect of NLO structure–function relationships. The contour surfaces for the distribution of the frontier molecular orbitals (FMOs) are used to explain the exchange of charges, as illustrated in Fig. 4.
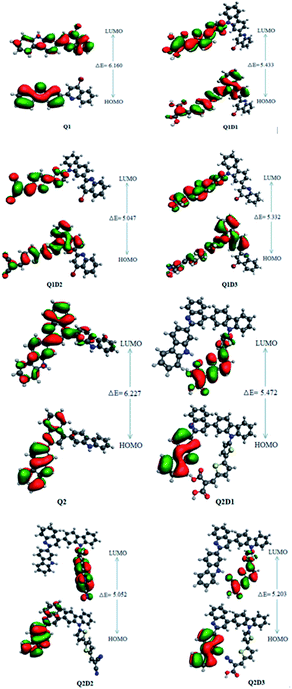 | ||
| Fig. 4 HOMOs and LUMOs of quinoline–carbazole based Q1 (A–D–π–A) and Q2 (D–A–D–π–A) families of molecules. | ||
In Q1, the HOMO is predominantly located on the donor carbazole unit while LUMO density is concentrated on the acceptor quinoline moiety. In Q1D1, Q1D2 and Q1D3, the HOMO is predominantly on the donor carbazole unit and partially on the π spacer while the LUMO is concentrated partially on the π spacer and largely on the terminal acceptor. Similarly, the HOMO in Q2 is on the donor carbazole segment and the LUMO is on the acceptor quinoline part. The HOMO charge density in Q2D1, Q2D2 and Q2D3 is positioned on one of the two donor carbazole units, while the LUMO charge density is positioned partially on the bridge unit and largely on the terminal acceptor parts. Thus, significant charge transfer in the studied compounds was directed from the donor HOMO to an acceptor via by the π-spacers. This facilitation of charge transfer indicates that all the designed compounds should be excellent NLO materials.
Global reactivity parameters
The energy values of FMOs (Egap = ELUMO − EHOMO) are useful for discovering global reactivity information, including global hardness (η), global softness (σ), global electrophilicity index (ω), electron affinity (EA), ionization potential (IP), electronegativity (X) and the chemical potential (μ)51–54 and calculated by utilizing eqn (3) and (4):| IP = −EHOMO | (3) |
| EA = −ELUMO | (4) |
The chemical hardness (η), chemical potential (μ) and electronegativity (X) have been calculated by utilizing Koopmans's theorem and the following eqn (5)–(7):55,56
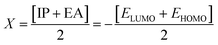 | (5) |
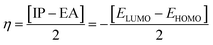 | (6) |
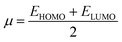 | (7) |
The global softness (σ) is described by eqn (8):
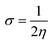 | (8) |
An electrophilicity index (ω) was introduced by Parr et al., as in eqn (9):
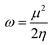 | (9) |
The results obtained from eqn (3)–(9) are collected in Table 2.
| Comp | IP | EA | X | η | μ | ω | σ |
|---|---|---|---|---|---|---|---|
| a IP = ionization potential, EA = electron affinity, X = electronegativity, μ = chemical potential, η = global hardness, σ = global softness and ω = global electrophilicity. Units are eV. | |||||||
| Q1 | 7.23 | 1.07 | 4.15 | 3.080 | −4.152 | 2.798 | 0.16 |
| Q1D1 | 7.22 | 1.79 | 4.51 | 2.716 | −4.509 | 3.742 | 0.18 |
| Q1D2 | 7.18 | 2.14 | 4.66 | 2.523 | −4.665 | 4.312 | 0.19 |
| Q1D3 | 7.36 | 2.03 | 4.70 | 2.666 | −4.696 | 4.135 | 0.18 |
| Q2 | 7.19 | 0.96 | 4.08 | 3.113 | −4.082 | 2.676 | 0.16 |
| Q2D1 | 7.17 | 1.70 | 4.43 | 2.736 | −4.435 | 3.594 | 0.18 |
| Q2D2 | 7.20 | 2.15 | 4.68 | 2.526 | −4.677 | 4.329 | 0.19 |
| Q2D3 | 7.13 | 1.93 | 4.15 | 2.601 | −4.535 | 3.953 | 0.19 |
The global reactivity parameters relate to the reactivity of the molecules studied. For example, ionization potential relates to electron-donating ability and electronegativity relates to the ability of a compound to attract electrons. The negative values of chemical potential (μ) shown in Table 2 indicate that all the studied molecules are chemically stable. Hardness, chemical potential and electronegativity depend on the value of Egap. The values of these parameters in Table 2 correlate, therefore, with the size of the band gap across the two families of molecules. Hence, the calculated hardness values across the two families lie in the order Q2 > Q1 > Q2D1 > Q1D1 > Q1D3 > Q2D3 > Q2D2 > Q1D2, exactly the same as the order of increase of Egap. The order of increasing softness is the reverse of this. Ionization potential, electron affinity, electronegativity and global electrophilicity correlate with Egap in the same manner.
Natural bond orbital (NBO) analysis
Natural bond orbital (NBO) studies are valuable for understanding the movement of charge between filled and empty orbitals.57 NBO information provides us with an understanding of intramolecular delocalization and of the charge densities which move in D–π–A structures from donor to acceptor segments.58 The stabilization energy of molecules in NBO analysis can be determined from eqn (10), which is derived using second-order perturbation theory:
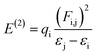 | (10) |
| Compounds | Donor (i) | Type | Acceptor (j) | Type | E(2)a | E(j)E(i)b (a.u.) | F(i,j)c (a.u.) |
|---|---|---|---|---|---|---|---|
| a E(2) is the energy of hyper conjugative interaction (stabilization energy in kcal mol−1).b Energy difference between donor and acceptor i and j NBO orbitals.c F(i;j) is the Fock matrix element between i and j NBO orbitals. | |||||||
| Q1 | C27–C32 | π | C28–C29 | π* | 372.21 | 0.01 | 0.095 |
| C1–C2 | π | C3–C4 | π* | 23.89 | 0.36 | 0.087 | |
| C2–H8 | σ | C3–C4 | σ* | 5.16 | 1.16 | 0.070 | |
| C3–C4 | σ | C9–Br24 | σ* | 6.93 | 0.88 | 0.070 | |
| N25 | LP(1) | C3–C4 | σ* | 11.98 | 0.98 | 0.097 | |
| N26 | LP(1) | C27–C32 | π* | 46.95 | 0.36 | 0.121 | |
| Q1D1 | C27–C28 | π | C29–C30 | π* | 34.05 | 0.37 | 0.100 |
| C12–N25 | π | C9–C13 | π* | 15.43 | 0.42 | 0.073 | |
| N26–C27 | ∂ | C37–C38 | ∂* | 0.55 | 1.50 | 0.026 | |
| C28–C29 | ∂ | N26–C27 | ∂* | 6.94 | 1.25 | 0.084 | |
| S46 | LP(2) | C47–C49 | π* | 30.57 | 0.33 | 0.090 | |
| C3 | LP(1) | C9–C13 | π* | 72.78 | 0.18 | 0.126 | |
| Q1D2 | C12–N25 | π | C9–C13 | π* | 15.44 | 0.42 | 0.073 |
| C47–C49 | π | C51–C53 | π* | 34.36 | 0.38 | 0.102 | |
| C2–C3 | ∂ | C3–C4 | ∂* | 4.65 | 1.34 | 0.071 | |
| C9–C13 | ∂ | C12–N25 | ∂* | 29.21 | 0.39 | 0.098 | |
| S46 | LP(2) | C47–C49 | π* | 28.96 | 0.34 | 0.088 | |
| N26 | LP(1) | C27–C32 | π* | 40.09 | 0.37 | 0.113 | |
| Q1D3 | C47–C49 | π | C51–C53 | π* | 32.17 | 0.38 | 0.100 |
| C12–N25 | π | C9–C13 | π* | 15.44 | 0.42 | 0.073 | |
| C1–H7 | ∂ | C1–C6 | ∂* | 0.61 | 1.20 | 0.024 | |
| C38–C40 | ∂ | N26–C37 | ∂* | 7.16 | 1.24 | 0.084 | |
| C22 | LP(1) | C16–C18 | π* | 78.49 | 0.19 | 0.133 | |
| S39 | LP(2) | C37–C38 | π* | 30.71 | 0.35 | 0.094 | |
| Q2 | C3–C4 | π | C11–N23 | π* | 20.03 | 0.34 | 0.076 |
| C45–C46 | π | C48–C51 | π* | 391.20 | 0.01 | 0.095 | |
| C1–H7 | σ | C1–C6 | σ* | 0.61 | 1.20 | 0.024 | |
| C26–C27 | σ | N24–C25 | σ* | 6.53 | 1.28 | 0.082 | |
| N23 | LP(1) | C3–C4 | σ* | 11.40 | 0.99 | 0.096 | |
| N55 | LP(1) | C39–C43 | π* | 47.19 | 0.36 | 0.121 | |
| Q2D1 | C3–C4 | π | C5–C6 | π* | 20.02 | 0.37 | 0.091 |
| C8–C12 | π | C11–N23 | π* | 34.85 | 0.37 | 0.102 | |
| C73–O75 | ∂ | C73–O77 | ∂* | 0.50 | 1.66 | 0.026 | |
| C58–C60 | ∂ | N55–C57 | ∂* | 6.99 | 1.23 | 0.083 | |
| O78 | LP(2) | C74–O80 | π* | 58.35 | 0.44 | 0.146 | |
| S66 | LP(2) | C67–C69 | π* | 30.83 | 0.33 | 0.091 | |
| Q2D2 | C3–C4 | π | C5–C6 | π* | 20.10 | 0.37 | 0.081 |
| C8–C12 | π | C11–N23 | π* | 34.49 | 0.37 | 0.102 | |
| C60–C62 | ∂ | N55–C57 | ∂* | 0.57 | 1.30 | 0.024 | |
| C73–C75 | ∂ | C75–N76 | ∂* | 9.51 | 1.78 | 0.117 | |
| N24 | LP(1) | C25–C30 | π* | 46.86 | 0.36 | 0.121 | |
| S66 | LP(2) | C67–C69 | π* | 29.10 | 0.34 | 0.089 | |
| Q2D3 | C73–N79 | π | C71–C72 | π* | 8.00 | 0.48 | 0.058 |
| C67–C69 | π | C71–C72 | π* | 34.54 | 0.39 | 0.105 | |
| C1–H7 | ∂ | C1–C6 | ∂* | 0.60 | 1.20 | 0.024 | |
| C72–C73 | ∂ | C73–N79 | ∂* | 10.18 | 1.79 | 0.121 | |
| N79 | LP(1) | C72–C73 | ∂* | 10.77 | 1.16 | 0.100 | |
| O75 | LP(2) | C74–O77 | π* | 57.92 | 0.45 | 0.146 | |
Four types of electronic transitions were commonly observed; σ → σ*, π → π*, LP → σ* and LP → π*. Among these π → π* were most prominent while σ → σ* were least dominant and LP → σ* and LP → π* were slightly dominant transitions. The presence of conjugation and charge transfer in these compounds can be examined by studying the π → π* transitions. The most significant π → π* electronic interactions are π(C27–C32) → π*(C28–C29), π(C27–C28) → π*(C29–C30), π(C47–C49) → π*(C51–C53) and π(C47–C49) → π*(C51–C53) with stabilization energies 372.21, 34.05, 34.36 and 32.17 kcal mol−1 found in Q1, Q1D1, Q1D2 and Q1D3, respectively. These excitations are the highest such transitions in the Q1 family.
Similarly the most feasible π → π* interactions among the Q2 family of molecules were π(C45–C46) → π*(C48–C51), π(C8–C12) → π*(C11–N23), π(C8–C12) → π*(C11–N23) and π(C67–C69) → π*(C71–C72) with stabilization energies of 391.20, 34.85, 34.49 and 34.54 kcal mol−1 in Q2, Q2D1, Q2D2 and Q2D3, respectively.
Significant resonance interactions were observed. In the Q1 family these are LP1(N26) → π*(C27–C32), LP2(C3) → π*(C9–C13), LP1(N26) → π*(C27–C32), and LP1(C22) → π*(C16–C18) with stabilization energies of 46.95, 72.78, 40.09, and 78.49 kcal mol−1 in Q1, Q1D1, Q1D2, and Q1D3, respectively. For the Q2 family the significant transitions from lone pair orbitals are LP1(N55) → π*(C39–C43), LP2(O78) → π*(C74–O80), LP1(N24) → π*(C25–C30), and LP2(O75) → π*(C74–O77) with stabilization energies of 47.19, 58.35, 46.86 and 57.92 kcal mol−1 in Q2, Q2D1, Q2D2, and Q2D3, respectively.
Hence NBO investigation of these molecules indicates that the extended hyper conjugation and strong intramolecular transfer of charge plays a significant role in stabilizing these systems and provides evidence of charge transfer characteristics that are crucial for potential NLO properties.
Nonlinear optical (NLO) properties
NLO compounds are extensively used in signal processing, optical switches, communication technology and optical memory devices. The electrical characteristics of the entire compound are responsible for the optical response, which in turn is related to the nonlinear response (hyperpolarizabilities, β and γ) and linear responses (polarizability, α, etc.).The linear and nonlinear responses of NLO materials arise from the electrical characteristics of the entire molecule. The NLO response properties of the Q1 and Q2 families of compounds have been estimated and the results for values of 〈α〉 and β are presented in Tables 4 and 5, respectively.
| System | αxx | αyy | αzz | αtotal |
|---|---|---|---|---|
| Q1 | 644.744 | 396.922 | 137.529 | 393.065 |
| Q1D1 | 955.102 | 788.767 | 359.700 | 701.1897 |
| Q1D2 | 938.708 | 836.458 | 368.775 | 714.647 |
| Q1D3 | 930.100 | 770.333 | 425.275 | 708.5693 |
| Q2 | 772.065 | 681.095 | 275.425 | 576.195 |
| Q2D1 | 1255.002 | 913.365 | 423.010 | 863.7923 |
| Q2D2 | 1060.912 | 849.048 | 755.935 | 888.6317 |
| Q2D3 | 1246.859 | 922.663 | 420.967 | 863.4963 |
| System | βxxx | βxxy | βxyy | βyyy | βxzz | βyzz | βzzz | βtotal |
|---|---|---|---|---|---|---|---|---|
| Q1 | 5702.17 | 884.16 | −229.03 | 183.80 | −10.97 | 11.08 | −2.17 | 5568.09 |
| Q1D1 | 9834.81 | −6526.60 | 397.07 | −3776.22 | −16.26 | 128.33 | 55.11 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420.20 420.20 |
| Q1D2 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 728.50 728.50 |
−11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 190.89 190.89 |
−4179.96 | −5623.95 | 19.92 | 70.96 | −65.46 | 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885.90 885.90 |
| Q1D3 | −11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 016.63 016.63 |
−7465.43 | −806.15 | −3690.90 | −193.28 | 46.25 | 92.98 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 392.40 392.40 |
| Q2 | −1653.41 | 2627.86 | −673.04 | 1288.99 | 27.04 | 22.09 | 32.91 | 4570.66 |
| Q2D1 | −6660.35 | 473.68 | −493.84 | 2352.61 | 193.75 | −65.34 | −31.74 | 7498.18 |
| Q2D2 | −3633.41 | 5694.79 | −7459.25 | 4279.34 | −573.46 | −298.39 | 510.96 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 748.70 748.70 |
| Q2D3 | −10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.88 000.88 |
−405.63 | −498.86 | 2153.84 | 186.47 | −79.76 | −1.95 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 452.70 452.70 |
Table 4 shows that the values of average polarizability for parent compounds Q1 and Q2 are 393.065 and 576.195 a.u., respectively. The most prominent transitions in all analysed molecules are along the x-axis (αxx) and modification with different acceptor moieties affects the polarization values. In both Q1 and Q2 families, the parent molecule has the lowest average polarizability and the presence of the strong acceptor unit EMN gives rise to the highest value of average polarizability. That is, the family maximum average polarizability is shown by Q1D2 and Q2D2, with the latter having the largest value for the molecules studied. Average polarizability decreases across the studied molecules in the order Q2D2 > Q2D1 > Q2D3 > Q1D2 > Q1D3 > Q1D1 > Q2 > Q1.
Dipole polarizability values (along the x-axis) are computed using eqn (11):
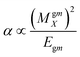 | (11) |
In this equation MgmX indicates the ground and mth excited state transition moment and Egm is the transition energy. In general, a molecule with large value of MgmX and a smaller value of Egm will exhibit a high hyperpolarizability value. Hence, dipole polarizability is a quantitative measure of the NLO response properties of compounds. Second-order polarizability – first hyperpolarizability (βtot) – values for the Q1 and Q2 families of compounds are shown in Table 5.
Table 5 shows that for the parent molecules the hyperpolarizability value of Q1 (5568.09 a.u.) is 1.2 times greater than that of Q2 (4570.66 a.u.). The values of βtot for the set of molecules increase in the order Q2 < Q1 < Q2D1 < Q2D3 < Q1D1 < Q1D3 < Q2D2 < Q1D2. That is, the hyperpolarizability increases in a manner compatible with the decrease in Egap. The highest βtot values are shown by molecules modified with the strong acceptor moiety EMN.
In these molecules, the highest and lowest NLO responses can be attributed to the efficiency of charge transfer from donor to acceptor through their corresponding π-associated connection. Briefly, increases in hyperpolarizability values in the molecules studied here arise in association with the delocalization of π-electrons. This delocalization decreases the HOMO–LUMO energy difference. Calculated values of average polarizability and second-order polarizability of the investigated molecules are significantly greater than for urea (βtot(urea) = 43 a.u.), a standard molecule for the analysis of NLO response.59 Hyperpolarizability values of Q1, Q1D1–Q1D3, Q2, Q2D1–Q2D3 are determined to be 129 times, 335 times, 555 times, 381 times, 106 times, 174 times, 389 times and 243 times higher than the second-order polarizability value of urea, respectively.
To examine the electronic excitations in the optimized geometries, TDDFT calculations were performed. TDDFT generally overestimates the excitation energies in case of charge transfer transitions and extended conjugated systems. It was therefore necessary to adopt a robust and high level of theory to model the UV-visible absorption spectrum of the studied compounds. For this purpose, TDDFT calculations were conducted using the CAM-B3LPY level with the 6-311G(d,p) basis set in DMSO solvent. In performing TDDFT calculations, the six most reduced singlet–singlet transitions were examined in Q1, Q2 and their derivatives. The results for the calculated absorption wavelength (λmax), transition energy, nature of transitions (Ege) and oscillator strength (fos) are listed in Tables S17–S23 (ESI)† while some important values of these compounds are shown in Table 6.
| Compounds | Ege (eV) | λmax (nm) | fos | LHE | MgmX (a.u.) | MO transitiona |
|---|---|---|---|---|---|---|
| a H = HOMO, L = LUMO, H − 1 = HOMO − 1, L + 1 = LUMO + 1 etc.b Experimental values in parentheses are from ref. 36. | ||||||
| Q1 | 3.860 | 321 [326]b | 1.447 | 0.964 | 1.989 | H − 1 → L (83%) |
| Q1D1 | 3.878 | 320 | 1.438 | 0.964 | 2.101 | H − 1 → L + 1 (85%) |
| Q1D2 | 2.844 | 436 | 1.450 | 0.965 | 3.366 | H → L (65%) |
| Q1D3 | 2.993 | 414 | 1.502 | 0.969 | 2.533 | H − 1 → L (60%) |
| Q2 | 3.885 | 319 [323]a | 1.459 | 0.965 | 0.830 | H − 1 → L (44%), H → L (32%) |
| Q2D1 | 3.912 | 317 | 1.283 | 0.948 | 0.140 | H − 1 → L + 1 (69%) |
| Q2D2 | 3.874 | 320 | 1.455 | 0.965 | 2.442 | H − 1 → L + 1 (55%) |
| Q2D3 | 3.954 | 314 | 1.184 | 0.934 | 2.046 | H − 1 → L + 1 (46%) |
UV-vis spectra analysis
All the molecules show absorbance in the visible region. The calculated λmax values for Q1 and Q2 of 321 and 319 nm, respectively, are in good agreement with the experimentally reported values of 326 and 323 nm, respectively.36 Of the designed molecules, Q1D2 and Q2D3 show the highest λmax values. The calculated absorption spectra are shown in Fig. 5. Among all the studied compounds, the maximum absorption wavelength and minimum transition energy are observed in Q1D2.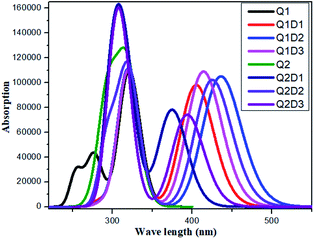 | ||
| Fig. 5 Simulated absorption spectra of quinoline–carbazole based compounds (Q1, Q1D1–Q1D3, Q2, Q2D1–Q2D3). | ||
Structural tailoring of compounds Q1 and Q2 modifies the contribution of different orbitals to the electronic transitions. In Q1, Q1D1–Q1D3, Q2, Q2D1–Q2D3, the crucial excited states are produced due to the promotion of electrons mainly from HOMO and HOMO − 1 to LUMO and LUMO + 1. This sort of charge transfer is required for NLO active compounds and forms the basis for the NLO responses of the compounds investigated here.
A crucial factor that determines the optical productivity of the molecules studied here is the light harvesting efficiency (LHE), which is determined using the fos values given by the TDDFT calculations. It is commonly observed that molecules with a large value of LHE exhibit high photocurrent properties. The value of LHE of the analyzed compounds is calculated using eqn (12) and the results are shown in Table 6.
| LHE = 1 − 10−f | (12) |
The LHE values of all studied compounds are similar to each other. Structure–property relationships help us to gain an understanding of the reason for an improved NLO in response to changing the nature of the acceptor units. Oudar and Chemla60 formulated a two-state model, eqn (13), which is frequently used in the literature for NLO estimation.
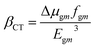 | (13) |
In this model the product of oscillation strength (fgm) and transition moment (Δμgm) is directly proportional and the transition energy cube Egm3 is inversely proportional to β. Thus, compounds exhibiting a large fgm and Δμgm and small Egm3 exhibit good NLO response properties. These parameters were estimated and their values are shown in Table 5. The relationship between βtot values and the corresponding two-level model (Δμgmfgm/Egm3) values for the studied molecules are displayed in Fig. 6, in which the βtot and two-level model values can be seen to be in very good agreement with each other.
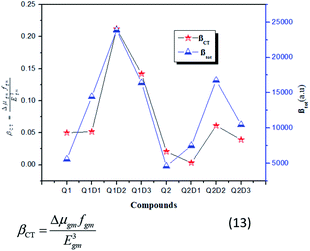 | ||
| Fig. 6 Relationship between the βtot (red star) values and the corresponding Δμgmfgm/Egm3 (blue triangles) values for the investigated compounds. | ||
Conclusions
The purpose of the work was to explore A–D–π–A and D–A–D–π–A configured novel quinoline–carbazole based highly efficient nonlinear optical compounds with promising NLO properties. All designed compounds Q1D1–Q1D3 and Q2D1–Q2D3 show absorbance wavelength in the visible region with low transition energy and oscillating strength. The largest reduction in band gap was shown by Q1D2 and Q2D2. As the NLO properties of the studied molecules were shown to correlate well with the band gap energy, this demonstrated that, of the three terminal groups investigated, EMN has the greatest impact on NLO properties. NBO results showed that electrons are effectively moved by means of the π-conjugated linker from D to A, facilitating the development of a charge transfer state. The FMOs analysis demonstrates that Egap in the designed compounds is found to be narrow relative to the parent compounds. Furthermore, the LUMO is arranged over the acceptor moiety and partially on the π linker while the HOMO is delocalized over the donor group and the π-conjugated linker, which represents the intramolecular charge transfer from donor to acceptor moieties mediated through π-bridge linkers. Global reactivity results showed that the decreasing order of softness is: Q1D2 > Q2D2 > Q2D3 > Q1D3 > Q1D1 > Q2D1 > Q1 > Q2, which is exactly the same as the order of decreasing Egap and the reverse of the order of global hardness values. In general, all the designed compounds in this study have demonstrated large theoretical βtot values in the range of 4570.66 to 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885.90 (a.u.). Among the studied compounds, Q2D2 has shown the highest 〈α〉 value of 888.63 (a.u.) while the highest βtot was shown to be 23
885.90 (a.u.). Among the studied compounds, Q2D2 has shown the highest 〈α〉 value of 888.63 (a.u.) while the highest βtot was shown to be 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 885.90 (a.u.) in Q1D2. Moreover, βtot values of the studied molecules were demonstrated to be in broad agreement with the two-level model (Δμgmfgm/ΔEgm3) values. The design of NLO materials is currently an active domain of research and this theoretical study provides valuable insight with which experimentalists can structure superior NLO materials for electronics and optics.
885.90 (a.u.) in Q1D2. Moreover, βtot values of the studied molecules were demonstrated to be in broad agreement with the two-level model (Δμgmfgm/ΔEgm3) values. The design of NLO materials is currently an active domain of research and this theoretical study provides valuable insight with which experimentalists can structure superior NLO materials for electronics and optics.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dr Akbar Ali is thankful to HEC, Pakistan for the IPFP grant.References
- M. G. Papadopoulos, A. J. Sadlej and J. Leszczynski, Non-linear optical properties of matter, Springer, Dordrecht, 2006 Search PubMed.
- M. Akram, M. Adeel and M. Khalid, et al., A combined experimental and computational study of 3-bromo-5-(2, 5-difluorophenyl) pyridine and 3, 5-bis (naphthalen-1-yl) pyridine: insight into the synthesis, spectroscopic, single crystal XRD, electronic, nonlinear optical and biological properties, J. Mol. Struct., 2018, 1160, 129–141 CrossRef.
- M. S. Ahmad, M. Khalid and M. A. Shaheen, et al., Synthesis and XRD, FT-IR vibrational, UV-vis, and nonlinear optical exploration of novel tetra substituted imidazole derivatives: a synergistic experimental-computational analysis, J. Phys. Chem. Solids, 2018, 265–276 CrossRef.
- M. Shahid, M. Salim and M. Khalid, et al., Synthetic, XRD, non-covalent interactions and solvent dependent nonlinear optical studies of Sulfadiazine-Ortho-Vanillin Schiff base: (E)-4-((2-hydroxy-3-methoxy-benzylidene) amino)-N-(pyrimidin-2-yl) benzene-sulfonamide, J. Mol. Struct., 2018, 1161, 66–75 CrossRef CAS.
- D. F. Eaton, Nonlinear Optical Materials: The Great and Near Great, ACS Publications, 1991 Search PubMed.
- Z. Peng and L. Yu, Second-order nonlinear optical polyimide with high-temperature stability, Macromolecules, 1994, 27(9), 2638–2640 CrossRef CAS.
- N. Tsutsumi, M. Morishima and W. Sakai, Nonlinear optical (NLO) polymers. 3. NLO polyimide with dipole moments aligned transverse to the imide linkage, Macromolecules, 1998, 31(22), 7764–7769 CrossRef CAS.
- E. M. Breitung, C.-F. Shu and R. J. McMahon, Thiazole and thiophene analogues of donor–acceptor stilbenes: molecular hyperpolarizabilities and structure–property relationships, J. Am. Chem. Soc., 2000, 122(6), 1154–1160 CrossRef CAS.
- P. S. Halasyamani and W. Zhang, Viewpoint: Inorganic Materials for UV and Deep-UV Nonlinear-Optical Applications, Inorg. Chem., 2017, 56(20), 12077–12085 CrossRef CAS PubMed.
- B. Zhang, G. Shi and Z. Yang, et al., Fluorooxoborates: Beryllium-Free Deep-Ultraviolet Nonlinear Optical Materials without Layered Growth, Angew. Chem., Int. Ed., 2017, 56(14), 3916–3919 CrossRef CAS PubMed.
- S. Yamashita, A tutorial on nonlinear photonic applications of carbon nanotube and graphene, J. Lightwave Technol., 2012, 30(4), 427–447 CAS.
- L. Guo, Z. Guo and X. Li, Design and preparation of side chain electro-optic polymeric materials based on novel organic second order nonlinear optical chromophores with double carboxyl groups, J. Mater. Sci.: Mater. Electron., 2018, 29(3), 2577–2584 CrossRef CAS.
- R. D. Fonseca, M. G. Vivas and D. L. Silva, et al., First-Order Hyperpolarizability of Triphenylamine Derivatives Containing Cyanopyridine: Molecular Branching Effect, J. Phys. Chem. C, 2018, 122(3), 1770–1778 CrossRef CAS.
- M. U. Khan, M. Khalid and M. Ibrahim, et al., First Theoretical Framework of Triphenylamine–Dicyanovinylene-Based Nonlinear Optical Dyes: Structural Modification of π-Linkers, J. Phys. Chem. C, 2018, 122(7), 4009–4018 CrossRef CAS.
- M. R. S. A. Janjua, M. U. Khan and B. Bashir, et al., Effect of π-conjugation spacer (C C) on the first hyperpolarizabilities of polymeric chain containing polyoxometalate cluster as a side-chain pendant: a DFT study, Comput. Theor. Chem., 2012, 994, 34–40 CrossRef CAS.
- M. R. S. A. Janjua, M. Amin and M. Ali, et al., A DFT Study on The Two-Dimensional Second-Order Nonlinear Optical (NLO) Response of Terpyridine-Substituted Hexamolybdates: Physical Insight on 2D Inorganic–Organic Hybrid Functional Materials, Eur. J. Inorg. Chem., 2012, 2012(4), 705–711 CrossRef CAS.
- M. U. Khan, M. Ibrahim and M. Khalid, et al., First theoretical probe for efficient enhancement of nonlinear optical properties of quinacridone based compounds through various modifications, Chem. Phys. Lett., 2019, 715, 222–230 CrossRef CAS.
- M. U. Khan, M. Ibrahim and M. Khalid, et al., Prediction of Second-Order Nonlinear Optical Properties of D–p–A Compounds Containing Novel Fluorene Derivatives: A Promising Route to Giant Hyperpolarizabilities, J. Cluster Sci., 2019, 30(2), 415–430 CrossRef CAS.
- M. U. Khan, M. Ibrahim and M. Khalid, et al., Quantum Chemical Designing of Indolo [3, 2, 1-jk] carbazole-based Dyes for Highly Efficient Nonlinear Optical Properties, Chem. Phys. Lett., 2019, 719, 59–66 CrossRef CAS.
- P. N. Prasad and D. J. Williams, Introduction to nonlinear optical effects in molecules and polymers, Wiley, New York, 1991, vol. 1 Search PubMed.
- D. S. Chemla, Nonlinear optical properties of organic molecules and crystals, Elsevier, 2012, vol. 1 Search PubMed.
- M. Wielopolski, J.-H. Kim and Y.-S. Jung, et al., Position-Dependent Extension of π-Conjugation in D-π-A Dye Sensitizers and the Impact on the Charge-Transfer Properties, J. Phys. Chem. C, 2013, 117(27), 13805–13815 CrossRef CAS.
- M. Katono, M. Wielopolski and M. Marszalek, et al., Effect of extended π-conjugation of the donor structure of organic D–A–π–A dyes on the photovoltaic performance of dye-Sensitized solar cells, J. Phys. Chem. C, 2014, 118(30), 16486–16493 CrossRef CAS.
- M. Panneerselvam, A. Kathiravan and R. V. Solomon, et al., The role of π-linkers in tuning the optoelectronic properties of triphenylamine derivatives for solar cell applications–A DFT/TDDFT study, Phys. Chem. Chem. Phys., 2017, 19(8), 6153–6163 RSC.
- S. Namuangruk, R. Fukuda and M. Ehara, et al., D–D–π–A-Type organic dyes for dye-sensitized solar cells with a potential for direct electron injection and a high extinction coefficient: synthesis, characterization, and theoretical investigation, J. Phys. Chem. C, 2012, 116(49), 25653–25663 CrossRef CAS.
- M. R. S. A. Janjua, Z.-M. Su and W. Guan, et al., Tuning second-order non-linear (NLO) optical response of organoimido-substituted hexamolybdates through halogens: quantum design of novel organic-inorganic hybrid NLO materials, Aust. J. Chem., 2010, 63(5), 836–844 CrossRef CAS.
- M. R. S. A. Janjua, S. Jamil and A. Mahmood, et al., Solvent-Dependent Non-Linear Optical Properties of 5, 5′-Disubstituted-2, 2′-bipyridine Complexes of Ruthenium (ii): A Quantum Chemical Perspective, Aust. J. Chem., 2015, 68(10), 1502–1507 CrossRef CAS.
- M. R. S. A. Janjua, Quantum mechanical design of efficient second-order nonlinear optical materials based on heteroaromatic imido-substituted hexamolybdates: first theoretical framework of POM-based heterocyclic aromatic rings, Inorg. Chem., 2012, 51(21), 11306–11314 CrossRef CAS PubMed.
- M. R. S. A. Janjua, S. Jamil and T. Ahmad, et al., Quantum chemical perspective of efficient NLO materials based on dipolar trans-tetraammineruthenium (II) complexes with pyridinium and thiocyanate ligands: first theoretical framework, Comput. Theor. Chem., 2014, 1033, 6–13 CrossRef CAS.
- M. Haroon, R. Mahmood and M. R. S. A. Janjua, An Interesting Behavior and Nonlinear Optical (NLO) Response of Hexamolybdate Metal Cluster: Theoretical Insight into Electro-Optic Modulation of Hybrid Composites, J. Cluster Sci., 2017, 28(5), 2693–2708 CrossRef CAS.
- M. R. S. A. Janjua, Z. H. Yamani and S. Jamil, et al., First principle study of electronic and non-linear optical (NLO) properties of triphenylamine dyes: interactive design computation of new NLO compounds, Aust. J. Chem., 2016, 69(4), 467–472 CrossRef CAS.
- R. Mahmood, M. R. S. A. Janjua and S. Jamil, DFT Molecular Simulation for Design and Effect of Core Bridging Acceptors (BA) on NLO Response: First Theoretical Framework to Enhance Nonlinearity Through BA, J. Cluster Sci., 2017, 28(6), 3175–3183 CrossRef CAS.
- A. Danel, E. Gondek and I. Kityk, 1H-pyrazolo [3, 4-b] quinoline and 1H-pyrazolo [3, 4-b] quinoxaline derivatives as promising materials for optoelectronic applications, Opt. Mater., 2009, 32(2), 267–273 CrossRef CAS.
- P.-I. Shih, C.-L. Chiang and A. K. Dixit, et al., Novel carbazole/fluorene hybrids: host materials for blue phosphorescent OLEDs, Org. Lett., 2006, 8(13), 2799–2802 CrossRef CAS PubMed.
- Y. Huo, J. Lu and S. Hu, et al., Photoluminescence properties of new Zn (II) complexes with 8-hydroxyquinoline ligands: dependence on volume and electronic effect of substituents, J. Mol. Struct., 2015, 1083, 144–151 CrossRef CAS.
- A. Slodek, D. Zych and A. Maroń, et al., Does the length matter?-Synthesis, photophysical, and theoretical study of novel quinolines based on carbazoles with different length of alkyl chain, Dyes Pigm., 2019, 160, 604–613 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, et al., D. 0109, Revision D. 01, Gaussian. Inc, Wallingford, CT, 2009 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393(1–3), 51–57 CrossRef CAS.
- A. Mahmood, M. I. Abdullah and S. U.-D. Khan, Enhancement of nonlinear optical (NLO) properties of indigo through modification of auxiliary donor, donor and acceptor, Spectrochim. Acta, Part A, 2015, 139, 425–430 CrossRef CAS PubMed.
- M. R. S. A. Janjua, First theoretical framework of di-substituted donor moieties of triphenylamine and carbazole for NLO properties: quantum paradigms of interactive molecular computation, Mol. Simul., 2017, 43(18), 1539–1545 CrossRef CAS.
- J. Autschbach, Charge-Transfer Excitations and Time-Dependent Density Functional Theory: Problems and Some Proposed Solutions, ChemPhysChem, 2009, 10(11), 1757–1760 CrossRef CAS PubMed.
- A. Dreuw and M. Head-Gordon, Single-reference ab initio methods for the calculation of excited states of large molecules, Chem. Rev., 2005, 105(11), 4009–4037 CrossRef CAS PubMed.
- V. Barone and M. Cossi, Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model, J. Phys. Chem. A, 1998, 102(11), 1995–2001 CrossRef CAS.
- A. Karakas, A. Elmali and H. Unver, Linear optical transmission measurements and computational study of linear polarizabilities, first hyperpolarizabilities of a dinuclear iron (III) complex, Spectrochim. Acta, Part A, 2007, 68(3), 567–572 CrossRef PubMed.
- A. Mahmood, S. U. D. Khan and U. A. Rana, et al., Effect of thiophene rings on UV/visible spectra and non-linear optical (NLO) properties of triphenylamine based dyes: a quantum chemical perspective, J. Phys. Org. Chem., 2015, 28(6), 418–422 CrossRef CAS.
- M. U. Khan, J. Iqbal and M. Khalid, et al., Designing triazatruxene-based donor materials with promising photovoltaic parameters for organic solar cells, RSC Adv., 2019, 9(45), 26402–26418 RSC.
- M. Adeel, A. A. Braga and M. N. Tahir, et al., Synthesis, X-ray crystallographic, spectroscopic and computational studies of aminothiazole derivatives, J. Mol. Struct., 2017, 1131, 136–148 CrossRef CAS.
- M. N. Arshad, A.-A. M. Al-Dies and A. M. Asiri, et al., Synthesis, crystal structures, spectroscopic and nonlinear optical properties of chalcone derivatives: a combined experimental and theoretical study, J. Mol. Struct., 2017, 1141, 142–156 CrossRef CAS.
- M. N. Tahir, M. Khalid and A. Islam, et al., Facile synthesis, single crystal analysis, and computational studies of sulfanilamide derivatives, J. Mol. Struct., 2017, 1127, 766–776 CrossRef CAS.
- S. S. Amiri, S. Makarem and H. Ahmar, et al., Theoretical studies and spectroscopic characterization of novel 4-methyl-5-((5-phenyl-1, 3, 4-oxadiazol-2-yl) thio) benzene-1, 2-diol, J. Mol. Struct., 2016, 1119, 18–24 CrossRef.
- R. G. Parr, L. V. Szentpaly and S. Liu, Electrophilicity index, J. Am. Chem. Soc., 1999, 121(9), 1922–1924 CrossRef CAS.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Electrophilicity index, Chem. Rev., 2006, 106(6), 2065–2091 CrossRef CAS PubMed.
- R. G. Parr, R. A. Donnelly and M. Levy, et al., Electronegativity: the density functional viewpoint, J. Chem. Phys., 1978, 68(8), 3801–3807 CrossRef CAS.
- A. Lesar and I. Milošev, Density functional study of the corrosion inhibition properties of 1, 2, 4-triazole and its amino derivatives, Chem. Phys. Lett., 2009, 483(4), 198–203 CrossRef CAS.
- T. Tsuneda, J.-W. Song and S. Suzuki, et al., On Koopmans' theorem in density functional theory, J. Chem. Phys., 2010, 133(17), 174101 CrossRef PubMed.
- T. Koopmans, Über die Zuordnung von Wellenfunktionen und Eigenwerten zu den einzelnen Elektronen eines Atoms, Physica, 1934, 1(1–6), 104–113 CrossRef.
- M. Szafran, A. Komasa and E. Bartoszak-Adamska, Crystal and molecular structure of 4-carboxypiperidinium chloride (4-piperidinecarboxylic acid hydrochloride), J. Mol. Struct., 2007, 827(1), 101–107 CrossRef CAS.
- C. James, A. A. Raj and R. Reghunathan, et al., Structural conformation and vibrational spectroscopic studies of 2, 6-bis (p-N, N-dimethyl benzylidene) cyclohexanone using density functional theory, J. Raman Spectrosc., 2006, 37(12), 1381–1392 CrossRef CAS.
- D. R. Kanis, M. A. Ratner and T. J. Marks, Design and construction of molecular assemblies with large second-order optical nonlinearities. Quantum chemical aspects, Chem. Rev., 1994, 94(1), 195–242 CrossRef CAS.
- J.-L. Oudar and D. Chemla, Hyperpolarizabilities of the nitroanilines and their relations to the excited state dipole moment, J. Chem. Phys., 1977, 66(6), 2664–2668 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02857f |
| This journal is © The Royal Society of Chemistry 2020 |