Effect of Zn doping on phase transition and electronic structures of Heusler-type Pd₂Cr-based alloys: from normal to all-d-metal Heusler

Abstract

Based on first-principles calculations, for Heusler alloys Pd₂CrZ (Z = Al, Ga, In, Tl, Si, Sn, P, As, Sb, Bi, Se, Te, Zn), the effect of Zn doping on their phase transition and electronic structure has been studied in this work. These alloys can be divided into two classes: (i) all-d-metal Heusler Pd₂CrZn and (ii) other normal Heusler alloys Pd₂CrZ (Z = Al, Ga, In, Tl, Si, Sn, P, As, Sb, Bi, Se, Te). For all-d-metal Heusler alloy Pd₂CrZn, transition metal element Zn behaves like a main group element due to its full 3d occupied state, and therefore the Zn atoms tend to occupy Wyckoff sites D (0.75, 0.75, 0.75) instead of replacing Pd atoms at A sites (0, 0, 0). The stable tetragonal L1₀ state is obtained via tetragonal deformation and the L1₀ stable state can be tuned by the uniform strain. The stability of the tetragonal state is analyzed and proved via calculation of the density of states (DOSs) and the phonon spectrum. For the series of normal Heusler alloys Pd₂CrZ, doping with Zn atoms can induce or strengthen the martensitic transformation, or regulate the large c/a ratios to a more reasonable range. It is hoped that this work can provide some guidance for further studies of the relationship between all-d-metal and normal Heusler alloys in the future.

---

Introduction

Magnetic phase transition materials¹ are novel smart materials that can sense and respond to environmental excitation and have been widely used in magnetic drives, magnetic sensors, magnetic storage, solid-state refrigeration, thermoelectric conversion and so on.^2,3 Searching for new magnetic phase transition materials is an essential study in the intelligent materials field. Magnetic shape memory alloys (MSMAs), one of the magnetic phase transition materials, play a pivotal role in magnetic actuation, magnetic refrigeration and the spintronics field.^4,5 Therefore, it is important to design and synthesize novel MSMAs.

Heusler alloys⁶ are the largest family in MSMAs, and their excellent characteristics make them a hot topic of study in such fields as modern electronic information technology, aerospace, and mechanical electronics. Heusler alloys become a favourable candidate for MSMAs due to their high Curie temperature,^7,8 tunable electronic structures,^9,10 adaptable semiconductor lattice constant¹¹ and novel magnetic and structural properties.^12–14 Normally, Heusler alloys have three classic types: half-Heusler alloys (XYZ),¹⁰ full-Heusler alloys (X₂YZ),^15,16 and equiatomic quaternary Heusler alloys (XYMZ).^13,17,18 Although the Heusler system has been proposed for more than 100 years, this system retains a high interest due to a series of novel physical phenomena and concepts were observed in this old system. A new category of Heusler family, all-d-metals,¹⁹ consists entirely of transition metal elements have been proposed recently. These alloys exhibit better phase space and versatility than conventional Heusler materials and feature magnetic martensitic transformation, magnetic drive shape memory, large magnetic drive strain, large magnetoresistance, large magnetocaloric effect, and large volume expansion.^19–22

Since the first MSMA Heusler alloy, Ni–Mn–Ga,²³ was proposed and studied in depth, other Heusler MSMA alloys have been widely investigated experimentally and theoretically, such as Ni₂FeGa,²⁴ Co–Ni–Ga (Al),²⁵ Mn₂NiGa,²⁶ and Fe–Mn–Ga.²⁷ Very recently, there have been some studies of all-d-metal Heusler alloys: (i) in the early 1900s, Muldawer et al. reported two all-d-metal Heusler alloys, Zn₂AuAg and Zn₂CuAu,²⁸ with ordered L2₁ or disordered B₂ structures. However, the nonmagnetic properties of these alloys limit the scope of application in magnetic materials, this study has spurred interest in all-d-metal Heusler alloys. (ii) Wei et al. achieved the multifunctional ferromagnetic shape memory effect in all-d-metal Ni_50−xCo_xMn_50−yTi_y in 2015.¹⁹ Doping transition group element Ti to the Ni–Mn system can benefit forming the cubic B₂ Heusler structures and stable the parent phase, further leading to the martensitic transformation. Based on the Ti–Ni–Mn phase, a strong ferromagnetic coupling in the Ni(Co)–Mn–Ti alloy was found via Co substitution. (iii) Wei et al. then conducted subsequent studies on the martensitic transformation and magnetic strain of the Ni_50−xCo_xMn_50−yTi_y system with large volume changes in 2016.²¹ They found that the martensitic transformation of Ni_50−xCo_xMn_50−yTi_y can occur at a magnetic strain of 6900 ppm and Ni_50−xCo_xMn_50−yTi_y polycrystalline samples exhibit a volume change of 2.54% near the room temperature. (iv) In 2018, Han et al. investigated the possible martensitic transformation of a series of all-d-metal equiatomic quaternary Heusler hypothetical alloys, ZnCdTMn (T = Fe, Ru, Os, Rh, Ir, Ni, Pd, Pt), by means of first-principle calculation.²⁰ (v) Ni et al. studied the magnetic structural transition of Mn₂Ni_1.5Ti_0.5 and Mn₂Ni_1.25Co_0.25Ti_0.5 and they found that the energy difference between the antiparallel and parallel configurations of the Mn (B) and Mn (D) moments can be increased by Co doping in Mn₂Ni_1.25Co_0.25Ti_0.5.²⁹ According to these previous studies, doping transition metal elements may be a favorable method to obtain all-d-metal Heusler alloys with magnetic phase transitions.

Therefore, in this work, we will study the doping effect of transition metal element Zn on Heusler alloys Pd₂CrZ, which may enable adjusting their phase transition and other magnetic properties for better applications under different conditions. To our best knowledge, there are no other studies focusing on the effect of Zn doping in Heusler alloys Pd₂CrZ, and therefore, current work can be seen as a reference for future theoretical and experimental investigations. The reasons we selected Zn element in this manuscript can be shown as follows: (i) currently, 3d metals doping to MSMAs is quite widespread. Among them, Zn has a full d (3d¹⁰4s²) occupied state of the atom, which causes the indirect interaction between Zn and other transition metal atoms in the Heusler alloys due to its low d-state energy, so the Zn atom may be regarded as the same role as a main group element. Some investigations have been carried out and found that Zn doping can improve the phase transition temperature or stability as well as the ordering of the structure;^30–32 however, a general first principle study to discuss the effect of Zn doping in normal Heusler alloys is still needed. (ii) The second reason is that the price of Zn is relatively lower than other transition metal elements, and thus it will be less costly for industrial applications.

Materials and methods

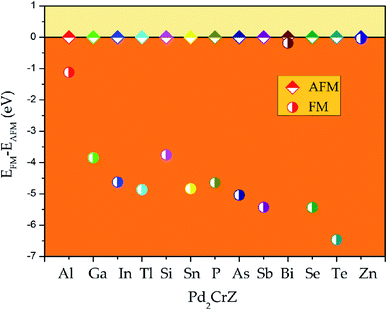
All the electronic structures have been computed via the density functional theory³³ which is realized in the VASP code³⁴ in this work. The exchange and related functions are described by Perdew–Burke–Ernzerhof (PBE)³⁵ for the parameterization of GGA.³⁶ And the projector augmented wave (PAW)³⁷ was chosen to handle the interaction between the valence electrons and ion cores. In all situations, the plane-wave basis set cutoff is set as 450 eV and the Monkhors–Pack special k-point mesh is fixed to 12 × 12 × 12 in all Brillouin zone integration whether in XA- or L2₁-type Heusler alloys. The unit cell was optimized until the force and total energy to less than 0.005 eV Å⁻¹ and 0.0000001 eV, respectively. The phonon energy calculation of Pd₂CrZ was performed in NanoAcademic Device Calculator (Nanodcal) code.³⁸

To determine the ground state of Pd₂CrZ (Z = Al, Ga, In, Tl, Si, Sn, P, As, Sb, Bi, Se, Te, Zn), the crystals of full Heusler-type alloys Pd₂CrZ were optimized. The site-preference rule (SPR)³⁹ is usually employed to determine the possible atomic preference of full-Heusler alloys X₂YZ. Normally, when X atoms have more valence electrons than Y, X atoms tend to locate at the Wyckoff A and C sites, the Y atoms tend to locate at B sites, as well as the main group element Z occupies the D sites, forming the L2₁-type Heusler alloys. The other form is the XA-type Heusler alloys, in which the valence electrons in X are less than Y atoms, so the A and B sites are occupied by X atoms. As shown in Fig. S1,† the crystal structures of XA- and L2₁-type of Pd₂CrZ are plotted. From Fig. 1, the energy differences between XA and L2₁ structures were given. From it, one can see that the L2₁ is the stable crystal structure due to its lower energy than the XA-type. Based on the L2₁ phase, the magnetic states, including ferromagnetic and antiferromagnetic (AFM), for Pd₂CrZ are also taken into consideration. For the AFM state, the antiparallel coupled spin moments between the Mn and Pd atoms are added. One can clearly see that the energy differences (E_FM − E_AFM) in Fig. 2 of all the Heusler alloys Pd₂CrZ are negative. That is, the FM state of all Pd₂CrZ Heusler alloys is more stable than the AFM state.

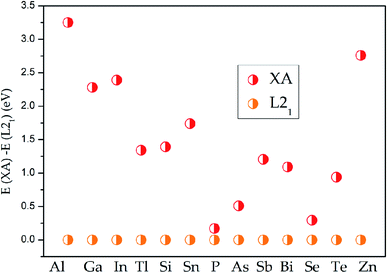Fig. 1 Energy differences between XA and L2₁ states for all the Pd₂CrZ alloys (Z = Al, Ga, In, Tl, Si, Sn, P, As, Sb, Bi, Se, Te, Zn).

Fig. 2 ΔE = E_FM − E_AFM per formula unit as a function of Z (Z = Al, Ga, In, Tl, Si, Sn, P, As, Sb, Bi, Se, Te, Zn) for all the Pd₂CrZ (Z = Al, Ga, In, Tl, Si, Sn, P, As, Sb, Bi, Se, Te, Zn) with L2₁ type structure.

Results and discussion

The phase transition and electronic structures of all-d-metal Pd₂CrZn

Based on above discussion, one can see that Pd₂CrZ prefers to exhibit the L2₁ structure, that is, these main group elements Z locate at Wyckoff site D (0.75, 0.75, 0.75). However, when the Z elements were substituted by the transition metal element Zn, the situation is complicated. We selected Pd₂CrAl_0.75Zn_0.25 as an example: there were two possible formed structures: one structure is that Zn enters the D site where it chemically replaces Al (see Fig. S2(b)†); the other structure is that Zn occupies the Pd (A or C) site and drives some Pd atoms to the D site (see Fig. S2(a)†). The second structure is based on the well-known SPR,^39,40 which the A or C sites prefer to be occupied by the transition metal elements with more valence electrons, here is the Zn atom. According to the energy differences (E_(Zn)D − E_(Zn)A) between the D-site doping and A-site doping for all the Pd₂CrZ_xZn_1−x alloys (x = 0.25, 0.5, 0.75) in Fig. 3, one can see that D-site Zn doping is preferred based on all the negative energy difference. Therefore, it can be inferred that Zn substitution Z does not change the atomic ordering sites (L2₁ structure) of Pd and Cr atoms in Pd₂CrZ_xZn_1−x, which can be explained by the filled 3d shell of Zn.^30–32 This is different from some other 3d transition metals such as Co. For instance, in Co-doped Mn₂NiGa, Co enters the Mn (A) site and drives Mn to the Ga (D) site.⁴¹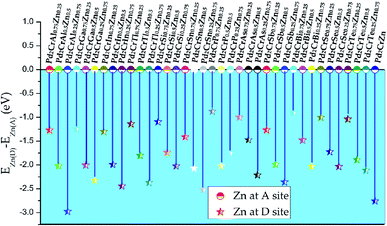

Fig. 3 The total energy differences between the alloys with Zn doping atoms at D site and at A site for all the Pd₂CrZ alloys (Z = Al, Ga, In, Tl, Si, Sn, P, As, Sb, Bi, Se, Te, Zn).

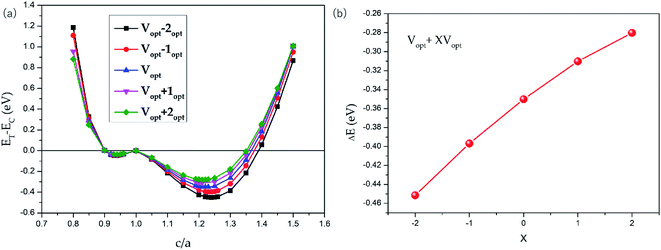
The possible L2₁ and L1₀ phase competition for all-d-metal Pd₂CrZn alloys have been carried out. The tetragonal strain was added to the L2₁-type cubic crystal to obtain the L1₀ tetragonal structure (see Fig. S3†). As shown in Fig. 4, via the tetragonal deformation, one can see that Pd₂CrZn has two local minimums of energy: one at c/a < 1 and the other at c/a > 1, indicating the stable tetragonal states of Pd₂CrZ than cubic states. The local minimum of shallow energy at c/a = ∼0.94 indicates the existence of the metastable phase here. The deeper energy local minimum occurs at c/a = ∼1.22 is about 0.35 eV energy difference. Moreover, changing of the uniform strain can tune the ΔE_M. In Fig. 4, we also plotted some phase transitions in different volumes, V_opt + X% V_opt (X = −2, −1, 0, 1, 2). One can see that the absolute values of energy difference (E_T − E_C) gradually increases from approximately 0.28 eV to 0.45 eV with X varying from +2 to −2, reflecting that the tetragonal L1₀ states become more and more stable with the volume reduction. In addition, the tetragonal L1₀ state occurs at around c/a = 1.2–1.3, similar to the normal tetragonal Heusler alloy Ni₂MnGa.²³

Fig. 4 (a) Total energies as functions of the c/a ratio for tetragonal Pd₂CrZn with contraction/expansion of the unit cell volume. The zero point of the total energy was set as the energy of the cubic (c/a = 1). (b) ΔE as functions of the (1 + X%) V_opt (X = −2, −1, 0, 1, 2) for Pd₂CrZn.

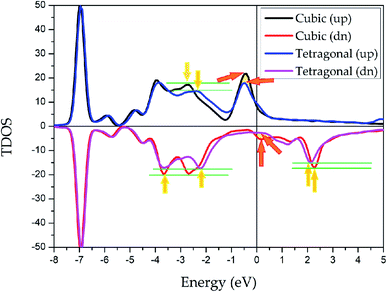
To explore the stability of tetragonal L1₀ state of Pd₂CrZ, we utilized the density of states (DOSs), including the total density of states (TDOSs) and partial density of states (PDOSs), to make a detailed discussion. Pd₂CrZn alloy was selected as an example and its TDOSs and PDOSs in both cubic and tetragonal states are shown in Fig. 5 and 6. Just considering the TDOSs in or at the vicinity of the Fermi level (E_F), smoother DOSs and lower peaks in the L1₀-state can be seen as an evidence that the tetragonal state⁴² is more stable than the cubic state of Pd₂CrZn. Further, whether in tetragonal or cubic phases, the d states of Zn mostly locate in a lower DOS region around −7 eV. Therefore, differ from other transition metal atoms, such as Mn and Co, in Heusler alloys, the direct hybridization between the d electrons of the Zn and Pd (Cr) atoms can be ignored. This also indicates that the Zn atoms behave as the main group elements near E_F. Meanwhile, the DOSs of Pd atoms are nearly symmetrical in both spin channels for the L2₁ and L1₀ states. Hence, the magnetic moments of Pd and Zn atoms are quite small. The main contribution to total magnetic moments is coming form the Cr atoms due to their strong spin splitting around the E_F. All the possible phase transitions as well as total and atomic magnetic moments of Pd₂CrZ were also calculated, and the results are shown in Tables S1 and S2.† In addition, during the tetragonal deformation, the c/a ratios for most of the Pd₂Cr-based alloys are approximately 1.2–1.3, while a small part exceeded 1.4, such as in the Pd₂CrSn and Pd₂CrP alloys.

Fig. 5 Total density of states (TDOSs) of Pd₂CrZn alloy in cubic and tetragonal phases.

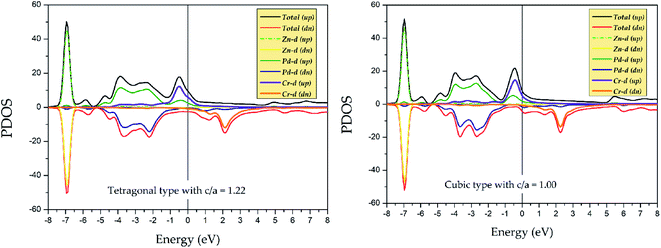Fig. 6 Partial density of states (PDOSs) of Pd₂CrZn alloy in tetragonal (c/a = 1.22) and cubic phases.

Zn doping of Pd₂Cr-based full-Heusler alloys: from normal to all-d-metal Heusler

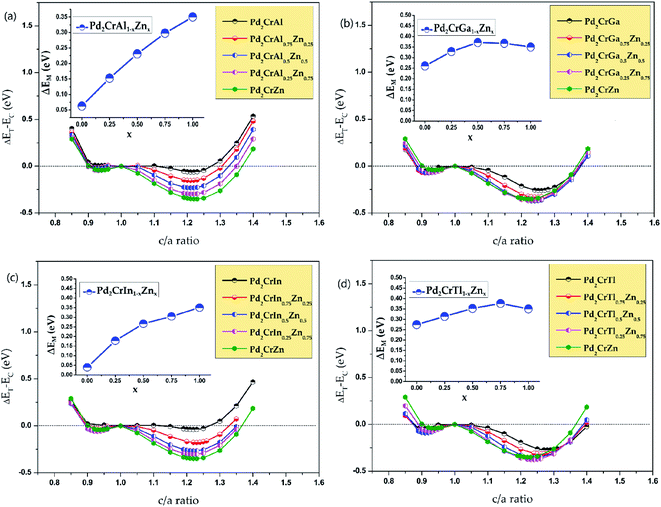
After studying the all-d-metal Heusler alloy Pd₂CrZn, the normal Heusler alloys Pd₂CrZ (Z = Al, Ga, In, Tl, Si, Sn, P, As, Sb, Bi, Se, Te) doping with Zn atom will now be further studied. Zn doping with varying degrees of 25%, 50%, 75% and 100% on the Z (D) site are investigated for all the Pd₂CrZ alloys, and the results are exhibited in Fig. 7 and S4.† There are three situations after Zn doping during the tetragonal deformation. (i) One is the degree of tetragonal transformation is enhanced; that is, the more stable L1₀ state was found during Zn doping. For Pd₂CrZ (Z = Al, Ga, In, Tl, Si, As, Te), a more stable state occurred at certain concentrations of Zn doping (see Fig. 7), reflecting that Zn doping in Pd₂CrZ (Z = Al, Ga, In, Tl, Si, As, Te) can increase the martensitic transformation temperature.³² (ii) For some normal Heusler alloys, such as Pd₂CrZ (Z = Sn, Sb, Bi) (see Fig. S4(b), (e) and (f)†), doping Zn in Pd₂CrZ (Z = Sn, Sb, Bi) can induce martensitic transformation. (iii) For the Pd₂CrP and Pd₂CrSe alloys (see Fig. S4(c) and (g)†), although the ΔE_M decreases during the Zn doping, the large unreachable c/a ratios may be regulated to a more reasonable range. In detail, the c/a ratios of Pd₂CrP and Pd₂CrSe are relatively large, approximately 1.5, which may not easy to achieve experimentally. As shown in Fig. S5,† the different degree of Zn doping as functions of the c/a ratio of Pd₂CrSe_1−xZn_x and Pd₂CrP_1−xZn_x are plotted as examples. From this, it can be seen that doping Zn in Pd₂CrP and Pd₂CrSe can gradually adjust the c/a ratio to a lower value, which may be easy to achieve experimentally.

Fig. 7 The total energy differences between tetragonal and cubic states as functions of the c/a ratio of different amount of Zn doping in Pd₂CrZ (Z = Al, Ga, In, and Tl). The zero point of the total energy was set as the energy of the cubic states (c/a = 1).

Finally, the phonon spectrums have been calculated and the stability of tetragonal Pd₂Cr-based Heusler alloys with different amounts of Zn doping was examined. Take the Pd₂CrAl_xZn_1−x system (see Fig. S6†) as an example, the absence of a virtual frequency guarantees the stability of the tetragonal state of Pd₂CrAl with increasing Zn content on the D site (see Fig. 8). Therefore, the tetragonal L1₀ states of Pd₂CrAl_xZn_1−x are structurally stable. Unfortunately, the possible L2₁–L1₀ phase transition of Pd₂CrZ have not been studied experimentally, and therefore, a comparison between the theoretical and experimental results can not be exhibited in this manuscript. However, the current study can help to understand the physics in all-d-metal alloys and to design new MSMAs in them. Furthermore, we would like point out that Bain paths are a sophisticated way⁴³ to investigate the reversible transformation between the L2₁ and L1₀ phases during the tetragonal distortion. This method has been widely used to design new MSMAs, some designed MSMAs have been experimentally verified, such as Mn–Ni–Co–Ti system.^22,29

Fig. 8 The calculated phonon energies of Pd₂CrAl (a), Pd₂CrAl_0.75Zn_0.25 (b), Pd₂CrAl_0.5Zn_0.5 (c), Pd₂CrAl_0.25Zn_0.75 (d) and Pd₂CrZn (e).

Conclusions

In this manuscript, we studied the effect of Zn doping on the phase transition and electronic structures of Heusler-type Pd₂Cr-based alloys based on spin-polarized first-principles calculations and the following conclusions were obtained:

(i) The L2₁ and XA competition of full-Heusler Pd₂CrZ Heusler alloys were examined, indicating that the L2₁ type is the stable atomic ordering than XA type for Pd₂CrZ Heusler alloys;

(ii) The FM and AFM magnetic states of the L2₁ type Pd₂CrZ Heusler alloys were discussed, and we found that all these alloys are in FM state;

(iii) In Pd₂CrZ_1−xZn_x, the Zn atom behaves similarly to the main group element Z, which is usually located at the D position, and the phenomenon of this mechanism is that the full 3d-shell of Zn atom. With the help of the calculated PDOS, in which the d state of Zn is quite far from the E_F. Thus, only the s and p states of Zn are located near the E_F to hybridize with the transition metal elements Pd and Cr;

(iv) The possible martensitic transition can be found in all-d-metal Pd₂CrZn alloys, and the austenite-martensitic energy difference ΔE_M in Pd₂CrZn can be regulated by uniform strain;

(v) The strong spin splitting of Cr atom around the E_F makes mainly contribution to the total magnetic moment of Pd₂CrZn. A lower DOSs around the E_F was used to explain the stability of the tetragonal state existed in Pd₂CrZn;

(vi) The martensitic transition and magnetism of Zn-doped Heusler alloys Pd₂CrZ_1−xZn_x (x = 0, 0.25, 0.5, 0.75, 1) were investigated, we found the ΔE_M or c/a ratio in Pd₂CrZ_1−xZn_x can be tuned on demand with the doping of Zn atoms;

(vii) The calculated phonon spectrums can be seen as a evidence for the stability of the tetragonal state of the Pd₂CrAl_xZn_1−x system;

(viii) Finally, it is hoped that all-d-metal alloys can receive some more attention from researchers; we firmly believe that there may be many other novel physical properties in all-d-metal alloys.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors declare no competing financial interest and this research was funded by the National Natural Science Foundation of China (grant No. 51801163).

References

1. V. Franco, J. . S. Blázquez and A. Conde, Appl. Phys. Lett., 2006, 89, 222512.
2. O. Gutfleisch, M. A. Willard, E. Brück, C. H. Chen, S. G. Sankar and J. P. Liu, Adv. Mater., 2011, 23, 821–842.
3. R. Kainuma, Y. Imano, W. Ito, Y. Sutou, H. Morito, S. Okamoto and K. Ishida, Nature, 2006, 439, 957.
4. O. Heczko, A. Sozinov and K. Ullakko, IEEE Trans. Magn., 2000, 36, 3266–3268.
5. H. D. Chopra, C. Ji and V. V. Kokorin, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, R14913.
6. S. A. Khandy, I. Islam, D. C. Gupta and A. Laref, J. Solid State Chem., 2019, 270, 173–179.
7. I. Galanakis and E. Şaşıoğlu, Appl. Phys. Lett., 2011, 99, 052509.
8. I. Galanakis, K. Özdoğan and E. Şaşıoğlu, Appl. Phys. Lett., 2013, 103, 142404.
9. X. Wang, Z. Cheng, G. Liu, X. Dai, R. Khenata, L. Wang and A. Bouhemadou, IUCrJ, 2017, 4, 758–768.
10. Y. J. Zhang, Z. H. Liu, Z. G. Wu and X. Q. Ma, IUCrJ, 2019, 6, 610–618.
11. Y. Feng, X. Chen, T. Zhou, H. Yuan and H. Chen, Appl. Surf. Sci., 2015, 346, 1–10.
12. W. Q. Zhao, X. F. Dai, X. M. Zhang, Z. J. Mo, X. T. Wang, G. F. Chen and G. D. Liu, IUCrJ, 2019, 6, 52–557.
13. G. Qin, W. Wu, S. Hu, Y. Tao, X. Yan, C. Jing and W. Ren, IUCrJ, 2017, 4, 506–511.
14. Z. H. Liu, Z. J. Tang, J. G. Tan, Y. J. Zhang, Z. G. Wu, X. T. Wang and X. Q. Ma, IUCrJ, 2018, 5, 794–800.
15. L. Boumia, F. Dahmane, B. Doumi, D. P. Rai, S. A. Khandy, H. Khachai, H. Meradji, A. H. Reshak and R. Khenata, Chin. J. Phys., 2019, 59, 281–290.
16. M. Wu, Y. Han, A. Bouhemadou, Z. Cheng, R. Khenata, M. Kuang and H. Yuan, IUCrJ, 2019, 6, 218–225.
17. L. Bainsla and K. G. Suresh, Appl. Phys. Rev., 2016, 3, 031101.
18. L. Bainsla, A. I. Mallick, M. M. Raja, A. K. Nigam, B. C. S. Varaprasad, Y. K. Takahashi and K. Hono, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 104408.
19. Z. Y. Wei, E. K. Liu, J. H. Chen, Y. Li, G. D. Liu, H. Z. Luo and G. H. Wu, Appl. Phys. Lett., 2015, 107, 022406.
20. Y. Han, M. Wu, M. Kuang, T. Yang, X. Chen and X. Wang, Results Phys., 2018, 11, 1134–1141.
21. Z. Y. Wei, E. K. Liu, Y. Li, X. L. Han, Z. W. Du, H. Z. Luo and G. H. Wu, Appl. Phys. Lett., 2016, 109, 071904.
22. Z. Y. Wei, W. Sun, Q. Shen, Y. Shen, Y. F. Zhang, E. K. Liu and J. Liu, Appl. Phys. Lett., 2019, 114, 101903.
23. S. Özdemir Kart, M. Uludogan, I. Karaman and T. Çagın, Phys. Status Solidi A, 2008, 205, 1026–1035.
24. Z. H. Liu, M. Zhang, Y. T. Cui, Y. Q. Zhou, W. H. Wang, G. H. Wu and G. Xiao, Appl. Phys. Lett., 2003, 82, 424–426.
25. K. Oikawa, T. Ota, F. Gejima, T. Ohmori, R. Kainuma and K. Ishida, Mater. Trans., 2001, 42, 2472–2475.
26. G. D. Liu, J. L. Chen, Z. H. Liu, X. F. Dai, G. H. Wu, B. Zhang and X. X. Zhang, Appl. Phys. Lett., 2005, 87, 262504.
27. T. Omori, K. Watanabe, R. Y. Umetsu, R. Kainuma and K. Ishida, Appl. Phys. Lett., 2009, 95, 082508.
28. L. Muldawer, J. Appl. Phys., 1966, 37(5), 2062–2066.
29. Z. Ni, X. Guo, X. Liu, Y. Jiao, F. Meng and H. Luo, J. Alloys Compd., 2019, 775, 427–434.
30. A. Dannenberg, M. Siewert, M. E. Gruner, M. Wuttig and P. Entel, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 214421.
31. L. S. Barton, R. T. Lazott and E. R. Marsten, J. Appl. Phys., 2014, 115, 17A908.
32. Z. Ni, X. Guo, Q. Li, Z. Liang, H. Luo and F. Meng, J. Magn. Magn. Mater., 2018, 464, 65–70.
33. R. G. Parr, Density functional theory of atoms and molecules, Horizons of Quantum Chemistry, Springer, Dordrecht, 1980, pp. 5–15.
34. J. Hafner, Comput. Phys. Commun., 2007, 177, 6–13.
35. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
37. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
38. J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 63, 245407.
39. X. Wang, Z. Cheng, H. Yuan and R. Khenata, J. Mater. Chem. C, 2017, 5, 11559–11564.
40. S. A. Khandy and J. D. Chai, J. Magn. Magn. Mater., 2019, 487, 165289.
41. L. Ma, W. H. Wang, C. M. Zhen, D. L. Hou, X. D. Tang, E. K. Liu and G. H. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 224404.
42. Y. Han, M. Wu, Y. Feng, Z. Cheng, T. Lin, T. Yang and X. Wang, IUCrJ, 2019, 6, 465–472.
43. Z. Wen, H. Hou, J. Tian, Y. Zhao, H. Li and P. Han, Intermetallics, 2018, 92, 15–19.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra02951c

‡ These authors contributed equally to this work.

---