Open Access Article
Open Access ArticleFe3+/Nb5+ Co-doped rutile–TiO2 nanocrystalline powders prepared by a combustion process: preparation and characterization and their giant dielectric response
Theeranuch Nachaithonga,
Pairot Moontragoon *bcd,
Narong Chanleke and
Prasit Thongbai
*bcd,
Narong Chanleke and
Prasit Thongbai d
d
aMaterials Science and Nanotechnology Program, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand
bInstitute of Nanomaterials Research and Innovation for Energy (IN-RIE), Research Network of NANOTEC-KKU (RNN), Khon Kaen University, Khon Kaen 40002, Thailand. E-mail: mpairo@kku.ac.th
cThailand Center of Excellence in Physics, Commission on Higher Education, Bangkok, 10400, Thailand
dDepartment of Physics, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand
eSynchrotron Light Research Institute (Public Organization), 111 University Avenue, Muang District, Nakhon Ratchasima 30000, Thailand
First published on 30th June 2020
Abstract
Fe3+/Nb5+ co-doped TiO2 (FeNb-TO) nanocrystalline powders were prepared by a combustion process. A pure rutile–TiO2 phase of powders and sintered ceramics with a dense microstructure was achieved. Both co-dopants were homogeneously dispersed in the ceramic microstructure. The presence of oxygen vacancies was confirmed by Raman and X-ray photoelectron spectroscopy techniques. The low-frequency dielectric permittivity enhanced as co-doping concentration increased. The thermally activated giant-dielectric relaxation of FeNb-TO ceramics was observed. Removing the outer-surface layer had a slight effect on the dielectric properties of FeNb-TO ceramics. Density functional theory (DFT) calculation showed that, in the energy preferable configuration, the 2Fe atoms are located near the oxygen vacancy, forming a triangle-shaped FeVoTi defect complex. This defect cluster was far away from the diamond-shaped 2Nb2Ti defect complex. Thus, the electron-pinned defect-dipoles (EPDD) cannot be formed. The giant-dielectric relaxation process of the FeNb-TO ceramics might be attributed to the interfacial polarization associated with electron hopping between Ti3+/Ti4+ ions inside the grains, rather than due to the surface barrier layer capacitor (SBLC) or EPDD effect.
1. Introduction
Giant dielectric oxides that can exhibit dielectric permittivity (ε′) values larger than 103 have intensively been investigated because of their potential applications in electronic devices, e.g., multilayer ceramic capacitors.1–12 Also, the interesting dielectric characteristics of many oxides have stimulated research activity on giant dielectric materials. To clarify the origin of the giant dielectric characteristics, several models have been represented, e.g., nano-barrier layer capacitor, electron-pinned defect-dipole (EPDD), surface barrier layer capacitor (SBLC), internal barrier layer capacitor (IBLC), and polaronic hopping models, as well as the sample-electrode contact effect.1,4,13–17 For the EPDD model, free electrons can be polarized in the defect clusters, giving rise to a high ε′. On the other hand, for the SBLC and IBLC models, the polarization that gives rise to a high ε′ occurs at the internal interfaces between the semiconducting and insulating parts.One of the most interesting giant dielectric oxides is a co-doped TiO2 ceramic system. For example, the In3+/Nb5+ co-doped TiO2 ceramic can exhibit excellent dielectric properties with high ε′ ∼ 6 × 104 and low loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ ≈ 0.02).1,18–20 The dielectric properties of this co-doped TiO2 system ceramics were described as follows: free electrons in the rutile-structure were induced by the substitution of Nb5+ ions. These free electrons would be confined in the clusters of defects, which associated with In3+ doping ions.1 This mechanism was referred to as an EPDD model.1 Under an applied electric field, free electrons can be polarized in a local structure, leading to an extremely increased ε′ with a low tan
δ ≈ 0.02).1,18–20 The dielectric properties of this co-doped TiO2 system ceramics were described as follows: free electrons in the rutile-structure were induced by the substitution of Nb5+ ions. These free electrons would be confined in the clusters of defects, which associated with In3+ doping ions.1 This mechanism was referred to as an EPDD model.1 Under an applied electric field, free electrons can be polarized in a local structure, leading to an extremely increased ε′ with a low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ.
δ.
Up to now, the giant dielectric properties of several co-doped rutile–TiO2 systems have been investigated, e.g., Yb3+/Nb5+,21 Zr4+/Nb5+,10 Zn2+/Nb5+,22 Al3+/Nb5+,23 Ga3+/Nb5+,13 V3+/Ta5+,24 Sm3+/Ta5+,25 Bi3+/Nb5+,26 Ga3+/Sb3+,27 and Ga3+/Ta5+.28 Almost systems showed very large ε′ and low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ. The cause(s) of such an excellent dielectric response was described using different models.1,13,14,18,23,26,28 The EPDD model was proposed and used to reasonably described the giant dielectric properties in many co-doped TiO2 systems.1,25,29,30 According to the micro-contact I–V measurements and impedance spectroscopy analysis,31,32 it was clearly shown that the In3+/Nb5+ co-doped TiO2 ceramic was electrical heterogeneous. The resistance of the grain boundary was very large, while the grain was a semiconductor. Hence, the giant dielectric response with a low tan
δ. The cause(s) of such an excellent dielectric response was described using different models.1,13,14,18,23,26,28 The EPDD model was proposed and used to reasonably described the giant dielectric properties in many co-doped TiO2 systems.1,25,29,30 According to the micro-contact I–V measurements and impedance spectroscopy analysis,31,32 it was clearly shown that the In3+/Nb5+ co-doped TiO2 ceramic was electrical heterogeneous. The resistance of the grain boundary was very large, while the grain was a semiconductor. Hence, the giant dielectric response with a low tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ in the In3+/Nb5+ co-doped TiO2 ceramics was attributed to the grain boundary capacitance effect following the IBLC model. Furthermore, it was also demonstrated that the resistive outer surface layer showed a great influence on the excellent dielectric properties,14,18,28,33 following the SBLC model. Therefore, the mechanism that gives rise to the enhanced dielectric properties of these ceramic systems was likely unclear now. Both experimental and theoretical studies should be simultaneously performed. Besides these co-doped TiO2 systems, investigation to seek a new co-doped TiO2 system is also important for future applications.
δ in the In3+/Nb5+ co-doped TiO2 ceramics was attributed to the grain boundary capacitance effect following the IBLC model. Furthermore, it was also demonstrated that the resistive outer surface layer showed a great influence on the excellent dielectric properties,14,18,28,33 following the SBLC model. Therefore, the mechanism that gives rise to the enhanced dielectric properties of these ceramic systems was likely unclear now. Both experimental and theoretical studies should be simultaneously performed. Besides these co-doped TiO2 systems, investigation to seek a new co-doped TiO2 system is also important for future applications.
According to the previous work,34 it was found that the Fe and Nb dopants can produce Ti3+ donor levels and trap states in the TiO2 structure. The creation of the shallow states had a significant effect on charge carrier transport via electron hopping and trapping/de-trapping. Thus, the Fe and Nb doping ions have an essential influence on the electronic conduction by increasing electron density. Thus, it is expected that the dielectric properties of Fe and Nb co-doped TiO2 ceramics could be obtained since the giant dielectric properties of co-doped TiO2 ceramics can be contributed by electron hopping.13
Therefore, in this current study, the dielectric behavior and theoretical calculation of TiO2 ceramics co-doped with Fe3+/Nb5+ ions were done. Experimentally, both powders and sintered ceramics were systematically characterized. The giant dielectric properties at different frequencies and temperatures of this co-doped system were measured to reveal the dielectric relaxation behavior. Theoretically, the density functional theory (DFT) was used to calculate the ground-state structure to know the origin of giant dielectric properties in Fe3+/Nb5+ co-doped TiO2 ceramics. The possible cause of the observed giant dielectric response was discussed.
2. Experimental details
(Fe0.5Nb0.5)xTi1−xO2 (FeNb-TO) nanoparticles (x = 1%, 2.5%, 5.0%, and 10%) as well as TiO2, Fe0.05Ti0.95O2 (Fe-TO), and Nb0.05Ti0.95O2 (Nb-TO) were prepared by a simple sol–gel method. C16H28O6Ti (Sigma-Aldrich), (FeN3O9)·9H2O (Sigma-Aldrich, >99.99%), NbCl5 (Sigma-Aldrich, >99.9%), deionized water, and citric acid were used as the starting raw materials. For each co-doping condition (x), the starting raw materials were weighed according to each chemical formula. First, (FeN3O9)·9H2O and NbCl5 were dissolved in an aqueous solution of 5 wt% citric acid with constant stirring at room temperature (RT). Second, a C16H28O6Ti solution was added into the solution with stirring at 130 °C until a viscous gel was observed. Third, the gel was heated for 1 h at 350 °C. Then, the resulting dried precursors for all doping concentrations were calcined in air at 1000 °C for 6 h using the heating rate of 5 °C min−1. Next, the calcined powders were carefully ground and pressed into pellets with 9.5 mm in diameter and 1.2 mm in thickness. The compressive stress for forming each pellet was ∼10 MPa. Finally, the pellets were sintered at 1400 °C for 5 h in air. The heating and cooling rates were 5 °C min−1.The prepared nanoparticles were characterized by transmission electron microscopy (TEM, FEI/TECNAI G2 20) and X-ray diffraction technique (XRD PANalytical, EMPYREAN). The XRD data were collected in the 2θ range of 20–80° by using a step increase of 0.01° per point. The lattice parameters were calculated using a Cohen's least mean square method. Surface morphologies of the sintered ceramics were characterized by a scanning electron microscopy (SEM) (SEC, SNE4500M). An accelerating voltage for electron microscopy was 20 kV. The distribution of all elements in the FeNb-TO ceramics was revealed using a field-emission scanning electron microscopy (FE-SEM, FEI, Hileos Nanolab G3CX). Raman spectra of sintered ceramics were collected with a UV-vis Raman System (NT-MDT Ntegra Spectra) using laser wavelength of 532 nm. The oxidation states in FeNb-TO ceramics were measured by an X-ray photoelectron spectroscopy (XPS), PHI5000 VersaProbe II, ULVAC-PHI, Japan) at the SUT-NANOTEC-SLRI Joint Research Facility, Synchrotron Light Research Institute (SLRI), Thailand. PHI MultiPak XPS software using Gaussian–Lorentzian lines was used to fit the XPS spectra.
Both sides of sintered ceramics were coated by Au sputtering technique. The dielectric parameters were corrected by a KEYSIGHT E4990A Impedance Analyzer. The measurement was performed in the frequency and temperature ranges of 102 to 106 Hz and −60 to 200 °C using an oscillation voltage of 0.5 V.
The stable configuration of the Fe and Nb co-doped TiO2 was studied using the density functional theory (DFT) implemented in the Vienna Ab initio Simulation Package (VASP). According to the pseudopotential used in this work, the projector augments wave approach and the Perdew–Burke–Ernzerhof (PBE) form of exchange-correlation functional was chosen. The 600 eV plane-wave energy cutoff and 3 × 3 × 3 k-point samplings with Monkhorst–Pack scheme were successfully tested. To move ion to the lowest energy configuration, the conjugate-gradient algorithm was carried out and the force acting on each ion was calculated by the Hellmann–Feynman theorem.
3. Results and discussion
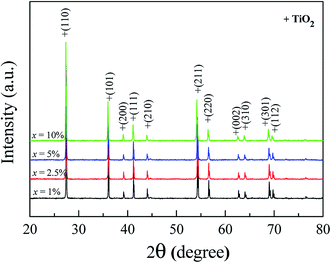
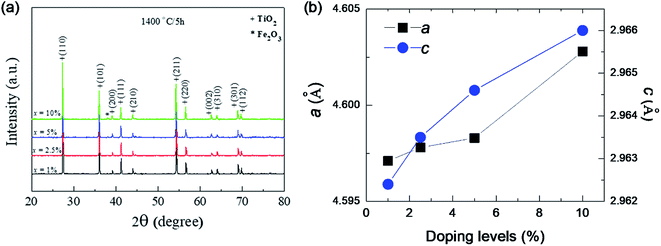
Fig. 1 shows the XRD patterns of FeNb-TO powders (x = 1, 2.5, 5, and 10%), which were calcined at sintered at 1000 °C for 6 h. All the XRD patterns show a single phase of rutile–TiO2. No impurity phase is observed. It was found that lattice parameters (a and c) slightly increased with increasing co-doping concentration. The a values of the 1%, 2.5%, 5%, and 10% co-doped powders were 4.5944, 4.5973, 4.6007, and 4.6070 Å, respectively, while the c values were 2.9625, 2.9626, 2.9643 and 2.9697 Å, respectively. As revealed in Fig. 2, the agglomeration of the FeNb-TO particles were observed with particle sizes of ∼200 nm.The phase formation and crystal structure of the sintered FeNb-TO ceramics were also studied, as illustrated in Fig. 3(a). All the XRD patterns of the FeNb-TO ceramics sintered at 1400 °C for 5 h also show a main phase of TiO2 with a rutile structure. The a values of the sintered ceramics with x = 1, 2.5, 5, and 10% were found to be 4.5971, 4.5978, 4.5983, and 4.6028 Å, respectively. The c values were 2.9624, 2.9635, 2.9646, and 2.9660 Å, respectively. As clearly seen in Fig. 3(b), both a and c values tend to enlarge as the co-doped concentration was increased. This means that Nb and Fe doping ions have substituted into the rutile–TiO2 structure. It is worth noting that the second phase of Fe2O3 was detected in the XRD pattern of the sample with x = 10%. This result may be caused by a high co-doping concentration, which was higher than the limit of solid solution in the TiO2 structure.
 | ||
| Fig. 3 (a) XRD pattern of the as-sintered FeNb-TO ceramics with difference co-doping levels. (b) Lattice parameters (a and c) for all doping levels. | ||
Fig. 4 displays the SEM images of sintered ceramic samples with x = 5% and 10%, revealing the morphologies of the ceramic samples. It is clearly seen that the microstructures of all sintered ceramics are fully dense without pores. It is found that the mean grain size tends to decrease with increasing co-doping concentration. This observation is similar to that observed in the Ga3+/Ta5+ co-doped TiO2.28 This indicates that Fe and Nb doping ions can inhibit the grain growth rate of TiO2.
Fig. 5(a) and (b) show the SEM-mapping images of the FeNb-TO ceramics with x = 5% and 10%, respectively. Both Fe and Nb co-dopants, as well as the major elements, i.e., Ti and O are homogeneously distributed in the microstructure. The cluster of both dopants is not observed in the SEM-mapping images.
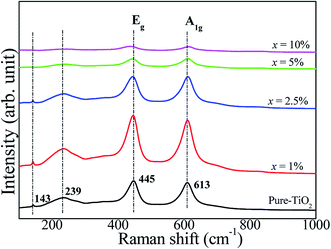
The Raman spectra of pure TiO2 and FeNb-TO ceramics with different co-doping levels were measured, as represented in Fig. 6. The strongest peaks of Eg and A1g modes are detected, which can be indicated to associate with oxygen vacancies and the O–Ti–O bonds, respectively.23 A1g peak very slightly shifted to higher wavenumbers when x > 2.5. Eg peak did not change when x ≤ 5%. Unfortunately, the obtained Raman spectrum of the FeNb-TO ceramic with x = 10% was not clear to justify the peak positions of these two modes. Nevertheless, the overall results showed that the positions of the peaks of Eg and A1g modes did not significantly change. Usually, TiO2−x is much sensitive to oxygen vacancy concentration. Hence, slightly shifting the position of Eg peak to lower a wave number indicated a slight increase in oxygen vacancies. As shown in Fig. 3, the secondary phase of Fe2O3 can be observed in the XRD patterns when x ≥ 2.5%. This result indicated that only a small portion of Fe ions can substitute into Ti site in the TiO2–rutile structure. On the other hand, the shifting of the A1g peak position indicates the influence of Fe and/or Nb on the Ti–O bond, which is owing to the different ionic radii between the host and co-dopant ions.
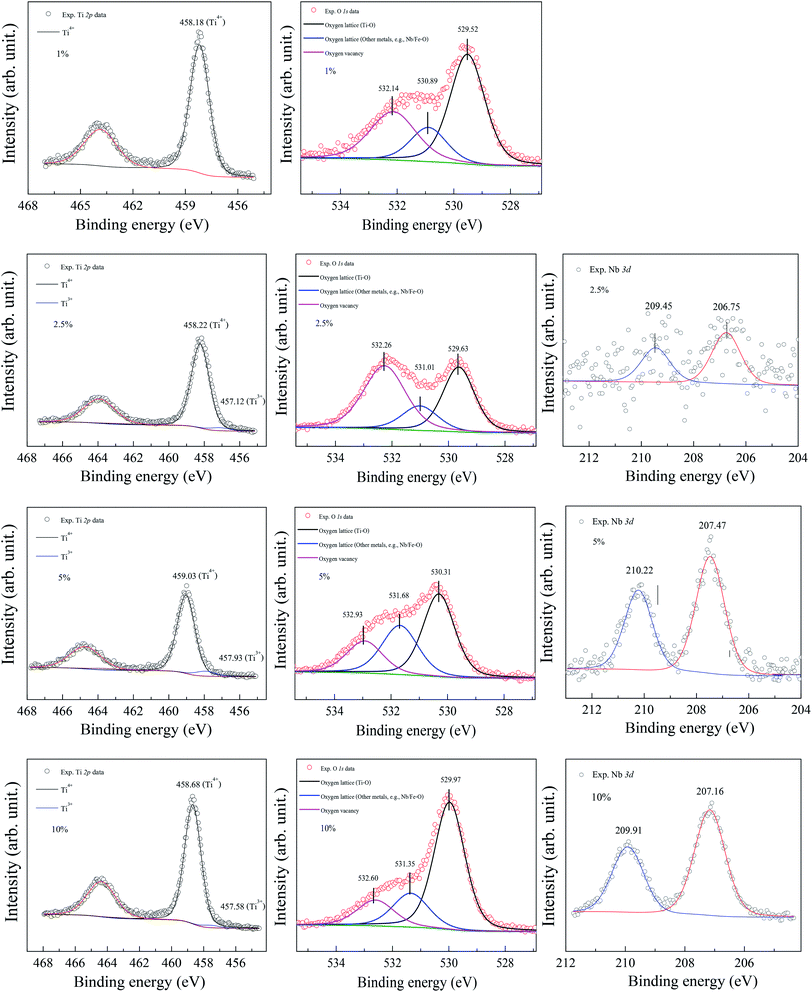
The XPS spectra of all the sintered FeNb-TO sample are shown in Fig. 7. Unfortunately, the Fe peak in all samples cannot be observed. The Nb peak of the x = 1% sample was not also detected in the XPS spectrum. Basically, an oxygen vacancy can be produced in the TiO2 structure by doping with trivalent cation (e.g., Fe3+) for neutral charge compensation. The XPS spectrum of O 1s profiles is shown in Fig. 7. Using the Gaussian–Lorentzian profile fitting, three peaks were separated. The major peak at 529.92 eV is suggested to the oxygen lattice (Ti–O bond).1,35,36 Two peaks located at 531.34 and 532.68 eV are indicated to associated oxygen–cation bonds (e.g., Fe–O and Nb–O bonds) and oxygen vacancies, respectively.1,26,35,36 The presence of oxygen vacancies in FeNb-TO ceramics is confirmed. Also, the binding energies of 3d3/2 and 3d5/2 of Nb 3d electrons are detected at 209.71 and 206.99 eV, respectively. The splitting of the spin-orbit of about 2.72 eV indicates the existence of Nb5+.1 Conduction electrons in TiO2 structure are existed by substitution of Nb5+, following the equations:
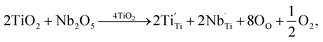 | (1) |
| Ti4+ + e → Ti3+. | (2) |
As demonstrated in Fig. 7, a small amount of Ti3+ is confirmed to exist in FeNb-TO ceramics.
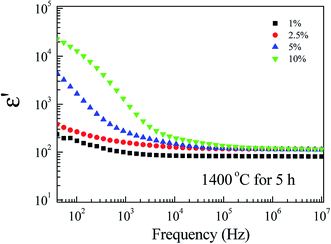
Fig. 8 depicts the frequency dependence of ε′ at RT of FeNb-TO ceramics at RT. Considering in a low-frequency range, ε′ increases with increasing co-doping concentration, whereas, ε′ slightly enhanced in frequencies higher than 104 Hz. tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peaks in a low-frequency range were observed (not shown). The overall dielectric behavior is likely to be the dielectric relaxation behavior. A slight change in ε′ in a high-frequency range indicates that Nb5+ and Fe3+ co-doping ions have a slight influence on the ionic polarization. Note that, in the high-frequency region, the ε′ values of all FeNb-TO ceramics are closed to the ε′ value of pure-rutile TiO2 ceramics. In contrast, the co-dopants have a remarkable effect on the dielectric response in a low-frequency region, which is usually caused by the interfacial polarization at the internal insulating layer that is contacting a semiconducting region. It is important to note that ε′ of FeNb-TO ceramics was lower than that of other co-doped TiO2 systems such as Yb3+/Nb5+,21 Zr4+/Nb5+,10 Zn2+/Nb5+,22 and Al3+/Nb5+.23
δ peaks in a low-frequency range were observed (not shown). The overall dielectric behavior is likely to be the dielectric relaxation behavior. A slight change in ε′ in a high-frequency range indicates that Nb5+ and Fe3+ co-doping ions have a slight influence on the ionic polarization. Note that, in the high-frequency region, the ε′ values of all FeNb-TO ceramics are closed to the ε′ value of pure-rutile TiO2 ceramics. In contrast, the co-dopants have a remarkable effect on the dielectric response in a low-frequency region, which is usually caused by the interfacial polarization at the internal insulating layer that is contacting a semiconducting region. It is important to note that ε′ of FeNb-TO ceramics was lower than that of other co-doped TiO2 systems such as Yb3+/Nb5+,21 Zr4+/Nb5+,10 Zn2+/Nb5+,22 and Al3+/Nb5+.23
To clarify the possible origin of the giant dielectric response in FeNb-TO ceramics, we further studied the temperature dependence of the dielectric properties at different frequencies and temperatures. As clearly seen in Fig. 9, the giant-dielectric relaxation behavior is observed in all FeNb-TO ceramics. Typically, the step-like decrease in ε′ and corresponding tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak shift to high frequencies as temperature increased. This confirmed the thermally-activated giant-dielectric relaxation behavior.37 We have observed that the giant-dielectric relaxation can be induced only in a temperature higher than RT, which would be more dominant in a high-temperature range. This dielectric behavior is not similar to those of other co-doped TiO2 ceramics.3,4,7,9,11,16,18,25,38 Thus, the primary cause of the giant-dielectric relaxation should be different from those of other co-doped TiO2 ceramics. The dielectric relaxation characteristic of the FeNb-TO ceramics is similar to that observed in the Ni1−x(Li1/2+Fe1/23+)xO ceramics.39
δ peak shift to high frequencies as temperature increased. This confirmed the thermally-activated giant-dielectric relaxation behavior.37 We have observed that the giant-dielectric relaxation can be induced only in a temperature higher than RT, which would be more dominant in a high-temperature range. This dielectric behavior is not similar to those of other co-doped TiO2 ceramics.3,4,7,9,11,16,18,25,38 Thus, the primary cause of the giant-dielectric relaxation should be different from those of other co-doped TiO2 ceramics. The dielectric relaxation characteristic of the FeNb-TO ceramics is similar to that observed in the Ni1−x(Li1/2+Fe1/23+)xO ceramics.39
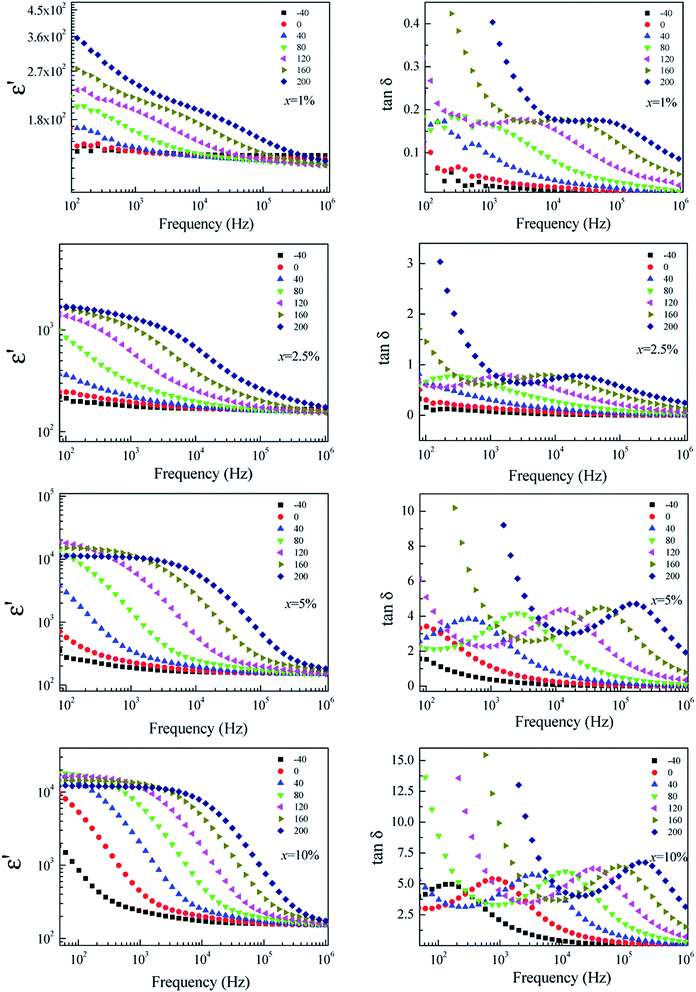 | ||
| Fig. 9 Temperature dependence of the dielectric properties at different frequencies for FeNb-TO ceramics with x = 1%, 2.5%, 5%, and 10%. | ||
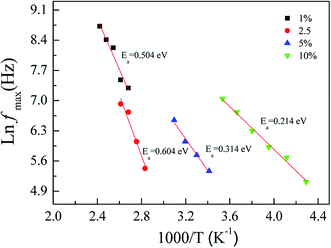
According to the observed dielectric relaxation behavior, the activation energy (Ea) for the relaxation process in the FeNb-TO ceramics can be calculated from the temperature dependence of the relaxation peak of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ (fmax), following the Arrhenius law. Fig. 10 displays the Arrhenius plots of all FeNb-TO ceramics. The activation energy required for the giant-dielectric relaxation in FeNb-TO ceramics was calculated from the slope of the ln
δ (fmax), following the Arrhenius law. Fig. 10 displays the Arrhenius plots of all FeNb-TO ceramics. The activation energy required for the giant-dielectric relaxation in FeNb-TO ceramics was calculated from the slope of the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fmax vs. 1000/T plots. The Ea values of the FeNb-TO ceramics with x = 1%, 2.5%, 5%, and 10% were, respectively, found to be 0.566, 0.604, 0.314, and 0.214 eV. The Ea values with 0.314 and 0.214 eV are closed to the Ea values of other giant dielectric oxides that contain Fe2+/Fe3+ ions such as BiFeO3 (0.325 eV)40 and LuFe2O4 (0.3 eV).41 Furthermore, the Ea = 0.566 and 0.604 eV may be resulted from the second ionization of oxygen vacancies.42 It is important to note that the dielectric relaxation should be associated with the electron hopping between Ti3+/Ti4+ and/or Fe2+/Fe3+ ions. The Ti3+/Ti4+ ratio could be increased with increasing the Nb5+ doping concentration. Therefore, the hopping can easily be activated when the Ti3+ or Fe3+ ions concentration increased, giving rise to a decrease in the Ea values for the FeNb-TO ceramics with x = 5% and 10%.
fmax vs. 1000/T plots. The Ea values of the FeNb-TO ceramics with x = 1%, 2.5%, 5%, and 10% were, respectively, found to be 0.566, 0.604, 0.314, and 0.214 eV. The Ea values with 0.314 and 0.214 eV are closed to the Ea values of other giant dielectric oxides that contain Fe2+/Fe3+ ions such as BiFeO3 (0.325 eV)40 and LuFe2O4 (0.3 eV).41 Furthermore, the Ea = 0.566 and 0.604 eV may be resulted from the second ionization of oxygen vacancies.42 It is important to note that the dielectric relaxation should be associated with the electron hopping between Ti3+/Ti4+ and/or Fe2+/Fe3+ ions. The Ti3+/Ti4+ ratio could be increased with increasing the Nb5+ doping concentration. Therefore, the hopping can easily be activated when the Ti3+ or Fe3+ ions concentration increased, giving rise to a decrease in the Ea values for the FeNb-TO ceramics with x = 5% and 10%.
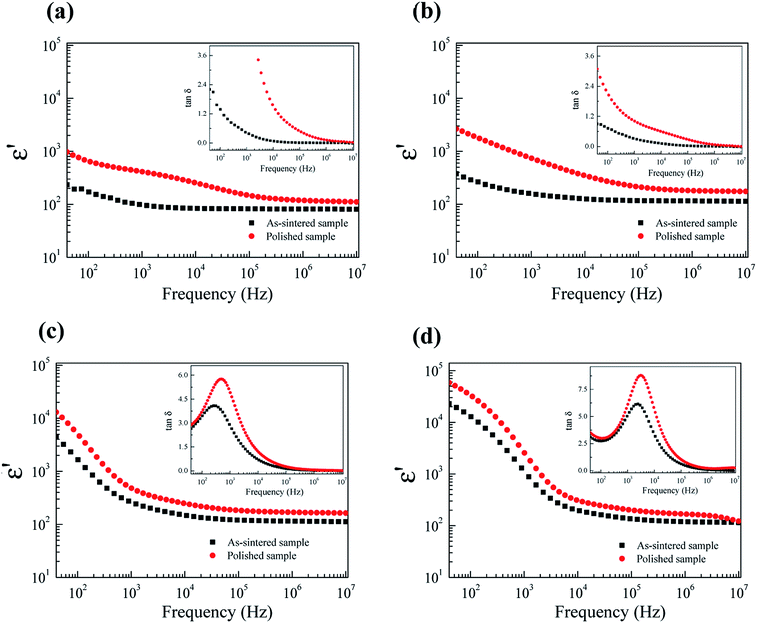
To further clarify the possible origin of the giant-dielectric relaxation in FeNb-TO ceramics, the effect of the outer surface layer on the dielectric properties was investigated since it had a great effect on the giant dielectric response in Ga3+/Ta5+ (ref. 28) and In3+/Nb5+ co-doped TiO2 oxides.14 Generally, the surface layer, which contains additional cations like Mn and Mg shows different element configurations from the core structure. This result may influence the dielectric and electrical properties of the FeNb-TO ceramics. Both sides of the outer surface with 0.5 mm in thickness (for each side) were removed by polishing. After removing the outer surface of the as-sintered samples, the dielectric properties changed significantly, especially for the dielectric properties in a low-frequency range of the FeNb-TO ceramic with x = 1% (Fig. 10). Both of the ε′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ increased. This indicates that the SBLC has a great effect on the overall dielectric properties of FeNb-TO ceramics. Thus, the outer surface layer is one of the most important factors contributing on the overall dielectric properties of FeNb-TO ceramics. The increase in a low-frequency tan
δ increased. This indicates that the SBLC has a great effect on the overall dielectric properties of FeNb-TO ceramics. Thus, the outer surface layer is one of the most important factors contributing on the overall dielectric properties of FeNb-TO ceramics. The increase in a low-frequency tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ indicates the increase in conductivity. Hence, the electrical properties of the outer surface layer of the FeNb-TO ceramics, which were prepared by a chemical method, are insulator compared to the inner core. Nevertheless, the investigation on the structure of the surface layer should be performed in the future work to clarify the different element configurations between the inner core and outer surface layer. Although the exact thickness of the outer surface layer cannot be estimated in this experiment, it was clearly shown that the outer surface layer plays an important role in dielectric responses of the FeNb-TO ceramics.
δ indicates the increase in conductivity. Hence, the electrical properties of the outer surface layer of the FeNb-TO ceramics, which were prepared by a chemical method, are insulator compared to the inner core. Nevertheless, the investigation on the structure of the surface layer should be performed in the future work to clarify the different element configurations between the inner core and outer surface layer. Although the exact thickness of the outer surface layer cannot be estimated in this experiment, it was clearly shown that the outer surface layer plays an important role in dielectric responses of the FeNb-TO ceramics.
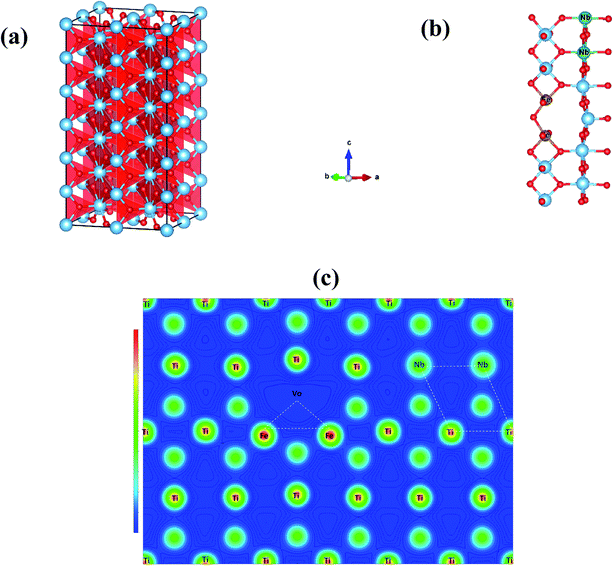
According to the Raman and XPS results, the presence of oxygen vacancies in FeNb-TO ceramics may be originated by Fe3+ ions. Oxygen vacancies and Ti3+ have been proved to occur. Thus, the giant-dielectric relaxation in FeNb-TO ceramics may be originated from the EPDD. To clarify this, calculations were performed using the GGA formalism with the VASP code. Periodic boundary conditions were employed on 2 × 2 × 6 super-cell of the rutile crystallographic unit cell as shown in Fig. 11(a). We firstly created one oxygen vacancy and then replaced two Ti atoms with two Nb atoms and another two Ti atoms with two Fe atoms in rutile TiO2. This structure is defined as 2NbVo2FeTiO2 (Vo stands for the oxygen vacancy). For each configuration, we allowed all atoms to relax fully. Based on our total energy calculations, we used the most stable configurations of 2FeVoTiO2 and 2NbTiO2 to further investigate the lowest energy configuration of the FeNb-TO ceramics, by placing the 2FeVo triangular and 2Nb diamond defects into the TiO2 structure simultaneously in 3 configurations, near opposite and far. When the 2FeVo triangular and 2Nb diamond defects were present in TiO2, the stable structure of 2NbTiO2 as shown in Fig. 11(b), we found that 2Nb atoms preferentially form a diamond-shaped structure. On the basis of total energy, we found that the 2FeVo triangular defect does not prefer to be close to the 2Nb diamond defect, as shown in Fig. 11(c) revealed that the case resulted in the lowest total energy. This result indicates that there is a small coupling between the 2FeVo triangular and 2Nb diamond defects (Fig. 12).
According to the experimental and theoretical investigations, it can be clearly suggested that the giant-dielectric relaxation behavior of FeNb-TO ceramics was not originated from both of the EPDD and IBLC models. Although the SBLC has an effect on the dielectric properties, it was not the primary cause for the observed giant dielectric relaxation in FeNb-TO ceramics. Instead, the electron hopping mechanism between Ti3+ ↔ Ti4+ ions was suggested to the most possible mechanism related to the giant-dielectric relaxation in FeNb-TO ceramics.
4. Conclusions
In the experimental investigation, FeNb-TO powders with pure rutile–TiO2 phase were successfully synthesized by a combustion process. The microstructure of all the sintered ceramics with homogeneous dispersion of dopants was highly dense microstructure without porosity. The presence of oxygen vacancies was confirmed by Raman and XPS techniques. The FeNb-TO ceramics exhibited the thermally activated giant-dielectric relaxation above RT. It was clearly shown that the outer surface layer had a little influence on giant-dielectric relaxation. Obviously, both the IBLC and SBLC effects cannot be used to clearly explain the dielectric behavior of FeNb-TO ceramics. In the theoretical investigation, we also used the density functional theory (DFT) to calculate the ground state structure to know the origin of colossal dielectric properties in the FeNb-TO ceramic by replacing four atoms Ti with two atoms of Fe and two atoms of Nb. An oxygen vacancy was introduced into the system. The calculation results showed that, in the energy preferable configuration, the 2Fe atoms are located near the oxygen vacancy and far away from the 2Nb atoms. These structures can form 2Nb2Ti diamond shape and FeVoTi triangle shape. Thus, the electron-pinned defect-dipoles cannot be formed in the FeNb-TO structure. Finally, we can suggest that the giant-dielectric relaxation behavior of FeNb-TO ceramics was not originated from both of the EPDD and IBLC/SBLC. The electron hopping mechanism was suggested to the most possible mechanism related to the giant-dielectric relaxation in FeNb-TO ceramics.Conflicts of interest
There is no conflicts to declare.Acknowledgements
This work has been supported by the Research Network NANOTEC (RNN) program of the National Nanotechnology Center (NANOTEC), NSTDA, Ministry of Higher Education, Science, Research and Innovation (MHESI) and Khon Kaen University, Thailand. The authors would like to thank the SUT-NANOTEC-SLRI (BL5.1) Joint Research Facility for use of their XPS facility. T. Nachaithong would like to thank the Thailand Research Fund under The Royal Golden Jubilee PhD Program [Grant Number PHD/0114/2559] for his PhD scholarship.References
- W. Hu, Y. Liu, R. L. Withers, T. J. Frankcombe, L. Norén, A. Snashall, M. Kitchin, P. Smith, B. Gong, H. Chen, J. Schiemer, F. Brink and J. Wong-Leung, Nat. Mater., 2013, 12, 821–826 CrossRef CAS PubMed.
- B. Guo, P. Liu, X. Cui and Y. Song, Ceram. Int., 2018, 44, 12137–12143 CrossRef CAS.
- Y. Yu, Y. Zhao, T.-D. Zhang, R.-X. Song, Y.-L. Zhang, Y.-L. Qiao, W.-L. Li and W.-D. Fei, Ceram. Int., 2018, 44, 6866–6871 CrossRef CAS.
- X. W. Wang, B. H. Zhang, L. Y. Sun, W. N. Qiao, Y. D. Hao, Y. C. Hu and X. E. Wang, J. Alloys Compd., 2018, 745, 856–862 CrossRef CAS.
- Y. Yu, W.-L. Li, Y. Zhao, T.-D. Zhang, R.-X. Song, Y.-L. Zhang, Z.-Y. Wang and W.-D. Fei, J. Eur. Ceram. Soc., 2018, 38, 1576–1582 CrossRef CAS.
- B. Shang, P. Liang, F. Li, X. Chao, L. Wei and Z. Yang, J. Alloys Compd., 2017, 704, 64–69 CrossRef CAS.
- B. Guo, P. Liu, X. Cui and Y. Song, J. Alloys Compd., 2018, 740, 1108–1115 CrossRef CAS.
- Y. Song, P. Liu, X. Zhao, B. Guo and X. Cui, J. Alloys Compd., 2017, 722, 676–682 CrossRef CAS.
- X.-g. Zhao and P. Liu, J. Alloys Compd., 2017, 715, 170–175 CrossRef CAS.
- Y. Chao, W. Xianhua and H. Jianhua, J. Am. Ceram. Soc., 2018, 101, 307–315 CrossRef.
- Z. Li, X. Luo, W. Wu and J. Wu, J. Am. Ceram. Soc., 2017, 100, 3004–3012 CrossRef CAS.
- L. Zhenwei, L. Xuan, W. Wenjuan and W. Jiagang, J. Am. Ceram. Soc., 2017, 100, 3004–3012 CrossRef.
- W. Dong, W. Hu, A. Berlie, K. Lau, H. Chen, R. L. Withers and Y. Liu, ACS Appl. Mater. Interfaces, 2015, 7, 25321–25325 CrossRef CAS PubMed.
- T. Nachaithong, P. Kidkhunthod, P. Thongbai and S. Maensiri, J. Am. Ceram. Soc., 2017, 100, 1452–1459 CrossRef CAS.
- W. Tuichai, P. Srepusharawoot, E. Swatsitang, S. Danwittayakul and P. Thongbai, Microelectron. Eng., 2015, 146, 32–37 CrossRef CAS.
- X. Zhu, L. Yang, J. Li, L. Jin, L. Wang, X. Wei, Z. Xu and F. Li, Ceram. Int., 2017, 43, 6403–6409 CrossRef CAS.
- W. C. Ribeiro, E. Joanni, R. Savu and P. R. Bueno, Solid State Commun., 2011, 151, 173–176 CrossRef CAS.
- W. Tuichai, S. Danwittayakul, N. Chanlek, P. Srepusharawoot, P. Thongbai and S. Maensiri, RSC Adv., 2017, 7, 95–105 RSC.
- J. Li, Z. Xu, F. Li, X. Zhu and S. Zhang, RSC Adv., 2016, 6, 20074–20080 RSC.
- W. Tuichai, S. Danwittayakul, S. Maensiri and P. Thongbai, RSC Adv., 2016, 6, 5582–5589 RSC.
- X.-g. Zhao and P. Liu, J. Am. Ceram. Soc., 2017, 100, 3505–3513 CrossRef CAS.
- N. Thongyong, W. Tuichai, N. Chanlek and P. Thongbai, Ceram. Int., 2017, 43, 15466–15471 CrossRef CAS.
- W. Hu, K. Lau, Y. Liu, R. L. Withers, H. Chen, L. Fu, B. Gong and W. Hutchison, Chem. Mater., 2015, 27, 4934–4942 CrossRef CAS.
- W. Tuichai, S. Danwittayakul, N. Chanlek and P. Thongbai, J. Alloys Compd., 2017, 725, 310–317 CrossRef CAS.
- Z. Li, J. Wu and W. Wu, J. Mater. Chem. C, 2015, 3, 9206–9216 RSC.
- X. Cheng, Z. Li and J. Wu, J. Mater. Chem. A, 2015, 3, 5805–5810 RSC.
- J. Fan, S. Leng, Z. Cao, W. He, Y. Gao, J. Liu and G. Li, Ceram. Int., 2018, 45, 1001–1010 CrossRef.
- W. Tuichai, N. Thongyong, S. Danwittayakul, N. Chanlek, P. Srepusharawoot, P. Thongbai and S. Maensiri, Mater. Des., 2017, 123, 15–23 CrossRef CAS.
- X. Wei, W. Jie, Z. Yang, F. Zheng, H. Zeng, Y. Liu and J. Hao, J. Mater. Chem. C, 2015, 3, 11005–11010 RSC.
- W. Dong, W. Hu, T. J. Frankcombe, D. Chen, C. Zhou, Z. Fu, L. Candido, G. Hai, H. Chen, Y. Li, R. L. Withers and Y. Liu, J. Mater. Chem. A, 2017, 5, 5436–5441 RSC.
- J. Li, F. Li, C. Li, G. Yang, Z. Xu and S. Zhang, Sci. Rep., 2015, 5, 8295 CrossRef CAS PubMed.
- Y. Q. Wu, X. Zhao, J. L. Zhang, W. B. Su and J. Liu, Appl. Phys. Lett., 2015, 107, 242904 CrossRef.
- T. Nachaithong, P. Thongbai and S. Maensiri, J. Eur. Ceram. Soc., 2017, 37, 655–660 CrossRef CAS.
- C.-T. Wang, H.-S. Lin and W.-P. Wang, Mater. Sci. Semicond. Process., 2019, 99, 85–91 CrossRef CAS.
- G. Liu, H. Fan, J. Xu, Z. Liu and Y. Zhao, RSC Adv., 2016, 6, 48708–48714 RSC.
- M.-Y. Tse, X. Wei and J. Hao, Phys. Chem. Chem. Phys., 2016, 18, 24270–24277 RSC.
- Y. Lin, L. Jiang, R. Zhao and C.-W. Nan, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 014103 CrossRef.
- W. Tuichai, S. Danwittayakul, N. Chanlek, P. Thongbai and S. Maensiri, J. Alloys Compd., 2017, 703, 139–147 CrossRef CAS.
- P. Thongbai, T. Yamwong and S. Maensiri, Appl. Phys. Lett., 2009, 94, 152905 CrossRef.
- S. Hunpratub, P. Thongbai, T. Yamwong, R. Yimnirun and S. Maensiri, Appl. Phys. Lett., 2009, 94, 062904 CrossRef.
- N. Ikeda, H. Ohsumi, K. Ohwada, K. Ishii, T. Inami, K. Kakurai, Y. Murakami, K. Yoshii, S. Mori, Y. Horibe and H. Kitô, Nature, 2005, 436, 1136 CrossRef CAS PubMed.
- Z. Wang, X. M. Chen, L. Ni, Y. Y. Liu and X. Q. Liu, Appl. Phys. Lett., 2007, 90, 102905 CrossRef.
| This journal is © The Royal Society of Chemistry 2020 |