Split or slip – passive generation of monodisperse double emulsions with cores of varying viscosity in microfluidic tandem step emulsification system

Abstract

We investigate the role of viscosities on the formation of double emulsion in a microfluidic step emulsification system. Aqueous droplets of various viscosities and sizes were engulfed in fluorocarbon oil and subsequently transformed into double droplets in the microfluidic step emulsifying device. We identify two distinct regimes of double droplet formation: (i) core droplets split into multiple smaller droplets, or (ii) cores slip whole into the forming oil shell. We show that the viscosity ratio of the core and shell phases plays a crucial role in determining the mode of formation of the double emulsions. Finally, we demonstrate that high viscosity of the core droplet allows for generation of double emulsions with constant shell thickness for cores of various sizes.

---

Introduction

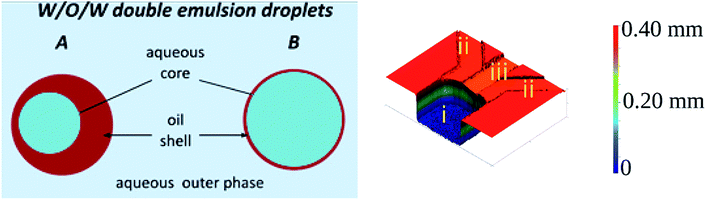
Double emulsions are liquid dispersion systems that are collections of double droplets. Double droplet is a droplet of one liquid engulfed in larger droplets of immiscible liquid and suspended in a third (outer) liquid.¹ For example, water-in-oil-in-water double emulsion (W/O/W DE) is composed of an aqueous (core) droplet nested in an oil droplet (shell), which is suspended in a continuous aqueous phase (see Fig. 1, left panel). Double droplets may contain one or more cores, of the same or various liquids.² Emulsions of higher orders can also be made by engulfing multiple layers of immiscible liquids.^1,3 Double emulsions are of high importance in pharmaceutical, cosmetic and food industries to encapsulate reactive or sensitive ingredients,^4–6 or in biotechnological research where they serve as containers to prepare high throughput screening assays,^7–10 templates for capsules and vesicles,^11,12 or models of lipid membranes within multisomes.¹³ In all of these applications the long term stability of the double emulsion, which largely depends on the structural properties of the double droplets,¹⁴ is of paramount importance. The two important structural parameters are the uniformity (monodispersity) of droplet's sizes and the shell thickness. Monodisperse emulsions are less prone to Ostwald ripening than polydisperse emulsions, therefore are more stable.¹⁵ Shell thickness determines how freely the core droplet can move inside the double droplet – with decreasing shell thickness the hydrodynamic resistance increases, decreasing the migration velocity of the core droplet. For sufficiently thin shells the middle phase fluid acts as a lubricant, hindering or preventing coalescence of the core droplet with the outermost continuous phase liquid.^16,17 Thus, double emulsions of monodisperse droplets and thin shells are preferred for the applications.

Fig. 1 (Left) Schematic drawing of water-in-oil-in-water double droplets. (A) Droplet with thick shell. (B) Droplet with thin shell. (Right) 3D scan of the device we used for double emulsion production (i) reservoir, (ii) side channels, (iii) supply channel. The color scale is artificial, added to visualize the height of the features. Width of the reservoir is 1 mm, supply channel is 220 μm, of the side channel 300 μm.

The emergence of droplet microfluidics opened new possibilities in production and utilization of single and multiple emulsions, offering exceptional control over their size and inner structure, such as the number, size and also arrangement of the core droplets.^1,18 As formation of droplets in microfluidic devices occurs on the scale of tens to hundreds of micrometers the inertial and gravitational effects can be neglected leaving the viscous and interfacial forces to govern the process. The ratio of the two forces – with the involvement of the characteristic fluid velocity – is expressed by the capillary number, Ca = μ × U/γ, where μ is the dynamic viscosity [Pa s], U is the characteristic fluid velocity [m s⁻¹], and γ is the interfacial tension [N m⁻¹]. Ca is commonly used to characterize the various regimes of droplet generation. There is however no uniform Ca number to characterize the droplet breakup or transition between various regimes and the balance between viscous and surface forces varies among the different geometries of the microfluidic droplet generators. For instance in flow-focusing^19–22 or T-junction^19,20,23,24 geometries the shear force generated by the flow of the individual fluid phases determine the local stresses which deform the interface and lead to droplet break-up. As a consequence the breakup dynamics and the size of the generated droplets strongly depends on the viscosity ratio and flow rates of all liquid phases.^19,20 In contrast, in step emulsification geometry the shear force has negligible effect on droplet formation.^25,26 In this geometry the to-be-dispersed phase is pushed from a shallow and wide rectangular microchannel to a wide and deep reservoir filled with the continuous phase liquid. At the sudden change of the confinement the tip of the squeezed liquid finger starts to form spherical shape and the resulting capillary pressure imbalance causes the liquid thread in the microchannel to thin (so called neck formation) and ultimately to break off as a droplet. In such passive systems the flow of continuous liquid is usually not required^27,28 and the droplet size is predominantly determined by the geometry of the nozzle. As a result, at sufficiently low capillary number step emulsification systems allow to generate tightly monodisperse droplets over a relatively wide range of flow rates.^25,29,30

Size distribution and throughput can be further improved by various modifications of the nozzle geometry such as introducing terraces,²⁹ bypasses,^27,31 triangular or ultra-wide nozzles,^30,32,33 or partially-separated nozzles.²⁸ Such small changes in the nozzle's geometry usually shift the balance between the viscous and surface forces in the droplet formation and breakup mechanism. For instance introducing a gradual widening of the nozzle (triangular shape in top view)³⁰ generates a different type of instability than the introduction of small terraces.³⁴ Although in both geometries droplet breakup is driven by the interfacial tension, the droplet size in the former geometry scales with the channel's height h, while in the latter geometry with h^1/3.³⁵ If the feeding microchannel is of an axisymmetric cylindrical geometry (instead of a rectangular with high aspect ratio) and a co-flow of the continuous phase is introduced along with the droplet phase, then the droplet formation is driven solely by the interfacial tension and droplet size is “almost insensitive to the viscosity ratio”.³⁶ In the standard step emulsification geometry, however, the dynamics of droplet formation (necking time and breakup frequency) depends both on the interfacial tension and viscosity of the inner and outer phase.^37,38

The formation of single emulsions in step emulsification systems has been thoroughly investigated,^25,26,39,40 but generation of double emulsion on the step has been proposed only recently and is not yet completely understood.^14,41 This can be accounted for the difficulties of selective surfaces modification protocols required for controlled generation of double emulsions. Indeed, even the presented methods use a tandem system of two separate devices with different surface characteristics to study the formation of double emulsion at the step. Authors identified the size of the core droplets as the key factor to determine the composition of the double droplet. The role of other physical parameters of the system that would make the technique transformable to arbitrary step emulsification system is yet to be determined.

Here, we use a similar tandem system to study how properties of the liquid phases influence the formation of double emulsion in a microfluidic step emulsification device. We describe the relationship between the viscosity and the size of the core droplet and the size of resulting double emulsion. Furthermore, we describe how viscosity ratio of used liquids determines whether the core droplets split or slip to the shell phase at the step of the microfluidic device. Finally, we investigate the dependence of the shell thickness on the size of injected core droplets.

Materials and methods

Preparation of the microfluidic chips

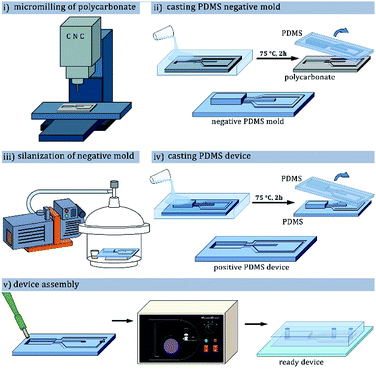
Throughout the experiments we used hybrid glass–poly(dimethylsiloxane) [PDMS] microfluidic chips.⁴² Procedure of microfluidic chip preparation was described in previous publications from our group,^43,44 and shown in the Fig. 2. Positive molds of the devices were milled in 5 mm-thick polycarbonate plate (Covestro, Germany) using a CNC-milling machine (Ergwind, Poland) and inspected under optical profilometer (ContourGT K0, Bruker, Germany). Negative mold was subsequently cast in PDMS mixed with curing agent (10 : 1 weight ratio, Sylgard 184, United States).

Fig. 2 PDMS microfluidic chip fabrication process using CNC-milled polycarbonate as the positive mold: (i) milling of the polycarbonate plate to form a positive mold; (ii) preparation of PDMS negative mold; (iii) protection of the PDMS negative mold with fluorosilane vapor deposition; (iv) preparation of PDMS device with positive channels; (v) bonding the device with glass plate after punching inlet holes and oxygen plasma treatment.

The surface of the baked cast was then activated with corona discharge (BD-20AC, Electrotechnic Products, USA) and silanized with tridecafluoro(-1,1,2,2-tetrahydrooctyl)-1-trichlorosilane (Alfa Aesar, Germany) vapor in vacuum for at least 1 h. The silanized master mold was filled with a mixture of PDMS and curing agent, degassed and baked for 1 hour at 75 °C. PDMS device was peeled from the mold, inlet and outlet holes were punched in it with a biopsy puncher, and the device was bonded to a glass slide by exposure to oxygen plasma (Harrick Plasma, United States) and bringing the pieces into contact.

Surface modification of the microfluidic chips

To prepare primary water-in-oil emulsion the microchannels of the microfluidic devices were rendered fluorophilic to allow wetting by fluorinated oils. The channels were filled with solution of fluoropolymer (HFE 1720, 3M, USA), and after evaporation of the oil baked 15 minutes at 130 °C to form a fluorosilane layer. In the other kind of device the hydrophilic surface of the channels was obtained by treating the bonded devices with 2% w/w PVA solution (13–23 kDa, 87–89% hydrolyzed, Sigma Aldrich, United States) around 4 hours after the plasma bonding.⁴⁵ The microchannels were filled with PVA solution, incubated at room temperature for 10 minutes, flushed clean with compressed air, and baked at 120 °C for 10 minutes. The filling-flushing-baking procedure was repeated three times for even surface coverage.

Used liquids

Core and outer phase liquids were 2% wt or 10% wt aqueous PVA solutions (the same as for channel modification). Oil (shell) phases were fluorinated oils (FC-40 and HFE-7500, 3M, USA) with 2% wt triblock fluorosurfactant PFPE–PEG–PFPE (Chemipan, Poland). Viscosities of the aqueous phases were measured with Malvern Kinexus rotational rheometer using cone-plate geometry (d = 50 mm, α = 1°) and are presented in Table 1. We calculated viscosity ratios for various core–shell-outer phase setups and presented them with measured interfacial tensions in Table 2.

Table 1 Viscosities of the used liquid phases at room temperature

Fluid	Phase	Viscosity, μ [mPa s]	Density, ρ (kg m^−3)
HFE-7500, 2% wt surf.	Oil	1.330	1614
FC-40, 2% wt surf.	Oil	4.231	1850
PVA 2% wt	Aqueous	2.0	∼1000
PVA 10% wt	Aqueous	23.2	∼1000

---

Table 2 Viscosity ratios, λ, and interfacial tensions, γ, of the tested liquid combinations. Interfacial tensions were measured using pendant droplet method. All oils contain 2% wt triblock PFPE–PEG–PFPE surfactant

Core liquid	Shell liquid	Outer liquid	λ [—] core/shell	λ [—] shell/outer	γ [mN m^−1] core/shell	γ [mN m^−1] shell/outer
PVA 2% wt	HFE-7500	PVA 2% wt	1.5	0.7	3.3 ± 0.1	3.3 ± 0.1
PVA 10% wt	HFE-7500	PVA 2% wt	18.1	0.7	3.2 ± 0.2	3.3 ± 0.1
PVA 2% wt	FC-40	PVA 2% wt	0.5	2.1	7.4 ± 0.6	7.4 ± 0.6
PVA 10% wt	FC-40	PVA 2% wt	5.6	2.1	8.0 ± 0.3	7.4 ± 0.6

---

Data capture and analysis

Optical detection setup was assembled using elements purchased from Thorlabs (Thorlabs, USA). Formation of droplets was observed and recorded using fast camera (1024PCI, Photron, Japan) mounted on Nikon stereoscope (SMZ 100, Nikon, Japan). Microchip was placed vertically in front of the horizontal imaging setup. Images were processed in ImageJ2 (ref. 46) (NIH, USA) and Automated Droplet Measurements software.⁴⁷ Analysis and plotting of the obtained results were performed using custom routines in Matlab 2018b (Mathworks, USA), RStudio 3.6.0 (R Studio Inc., USA), MS Excel 2013 (Microsoft, USA), and Origin Pro 8 (OriginLab, USA).

Results and discussion

Architecture of step emulsification device

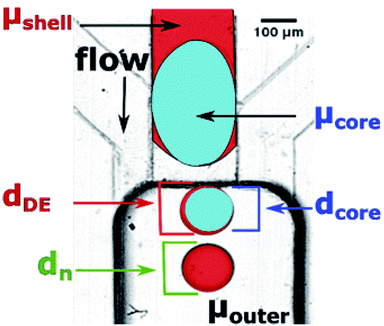
Microfluidic step emulsification device for DE production comprised three main elements, marked in Fig. 1, right panel: (i) large channel (reservoir) pre-filled with the outer phase fluid, (ii) shallow supporting side channels used to pre-fill the reservoir with the outer phase, (iii) rectangular main channel supplying the to-be-dispersed phase to the reservoir. The microphotograph of the device is also presented in Fig. 3.

Fig. 3 Physical parameters investigated in our system: viscosities of core phase, shell phase, and outer phase (μ_core, μ_shell, and μ_outer, respectively), diameters of core and core + shell in double droplets (d_core and d_DE, respectively), and diameter of O/W emulsion (‘double emulsion without core’), d_n. Black arrow marks the flow direction, which is aligned with gravity field. The colors in this figure were added in image-processing as guide to the eye.

The main channel was 220 μm wide and 45 μm deep. Supporting side channels (300 μm wide, 20 μm deep) served as bypasses that facilitate continuous phase to access the neck of the thinning thread during droplet formation, as shown in our previous work.²⁸ We used these side channels also to supply the continuous phase to the reservoir prior to the experiments. We didn't apply flow from these channels during the experiments. To prevent the to-be-dispersed phase from entering the side channels we kept their height below half of the main channel height.²⁷ We operated the chip in vertical position, to transport the formed droplets away from the step by buoyancy (W/O emulsion) or by gravity (W/O/W double emulsion).^27,28,48,49

Step emulsification systems are known to produce tightly monodisperse droplets in the dripping regime characterized by relatively low flow rates. Above a certain threshold of the flow rate the system turns to jetting regime and generates large, polydisperse droplets. We prepared both fluorophilic and hydrophilic step emulsification devices and generated both W/O and O/W single emulsions over a wide range of flow rates to determine the critical value 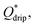above which jetting regime occurs (see ESI† for details). We found that at Q_drip ≤ 0.5 μL min⁻¹ all systems produce droplets (both W/O and O/W) in the dripping regime (see ESI Fig. S2†). Thus, we used 0.5 μL min⁻¹ throughout our experiments to transform single emulsions into double emulsions.

Workflow of double emulsion production

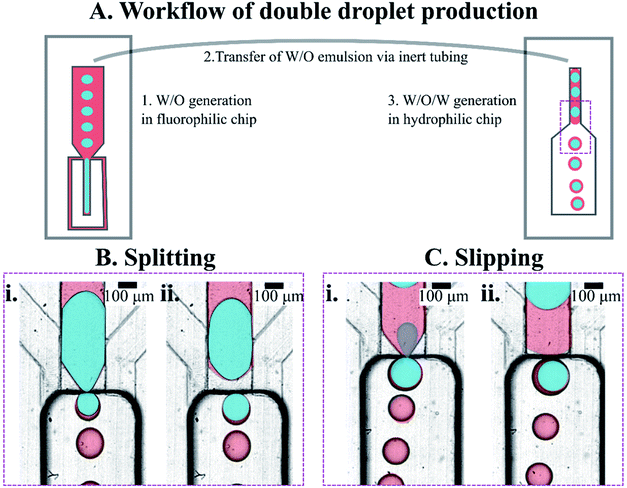
We prepared double emulsions in a two-step process, using tandem of microfluidic devices connected with a tubing, as shown in Fig. 4A. In the first device, a flow-focusing microsystem with fluorophilic walls, we produced W/O emulsion that was directly transported to the second device via PTFE tubing. We prefilled the second, step emulsification microfluidic device (having hydrophilic walls) with the aqueous outer phase before transforming W/O into W/O/W droplets there.

Fig. 4 Generation of double emulsion droplets using tandem step microfluidics. (A) Workflow of the production of the double droplets. (B and C) Magnification of area where droplets are formed. Snapshots from the step emulsification experiments – in each, the frames (i) and (ii) were taken a few milliseconds apart. Two observed behaviors of the core droplets during DE production on a step. Either the core droplet split into multiple droplets ((B), two panels in the left) or slipped whole to the DE ((C), two panels in the right). Core droplets in splitting regime (B) are made of PVA 2% wt, core droplets in slipping regime (C) are made of PVA 10% wt. Water phase is colored blue in the image, but is transparent in reality; oil phase – red in the image, transparent in reality; outer phase – transparent both in image and in reality. Colors were added for clarity in the post-processing of the image.

Establishing nominal droplet sizes

Step-emulsification modules with bypasses yield single emulsion droplets of stable size when operating in the dripping regime, and the size of the droplets produced in the dripping regime depends only very weakly on the flow rate. This is well-reported for single emulsions^25,26,38 but may not be true when emulsifying two liquid phases (core and shell) simultaneously. Therefore, we chose a baseline for comparison of the double droplet sizes, the nominal droplet size, d_n, which we define as the diameter of droplets formed in our step emulsification devices at Q_drip (see Fig. 3 and Table S1†).

We use d_n to express diameters of produced double droplets in terms of relative droplet size, i.e. as the ratio of measured double droplet diameter d_DE to d_n of the phase being dispersed in the outer phase. In case of W₁/O/W₂ emulsions the d_n used to calculate the relative droplet size is the d_n of O/W₂ emulsion.

We observed that the flow of core droplets into the double droplet exhibited two qualitatively distinct behaviors. The core droplets either split into multiple subsequent smaller droplets (see Fig. 4B and 5C) or slipped as a whole into the double droplet (see Fig. 4C and 5B). These two scenarios were observed previously by Ofner et al.¹⁴ and explained by the core/DE diameter ratio. Here we investigate both droplet diameter and viscosity ratios to verify the factors that promote either of the two behaviors.

Fig. 5 Droplets produced in the hydrophilic step emulsification device upon supplying W/O droplets of varying size. (A) Histogram of sizes of droplets produced using step emulsification device. Sizes of the cores are denoted by the purple dashed lines, black dashed line shows the value of nominal droplet size, d_n. SE, DE, SE + DE, and R denote single emulsion droplets, double emulsion droplets, mix of single and double droplets, and residual single emulsion droplets formed from double droplet rupture, respectively. Top row: PVA 10% wt cores, bottom row: PVA 2% wt cores. Oil phase is HFE-7500 2% surfactant and outer phase is PVA 2% wt. (B and C) Example of analysed emulsions. In slipping regime (B) cores consist of PVA 10% wt and the produced double droplets do not disintegrate, in splitting regime (C) the cores split into subsequent droplets (SE and DE), sometimes breaking and releasing residual oil in water droplet (R).

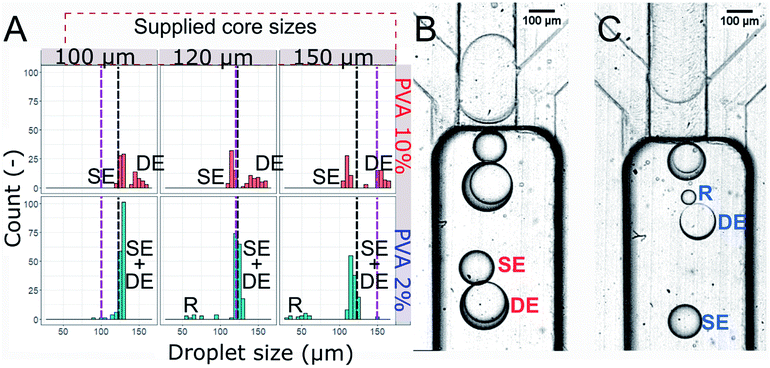
Investigation of the core size and viscosity on DE formation

We generated three sizes of the core droplets in the flow focusing device and fed them into the step emulsification device: (i) core droplets smaller than the nominal droplet size d_n (100 μm), (ii) core droplets similar in size to the nominal droplet d_n (120 μm), (iii) core droplets larger than the nominal droplet size d_n (150 μm). Sizes of all droplets produced in the step emulsification system were measured. The distribution of the sizes of the mixed population (comprising W/O/W double droplets and single O/W droplets – emulsified excess oil phase of the W/O feed emulsion) is presented in Fig. 5. Both single and double droplets were registered in the experiment and presented in Fig. 5, as it was challenging to distinguish between them by size only.

For systems with low core–shell viscosity ratio λ (cores of PVA 2% wt, λ = 1.5), i.e. for core droplets with similar viscosity that of the shell phase, we observed splitting of the core droplets into multiple double emulsion droplets, even for d_core < d_n (see bottom of Fig. 5A for size distribution and Fig. 5C for microphotograph of the result). In systems with high core–shell viscosity ratio (cores of PVA 10% wt, λ = 5.6–18.1 depending on the shell) the core droplets slipped entirely into the double emulsion for both investigated oils and all investigated core sizes (see top of the Fig. 5A for droplet size distribution, and Fig. 5B for microphotograph). This is in sharp contrast with previous reports claiming that structure of double emulsion generated during step emulsification for a fixed volume of the feeding droplet is defined solely by the nozzle's geometry and rates of flows.^15,30

Double droplets containing the less viscous cores were roughly the size of the nominal droplet for every investigated core size (see bottom of Fig. 5A). It is due to fact that the cores larger than d_n split during double emulsion formation. We measured shell thickness only for a few double droplets as it was clear that there is a high degree of variability (Fig. 5C, which features two double droplets with shells ∼10 μm and ∼40 μm, measured as difference between double droplet diameter and core droplet diameter). We did not observe coalescence incidents between droplets, other than occasional double droplet rupture for system with cores of low viscosity. This led to formation of a population of small droplets (diameter below 100 μm, denoted R in the Fig. 5). When the core of the double droplet coalesced with the outer phase the oil layers were released and formed single emulsion droplet.

Double droplets containing the more viscous cores (10% wt PVA) were significantly larger than the corresponding nominal droplets (d_n = 127.9 μm) for all the investigated core sizes. The only droplets that we observed to be smaller than the nominal droplet size were single droplets made of excess oil from between subsequent inflowing cores. We observed that even the cores with d_core > d_n did not split upon formation of the double droplet.

Using different oil (shell) phases results in differences in nominal droplet size for various combinations of liquids (see Table S1†). However, in our investigations generation of O/W droplets of HFE-7500 and FC-40 in PVA 2% using the same microfluidic chip and flow rate resulted in comparable nominal droplet sizes (118.2 μm vs. 113.6 μm). We observed the same situation for W/O droplets of PVA 10% generated in HFE-7500 and FC-40 (127.9 μm vs. 126.8 μm). In case of the W/O droplet of low viscosity PVA 2% generated in HFE-7500 and FC-40 oils the nominal droplet size differed by 10% (122.4 μm vs. 136.1 μm). Nevertheless, we observed similar qualitative behavior in experiments with FC-40 oil used instead of HFE-7500: splitting of less viscous cores (PVA 2%) to the nominal droplet size and slipping of more viscous cores (PVA 10%) larger than the nominal droplet size.

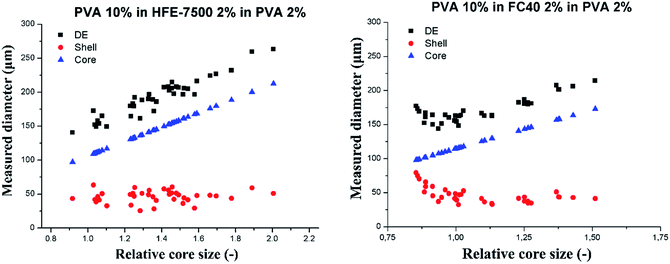
Investigation of the shell thickness

In a subsequent experiment we investigated in greater details the dependence of the shell thickness on the core size for high core–shell viscosity ratio. We used the flow-focusing microfluidic device to generate single emulsions – droplets of PVA 10% wt in fluorinated oils (HFE-7500 or FC-40). We produced W/O emulsions, differing by the shell phase and varying diameter of the aqueous droplets. We injected sequentially such W/O emulsions into the hydrophilic step emulsification device filled with 2% wt solution of PVA in water. This resulted in transformation of the W/O into W/O/W double droplets. We measured the core diameter, shell thickness and total double droplet diameter and presented them in Fig. 6. Each core size (blue triangles in the plots) was normalized by the nominal droplet size for each system to yield relative core size.

Fig. 6 Slipping behavior of PVA 10% wt core droplets-in-oil-in-PVA 2% wt. Oil was HFE-7500 with 2% wt surfactant (left) and FC-40 (right). Black squares denote the total DE droplet size, blue triangles denote the relative core size and red circles represent the shell thickness. The double droplets were produced at 0.5 μL min⁻¹.

PVA 10% wt cores slipped into the double emulsion for the investigated range of core sizes for both tested oils (shell phase). DE droplet diameter increases linearly with the increase of the core size, and the shell thickness decreases down to the stable level of 40 ± 5 μm for HFE7500 and 46 ± 9 μm for FC-40. Averaged shell thickness values were measured for DE comprising cores larger than nominal droplet size (relative core size > 1).

Influence of the viscosity on core droplet integrity

In presented step emulsification geometry the outer phase invading the necking area comes mainly from the reservoir, flowing through the side channels to get to the necking area around the forming droplet.²⁸ Shell phase does not wet the walls of the microchannels and is confined by the feed channel until it reaches the reservoir, where spatial confinement is released and liquid expands.²⁵ Thus, oil phase and core droplet confined within can only move towards the reservoir, pushed by the syringe-pump-induced flow. During necking, the shell and core phase form the growing head of the thread. The core droplet confined in microchannel in the shell phase thread is squeezed further by the constricting shell-phase thread. The inner core droplet may yield to the constricting force i.e. splitting in the necking area. In case the viscous resistance of the core droplet is large enough, the core droplet can apparently withstand the force exerted by the thinning interface until the whole droplet passes through the necking region. In presented investigation the sufficient viscosity to withstand splitting was observed when core viscosity was over 20 mPa s and core-to-shell viscosity ratio was 5–18 (depending on the used oil). From the perspective of elucidating mechanism of double emulsion formation at the step it would be interesting to establish exact values of the core-to-shell viscosity ratio that enables core slipping. This finding paves a way for future studies targeted at establishing the exact viscosity ratios governing split to slip regime transition.

Conclusions

We showed that the core-to-shell viscosity ratio determines the structure of the double droplet formed via step emulsification. When cores are less or only slightly more viscous than the shell liquid (λ ≤ 1.5) the core droplets split into multiple smaller droplets at the step. For higher values of core-to-shell viscosity ratio (λ ≥ 5.6) the core droplets maintained integrity and slipped intact into double droplets. ‘Slipping’ of the intact cores into double droplets warrants more uniform shell thickness of the double droplets, while splitting of cores generates higher variance of the thickness of the shell.

We demonstrated that shell thickness can be controlled independently of the cores size – allowing for encapsulation of the single emulsion into oily shells, while maintaining the integrity of the liquid cores. This minimizes the risk of cross-contamination between droplets when carrying out biological assays, e.g. core droplets contain single cells and are encapsulated into DE for sorting in directed evolution experiment.

Author contribution

A. S. O., K. M., L. D and P. G. designed the experiments. A. S. O. performed the experiments. A. S. O. and K. M. analyzed the data. A. S. O. and L. D. provided the graphics. A. S. O., K. M., L. D., and P. G. discussed and wrote the manuscript.

Conflicts of interest

Authors declare no conflict of interest.

Acknowledgements

The authors would like to thank Patryk Adamczuk, Bogdan Dąbrowski, and Karol Patyrak for microfabrication of the devices, Agnieszka Wiśniewska for viscosity measurements, Tomasz S. Kamiński, Ott Scheler, Jan Guzowski and Witold Postek for discussions. A. S. O., K. M. and P. G. were supported by the National Science Centre, Poland, within the projects Preludium 2016/23/N/ST4/01020, Sonata 2016/21/D/ST3/00988 and Symfonia 2014/12/W/NZ6/00454, respectively. A. S. O. and L. D. were supported by the Foundation for Polish Science within the project TEAM TECH POIR.04.04.00-00-2159/16-00.

References

1. G. T. Vladisavljević, R. Al Nuumani and S. Nabavi, Micromachines, 2017, 8, 75.
2. L. A. Adams, T. E. Kodger, S.-H. Kim, H. C. Shum, T. Franke and D. A. Weitz, Soft Matter, 2012, 8, 10719.
3. A. R. Abate and D. A. Weitz, Small, 2009, 5, 2030–2032.
4. F. Fontana, M. P. A. A. Ferreira, A. Correia, J. Hirvonen and H. A. Santos, J. Drug Delivery Sci. Technol., 2016, 34, 76–87.
5. B. Tal-Figiel, Chem. Eng. Res. Des., 2007, 85, 730–734.
6. V. Eisinaite, D. Juraite, K. Schroën and D. Leskauskaite, Food Chem., 2016, 206, 59–66.
7. K. Bernath, M. Hai, E. Mastrobattista, A. D. Griffiths, S. Magdassi and D. S. Tawfik, Anal. Biochem., 2004, 325, 151–157.
8. Z. Tan and J. M. Heemstra, ChemBioChem, 2018, 19, 1853–1857.
9. A. Zinchenko, S. R. A. Devenish, B. Kintses, P. Y. Colin, M. Fischlechner and F. Hollfelder, Anal. Chem., 2014, 86, 2526–2533.
10. P. Mair, F. Gielen and F. Hollfelder, Curr. Opin. Chem. Biol., 2017, 37, 137–144.
11. A. Vian and E. Amstad, Soft Matter, 2019, 15, 1290–1296.
12. J. Petit, I. Polenz, J. C. Baret, S. Herminghaus and O. Bäumchen, Eur. Phys. J. E, 2017, 39, 59.
13. G. Villar, A. J. Heron and H. Bayley, Nat. Nanotechnol., 2011, 6, 803–808.
14. A. Ofner, I. Mattich, M. Hagander, A. Dutto, H. Seybold, P. A. Rühs and A. R. Studart, Adv. Funct. Mater., 2018, 1806821.
15. T. F. Tadros, in Emulsion Formation and Stability, ed. T. F. Tadros, WILEY-VCH Verlag GmbH, Hoboken, 1st edn, 2013, pp. 1–75.
16. S.-H. Kim, J. W. Kim, J.-C. Cho and D. A. Weitz, Lab Chip, 2011, 11, 3162–3166.
17. A. Vian, V. Favrod and E. Amstad, Microfluid. Nanofluid., 2016, 20, 159.
18. A. S. Opalski, T. S. Kaminski and P. Garstecki, KONA Powder Part. J., 2019, 36, 50–71.
19. P. Garstecki, I. Gitlin, W. Diluzio, G. M. Whitesides, E. Kumacheva and H. A. Stone, Appl. Phys. Lett., 2004, 85, 2649–2651.
20. P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437.
21. Z. Nie, M. S. Seo, S. Xu, P. C. Lewis, M. Mok, E. Kumacheva, G. M. Whitesides, P. Garstecki and H. A. Stone, Microfluid. Nanofluid., 2008, 5, 585–594.
22. T. Nisisako, T. Torii, T. Takahashi and Y. Takizawa, Adv. Mater., 2006, 18, 1152–1156.
23. J. Yao, F. Lin, H. S. Kim and J. Park, Micromachines, 2019, 10(12), 808.
24. Z. Nie, S. Xu, M. Seo, P. C. Lewis and E. Kumacheva, J. Am. Chem. Soc., 2005, 127, 8058–8063.
25. R. Dangla, E. Fradet, Y. Lopez and C. N. Baroud, J. Phys. D: Appl. Phys., 2013, 46, 114003.
26. A. Montessori, M. Lauricella, S. Succi, E. Stolovicki and D. Weitz, Phys. Rev. Fluids, 2018, 7, 1–7.
27. F. Dutka, A. S. Opalski and P. Garstecki, Lab Chip, 2016, 16, 2044–2049.
28. A. S. Opalski, K. Makuch, Y.-K. Lai, L. Derzsi and P. Garstecki, Lab Chip, 2019, 19, 1183–1192.
29. S. Sugiura, M. Nakajima, J. Tong, H. Nabetani and M. Seki, J. Colloid Interface Sci., 2000, 227, 95–103.
30. E. Amstad, M. Chemama, M. Eggersdorfer, L. R. Arriaga, M. P. Brenner and D. A. Weitz, Lab Chip, 2016, 16, 138–155.
31. A. G. Håti, T. Szymborski, M. Steinacher and E. Amstad, Lab Chip, 2018, 18, 648–654.
32. A. Ofner, D. G. Moore, P. A. Rühs, P. Schwendimann, M. Eggersdorfer, E. Amstad, D. A. Weitz and A. R. Studart, Macromol. Chem. Phys., 2017, 218, 1600472.
33. K. van Dijke, G. Veldhuis, K. Schroën and R. Boom, Lab Chip, 2009, 9, 2824–2830.
34. S. Sugiura, M. Nakajima and M. Seki, Langmuir, 2002, 18, 3854–3859.
35. E. Amstad and D. A. Weitz, Lab Chip, 2017, 17, 2332–2333.
36. I. Chakraborty, J. Ricouvier, P. Yazhgur, P. Tabeling and A. M. Leshansky, Lab Chip, 2017, 17, 3609–3620.
37. N. Mittal, C. Cohen, J. Bibette and N. Bremond, Phys. Fluids, 2014, 26, 082109.
38. E. Crestel, L. Derzsi, H. Bartolomei, J. Bibette and N. Bremond, Phys. Rev. Fluids, 2019, 4, 073602.
39. S. Sugiura, M. Nakajima, T. Oda, M. Satake and M. Seki, J. Colloid Interface Sci., 2004, 269, 178–185.
40. K. van Dijke, R. de Ruiter, K. Schroën and R. Boom, Soft Matter, 2010, 6, 321–330.
41. M. L. Eggersdorfer, W. Zheng, S. Nawar, C. Mercandetti, A. Ofner, I. Leibacher, S. Koehler and D. A. Weitz, Lab Chip, 2017, 17, 936–942.
42. E. Berthier, E. W. K. Young and D. Beebe, Lab Chip, 2012, 12, 1224–1237.
43. W. Postek, T. S. Kaminski and P. Garstecki, Lab Chip, 2017, 17, 1323–1331.
44. W. Postek, T. S. Kaminski and P. Garstecki, Analyst, 2017, 142, 2901–2911.
45. S. Deshpande and C. Dekker, Nat. Protoc., 2018, 13, 856–874.
46. C. T. Rueden, J. Schindelin, M. C. Hiner, B. E. DeZonia, A. E. Walter, E. T. Arena and K. W. Eliceiri, BMC Bioinf., 2017, 18, 1–26.
47. Z. Z. Chong, S. B. Tor, A. M. Gañán-Calvo, Z. J. Chong, N. H. Loh, N. T. Nguyen and S. H. Tan, Microfluid. Nanofluid., 2016, 20, 1–14.
48. M. Schulz, F. von Stetten, R. Zengerle and N. Paust, Langmuir, 2019, 35(30), 9809–9815.
49. E. Stolovicki, R. Ziblat and D. A. Weitz, Lab Chip, 2018, 18, 132–138.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra03007d

---