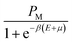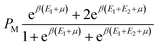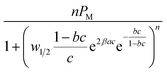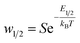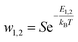Open Access Article
Open Access ArticleNew insights in the physicochemical investigation of the vitamin B12 nucleus using statistical physics treatment: interpretation of experiments and surface properties
Manel Ben Yahia*a and
Mohamed Ben Yahia *b
*b
aPhysics Department Rabigh College of Science and Arts, King Abdulaziz University, Jeddah, PO box 344, Rabigh 21911, Saudi Arabia. E-mail: mbinyhea@kau.edu.sa
bPhysics department, Laboratory of Quantum and Statistical Physics, LR18ES18, Faculty of Sciences of Monastir, University of Monastir, Monastir, 5000, Tunisia. E-mail: ben_yahia_med@hotmail.fr
First published on 8th June 2020
Abstract
In this research paper, the equilibrium isotherms for the adsorption of cobalt(II)nitrate and cobalt(II)chloride on tetrakis(4-tolylphenyl)porphyrin (H2TTPP) were obtained at four temperatures for modeling analysis. The experimental data describing the adsorbed quantity of cobalt particles were measured using the quartz crystal microbalance (QCM) strategy. Then, statistical physics formalism was employed to interpret the complexation mechanism by applying the real gas law that contemplates the interaction between the adsorbate particles in the free state. Advanced models treated with the law of van der Waals were applied for the single and L.B.L adsorptions of Co2+ at various temperatures (288–318 K). The experimental adsorption data of CoCl2 on porphyrins were satisfactorily fitted with the monolayer equation, showing that the chlorine particles had no effect on the complexation system, while the nitrate particles were involved in the adsorption of Co(NO3)2 and contributed to the layer formation. The physicochemical parameters of statistical physics models were estimated and used to compare the complexation mechanisms of both adsorbates. The study of the cohesion pressure (a) and the co-volume (b) confirmed that cobalt chloride guaranteed more stability during the formation of the vitamin B12 nucleus. Deeper energetic analysis demonstrated that cobalt ions were complexed by ionic or covalent bonds in the case of cobalt chloride (complexation energy (–E1/2) varies from −48.2 to −50.3), while a physisorption process took place in the case of cobalt nitrate ((–E1) varies from −33.6 to −36.1), thus indicating that CoCl2–H2TTPP was the most stable complex. The statistical physics models were also used to investigate two thermodynamic functions that govern the adsorption mechanisms, namely, the configurational entropy and the Gibbs free enthalpy.
1. Introduction
In recent studies, the adsorption of various cationic ions (zinc, iron, magnesium, etc.) on complexing macrocycle molecules (helicenes, porphyrins, cyclodextrins, etc.) has been investigated due to their interesting contribution to several biological responses.1,2 To study the complexation mechanism of biosensors in adsorption systems, experimental adsorption isotherms were obtained using the quartz crystal microbalance strategy.3 A theoretical description of experimental data was carried out by applying statistical physics formalism to evaluate the physicochemical properties of the sorption process at the solid–liquid interface.4 In particular, it has been demonstrated that tetraphenylporphyrin can be used as a sensor for Fe2+ and Fe3+ and forms a steady complex called heme, which assumes a significant contribution to the dioxygen transport in the human body.1 Also, it has been proved that tolylphenylporphyrin can complex with the Mg2+ ion, which comprises the chlorophyll core.5 However, the complexation mechanism of other particles on porphyrin has not been totally considered and understood. In this paper, we have focused on another complex of porphyrin which is more imporant than the other metalloporphyrins. It is a cobalt–porphyrin complex (Fig. 1), which constitutes the nucleus of vitamin B12.6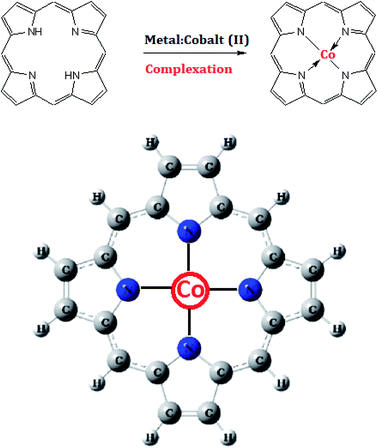 | ||
| Fig. 1 Illustration of the complexation reaction of the tetrakis(4-tolylphenyl)porphyrin (H2TTPP) with cobalt(II) particles, resulting in the chemical structure of the vitamin B12 nucleus. | ||
Vitamin B12, named cobalamin, is necessary for the ordinary working of the brain and the nervous system. In addition, it plays an important role in the formation of blood. It is included as a cofactor in the cell metabolism of the human body, particularly in DNA synthesis and its regulation, as well as in the synthesis of fatty acids and in energy production. Plants and animals cannot produce this vitamin.6 Only a few bacteria, archaea, micro-fungi and microalgae7 have the necessary enzymes for its biosynthesis.
A definitive thought on this examination is to provide another strategy for the fabrication of this vitamin. The Quartz Crystal Microbalance (QCM) is proposed to control the possibility of complexing the tetrakis(4-tolylphenyl)porphyrin (H2TTPP) with cobalt ions.8,9 The QCM technique is used because the experimental setup devoted to the achievement of experimental isotherms is a precious mass detecting technique at the nanogram scale. Moreover, this experimental strategy offers the possibility to calculate the complexed amount of cationic metal to the upper functional electrode while simultaneously carrying out the complexation of porphyrin in solution.10 This is possibly a unique property that cannot be found in other experimental apparatus.
On the other hand, from the field of interest and by decomposing various outcomes presented in numerous investigations, it can be inferred that in most situations, scientists can apply mathematical expressions to the experimental data.11,12 Many specialists have demonstrated that the interpretation of the sorption isotherms can be given by several model expressions.11–13 Many of them are absolutely mathematical and have no critical discussions.11–15 Indeed, a fundamental thought of this paper is the use of statistical physics treatment, which permits the establishment of advanced models based on the grand-canonical ensemble of Gibbs. These advanced models are applied for the microscopic description of the complexation processes of porphyrins by the intermediate of the physicochemical parameters involved in their analytical expressions.1,2,4,5
Interestingly, the goals of this research work are as follows: (1) providing another technique for making the central core of the vitamin B12, which can be exceptionally valuable for producing this vitamin in industry. (2) Application of the QCM strategy for the achievement of sorption isotherms. (3) Choosing the appropriate type of adsorbate (cobalt nitrate or cobalt chloride) for the fabrication of vitamin B12. (4) Providing theoretical analysis of the experimental results by the intermediate of statistical physics treatment. (5) Verifying experimental results by statistical physics modeling. (6) Interpreting the complexation process at the microscopic level through the parameters given by the statistical physics models. (7) Providing industrial recommendations for the fabrication of vitamin B12 based on experimental results and theoretical interpretations.
2. Experimental methodology: QCM measurement
2.1. Materials
The adsorbent used in the experimental measurement is the tetrakis(4-tolylphenyl)porphyrin (H2TTPP), which was synthesized by the standard literature strategy (Adler-Longo technique).16 These porphyrins were chosen to be investigated in this work because practically all metals can be coordinated with their complexing cavities. Thus, since the experimental setup of the QCM method implies the use of compounds that are soluble in water, we chose to investigate the cobalt chloride and the cobalt nitrate in the porphyrin adsorption. These two adsorbates are the most commonly used cobalt compounds in the lab and they occur in the form of the hexahydrate (CoCl2·6H2O and Co(NO3)2·6H2O). Other compounds (e.g. cobalt sulfide) are insoluble in water so they cannot be used for the achievement of experimental isotherms using the QCM technique. Moreover, these two adsorbates provide the metallic cobalt particle Co2+. The complexation of the tetrakis(4-tolylphenyl)porphyrin (H2TTPP) with cobalt(II) produces the core of the second form of vitamin B12.17 However, the use of a compound that delivers cobalt(III) (for example, cobalt(III) nitrate) leads to the formation of the third form of vitamin B12 (hydroxocobalamin) which cannot be achieved by means of our experimental setup.18In this work we attempted to choose the reasonable adsorbate for the fabrication of vitamin B12 by comparing the complexed quantities of cobalt ions that were estimated using the QCM strategy.
2.2. QCM method
Generally, the QCM strategy is an advanced measurement methodology that is devoted to the investigation of a large scope of molecular systems at the solid–liquid interface, in particular, biochemical and biopolymer systems.19 Thus, the QCM setup is an effective mass-sensing strategy dependent on the piezoelectric property of quartz crystal, i.e., the microbalance device detects all mass changes at the surface of the quartz crystal. In addition, it is well established that porphyrins are suitable materials for giving significant reactivity to an electrode coating and different supporting porphyrin systems are known for their excellent electro-catalytic characteristics in the detection of many important analytes, for example, neurotransmitters, nitric oxide and many others.20–23 Indeed, this experimental choice is due to the great interest given to the preparation of functionalized electrodes with porphyrins.The quartz crystal is the key constituent of the QCM setup. It is AT-cut quartz that is covered on both sides with gold of thickness varying from 100 to 1000 nm. Note also that all crystals are polished with a fundamental resonance frequency of 5 MHz. The thickness of the crystal is about 331 μm and its diameter is about 2.54 cm. The commercial quartz crystal is protected by a resin layer, which should be removed using a well-known cleaning protocol20 in which the material is rinsed with acetone and deionized water, followed by drying, then, it is cleaned with a Piranha solution at room temperature for 1 to 5 minutes. After this cleaning treatment, the crystals are completely rinsed with deionized water and ethanol, and then dried by applying high purity nitrogen to remove any remaining water. Modification of the active surface of the crystal is then carried out by coating the porphyrin adsorbent.
Many techniques have been applied and used to immobilize porphyrins and similar composites on the electrode surface. Macromolecule coatings are commonly achieved either by applying preformed polymer or by spin coating directly on the electrode surface. Among these, the latter methodology is attractive because it can easily follow the characteristics of the resulting film by fitting the experimental results with mathematical models.21 In this direction, modifying the surface of the gold electrodes of quartz crystal with macrocyclic complexes is appealing on several grounds. Specifically, exceptional attention has been targeted to porphyrin and metalloporphyrin-based films.9,19
In the present work, the QCM strategy consists of the deposition of substrate volume (porphyrin H2TTPP) by spin coating onto the gold electrode of quartz.22,23 Here, 30 μl of adsorbent is deposited at 3000 rpm for 1 min onto the quartz crystal surface. The covered crystals are then dried at 100 °C for 2 hours. The goal is to obtain appropriate films, which should be homogeneous over the entire surface of the quartz crystal. The structure of such artificially modified electrodes controls whether the cobalt ions are captured by the macromolecules in order to form a stable vitamin B12 product.
After the chemical functionalization of the gold electrode of the quartz crystal with porphyrins, we proceeded with the isotherm measurement.
2.3. Measurement protocol: adsorption isotherms
In the reactor filled with the buffer solution (Vs = 100 ml), the adsorption cell (porphyrin coated on quartz crystal) is immersed until the stabilization of the frequency is reached. Once the crystal is immersed in water, a change in frequency is observed due to the hydrostatic pressure. The resonant frequency of the polymer-coated crystal (F0) is measured by a Maxtek frequency-meter PM700 (plating monitor). This frequency will be used as a reference for our measurement. Then, volumes of adsorbate solution are injected in order to increase the cobalt concentration in the reactor. The slight variation in the mass of one of the electrodes induces a slight decrease in the quartz resonance frequency so the monitor displays the values of the quartz resonant frequencies corresponding to each concentration during the experiment.In 1959, Sauerbrey24 hypothesized that for small mass changes, the added mass could be treated in the same way as an additional mass of quartz. Therefore, the frequency–mass relation is described as follows:24,25
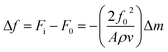 | (1) |
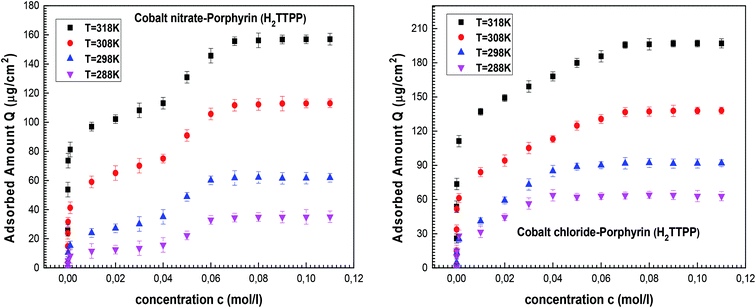
Finally, we obtain the equilibrium adsorption data for cobalt(II)nitrate and cobalt(II)chloride on tetrakis(4-tolylphenyl)porphyrin (H2TTPP), which are plotted in Fig. 2 at four different temperatures. These experimental data are analyzed in order to choose the most effective adsorbate for the achievement of the vitamin B12 nucleus by comparing the adsorption capacities of both porphyrins.
2.4. Discussion of experimental data
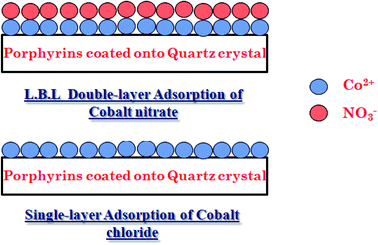
The experimental adsorption data indicate that the two complexation processes tend toward a saturation phenomenon at high adsorbate concentrations. One saturation level appeared for the cobalt(II)chloride adsorption and two saturation levels were observed for the cobalt(II)nitrate. It can be concluded that the adsorbate is the prevailing component in the complexation mechanism. Moreover, the experimental results demonstrated that the adsorption capacities were reduced for cobalt(II)nitrate isotherms as compared to cobalt(II)chloride, indicating that CoCl2 is more suitable for the porphyrin complexation. In light of this initial experimental result, we suggest that cobalt(II)chloride is suitable for a real industrial application.This was analyzed by theoretical examination through innovative statistical physics treatment. In light of sketching the experimental isotherms, monolayer and double-layer models can be adopted to analyze the adsorption curves via the fitted parameters of advanced models. Consequently, the target of the following stage is to incorporate experimental data and theoretical discoveries using these referenced models to acquire new clarifications on the complexation mechanism of cobalt(II) on porphyrin cavities.
3. Theoretical methodology: statistical physics treatment
In recent works, Langmuir, Freundlich and other common isotherm models have been successfully applied to estimate the affinity and the adsorption capacity of adsorbent but they did not provide any interpretation regarding the steric and energetic perspectives.11,15 A deeper physicochemical investigation of cobalt complexation on porphyrins was performed through innovative statistical physics treatment that permits physical explanations of the sorption mechanism at the ionic scale.1,4 Single-layer and L.B.L double-layers models were employed to elucidate the complexation of cobalt on tetrakis(4-tolylphenyl)porphyrin.2,43.1. Statistical physics modeling
In order to develop the analytical expressions of statistical physics models, some assumptions should be integrated:(a) The reservoir of cobalt ions in solution is considered as a reservoir of particles in equilibrium with the solid surface of the adsorbent. Thus, the equilibrium between the free reservoir (cobalt(II)nitrate or cobalt(II)chloride) and the adsorbed state (solid support of tetrakis(4-tolylphenyl)porphyrin (H2TTPP)) is described through the following equation:5,26
| n(Co) + Pr⇌(Co)n − Pr | (2) |
(b) It is supposed that the studied system is in the grand-canonical situation so the starting stage of analytical development is the grand-canonical partition function (zgc). Moreover, we just considered the translation degrees of freedom since the adsorbate in the present investigation is a mono-atomic ion. In this situation, we neglected all other degrees of freedom (vibrational, rotational, electronic and nuclear degrees of freedom).1,4,26
It should be also referenced that for the advanced single-layer model, it is assumed that a single adsorbed layer is formed and that the cobalt ions are adsorbed with the same energy (–E). In the case of double-layer ionic adsorption, we used a model that describes a layer-by-layer adsorption (L.B.L) as we have shown in previous work.1,22 In this case, the formation of the two adsorbed layers is founded on the alternating adsorption of materials containing complementary charges. This method is dependent on charge neutralization between polycations and polyanions. First, the solid surface acts as a template, and after the adsorption of cationic ions, it is refunctionalized and acts as a new template for the subsequent adsorption of anionic ions. We define the energy (–E1) that characterizes the adsorption of the first layer (cationic ions Co2+) and the energy (–E2) that reflects the arrangement of the second adsorbed layer (anionic ion Cl− or NO3−).1,22
The subsequent stage in the statistical physics methodology published in previous works comprises the calculation of the average occupation number (N0) of identical porphyrin sites (PM).26
(c) Finally, the last assumption consists of applying the chemical potential of a real gas in order to introduce the lateral interactions between the adsorbates, which are depicted by the van-der-Waals parameters a and b:27
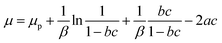 | (3) |
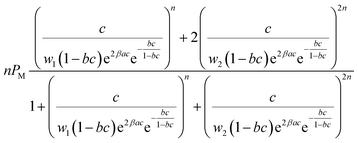
The final analytical expression of the adsorbed quantity (Q) corresponding to the single-layer model and the L.B.L double-layer model is determined from the resulting product of the number of ions per site n and the average occupation number N0 corresponding to each model.26,27
| Q = nN0 | (4) |
The grand-canonical partition function, the average occupation number and the analytical expression of each advanced model are reported in Table 1.
All the sorption isotherms were adjusted with the two advanced models.
From the numerical simulation of the experimental isotherms, three error coefficients were derived:28
(1) The first correlation coefficient R2 demonstrated the good quality of the adjustment when its value is close to unity.
(2) The second coefficient RMSE indicates that the distinction between the theoretical values and the experimental values is negligible when its value is less than 2.
(3) The third error coefficient AIC is a helpful factor for comparison of the adjustment with the two models: the model with the lowest AIC value is the most appropriate for the microscopic explanation of the experimental data.
The numerical values of the adjustment errors of the two models are given in Table 2.
| Temperature (K) | 288 | 298 | 308 | 318 | ||||||||
| Adjustment coefficient | R2 | RMSE | AIC | R2 | RMSE | AIC | R2 | RMSE | AIC | R2 | RMSE | AIC |
| CoCl2/(S–L–M) | 0.98 | 1.1 | 9.7 | 0.99 | 0.9 | 8.3 | 0.98 | 0.8 | 7.4 | 0.99 | 0.7 | 8.1 |
| CoCl2/(D–L–M) | 0.96 | 2.4 | 14.3 | 0.97 | 3.2 | 15.2 | 0.97 | 3.1 | 15.1 | 0.97 | 3.5 | 14.6 |
| Co(NO3)2/(S–L–M) | 0.94 | 4.8 | 16.3 | 0.92 | 5.2 | 16.1 | 0.93 | 4.9 | 17.4 | 0.92 | 5.1 | 16.5 |
| Co(NO3)2/(D–L–M) | 0.97 | 1.2 | 11.2 | 0.98 | 0.8 | 11.9 | 0.98 | 0.9 | 11.3 | 0.99 | 1.1 | 10.9 |
Based on the numerical values of error coefficients, the L.B.L double-layer model was satisfactorily chosen for the theoretical analysis of cobalt(II) nitrate isotherms (R2 ∼ 1, AIC and RMSE are the lowest values for all temperatures). On the other hand, the advanced single-layer model shows the best numerical adjustment with the cobalt(II) chloride–H2TTPP system (0.98 < R2 < 0.99, 7.4 < AIC <9.7 and 0.7 < RMSE <1.1). This leads to the conclusion that the anionic ions Cl− do not influence the complexation mechanism, while the nitrate ions take part in the formation of adsorbed layers in keeping with the previous examinations of Zn(NO3)2 and Fe(NO3)2 on similar adsorbents.1,5,22
As per the fitting results, we illustrate an approximate image in Fig. 3 describing the single-layer complexation of cobalt(II)chloride and the layer by layer adsorption of cobalt(II) nitrate on tetrakis(4-tolylphenyl)porphyrin. From this numerical deduction, we can confirm the experimental results given in Section 2.4: cobalt chloride is affirmed to be the best adsorbate since the chlorine (Cl−) ions remain in solution and have no impact on the procedure for the complexation phenomenon.
3.2. Microscopic interpretation of the complexation process through model parameters
The two adsorption models have common parameters which are the number of cobalt ions per porphyrin site n, the porphyrin density PM and the van-der-Waals variables (cohesion pressure a and co-volume b). n and PM are considered as steric checking parameters. The role of n is to gauge the maximum number of cobalt ions that can be brought into the porphyrinic cavity. The adjusted values of PM give information about the number of sites accessible to ions for every temperature. These two parameters are related to the monolayer adsorption capacity (Qmono = nPM) so they characterize the complexation phenomenon in a quantitative manner at the first adsorbed layer level. Since the difference between the two complexation processes is basically energetic, we consider that the interpretation of the adsorption of cobalt chloride and cobalt nitrate from the comparison of the two models by means of these common steric parameters will not give any obvious and helpful information. However, the cohesion pressure a and the co-volume b describe the lateral interactions between the adsorbates. As such, the study of these parameters can give useful results on comparison of the two adsorbates.Moreover, the distinction between the two models is essentially seen in the energetic parameters. The monolayer model gives rise to a single energetic parameter w1/2 and the L.B.L model involves two energy levels via w1 and w2. From this finding, one can conclude that the sorption energies have the most relevant influence on the sorption capacities. In this way, it suffices to compare the adsorption energies of the two adsorbates to select the adsorbate that can form the steadiest complex with porphyrins.
The fitting values of the van-der-Waals parameters and the energetic parameters influencing the complexation of cobalt chloride and cobalt nitrate on porphyrin (H2TTPP) are given in Table 3.
| Adsorption system | CoCl2/(S–L–M) | Co(NO3)2/(D–L–M) | |||||
| Physicochemical parameters | a (10−22 J mL mol−1) | b (10−7 mL mol−1) | w1/2 (J mol−1) | a (10−22 J mL mol−1) | b (10−7 mL mol−1) | w1 (J mol−1) | w2 (J mol−1) |
| 288 K | 12.3 | 9.4 | 0.011 | 18.6 | 15.4 | 0.005 | 0.099 |
| 298 K | 9.4 | 12.6 | 0.012 | 15.6 | 18.7 | 0.0059 | 0.096 |
| 308 K | 5.9 | 14.8 | 0.014 | 11.4 | 20.2 | 0.0061 | 0.092 |
| 318 K | 4.8 | 15.8 | 0.013 | 10.2 | 22.4 | 0.006 | 0.09 |
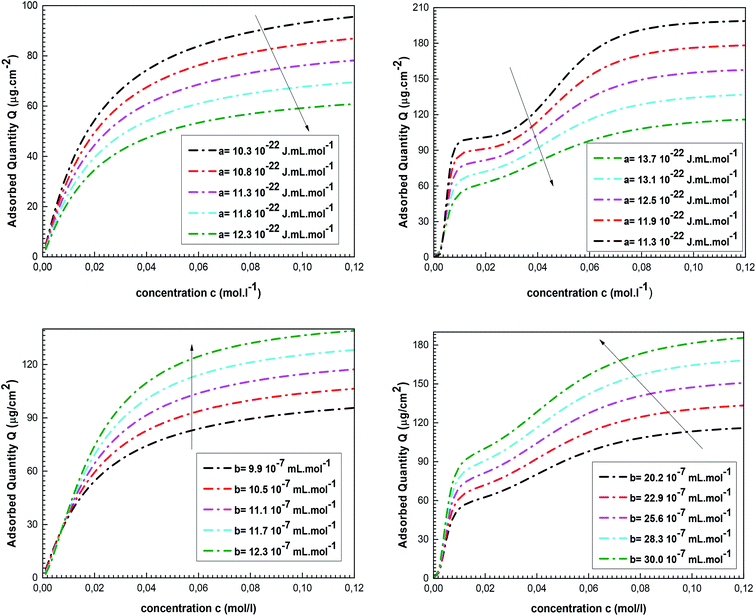
First of all, it is helpful to comprehend the impact of these parameters on the adsorbed quantity. The effects of the van-der-Waals parameters on the isotherms behaviors are reported in Fig. 4.
We note that the adsorbed amount Q decreases with the increase in the value of a. The increase in the cohesion pressure reflects an expansion in the lateral interactions involving the adsorbates. In this situation, the free state is more attractive than the adsorbed phase and the adsorption of cobalt ions on tetrakis(4-tolylphenyl)porphyrin is difficult. An opposite impact is noted for b since the expansion in co-volume induces a rise in the complexed quantity Q. In reality, the rise in the value of b reflects the increase in the distance between the adsorbates, which supports their adsorption by the porphyrin surface.
The values of these parameters and their variations versus temperature for the two complexation processes are shown in Fig. 5.
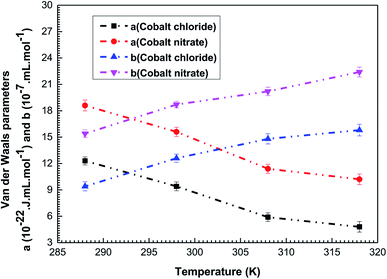 | ||
| Fig. 5 Variations in the adjusted values of the interaction parameters (cohesion pressure a and co-volume b) versus temperature for the cobalt chloride and the cobalt nitrate complexation processes. | ||
As shown in Fig. 5, the cohesion pressure declines with the increase in the temperature for the two adsorption systems. The impact of this variable is greater at low temperatures, so the interaction between the adsorbates is low at high temperature. Therefore, it was concluded that the cobalt ions are easily caught by the tetrakis(4-tolylphenyl)porphyrin at high temperatures. Conversely, it was noticed that an increase in the temperature results in an expansion of b, meaning that the repulsion between adsorbate ions is stronger at high temperatures, which encourages their adsorption by the porphyrinic surface. Consequently, the behavior of these two parameters clarifies the reproducibility of cobalt adsorption at high temperatures and demonstrates the endothermic nature of the complexation processes.
The fitted values of a and b are the highest for the adjustment with the adsorption isotherms of cobalt nitrate: a(Co(NO3)2) > a(CoCl2) and b(Co(NO3)2) > b(CoCl2). This leads to the conclusion that the lateral interactions and the disturbances during the complexation processes are the lowest in the case of cobalt chloride. The use of this type of adsorbate guarantees greater stability during the formation of the vitamin B12 nucleus. This interpretation is in agreement with the experimental results but it obviously requires confirmation through the calculation of the adsorption energies of both complexation systems.
The energetic parameters that govern the complexation process dynamics are w1/2 for cobalt chloride and w1 and w2 for cobalt nitrate. Note that these variables present the affinity of tetrakis(4-tolylphenyl)porphyrin sites for related particles.
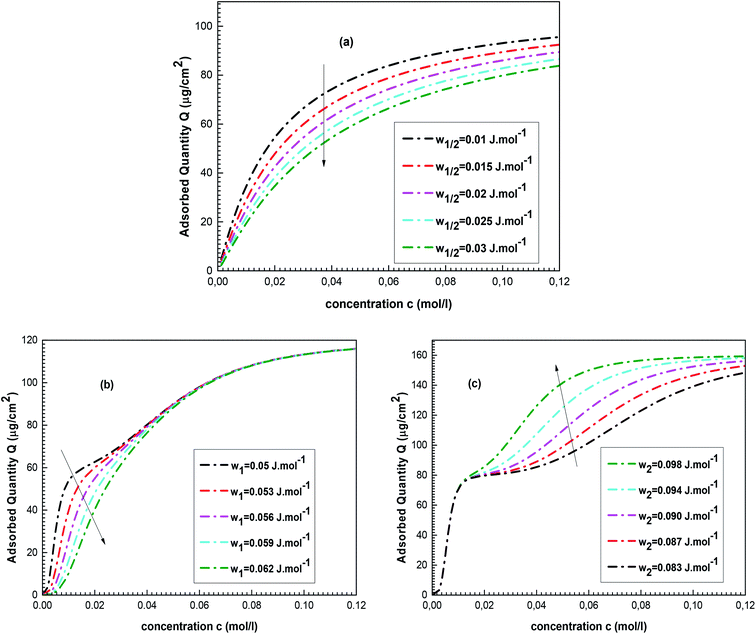
Fig. 6a shows the evolution of the complexed quantity Q of cobalt chloride for various w1/2 values.
One can see that a rise in the value of the energetic parameter w1/2 causes a decrease in Q. Table 1 includes a relation between the complexation energy –E1/2 and w1/2. This relation demonstrates that high values of w1/2 reflect low values of complexation energy –E1/2, i.e., a low complexed quantity Q.
The impacts of w1 and w2 on the complexed quantity Q of cobalt nitrate are illustrated in Fig. 6b and c.
First, it should be noted that an expansion in the values of w1 influences the isotherm plot at low cobalt nitrate concentrations. The influence of w1 on Q is similar to the impact of w1/2 because both characterize the cobalt-tetrakis(4-tolylphenyl)porphyrin interaction. Thus, Q increases as w1 decreases but only in the low concentration range. On the other hand, w2 acts on the isotherm behaviors at high cobalt nitrate concentration because it characterizes the interaction between the two adsorbed layers. At saturation, an increase in the value of w2 causes an expansion of the complexed quantity Q: a high w2 value corresponds to low interaction between the two adsorbed layers (low value of sorption energy –E2), reflecting that the adsorbed ions of the second layer are more attractive to the porphyrin surface and then Q increases.
The description and identification of the interaction type were carried out through complexation energy calculations. The adjusted values of the energetic parameters, w1/2 deduced from the single-layer adsorption and w1 and w2 deduced from the L.B.L double-layer model, were used to compute the complexation energies.
The adsorption energies |(–E1/2)|, |(–E1)| and |(–E2)| were determined under various temperatures by the following formulas:
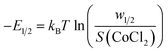 | (5) |
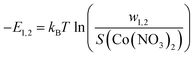 | (6) |
The values of the calculated energies (in modulus) are given in Table 4. Their variations via temperature are delineated in Fig. 7.
| Adsorbate–adsorbent system | (Co(NO3)2)–H2TTPP | (CoCl2)–H2TTPP | |
| Sorption energy | |−E1| (kJ mol−1) | |−E2| (kJ mol−1) | |−E1/2| (kJ mol−1) |
| 288 K | 30.6 | 19.1 | 48.2 |
| 298 K | 35.6 | 17.6 | 50.3 |
| 308 K | 38.9 | 17.1 | 53.9 |
| 318 K | 39.1 | 16.7 | 56.3 |
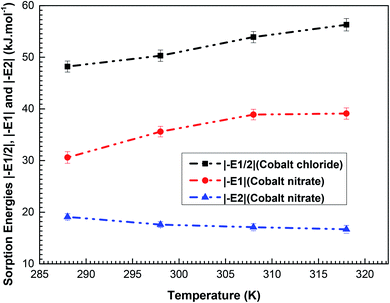 | ||
| Fig. 7 Variations in the adsorption energies |−E1/2| of cobalt chloride and |−E1| and |(−E2)| of cobalt nitrate as a function of temperature (288–318 K). | ||
In light of Fig. 7, one can see that the adsorption energy |(–E1/2)| and |(–E1)| increases (in modulus) with the increase in temperature. It can be clarified by the endothermic nature of the cobalt particle complexation. Conversely, we find that an increase in temperature causes a decrease in the sorption energy |(–E2)|. Since the two adsorption processes are endothermic, it can be established that |(–E1/2)| and |(–E1)| are the deciding factors in the complexation mechanisms. In addition, based on Table 4, for the L.B.L adsorption system, the estimated values of the energy |(–E1)| are higher than those of |(–E2)|. This is entirely logical since (–E1) portrays the connection between the first layer formed with cobalt ions and the complexing surface of porphyrins, whereas (–E2) reflects the interaction between the two adsorbed layers (adsorbate–adsorbate interaction).30
Looking at the values |(–E1/2)| and |(–E1)| of the two adsorption systems, we can note that the (CoCl2)–H2TTPP interaction is stronger than the (Co(NO3)2)–H2TTPP association. This affirms the previous outcome that cobalt chloride is the best adsorbate suited for the complexation of the cationic cobalt ions. The sorption energies |(–E1)| of cobalt nitrate are lower than 40 kJ mol−1, so the binding between cobalt nitrate and the H2TTPP sites takes place via physical adsorption.30,31 All the complexing energies of cobalt chloride are greater than 40 kJ mol; accordingly, we concluded that the complexation of porphyrin H2TTPP by cobalt chloride is a chemical sorption process and this solid binding occurs through covalent or ionic bonds.32
In the next part, thermodynamic properties33 are determined according to the statistical physics treatment in order to get macroscopic information about the double layer adsorption of cobalt nitrate and the single-layer adsorption of cobalt chloride.
3.3. Thermodynamics of the adsorption processes: configurational entropy and Gibbs free enthalpy
The information given by the entropy is very important in the characterization of the behavior of adsorbed particles. The entropy is defined as a quantity that describes the disorder of a studied system, which is proportional to the configurational number needed to achieve this process.2–33 It is therefore the configurational entropy that is considered. The entropy can be calculated on the basis of statistical physics formalism by exploiting the grand potential J and the grand-canonical partition function zgc of the considered system. It can be written in the following formula:1,2,33
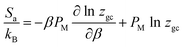 | (7) |
The second thermodynamic function is the Gibbs free enthalpy, which describes the spontaneity of the studied adsorption system. Thanks to the grand canonical formalism in statistical physics, the Gibbs free enthalpy values were calculated as follows:1,33
| G = μ × Q | (8) |
The analytical expressions of the entropy and the free enthalpy determined for the two complexation systems are given Table 5. Fig. 8 depicts the evolution of the entropy and the free enthalpy versus concentration for the single-layer adsorption of cobalt chloride and the L.B.L double-layer adsorption of cobalt nitrate.
a 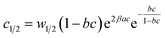 , , 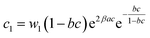 and and 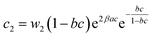 . . |
||
|---|---|---|
| Adsorption system | Single-layer adsorption of cobalt chloride | Double-layer adsorption of cobalt nitrate |
| Entropy Sa/kB | 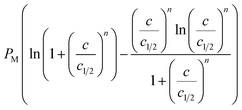 |
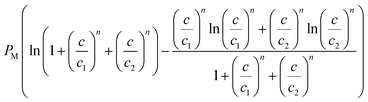 |
| Free enthalpy G/kBT | 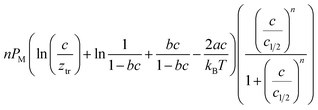 |
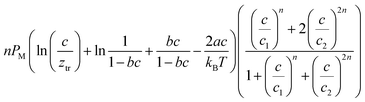 |
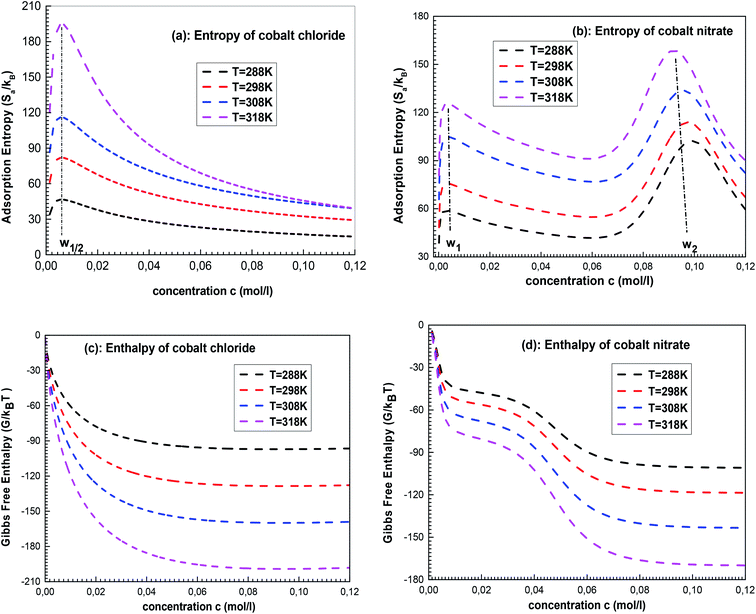
According to Fig. 8a, for cobalt chloride, the entropy has two different behaviors below and above w1/2. Indeed, the entropy increases with concentration before w1/2 and decreases after this particular point. At the beginning of the single-layer adsorption, the disorder at the adsorbent surface increases where the mobility of cobalt particles is important since the adsorbate ion has many possibilities to find an empty site. Then the disorder reaches a maximum value at w1/2. After w1/2, the adsorbate particle has a low probability for choosing an adsorbent site because the surface tends toward monolayer saturation and therefore tends toward the order.
For the double-layer adsorption of cobalt nitrate (Fig. 8b), the entropy reaches two maximum values at w1 and w2, and the peak corresponding to w2 is higher than that corresponding to w1. This can be possibly explained by the nature of the interaction of the energetic parameters: w1 describes the adsorbate–adsorbent interaction and therefore the first peak of the entropy translates to the disorder resulting from the interaction between the cobalt ions and the solid surface only at the first layer level. w2 is linked to the adsorbate–adsorbate interaction; at this particular point, we can speak of a total disorder at the whole system level. The disorder decreases when the saturation is reached.
Fig. 8c and d show that all the values of enthalpy are negative, indicating that the two adsorption processes of CoCl2 and Co(NO3)2 evolve spontaneously. It was also noted that the free enthalpy becomes constant at high concentrations, i.e. the singe-layer and the double-layer systems become more stable when saturation is reached. Interestingly, one can see that the enthalpy of cobalt chloride presents only one stability state (Fig. 8c). However, Fig. 8d shows two states of stability of cobalt-nitrate adsorption: the first partially stable state returns to the saturation of the first layer and the second corresponds to the total state of stability after the formation of the two adsorbed layers.
4. Conclusion, comparison with other works and recommendations
The objective of this paper is to provide an experimental strategy for fabricating the vitamin B12 nucleus based on the Quartz Crystal Microbalance method. Thus, it was ensured that the QCM method was a helpful experimental tool for the measurement of experimental complexation isotherms of cobalt(II) chloride and cobalt(II) nitrate on tetrakis(4-tolylphenyl)porphyrin (H2TTPP). The experimental data were analyzed in order to estimate the best adsorbate that can be used for the achievement of the vitamin B12 nucleus.Two advanced models were established in light of the grand canonical formalism and the real gas law. The single-layer model was found to be the best for the theoretical characterization of cobalt(II) chloride adsorption, demonstrating that the chlorine particles are not engaged in the complexation process. The advanced L.B.L model, which assumed that two layers of adsorbed ions were formed, was affirmed to be the best-embraced model for the hypothetical portrayal of cobalt(II) nitrate adsorption. These modeling results are in acceptable concurrence with recent works dedicated to the adsorption of cationic metals on porphyrins. For example, it was shown that the adsorption of magnesium nitrate, iron nitrate and zinc nitrate onto porphyrin molecules took place via layer-by-layer adsorption, so the anionic particles NO3− are associated with the sorption mechanism and contribute to the layer arrangement. It was likewise shown that the chlorine particles are not associated with the adsorption of magnesium chloride on porphyrins, which is in agreement with the present examination of the cobalt chloride. However, in the case of the L.B.L adsorption, the difference between cobalt nitrate adsorption and the others specially appeared in the number of formed layers. In the referenced works, it was established that a vast number, sometimes an infinite number, of layers was adsorbed onto the porphyrin surface, whereas in the case of cobalt nitrate it was demonstrated that only two layers of adsorbed ions were formed, which led to the use of a double-layer L.B.L model for the theoretical modeling. Moreover, the L.B.L model used in this paper is an advanced form of the double-layer model, which considers the lateral interactions (parameters a and b) between the adsorbates and it has not been used in any previous papers. Without considering the lateral interactions, we acquire another type of the double-layer model established on the basis of the ideal gas approach. This model expression was developed and published in previous papers.13 Both model expressions were developed through statistical physics formalism and constitute advanced model expressions as opposed to the empirical models whose parameters generally have no physical significance. We have shown in the present work the helpfulness of the van-der-Waals variables a and b in elucidating the nature of the complexation mechanisms (endothermic type). In addition, it was demonstrated that the lateral interactions act strongly in the case of cobalt nitrate and that Co(Cl)2–H2TTPP is the most stable complex.
The energetic study showed that (–E1) is the determining factor for the choice of the best complexing porphyrin. By looking at the complexation energy (–E1/2) and (–E1) of each adsorption system, we found that the interaction between cobalt chloride and tetrakis(4-tolylphenyl)porphyrin (H2TTPP) can be covalent or ionic bonds. The thermodynamic study showed that the disorder reaches its maximum value at w1/2 for the single-layer adsorption of cobalt chloride and presented two peaks at w1 and w2 for cobalt nitrate. The study of the Gibbs free enthalpy indicated that the complexation process is spontaneous for the single-layer and the double-layer adsorptions on porphyrins. It was concluded that the statistical physics development can be a fascinating strategy for the description of experimental isotherms and that this physics formalism assists with ascribing physical hugeness to the model parameters.
Finally, relating the experimental results, the numerical findings and the theoretical interpretations, we suggest the use of cobalt chloride as material for producing the nucleus of the vitamin B12 in a genuine industrial application.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. (D-081-662-1441). The authors, therefore, gratefully acknowledge DSR technical and financial support.References
- M. Ben Yahia, S. Knani, L. B. H. Hsan, M. Ben Yahia, H. Nasri and A. B. Lamine, Statistical studies of adsorption isotherms of iron nitrate and iron chloride on a thin layer of porphyrin, J. Mol. Liq., 2017, 248, 235–245 CrossRef CAS.
- S. Knani, N. Khalifa, M. Ben Yahia, F. Aouaini and M. Tounsi, Statistical physics study of the interaction of the 5,10,15,20-tetrakis(4-tolylphenyl)porphyrin (H2TTPP) with magnesium ion: new microscopic interpretations, Arabian J. Chem., 2020, 13, 4374–4385 CrossRef CAS.
- G. McHale, C. Hardacre, R. Ge, N. Doy, R. W. K. Allen, J. M. MacInnes, M. R. Brown and M. I. Newton, Density − viscosity product of small-volume ionic liquid samples using quartz crystal impedance analysis, Anal. Chem., 2008, 80, 5806–5811 CrossRef CAS PubMed.
- A. Nakbi, M. Bouzid, F. Ayachi, F. Aouaini and A. B. Lamine, Investigation of caffeine taste mechanism through a statistical physics modeling of caffeine dose-taste response curve by a biological putative caffeine adsorption process in electrophysiological response, Prog. Biophys. Mol. Biol., 2019, 147, 70–85 CrossRef PubMed.
- M. B. Yahia, F. Aouaini, M. Yahia, E. S. Almogait and H. Al-Ghamdi, Theoretical investigation of the chlorophyll nucleus adsorption monitored with Quartz Crystal Microbalance technique: New insights on physicochemical properties, J. Mol. Liq., 2019, 289, 111188 CrossRef CAS.
- D. Hodgkin, J. Kamper, M. Mackay, J. Pickworth, K. N. Trueblood and J. G. White, Structure of Vitamin B12, Nature, 1956, 178, 64–66 CrossRef CAS PubMed.
- E. M. Bertrand, M. A. Saito, J. J. Young and B. A. Neilan, Vitamin B12 biosynthesis gene diversity in the Ross Sea: the identification of a new group of putative polar B12 biosynthesis, Environ. Microbiol., 2011, 13, 1285–1298 CrossRef CAS PubMed.
- J. A. J. Brunink, C. Di Natale, F. Bungaro, F. A. M. Davide, A. D'Amico, R. Paolesse, T. Boschi, M. Faccio and G. Ferri, The application of metalloporphyrins as coating material for quartz microbalance – based chemical sensors, Anal. Chim. Acta, 1996, 325, 53–64 CrossRef CAS.
- C. D. Natale, A. Macanano, G. Repole, G. Saggio, A. D'Amico, R. Paolesse and T. Boschi, The exploitation of metalloporphyrins as chemically interactive material in chemical sensors, Mater. Sci. Eng., C, 1998, 5, 209–215 CrossRef.
- L. Sun, C. Gu, K. Wen, X. Chao, T. Li, G. Hu and J. Sun, A gas sensor fabricated with field-effect transistors and Langmuir-Blodgett film of porphyrin, Thin Solid Films, 1992, 210–211, 486–488 Search PubMed.
- I. Langmuir, The adsorption of gases on plane surfaces of glass, mica and platinum, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- S. Brunauer, L. S. Deming and E. Teller, On a theory of Van der Waals adsorption of gases, J. Am. Chem. Soc., 1940, 62, 1723–1732 CrossRef CAS.
- S. A. C. Hill, J. A. Norton and G. Newman, The water vapour soption properties of Sitka spruce determined using a dynamic vapor sorption apparatus, Wood Sci. Technol., 2010, 44, 497–514 CrossRef.
- M. Peleg, Assessment of a semi-empirical four parameter general model for sigmoid moisture sorption isotherms, J. Food Process Eng., 1993, 16, 21–37 CrossRef.
- F. M. H. Freundlich, Over the adsorption in solution, J. Phys. Chem., 1906, 57, 385–471 Search PubMed.
- A. D. Adler, F. R. Longo, J. D. Finarelli, J. Goldmacher, J. Assour and L. Korakoff, A simplified synthesis for meso-tetraphenylporphine, J. Org. Chem., 1967, 32, 476 CrossRef CAS.
- J. C. Linnell and D. M. Matthews, Cobalamin metabolism and its clinical aspects, Clin. Sci., 1984, 66, 113–121 CrossRef CAS PubMed.
- R. C. Dart, Hydroxocobalamin for Acute Cyanide Poisoning, Clin. Toxicol., 2006, 44, 1–3 CAS.
- K. Kurzątkowska, D. Shpakovsky, J. Radecki, H. Radecka, Z. Jingwei and E. Milaeva, Iron (III) porphyrin bearing 2,6-di-tert-butylphenol pendants deposited onto gold electrodes for amperometric determination of l-histidine, Talanta, 2009, 78, 126–131 CrossRef PubMed.
- C. Kôfilinger, S. Drost, F. Aberl, H. Wolf, S. Koch and P. Woias, A quartz crystal biosensor for measurement in liquids, Biosens. Bioelectron., 1992, 7, 397–404 CrossRef.
- D. Wang, P. Mousavi, P. J. Hauser, W. Oxenham and C. S. Grant, Quartz crystal microbalance in elevated temperature viscous liquids: Temperature effect compensation and lubricant degradation monitoring, Colloids Surf., A, 2005, 268, 30–39 CrossRef CAS.
- M. Ben Yahia, H. B. L. Hsan, S. Knani, M. B. Yahia, H. Nasri and A. B. Lamine, Modeling of adsorption isotherms of zinc nitrate on a thin layer of porphyrin, J. Mol. Liq., 2016, 222, 576–585 CrossRef.
- B. Ballarin, S. Masiero, R. Seeber and D. Tonelli, Modification of electrodes with porphyrin-functionalised conductive polymers, J. Electroanal. Chem., 1998, 449, 173–180 CrossRef CAS.
- G. Sauerbrey, Use of quartz vibration for weighing thin films of a microbalance, Z. Phys., 1959, 155, 206–212 CrossRef CAS.
- D. Johannsmann, K. Mathauer, G. Wegner and W. Knoll, Viscoelastic properties of thin films probed with a quartz crystal resonator, Phys. Rev. B, 1992, 46, 7808–7815 CrossRef PubMed.
- A. Ben Lamine and Y. Bouazra, Application of statistical thermodynamics to the olfaction mechanism, Chem. Senses, 1997, 22, 67–75 CrossRef CAS PubMed.
- M. Ben Yahia, M. B. Yahia, F. Aouaini, S. Knani, H. Al-Ghamdi, E. S. Almogait and A. B. Lamine, Adsorption of sodium and lithium ions onto helicenes molecules: Experiments and phenomenological modeling, J. Mol. Liq., 2019, 288, 110988 Search PubMed.
- W. D. Marquardt, An algorithm for least-squares-estimation of nonlinear parameters, J. Soc. Ind. Appl. Math., 1963, 11, 431–441 CrossRef.
- M. Ben Yahia, M. Tounsi, F. Aouaini, S. Knani, M. B. Yahia and A. Ben Lamine, A Statistical Physics Study of the Interaction of [7]-Helicene with Alkali Cations (K+ and Cs+): New Insights on Microscopic Adsorption Behavior, RSC Adv., 2017, 7, 44712–44723 RSC.
- M. Bouzid, Q. Zhu, D. M. Geoff and A. Ben Lamine, New insight in adsorption of pyridine on the two modified adsorbents types MN200 and MN500 by means of grand canonical ensemble, J. Mol. Liq., 2018, 263, 413–421 CrossRef.
- S. Wjihi, C. E. Peres, L. G. Dotto and A. Ben Lamine, Physicochemical assessment of crystal violet adsorption on nanosilica through the infinity multilayer model and sites energy distribution, J. Mol. Liq., 2019, 280, 58–63 CrossRef CAS.
- L. Sellaoui, E. F. Soetaredjo, S. Ismadji, B. A. Petriciolet, C. Belver, J. Bedia, B. A. Lamine and A. Erto, Insights on the statistical physics modeling of the adsorption of Cd2+ and Pb2+ ions on bentonite-chitosan composite in single and binary systems, Chem. Eng. J., 2018, 354, 569–576 CrossRef CAS.
- B. Diu, C. Guthmann, D. Lederer and B. Roulet, Physique statistique, Hermann, Paris, 1989 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |