Open Access Article
Open Access ArticleObjective quantification of surface roughness parameters affecting superhydrophobicity†
Yoonkyung Cho and
Chung Hee Park
and
Chung Hee Park *
*
Department of Textiles, Merchandising and Fashion Design, Seoul National University, Seoul, 08826, Republic of Korea. E-mail: junghee@snu.ac.kr
First published on 24th August 2020
Abstract
This study proposes new optical roughness parameters that can be objectively quantified using image processing techniques, and presents an analysis of how these parameters are correlated with the degree of superhydrophobicity. To this end, photolithography and dry etching processes were used to form regular square pillars with different heights and spacings with a length of tens of micro-meters on silicon wafers. Optical roughness parameters of the specimens were obtained using image processing, and surface wettability was characterized using static contact angle and sliding angle measurements for water droplets of volume VD = 3.5 μl or 12 μl. As a result, seven optical roughness parameters were derived to describe the surface roughness topography in a multi-faceted way. Between the Cassie–Baxter state and the Wenzel state, two distinct wetting states intermediate state I, and intermediate state II were observed. Multiple linear regression of optical roughness parameters and superhydrophobicity demonstrated that in the stable Cassie–Baxter state, the contact angle can be increased or sliding angle decreased more effectively by adjusting the spacing between pillars than by just tuning the solid area fraction. However, in the metastable state where the Cassie–Baxter state can be changed to intermediate state I and vice versa by adjusting VD or surface geometry, reducing the solid area fraction is a priority to ensure a stable Cassie–Baxter state. Horizontal-perspective roughness parameters had a great effect on dynamic wettability in the Cassie–Baxter state. The results confirmed that the proposed optical roughness parameters may be useful for quantitative analysis of the complex effects of roughness on superhydrophobic surfaces.
1. Introduction
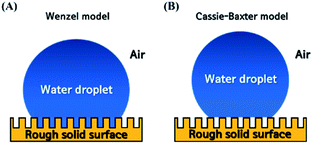
Superhydrophobic surfaces have many uses, including self-cleaning textiles, anti-fogging/anti-icing coatings, and micro-fluidic systems.1–6 For water droplets, the maximum static contact angle can be increased to 120° (ref. 1) on a flat surface by decreasing the surface energy without roughness, whereas a superhydrophobic surface has a high contact angle ≥150° and also a low sliding angle <10°. Thus, to create superhydrophobicity, surface roughness must be formed and controlled to minimize the contact area and interaction between water and the solid surface. Many studies1–9 have been conducted to understand the effect of surface roughness on the surface wettability, with the goal of increasing the ability to obtain superhydrophobic surfaces. Theoretical models and experimental studies have determined how surface roughness affects surface wettability.7,9–13 The most basic models for describing wettability on rough surfaces are the Wenzel model10 and the Cassie–Baxter model.11 The Wenzel model10 is
cos(θW) = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ0) cos(θ0)
| (1) |
cos(θCB) = f![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ0) + f − 1 cos(θ0) + f − 1
| (2) |
The two models consider different behaviors of a water droplet on a surface. The Wenzel model considers a water droplet that seeps in between the irregularities of a rough surface (Fig. 1A). The Cassie–Baxter model considers a water droplet that sits on top of the irregularities, with a layer of air trapped between the irregularities beneath it (Fig. 1B).
The Wenzel and Cassie–Baxter models are widely used to describe and predict the static contact angle of rough surfaces. However, some wetting phenomena (e.g., transition state,5 rose-petal effect8) cannot be described by either of the two models. A droplet's attachment to, and rolling off from a surface are mainly associated with the dynamics of the three-phase contact line.19 The balance of adhesion, shear, gravitational and air drag forces along the contact line governs acceleration of droplet rolling (or the droplet can be pinned on the surface by the balance).19 Surface energy, roughness topography, water droplet volume and environmental conditions all affect each of these force. In the petal effect, water contact angle is high but the droplets stick to the surface even in the case of reversing. As the structure is in a Cassie impregnating wetting state, the droplets on the surface penetrate through the microstructures but cannot penetrate through the nanostructures, with a strong negative pressure owing to the small volume of sealed air between the nanostructures.25 However, the Wenzel and Cassie–Baxter models predict water contact angle by using only surface energy (cos(θ0)) and simplified roughness factors (r, f) and therefore disregarded important factors. Furthermore, they only consider situations in which the droplet completely wets the surface (Wenzel) or touches the tops of surface structure without much penetration (Cassie–Baxter). For these reasons, these models are valid only in some range of wetting states21 so numerous follow-up studies20–23 have been conducted to complement these models.
Especially, regarding the effect of surface roughness, it was experimentally proven that surface superhydrophobicity is considerably affected not only by the vertical-perspective roughness factors (r in the Wenzel model, f in the Cassie–Baxter model) but also by the horizontal-perspective roughness factors, including spacing between surface irregularities and the shape of surface irregularities.7,9,12,13
Rahmawan et al.12 explained the effect of surface roughness on superhydrophobicity by combining the Wenzel and Cassie–Baxter models for the surface that has dual micro-nanoscale roughness. The superhydrophobicity greatly decreases when the spacing between micro-pillars becomes wider than a certain threshold.12 Han and Gao13 evaluated the wettability of the film surfaces having hexagonal ZnO nano-rods, and found that the contact angle depends on ZnO nano-rods' length, density and diameter.13 To represent these results, the Cassie–Baxter f is modified to13
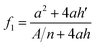 | (3) |
According to Yoshimitsu et al.,7 to increase the shedding of water droplets, adjustment of the shape and scale of the solid–liquid–gas triple phase boundary is better than simply reducing the solid area fraction f. Heavy droplets can easily overcome sliding resistance because of the effect of gravity, so they have low sliding angle, and their weight has a larger effect on sliding angle than on static contact angle.7
Zheng et al.9,14,15 mathematically analyzed the wetting transition state between Wenzel state and Cassie–Baxter state as a function of hydraulic pressure P. They proposed a critical hydraulic pressure Pc, which is the maximum at which the Cassie–Baxter state can be maintained (eqn (4)).9 Pc can be increased by reducing the droplets surface tension (γ), the solid fraction (f), and the solid surface energy (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∅0), while also adjusting the shape of the pillar tops (λ):
∅0), while also adjusting the shape of the pillar tops (λ):
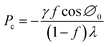 | (4) |
These studies showed how horizontal-perspective roughness factors such as pillar density and shapes affect superhydrophobicity. However, the results reached conclusions that have limited applications for given surfaces or are partially contradictory. Moreover, surface roughness topography affects superhydrophobicity of surfaces in ways that have not been clarified.16 Until now, it was only possible to quantitatively obtain vertical-perspective surface roughness parameters such as average deviation Ra and standard deviation Rq due to the limitations of the roughness evaluation methods. Even though the horizontal-perspective has importance in the superhydrophobic properties on surfaces, there are not universal and easy-to-handle characterization methods of horizontal-perspective roughness. Thus, quite frequently, the visual observation of microscopic images of superhydrophobic surfaces is reduced to expressions such as “the grain sizes varied”13 or “similar rod density”,13 which estimate the number, shape, density and spacing of irregularities on surfaces. The reader might be then led to the subjective point of view of the writer.17 On the other hand, descriptions such as “at least ten measurements were made manually for analysis of the geometry of the nano-rods”6 can also be found, but ranges are normally limited to the selected area and cannot represent the overall characteristics of the surface. As such, we consider that an effort on quantification of various roughness parameters and their effects on superhydrophobicity should be made.
Therefore, the goal of this study was to obtain quantitative roughness parameters that describe surface topography by using simple image-processing techniques, and to examine the effect of each parameter on superhydrophobicity to establish an understanding of how surface roughness affects surface wettability at surface roughness range of several tens of micro-meters. For this purpose, Si wafers with pillars of different heights and spacing on the surface were prepared, and the surface roughness was quantitatively evaluated from binarized grayscale digital images. The reliability and accuracy of the proposed parameters were verified by comparison with actual values. To estimate superhydrophobicity, contact angle and sliding angle were measured, then the relationship between these optical roughness parameters and superhydrophobicity was quantified using multiple linear regression analysis.
2. Experimental section
2.1 Fabrication of samples with controlled micro-roughness
To create samples that had regular roughness with micro-scale square pillars, p-type Si wafers (4′′ diameter) were etched by photolithography and dry etching. Tops of the pillars were square with sides of 10 μm. The pillar heights H were 10 μm or 50 μm, the spacing between pillars S was 10 μm, 20 μm or 30 μm (Table 1). Samples were coded H, S, and a number that represents the length (μm).| Pillar top size (μm) | 10 × 10 | ||
| Pillar top shape | Square | ||
| Pillar height (μm) | 10 | 50 | |
| Spacing between pillars (μm) | 10 | 20 | 30 |
2.2 Measurement of surface wettability
To analyze the superhydrophobicity of the samples with different roughness, they were hydrophobized using 1H,1H,2H,2H-perfluorodecyltriethoxysilane (C12H15F17O3Si, FAS-17, 97%, Sigma Aldrich Co., Ltd.). Samples were placed in a vacuum oven at 400 Torr and 200 °C with 100 μl of FAS-17, then physical vapor deposition by thermal evaporation was performed for 40 min.7 The samples were dried for 30 min at 80 °C. Static contact angles (SCA) and sliding angles (SA) were measured for distilled water droplets of VD = 3.5 μl or 12 μl, using a contact-angle goniometer (Theta Lite Optical Tensiometer, KSV Instruments Co., Ltd., Finland). SCA was measured at five places on each sample, then averaged out of the three samples. To measure SA, conventional tilted-plate method was used (droplets placed on a level surface, which was then inclined24). The water droplet was dropped from a height of 1 cm vertically above the sample and the sample was tilted at 0.5° intervals; SA is defined as the tilt angle at which the droplet starts to roll off the surface. This measurement was repeated three times and averaged.2.3 Surface roughness evaluation by image processing
| Region of interest (μm) | 120 × 90 |
| Magnification | ×100 |
| Distance from lens to sample (cm) | 1 |
| Brightness | 128 |
| Image size (px) | 1024 × 769 |
| Resolution (DPI) | 600 |
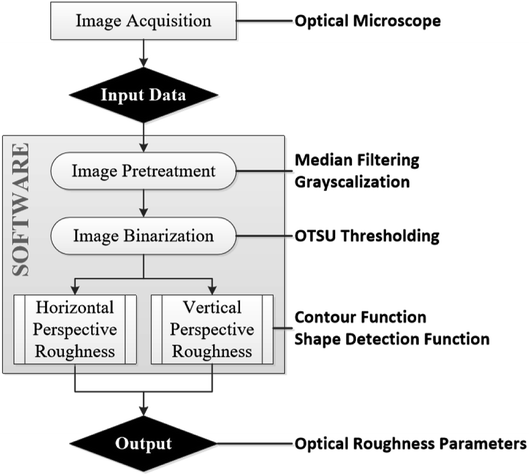
Original images were 1024 × 769 pixel matrices, and were used without any size change during image processing. As input data to extract roughness parameters, the images were pretreated by median filtering to remove noise, then converted to grayscale, then binarized. To distinguish pillar tops in the images, the OTSU thresholding algorithm was used; it binarizes grayscale images by classifying the brightness values (0–255) into two groups relative to a threshold value 0 < t < 255 that creates maximum variance between groups, and minimum variance within them. Therefore, the binarization could be performed automatically on the sample images. As a result, the pixel values of images are divided into 1 (white) or 0 (black), where the white pixels represent pillar tops, and the black pixels represent background.
 and solid area fraction (f*).11 The asterisks distinguish measured optical parameters from actual values of geometric characteristics of samples.
and solid area fraction (f*).11 The asterisks distinguish measured optical parameters from actual values of geometric characteristics of samples.
The image processing method for extracting optical roughness parameters considers the actual area and length of single pixels in the image, and the number and location of the pixels that consist of the pillar tops. The areas of the region of interest and of the image are known (Table 2), so the actual area that one pixel represents can be calculated as:
Actual area represented by one pixel (μm2)
For shape analysis, object detection and recognition in this study, the contour and shape-detection OpenCV programming functions were used. The contour function detected boundaries of each group of white pixels, then calculated the number of pixels in the boundary. The shape-detection function detected square pillar tops, and recorded the coordinates of the four vertexes of each top.
3. Results and discussion
3.1 Superhydrophobicity of the micro-roughness samples
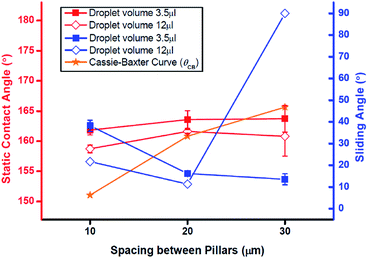
The flat sample had SCA = 120° after hydrophobization. This result confirms that a FAS-17 monolayer was deposited on the sample surface.16 The tilted flat sample showed no shedding effect.Fig. 3 and 4 shows the effect of pillar spacing S and water droplet volume VD on the SCA and SA of the hydrophobized specimens with pillars that had height H = 50 μm or 10 μm, respectively. At H = 50 μm (Fig. 3), SCA of 3.5 μl water droplet increased as S increased; the reason is that the contact area between water and solid decreases as S increases. At S = 30 μm, the droplet could not remain on the surface, and fell off immediately (SCA = 180°). These measured SCA were higher than the predictions θCB of the Cassie–Baxter model. However, at VD = 12 μl, SCA increased in the range 10 ≤ S ≤ 20 μm, but maintained similar values at 20 ≤ S ≤ 30 μm. Droplets of VD = 12 μl on S = 30 μm had SCA < θCB. At both VD, SA decreased as S increased. Here we found two surface-wetting cases: (1) a stable Cassie–Baxter state in which the water droplet has SCA > θCB and the water slides off the surface; and (2) an intermediate state I in which SCA < θCB and the water also slides off the surface. The 12 μl droplet on H50–S30 had SCA < θCB and was therefore in intermediate state I, because the shedding effect of the droplet was maintained (SA < 10°).
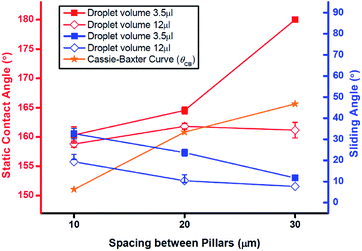 | ||
| Fig. 3 Static contact angle (red lines, left axis) and sliding angle (blue lines, right axis) of samples with pillars with height = 50 μm. Orange line: prediction of Cassie–Baxter model. | ||
 | ||
| Fig. 4 Static contact angle (red lines, left axis) and sliding angle (blue lines, right axis) of samples with pillars height = 10 μm. Orange line: prediction of Cassie–Baxter model. | ||
When the H was 10 μm (Fig. 4), SCA of 3.5 μl and 12 μl droplets increased as S increased from 10 μm to 20 μm. At S = 30 μm, SCA decreased slightly to <θCB. However, the effect of S on SA was different for the two VD. For the 3.5 μl droplet, SA decreased as S increased. In contrast, for the 12 μl droplets, SA decreased in as S increased from 10 μm to 20 μm, but the droplet became pinned at S = 30 μm. In the H10–S30 specimen, a 12 μl droplet showed another wetting case: intermediate state II in which SCA < θCB and the water does not run off the surface. Intermediate state II is distinct from the Wenzel state because the SCA of intermediate state II does not correspond to the static contact angles θW predicted by Wenzel model (Table 5).
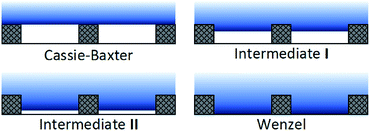
Therefore, we observed four wetting states of water droplet on solid surface (Fig. 5): the Cassie–Baxter and Wenzel states, and two distinct intermediate states between them. During intermediate state I, the water starts moving down and entering the valleys between the pillars,18 but this movement does not affect the ability to shed water. During intermediate state II the water has filled the grooves but does not completely penetrate into the valleys; in this state, shedding of water is impaired. Both intermediate states occur when S is sufficiently wide or the water droplet is sufficiently heavy, or H is sufficiently low.
The predicted contact angles by Cassie–Baxter and Wenzel model, measured contact angles and wetting states of the specimens are summarized in Table 5. The measured contact angles were generally closer to the predictions of the Cassie–Baxter model than of the Wenzel model. However, sometimes the measured values are way off than theoretical values. The large gaps might result from the limitations of the Wenzel and Cassie–Baxter models, which cannot perfectly incorporate the effects of water droplet volume and surface geometry on SCA. Furthermore, some small gaps might be due to fine surface scratches that are inevitably created on the pillar tops during sample fabrication.
VD affected surface wettability. SCA was higher for 3.5 μl droplets than for 12 μl droplets. The inner pressures (Table 4) of the droplets were calculated as9
| P = (4/D) × γ | (5) |
| Water volume (μl) | 3.5 | 12 | 1000 |
| Surface tension (dyne cm−1) | 72.8 | ||
| Droplet diameter (mm) | 1.9 | 2.9 | 12.4 |
| Inner pressure (Pa) | 1531.58 | 1003.45 | 234.68 |
| Sample | Predicted contact angle | Measured contact angle and wetting state | ||||
|---|---|---|---|---|---|---|
| θW | θCB | Droplet volume 3.5 μl | Droplet volume 12 μl | |||
| θMea | Wetting state | θMea | Wetting state | |||
| a θW: predicted contact angle by Wenzel;10 θCB: predicted contact angle by Cassie–Baxter;11 θMea: averaged actual measured contact angle by experiment. | ||||||
| H10–S10 | 180 | 151 | 161 | Cassie–Baxter | 159 | Cassie–Baxter |
| H10–S20 | 136 | 160 | 164 | Cassie–Baxter | 162 | Cassie–Baxter |
| H10–S30 | 128 | 165 | 164 | Intermediate I | 161 | Intermediate II |
| H50–S10 | NA | 151 | 160 | Cassie–Baxter | 159 | Cassie–Baxter |
| H50–S20 | NA | 160 | 165 | Cassie–Baxter | 162 | Cassie–Baxter |
| H50–S30 | NA | 165 | >180 | Cassie–Baxter | 161 | Intermediate I |
VD also affected dynamic wettability. SA tended to be smaller for the 12 μl droplets than for the 3.5 μl droplets. This was possibly because the weight influenced more strongly on SA for large-volume drops and thus made the water droplet overcome the sliding resistance more easily.7
However, this tendency with VD was applicable only for the Cassie–Baxter state and intermediate state I. Therefore, within a range of VD, the Cassie–Baxter state can be maintained at a given surface roughness; from the opposite perspective, a suitable range of roughness values can maintain a stable Cassie–Baxter state according to the VD and pressure. In this study, SA was measured while the droplet is at rest on the level surface, so that measurements exclude the effect of outer hydraulic pressure that is exerted when the droplet strikes a surface.
Fig. 6 shows the photographic images of a 3.5 μl droplet and a 12 μl droplet on the sample surface. We can see that the 12 μl droplet has a distorted appearance compared to the 3.5 μl droplet due to its weight.
3.2 Optical roughness parameters of the micro-roughness samples
Tables 6 and 7 show the original optical microscope images of the samples and binary images obtained using the OTSU thresholding algorithm. When the H was 50 μm (Table 6), the contrast between the pillar tops and bottom was clear in all specimens, although the contrast decreased slightly as S increased. The high pillars can cast shadows by blocking the incident light from the microscope, and can increase the amount of diffused reflection between the pillars (Fig. 7A); this effect causes a difference in light intensity collected by the sensor from the pillar tops and bottom. Thus, in the grayscale image, the pixels that represent pillar tops were significantly whiter than those of bottom, so OTSU extracted the tops successfully. The optimal threshold values of each sample image were set automatically; 102 (H50–S10), 107 (H50–S20) and 166 (H50–S30) (Table 6).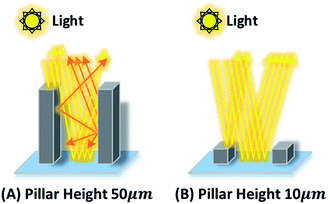 | ||
| Fig. 7 Simple schematic illustration of reflection of light rays: (A) pillars height H = 50 μm; (B) pillars height H = 10 μm. | ||
However, in specimens that had pillars H = 10 μm, the contrast between the pillar tops and bottom was not clear. The distinction between the pillar tops and bottom became difficult as S increased. As shown in Fig. 7B, the H was not sufficient to cast a shadow or to scatter the reflected light between pillars; the result was a weak difference in light intensity reflected from the pillar tops and bottom. As a result, image binarization could not be performed successfully with these samples. Therefore, to extract pillar tops from the images, we converted the white pixels of the bottom except the pillar tops into black after OTSU binarization (Table 7). Further considerations must be taken into account to develop an objective binarization method to extract meaningful features in this case.
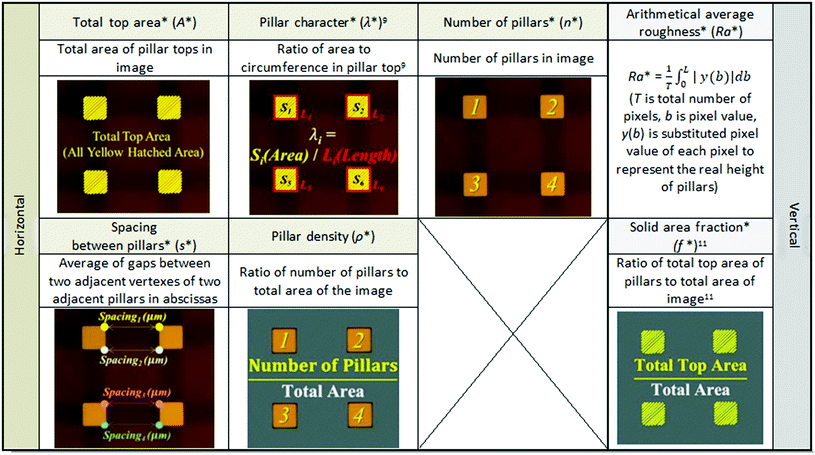
Table 8 shows several geometric characteristics of the specimens and the optical roughness parameters by binary images. Geometric characteristics are calculated as:
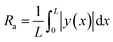 | (6) |
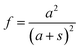 | (7) |
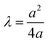 | (8) |
| Sample | Geometric characteristics | Optical roughness parameters | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Horizontal | Vertical | Horizontal | |||||||||||||
| s | Ra | f11 (%) | λ9 | s* (μm) | s* |Δ| | |Δ| | f* (%) | f* |Δ| | λ* | λ* |Δ| | n* | ρ* (n*/mm2) | ρ* (μm2) | ||
a s: spacing between pillars; Ra: arithmetical average roughness; f: area fraction by Cassie–Baxter;11 λ: pillar characteristic parameter by Zheng et al.;9 A*: total top area*; λ*: pillar character*; f*: solid area fraction*; n*: number of pillars*; s*: spacing between pillars*; ρ*: pillar density*; 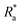 : arithmetical average roughness* (asterisk denotes optical roughness parameters), Δ: uncertainties of optical roughness parameters (s*, : arithmetical average roughness* (asterisk denotes optical roughness parameters), Δ: uncertainties of optical roughness parameters (s*, 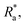 f*, λ*). f*, λ*). |
|||||||||||||||
| H10–S10 | 10 | 5.0 | 25 | 2.5 | 10.2 (±0.03) | 0.2 | 3.66 | 1.34 | 24.1 | 0.9 | 2.65 (±0.04) | 0.15 | 20 | 1851.9 | 2601.1 |
| H10–S20 | 20 | 4.8 | 11 | 2.5 | 20.3 (±0.1) | 0.3 | 2.17 | 2.63 | 12.4 | 1.4 | 2.61 (±0.07) | 0.11 | 12 | 1111.1 | 1334.5 |
| H10–S30 | 30 | 4.2 | 6 | 2.5 | 30.7 (±0.2) | 0.7 | 1.13 | 3.07 | 6.0 | 0 | 2.44 (±0.20) | 0.06 | 6 | 555.6 | 649.6 |
| H50–S10 | 10 | 25.0 | 25 | 2.5 | 11.2 (±0.08) | 1.2 | 18.25 | 6.75 | 24.0 | 1.0 | 2.42 (±0.02) | 0.08 | 24 | 2222.2 | 2587.7 |
| H50–S20 | 20 | 24.0 | 11 | 2.5 | 21.5 (±0.05) | 1.5 | 8.93 | 15.07 | 9.9 | 1.1 | 2.30 (±0.02) | 0.20 | 12 | 1111.1 | 1067.7 |
| H50–S30 | 30 | 21.0 | 6 | 2.5 | 33.3 (±0.06) | 3.3 | 5.15 | 15.85 | 5.5 | 0.5 | 2.47 (±0.01) | 0.03 | 6 | 555.6 | 587.3 |
Versatile explanation of surface topography was possible by using the optical roughness parameters A*, n* or ρ*. The common roughness factors Ra, f and λ were also obtainable from the optical roughness parameters 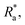 f* and λ*. Comparison of optical roughness parameter values with geometric characteristic values of specimens revealed little difference, so the results of image processing were considered reliable and applicable.
f* and λ*. Comparison of optical roughness parameter values with geometric characteristic values of specimens revealed little difference, so the results of image processing were considered reliable and applicable.
3.3 Relationship between superhydrophobicity and the optical roughness parameters
The relationship between the optical roughness parameters and superhydrophobicity of specimens was quantified by linear regression. First, the optical roughness parameters A* and n* were adjusted to ad. A* and ad. n* by normalization to the droplets contact area with the solid surface (Table 9). This area was calculated using the actual length l of droplet baseline that touches the solid surface.| Sample | l (mm) | Adjusted A* (mm2) | Adjusted n* | |||
|---|---|---|---|---|---|---|
| 3.5 μl | 12 μl | 3.5 μl | 12 μl | 3.5 μl | 12 μl | |
| H10–S10 | 0.84 | 1.52 | 0.13 | 0.44 | 1026 | 3360 |
| H10–S20 | 0.85 | 1.52 | 0.07 | 0.22 | 631 | 2016 |
| H10–S30 | 0.85 | 1.62 | 0.03 | 0.12 | 315 | 1145 |
| H50–S10 | 0.85 | 1.54 | 0.14 | 0.45 | 1261 | 4139 |
| H50–S20 | 0.85 | 1.53 | 0.06 | 0.18 | 631 | 2043 |
| H50–S30 | 0 | 1.56 | 0 | 0.10 | 0 | 1062 |
Linear regressions were performed to determine the relationships between optical parameters and SCA/SA for each H and VD (Table 10, ESI Fig. 1a–h†). At H = 10 μm and VD = 3.5 μl, f* and SCA showed the highest correlation (correlation coefficient >0.95, R2 > 0.90). For SA, f* and ad. A* showed the highest correlation (correlation coefficient >0.95, R2 > 0.90). At H = 50 μm and VD = 3.5 μl, the optical roughness parameter s* was the most influential factor on SCA, and s* × ρ* × ad. A* × ad. n* were the most influential factors on SA. The R2 values of parameters were high enough to prove the validity of the regression models. However, at H = 50 μm pillars and VD = 12 μl, f* and ad. A* had the greatest correlation with SCA (R2 > 0.80), and f* × ρ* × 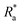 × ad. A* × ad. n* had the most significant relationship with SA. At H = 10 μm and VD = 12 μl, none of the optical roughness parameters had a significant correlation with either SCA or SA. Another notable point is that at H = 50 μm and VD = 3.5 μl, the dynamic wettability SA was more affected by horizontal-perspective roughness parameters (s* × ρ* × ad. A* × ad. n*) than by vertical-perspective roughness parameters
× ad. A* × ad. n* had the most significant relationship with SA. At H = 10 μm and VD = 12 μl, none of the optical roughness parameters had a significant correlation with either SCA or SA. Another notable point is that at H = 50 μm and VD = 3.5 μl, the dynamic wettability SA was more affected by horizontal-perspective roughness parameters (s* × ρ* × ad. A* × ad. n*) than by vertical-perspective roughness parameters 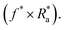
These results lead to the following conclusions. First, in the range of the stable Cassie–Baxter state (H = 50 μm VD = 3.5 μl), the best way to increase SCA or decrease SA is to increase s* rather than f*. Second, at a metastable state that the Cassie–Baxter state and intermediate state I can be switched depending on VD or surface geometry (H = 10 μm VD = 3.5 μl; H = 50 μm VD = 12 μl), the best way to increase SCA and SA is to tune f*; the result is a stable Cassie–Baxter state. Third, to increase the dynamic wettability in the Cassie–Baxter state, horizontal parameters are more important than vertical ones. Consequently, depending on the wetting state, the influence of each optical roughness parameter on superhydrophobicity changes. Therefore, strategies to control static or dynamic hydrophobicity by coordinating surface roughness must consider the wetting state.
The roughness factor λ was the same in all specimens, influence of λ* on superhydrophobicity could not be analyzed in this study. According to previous study,9 λ depends on the shape and size of the pillar tops. Smaller λ can be driven by more complicated or multi-connected pillar tops, and lead higher superhydrophobicity.9 The influence of the optical roughness parameter λ* should be explored in further study with various samples of different λ*.
4. Conclusions
This study was intended to propose objective optical parameters to quantify surface roughness and to establish the relationship between these parameters and the superhydrophobicity of the surface. For this purpose, microscale pillars were formed on silicon wafers by photolithography followed by etching, and their roughness topographies were evaluated using image processing techniques.Six specimens with various roughness were vapor deposited with FAS-17. Their wetting behaviors were affected by pillar height H, spacing between pillars S and water droplet volume VD. The wetting states of the specimens by water droplets of two volumes were divided into four states: Cassie–Baxter state, intermediate state I, intermediate state II and Wenzel state. Increase in water droplet volume yielded enhanced sliding of the droplet only in the Cassie–Baxter state and intermediate state I.
For quantitative evaluation of the surface roughness, the developed image processing program yielded seven optical roughness parameters. The values were very similar to the geometric characteristic values of specimens. Optical roughness parameters A*, n* and ρ* provided additional information to existing roughness factors. Therefore, these optical roughness parameters provide reliable and complementary methods to describe surface topography of silicon wafers that have micro-scale roughness. This is the first step to eliminate the need for subjective assessment of the morphological aspects of superhydrophobic surfaces.
The relationship between optical roughness parameters and superhydrophobicity was analyzed by linear regression. In samples with H = 50 μm and VD = 3.5 μl, the wetting state was stable Cassie–Baxter state; increase of SCA and decrease of SA can be achieved more effectively by increasing s* than by reducing f*. However, with H = 10 μm and VD = 3.5 μl, or H = 50 μm and VD = 12 μl, the wetting state was switchable from Cassie–Baxter state to intermediate I, so increase in SCA or decrease in SA can be accomplished best by reducing f* to make the wetting state enter a stable Cassie–Baxter state. In the stable Cassie–Baxter state, horizontal parameters had a strong effect on dynamic wettability. Therefore, to obtain extreme superhydrophobic phenomena, e.g. lotus effect, horizontal parameters should be considered.
The validation of these relationships improves over earlier studies of superhydrophobic surface, which focused mainly on the relationship between f and superhydrophobicity. The relationships identified in this study can be used to optimize superhydrophobic surface by controlling an appropriate optical roughness parameter according to the surfaces wetting states and VD. However, as an early attempt to objectively quantify superhydrophobic surface roughness, this study only focuses on the regular micro-scale roughness parameters. Most industrial superhydrophobic surfaces have uncontrolled roughness scale less than several micrometers, or even nanometers, so further study should be conducted to expand objective characterization of irregular nano-scaled roughness and its effect on superhydrophobicity.
The proposed optical roughness parameters have potential applications for comprehensive quantitative analysis of the effects of roughness on superhydrophobic surfaces.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MEST – 2018R1A2B6003526, MOE – 2020R1A6A3A13073063).References
- A. Lafuma and D. Quere, Superhydrophobic states, Nat. Mater., 2003, 2, 457–460 CrossRef CAS PubMed.
- M. H. Shim, C. H. Park and J. Y. Kim, The effects of surface energy and roughness on the hydrophobicity of woven fabrics, Text. Res. J., 2014, 84(12), 1268–1278 CrossRef.
- S. O. Kwon, T. J. Ko, E. S. Yu, J. Y. Kim, M. W. Moon and C. H. Park, Nanostructured self-cleaning lyocell fabrics with asymmetric wettability and moisture absorbency (part I), RSC Adv., 2014, 4(85), 45442–45448 RSC.
- M. Miwa, A. Nakajima, A. Fujishima, K. Hashimoto and T. Watanabe, Effects of the surface roughness on sliding angles of water droplets on superhydrophobic surfaces, Langmuir, 2000, 16(13), 5754–5760 CrossRef CAS.
- S. H. Park, J. Y. Kim and C. H. Park, Influence of micro and nano-scale roughness on hydrophobicity of a plasma treated woven fabric, Text. Res. J., 2017, 87(2), 193–207 CrossRef CAS.
- Y. W. Park, C. H. Park and J. Y. Kim, A quantitative analysis on the surface roughness and the level of hydrophobicity for superhydrophobic ZnO nanorods grown textiles, Text. Res. J., 2014, 84(16), 1776–1788 CrossRef.
- Z. Yoshimitsu, A. Nakajima, T. Watanabe and K. Hashimoto, Effects of surface structure on the hydrophobicity and sliding behavior of water droplets, Langmuir, 2002, 18, 5818–5822 CrossRef CAS.
- B. Bhushan and M. Nosonovsky, The rose petal effect and the modes of superhydrophobicity, Philos. Trans. R. Soc., A, 2010, 368, 4713–4728 CrossRef CAS PubMed.
- Q. S. Zheng, Y. Yu. and Z. H. Zhao, Effects of hydraulic pressure on the stability and transition of wetting modes of superhydrophobic surfaces, Langmuir, 2005, 21, 12207–12212 CrossRef CAS PubMed.
- R. N. Wenzel, Resistance of solid surfaces to wetting by water, Ind. Eng. Chem., 1936, 28, 988–994 CrossRef CAS.
- A. B. D. Cassie and S. Baxter, Wettability of porous surfaces, Trans. Faraday Soc., 1944, 40, 546–551 RSC.
- Y. Rahmawan, M. W. Moon, K. S. Kim, K. R. Lee and K. Y. Suh, Wrinkled, dual-scale structures of diamond-like carbon (DLC) for superhydrophobicity, Langmuir, 2010, 26(1), 484–491 CrossRef CAS PubMed.
- J. Han and W. Gao, Surface wettability of nanostructured zinc oxide films, J. Electron. Mater., 2008, 38(4), 601–608 CrossRef.
- Q. S. Zheng, C. J. Lu, P. F. Hao and J. Sheridan, Small is beautiful, and dry, Sci. China: Phys., Mech. Astron., 2010, 53(12), 2245–2259 CAS.
- Q. S. Zheng and C. Lu, Size effects of surface roughness to superhydrophobicity, Procedia IUTAM, 2014, 10, 462–475 CrossRef.
- S. A. Kulinich and M. Farzaneh, Hydrophobic properties of surfaces coated with fluoroalkylsiloxane and alkylsiloxane monolayers, Surf. Sci., 2004, 573, 379–390 CrossRef CAS.
- M. Vidal, M. Ostra, N. Imaz, E. Garcia-Lecina and C. Ubide, Analysis of SEM digital images to quantify crack network pattern area in chromium electrodeposits, Surf. Coat. Technol., 2016, 285, 289–297 CrossRef CAS.
- N. A. Patankar, Transition between superhydrophobic states on rough surfaces, Langmuir, 2004, 20, 7097–7102 CrossRef CAS PubMed.
- S. Y. Bekir, A. S. Abudllah, A. Haider and A. A. Nasser, Dynamics of a water droplet on a hydrophobic inclined surface: influence of droplet size and surface inclination angle on droplet rolling, RSC Adv., 2017, 7, 48806–48818 RSC.
- G. McHale, Cassie and Wenzel: Were they really so wrong?, Langmuir, 2007, 23(15), 8200–8205 CrossRef PubMed.
- L. Gao and T. J. McCarthy, How Wenzel and Cassie were wrong, Langmuir, 2007, 23(7), 3762–3765 CrossRef CAS PubMed.
- M. V. Panchagnula and S. Vedentam, Comment on how wenzel and Cassie were wrong by Gao and McCarthy, Langmuir, 2007, 23(26), 13242 CrossRef CAS PubMed.
- H. Y. Erbil and C. E. Cansoy, Range of applicability of the Wenzel and Cassie-Baxter equations for superhydrophobic surfaces, Langmuir, 2009, 25(24), 14135–14145 CrossRef CAS PubMed.
- E. Pierce, F. J. Carmona and A. Amirfazil, Understanding of sliding and contact angle results in tilted plate experiments, Colloids Surf., A, 2008, 323, 73–82 CrossRef CAS.
- L. Feng, Y. Zhang, J. Xi, Y. Zhu, N. Wang, F. Xia and L. Jiang, Petal effect: A superhydrophobic state with high adhesive force, Langmuir, 2008, 24(8), 4114–4119 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra03137b |
| This journal is © The Royal Society of Chemistry 2020 |