Aluminum nanocomposites reinforced with monolayer polyaniline (C₃N): assessing the mechanical and ballistic properties

Abstract

This study unveils C₃N, a new material that serves as an excellent reinforcement to enhance the mechanical properties of aluminum using a molecular dynamics simulation method. Results show that the C₃N nanosheets greatly improve the mechanical properties of aluminum-based nanocomposites. With only 1.3 wt% C₃N, the Young's modulus, fracture strength, and fracture strain increased by 27, 70, and 51 percent, respectively. A comparison between the reinforcement of graphene and C₃N in an aluminum (Al) matrix shows that in terms of the mechanical properties, the graphene–aluminum composite is weaker than the C₃N–aluminum composite in the tensile tests, but slightly stronger in the energy adsorption tests. Our findings show that the mechanical properties are highly dependent on the strain rate and temperature. The effects of various imperfections, such as the vacancy, crack, and void defects, on the mechanical properties were also studied. Results show that in the presence of void defects, the structure exhibited higher mechanical properties than when there were other defects. This phenomenon was found to be related to the decrease in the effective load transfer from aluminum to C₃N. Furthermore, by increasing the weight percent of the nanosheets up to 5%, the energy absorption rate increased by 25% compared to the pure aluminum. When C₃N was placed on top of the aluminum surface, the silicon nanoparticles were associated with a 35% energy adsorption by the nanocomposite. The results of this paper could be used to help understand and overcome some limitations in the fabrication of metallic nanocomposites with 2D material reinforcement.

---

1 Introduction

In recent years, two-dimensional monolayer materials consisting of various atoms such as carbon, nitrogen and boron in a honeycomb structure have been used as a promising way for new applications in various industries such as nanoelectronics and energy storage technologies. To date, different methods have been proposed to fabricate and synthesize such materials.^1–4 Due to their outstanding mechanical and thermal properties, such materials serve as building blocks in the composite industry, nanorobots, mechanical actuators, nano-electromechanical systems, automotive and aerospace industries, as well as a heat transfer-improving factor in high-temperature systems. Consequently, as appealing reinforcements, they have attracted the attention of many researchers.^5–9 Aluminum (Al) and copper (Cu) nanocomposites reinforced with 2D materials are two of the most widely used composites in the aforementioned industries. It is worth noting that pure aluminum is a commonly used material in the aerospace, marine, and medical industries.

Previously, most researchers in the nanocomposite industry focused on graphene and boron nitride monolayers, and using such materials in various applications has posed some challenges. For example, attempts to use graphene, a semiconductor with zero bandwidth, has caused practical problems in the electronics industry.^10,11 Replacing carbon atoms with nitrogen in graphene is a reliable approach for synthesizing 2D graphene-like materials. Crystalline materials such as C₃N₄, as well as C₂N, are examples of these structures.^12,13 However, in 2017, Yang et al. synthesized a 2D non-defective C₃N nanostructure through the polymerization of 2,3-diaminophenazine. Like graphene, C₃N contains a homogeneous honeycomb structure with a regular distribution of nitrogen atoms, in which the C and N atoms exhibit a D_6h symmetry. Both theoretically and experimentally, it has been shown that C₃N has an indirect bandgap of 0.39 eV.¹⁴ In addition, compared to pure graphene, which is not capable of adsorbing metal atoms such as sodium (Na) and lithium (Li), the presence of highly electronegative nitrogen atoms can enhance the interaction between carbon with metal atoms.¹⁵ The C₃N features are not just limited to the electronic and optical properties. Other interesting features, such as the high thermal stability,¹⁶ the highest thermal conductivity after graphene between the 2D materials, and a strong Young's modulus of about 1090 GPa,¹⁷ can be mentioned for this structure. These specifications show C₃N as a promising candidate for the replacement of graphene and other 2D materials in various nanoscale applications.^4,15

Extensive experimental and theoretical studies have been conducted in the field of nanocomposites reinforced with 2D materials such as graphene, CNT and boron nitride in recent years.^18–21 Recently, Kumar investigated the orientation of aluminum atoms with the mechanical properties of graphene/aluminum composites using molecular dynamics simulations. His studies showed that the mechanical properties of aluminum/graphene composites are significantly improved in comparison with those consisting of pure aluminum. The results of this work showed that a better Young's modulus will be observed when the tensile test is performed along the graphene thickness. Young's modulus in this direction is expected to increase by 61%.²² In 2017, Dixit et al. experimentally and theoretically investigated the properties of laminated graphene-reinforced aluminum. The formation of such nanocomposite and optimizing its process parameters showed a two-fold increase in hardness without any changes in ductility due to the graphene scattering in aluminum. Their results showed a 94 MPa yield stress and ultimate stress of 147 MPa for the composite structure.²³ Using an experimental study, Niteesh et al. reported a significant increase in the Young's modulus and tensile strength of the composite over non-reinforced aluminum. Almost 46% of the final composite strength of pure aluminum was improved.²⁴ Choi and his colleagues investigated the mechanical behavior of carbon nanotube-reinforced aluminum composites by molecular dynamics simulation, which showed that, compared with pure aluminum, the Young's modulus for CNT(4,4)-Al, CNT(6,6)-Al and CNT(8,8)-Al increased by 31%, 33%, and 39%, respectively. Furthermore, the toughness values improved significantly by 37%, 72%, and 100%, respectively.²⁵ Sedigh and colleagues recently determined that BN nanotubes have a significant effect on improving the mechanical properties of aluminum composites. Their work comprehensively investigated the effects of various defects, as well as temperature effects. Results showed that the Young's modulus of Al/BNNS and Al/BNNT composites increased by 52% and 42%, respectively, compared to pure aluminum.²⁶ Recently, Khoshghadam et al. used a novel experimental method to synthesize the graphene-reinforced nanocomposite, in addition to studying its microstructure and mechanical properties. Their results revealed that the mechanical properties of the sintered nanocomposites, such as the yield stress, ultimate stress, and Vickers hardness improved to 79, 49, and 44%, respectively, with only 1 wt% graphene as reinforcement over the Al–4Cu alloy.²⁷

The mechanical properties of pure 2D materials such as graphene, boron nitride, and C₃N have been studied in detail using molecular dynamics simulations.^28–30 Reports indicate that the 2D hexagonal structures greatly influence the properties, and especially mechanical characteristics of aluminum composites. Also, given the high structural similarity of C₃N to graphene and boron nitride, this material can be generally used in processes where graphene is used. Given the different chemical, electronic, thermal, and mechanical properties of C₃N versus graphene, there are several distinct applications for this material. Therefore, it is important to investigate how C₃N alters the mechanical properties of the reinforced aluminum nanocomposites. Such effects are explained by various mechanisms, such as the effective load transfer, grain refinement, dislocation looping, and mismatch of elastic modulus, thermal expansion coefficient, and the geometry of reinforcement and metallic matrix, all of which are predictable using different mathematical models. The most important of these models are the shear lag model, the orowan looping effect, and the hall–petch equation.²⁷ Therefore, in this paper, using a molecular dynamics simulation technique, the mechanical parameters (such as yield stress and strain) were investigated along with Young's modulus of an aluminum nanocomposite reinforced with different weight percentages of C₃N. The effect of temperature, strain rate, and various defects, including vacancy, crack, and void defects, were also studied in this work. The results of this paper may provide the basis for the emergence of new nanocomposites reinforced with carbon and nitrogen atoms.

2 Materials and methods

Molecular dynamics simulations have been performed using a large-scale atomic/molecular massively parallel simulator (LAMMPS).³¹ Using the embedded-atom method (EAM) potential, the interaction between the Al atoms was defined.³² The interaction between the carbon and nitrogen atoms in C₃N was defined with the Tersoff potential reported by Kinnaki et al.³³ To validate the final results, some modifications to the coefficients of this potential were made.³⁰ To interact between the carbon and nitrogen atoms with aluminum and silicon atoms, which is a non-bonded van der Waals interaction, the Lennard-Jones potential was used. The values of ε and σ can be seen using the following formulas in Table 1.

Table 1 Lennard-Jones potential coefficients between different atoms in this study

Pair	σ (Å)	ε (eV)
C–Al^22	3.0135	0.035078
N–Al^34	2.9925	0.05109
Si–Al^35	3.223	2.6135 × 10^−5
Si–N^36	3.54354965	0.00722234
Si–C^37	3.61285	0.00805

---

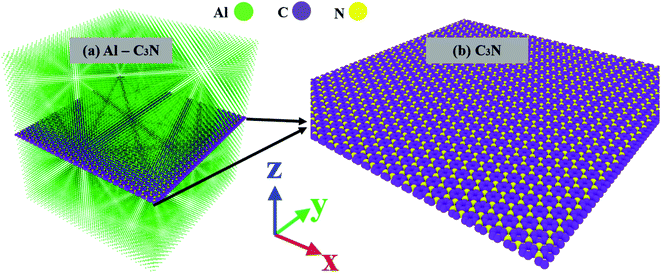
Initially, the total number of atoms was 121 229 with a dimension of 125.5 × 125.5 × 125.5 ų. Of these, the proportion of the Al, C, and N atoms was 115 320, 4459, and 1450, respectively, with the C₃N structure at the center of the FCC aluminum structure with 2.3 weight percent (Fig. 1). The present simulations are considered to be in an equilibrium state, and all boundaries are periodic. For all simulations, the structure was first equilibrated using the Nose–Hoover algorithm at constant temperature and pressure at 300 K and 0 atm for 50 ps with 1 fs time step. The system was then subjected to a tensile load (in the x-direction) with a strain rate of 0.001 ps⁻¹. The virial stress resulting from the tensile load was calculated and plotted versus the resulting strain.

Fig. 1 The initial configuration in the present simulation consists of (a) Al–C₃N nanocomposite with 2.3 wt% C₃N embedded in the center of the aluminum plate. (b) C₃N monolayer. The aluminum, carbon, and nitrogen atoms are shown in green, purple, and yellow, respectively.

3 Results and discussion

3.1 Mechanical properties of the Al/C₃N nanocomposite

To validate the performed simulations, the stress–strain curve of pure aluminum and C₃N nanosheets were compared with previous works under the identical condition in Fig. 2.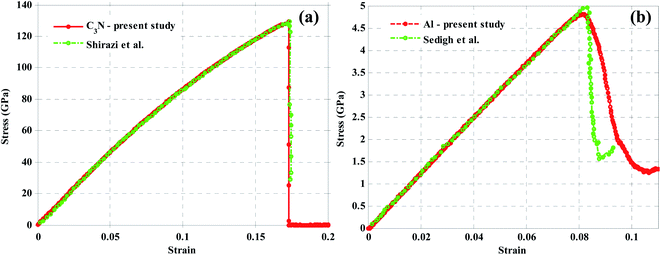

Fig. 2 Stress–strain curves of (a) C₃N nanosheets (in comparison with Shirazi³⁰) and (b) pure aluminum (in comparison with Sedigh²⁶).

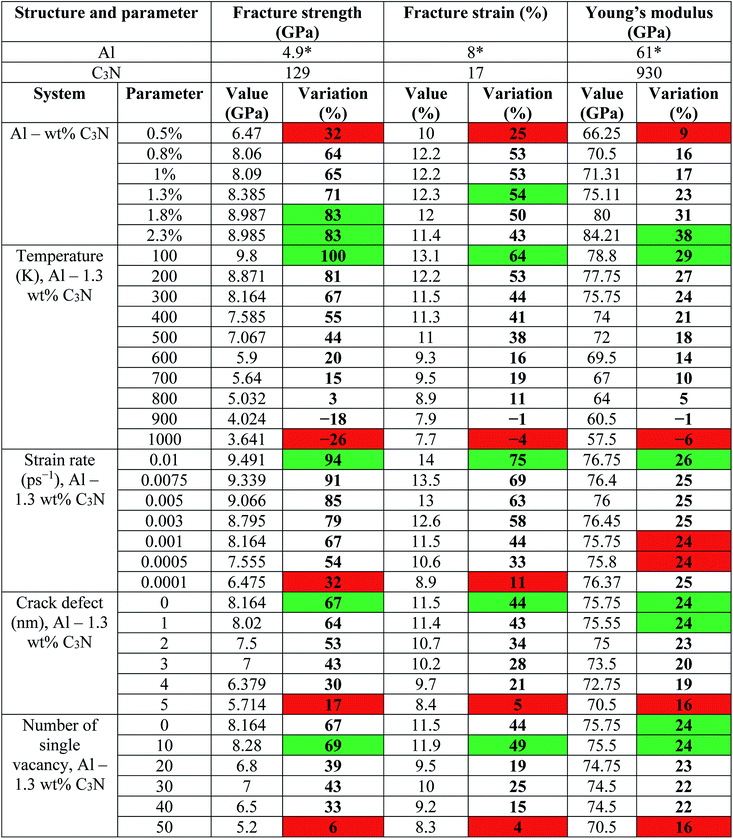
Table 2 also shows the results of the mechanical parameters (Young's modulus and fracture strength and strain) of the aforementioned structures. In Table 2, all results obtained in this study are compared with previous works, and a relatively complete comparison is made between the results of the reinforcement of graphene in the Al matrix with the results of the reinforcement of C₃N in the Al matrix. The second and third sections of this table show that in terms of the mechanical properties, the graphene–aluminum composite is weaker than the C₃N–aluminum composite in the tensile test and slightly stronger in the impact and energy adsorption tests.

Table 2 Comparison of Young's modulus, fracture strength and strain of pure Al and 2D material-reinforced aluminum nanocomposites using molecular dynamics simulations

	Tensile test	Assessment method (potential)	Fracture strain (%)	Fracture strength (GPa)	Young's modulus (GPa)
Previous reports	Pure Al^38	EAM	8	15	60
	Pure Al^26	EAM	5	8	63
	Pure Al^25	EAM	5	9	74
	Pure Al^22	EAM	2.7	10	43.63
	Pure Al^39	Experiment	0.364	12	40
	Pure Al^40	Experiment	0.22	7.5	32
	Pure Al^41	Experiment	0.125	1.9	10
	Pure Al^42	Experiment	0.195	13	12.5
	Al–graphene^22	EAM–Airebo	6	8	70.96
	Al–graphene^39	Experiment	0.454	12	40
	Al–graphene^42	Experiment	0.36	11	25
	Al–BN^26	EAM–Tersoff	5.1	6	96.27
	Al–CNT^25	EAM–Airebo	8.65	18.9	103.3
	Al–CNT^43	Experiment	0.141	—	70
Present study	Pure Al	EAM	4.9	8	61
	Pure C3N	Tersoff	129	17	129
	1.3 wt% reinforcement	Al–Gr	6.5	9	76.55
		Al – C3N	8	11.5	75.75
	Temperature 500 K	Al–Gr	5.038	7.3	71.85
		Al – C3N	7	10	72
	Strain rate 0.0005 (ps^−1)	Al–Gr	5.9	8	76.6
		Al–C3N	7.5	10.5	75
	Crack defect (3 nm)	Al–Gr	5.5	8.7	73.75
		Al–C3N	6.9	9.9	72
	Vacancy	Al–Gr	5.6	9	69
		Al–C3N	7.7	11	74
	Divacancy	Al–Gr	5.5	8.8	69
		Al–C3N	7.5	10.9	73
	Vacancy and divacancy	Al–Gr	5.3	8.4	72
		Al–C3N	7	10	73.5
	Void defect	Al–Gr	5.5	7.8	73
		Al–C3N	7.09	10.4	73

---

			ΔK (|ν2^2 − ν1^2|/ν1^2)
	Value	Variation (%)	Value	Variation (%)
Pure Al	0.477	—	0.7663	—
Al–Gr	0.379	20.5	0.8570	11.8
Al–C3N	0.381	20.1	0.8527	11.2

---

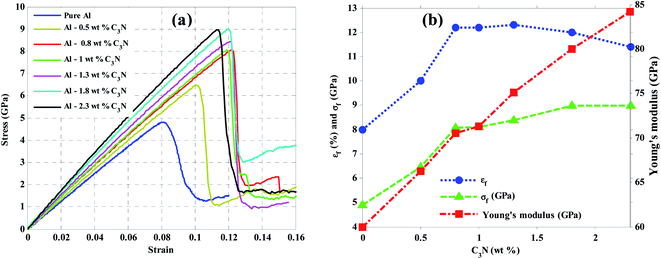
The results are shown in Fig. 2 and Table 2. In addition to guaranteeing the validation of the simulations, these results reveal that C₃N is strongly competitive with other 2D materials as a composite reinforcement due to a unique increase in the aluminum mechanical properties. Therefore, enhancing the mechanical properties of the aluminum nanocomposites reinforced with this new 2D material under different conditions is discussed here. Fig. 3 shows the stress–strain curve, the fracture strain and stress variations, as well as the Young's modulus of the Al–C₃N nanocomposites with different weight percentages of C₃N as the filler at 300 K.

Fig. 3 (a) Stress–strain curve, and (b) the fracture strain and stress variations, as well as the Young's modulus of Al– C₃N nanocomposites with different weight percentages of C₃N as the filler at 300 K.

Experimental reports suggest that adding 1 to 2% by weight of graphene to the aluminum structure is ideal and sufficient for new properties to emerge. The results show that by adding 1.3 wt% C₃N to the aluminum structure, the Young's modulus, fracture strength, and strain increased by 27, 70 and 51%, respectively. Similar results were reported in previous works for different nanocomposites (Table 2). Grain refinement could be mentioned as an enhanced mechanism, as well as a load transfer from aluminum to the 2D sheets. The grain boundary pinning resulted in a high volume of grain boundaries due to the finer grain sizes, which strengthened the composite by preventing the motion of dislocations. The presence of C₃N and the large volume of grain boundaries limited the dislocation motion in the aluminum–C₃N interface. Therefore, C₃N resulted in a dramatic increase in the mechanical properties.

3.2 Effect of temperature and strain rate

One of the prominent features of nanomaterials is their applicability at high temperatures, especially aluminum nanocomposites that are used in some industries at high temperatures.²³ In this section, the mechanical properties of the structure at different temperatures were investigated. Fig. 4(a) shows the Young's modulus and fracture strength and strain as a result of increasing the temperature from 100 to 1000 K for an aluminum nanocomposite with 1.3 wt% C₃N. Our findings show that when the system temperature rose from 100 to 1000 K, Young's modulus, as well as the fracture strength and strain, decreased by 27, 58, and 39%, respectively. The temperature of 1000 K is approximately the temperature used by the aluminum structures for high-temperature applications. It was found that the temperature greatly influenced the mechanical properties of the nanocomposites. Naturally, the distance between the adjacent atoms increased with increasing temperature, whereas the interaction energy and bonding between the atoms decreased, so the ultimate strength tended to decrease. On the other hand, the effect of increasing temperature on Young's modulus was less than the fracture strength.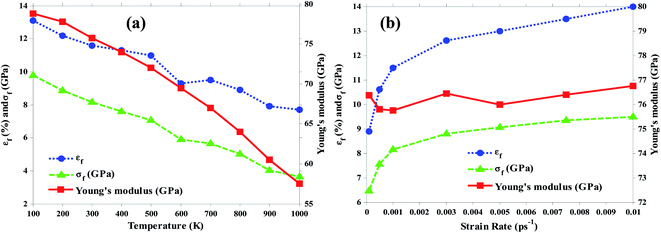

Fig. 4 Variation of Young's modulus, fracture strength and strain of nanocomposite with 1.3 wt% C₃N by (a) temperature rise and (b) strain rate increase.

One of the factors influencing Young's modulus is the coupling forces. Because increasing temperature is directly related to a decrease in the potential energy, there will be a decrease in Young's modulus in the structure. It is also important to note that on atomic scales, Young's modulus is associated with chemical bonds that are strongly attenuated at high temperatures. It should also be noted that the kinetic energy increases with increasing temperature. This energy is converted to strain energy in the tensile test, which therefore reduces the resistance level of the interatomic bonds. This will break the bonds sooner, reducing the fracture strain.

The effect of the strain rate on the mechanical properties of the Al–C₃N nanocomposite containing 1.3 wt% C₃N at 300 K was then investigated. The changes in Young's modulus, as well as the fracture strength and strain, were visible as a function of the increase in the strain rate in Fig. 4. The system was studied at seven different strain rates. The results show that by increasing the strain rate from 0.0001 to 0.01 ps⁻¹, the fracture strength and strain increased 46 and 57 percent, respectively. The modifications of Young's modulus were negligible (an increase of 2%), and were therefore ignored. However, the fracture strength and strain were highly significant, and the fracture strain increase was higher than the fracture strength. A higher strain rate meant less time for the materials to respond to different loads, thus resulting in the improvement of the mechanical properties.

3.3 Effect of defect density

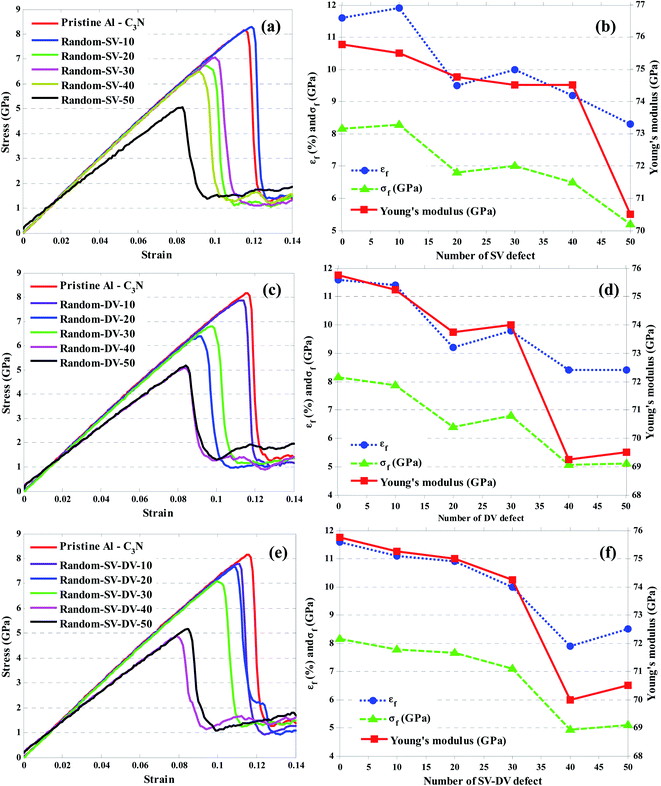
From a thermodynamic point of view, as well as taking the synthesis conditions into account, producing the pure nanomaterials is almost impossible. Defects in the 2D materials are crucial to properly understanding the physical, chemical, electrical, optical, thermal, and mechanical properties. Therefore, it is important to investigate the effect of these defects on the properties of nanomaterials.^44,45 It should be noted that while the presence of defects in nanomaterials seems to be harmful if these defects are controlled in the structure, they may give rise to new properties such as the creation of a bandgap, which sometimes changes the system from insulator to metal.⁴⁶ In this work, three types of defects including vacancy, crack, and void defects were investigated. The vacancy defects and the voids were distributed randomly on the C₃N sheet and in the Al–C₃N interface, respectively. Furthermore, the crack defects were located perpendicular to the elongation direction.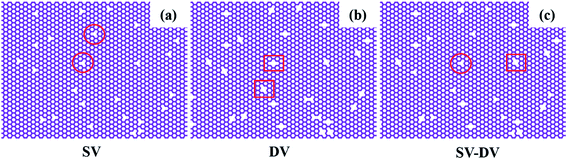

3.3.1 Single and double vacancies. One of the most common defects in the structure of nanomaterials is the lack of one or more atoms in the structure due to the lack of sufficient energy to form essential bonds in the network, such as single and di-vacancies (SV and DV). Single vacancy, especially in 2D materials, was the focus of many researchers in recent years.⁴⁷ Here, three different defects, including SV, DV, and SV–DV (simultaneously applied), were created in the C₃N structure. The number of defects was assumed to be 10, 20, 30, 40, and 50 for all three types separately (Fig. 5).

Fig. 5 The initial configuration of the C₃N nanosheets containing (a) single vacancies (inside circles), (b) divacancies (inside squares) and (c) homogeneously both types.

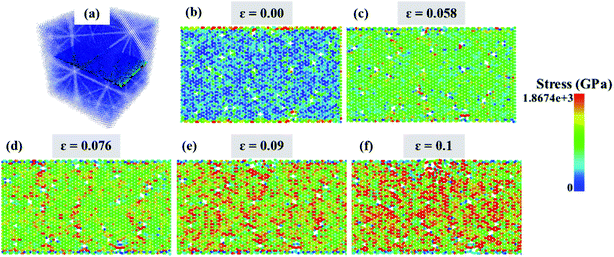
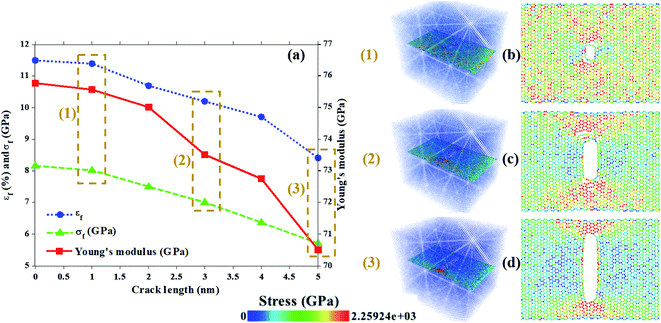
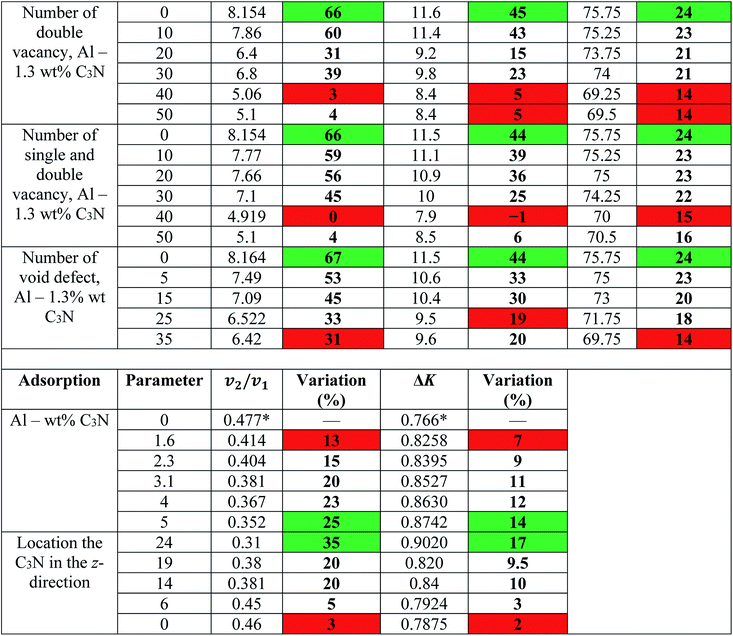
The stress–strain curve for these three different problems can be seen in Fig. 6. The effect of the defect concentration on the mechanical properties of nanocomposites was investigated. As shown in Fig. 6(a), Young's modulus, fracture strength, and strain decreased significantly with increasing SV defect numbers 6, 36, and 28%, respectively. Whereas when there was only DV defect, Young's modulus, fracture strength, and strain reduction were higher than the SV defect case, with a decrease of 8, 37, and 27%, respectively. Finally, when there were both SV and DV defects, Young's modulus, fracture strength, and strain were reduced by 7, 37 and 26%, respectively. It can be said that the results for almost all cases were similar. However, the SV–DV defect was better than the DV defect, but weaker than the SV defect. The attenuation of the mechanical properties in the presence of different defects depends on several parameters, including the number of atoms removed, as well as the location and the shape of the defect; however, their effects may not be as straightforward. For example, it is sometimes possible to eliminate the stress concentration at a particular point by removing an atom or changing the position of defects, or transfer the stress concentration position to a less stressful position, thereby creating a more appropriate stress distribution in the structure. This is why, in some cases, increasing the number of atoms removed does not necessarily lead to a weakening of the mechanical properties. As a result, it appears that the mechanical pressures and loads transferred from the aluminum to the nanosheets at that point are very high. By removing the atoms, the stress concentration is removed from that region, and the mechanical properties are slightly improved. On the other hand, as the vacancy concentration increases, the 2D structures exhibit brittle behavior. Therefore, the stress distribution is almost uniform. To better understand such behaviors, the present work has investigated the distribution of stress in the structure using the Von Mises stress formula. For this purpose, the stress distribution in a sample with SV–DV defects containing 30 SV, and the DV defects are shown in Fig. 7. As can be seen with increasing strain, the stresses were concentrated around these defects such that the structural failure eventually occurred in the same areas. It should be noted that the closer these defects were to the boundaries, the greater the mechanical loads perpendicular to the loading direction were, and the greater the stress concentration was in these areas.

Fig. 6 (a), (b), and (c) The stress–strain curve of Al– C₃N nanocomposites in the presence of SV, DV and SV–DV defects, respectively, as a function of increasing the number of defects in the C₃N 2D nanosheets. The Young's modulus, fracture strength, and strain are shown by increasing the number of defects for SV (d), DV (e), and SV–DV (f).

Fig. 7 Von Mises stress distribution of the (a) nanocomposite before the tensile test, (b) C₃N nanosheets when strain is ε = 0, (c) when strain is ε = 0.058, (d) when strain is ε = 0.076, (e) when strain is ε = 0.09, (f) when strain is ε = 0.1.

3.3.2 Crack defect. Like the SV, a crack is a defect with a high probability of material formation, and its propagation is affected by the orientation of the atoms in the structures.⁴⁸ Therefore, this work investigates the effect of CD on the mechanical properties of the Al–C₃N nanocomposites. Here, CDs of various sizes were created in C₃N, and the mechanical properties of the nanocomposites were studied. Cracks of 1 to 5 nm with an interval of 1 nm in the C₃N nanosheets were created. The results show that when a crack with 10 Å in length was created, the Young's modulus, fracture strength, and strain were 75.55 GPa, 8 GPa, and 0.11, respectively. However, increasing the crack length to 50 Å led to a decrease in the values to 70.5 GPa, 5.71 GPa and 0.08, respectively. When a crack of 5 nm in length was created, the aforementioned parameters were reduced by 7 GPa, 30 GPa, and 26, respectively (Fig. 8(a)). The Von Mises stress distribution for the three cases with crack lengths of 1, 3, and 5 nm on the C₃N nanosheet is shown in Fig. 8(b), (c) and (d), respectively. At the nanoscale, various factors such as the atomic lattice, defect concentration, edge structure, as well as the residual intrinsic strains influence the fracture behavior of the 2D materials. However, the cracking in these materials may be caused by an increase in the number of vacancies in the structure. In addition, they sometimes can be caused by creating several types of SV or DV defects together, which causes C–N bond breakages and stress concentration. As a result, failure occurs in the crack location. As can be seen from the Von Mises stress, stress is highly concentrated at the crack tip. As the crack length increased, the stress concentration in these areas increased and the fracture at lower strains occurred.

Fig. 8 (a) Changes of the Young's modulus, fracture strength and strain with increasing crack length in the Al–C₃N nanocomposites. (b), (c) and (d) The stress distribution in the C₃N nanosheets in the presence of cracks with lengths of 1, 3, and 5 nm at the beginning of the disruption.

3.3.3 Void defect. This type of defect is more common in nanocomposites, is one of the clustered defect subdivisions, and is a reduced type of the porosity defect in the structure. Moreover, often in nanocomposites, this kind of defect will appear at the interface between materials. Research on the sources, effects, and consequences of void defects can be found in several recently published articles.^49–55 Since aluminum is a soft material, the possibility of such defects increases when aluminum is combined with a hard material such as C₃N. Therefore, in this section, the effect of the VD defect on the mechanical properties of the Al–C₃N nanocomposite is investigated. As depicted in Fig. 9, in this work, 5, 15, 25, and 35 void defects were formed randomly in the nanocomposite structure.

Fig. 9 Initial configuration of the Al–C₃N nanocomposite in the presence of a cylindrical void defect with a diameter of 4 to 6 Å and a height of 7 to 15 Å in the interface between Al and the C₃N nanosheets.

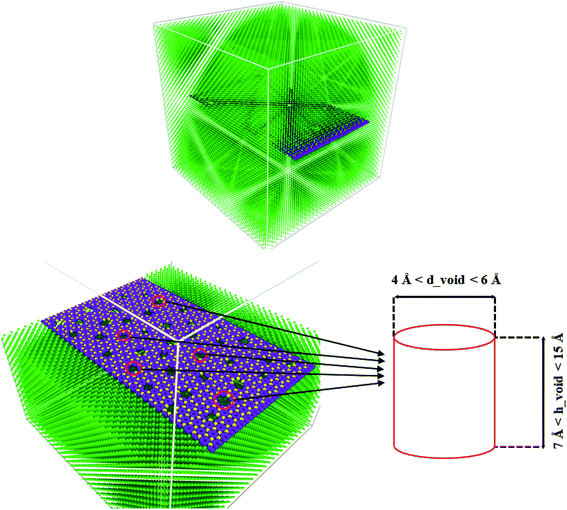
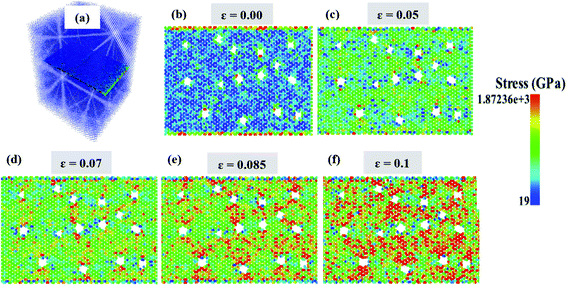
The defects are similar to a cylinder with different radii between 2 and 3 Å and different heights between 7 and 15 Å. The results show that by increasing the number of defects, mechanical parameters such as Young's modulus, fracture strength, and strain decreased by 6%, 21%, and 17%, respectively (Fig. 10). It is worth noting this defect, although the removal of more atoms from the system exhibited better mechanical properties than the vacancy and crack defects. The reason for the higher mechanical properties in the presence of this defect than other defects can be attributed to the reduction of the effective load transfer from the aluminum atoms to the N–C bonds. Thus, in the case of the void defects, not only will the carbon and nitrogen atoms in the C₃N be removed, but the aluminum atoms will also be removed from the nanocomposite structure. Therefore, the transfer of the mechanical pressures and loads will eventually be reduced to better mechanical properties than other defects.

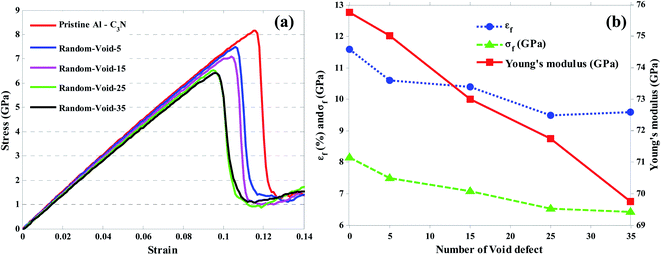Fig. 10 (a) Stress–strain curve and (b) Young's modulus, fracture strength and strain of the Al–C₃N nanocomposite with increasing void defect concentration.

Fig. 11 shows the stress distribution and concentration in the presence of these defects. It is natural that with the increasing strain in the structure, the stress concentration around these defects will increase. Eventually, a system rupture will occur in these areas. These defects further affect the density of the structure.

Fig. 11 (a) Initial configuration of the nanocomposite. (b to f) Stress distribution and concentration in the Al–C₃N nanocomposites in the presence of 15 void defects at different strains after equilibrium (b) ε = 0.0, (c) ε = 0.05, (d) ε = 0.07, (e) ε = 0.085 and (f) ε = 0.1 (at the beginning of the structure disruption).

3.4 Energy adsorption; ballistic impact test

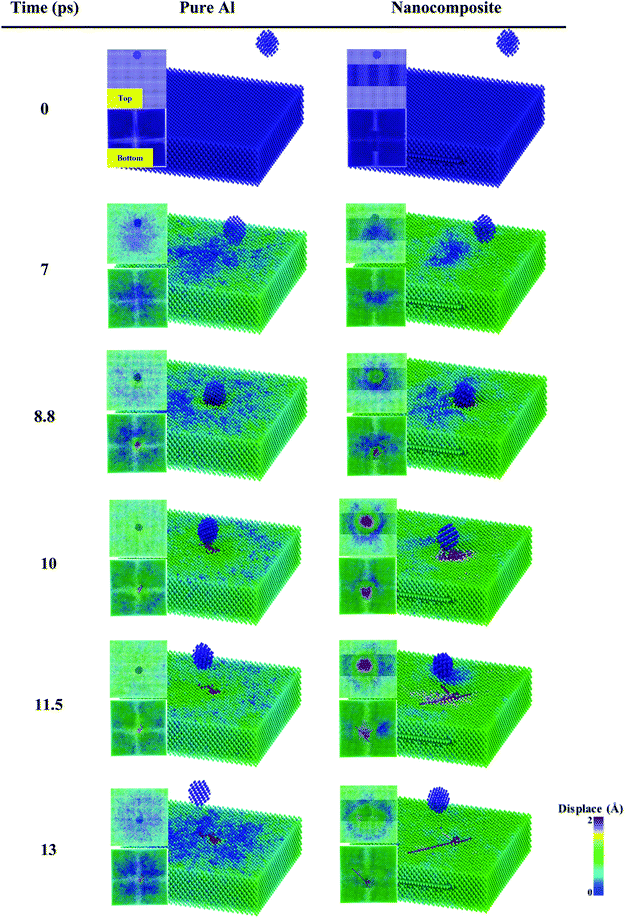
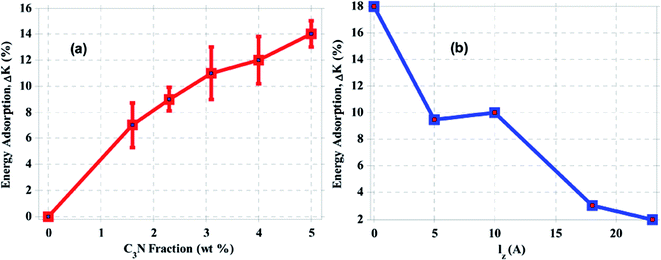
In the following section, the resistance of aluminum–C₃N nanocomposite to a projectile in a ballistic test was studied for energy adsorption. By throwing a silicon nanoparticle into the Al–C₃N composite, the amount of kinetic energy reduction (ΔK = |K_a − K_b|/K_b × 100) of the particle as a rate of energy adsorption percent by the nanocomposite was studied. K_a and K_b are the kinetic energy of a nanoparticle before and after impact with the structure, respectively. Then ΔK = |V_a² − V_b²|/V_b² × 100, where V is the speed of the particle. For this purpose, a silicon nanoparticle with a lattice constant of 5.431 Å with a radius of 9 Å containing 151 Si atoms with a definite distance from the surface (Fig. 12) was launched in the z-direction to the desired barrier, at a constant angle of 42°. The nanoparticle returned to the z-direction after a collision with the desired structure. In this figure, the top and bottom images of the Al plate were depicted with a contour of atom displacements in the z-direction. As can be seen from these images, in the composite state, more displacement occurred for the atoms. Given the similar input energy to the systems, the resulting stress in the nanocomposite would be much lower than that of pure aluminum. In addition, the displacement distribution, and thus the strain and stress distribution in the nanocomposite, is much broader. This indicates that the nanocomposites are more susceptible to stress concentration, and are more robust. These displacements have also led to the adsorption of more strain energy by the nanocomposites.

Fig. 12 Configuration of 1.8 nm diameter silicon nanoparticle launch and impact on the Al–C₃N nanocomposite with dimensions of 12.5 × 12.5 × 2.4 nm along the angle (42°) concerning the yz plane at different times.

The results show that by increasing the weight percent of the nanosheets up to 5%, the energy absorption rate increased by 25% compared to pure aluminum (Fig. 13). Therefore, it can be concluded that the presence of the 2D structure of C₃N in the Al–C₃N nanocomposite had a significant effect on increasing the energy absorption of the structure.

Fig. 13 (a) The energy changes adsorbed by the Al–C₃N nanocomposite. (b) The energy changes adsorbed by the nanocomposite by varying the C₃N nanoparticle positioning distance from the aluminum surface.

In addition, the effect of changing the position of the C₃N nanosheets in the z-direction was investigated. In this case, the C₃N sheet was placed at five different distances (0, 6, 12, 19 and 24 angstroms in the z-direction) from the top surface of the nanocomposites.

The results show that as the nanosheet approached the aluminum surface, the energy adsorption was significantly increased. That is, when the C₃N was placed on the top of the aluminum surface, silicon nanoparticles were associated with a 35% energy adsorption by the nanocomposite after being hit by the C₃N (Fig. 13).

3.5 General findings

Based on the simulations and previous experiences, a comprehensive assessment of the mechanical applications of C₃N was conducted. The results obtained in this study are listed in Table 3.

Table 3 Comprehensive assessment of the mechanical applications of C₃N

---

In Table 3, the most changes in each part are shown in green and the least in red. As for the effect of temperature, up to 800 °C, the nanocomposite had not yet become mechanically weaker than pure aluminum at ambient temperature. This suggests that using C₃N can be largely useful in high-temperature applications of aluminum. The energy adsorption section at the bottom of the table shows the C₃N on the aluminum surface with the highest weight fraction as the best energy absorber.

4 Conclusions

In summary, this work presents, the mechanical properties of the Al–C₃N nanocomposites using molecular dynamics simulation under different conditions. The obtained results were compared with previous works, and a relatively complete comparison was made between the results of reinforcement of graphene in the Al matrix with the results of reinforcement of C₃N in the Al matrix. In terms of the mechanical properties, the graphene–aluminum composite is weaker than C₃N–aluminum composite in the tensile tests, but slightly stronger in the impact and energy adsorption tests. The effects of the C₃N fraction on the aluminum matrix were investigated. The results showed that by increasing the C₃N nanosheet weight fraction to 2.3%, the mechanical properties of the nanocomposite were significantly improved so that it was competitive with other 2D materials. The effects of the strain rate and temperature, which are important parameters in the mechanical properties of materials, were investigated in this work. The results show that the proposed system is strongly dependent on the temperature and strain rate. Furthermore, it was found that with increasing temperature from 100 to 1000 K, the Young's modulus and fracture strength and strain decreased by 27%, 58%, and 39%, respectively. Also, when the strain rate increased from 0.0001 to 0.01, the Young's modulus and fracture strength and strain increased by 2%, 46%, and 57%, respectively. Finally, the effect of different defects on the mechanical properties of the structure was investigated, revealing that the void defect exhibited better mechanical properties than the other defects. The crack and vacancy defects (single-vacancy and di-vacancy) were created on the C₃N nanosheets. The effect of the crack length and vacancy concentration on the mechanical properties of the nanocomposites was then investigated. It was shown that the mechanical properties could sometimes be improved by increasing the defect numbers in the structure because by removing some atoms from the structure, it is possible to remove the stress concentration from some parts of the structure. This allowed the local stresses of the structure to be better distributed throughout the structure, resulting in an improvement in the mechanical properties. Finally, the results of the ballistic tests indicated that the C₃N on the aluminum surface with the highest weight fraction was the best energy absorber.

Conflicts of interest

There are no conflicts to declare.

References

1. A. K. Geim and K. S. Novoselov, The rise of graphene, in Nanoscience and Technology, Co-Published with Macmillan Publishers Ltd, UK, 2009, pp. 11–19.
2. C. Berger, et al., Electronic Confinement and Coherence in Patterned Epitaxial Graphene, Science, 2006, 312(5777), 1191.
3. V. Barone and J. E. Peralta, Magnetic Boron Nitride Nanoribbons with Tunable Electronic Properties, Nano Lett., 2008, 8(8), 2210–2214.
4. S. Yang, et al., C₃N—A 2D Crystalline, Hole-Free, Tunable-Narrow-Bandgap Semiconductor with Ferromagnetic Properties, Adv. Mater., 2017, 29(16), 1605625.
5. S. Stankovich, et al., Graphene-based composite materials, Nature, 2006, 442(7100), 282–286.
6. W.-L. Song, et al., Polymer/Boron Nitride Nanocomposite Materials for Superior Thermal Transport Performance, Angew. Chem., Int. Ed., 2012, 51(26), 6498–6501.
7. T. Ramanathan, et al., Functionalized graphene sheets for polymer nanocomposites, Nat. Nanotechnol., 2008, 3(6), 327–331.
8. H. Chen, et al., Mechanically Strong, Electrically Conductive, and Biocompatible Graphene Paper, Adv. Mater., 2008, 20(18), 3557–3561.
9. S. C. Tjong, Recent progress in the development and properties of novel metal matrix nanocomposites reinforced with carbon nanotubes and graphene nanosheets, Mater. Sci. Eng., R, 2013, 74(10), 281–350.
10. F. Schwierz, Graphene transistors, Nat. Nanotechnol., 2010, 5(7), 487–496.
11. K. E. Eshkalak, S. Sadeghzadeh and M. Jalaly, Thermal resistance analysis of hybrid graphene-boron nitride nanosheets: the effect of geometry, temperature, size, strain and structural defects, Comput. Mater. Sci., 2020, 174, 109484.
12. J. Mahmood, et al., Nitrogenated holey two-dimensional structures, Nat. Commun., 2015, 6, 6486.
13. S. Muhl and J. M. Méndez, A review of the preparation of carbon nitride films, Diamond Relat. Mater., 1999, 8(10), 1809–1830.
14. S. Yang, et al., C₃N—A 2D Crystalline, Hole-Free, Tunable-Narrow-Bandgap Semiconductor with Ferromagnetic Properties, Adv. Mater., 2017, 29(16), 1605625.
15. Y. Mao, et al., Lithium storage in nitrogen-rich mesoporous carbon materials, Energy Environ. Sci., 2012, 5(7), 7950–7955.
16. B. Mortazavi, Ultra high stiffness and thermal conductivity of graphene like C₃N, Carbon, 2017, 118, 25–34.
17. H. Wang, H. Wu, and J. Yang, C₃N: a Two Dimensional Semiconductor Material with High stiffness, Superior Stability and Bending Poisson's Effect, arXiv:1703.08754, 2017.
18. L. Tong, et al., Recent progress in the preparation and application of quantum dots/graphene composite materials, RSC Adv., 2017, 7(76), 47999–48018.
19. S. Pande, et al., Mechanical and electrical properties of multiwall carbon nanotube/polycarbonate composites for electrostatic discharge and electromagnetic interference shielding applications, RSC Adv., 2014, 4(27), 13839–13849.
20. G. Zhu, et al., Microstructure, mechanical properties and oxidation resistance of SiCf/SiC composites incorporated with boron nitride nanotubes, RSC Adv., 2016, 6(86), 83482–83492.
21. A. K. Pandey, et al., Mechanical and thermal behaviours of graphite flake-reinforced acrylonitrile–butadiene–styrene composites and their correlation with entanglement density, adhesion, reinforcement and C factor, RSC Adv., 2016, 6(56), 50559–50571.
22. S. Kumar, Graphene Engendered aluminium crystal growth and mechanical properties of its composite: an atomistic investigation, Mater. Chem. Phys., 2018, 208, 41–48.
23. S. Dixit, et al., Multi-layer graphene reinforced aluminum – manufacturing of high strength composite by friction stir alloying, Composites, Part B, 2018, 136, 63–71.
24. S. J. Niteesh Kumar, et al., Mechanical Properties of Aluminium-Graphene Composite Synthesized by Powder Metallurgy and Hot Extrusion, Trans. Indian Inst. Met., 2017, 70(3), 605–613.
25. B. K. Choi, G. H. Yoon and S. Lee, Molecular dynamics studies of CNT-reinforced aluminum composites under uniaxial tensile loading, Composites, Part B, 2016, 91, 119–125.
26. P. Sedigh, A. Zare and A. Montazeri, Evolution in aluminum applications by numerically-designed high strength boron-nitride/Al nanocomposites, Comput. Mater. Sci., 2020, 171, 109227.
27. M. Khoshghadam-Pireyousefan, et al., Application of a novel method for fabrication of graphene reinforced aluminum matrix nanocomposites: synthesis, microstructure, and mechanical properties, J. Mater. Sci. Eng. A, 2020, 772, 138820.
28. K. Einalipour Eshkalak, S. Sadeghzadeh and M. Jalaly, The mechanical design of hybrid graphene/boron nitride nanotransistors: geometry and interface effects, Solid State Commun., 2018, 270, 82–86.
29. K. E. Eshkalak, S. Sadeghzadeh and M. Jalaly, Studying the effects of longitudinal and transverse defects on the failure of hybrid graphene-boron nitride sheets: a molecular dynamics simulation, Phys. E, 2018, 104, 71–81.
30. A. H. N. Shirazi, et al., Mechanical responses of pristine and defective C₃N nanosheets studied by molecular dynamics simulations, Comput. Mater. Sci., 2018, 147, 316–321.
31. S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117(1), 1–19.
32. Y. Mishin, et al., Interatomic potentials for monoatomic metals from experimental data and ab initio calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(5), 3393–3407.
33. A. Kınacı, et al., Thermal conductivity of BN-C nanostructures, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(11), 115410.
34. Z. Cong and S. Lee, Study of mechanical behavior of BNNT-reinforced aluminum composites using molecular dynamics simulations, Compos. Struct., 2018, 194, 80–86.
35. P. Peng, et al., Molecular dynamic simulations of nanoindentation in aluminum thin film on silicon substrate, Appl. Surf. Sci., 2010, 256(21), 6284–6290.
36. R. Abadi, et al., Fabrication of nanopores in polycrystalline boron-nitride nanosheet by using Si, SiC and diamond clusters bombardment, Comput. Mater. Sci., 2018, 145, 280–290.
37. N. Inui and S. Iwasaki, Interaction Energy between Graphene and a Silicon Substrate Using Pairwise Summation of the Lennard-Jones Potential, e-J. Surf. Sci. Nanotechnol., 2017, 15, 40–49.
38. T. Bin and Y. Rong, Molecular Dynamics Study of Uniaxial Deformation in Perfect and Defective Aluminum, Chin. J. Phys., 2015, 53(7), 120802.
39. S.-j. Yan, et al., Research of Graphene-reinforced Aluminum Matrix Nanocomposites, J. Mater. Eng., 2011, 1(4), 1–6.
40. C.-H. Jeon, et al., Material properties of graphene/aluminum metal matrix composites fabricated by friction stir processing, Int. J. Precis. Eng. Manuf., 2014, 15(6), 1235–1239.
41. L. Li, et al., Microstructure and tensile properties of bulk nanostructured aluminum/graphene composites prepared via cryomilling, J. Mater. Sci. Eng. A, 2015, 626.
42. S. Kumar, et al., Mechanical Properties of Aluminium-Graphene Composite Synthesized by Powder Metallurgy and Hot Extrusion, Trans. Indian Inst. Met., 2017, 70.
43. R. George, et al., Strengthening in carbon nanotube/aluminum (CNT/Al) composites, Scr. Mater., 2005, 53, 1159–1163.
44. K. E. Eshkalak, S. Sadeghzadeh and M. Jalaly, Mechanical properties of defective hybrid graphene-boron nitride nanosheets: a molecular dynamics study, Comput. Mater. Sci., 2018, 149, 170–181.
45. J. Zhang, et al., Characterization of atomic defects on the photoluminescence in two-dimensional materials using transmission electron microscope, InfoMat, 2019, 1(1), 85–97.
46. N. Ding, X. Chen and C.-M. L. Wu, Mechanical properties and failure behaviors of the interface of hybrid graphene/hexagonal boron nitride sheets, Sci. Rep., 2016, 6(1), 31499.
47. S. Sadeghzadeh, Effects of vacancies and divacancies on the failure of C₃N nanosheets, Diamond Relat. Mater., 2018, 89, 257–265.
48. D. Gross and T. Seelig, Fracture mechanics: with an introduction to micromechanics, Springer, 2017.
49. G. H. Michler and H.-H. K.-B. von Schmeling, The physics and micro-mechanics of nano-voids and nano-particles in polymer combinations, Polymer, 2013, 54(13), 3131–3144.
50. W.-W. Pang, et al., Dislocation creation and void nucleation in FCC ductile metals under tensile loading: a general microscopic picture, Sci. Rep., 2014, 4(1), 6981.
51. X. Xia, et al., A unified theory of plasticity, progressive damage and failure in graphene-metal nanocomposites, Int. J. Plast., 2017, 99, 58–80.
52. A. Mikhalchan, T. Gspann and A. Windle, Aligned carbon nanotube–epoxy composites: the effect of nanotube organization on strength, stiffness, and toughness, J. Mater. Sci., 2016, 51(22), 10005–10025.
53. M. A. Irfan, et al., Porosity reduction and mechanical properties improvement in die cast engine blocks, J. Mater. Sci. Eng. A, 2012, 535, 108–114.
54. S. N. Ahmad, J. Hashim and M. I. Ghazali, The Effects of Porosity on Mechanical Properties of Cast Discontinuous Reinforced Metal–Matrix Composite, J. Compos. Mater., 2005, 39(5), 451–466.
55. V. Narain and S. Ray, Variation in mechanical properties with MnO₂ content in cast and forged in situ Al-8Mg-MnO₂ composites, J. Mater. Res. Technol., 2019, 8(5), 4489–4497.

---