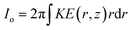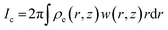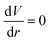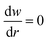DOI:
10.1039/D0RA04214E
(Paper)
RSC Adv., 2020,
10, 25022-25028
Phase-field simulations of electrohydrodynamic jetting for printing nano-to-microscopic constructs
Received
11th May 2020
, Accepted 25th June 2020
First published on 30th June 2020
Abstract
A numerical simulation is presented for predicting the transient ejection of micro-/nano-scopic jets from microscale nozzles, when a liquid confined within the nozzle is subjected to an external electric field. This simulation is based on the Taylor–Melcher leaky dielectric model, and uses the phase field method for interface tracking. The presented model is able to successfully simulate the deformation of a flat liquid meniscus into a Taylor cone, eventually leading to jet formation and breakup into droplets. Several simulations are performed to understand the effect of process parameters like applied voltage, liquid flow rate and properties on jet ejection dynamics. The results reveal the dependence of the ejected jet diameter and current primarily on the applied electric potential, liquid flow rate and electrical conductivity of the liquid. For high conductivity liquids, it is found that the convection current is of the same order of magnitude as the conduction current. In contrast, the convection current dominates the conduction current during jet ejection in the case of low conductivity liquids, regardless of the flow rate. It is also found that stable jets smaller than 200 nm can be produced from a 2 μm nozzle, which would facilitate patterning structures at the nanoscale. This model presents an approach to analyze the effect of process parameters on electrojet ejections and can effectively guide the design of printheads for e-jet systems that pattern nanoscale features in jetting and nano-dripping modes from microscopic nozzles.
Introduction
Electrohydrodynamic jetting (E-jetting) of liquid precursors from microscopic nozzles and their subsequent vaporization upon substrate landing to leave behind solid-state products has emerged as a technique of choice for patterning structures in size regimes that extend from several tens of nanometres to microns. This technique, which is characterized by a strong coupling between electrical and hydrodynamic forces, has gained recognition because of its high patterning resolution, controllability, and applicability to wide material compositions.1 It is used in a variety of applications including printed electronics,2 biotechnology,3 photonic and plasmonic devices,4 sensors,5 self-assembly of nanomaterials,6 and 3D printing.7 In a typical configuration, an E-jet is generated by injecting a liquid into a nozzle at low flow rates. At the tip of the nozzle, this liquid is electrified through the application of an electric potential (on the order of kilovolts) to the tip with respect to a grounded bottom electrode. The potential difference creates an electric field around the liquid meniscus that is formed at the nozzle tip and brings electric charges/ions to the meniscus surface, causing its elongation and eventual breakup in the direction of the applied electric field. Depending on the applied voltage and flow rate, a range of emission modes from the nozzle apex are possible: dripping, pulsating, spindle, cone-jet, and multi-jet modes.8 One of the most extensively researched and useful modes for commercial applications is the cone-jet mode wherein the liquid meniscus takes the form of a cone (commonly called Taylor cone9) that emits a thin jet from its apex. This jet subsequently breaks up into electrically charged droplets, which are deposited onto a substrate and result in patterned micro/nano-scale structures upon evaporation of the volatile components in the liquid. The force components, which act on a Taylor cone during its jetting process, are shown in Fig. 1. In this process, electric forces (both, Coulomb and dielectric) develop at the interface and are balanced by surface tension as well as reverse viscous flow induced in the liquid.
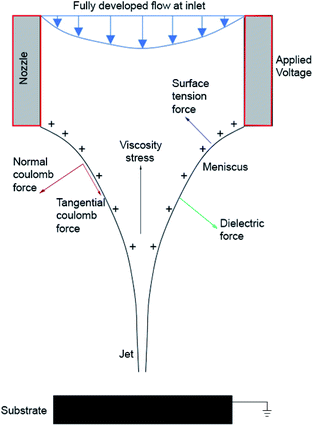 |
| | Fig. 1 Forces acting on a Taylor cone during its electro-jetting process. | |
The electro-jetting process is dependent on several factors such as operating parameters, physical properties of the liquid, geometrical factors, and surrounding conditions. A number of experimental studies have been undertaken in the past to understand the effect of these factors on electro-jetting. However, there have been isolated numerical efforts for modelling and understanding electrohydrodynamic jetting. Recently, with the emergence of interface tracking methods like volume-of-fluid (VOF),10 level set11 and phase field methods,12 interest has renewed in numerical modelling of electro-jetting/spraying to understand jet growth and breakup. Initial efforts in numerical modelling predominantly investigated the steady-state ejection of liquid from a capillary nozzle in the cone-jet mode. One of the first numerical study was conducted by Hartman et al.13 where an iterative one-dimensional model was used to calculate the steady-state shape of a liquid cone and its jet. Later, Yan et al.14 improved this model by solving axisymmetric Navier–Stokes (N–S) equations to predict the shape of the cone-jet and the velocity distribution within the liquid meniscus based on the liquid flow rate, liquid properties, and the electrode configuration. Lastow and Balachandran15 presented a commercial CFD code to simulate the EHD atomization process and to predict its voltage operating window. This model modified a commercial heat conduction (Laplace) equation solver and utilized it to solve the electric field equations, assuming the liquid behaviour to be dielectric. The electric force calculated from these equations was then used in the N–S equation to predict fluid motion. In contrast to previous models,13,14 this model did not make an initial assumption of a conical shape for the meniscus and rather started with a flat meniscus where no charges were present at the beginning. However, the models developed by Yan et al.,14 and Lastow and Balachandran15 did not account for the electric current flow along the charged cone-jet. Later, Herrada et al.16 developed a model based on the VOF method to accurately predict the flow pattern within the liquid domain and to compute the emitted electric current. However, each of the models described above have not considered droplet breakup from the cone jet and have predicted droplet sizes purely based on jet diameter. Recently, a few numerical models have been presented that account for droplet formation, breakup, and motion under the action of electric forces. Collins et al.17 developed a numerical scheme to simulate the complete electrohydrodynamic tip streaming process, including cone-jet formation and droplet pinch-off. Ouedraogo et al.18 developed a VOF numerical approach that involves a coupled solution to the multiphase flow problem using charge conservation equations, to investigate droplet generation and breakup characteristics as a function of the applied voltage. Most of these past numerical studies involving EHD cone-jet/droplet ejection have only been performed for millimetre scale geometries, which in turn generate microscale jets/droplets. With the emergence of E-jets as a viable method for patterning nanoscale features, there is a need for numerical modelling capabilities that address EHD enabled jet/droplet ejection from microscale nozzles, which are essential to realize printed features in the nanoscopic size regime.
The current effort addresses this critical need and delivers a computationally robust numerical model, which is enabled by the phase field method,12,19 for simulating the EHD driven ejection of nanoscopic cone-jets from a microscale nozzle. The equations solved in this model are based on leaky dielectric theory,20 and can predict jet formation, elongation, and its subsequent breakup into constituent droplets at the nanoscopic size regimes.
Problem formulation
A simulation of the electro-jetting process involves two components: (i) a numerical solution to equations that govern the underlying electro-hydrodynamics system (i.e., coupled fluid flow and electrostatic phenomena), and (ii) a tracking of the liquid–gas interface, which has been accomplished in this effort through the phase-field method. The mass conservation for incompressible flow is implemented by solving the continuity equation, which is given as:| |
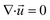 | (1) |
where 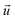 is the fluid velocity. The incompressible form of Navier–Stokes equation for solving fluid flow is given by:
is the fluid velocity. The incompressible form of Navier–Stokes equation for solving fluid flow is given by:| |
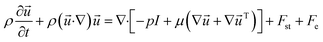 | (2) |
where p is the fluid pressure, ρ is fluid density, μ is dynamic viscosity, while Fst and Fe represent surface tension and electric forces, respectively. The surface tension and electric forces are added to Navier–Stokes equation as body forces on the fluid, and are given, respectively, as:| |
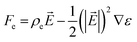 | (4) |
where, G is the chemical potential and φ is the phase field variable, which is discussed in detail later. The chemical potential G is defined as:| |
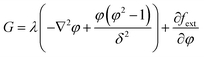 | (5) |
where, λ is the mixing energy density, δ is the capillary width, which is dictated by the interface thickness, and fext is the external free energy. In the calculation of electric force, ρe is the volumetric charge density, 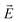 is the electric field, and (ε = εrε0) is the fluid permittivity. The first term on the right-hand side of eqn (4) is the Coulomb force, which is a result of electric field interactions with the charges that are induced at the liquid–gas interface. The second term represents the dielectric force due to the polarization of liquid. While the dielectric force always acts perpendicular to the liquid–air interface, the coulombic force includes a tangential component in addition to a normal component (refer Fig. 1). This tangential force causes a shearing action at the jet surface and thereby, results in its breakup into droplets.
is the electric field, and (ε = εrε0) is the fluid permittivity. The first term on the right-hand side of eqn (4) is the Coulomb force, which is a result of electric field interactions with the charges that are induced at the liquid–gas interface. The second term represents the dielectric force due to the polarization of liquid. While the dielectric force always acts perpendicular to the liquid–air interface, the coulombic force includes a tangential component in addition to a normal component (refer Fig. 1). This tangential force causes a shearing action at the jet surface and thereby, results in its breakup into droplets.
The electric field 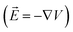 is governed by the Poisson and charge conservation equations as:
is governed by the Poisson and charge conservation equations as:
| |
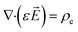 | (6) |
| |
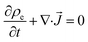 | (7) |
where
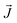
is the electric current density and is defined as:
| |
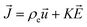 | (8) |
Here,
K is the electrical conductivity of fluid. The first part on the right-hand side of
eqn (8) denotes the electric current due to charge convection along the jet, whereas the second part represents electric current due to charge conduction through the jet.
For interface tracking during the transient evolution of a two-phase laminar flow, the conservative form of the phase field method for incompressible flows is employed. This form is given by the Cahn–Hilliard equation as:19,21
| |
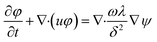 | (9) |
| |
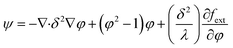 | (10) |
Here, the derivative of the external free energy
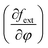
is set to zero. The value of phase field variable (
φ) varies smoothly over the liquid–gas interface with values of
φ = +1 in liquid phase and
φ = −1 in gas phase. In implementation of the phase field method for two-phase interface tracking, the two fluids are considered as a single effective fluid whose properties are defined as:
| | |
Π = Πg (1 − φ)/2 + Πl (1 + φ)/2
| (11) |
where Π is an effective fluid property, which could be density (
ρ), dynamic viscosity (
μ), electrical conductivity (
K), or permittivity (
ε) of the fluid. The subscript g and l denote the gas and liquid phase properties, respectively.
Numerical simulation
The electrohydrodynamic system described above represents a tightly coupled system involving an externally applied electric field and its resultant fluid flow. Here, the electric currents and Laminar Two-Phase Flow (Phase Field) physics modules in COMSOL Multiphysics 5.4 software are utilized to numerically solve this coupled problem. The computational domain used for electro-jet simulation is shown in Fig. 2(a). The geometrical configuration used in these simulations are like that used in experiments by Choi et al.22 The model reduces the computational complexity through an axisymmetric representation of the underlying system. The nozzle inner diameter (D) is maintained at either 10 μm or 2 μm, and its outer diameter is set at 20 μm or 4 μm, respectively. The separation between the nozzle and the substrate (H) is kept at 100 μm. The boundary conditions of electrostatic and hydrodynamic fields are listed in Table 1. The liquid is injected through the nozzle at different flow rates (Q) ranging from 10−13 to 10−10 m3 s−1, assuming a fully developed flow at the inlet. Furthermore, the nozzle is maintained at a constant electric potential (Voltage) of 2000 V in all simulations (except Fig. 5). This electric potential has been chosen to achieve the ejection of extremely fine jets (in the sub-200 nm regime for Octanol) and are similar to those used in past miniaturized electrospray studies.23–25 Because of the small values for bond number, gas density and viscosity, the effect of gravity has been neglected in these simulations.
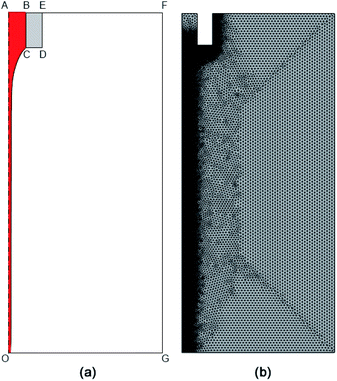 |
| | Fig. 2 (a) A schematic diagram of the computational domain, which was chosen to model the electro-jetting system, and (b) the finite-element mesh employed in this effort. The boundary conditions associated with this computational domain are listed in Table 1. | |
Table 1 Boundary conditions
| Boundary |
Electrostatic |
Hydrodynamic |
| AB: inlet |
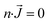 |
w = 2Q/A × (1 − 4r2/D2) |
| BCDE: nozzle wall |
V = V0 |
u = 0, w = 0 |
| EFG: outlet |
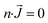 |
p = 0 |
| OA: symmetry |
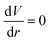 |
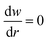 |
| OG: substrate |
V = 0 |
u = 0, w = 0 |
This time-dependent problem is solved using the MUMPS direct method with a Backward Differentiation Formula (BDF) for time stepping in COMSOL. A non-uniform triangular mesh is used, with a very fine mesh (minimum element size: 0.01 μm) along the centre-line of the domain where the jet passes through, and a courser mesh away from the central region, as shown in Fig. 2(b). This reduces the computational load, while still maintaining a high mesh density at critical regions and helps in properly resolving the two-phase interface. A mesh independence study was also carried out to validate that the simulation results were insensitive to further mesh refinement. Two different liquids have been employed as ink in these simulations: (a) octanol, which is representative of a highly conducting liquid, and (b) tetra-decane, which is weakly conducting. The physical properties of these two liquids are listed in Table 2. In the context of simulations that predict ejection characteristics (droplet/jet diameter, current, etc.) from a nozzle, the prediction accuracy would further improve through a suitable accounting of the presence of nanomaterial precursors in the solvent-based ink. These are typically accounted for by using experimentally measured, effective fluid properties for the nanomaterial-containing ink and represents one potential future direction for work presented in this effort.
Table 2 Physical properties26,27 of liquids used in simulations
| Liquid |
ρ (kg m−3) |
μ (mPa s) |
ε |
K (S m−1) |
γ (N m−1) |
| Air |
1.225 |
1.81 × 10−2 |
1 |
1 × 10−15 |
— |
| Octanol |
827 |
7.2 |
9.93 |
2.27 × 10−4 |
0.024 |
| Tetra-decane |
762 |
2.59 |
2.08 |
6.68 × 10−8 |
0.026 |
Results and discussion
The time-evolution of an octanol cone-jet from a 2 μm nozzle as predicted by the numerical model is shown in Fig. 3. As seen, the flat meniscus deforms into a conical shape due to the downward pull exerted by the electric force. As the conical meniscus elongates, the electric force at the cone tip overcomes surface tension and a jet emanates from the Taylor cone. The evolution of the cone-jet profile at 0 μs, 0.4 μs, 0.6 μs, and 1.7 μs are shown in panels (a–d) of Fig. 3 for a flow rate of 1 × 10−12 m3 s−1. The length of the emanating jet is dependent on the liquid flow rate, with shorter jets appearing at smaller flow rates. These shorter jets break into constituent droplets before hitting the substrate. In contrast, at high flow rates, the jet remains intact over greater lengths and impinges on the substrate in continuous form. The inset of panel ‘d’ shows a 280 nm droplet breaking off from the tip of a 160 nm diameter jet, clearly establishing the capability of the presented phase field-based modelling approach in predicting jet evolution, deformation, and sizing, and droplet formation at the nanoscopic size regimes. Furthermore, it is important to emphasize the difference in size between the jet and droplet diameters. Since the size of EHD printed solid-state structure is dependent on the form (droplet27 or continuous jet29) in which precursor ink impinges on the substrate, the presented model which can predict the form of such precursors offers an avenue to much better estimate the printing resolution of EHD systems, compared to past efforts which estimated size of printed structures just based on diameter of ejected jets. Note that the smallest printed feature would correspond to the underlying droplet size only if the nozzle movement is carefully controlled with respect to the substrate, such that a build-up of liquid droplets and consequent enlargement of printed features is avoided.27
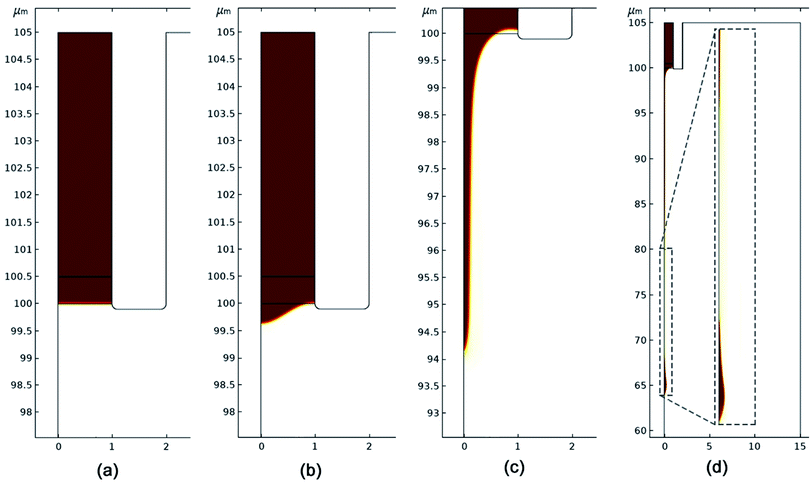 |
| | Fig. 3 Simulated octanol cone-jet from a 2 μm nozzle for flow rate of 1 × 10−12 m3 s−1 using the COMSOL electrohydrodynamic model at different time instants: (a) 0 s, (b) 4 × 10−7 s, (c) 6 × 10−7 s and (d) 1.7 × 10−6 s. The capability of the phase-field model in predicting droplet breakup is established in panel ‘d’. | |
Another important quantity in electro-jetting is the electric current transported by the jet. Electric current is a characteristic of the mode of operation of electrospray, and its measurement is essential for predicting/controlling the jet behaviour.30 For example, a temporally uniform current is indicative of a stable cone jet, which would lead to a much more precise and controllable printing process. However, a time varying current would be indicative of pulsating or micro-dripping mode of jetting, which is not suitable for high yield electrohydrodynamic printing. Moreover, the quantification of electric current is also indicative of the charge transfer which can be used to determine the fluid behaviour. The total electric current transported within the jet is governed by both, charge convection and bulk charge conduction:26,31
where, the conduction (
Io) and convection (
Ic) currents can be calculated using:
| |
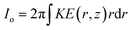 | (14) |
| |
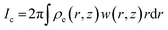 | (15) |
In the above equations,
E(
r,
z) and
w(
r,
z) represent the electric field and downward jet velocity distribution, respectively, within the liquid jet.
In this effort, the jet diameter and electric current have been quantified as a function of the flow rate. This involves an averaging of their values at different locations along the jet path as the jet extends from the nozzle up to its location of breakup or impingement on substrate. Specifically, these parameters are averaged from their respective values at nodes, which are separated by 5 μm intervals and extend between 10 μm and 90 μm from the nozzle tip. Fig. 4 shows the resulting averaged jet diameter and total current for three different simulation cases: (a) octanol & Dnozzle = 2 μm; (b) octanol & Dnozzle = 10 μm; and (c) tetradecane & Dnozzle = 10 μm. An increase in flow rate leads to a thicker emitted jet for all the three cases. This is because a higher liquid velocity necessitates a larger shear force at the liquid–air interface for squeezing the meniscus into a smaller cross-sectioned jet. If the electric field is not increased, the shear electric force becomes insufficient to squeeze the meniscus into a thin jet, and this results in larger jet diameters at increasing flow rates.26
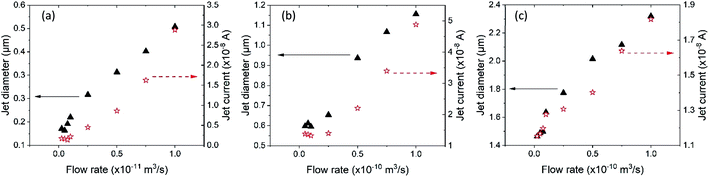 |
| | Fig. 4 Calculated jet diameter and current for different simulation cases: (a) octanol & Dnozzle = 2 μm; (b) octanol & Dnozzle = 10 μm; (c) tetradecane & Dnozzle = 10 μm. | |
Another interesting element that emerges in the octanol data presented in Fig. 4(a) and (b) is the nearly invariant jet diameter and current at flow rates that are near and below 1 × 10−12 m3 s−1. The evolution of jetting in these data points reveals its break-up to form droplets, prior to the liquid reaching the underlying substrate. On the other hand, a pure jetting-only mechanism (i.e., without the formation of droplets) was observed at higher flow rates. Thus, the trend of decreasing jet diameters and currents stops to form a plateau at this low flow-rate regime involving jet break-up into droplets. Therefore, for printing the smallest features in the jetting mode at a given EHD voltage, the inlet flow rate has to be adjusted to its lowest possible value that permits the formation of a stable continuous jet (this in-turn will be characteristic to the liquid employed). An additional parameter that may be tuned to realize thinner jets (and thereby, smaller feature sizes) is the applied electric potential.27,32 The effect of electric potential on jet diameter and current has been examined in Fig. 5 by considering the ejection of tetradecane from a 10 μm nozzle and at an inflow rate of 5 × 10−11 m3 s−1. It is found that an increase in the applied potential leads to the generation of finer jets. This is a result of the larger electric forces that are induced at the liquid–air interface under higher electric potentials. However, the jet current increases with an increase in electric potential due to the generation of higher flow velocities and charges in the jet. This observation of a smaller jet diameter and a higher jet current with an increase in electric potential is consistent with those reported in past experimental studies.27,32 The electric potential can be increased up to the threshold value that results in tilted-jet or twin-jet operational mode.28 Lastly, printing with a smaller diameter nozzle also facilitates smaller feature printing, as can be seen from Fig. 4(a) where features as small as 160 nm can be produced with 2 μm nozzles. On the other hand, the smallest jet diameters and feature sizes are limited to 600 nm for jetting induced from a 10 μm nozzle. A finer sized droplet or jet impinging onto the substrate will leave behind finer printed structure upon evaporation of volatile component, leading to higher resolution of printing.
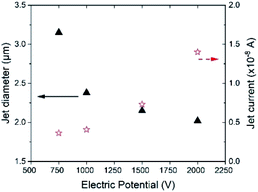 |
| | Fig. 5 The impact of voltage on the resultant jet diameter and current in the case of tetradecane. Here, Qin= 5 × 10−11 m3 s−1 and Dnozzle = 10 μm. | |
Just as with the jet diameter, the transported total jet current also increases with the flow rate of liquid. This is because a higher flow rate liquid transports more charge per unit time (higher liquid velocity). In addition, the calculated total current for octanol is obviously larger than tetradecane due to its much higher conductivity. Both observations agree with the trend observed by Li et al.31 Comparing Fig. 4(b) and (c), for the same applied voltage and flow rate in a 10 μm nozzle, octanol produces a finer jet than tetradecane. This is also attributed to the ability of octanol to transport higher charges (because of its larger conductivity in comparison to tetradecane), which results in larger electric forces.
Lastly, the ratio Ic/Io is plotted for all three simulation cases at different flow rates in Fig. 6. This ratio is found to be of the order of 10 for octanol and 103 for tetradecane. This order of magnitude difference arises from the lower conductivity of tetradecane, thereby leading to the charge convection component dominating over the charge conduction contribution. On the other hand, the higher conductivity of octanol makes its charge conduction component of the same order of magnitude as its charge convection. A similar trend was observed by Li et al.31 for weakly conducting (Glycerol) and high conductivity (poly-ethylene oxide) liquids. The simulation results presented here demonstrate that nanometre scale patterns can be printed from a microscale nozzle by using an appropriately thin nozzle and a conductive liquid. Since the model can predict both liquid deformation and breakup, it can be used for analysing and optimizing conditions that are required for nanoscale printing from an electrified nozzle in both, jetting and dripping modes. Lastly, the ability of the presented method to capture transient interface dynamics also makes it suitable for analysing the effect of time varying electric field/voltage on the ejection process.
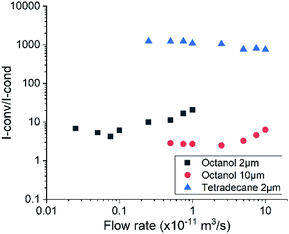 |
| | Fig. 6 Ratio of calculated convection and conduction current for different simulation cases. | |
Conclusions
A simple and efficient numerical model based on phase-field interface tracking methodology has been presented to simulate micro-/nano-electrohydrodynamic jet ejection from an electrified nozzle. The model is based on the assumption of a leaky dielectric fluid, and solves the coupled Navier–Stokes and charge conservation equations to predict liquid motion. In addition to simulating the jet deformation and elongation, the model also predicts jet breakup into constituent droplets. From the simulations, it is found that the jet stability is dictated by its inlet liquid flow rate and breaks up into droplets before hitting substrate at low flow rates. The predicted jet diameter and current are found to depend on the applied electric potential, liquid's flow rate and electrical conductivity, as well as the nozzle diameter. A high electric potential, lower flow rate and higher electrical conductivity leads to an ejection of finer jets. Furthermore, smaller nozzles are found to further decrease the jet diameter. Within the presented results, jet diameters as small as 160 nm were observed under the simulated conditions from 2 μm nozzle. Therefore, an ideal combination for printing nanoscale features would involve ejection of a high conductivity cone jet at low flow rates from a small diameter nozzle maintained at high electric potential. The developed numerical model has allowed us to evaluate the effect of these operating parameters and would be very useful in optimizing conditions for implementing stable electrohydrodynamic nanoprinting in cone jet or nano-dripping modes.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A. S. and S. K. S. acknowledge support for this work, in part, from the National Science Foundation under Grant No. 1609303.
References
- M. S. Onses, E. Sutanto, P. M. Ferreira, A. G. Alleyne and J. A. Rogers, Small, 2015, 11, 4237–4266 CrossRef CAS PubMed.
- Y. Liang, J. Yong, Y. Yu, A. Nirmalathas, K. Ganesan, R. Evans, B. Nasr and E. Skafidas, ACS Nano, 2019, 13, 13957–13964 CrossRef CAS PubMed.
- K. Shigeta, Y. He, E. Sutanto, S. Kang, A.-P. Le, R. G. Nuzzo, A. G. Alleyne, P. M. Ferreira, Y. Lu and J. A. Rogers, Anal. Chem., 2012, 84, 10012–10018 CrossRef CAS PubMed.
- S. J. P. Kress, P. Richner, S. V. Jayanti, P. Galliker, D. K. Kim, D. Poulikakos and D. J. Norris, Nano Lett., 2014, 14, 5827–5833 CrossRef CAS PubMed.
- K. H. Choi, M. Zubair and H. W. Dang, Jpn. J. Appl. Phys., 2014, 53, 05HB02 CrossRef.
- M. S. Onses, C. Song, L. Williamson, E. Sutanto, P. M. Ferreira, A. G. Alleyne, P. F. Nealey, H. Ahn and J. A. Rogers, Nat. Nanotechnol., 2013, 8, 667 CrossRef CAS PubMed.
- Q. Lei, J. He and D. Li, Nanoscale, 2019, 11, 15195–15205 RSC.
- A. Jaworek and A. Krupa, J. Aerosol Sci., 1999, 30, 873–893 CrossRef CAS.
- J. F. D. L. Mora, Annu. Rev. Fluid. Mech., 2007, 39, 217–243 CrossRef.
- J. M. Lopez-Herrera, A. M. Ganan-Calvo, S. Popinet and M. A. Herrada, Int. J. Multiphase Flow, 2015, 71, 14–22 CrossRef CAS.
- Y. Lin, Electrophoresis, 2013, 34, 736–744 CrossRef CAS PubMed.
- Y. Lin, P. Skjetne and A. Carlson, Int. J. Multiphase Flow, 2012, 45, 1–11 CrossRef CAS.
- R. P. A. Hartman, D. J. Brunner, D. M. A. Camelot, J. C. M. Marijnissen and B. Scarlett, J. Aerosol Sci., 1999, 30, 823–849 CrossRef CAS.
- F. Yan, B. Farouk and F. Ko, J. Aerosol Sci., 2003, 34, 99–116 CrossRef CAS.
- O. Lastow and W. Balachandran, J. Electrost., 2006, 64, 850–859 CrossRef CAS.
- M. A. Herrada, J. M. Lopez-Herrera, A. M. Ganan-Calvo, E. J. Vega, J. M. Montanero and S. Popinet, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 026305 CrossRef CAS PubMed.
- R. T. Collins, J. J. Jones, M. T. Harris and O. A. Basaran, Nat. Phys., 2008, 4, 149–154 Search PubMed.
- Y. Ouedraogo, E. Gjonaj, T. Weiland, H. D. Gersem, C. Steinhausen, G. Lamanna, B. Weigand, A. Preusche, A. Dreizler and M. Schremb, Int. J. Heat Fluid Flow, 2017, 64, 120–128 CrossRef.
- P. Yue, J. F. Feng, C. Liu and J. Shen, J. Fluid Mech., 2004, 515, 293–317 CrossRef CAS.
- D. A. Saville, Annu. Rev. Fluid. Mech., 1997, 29, 27–64 CrossRef.
- User’s guide, Microfluidics Module, COMSOL Multiphysics 5.4 Search PubMed.
- H. K. Choi, J.-U. Park, O. O. Park, P. M. Ferreira, J. G. Georgiadis and J. A. Rogers, Appl. Phys. Lett., 2008, 92, 123109 CrossRef.
- O. Yogi, T. Kawakami, M. Yamauchi, J. Y. Ye and M. Ishikawa, Anal. Chem., 2001, 73, 1896–1902 CrossRef CAS PubMed.
- C.-H. Chen, D. A. Saville and I. A. Aksay, Appl. Phys. Lett., 2006, 89, 124103 CrossRef.
- A. M. Ganan-Calvo, J. M. Lopez-Herrera and P. Riesco-Chueca, J. Fluid Mech., 2006, 566, 421–445 CrossRef.
- A. M. Ganan-Calvo, J. Davila and A. Berrero, J. Aerosol Sci., 1997, 28, 249–275 CrossRef CAS.
- P. Galliker, J. Schneider, H. Eghlidi, S. Kress, V. Sandoghdar and D. Poulikakos, Nat. Commun., 2012, 3, 890 CrossRef CAS PubMed.
- A. Lee, H. Jin, H.-W. Dang, K.-H. Choi and K. H. Ahn, Langmuir, 2013, 29, 13630 CrossRef CAS PubMed.
- S.-Y. Kim, Y. Kim, J. Park and J. Hwang, J. Micromech. Microeng., 2010, 20, 055009 CrossRef.
- X. Wang, G. Zheng, Z. Luo and W. Li, AIP Adv., 2015, 5, 127120 CrossRef.
- W. Li, X. Wang, G. Zheng, L. Xu, J. Jiang, Z. Luo, S. Guo and D. Sun, Appl. Phys. A: Mater. Sci. Process., 2018, 124, 711 CrossRef.
- V. R. Gundabala, N. Vilanova and A. Fernandez-Nieves, Phys. Rev. Lett., 2010, 105, 154503 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article and
Arunkumar Subramanian
and
Arunkumar Subramanian *
*
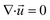
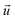 is the fluid velocity. The incompressible form of Navier–Stokes equation for solving fluid flow is given by:
is the fluid velocity. The incompressible form of Navier–Stokes equation for solving fluid flow is given by: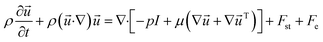
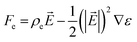
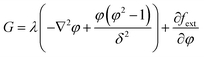
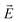 is the electric field, and (ε = εrε0) is the fluid permittivity. The first term on the right-hand side of eqn (4) is the Coulomb force, which is a result of electric field interactions with the charges that are induced at the liquid–gas interface. The second term represents the dielectric force due to the polarization of liquid. While the dielectric force always acts perpendicular to the liquid–air interface, the coulombic force includes a tangential component in addition to a normal component (refer Fig. 1). This tangential force causes a shearing action at the jet surface and thereby, results in its breakup into droplets.
is the electric field, and (ε = εrε0) is the fluid permittivity. The first term on the right-hand side of eqn (4) is the Coulomb force, which is a result of electric field interactions with the charges that are induced at the liquid–gas interface. The second term represents the dielectric force due to the polarization of liquid. While the dielectric force always acts perpendicular to the liquid–air interface, the coulombic force includes a tangential component in addition to a normal component (refer Fig. 1). This tangential force causes a shearing action at the jet surface and thereby, results in its breakup into droplets.
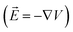 is governed by the Poisson and charge conservation equations as:
is governed by the Poisson and charge conservation equations as: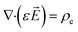
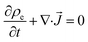
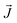 is the electric current density and is defined as:
is the electric current density and is defined as: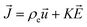
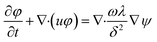
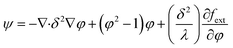
 is set to zero. The value of phase field variable (φ) varies smoothly over the liquid–gas interface with values of φ = +1 in liquid phase and φ = −1 in gas phase. In implementation of the phase field method for two-phase interface tracking, the two fluids are considered as a single effective fluid whose properties are defined as:
is set to zero. The value of phase field variable (φ) varies smoothly over the liquid–gas interface with values of φ = +1 in liquid phase and φ = −1 in gas phase. In implementation of the phase field method for two-phase interface tracking, the two fluids are considered as a single effective fluid whose properties are defined as: