Open Access Article
Open Access ArticleFull crystal structure, hydrogen bonding and spectroscopic, mechanical and thermodynamic properties of mineral uranopilite†
Francisco Colmenero *a,
Jakub Plášil
*a,
Jakub Plášil b,
Vicente Timón
b,
Vicente Timón a and
Jiří Čejkac
a and
Jiří Čejkac
aInstituto de Estructura de la Materia (IEM-CSIC), C/ Serrano, 113, 28006 Madrid, Spain. E-mail: francisco.colmenero@iem.cfmac.csic.es
bInstitute of Physics ASCR, v.v.i., Na Slovance 2, 182 21, Praha 8, Czech Republic
cMineralogicko-petrologické oddělení, Národní muzeum, Cirkusová 1740, 193 00 Praha 9, Czech Republic
First published on 27th August 2020
Abstract
The determination of the full crystal structure of the uranyl sulfate mineral uranopilite, (UO2)6(SO4)O2(OH)6·14H2O, including the positions of the hydrogen atoms within the corresponding unit cell, has not been feasible to date due to the poor quality of its X-ray diffraction pattern. In this paper, the complete crystal structure of uranopilite is established for the first time by means of first principles solid-state calculations based in density functional theory employing a large plane wave basis set and pseudopotential functions. The computed unit-cell parameters and structural data for the non-hydrogen atoms are in excellent agreement with the available experimental data. The computed X-ray diffraction pattern is also in satisfactory agreement with the experimental pattern. The infrared spectrum of uranopilite is collected from a natural crystal specimen originating in Jáchymov (Czech Republic) and computed employing density functional perturbation theory. The theoretical and experimental vibrational spectra are highly consistent. Therefore, a full assignment of the bands in the experimental infrared spectrum is performed using a normal mode analysis of the first principles vibrational results. One overtone and six combination bands are recognized in the infrared spectrum. The elasticity tensor and phonon spectra of uranopilite are computed from the optimized crystal structure and used to analyze its mechanical stability, to obtain a rich set of elastic properties and to derive its fundamental thermodynamic properties as a function of temperature. Uranopilite is shown to have a large mechanical anisotropy and to exhibit the negative Poisson's ratio and negative linear compressibility phenomena. The calculated specific heat and entropy at 298.15 K are 179.6 and 209.0 J K−1 mol−1, respectively. The computed fundamental thermodynamic functions of uranopilite are employed to obtain its thermodynamic functions of formation in terms of the elements and the thermodynamic properties of a set of chemical reactions relating uranopilite with a representative group of secondary phases of spent nuclear fuel. From the reaction thermodynamic data, the relative stability of uranopilite with respect to these secondary phases is evaluated as a function of temperature and under different hydrogen peroxide concentrations. From the results, it follows that uranopilite has a very large thermodynamic stability in the presence of hydrogen peroxide. The high stability of uranopilite under this condition justify its early crystallization in the paragenetic sequence of secondary phases occurring when uranium dioxide is exposed to sulfur-rich solutions.
1 Introduction
The uranyl sulfate oxyhydroxide tetradecahydrate mineral uranopilite,1–6 (UO2)6(SO4)O2(OH)6·14H2O, is one of the most environmentally important and abundant uranyl sulfate minerals.7–12 This mineral was first described in 1854 by Dauber13 from Jáchymov (former Bohemia, as part of the Austrian empire, now Czech Republic) and by Weisbach14 from Johanngeorgenstadt (Saxony, Germany). Uranopilite is a highly hydrated mineral whose crystal structure2 has a topology which is not present in the structure of any other uranyl sulfate material.7–12 The crystal structure of uranopilite contains layers composed of hydrogen-bonded infinite chains or bands. The structure of these bands in uranopilite is one of the most complex found so far in the structure of a uranyl mineral. The determination of the hydrogen bond structure of uranopilite is a long standing problem2,5,6 whose solution has not been possible due to the complexity of its X-ray diffraction pattern and the paucity of well-developed crystals. The twinning of the uranopilite crystals leads to the existence of a large number overlapping reflections and unresolved artifacts which, together with a poor absorption correction, are the cause of highly positive difference Fourier maps in the proximity of the uranium atoms within the uranopilite chains, which hinders the determination of the hydrogen atom positions within its unit cell.6 However, this problem may be lifted by using theoretical approaches to determine the complete crystal structure of uranopilite. The first principles solid-state methodology based on Density Functional Theory (DFT) has been previously employed successfully to determine the complete crystal structures of fundamental uranyl-containing minerals such as schoepite,15 metaschoepite,16 becquerelite,17 kasolite,18 uranophane-β,19 vandenbrandeite,20 uranosphaerite21 and bayleyite.22 The hydrogen bond network structure present in the unit cell of uranopilite is unveiled in this work.Uranyl sulfate minerals are invariably found in uranium deposits where uraninite commonly coexists with sulfide minerals. Uranopilite is frequently found on the surface of altered uraninite or in its vicinity.6,8 In these deposits, the oxidative dissolution processes of sulfide minerals lead to the formation of sulfur rich solutions with low pH known as acid-mine drainage.23–26 These acid solutions, generated after mining and ore processing contain high concentrations of metals and toxic elements (such as U, Cd, Cr, Pb and As) and drain from stockpiles of waste rock, mill tailings and open pits at or near the mine site, into surface streams, rivers and lakes leading to the deterioration of the water quality. The precipitation and dissolution of uranyl sulfate minerals are among the most important processes limiting the solubility of uranium in these deposits. The dissolution of these minerals leads to the formation of highly mobile aqueous uranyl sulfate complexes27–40 which may be transported long distances away from the deposit and, therefore, control the migration of uranium at the large scale.41–44 The oxidative dissolution processes of sulfide minerals and the presence of large metal water concentrations in soils with high sulfate contents can also occur in the absence of mining and may have both anthropogenic and non-anthropogenic origin.23,45–50 The presence of sulfur compounds48,49 and biogenic processes50 were fundamental for the genesis of many uranium ore deposits.51 The study of the precipitation/dissolution processes of uranyl sulfate minerals is also highly relevant for the performance assessment of spent nuclear fuel repositories.52–57
In order to make progress in all the fields related to the confinement of uranium containing wastes, a substantial amount of research should be made to perform large scale numerical modeling calculations to identify the main geochemical processes involved and to assess the effectiveness of the barrier systems used to prevent the long term migration of contaminants.58,59 Numerical simulations are the only method that allows to recognize the highly multidisciplinary nature of the problem and takes in account the complex coupled interaction between geology, hydrology, mechanics, chemistry, biogeochemistry and thermodynamics for the precise geometry of the site being studied. Appropriate numerical simulations using highly developed and augmented reactive transport codes are an essential ingredient of the long-term performance assessment of nuclear waste repositories.28,29,60–65 A serious weakness in the current knowledge base is the lack of reliable temperature dependent thermodynamic information for the most important chemical species and chemical reactions involved.31,66–68 The elaboration of a complete chemical thermodynamic database27,28,69,70 is mandatory if we desire to bring the results of such simulations in agreement with the experimental information. The stabilities and the dissolution reaction constants of a given mineral are dependent on the temperature, composition and local conditions (pH and EH), and the knowledge of its Gibbs free energy, enthalpy, and entropy thermodynamic functions of formation, including their variation with temperature, is required for their prediction. The case of the uranyl sulfate minerals is particularly important because, saving the minerals of the zippeite group,71,72 there is not thermodynamic information for the most of these environmentally important minerals even at room temperature. The need of thermodynamic data for uranyl sulfate minerals, due to its enormous relevance under acidic conditions, has been recognized in the past29,73 and has still not been addressed. The availability of accurate thermodynamic data for uranyl sulfate minerals should allow to obtain a deep knowledge about the formation processes of these minerals and of the interaction of uranium and sulfide minerals at several time scales and environmental conditions which is currently poorly understood.74 One of the main purposes of this paper is to provide precise temperature dependent thermodynamic data for one of the most important uranyl sulfate minerals, uranopilite,1–6 and, from them, to investigate its connection with the dissolution/precipitation processes occurring when uranium dioxide is exposed to oxidizing conditions in the presence of SO42− anions. Uranopilite has very high uranium content and is the earliest uranyl sulfate mineral appearing in the paragenetic sequence of uranyl-containing minerals occurring due to the corrosion of uranium ore deposits when the ore is exposed to oxidizing low pH sulfur-rich solutions. It should be noticed that a closely related mineral phase, referred to as metauranopilite, is usually described as its dehydration product. However, this mineral phase, described from a single specimen by Nováček75,76 in 1935, is dubious.8,77 Another, closely related mineral is jáchymovite,78 (UO2)8(SO4)(OH)14·13H2O. Despite of the absence of structural data, it is clear that this mineral differs significantly from uranopilite in the U![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio and total water content.
S ratio and total water content.
In this work, the infrared spectrum, the elasticity tensor and the phonon spectra of uranopilite were determined from the computed equilibrium crystal structure by using large-scale first-principles calculations (see the Appendix A of the ESI†). The experimental infrared spectrum of uranopilite was collected from a natural mineral specimen originating in Jáchymov (Czech Republic). The collected spectrum was found to be in excellent agreement with the theoretical spectrum and, therefore, all the infrared bands were assigned to specific vibrational atomic motions by performing a normal coordinate analysis of the theoretical vibrational results. The study of the spectral signatures of uranium containing materials is crucial in many research fields ranging from nuclear forensics to nuclear waste storage for their precise identification.10,79,80 Therefore, a detailed spectroscopic characterization is given. From the computed elasticity tensor, the mechanical stability of uranopilite crystal structure was analyzed and a rich set of relevant mechanical properties of this mineral, unknown as far as we know, were determined. The fundamental thermodynamic properties of uranopilite as a function of temperature were derived from the computed phonon spectra. As the mechanical properties, the thermodynamic parameters of uranopilite have not being measured experimentally and are reported here for the first time. The computed fundamental thermodynamic functions were then employed to obtain the thermodynamic properties of formation of uranopilite in terms of the elements and the thermodynamic properties of reaction of a series of reactions involving uranopilite and a subset of the most prominent secondary phases of spent nuclear fuel (SNF). From the temperature dependent thermodynamic reaction data, the relative thermodynamic stability of uranopilite with respect to these secondary phases of SNF were obtained as a function of temperature and under the presence of different concentrations of hydrogen peroxide (H2O2).
2 Results and discussion
2.1. The crystal structure of uranopilite
The fundamental building units in uranopilite crystal structure are shown in Fig. 1. The uranium atom in uranopilite displays pentagonal bipyramidal coordination and the sulfur atom, as usual, displays tetrahedral coordination. Each uranyl pentagonal bipyramid shares two edges with other two bipyramids to form a trimer, [(UO2)3O2(OH)4(H2O)3]2−. Two trimers and one sulfate tetrahedron, SO42−, combine to form a basic uranyl sulfate unit, [(UO2)6O4(OH)6(SO4)(H2O)6]4− as represented schematically in Fig. 1. The computed full crystal structure of uranopilite is plotted in Fig. 2.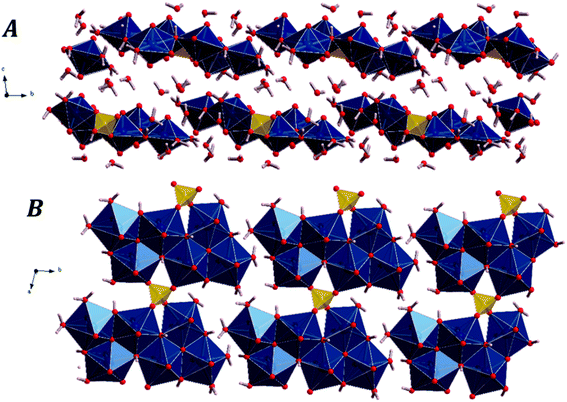 | ||
| Fig. 2 The crystal structure of uranopilite: (A) view of two uranyl sulfate layers and their interlayer space from [100] direction; (B) view of a single uranyl sulfate layer from [001] direction. | ||
As shown in Fig. 2B, the uranyl sulfate units share the two free vertices of the sulfate tetrahedra to form neutral chains expanding along [100] crystallographic direction. These chains are between three and four uranyl-polyhedra wide and, therefore, are better described as bands. The different bands, although slightly tilted, are placed around a given plane and linked by means of hydrogen bonds to form complex layers (or pseudo-layers) parallel to the (110) plane. The space between the layers is occupied by water molecules. Two uranopilite parallel layers and their interlayer space are shown in Fig. 2A. Fig. 2B displays a single layer from [001], the direction perpendicular to the layers.
The computed unit-cell parameters of uranopilite and the corresponding unit-cell volume and density are reported in Table 1. In this table, the experimental values obtained up to date are also given for comparison. The computed values using the DFT-D2 approach are in very good agreement with the experimental values. The deviation between the calculated and experimental volumes is only about 0.4% with respect to the value reported by Burns2 and 1.6% with respect to the value reported by Plášil et al.6 The inclusion of dispersion corrections improves substantially the computed crystal structure since, as can be observed in the first row of Table 1, if the uncorrected PBE functional is used, the error in the computed volume increases up to 4.8% with respect to the volume given by Burns.2
| Parameter | a (Å) | b (Å) | c (Å) | α (deg) | β (deg) | γ (deg) | Vol. (Å3) | ρ (g cm−3) |
|---|---|---|---|---|---|---|---|---|
| PBE | 9.0171 | 14.3018 | 14.6067 | 93.74 | 99.67 | 101.70 | 1808.69 | 3.861 |
| DFT-D2 | 8.9466 | 14.1497 | 14.2549 | 94.57 | 99.16 | 101.59 | 1733.59 | 4.028 |
| DFT-D2+U | 8.9467 | 14.1499 | 14.2552 | 94.57 | 99.16 | 101.59 | 1733.67 | 4.028 |
| Exp.6 | 8.8556(9) | 13.9819(15) | 14.3070(30) | 96.749(12) | 98.754(12) | 99.726(9) | 1706.91 | 4.091 |
| Exp.2 | 8.896(2) | 14.029(3) | 14.339(3) | 96.610(4) | 98.472(4) | 99.802(4) | 1726.03 | 4.046 |
| Exp.5 | 8.901(2) | 14.042(3) | 14.521(3) | 97.41(3) | 98.97(3) | 99.69(3) | 1744.58 | 4.003 |
| Exp.3 | 8.896(6) | 14.025(9) | 14.299(6) | 96.68(4) | 98.60(6) | 99.92(6) | 1719.01 | 4.062 |
| Exp.4 | 8.857(6) | 13.975(8) | 14.335(4) | 96.70(4) | 98.63(4) | 99.56(6) | 1711.55 | 4.080 |
As can also be seen in Table 1 (third row), the Hubbard correction, which was used with a value of the effective Hubbard parameter81 of Ueff = 4.0 eV, does not introduce significant variations of the computed crystal structure. The insignificance of the Hubbard correction may be understood from Fig. S.2 and S.3 of the ESI† in which the computed electron density of states of uranopilite and the frontier band functions (the highest occupied and lowest unoccupied one-electron wavefunctions) are plotted, respectively. The DFT-D2 approach predicts correctly that uranopilite is an insulator with a band gap of 2.27 eV (Fig. S.2†). Furthermore, the highest occupied band function is mainly composed of contributions localized in p orbitals of oxygen atoms and d orbitals of uranium and the lowest unoccupied wavefunction is highly localized in f orbitals of uranium atoms. Because the f orbitals in uranium are empty and separated by almost 2.3 eV from the highest occupied band function, the Hubbard correction, improving the description of the strong correlation between electrons occupying f orbitals, is not needed. As an additional check, the infrared spectrum of uranopilite was determined using the Hubbard correction and the results were essentially the same as those reported in Sec. 2.4 obtained without the Hubbard correction. Due to the small impact of this correction for uranopilite, it was not employed to obtain its mechanical and thermodynamic properties.
There are six symmetrically independent uranium atoms (referred to as U1 to U6) and only one independent sulfur atom (S1) in the structure of uranopilite. The interatomic distances derived from the computed crystal structure are reported in Table S.1 of the ESI†. The experimental values of these distances reported by Burns2 are also given in Table S.1.† Both sets of distances are in excellent agreement. The experimental average U–O distances for the upper and lower apical oxygen atoms in the uranyl pentagonal bipyramids are 1.81(2), 1.82(2), 1.80(2), 1.79(2), 1.76(2) and 1.76(2) Å and the corresponding computed values 1.80, 1.80, 1.80, 1.79, 1.80 and 1.80 Å, respectively. The computed values agree also very well with the mean value of 1.79 Å obtained from many well-refined uranyl mineral crystal structures.82 Likewise, the experimental average U–O distances for the oxygen atoms in the equatorial positions in the uranyl bipyramids are 2.41(2), 2.39(2), 2.41(2), 2.39(2), 2.39(2) and 2.41(2) Å, which can be compared with the corresponding theoretical values: 2.40, 2.39, 2.40, 2.44, 2.41 and 2.39 Å, respectively. Again, these values agree well with the value of 2.37 Å obtained by Burns et al.82 by averaging the corresponding values for a numerous set of well-refined structures involving pentagonal bipyramidal coordination on uranium atom. The theoretical and experimental average S–O distances are the same, 1.49 Å. The computed full crystal structure of uranopilite is included in the ESI† in a file with CIF (Crystallographic Information File) format.
2.2. Hydrogen bonding
The hydrogen bonding network structure in uranopilite is very complex as expected for a highly hydrated mineral with a unit cell containing twenty-eight water molecules (fourteen per formula unit). The computed hydrogen bond parameters are reported in Table 2. Thirty-two different hydrogen bonds were found. Six of them are associated to the hydroxyl ions and twenty-six to the interlayer water molecules.| Hydrogen bond | O1⋯O2 | H⋯O2 | A(O1–H⋯O2) |
|---|---|---|---|
| O1(hydroxyl)–H⋯O2 | |||
| OH19–H19···OW33 | 2.668 | 1.663 | 175.20 |
| OH20–H20···OW29 | 2.788 | 1.816 | 170.17 |
| OH21–H21···OW28 | 2.968 | 1.991 | 175.61 |
| OH22–H22···OW32 | 2.812 | 1.822 | 172.91 |
| OH23–H23···OW26 | 3.030 | 2.074 | 164.47 |
| OH24–H24···OW30 | 2.861 | 1.884 | 171.79 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| O1(water)–H⋯O2 | |||
| OW25–H25a⋯OW31 | 2.585 | 1.622 | 158.44 |
| OW25–H25b⋯OW34 | 2.664 | 1.681 | 166.97 |
| OW26–H26b⋯OW31 | 2.727 | 1.745 | 166.50 |
| OW26–H26a⋯OW35 | 2.738 | 1.771 | 162.33 |
| OW27–H27b⋯OW25 | 2.686 | 1.694 | 171.36 |
| OW27–H27a⋯OW37 | 2.571 | 1.585 | 164.43 |
| OW28–H28b⋯O11 | 2.679 | 1.692 | 169.18 |
| OW28–H28a⋯O5 | 2.935 | 2.103 | 141.88 |
| OW29–H29b⋯OW34 | 3.221 | 2.503 | 130.65 |
| OW29–H29a⋯OW38 | 2.593 | 1.587 | 168.84 |
| OW30–H30b⋯OW38 | 2.736 | 1.757 | 167.34 |
| OW30–H30a⋯OW36 | 2.657 | 1.648 | 176.58 |
| OW31–H31b⋯OW32 | 2.703 | 1.713 | 174.45 |
| OW31–H31a⋯OH21 | 2.723 | 1.735 | 170.26 |
| OW32–H32a⋯OW35 | 2.716 | 1.729 | 168.97 |
| OW33–H33a⋯OW34 | 2.727 | 1.740 | 170.06 |
| OW34–H34a⋯O8 | 2.977 | 2.109 | 147.16 |
| OW34–H34b⋯OH24 | 2.757 | 1.766 | 171.55 |
| OW35–H35b⋯OW33 | 2.659 | 1.673 | 167.39 |
| OW35–H35a⋯O12 | 2.913 | 2.273 | 122.43 |
| OW36–H36a⋯O1 | 2.771 | 1.817 | 161.70 |
| OW36–H36b⋯O5 | 2.789 | 1.831 | 164.01 |
| OW37–H37b⋯O3 | 2.760 | 1.776 | 174.28 |
| OW37–H37a⋯OW36 | 2.730 | 1.764 | 163.17 |
| OW38–H38a⋯O10 | 2.721 | 1.793 | 155.98 |
| OW38–H38b⋯OW37 | 2.682 | 1.690 | 171.67 |
From the positions of the non-hydrogen atoms, Burns2 suggested a possible hydrogen bond distribution in uranopilite using crystal chemical considerations. The hydrogen bond structure afforded by the first principles calculations is slightly different to the qualitative picture inferred by Burns.2 The differences can be mainly attributed to temperature effects, because the computed structure corresponds to zero temperature and the experimental one to room temperature, and to the qualitative nature of the picture inferred by Burns.2 The determination of the energy-optimized positions of the hydrogen atoms in a given crystal structure is a significant addition because it specifies the hydrogen bond structure in a precise way. Furthermore, from the theoretical point of view, it allows to determine the vibrational spectra and material properties using the first principles methodology.
2.3. X-ray powder diffraction patterns
The X-ray diffraction patterns of uranopilite associated to the computed and experimental2 (without the hydrogen atoms) crystal structures were determined utilizing the program REFLEX belonging to the Materials Studio package of programs.83 The patterns were determined with a X-ray radiation wavelength of λ = 1.540598 Å (CuKα radiation). The patterns obtained are compared in Fig. 3 and as can be observed they agree faithfully. Table S.2 of the ESI.† provides an exhaustive comparison of the computed and experimental positions and intensities of the nineteen more intense reflections. The X-ray powder pattern of uranopilite is quite complex and contains many reflections with intensities larger than 10%. The largest variation in the computed positions is obtained for the [−241] reflection (2θ ∼ 30.8°), the difference being only about 0.8 degrees.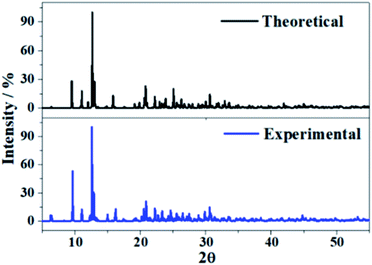 | ||
| Fig. 3 X-ray powder diffraction patterns of uranopilite. The upper diffractogram was determined from the computed geometry and the lower one from the experimental one.2 | ||
2.4. Infrared spectroscopy
The experimental infrared spectrum of uranopilite was acquired from a natural crystal specimen originating in Jáchymov (Czech Republic). The spectrum was also evaluated by employing first principles methods utilizing Density Functional Perturbation Theory (DFPT). Both spectra are displayed in Fig. 4 and as may be observed they are in very good accord. The bands in the experimentally determined spectrum are very wide and were resolved into single constituents (see Fig. S.4 of the ESI†) employing the method depicted in a previous paper.18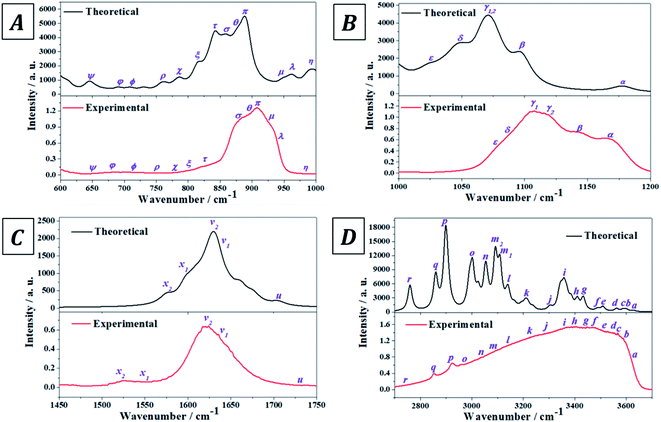 | ||
| Fig. 4 Experimental and theoretical infrared spectra of uranopilite: (A) region 600–1000 cm−1; (B) region 1000–1200 cm−1; (C) region 1450–1750 cm−1; (D) region 2700–3700 cm−1. | ||
The infrared spectrum of uranopilite samples from several different localities was measured in a previous work by Frost et al.84 The vibrational frequencies obtained in the present work are compared with those reported by Frost et al.84 in Table S.3 of the ESI.† While the obtained frequencies are quite consistent, the results provided in this work are apparently more exhaustive and the rigorous assignment of the infrared bands afforded from the first principles calculation is quite different from the empirical assignment performed by Frost et al.84 In fact, the assignment by Frost et al.84 is very incomplete and the authors called the attention on the great difficulty of assigning many of the infrared bands due to its overlap with other bands. Furthermore, the existence of an overtone and a large number of combination bands (described in detail here) was not noticed by Frost et al.84
The experimental and computed infrared band vibrational frequencies and the corresponding calculated intensities and assignments are given in Table S.4 of the ESI.† Additionally, Fig. S.5 (ESI†) shows images of the vibrational atomic motions in a selection of the infrared active normal modes of uranopilite. The detailed analysis of the infrared spectrum was divided in five main different spectral regions: (i) The region from 2200 to 3750 cm−1 (Fig. 4D, 5C and D); (ii) the region from 1300 to 1750 cm−1 (Fig. 4C and 5B); (iii) The region from 1000 to 1200 cm−1 (Fig. 4B and 5A); (iv) the region from 600 to 1000 cm−1 (Fig. 4A); and (v) the region from 400 to 600 cm−1. The last region, from 400 to 600 cm−1, is analyzed using the theoretical approach only. The study of the bands from this region is needed to identify the origin of some bands from the other spectral regions. The individual infrared bands pertaining to each spectral region are provided in separate sections of Table S.4.† The detailed analysis of the infrared spectrum of uranopilite and its assignment are given in Appendix B of the ESI.†
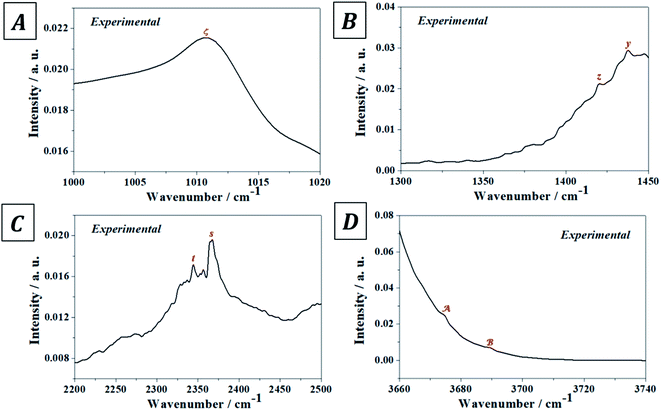 | ||
| Fig. 5 Overtone and combination infrared bands in uranopilite: (A) region 1000–1020 cm−1; (B) region 1300–1350 cm−1; (C) region 2200–2500 cm−1; (D) region 3660–3740 cm−1. | ||
2.5. Mechanical properties
| Property | Value | |
|---|---|---|
| B | Bulk modulus | 21.52 |
| G | Shear modulus | 10.94 |
| E | Young modulus | 28.06 |
| N | Poisson ratio | 0.28 |
| D | Ductility index | 1.97 |
| H | Hardness index | 0.67 |
| AU | Universal anisotropy | 6.65 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| EOS | ||
| B | Bulk modulus | 20.74 ± 0.44 |
| B′ | Bulk modulus first derivative | 7.30 ± 0.58 |
| B′′ | Bulk modulus second derivative | −2.21 ± 0.50 |
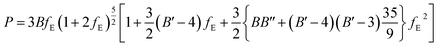 | (1) |
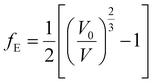 | (2) |
The fitting parameters, B, B′ and B′′ in eqn (1), are the bulk modulus and its first and second derivatives with respect to pressure. The values found are reported in Table 3. The bulk moduli obtained from the EOS and from the computed elastic constants, B = 20.74 ± 0.44 GPa and B = 21.52 ± 1.32 GPa, respectively, are in very good agreement.
The underlying structural mechanism responsible for the NLC phenomenon in uranopilite and the precise values of the compressibility are studied in the next section by means of the analysis of the deformation of uranopilite crystal structure under pressure. It must be noticed that uranopilite shows a perfectly normal mechanical behavior under isotropic pressure. As shown in Fig. S.6 of the ESI,† the volume and unit-cell parameters of uranopilite decrease under isotropic compression up to 5 GPa. The calculated values of the volumetric compressibility, kV = −1/V(∂V/∂P)P, in the pressure range from −0.5 to 4.0 GPa are provided in Table S.6 and plotted in Fig. S.7.† The presence of negative compressibility under anisotropic pressure and its absence under hydrostatic pressure has been also observed recently for the zinc and cadmium oxalates.100
2.5.4.1. Deformation of the crystal structure under pressure. The crystal structure of uranopilite was optimized under the effect of thirteen different pressures directed along the minimum compressibility direction, Uk-min. The computed unit cell volumes are reported in Table S.7† and can be visualized in Fig. 7. The unit cell volume increases from P = 0.007 GPa to P = 0.015 GPa and, therefore, the compressibility is negative in this pressure range. The computed values of the compressibility, kV = −1/V(∂V/∂P)P, in the pressure range from P = 0.005 to P = 0.025 GPa are provided in Table S.8† and plotted in Fig. 7. The minimum value of the compressibility, kV = −77.9 TPa−1, is reached at P = 0.011 GPa.
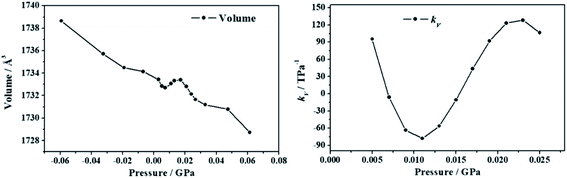 | ||
| Fig. 7 Unit cell volumes and compressibilities (kV) of uranopilite calculated as a function of the external pressure applied along the minimum compressibility direction. | ||
In order to understand the structural variations leading to the NLC effect in uranopilite, the variation of the interatomic distances and angles and lattice parameters for the optimized structures corresponding to different pressures applied in the minimum compressibility direction were analyzed. The changes observed in the interatomic distances and angles within the uranium and sulfur coordination polyhedra and the hydrogen bond parameters were quite small. The largest structural variations occurring under the application of pressure were observed in the interlayer distance. The c lattice parameter in uranopilite is exactly equal to two times the interlayer space. As can be seen in Table S.7,† from P = 0.0029 GPa to P = 0.0073 GPa, the unit cell volume decreases mainly due to the decrease of the a and c lattice parameters. However, from P = 0.0073 GPa to P = 0.0131 GPa, while the a lattice parameter decreases, the interlayer space (and the c lattice parameter) increases leading to the increase of the total unit-cell volume. Therefore, the increase of the interlayer space is the main reason for the NLC effect in uranopilite. It is a physical effect related to the increase of the non-bonding distances along the [001] crystallographic direction under pressure.
The structure of uranopilite was also optimized for twelve different pressures directed along the minimum Poisson's ratio direction, ULν-min. The resulting unit cell volumes are reported in Table S.9† and plotted in Fig. S.8 of the ESI.† In this case, the unit cell volume increases from P = 0.014 GPa to P = 0.024 GPa. Hence, negative values of the compressibility are present in this pressure range as can be observed in Fig. S.8.† The calculated values of compressibility from P = 0.003 GPa to P = 0.029 GPa are given in Table S.10.† The minimum value of the compressibility is kV = −34.2 TPa−1 and occurs at P = 0.019 GPa. Therefore, uranopilite displays also significant negative compressibilities for external pressures applied along the direction of minimum Poisson's ratio. The variation of the geometric parameters under pressure was also analyzed and it was found that the increase of the interlayer space was, as in the case of pressures applied along the direction of minimum compressibility, the main responsible of the increase of volume.
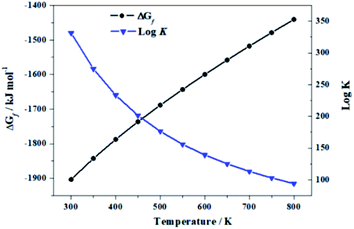
2.6. Thermodynamic properties
| T (K) | ΔfH | ΔfG | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K K |
|---|---|---|---|
| 298.15 | −2163.76 | −1905.40 | 333.81 |
| 300 | −2163.03 | −1903.02 | 331.34 |
| 350 | −2146.80 | −1842.35 | 274.95 |
| 400 | −2135.74 | −1787.25 | 233.39 |
| 450 | −2128.41 | −1736.25 | 201.53 |
| 500 | −2123.91 | −1688.40 | 176.38 |
| 550 | −2121.64 | −1643.04 | 156.04 |
| 600 | −2121.17 | −1599.71 | 139.26 |
| 650 | −2122.19 | −1558.05 | 125.20 |
| 700 | −2124.46 | −1517.82 | 113.26 |
| 750 | −2127.81 | −1478.79 | 102.99 |
| 800 | −2132.09 | −1440.81 | 94.07 |
| UO3(cr) + 1/6SO3(g) + 17/6H2O(l) → 1/6(UO2)6(SO4)O2(OH)6·14H2O(cr) | (A) |
| UO3·H2O(cr) + 1/6SO3(g) + 11/6H2O(l) → 1/6(UO2)6(SO4)O2(OH)6·14H2O(cr) | (B) |
| UO2CO3(cr) + 1/6SO3(g) + 17/6H2O(l) → 1/6(UO2)6(SO4)O2(OH)6·14H2O(cr) + CO2(g) | (C) |
| 1/2(UO2)2(SiO4)·2H2O(cr) + 1/6SO3(g) + 11/6H2O(l) → 1/6(UO2)6(SO4)O2(OH)6·14H2O(cr) + 1/2SiO2(cr) | (D) |
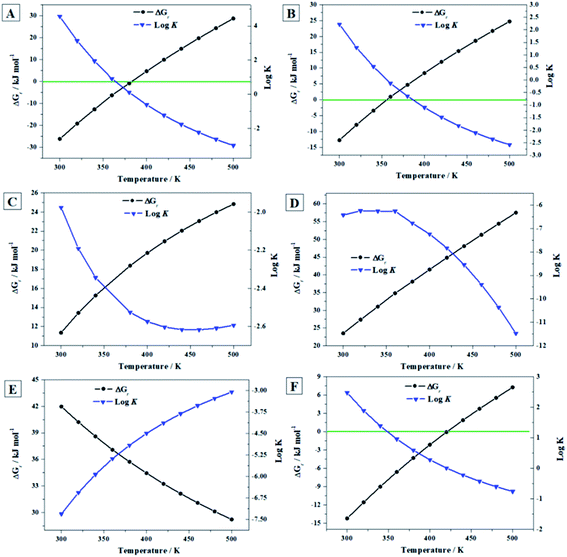 | ||
| Fig. 9 Computed Gibbs free energies of reaction and corresponding reaction constants for the reactions (A) to (F) as a function of temperature. | ||
2.6.3.1. The presence of hydrogen peroxide. The ThFORs of the reactions of conversion of uranopilite into schoepite, [(UO2)8O2(OH)12]·12H2O, and studtite, (UO2)O2·4H2O:
| 1/6(UO2)6(SO4)O2(OH)6·14H2O(cr) + 7/48O2 → 1/8[(UO2)8O2(OH)12]·12H2O(cr) + 1/6SO3(g) + 7/24H2O(l) + 7/24H2O2(l) | (E) |
| 1/6(UO2)6(SO4)O2(OH)6·14H2O(cr) + 7/6H2O2(l) → (UO2)O2·4H2O(cr) + 1/6SO3(g) + 1/12 O2(g) | (F) |
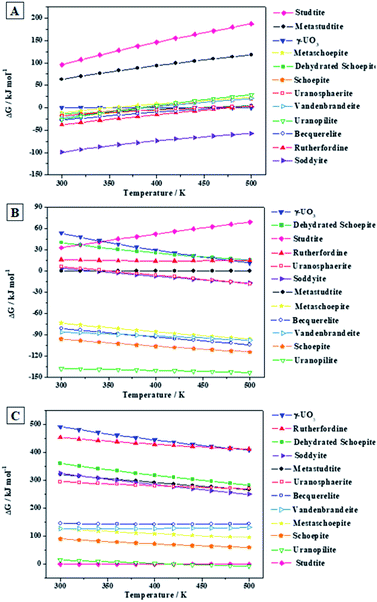
Under H2O2-free conditions (Fig. 10A), the most stable phase from 300 to 500 K is the uranyl silicate soddyite. At 300 K, uranopilite is the fourth more stable mineral phase after soddyite, rutherfordine and becquerelite. Hence, uranopilite should be replaced by other phases in the absence of H2O2 and in the presence of, for instance, silicate or carbonate ions. However (Fig. 10B), uranopilite is highly stabilized under the presence of H2O and H2O2 and becomes the most stable phase among those studied in this paper. Lastly, as shown in Fig. 10C, under high concentration of H2O2, the uranyl peroxide hydrate phase studtite is the most stable one in line with the results obtained in previous papers16,17,20,21,67,68 and uranopilite becomes the second most stable secondary phase of SNF among those considered in the present paper. However, this is true only for temperatures lower than 148 °C (421 K), and for larger temperatures uranopilite is more stable than studtite. Due to the importance of these results, the precise experimental measurement of the standard state enthalpy of formation of uranopilite in terms of the elements appears to be required to reduce the uncertainty in the estimate used here. Although at temperatures higher than 148 °C, it may be thought that some degree of dehydration of uranopilite may occur, it should be emphasized that the present results refer to the condition of presence of H2O2 and absence of H2O. Under this condition, the most hydrated phases appear to be more stable than the corresponding phases appearing due to its dehydration at H2O2-free conditions. For example, as showed in Fig. 10E, studtite is more stable than metastudtite from 300 to 500 K68 and the same occurs for schoepite and metaschoepite.17 Furthermore, mineral metauranopilite is highly dubious8,77 and no one report on the existence of this phase has been published since 1941.75,76 Theoretical computations aimed to find this phase have also being unsuccessful so far. The thermal decomposition curve of uranopilite, reported in Appendix C of the ESI† does not support the existence of this phase due to the monotonous dehydration thermogravimetric (TG) curve.
3 Conclusions
The complete crystal structure of mineral uranopilite was determined using first principles solid-state methods based on DFT. Since the calculated structural information and X-ray powder diffraction pattern were in excellent agreement with the experimental information, the hydrogen bonding network resulting from the computed positions of the hydrogen atom must be reliable. The infrared spectrum of uranopilite was collected from a natural crystal sample from Jáchymov (Czech Republic) and computed using DFPT. The good agreement between both spectra provided additional support for the computed structure. The high degree of consistency between both spectra allowed for the assignment of all the bands in the experimental spectrum to specific vibrational atomic motions. The proposed assignment is very different to the one performed previously84 using empirical arguments. Besides, one infrared band was recognized as an overtone and six additional bands were identified as combination bands.The access of the energy-optimized crystal structure facilitated the determination of the elasticity matrix and phonon spectra of uranopilite employing the first principles methodology. From the calculated elasticity matrix, the mechanical stability of the crystal structure of uranopilite was stablished and an abundant set of elastic properties were determined. Uranopilite was found to have a large mechanical anisotropy and to exhibit the negative Poisson's ratio and negative linear compressibility phenomena. The mechanism responsible for the negative linear compressibility effect of uranopilite under the effect of external pressures applied along the direction of minimum compressibility was investigated by analyzing the deformation of the crystal structures under pressure. The anomalous expansion of the interlayer space was found to be the main cause of the increase of the unit cell volume of uranopilite under the effect of compressive pressure. The minimum value of the compressibility was found to be kV = −77.9 TPa−1, for an applied external pressure of 0.011 GPa.
The fundamental thermodynamic functions of uranopilite, unknown so far, were obtained from the computed phonon spectra as a function of the temperature. These thermodynamic functions were used to determine the thermodynamic functions of formation of uranopilite in terms of the elements and the thermodynamic functions of reaction for a set of reactions relating uranopilite and a subgroup of the most prominent secondary phases of spent nuclear fuel. The thermodynamic reaction data was used in order to obtain the relative thermodynamic stability of uranopilite with respect to these phases as a function of temperature and under different concentrations of hydrogen peroxide. The results show that uranopilite is highly stable under the presence of hydrogen peroxide and becomes the most stable phase under the simultaneous presence of water and hydrogen peroxide. Besides, under the presence of hydrogen peroxide and absence of water, uranopilite is the second most stable phase after studtite at low temperatures and become the most stable phase at 148 °C. The high stability of uranopilite under these conditions explains its early crystallization in the paragenetic sequence of secondary phases occurring when natural uraninite is exposed to low-pH sulfur-rich solutions. From the point of view of nuclear waste disposal, sulfur-free conditions should be insured in a repository to avoid the possible formation of uranyl sulfate minerals. With the attenuation of the intensity of the strong radiation fields associated to the SNF over time, the concentration of hydrogen peroxide should decrease significantly and these minerals should dissolve into water forming very mobile uranyl sulfate complexes.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The computation time provided by the Centro Técnico de Informática from CSIC is deeply acknowledged. This work has been performed in the framework of a CSIC–CIEMAT collaboration agreement: “Caracterización experimental y teórica de fases secundarias y óxidos de uranio formados en condiciones de almacenamiento de combustible nuclear”. We thank Jana Ederová (Institute of Chemical Technology in Prague, Czech Republic) for the carefully undertaken thermal analysis. JP acknowledges the support of the Czech Science Foundation through the project GACR 20-11949S. VT is grateful for the financial support of the Ministry of Science, Innovation and Universities of Spain through Project FIS2016-77726-C3-1-P. JČ acknowledge the financial support of the Ministry of Culture of the Czech Republic (long-term project DKRVO 2019-2023/1.II.b; National Museum, 00023272).References
- C. Frondel, Am. Mineral., 1952, 37, 950–959 CAS.
- P. C. Burns, Can. Mineral., 2001, 39, 1139–1146 CrossRef CAS.
- J. Plášil, J. Sejkora, P. Škácha, V. Goliaš and M. Hušák, Bull. Mineral. Petrol., 2005, 13, 192–196 Search PubMed.
- J. Sejkora, J. Litochleb, B. Bureš and J. Jindra, Bull. Mineral. Petrol., 2004, 12, 171–174 Search PubMed.
- N. Meisser, Beitr. Geol. Schweiz, Geotech. Ser., 2012, 96, 1–183 Search PubMed.
- J. Plášil, J. Sejkora, R. Škoda and P. Škácha, J. Geosci., 2014, 59, 223–253 CrossRef.
- R. J. Finch and T. Murakami, Rev. Mineral. Geochem., 1999, 38, 91–179 CAS.
- S. V. Krivovichev and J. Plášil, in Uranium: From Cradle to Grave, ed. P. C. Burns and G. E. Sigmon, Mineralogical Association of Canada, Winnipeg, MB, Canada, 2013, Short Course 43, pp. 15–119 Search PubMed.
- J. Plášil, J. Geosci., 2014, 59, 99–114 CrossRef.
- R. J. Baker, Coord. Chem. Rev., 2014, 266–267, 123–136 CrossRef CAS.
- A. J. Lussier, R. A. K. Lopez and P. C. Burns, Can. Mineral., 2016, 54, 177–283 CrossRef CAS.
- V. V. Gurzhiy and J. Plášil, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2019, 75, 39–48 CrossRef CAS PubMed.
- H. Dauber, Ann. Phys., 1854, 92, 237–251 CrossRef.
- A. Weisbach, Neu. Jb. Geol. Paläont, 1882, 2, 249–259 Search PubMed.
- F. Colmenero, J. Cobos and V. Timón, Inorg. Chem., 2018, 57, 4470–4481 CrossRef CAS PubMed.
- F. Colmenero, A. M. Fernández, J. Cobos and V. Timón, ACS Earth Space Chem., 2019, 3, 17–28 CrossRef CAS.
- F. Colmenero, A. M. Fernández, V. Timón and J. Cobos, RSC Adv., 2018, 8, 24599–24616 RSC.
- F. Colmenero, J. Plášil, J. Cobos, J. Sejkora, V. Timón, J. Čejka and L. J. Bonales, RSC Adv., 2019, 9, 15323–15334 RSC.
- F. Colmenero, J. Plášil and J. Sejkora, Dalton Trans., 2019, 48, 16722–16736 RSC.
- F. Colmenero, J. Plášil, J. Cobos, J. Sejkora, V. Timón, J. Čejka, A. M. Fernández and V. Petříček, RSC Adv., 2019, 9, 40708–40726 RSC.
- F. Colmenero, J. Plášil and I. Němec, J. Phys. Chem. Solids, 2020, 141, 109400 CrossRef CAS.
- F. Colmenero, J. Plášil and P. Škácha, Spectrochim. Acta, Part A, 2020, 234, 118216 CrossRef CAS PubMed.
- D. K. Nordstrom and C. N. Alpers, in Reviews in Economic Geology, ed. G. S. Plumlee and M. J. Logsdon, Society of Economic Geologists, Littleton, CO, 1999, ch. 6, vol. 6A, pp. 133–160 Search PubMed.
- K. J. Edwards, P. L. Bond, G. K. Druschel, M. M. Mcguire, R. J. Hamers and J. F. Banfield, Chem. Geol., 2000, 169, 383–397 CrossRef CAS.
- Z. Bian, X. Miao, S. Lei, S. Chen, W. Wang and S. Struthers, Science, 2002, 37, 702–703 Search PubMed.
- H. E. Jamieson, S. R. Walke and M. B. Parsons, Appl. Geochem., 2015, 57, 85–105 CrossRef CAS.
- I. Grenthe, J. Fuger, R. J. M. Konings, R. J. Lemire, A. B. Muller, C. Nguyen-Trung, H. Wanner, Chemical Thermodynamics of Uranium, Nuclear Energy Agency Organisation for Economic Co-Operation and Development, OECD, Issy-les-Moulineaux, France, 2004 Search PubMed.
- N. Y. R. Guillaumont, T. Fanghänel, V. Neck, J. Fuger, D. A. Palmer, I. Grenthe and M. H. Rand, Update on the Chemical Thermodynamics of Uranium, Neptunium, Plutonium, Americium, and Technetium, ed. F. J. Mompean, M. Illemassene, C. Domenech-Orti and K. Ben Said, OECD Nuclear Energy Agency, Data Bank, Issy-les-Moulineaux, France, 2003 Search PubMed.
- S. A. Cumberland, G. Douglas, K. Grice and J. W. Moreau, Earth-Sci. Rev., 2016, 159, 160–185 CrossRef CAS.
- D. Langmuir, Geochim. Cosmochim. Acta, 1978, 42, 547–569 CrossRef CAS.
- D. Langmuir, Aqueous Environmental Geochemistry, Prentice-Hall, New York, 1997; pp. 486−557 Search PubMed.
- C. Nguyen-Trung, G. M. Begun and D. A. Palmer, Inorg. Chem., 1992, 3, 5280–5287 CrossRef.
- A. Gianguzza, D. Milea, F. J. Millero and S. Sammartano, Mar. Chem., 2004, 85, 103–124 CrossRef CAS.
- V. Vallet, I. Grenthe, C. R. Chimie, 2007, 10, 905–915 CrossRef CAS.
- C. Hennig, K. Schmeide, V. Brendler, H. Moll, S. Tsushima and A. C. Scheinost, Inorg. Chem., 2007, 46, 5882–5892 CrossRef CAS PubMed.
- C. Hennig, S. Tsushima, V. Brendler, A. Ikeda, A. C. Scheinost and G. Bernhard, in Uranium, Mining and Hydrogeology, ed. B. J. Merkel and A. Hasche-Berger, Springer, Berlin, 2008; pp. 603–614 Search PubMed.
- D. Vopálka, K. Štamberg, A. Motl and B. Drtinová, J. Radioanal. Nucl. Chem., 2010, 286, 681–686 CrossRef.
- L. Rao, G. Tian, Y. Xia, J. I. Friese, P. Zanonato and P. Di Bernardo, in Nuclear Energy and the Environment, American Chemical Society, Washington DC, 2010 Search PubMed.
- S. Berto, F. Crea, P. G. Daniele, A. Gianguzza, A. Pettignano and S. Sammartano, Coord. Chem. Rev., 2012, 256, 63–81 CrossRef CAS.
- A. Kalintsev, A. Migdisov, H. Xu, R. Roback and J. Brugger, Geochim. Cosmochim. Acta, 2019, 267, 75–91 CrossRef CAS.
- H. M. Fernandes, L. H. S. Veiga, M. R. Franklin, V. C. S. Prado and J. F. Taddei, J. Geochem. Explor., 1996, 52, 161–173 CrossRef.
- J. Brugger and P. C. Burns, N. Meisser, Am. Mineral., 2003, 88, 676–685 CrossRef CAS.
- K. Maher, J. R. Bargar and G. E. Brown, Inorg. Chem., 2013, 52, 3510–3532 CrossRef CAS PubMed.
- B. Novotnik, W. Chen and R. D. Evans, Appl. Geochem., 2018, 91, 36–44 CrossRef CAS.
- D. D. Runnells, T. A. Sheperd and E. E. Angino, Environ. Sci. Technol., 1992, 26, 2316–2323 CrossRef CAS.
- K. D. Kelley and C. D. Taylor, Appl. Geochem., 1997, 12, 397–409 CrossRef CAS.
- R. A. Zielinski, W. H. Orem, K. R. Simmons and P. J. Bohlen, Water, Air, Soil Pollut., 2006, 176, 163–183 CrossRef CAS.
- C. G. Warren, Econ. Geol., 1972, 67, 759–767 CrossRef CAS.
- R. L. Reynolds and M. B. Goldhaber, Econ. Geol., 1983, 78, 105–120 CrossRef CAS.
- A. Bhattacharyya, K. M. Campbell, S. D. Kelly, Y. Roebbert, S. Weyer, R. Bernier-Latmani and T. Borch, Nat. Commun., 2007, 8, 15538 CrossRef PubMed.
- J. A. Plant, P. R. Simpson, B. Smith and B. F. Windley, Rev. Mineral. Geochem., 1999, 38, 255–319 CAS.
- R. J. Finch and R. C. Ewing, Uraninite Alteration in an Oxidizing Environment and its Relevance to the Disposal of Spent Nuclear Fuel, SKB Technical Report 91–15, Swedish Nuclear Fuel and Waste Management Co, Stockholm, Sweden, 1994 Search PubMed.
- R. S. Forsyth and L. O. Werme, J. Nucl. Mater., 1992, 90, 3–19 CrossRef.
- E. C. Pearcy, J. D. Prikryl, W. M. Murphy and B. W. Leslie, Appl. Geochem., 1994, 9, 713–732 CrossRef CAS.
- D. J. Wronkiewicz, J. K. Bates, T. J. Gerding, E. Veleckis and B. S. Tani, J. Nucl. Mater., 1992, 190, 107–127 CrossRef CAS.
- D. J. Wronkiewicz, J. K. Bates, S. F. Wolf and E. C. Buck, J. Nucl. Mater., 1996, 238, 78–95 CrossRef CAS.
- J. Bruno, I. Casas, E. Cera, R. C. Ewing, R. J. Finch and L. O. Werme, Mater. Res. Soc. Symp. Proc., 1994, 353, 633–639 CrossRef.
- J. Bruno and R. C. Ewing, Elements, 2006, 2, 343–349 CrossRef CAS.
- R. C. Ewing, Nat. Mater., 2015, 14, 252–255 CrossRef CAS PubMed.
- Modelling in Aquatic Chemistry, ed. I. Grenthe and I. Puigdomenech, OECD Nuclear Energy Agency Data Bank, OECD/NEA, Stockholm. 1997 Search PubMed.
- C. J. Chisholm-Brause, J. M. Berg, K. M. Little, R. A. Matzner and D. E. Morr, J. Colloid Interface Sci., 2004, 277, 366–382 CrossRef CAS PubMed.
- T. Behrends, E. Krawczyk-Bärsch and T. Arnold, Appl. Geochem., 2013, 27, 453–462 CrossRef.
- C. Tournassat and C. I. Steefel, Rev. Mineral. Geochem., 2019, 85, 75–109 CrossRef.
- V. Lagneau, O. Regnault and M. Descostes, Rev. Mineral. Geochem., 2019, 85, 499–528 CrossRef.
- O. Bildstein, F. Claret and P. Frugier, Rev. Mineral. Geochem., 2019, 85, 419–457 CrossRef.
- F. Endrizzi, X. Gaona, M. Marques-Fernandes, B. Baeyens and M. Altmaier, J. Chem. Thermodyn., 2018, 120, 45–53 CrossRef CAS.
- F. Colmenero, A. M. Fernández, J. Cobos and V. Timón, J. Phys. Chem. C, 2018, 122, 5254–5267 CrossRef CAS.
- F. Colmenero, A. M. Fernández, J. Cobos and V. Timón, J. Phys. Chem. C, 2018, 122, 5268–5279 CrossRef CAS.
- NEA Data Bank, Thermochemical Database (TDB), accessed 15 April, 2020, https://www.oecd-nea.org/dbtdb/.
- Thermo-Chimie database (Consortium Andra-Ondraf/Niras-RWM), accessed 15 April, 2020, http://www.thermochimie-tdb.com/.
- M. Sharifironizi, J. E. S. Szymanowski, G. E. Sigmon, A. Navrotsky, J. B. Fein and P. C. Burns, Chem. Geol., 2016, 447, 54–58 CrossRef CAS.
- M. Sharifironizi and P. C. Burns, Can. Mineral., 2018, 56, 7–14 CrossRef CAS.
- D. Gorman-Lewis, P. C. Burns and J. B. Fein, J. Chem. Thermodyn., 2008, 40, 335–352 CrossRef CAS.
- P. Wersin, M. F. Hochella, P. Persson, G. Redden, J. O. Leckie and D. W. Harris, Geochim. Cosmochim. Acta, 1998, 58, 2829–2843 CrossRef.
- R. Nováček, Věstník Královské České Společnosti Nauk, 1935, vol. 7, pp. 1–36 Search PubMed.
- R. Nováček, Věstník Královské České Společnosti Nauk, Třída matematicko-přírodovědná, 1941, pp. 1–15 Search PubMed.
- P. Ondruš, F. Veselovský, J. Hlousek, R. Skála, J. Vavřín, J. Frýda, J. Čejka and A. Gabašová, J. Czech Geol. Soc., 1959, 42, 3–76 Search PubMed.
- J. Čejka, J. Sejkora, Z. Mrázek, Z. Urbanec and T. Jarchovsky, Neues Jahrbuch Mineral. Abhand., 1996, 170, 155–170 Search PubMed.
- G. Lu, A. Haes and T. Z. Forbes, Coord. Chem. Rev., 2018, 374, 314–344 CrossRef CAS PubMed.
- R. J. P. Driscoll, D. Wolverson, J. M. Mitchels, J. M. Skelton, S. C. Parker, M. Molinari, I. Khan, D. Geeson and G. C. Allen, RSC Adv., 2014, 4, 59137–59149 RSC.
- P. F. Weck, E. Kim, C. F. Jové-Colón and D. C. Sassani, Dalton Trans., 2013, 42, 4570–4578 RSC.
- P. C. Burns, R. C. Ewing and F. C. Hawthorne, Can. Mineral., 1997, 35, 1551–1570 CAS.
- MaterialsStudio, 15 April, 2020, http://3dsbiovia.com/products/collaborative-science/biovia-materials-studio/.
- R. L. Frost, J. Čejka, M. L. Weier, W. N. Martens and G. A. Ayoko, J. Raman Spectrosc., 2007, 38, 398–409 CrossRef CAS.
- P. F. Weck, E. Kim and E. C. Buck, RSC Adv., 2015, 5, 79090–79097 RSC.
- F. Mouhat and F. X. Coudert, Phys. Rev. B, 2014, 90, 224104 CrossRef.
- W. Voigt, Lehrbuch der Kristallphysik, Teubner, Leipzig, 1962 Search PubMed.
- A. Reuss, Z. Angew. Math. Mech., 1929, 9, 49–58 CrossRef CAS.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354 CrossRef.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CAS.
- H. Niu, P. Wei, Y. Sun, C. X. Chen, C. Franchini, D. Li and Y. Li, Appl. Phys. Lett., 2011, 99, 031901 CrossRef.
- S. I. Ranganathan and M. Ostoja-Starzewski, Phys. Rev. Lett., 2008, 101, 055504 CrossRef PubMed.
- EOSFIT 5.2 software, http://programming.ccp14.ac.uk/ccp/web-mirrors/ross-angel/crystal/software.html, accessed 15 April, 2020 Search PubMed.
- F. Birch, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- Z. A. D. Lethbridge, R. I. Walton, A. S. H. Marmier, C. W. Smith and K. E. Evans, Acta Mater., 2010, 58, 6444–6451 CrossRef CAS.
- F. Colmenero, J. Cobos and V. Timón, J. Phys.: Condens. Matter, 2019, 31, 175701 CrossRef CAS PubMed.
- F. Colmenero, Mater. Res. Express, 2019, 6, 045610 CrossRef.
- F. Colmenero, Phys. Chem. Chem. Phys., 2019, 21, 2673–2690 RSC.
- F. Colmenero, Adv. Theory Simul., 2019, 2, 1900040 CrossRef.
- F. Colmenero and V. Timón, J. Mater. Sci., 2020, 55, 218–236 CrossRef CAS.
- F. Colmenero, J. Sejkora and J. Plášil, Sci. Rep., 2020, 10, 7510 CrossRef CAS PubMed.
- R. S. Lakes, Science, 1987, 235, 1038–1040 CrossRef CAS PubMed.
- R. S. Lakes, Annu. Rev. Mater. Res., 2017, 47, 63–81 CrossRef CAS.
- R. H. Baughman, S. Stafström, C. Cui and S. O. Dantas, Science, 1998, 279, 1522–1524 CrossRef CAS PubMed.
- A. B. Cairns and A. L. Goodwin, Phys. Chem. Chem. Phys., 2000, 17, 20449–20465 RSC.
- Y. Tardy and R. M. Garrels, Geochim. Cosmochim. Acta, 1976, 41, 1051–1056 CrossRef.
- R. J. Finch, Mater. Res. Soc. Symp. Proc., 1997, 465, 1185–1192 CrossRef CAS.
- S. B. Clark, R. C. Ewing and J. C. Schaumloffel, J. Alloys Compd., 1998, 271–273, 189–193 CrossRef CAS.
- F. Chen, R. C. Ewing and S. B. Clark, Am. Mineral., 1999, 84, 650–664 CrossRef CAS.
- M. W. Chase, C. A. Davies, J. R. Downey, D. J. Frurip, R. A. McDonald and A. N. Syverud, J. Phys. Chem. Ref. Data, 1985, 14(Suppl. 1), 1–1856 CAS.
- I. Barin, Thermochemical Data of Pure Substances, VCH, Weinheim, Third edn, 1995 Search PubMed.
- E. Ekeroth, O. Roth and M. Jonsson, J. Nucl. Mater., 2006, 355, 38–46 CrossRef CAS.
- A. Barreiro-Fidalgo, Y. Kumagai and M. Jonsson, J. Coord. Chem., 2018, 71, 1799–1807 CrossRef CAS.
- A. C. Maier, P. Kegler, M. Klinkenberg, A. Baena, S. Finkeldei, F. Brandt and M. Jonsson, Dalton Trans., 2020, 49, 1241–1248 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: (a) Calculated positions of the atoms within the unit cell of uranopilite. (b) Experimental and first principles methods employed in this work; (c) detailed description of the experimental and computed infrared spectra; (d) thermal decomposition curve (Fig. S.1); (e) computed density of states and frontier band functions; (f) interatomic distances; (g) most intense reflections in the X-ray powder pattern; (h) resolution of the infrared bands into single components; (h) depictions of the vibrational motions associated to a subset of the most important infrared active normal modes (i) comparison of the experimental infrared band wavenumbers and those from the literature (j) computed elastic constants; (k) calculated unit-cell volume and parameters as a function of the applied external pressures; (l) compressibility values as a function of the external pressure; (m) calculated fundamental thermodynamic functions; (n) thermodynamic properties of reaction. CCDC 1961689. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ra04596a |
| This journal is © The Royal Society of Chemistry 2020 |