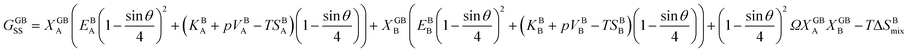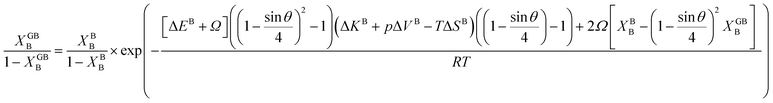DOI:
10.1039/D0RA04682E
(Paper)
RSC Adv., 2020,
10, 26728-26741
A model for grain boundary thermodynamics
Received
27th May 2020
, Accepted 29th June 2020
First published on 17th July 2020
Abstract
Systematic microstructure design requires reliable thermodynamic descriptions of each and all microstructure elements. While such descriptions are well established for most bulk phases, thermodynamic assessment of microstructure defects is challenging because of their individualistic nature. In this paper, a model is devised for assessing grain boundary thermodynamics based on available bulk thermodynamic data. We propose a continuous relative atomic density field and its spatial gradients to describe the grain boundary region with reference to the homogeneous bulk and derive the grain boundary Gibbs free energy functional. The grain boundary segregation isotherm and phase diagram are computed for a regular binary solid solution, and qualitatively benchmarked for the Pt–Au system. The relationships between the grain boundary's atomic density, excess free volume, and misorientation angle are discussed. Combining the current density-based model with available bulk thermodynamic databases enables constructing databases, phase diagrams, and segregation isotherms for grain boundaries, opening possibilities for studying and designing heterogeneous microstructures.
1. Introduction
Grain boundaries (GBs) are one of the main sources of heterogeneity in polycrystalline microstructures; they interact with various microstructure elements, e.g. GB networks,1 secondary-phase particles,2–4 dislocations,5–7 and vacancies,8,9 while they themselves possess distinct physical properties similar to the bulk phases. A critical source of microstructure heterogeneity is GBs' interaction with solute atoms that influences both the local and global chemistry of the microstructure. Solute segregation to GBs can mediate a whole different sort of phenomena such as segregation-assisted GB premelting,10 phase transition,11–13 precipitation14,15 and embrittlement16,17 as well as stabilization of nanocrystalline materials.18–20 Hence, understanding and controlling GBs and their spatial interactions with other microstructure elements can unravel new ideas for designing heterogeneous microstructures.
The studies on interfacial segregation can be traced back to the works of Gibbs,21 Langmuir,22 McLean23 and Fowler and Guggenheim24 on the adsorption. Since then, numerous studies on the segregation phenomena have been conducted.25–42 van der Waals,43 Cahn and Hilliard44 and Cahn45 worked out free energy functionals that account for heterogeneous interfacial features on the mesoscale. Based on this idea, several models for GB segregation were proposed. Ma et al.46 developed a phase-field model for studying GB segregation in which GB region was described by its reduced atomic coordination number. Based on Kobayashi–Warren–Carter's work,47 Tang et al. developed models for order-disorder transition48,49 and phase transition50 at GBs. Heo et al.51 proposed a model for GB segregation and drag including misfit elastic interactions. The common feature of these models is the non-vanishing gradients in GB structure and/or composition. Due to this fact, GB phases are sometimes referred to as ‘complexions’52–54 to emphasize their confined heterogeneous nature in contrast to a bulk phase that is – by definition – homogeneous.
Despite the enormous knowledge accumulated over the last century about the fundamental aspects of GBs,39,40,55,56 its application at a technical level is awaiting more comprehensive tools to allow systematic GB engineering. In particular, databases on GBs' properties are less popular; while thermodynamic and kinetic descriptions for most bulk phases are well established, analogous systematic and general descriptions for GBs are rarely investigated. This is because of the individualistic nature of GBs as every GB can be different depending on its crystallographic properties.55 Although GB properties are functions of a large space of crystallographic variables, one may not neglect the fact that they are made of the same constituents as for the grain interior (bulk), albeit deviating in local structure. An alternative view, therefore, can be to picture GBs with reference to their corresponding bulk phases. Thus, parallel to the current characterization techniques57 and automated simulation methods58,59 that are mainly focused on studying individual GBs, a general approach could be assessing the thermodynamic and kinetic properties of GBs with reference to the known bulk. For this purpose, we need to establish a physical framework that allows an approximation of the GB environment with respect to its reference bulk material.
In the current study, I propose a continuous atomic density field and its spatial variations to describe the GB region, relative to its adjacent homogeneous bulk material, in a regular substitutional binary solution. Based on this idea, (i) the GB's Gibbs free energy is approximated, (ii) GB segregation and the coexistence of the bulk and GB phases are discussed and, (iii) a concept for computing GB phase diagram is described. The novelty of the current model is that it enables a rapid, pragmatic assessment of GB properties based on available bulk thermodynamic data. To demonstrate the application of the current model, GB segregation and interfacial phase separation in the Pt–Au system are qualitatively studied. Furthermore, the relationships between the relative atomic density field and the GB nature in terms of GB excess free volume and misorientation angle are discussed. In two parallel studies, the applications of this model are further demonstrated in understanding segregation and interfacial phase separation in different alloy systems. In one case, we apply the density-based formulation to realize the Fowler–Guggenheim segregation isotherm for co-segregating Ni and Mn atoms at various types of GBs in a FeMnNiCrCo high-entropy alloy.60 A simpler version of the model has been applied to studying Mn segregation in the binary FeMn alloy system.61 The current density-based model offers a pragmatic approach to build GB thermodynamic databases, segregation isotherms and phase diagrams for studying heterogeneous polycrystalline microstructures.
2. Density-based model for GB thermodynamics
In his seminal work, van der Waals proposed that an interface can be described by a continuous density field43 and its spatial variations. For a GB, that needs to accommodate for the geometrical mismatch between two adjacent grains, an analogous picture can be portrayed in which the density of the GB will be different than that of the bulk materials. This is, on the one hand, even a simpler case than the van der Waals's setup, as the bulk density on the two sides of the GB are the same. On the other hand, however, it can be more complex because of the crystalline nature of the bulk material that may extend into the GB region. As a first attempt, here we neglect the heterogeneity of GB density (the density variation within the GB plane due to the crystallinity) and instead focus on the possibility of considering an ‘average’ atomic density parameter and density gradient terms to describe GB region.
In the following, we derive the density-based Gibbs free energy of a GB in unary (Section 2.1) and a substitutional binary regular solution (Section 2.2) systems. To do so, we take a variational approach to obtain density-based free energy density and cast this into the conventional thermodynamic framework, as used in CALPHAD approaches. We obtain the Gibbs free energy functional as a function of the atomic density field, concentration field, and their respective spatial variations. Using this free energy description, we obtain the GB phase diagram and segregation isotherm, Section 3. The model is demonstrated on the Pt–Au system. Different aspects of the current model, i.e., the coexistence of the bulk and GB phases and the relationship between the GB density, GB excess free volume, and GB misorientation angle, are discussed in Section 4.
2.1 A GB in a pure substance
At constant temperature T and pressure p, the Gibbs free energy functional of a system made of pure substance A can be written as| |
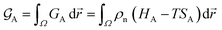 | (1) |
where ρn(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the atomic density field equivalent to the inverse molar volume field (Vm(
) is the atomic density field equivalent to the inverse molar volume field (Vm(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ))−1, HA is enthalpy per unit mole with HA = KA + EA + pVA (KA: kinetic energy, EA: potential energy and pVA: mechanical energy), and SA is entropy per unit mole, respectively. van der Waals has shown43 that the potential energy of a heterogeneous system depends on the (local) density as well as (nonlocal) density gradients. In this study, we consider a symmetric flat GB separating two infinitely large homogeneous grains. For this system, breaking the symmetry only normal to the GB plane, the interactions can be realized considering only one spatial dimension. The potential energy density will be
))−1, HA is enthalpy per unit mole with HA = KA + EA + pVA (KA: kinetic energy, EA: potential energy and pVA: mechanical energy), and SA is entropy per unit mole, respectively. van der Waals has shown43 that the potential energy of a heterogeneous system depends on the (local) density as well as (nonlocal) density gradients. In this study, we consider a symmetric flat GB separating two infinitely large homogeneous grains. For this system, breaking the symmetry only normal to the GB plane, the interactions can be realized considering only one spatial dimension. The potential energy density will be| |
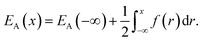 | (2) |
Here EA(−∞) is the potential energy inside the homogeneous grain at x = −∞ and the second term describes the energy stored in matter when brought from −∞ to a given position x. f(r) is the sum of all forces acting on point r:| |
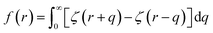 | (3) |
where ζ(r ± q) is the force density at point r upon the interaction between the two material points separated by a distance ±q. The interaction forces between atoms depend on the interatomic potential U(r ± q) with 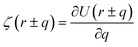 .
.
Although the detailed form of the interatomic potentials/forces can vary for different types of atoms, it is well-known that the atomistic interactions rapidly decays over the distance between atoms. For the sake of our discussion, we consider here a simple functional form
| |
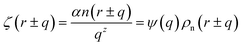 | (4) |
where
α is a material constant,
n(
r ±
q) is the number of atoms,
z is a positive exponent and we define
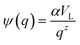
.
Eqn (4) with
z ≫ 1 is inspired by interatomic force relations in the absence of the long-range electrostatic interactions.
62 Here
VL is the characteristic coarse-graining volume over which the mesoscale atomic density field is measured by
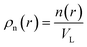
. Similar coarse-graining descriptions are worked out in defining mesoscale free energy formulations.
63,64 The specific form of
ψ(
q) can be obtained from atomistic simulations. The second- or higher-order dependencies of the interaction forces on the atomic density (including repulsive atomic interactions) can also be assumed. In the current treatment, however, we limit ourselves to the simplest first-order linear approximation as in
eqn (4).
In the theories of atomistic simulations, the atomic forces are practically calculated up to a cut-off radius Rc beyond which the interatomic forces are neglected.62 Hence, one reasonable approximation for the coarse-graining volume would be 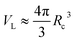 which can relate the atomistic simulation length-scale with the current mesoscale density-based formulation. Inserting eqn (4) in eqn (3), and integrating by part we can write
which can relate the atomistic simulation length-scale with the current mesoscale density-based formulation. Inserting eqn (4) in eqn (3), and integrating by part we can write
| |
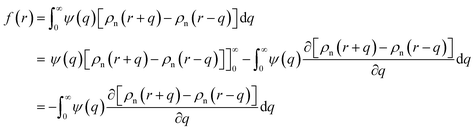 | (5) |
with
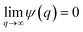
and
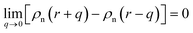
. Applying the Taylor expansions
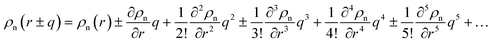
,
eqn (5) gives
| |
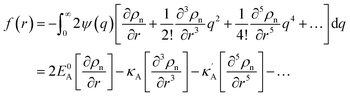 | (6) |
where we define
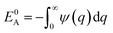
,
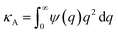
and
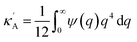
. Using
eqn (2) and
(6) with the boundary values
EA(−∞) =
E0Aρn(−∞),
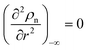
and
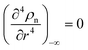
, we obtain the potential energy as a function of atomic density:
| |
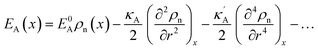 | (7) |
As a consequence of the Tylor expansions, it is clear that the sixth and higher-order spatial derivatives of the atomic density field can still contribute to the potential energy. These are, however, neglected in the following. Thus, the free energy functional in eqn (1) can be written as
| |
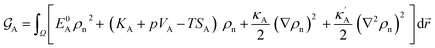 | (8) |
where we use a three-dimensional notation, ∫(∇
ρn)
2 d
V = −∫
ρn∇
2ρn d
V and ∫(∇
2ρn)
2 d
V = −∫
ρn∇
4ρn d
V with ∇
ρn = 0 and ∇
3ρn = 0 at the boundaries of the integrals. Here two density-dependent terms (
KA +
pVA −
TSA)
ρn and
E0Aρn2 appear in the free energy functional that scale differently with respect to the density
ρn.
The bulk atomic densities on the two sides of the GB can have different isotropy, depending on the crystallographic planes that meet at the GB plane. This can result in asymmetric GB structure and density profile. In the current study, however, we neglect this possibility and assume the same bulk density on the two sides of the GB. Thus we can further simplify our description by defining a dimensionless density parameter 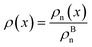 with ρBn = ρn(−∞) and writing
with ρBn = ρn(−∞) and writing
| |
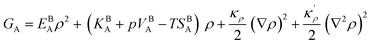 | (9) |
in which
EBA =
E0A(
ρBn)
2,
κρ =
κA(
ρBn)
2,
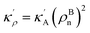
,
KBA =
KAρBn,
pVBA =
pVAρBn,
SBA =
SAρBn and, the Gibbs free energy of the homogeneous bulk phase (for
ρ = 1) recovers as
| | |
GBA = EBA + KBA + pVBA − TSBA = HBA − TSBA.
| (10) |
To obtain the GB free energy, one can compare a heterogeneous system including a GB against a homogeneous bulk system (without the boundary). Thus, subtracting eqn (10) from eqn (9) we obtain
| |
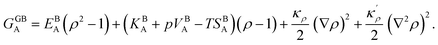 | (11) |
Eqn (11) gives an approximation of the GB Gibbs free energy density, GGBA. For the symmetric flat GB centered at position x = 0, the equilibrium density profile across the GB region (for 0 ≤ x ≤ η) will be
| |
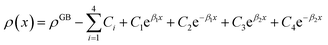 | (12) |
which satisfies
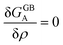
with
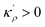
. The coefficients
Cis need to fulfill boundary conditions
ρ(
x = 0) =
ρGB,
ρ(
x =
η) = 1 and the continuity conditions
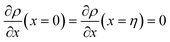
. Here
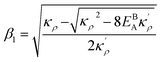
,
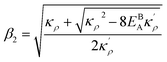
and
η is the GB half width. For a simpler case, assuming
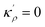
, the equilibrium density profile across the GB region reads
| |
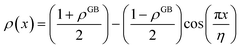 | (13) |
with
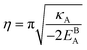
.
Eqn (12) or
(13) give a continuous atomic density profile across the GB. For more details on these equations see Appendix A. The continuity of atomic density profile across the GB region is confirmed by atomistic simulations.
61 Fig. 1 compares the atomic density profile
eqn (13) versus previous phase-field models for GBs
47–50 (
Fig. 1(c)) as well as the classical phase-field profile across an interface
65–67 (
Fig. 1(d)). Using
eqn (13) with
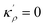
, the GB energy
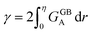
can be analytically obtained as
with
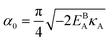
. This equation approximates the direct relation between
γ and
ρGB for an equilibrium density profile across the GB.
Fig. 1(e) shows the normalized value
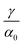
as a function of
ρGB. In the following,
ρGB, the average relative atomic density within the GB plane, will be referred to as ‘GB density’. The significance of the GB density and its relationship with the GB character is discussed in Section 4.2.
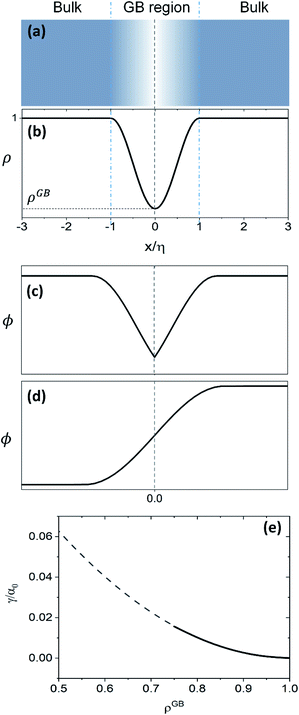 |
| | Fig. 1 (a) and (b) Continuous density profile across a symmetric flat GB with a density ρ(x = 0) = ρGB (eqn (13)). The GB width is related to the model parameters EBA and κA. The current density profile across GB is compared versus schematic drawing of order parameters from (c) the KWC phase-field model for GBs47 usually applied for studying GB phase transitions48–50 and (d) the classical phase-field profile (see for instance ref. 65). (e) The energy of the GB as a function of its density (eqn (14)) is shown (see Section 4.2 for discussions). | |
2.2 A GB in a regular binary alloy
In order to extend the current density-based model for a GB in a binary alloy, we need to discuss the significance of mixing energy as a function of atomic density. For a bulk regular solution made of A (solvent) and B (solute) atoms, the change in the Gibbs free energy due to the mixing can be approximated as68| |
ΔGBmix(XB) = ΔHBmix − TΔSBmix = ΩXAXB + RT[XA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XA + XB XA + XB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XB] XB]
| (15) |
within which R is the gas constant, Ω is the mixing enthalpy coefficient, Na is Avogadro number and Z is the coordination number. 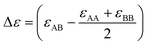 is bonding energy in which εij is the bonding energy between atoms i and j and XA (XB) is the mole fraction of atoms A (B). In principle, the mixing energy terms in eqn (15) can be assumed to follow the same scaling found in eqn (9). The effect of changing the coordination number Z on the GB enthalpy of mixing and GB segregation has been previously discussed (see for instance ref. 40, 46 and 69 and references therein). While the coordination number is proportional to the local density, the stretch in the bonding energy Δε is also expected to change with the density in the limit of linear elasticity. Considering these facts and neglecting the dependency of configurational entropy for the sake of simplicity, we can write
is bonding energy in which εij is the bonding energy between atoms i and j and XA (XB) is the mole fraction of atoms A (B). In principle, the mixing energy terms in eqn (15) can be assumed to follow the same scaling found in eqn (9). The effect of changing the coordination number Z on the GB enthalpy of mixing and GB segregation has been previously discussed (see for instance ref. 40, 46 and 69 and references therein). While the coordination number is proportional to the local density, the stretch in the bonding energy Δε is also expected to change with the density in the limit of linear elasticity. Considering these facts and neglecting the dependency of configurational entropy for the sake of simplicity, we can write| | |
ΔGmix(XB, ρ) ≈ ρ2ΔHBmix − TΔSBmix.
| (17) |
Following Cahn and Hilliard,44 an energy term due to the concentration gradients – in the presence of chemical heterogeneity – enters the free energy description as well. Thus, using eqn (9) and (17), the density-based Gibbs free energy of a regular solid solution (SS) can be written as
| |
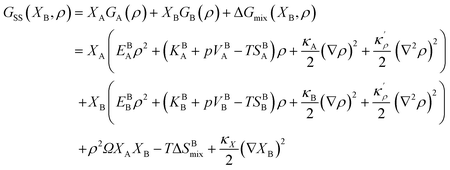 | (18) |
where
κX is the concentration gradient coefficient. In
eqn (18), corresponding molar fractions
XBi and
XGBi will be considered for the bulk and GB regions, respectively. For the homogeneous bulk phase, one recovers
| | |
GBSS(XBB, ρ = 1) = XBA(HBA − TSBA) + XBB(HBB − TSBB) + ΩXBAXBB − TΔSBmix.
| (19) |
Using eqn (18) we are able now to study the GB phase equilibria and segregation isotherms as presented in the next section.
3. Applications of the density-based model
3.1 Equilibrium GB phase diagram
Obviously, a GB may not exist without its corresponding bulk phase(s). It is, however, useful to study the equilibrium phase diagram of a hypothetical GB as a function of its atomic density. As eqn (18) suggests, for such hypothetical GB with ρ < 1 the phase equilibria should differ from that of the corresponding bulk material with ρ = 1. The equilibrium states are evaluated by minimizing the Gibbs free energy functional with respect to the concentration and atomic density fields, i.e. 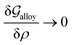 and
and 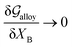 with
with 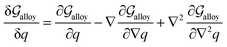 and
and  . A numerical solution of these equations can provide information about the spatiotemporal evolution of phases in the GB region. This has been quantitatively demonstrated in a parallel study on the Mn segregation in Fe–Mn system.61 The aim of the current study, however, is to provide analytical descriptions for equilibrium GB thermodynamics. Hence, in the following, we rather investigate a single material point at the GB center where spatial gradients of the atomic density field vanish, i.e. ∇ρ(x = 0) = 0. We further assume that for this point the concentration gradient and higher-order density gradients can be neglected. Thus, with ρ(x = 0) = ρGB and XB(x = 0) = XGBB, the density-based Gibbs free energy description at this material point simplifies to
. A numerical solution of these equations can provide information about the spatiotemporal evolution of phases in the GB region. This has been quantitatively demonstrated in a parallel study on the Mn segregation in Fe–Mn system.61 The aim of the current study, however, is to provide analytical descriptions for equilibrium GB thermodynamics. Hence, in the following, we rather investigate a single material point at the GB center where spatial gradients of the atomic density field vanish, i.e. ∇ρ(x = 0) = 0. We further assume that for this point the concentration gradient and higher-order density gradients can be neglected. Thus, with ρ(x = 0) = ρGB and XB(x = 0) = XGBB, the density-based Gibbs free energy description at this material point simplifies to| | |
GSS(XGBB, ρGB) = XGBA(EBA(ρGB)2 + (KBA + pVBA − TSBA)ρGB) + XGBB(EBB(ρGB)2 + (KBB + pVBB − TSBB)ρGB) + (ρGB)2ΩXGBAXGBB − TΔSBmix.
| (20) |
Eqn (20) allows to approximate the GB thermodynamic properties, analytically. To demonstrate application of the current density-based model, we consider a hypothetical GB with ρGB = 0.75 in the Pt–Au system. In this alloy system, the only difference to the theoretical regular solution is in the enthalpy of mixing that extends to the second term in Redlich–Kister polynomial:
| | |
ΩPtAu = L0 + L1(XBPt − XBAu).
| (21) |
Inserting eqn (21) in eqn (20) we obtain
| | |
GSS(XGBAu, ρGB) = XGBPt(EBPt(ρGB)2 + (KBPt + pVBPt − TSBPt)ρGB) + XGBAu(EBAu(ρGB)2 + (KBAu + pVBAu − TSBAu)ρGB) + (ρGB)2ΩPtAuXGBPtXGBAu − TΔSBmix.
| (22) |
Grolier et al.70 have assessed the bulk thermodynamic data for binary the Pt–Au and reported L0 = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 + 8.3104T and L1 = −12
625 + 8.3104T and L1 = −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616 + 5.8186T [J mol−1] for the FCC Pt–Au solid solution. The rest of the thermodynamic data for pure Pt and Au are extracted from SGTE compilation by Dinsdale.71 Inserting these values in eqn (21) and (22), one obtains the Gibbs free energy as a function of GB density and composition. Fig. 2 shows a 3D map of the Gibbs free energy for the Pt–Au system at 300 K as a function of composition XAu and GB density ρGB. We found that as the GB density decreases, the Gibbs free energy increases and deviates larger from the corresponding bulk values. Fig. 3 compares bulk and GB Gibbs free energy for ρGB = 0.75 at different temperatures.
616 + 5.8186T [J mol−1] for the FCC Pt–Au solid solution. The rest of the thermodynamic data for pure Pt and Au are extracted from SGTE compilation by Dinsdale.71 Inserting these values in eqn (21) and (22), one obtains the Gibbs free energy as a function of GB density and composition. Fig. 2 shows a 3D map of the Gibbs free energy for the Pt–Au system at 300 K as a function of composition XAu and GB density ρGB. We found that as the GB density decreases, the Gibbs free energy increases and deviates larger from the corresponding bulk values. Fig. 3 compares bulk and GB Gibbs free energy for ρGB = 0.75 at different temperatures.
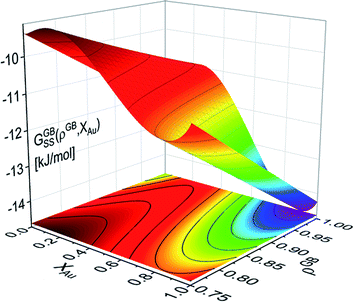 |
| | Fig. 2 Gibbs free energy density of the Pt–Au system (eqn (22)) is shown as a generalized function of composition and atomic density at T = 300 K. For ρGB = 1 = ρB, the Gibbs free energy of the reference bulk is recovered. For ρGB < 1 the free energy increases. | |
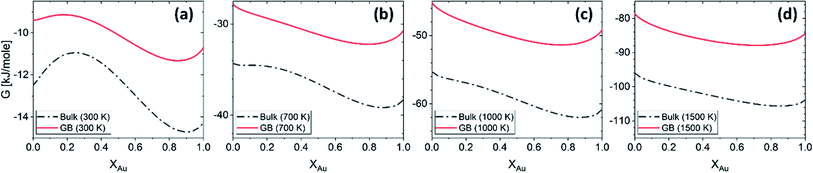 |
| | Fig. 3 The Gibbs free energy density of the bulk and our hypothetical GB with ρGB = 0.75 in the Pt–Au system obtained from eqn (22) are compared at different temperatures. As expected, the GB Gibbs free energy density is higher than the bulk. | |
Using eqn (22), the equilibrium phase diagrams of the bulk and any specific standalone GB (with a given GB density) in the Pt–Au system can be generated. Fig. 4 compares the phase diagrams of the bulk and our hypothetical GB (with ρGB = 0.75) in the Pt–Au solid solution. The results show that, inside a (hypothetically standalone) GB, the interfacial phase separation becomes possible but for smaller ranges of temperature and composition when compared to the bulk phase diagram.
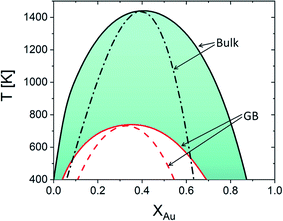 |
| | Fig. 4 Equilibrium phase diagram for the bulk ρ = ρB = 1 and our hypothetical GB with ρ = ρGB = 0.75 are obtained for the Pt–Au system. The dash lines represent the chemical spinodals. The colored area marks the possible domain where GB phase diagrams for 0.75 < ρGB < 1 can appear. Note that the equilibrium bulk and GB phase diagrams are plotted independently. The coexistence of the bulk and GB phases will be discussed in Sections 3.2 and 4.1 and Fig. 6. | |
As it is evident from the Gibbs free energy plots (Fig. 2 and 3), the GB thermodynamics strongly depend on the GB density ρGB. Although the phase diagram is a nonlinear function of the GB density, the possible values for GB density ρGB are finite and vary close to 1. For instance, the colored area in Fig. 4 indicates where the GB phase diagram can appear for 0.75 < ρGB < 1. Thus, once the range of GB density is determined, the equilibrium GB phase diagrams can be approximated. The GB density represents the nature (type) of the GB and correlates with the GB energy and misorientation angle. These aspects of the current density-based model are discussed in Section 4.2.
3.2 GB segregation behavior
In Section 3.1 a hypothetical standalone GB was discussed. For a complete description of GB phase equilibria, however, the coexistence between the GB and bulk phases must be understood. In a binary system, this requires equality of the (relative) chemical potentials μBB − μBA = μGBB − μGBA all across the system (parallel tangent construction).24,72 In reality, these are not sufficient conditions as a minimum energy state with respect to the atomic density field must be satisfied as well. However, if we consider the same material point at the GB center as above, we can simplify the problem and solve for the equality of the (relative) chemical potentials using eqn (20) which gives| |
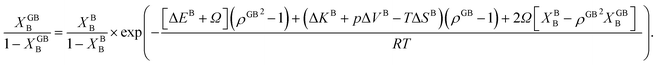 | (23) |
In eqn (23), XGBB is the composition of the GB with ρ = ρGB, XBB is the composition of the bulk far from the GB, ΔEB = EBB − EBA, ΔKB = KBB − KBA, pΔVB = pVBB − pVBA, and ΔS = SBB − SBA. Eqn (23) resembles the Fowler–Guggenheim segregation isotherm24 but also takes the specific effect of a given GB, represented by its density ρGB, into account. For the Pt–Au system, we obtain| |
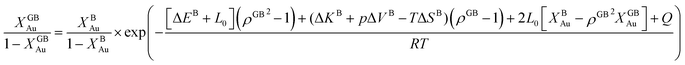 | (24) |
with 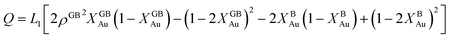 , ΔEB = EBAu − EBPt, ΔKB = KBAu − KBPt, pΔVB = pVBAu − pVBPt, and ΔS = SBAu − SBPt. Eqn (23) and (24) use GB density and bulk thermodynamic data as the inputs and give the corresponding GB segregation isotherms.
, ΔEB = EBAu − EBPt, ΔKB = KBAu − KBPt, pΔVB = pVBAu − pVBPt, and ΔS = SBAu − SBPt. Eqn (23) and (24) use GB density and bulk thermodynamic data as the inputs and give the corresponding GB segregation isotherms.
Fig. 5 presents the (relative) chemical potentials and the segregation isotherms for the bulk and the exemplar GB with ρGB = 0.75 in the Pt–Au system at three different temperatures. The chemical potential of the GB which is a function of GB density differs from the corresponding bulk chemical potential. The Maxwell construction (defining the two-phase regions) and the spinodal compositions for both GB and bulk materials are built. The graphs show that the GB spinodal decomposition (interfacial spinodal) can occur for lower chemical potential values below the bulk spinodal (e.g. in Fig. 5(a)). As a result, the two-phase GB can be in equilibrium with a single-phase bulk. As a matter of fact, it has been reported that a segregation-assisted interfacial phase separation can occur in Pt–Au system which results in the formation of two-phase GBs coexisting with a single-phase bulk.73,74 The results in Fig. 5 suggest that the two-phase bulk will be in equilibrium with a single-phase GB. In fact, at a given temperature, for any bulk composition within the two-phase region of the phase diagram, the two-phase bulk is expected to be in equilibrium with a single phase/composition GB. These are because of a vertical shift in the GB chemical potential (with respect to the bulk chemical potential) that can be seen in Fig. 5(a). Combining these results with the equilibrium bulk and GB phase diagrams (Section 3.1), we are able now to study the complete GB thermodynamic phase diagram. This is discussed in Section 4.1.
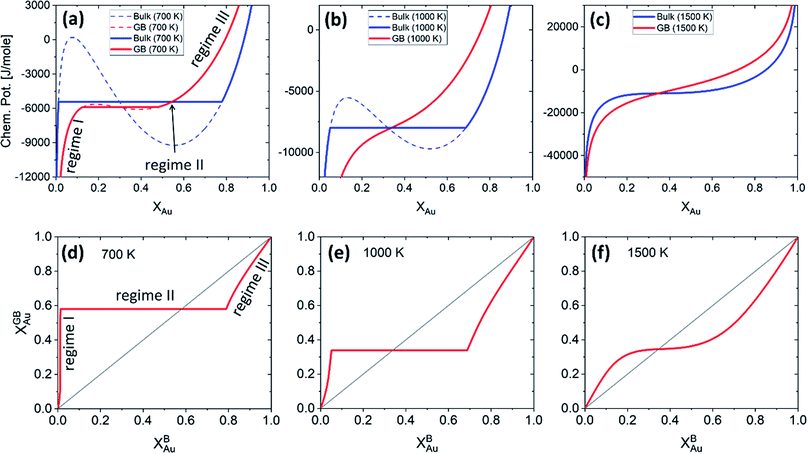 |
| | Fig. 5 (a)–(c) The chemical potentials of the Au atoms in bulk and a GB (with ρGB = 0.75) Pt–Au are plotted for three different temperatures. (d)–(f) Using the parallel tangent condition the segregation isotherms are obtained for the corresponding temperatures. Different regimes of segregation appear depending on the GB density and temperature. See discussions in Section 4.2. | |
4. Discussion
4.1 Coexistence of GB and bulk phases
In this model, the GB region is described by a continuous atomic density and its spatial gradients. For the sake of simplicity, here we have limited our derivations to the first-order approximation of the potential energy with respect to ρ and its spatial variations. The current density-based model provides a simple method for approximating the Gibbs free energy of a given GB based on available bulk thermodynamic data. The continuity of the atomic density field across GB allows further simplifying the Gibbs free energy description at the GB plane where the gradient term ∇ρ vanishes. The results of the current study are obtained for this single material point within the GB region. The model can be applied in full-field simulations of GBs as well, to evaluate the temporal evolution of the atomic density and concentration fields. In two parallel study, we have demonstrated the application of the density-based model for studying GB segregation in a FeMnNiCrCo high entropy alloy60 and segregation engineering of Fe–Mn alloys.61
In the current study, we focus on the equilibrium GB properties in a binary substitutional solid solution. Using the density-based formulation we extend the concept of the phase diagram for GBs, Fig. 6(b). To arrive there, we started with the equilibrium phase diagram for the bulk and a hypothetical standalone GB, with ρGB = 0.75, in the Pt–Au solid solution (Fig. 4). The results show that similar to the bulk materials, GBs in the Pt–Au system can also undergo an interfacial spinodal phase separation. In this case, we show that GB two-phase region is confined to smaller temperature and composition ranges. As the GB density deviates larger from the bulk density, the GB miscibility gap in the phase diagram becomes smaller.
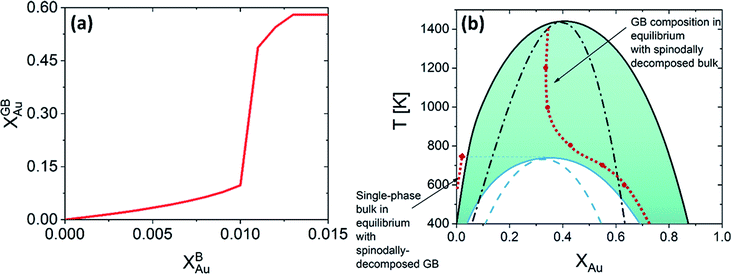 |
| | Fig. 6 (a) For Pt–Au system at 700 K, a jump (GB spinodal) occurs before the bulk spinodal decomposition takes place. This is a zoomed in plot in Fig. 5(d) (left corner), see also Fig. 5(a). (b) Based on the current density-based model the coexistence of the bulk and GB phases is depicted in the phase diagram for the Pt–Au system. A two-phase bulk will be in equilibrium with a single-phase GB while a two-phase (spinodally-decomposed) GB is shown to be in equilibrium with a single-phase bulk. | |
The coexistence of the bulk and GB phases can be studied using the equal chemical potential condition.24,72 Here the bulk phase, which is the dominant part of the microstructure, is assumed to dedicate the ultimate thermodynamic states and behavior of the GBs. According to eqn (23) (or eqn (24) for the Pt–Au system), the GB segregation level depends on the temperature, bulk composition, as well as GB type represented by its density ρGB. For a regular solution discussed here, the driving forces for the segregation can be divided into two parts: the first contribution is the ideal segregation energy 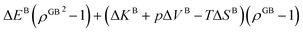 that is analogous to the segregation driving force in Langmuir–McLean isotherm.72 If we neglect the energetic contributions due to the mixing (Ω = 0), we obtain a density-based version of Langmuir–McLean relation as:
that is analogous to the segregation driving force in Langmuir–McLean isotherm.72 If we neglect the energetic contributions due to the mixing (Ω = 0), we obtain a density-based version of Langmuir–McLean relation as:
| |
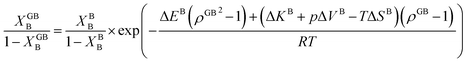 | (25) |
that describes solute segregation for a given GB in an ideal solution. The second contribution in
eqn (23) is
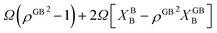
due to the mixing which contains a term with the GB concentration
XGBB. The two contributions discussed above can have cooperative or competitive effects on the segregation level, depending on the magnitude and sign of
Ω and Δ
EB.
Fig. 5 presents the chemical potentials and segregation isotherms for the Pt–Au system. In this system, three regimes of bulk-GB coexistence could be identified as a function of the bulk composition. First, segregation to the GB occurs as the Au content increases in Pt-rich alloys (regime I). For a two-phase bulk, the GB composition becomes fixed (regime II) that applies to the entire range of bulk composition in the two-phase bulk region. Any further increase of the Au content results in solute depletion in the GB (regime III) with respect to the bulk. In Fig. 5(a) and (d) different regimes of segregation are marked.
For a Pt-rich Pt–Au alloy (regime I), the GB, which is enriched in Au due to the segregation, can undergo an interfacial spinodal decomposition before a bulk spinodal becomes possible. At 700 K, for instance, a jump in the GB segregation, associated with the interfacial phase separation, is revealed in the Pt–Au system. Fig. 6(a) shows this jump in the GB composition as a function of bulk composition (this is a zoomed-in plot of the left corner in Fig. 5(d)). At this jump, the GB decomposes into low-concentration and high-concertation domains that occurs in the presence of a single-phase bulk. This means that for a specific bulk composition (in the single-phase region of the bulk phase diagram) a spinodally-decomposed two-phase GB will form. Consistent with the current predictions, a segregation-assisted interfacial spinodal decomposition has been indeed reported in nanocrystalline Pt–Au alloy.73 Also, atomistic simulations of the Pt–Au system confirmed such interfacial spinodal phase separation for bulk compositions well below the bulk spinodal range.74 GB spinodal phase separation is also evidenced in other material systems with technological significance.75,76
For the two-phase Pt–Au bulk materials (regime II), the model predicts that a single-phase GB comes to coexist. This is because of the vertical shift in the GB chemical potential with respect to the corresponding bulk chemical potential curve, as depicted in Fig. 5(a). In practice, a range of atomic densities and compositions exists in the GB region (between the GB plane and bulk interior) that can enable interfacial phase separation in the GB region. Combining the equilibrium GB phase diagram (Fig. (4)) and the GB segregation isotherms (Fig. (5)), we can obtain the complete GB phase diagram as presented in Fig. 6(b).
The discontinuous jump in the GB segregation isotherm (Fig. 6(a)) is a result of the difference in the free energy functional and chemical potentials of the bulk and GB phases, captured by the density-based model. Depending on the sign of ΔEB and the shape of Ω(XB) function (in composition space), the GB chemical potential and its corresponding spinodal decomposition can lie ‘Above’ or ‘Below’ the bulk spinodal (Fig. 7). In either case, one can activate a segregation-assisted interfacial phase separation, that can act as a precursor for subsequent nucleation, before reaching the bulk two-phase region. It has been shown that a segregation-assisted transient spinodal phase separation comes to exist at GBs for a larger range of bulk compositions61 which enables manipulation of GB segregation by desired heat treatments.
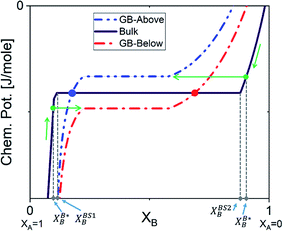 |
| | Fig. 7 The GB chemical potential can be ‘Below’ or ‘Above’ the bulk's curve. XBS1B and XBS2B show the bulk equilibrium compositions in the two-phase region. The two-phase GB will be in equilibrium with a single-phase bulk material as marked by the arrows. The dots on the bulk chemical potential curve indicates the single-phase GB is equilibrium with the two-phase bulk. | |
In a polycrystalline material having a large population of GBs of various types (with different crystallographic properties), the GB densities are expected to differ from one GB to another. A quantitative application of the current model to technical materials, therefore, requires determination of the GB structure and densities for different types of GBs. For this purpose, atomistic simulations, for instance, can provide the necessary means to evaluate GB density profiles. Though atomistic simulation of GBs is beyond the scope of this study, in the following we briefly analyze the relationships between the ρGB, GB excess free volume and GB misorientation angle that can provide more insights to the density-based concept.
4.2 The relation between the GB density and GB nature
In order to make use of the current model, it is helpful to explore the significance of the average GB density and its relationship with the GB nature. Using atomistic simulations and an appropriate numerical coarse-graining scheme, 3D density map of any GB can be extracted from its equilibrium atomic configuration that gives η and ρGB.61 GB energy γ can be related to the η and ρGB values. Eqn (14) approximates the relationship between GB energy and its density ρGB when 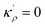 is assumed. It is observed that GBs with higher energies, i.e., lower GB densities, attract more solute content during the segregation.77 Using eqn (14) and (20), the GB Gibbs free energy of a regular solution can be written as a function of its initial GB energy. Accordingly, we can rewrite eqn (23) as
is assumed. It is observed that GBs with higher energies, i.e., lower GB densities, attract more solute content during the segregation.77 Using eqn (14) and (20), the GB Gibbs free energy of a regular solution can be written as a function of its initial GB energy. Accordingly, we can rewrite eqn (23) as| |
 | (26) |
that gives a useful approximation for describing GB's tendency for segregation as a function of its initial energy.
One way to elaborate about the GB density ρGB is to find its relationship with the GB excess free volume defined as78
| |
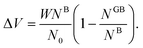 | (27) |
Here
W is the atom diameter,
NGB is the number of atoms in the GB,
NB is the number of atoms in the bulk within the same volume and
N0 is the number of atoms per unit area of the GB. In principle, the ‘excess’ volume represents the ‘shortage’ of atoms in the GB plane. On the other hand, comparing a GB against the bulk of the same volume and using
eqn (13), the relative number of atoms in a GB will be
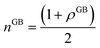
(where
nB = 1) and the relative difference (with respect to the bulk) will be
where
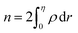
is the (relative) total number of atoms in the GB. Comparing
eqn (27) and
(28) one can find the one-to-one relationship between Δ
n and Δ
V, where we can identify Δ
V ∝ (1 −
ρGB). Extensive works have been devoted to calculate and measure GB excess free volume (see for instance
ref. 79–81). Aaron and Bolling
78 have shown that the energy of different types of GBs can be associated with their excess free volume which can be extended as well for the GB density parameter
ρGB.
The lower limit of the GB density value (highest excess free volume) shall be obtained for general high angle GBs (HAGBs). Aaron and Bolling remarked that the excess free volume in a general HAGB is comparable to that of a liquid phase.78 On the other hand, the maximum GB density value is the corresponding bulk density ρB = 1. Special GBs such as coherent twin boundaries (TBs) with low coincidence values show small GB energy and excess free volumes.78 This is well consistent with the current model in which as ΔV goes to zero, ρGB approaches ρB = 1 and γ approaches zero (eqn (14)).
For a low-angle GB (LAGB), the situation becomes a bit more complex because of the dislocations. Since dislocations are localized defects with a lower atomic density in their core, one expects the local GB density ρGB within the LAGB plane to fluctuate accordingly. In addition, elastic interactions between dislocations can play a role in determining ρGB for LAGBs. For a simple case neglecting these elastic interactions, we can approximate the average GB density for a LAGB by a simple volume averaging of regularly spaced dislocations, as detailed in Appendix B. For a tilt GB, a simple geometrical construction of a LAGB gives the average GB density 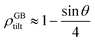 with the GB misorientation θ, and the edge dislocation core density ρD ≈ 0.75. For a larger misorientation angle, the GB density will be smaller, deviating larger from bulk properties. We also obtain a misorientation-dependent
with the GB misorientation θ, and the edge dislocation core density ρD ≈ 0.75. For a larger misorientation angle, the GB density will be smaller, deviating larger from bulk properties. We also obtain a misorientation-dependent 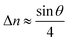 and thus a corresponding GB excess free volume ΔV ∝ sin
and thus a corresponding GB excess free volume ΔV ∝ sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ that is consistent with the previous studies.78,82 GB segregation as a function of GB misorientation has been studied in the Pt–Au system. Seki et al.83,84 and Seidman85 studied Au segregation to twist boundaries and have shown that although the GB segregation is not homogeneous, its average level increases as the misorientation angle increases (with the exception of special GBs). These observations confirm the results from the current density-based model where a higher misorientation angle corresponds to a lower GB density. An in-depth study of LAGBs requires consideration of elastic energy contributions which is left for a future study.
θ that is consistent with the previous studies.78,82 GB segregation as a function of GB misorientation has been studied in the Pt–Au system. Seki et al.83,84 and Seidman85 studied Au segregation to twist boundaries and have shown that although the GB segregation is not homogeneous, its average level increases as the misorientation angle increases (with the exception of special GBs). These observations confirm the results from the current density-based model where a higher misorientation angle corresponds to a lower GB density. An in-depth study of LAGBs requires consideration of elastic energy contributions which is left for a future study.
5. Summary and outlook
In this work, we have derived a density-based model for assessing GB thermodynamics. The current model uses available bulk thermodynamic data, as input, and gives a rather general formulation for GB's Gibbs free energy. GB segregation isotherm and phase diagram for a regular binary solid solution have been obtained. We further discussed the relationships between GB density, GB excess free volume and, GB misorientation angle. The results are qualitatively demonstrated on the Pt–Au system. We show that in a Pt-rich Pt–Au alloy, Au atoms tend to segregate to the GB. The average level of segregation increases with decreasing GB density, i.e., increasing GB misorientation angle (with the exception of special GBs). We also show that an interfacial spinodal decomposition can occur in these alloys for single-phase bulk alloys. A comparison with previous studies on the Pt–Au system confirms these predictions.
The current density-based model offers a simple, pragmatic approach to develop GB thermodynamic databases. Despite its simplicity, applications of this model can unroll new microstructure design concepts by segregation engineering of GBs.60,61 A systematic atomistic study of the coarse-grained atomic density profiles for different types of GBs can enrich the development of this model. In order to assess engineering alloys with interstitial solute atoms, the density-based free energy description needs to be extended for multi-component materials and including elastic energy contributions.
Appendix
A Equilibrium GB density profile
The equilibrium GB density profile across a symmetric flat GB in a pure substance can be obtained by minimizing the GB free energy functional with respect to the relative atomic density. For a 1D setup,| |
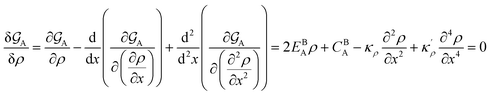 | (A.1) |
where CBA = KBA + pVBA − TSBA (see eqn (9)). The general solution for this higher-order linear ordinary differential equation reads| |
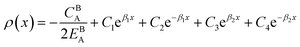 | (A.2) |
with 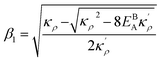 and
and 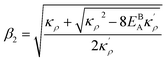 . We also obtain
. We also obtain| |
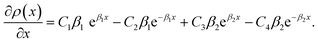 | (A.3) |
Applying the boundary conditions ρ(x = 0) = ρGB, ρ(x = η) = 1 and the continuity conditions 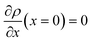 and
and 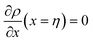 , we obtain
, we obtain
| |
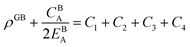 | (A.4) |
| |
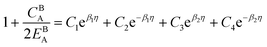 | (A.5) |
| |
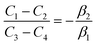 | (A.6) |
| |
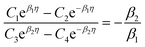 | (A.7) |
The solution to eqn (A.4)–(A.7) can be computed numerically. The continuity of the average atomic density profile across the GB region is confirmed using atomistic simulations.61 For a simpler case assuming 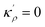 , we find another general solution for eqn (A.1):
, we find another general solution for eqn (A.1):
| |
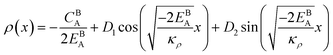 | (A.8) |
where
D1 and
D2 are constants and
| |
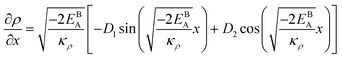 | (A.9) |
Applying the boundary conditions to this solution we obtain
| |
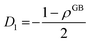 | (A.10) |
| |
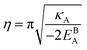 | (A.12) |
| |
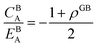 | (A.13) |
Although solution eqn (A.8) is limiting, it provides a possibility for further analytical treatment of the density profile and therefore is used for approximating GB energy, eqn (14). For more details see Section 2.1.
B A simple geometrical calculation of GB density
The objective of this appendix is to provide a simple analysis of the GB density and its dependence on the misorientation angle. We consider a LAGB that can be mapped with a set of regularly spaced dislocations separated by a distance68| |
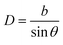 | (B.1) |
in which b is the Burgers vector of the dislocations and θ is the GB misorientation angle. The ‘average’ relative GB density can be obtained by averaging the density of a dislocation in the unit area of the LAGB. For a tilt LAGB one obtains| |
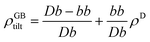 | (B.2) |
where ρD is the relative atomic density at the core of an edge dislocation. Inserting eqn (B.1) in eqn (B.2)| |
ρGBtilt = 1 − (1 − ρD)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. θ.
| (B.3) |
Here it is assumed that the volume between the two dislocations has the same density as bulk (ρB = 1). For an edge dislocation depicted in Fig. 8(a), one can approximate 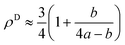 where a is the interatomic distance normal to the edge dislocation line – here we neglect the effect of elastic energy of the dislocation on its core density. Neglecting the second term inside the parenthesis then we have ρD ≈ 0.75 that gives the atomic density of a tilt GB as
where a is the interatomic distance normal to the edge dislocation line – here we neglect the effect of elastic energy of the dislocation on its core density. Neglecting the second term inside the parenthesis then we have ρD ≈ 0.75 that gives the atomic density of a tilt GB as
| |
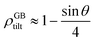 | (B.4) |
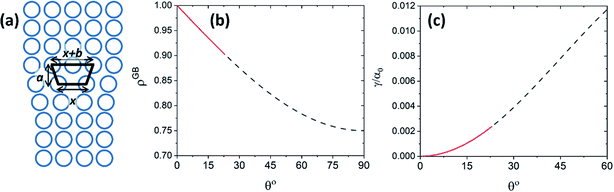 |
| | Fig. 8 (a) The core of an edge dislocation has a lower density than that of the bulk that is captured by a simple geometrical analysis. GB density (b) and energy (c) as a function of the misorientation angle, with the exception of special GBs, are plotted (eqn (B.4) and (B.5)). | |
In this relation, as θ approaches zero, ρGB approaches ρB = 1 and the GB energy (according to eqn (7)) decreases towards zero. Inserting eqn (B.4) into eqn (14), we obtain
| |
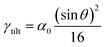 | (B.5) |
that is the tilt GB energy as a function of the misorientation angle.
Eqn (14),
(B.4) and
(B.5) give the relationship between the GB density, energy and misorientation angle based on the current simple analysis. From
eqn (28) and
(B.4),
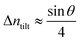
and thus the corresponding average GB excess free volume will be proportional to the misorientation angle as Δ
V ∝ sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ.
Fig. 8(b) and (c) show the variation of GB density and energy as a function of the misorientation angle according to this analysis.
Although eqn (B.4) and (B.5) are based on a very simplified averaging method that does not account for the elastic energy of the dislocations, the current analysis is solid in establishing the trend in GB densities as a function of its misorientation angle, with the exception of special GBs. It is useful to show that the GB density converges to the expected GB energies in the limiting cases, consistent with the previous derivations of GB energy based on the excess free volume concept.78 In order to connect the GB segregation isotherm with its initial misorientation angle, we can approximate by replacing the atomic density parameter using eqn (B.4). From eqn (B.4) and (20)
| |
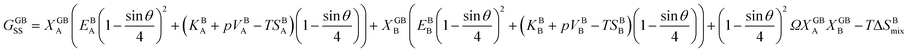 | (B.6) |
Thus, using eqn (B.6) and (23) the GB segregation isotherm follows
| |
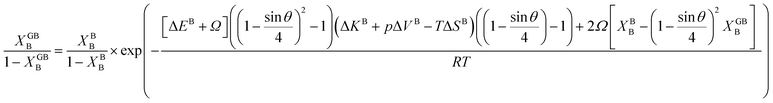 | (B.7) |
Data availability
The numerical data from this study are available upon reasonable request.
Conflicts of interest
The author declares no conflict of interest.
Acknowledgements
This work is being performed under the project DA 1655/2-1 within the Heisenberg program by the Deutsche Forschungsgemeinschaft (DFG). The author gratefully acknowledges financial supports within this program.
References
- R. Darvishi Kamachali, Grain boundary motion in polycrystalline materials, Univ.-Bibliothek, 2013 Search PubMed.
- N. Louat, The inhibition of grain-boundary motion by a dispersion of particles, Philos. Mag. A, 1983, 47(6), 903–912 CrossRef CAS.
- C. Schwarze, R. Darvishi Kamachali and I. Steinbach, Phase-field study of zener drag and pinning of cylindrical particles in polycrystalline materials, Acta Mater., 2016, 106, 59–65 CrossRef CAS.
- X. Li, J. Liang, T. Shi, D. Yang, X. Chen, C. Zhang, Z. Liu, D. Liu and Q. Zhang, Tribological behaviors of vacuum hot-pressed ceramic composites with enhanced cyclic oxidation and corrosion resistance, Ceram. Int., 2020, 12911–12920 CrossRef CAS.
- D. Dingley and R. Pond, On the interaction of crystal dislocations with grain boundaries, Acta Metall., 1979, 27(4), 667–682 CrossRef CAS.
- J. Kacher, B. Eftink, B. Cui and I. Robertson, Dislocation interactions with grain boundaries, Curr. Opin. Solid State Mater. Sci., 2014, 18(4), 227–243 CrossRef CAS.
- X. Li, T. Shi, B. Li, X. Chen, C. Zhang, Z. Guo and Q. Zhang, Subtractive manufacturing of stable hierarchical micro–nano structures on AA5052 sheet with enhanced water repellence and durable corrosion resistance, Mater. Des., 2019, 183, 108152 CrossRef CAS.
- R. Darvishi Kamachali, J. Hua, I. Steinbach and A. Hartmaier, Multiscale simulations on the grain growth process in nanostructured materials: paper presented at the 2nd Sino-German symposium on computational thermodynamics and kinetics and their applications to solidification, Int. J. Mater. Res., 2010, 101(11), 1332–1338 CrossRef.
- D. Chen, J. Wang, T. Chen and L. Shao, Defect annihilation at grain boundaries in alpha-Fe, Sci. Rep., 2013, 3, 1450 CrossRef PubMed.
- J. Luo, V. Gupta, D. Yoon and H. Meyer III, Segregation-induced grain boundary premelting in nickel-doped tungsten, Appl. Phys. Lett., 2005, 87(23), 231902 CrossRef.
- K. E. Sickafus and S. Sass, Grain boundary structural transformations induced by solute segregation, Acta Metall., 1987, 35(1), 69–79 CrossRef CAS.
- Y. Yan, M. Chisholm, G. Duscher, A. Maiti, S. Pennycook and S. Pantelides, Impurity-induced structural transformation of a MgO grain boundary, Phys. Rev. Lett., 1998, 81(17), 3675 CrossRef CAS.
- T. Frolov, M. Asta and Y. Mishin, Segregation-induced phase transformations in grain boundaries, Phys. Rev. B, 2015, 92(2), 020103 CrossRef.
- D. Vaughan, Grain boundary precipitation in an Al–Cu alloy, Acta Metall., 1968, 16(4), 563–577 CrossRef CAS.
- M. De Hass and J. T. M. De Hosson, Grain boundary segregation and precipitation in aluminium alloys, Scr. Mater., 2001, 44(2), 281–286 CrossRef CAS.
- R. Messmer and C. Briant, The role of chemical bonding in grain boundary embrittlement, Acta Metall., 1982, 30(2), 457–467 CrossRef CAS.
- P. Lejček, M. Šob and V. Paidar, Interfacial segregation and grain boundary embrittlement: an overview and critical assessment of experimental data and calculated results, Prog. Mater. Sci., 2017, 87, 83–139 CrossRef.
- J. R. Trelewicz and C. A. Schuh, Grain boundary segregation and thermodynamically stable binary nanocrystalline alloys, Phys. Rev. B, 2009, 79(9), 094112 CrossRef.
- T. Chookajorn, H. A. Murdoch and C. A. Schuh, Design of stable nanocrystalline alloys, Science, 2012, 337(6097), 951–954 CrossRef CAS PubMed.
- M. Kapoor, T. Kaub, K. A. Darling, B. L. Boyce and G. B. Thompson, An atom probe study on Nb solute partitioning and nanocrystalline grain stabilization in mechanically alloyed Cu–Nb, Acta Mater., 2017, 126, 564–575 CrossRef CAS.
- J. W. Gibbs, The Collected Works of J. Willard Gibbs, Ph. D., LLD, Yale University Press, London, England, 1957, vol. 1–2 Search PubMed.
- I. Langmuir, The adsorption of gases on plane surfaces of glass, mica and platinum, J. Am. Chem. Soc., 1918, 40(9), 1361–1403 CrossRef CAS.
- D. MacLean, Grain boundaries in metals, 1957 Search PubMed.
- R. H. Fowler and E. A. Guggenheim, Statistical thermodynamics: a version of statistical mechanics for students of physics and chemistry, The University Press, 1939 Search PubMed.
- E. W. Hart, Two-dimensional phase transformation in grain boundaries, Scr. Metall., 1968, 2(3), 179–182 CrossRef.
- E. W. Hart, Grain boundary phase transformations, The nature and behavior of grain boundaries, Springer, 1972, pp. 155–170 Search PubMed.
- M. Guttmann, P. Krahe, F. Abel, G. Amsel, M. Bruneaux and C. Cohen, Temper embrittlement and intergranular segregation of antimony: a quantitative analysis performed with the backscattering of energetic ions, Metall. Trans., 1974, 5(1), 167 CAS.
- M. Guttmann, Grain boundary segregation, two dimensional compound formation, and precipitation, Metall. Trans. A, 1977, 8(9), 1383–1401 CrossRef.
- D. Mervyn, R. Baird and P. Wynblatt, Surface segregation in a Ni-1 at% Pd alloy, Surf. Sci., 1979, 82(1), 79–92 CrossRef CAS.
- S. Dregia and P. Wynblatt, Equilibrium segregation and interfacial energy in multicomponent systems, Acta Metall. Mater., 1991, 39(5), 771–778 CrossRef CAS.
- S. Hu and L. Chen, Solute segregation and coherent nucleation and growth near a dislocation—a phase-field model integrating defect and phase microstructures, Acta Mater., 2001, 49(3), 463–472 CrossRef CAS.
- S. Hu and L. Chen, Diffuse-interface modeling of composition evolution in the presence of structural defects, Comput. Mater. Sci., 2002, 23(1–4), 270–282 CrossRef.
- P.-R. Cha, S. G. Kim, D.-H. Yeon and J.-K. Yoon, A phase field model for the solute drag on moving grain boundaries, Acta Mater., 2002, 50(15), 3817–3829 CrossRef CAS.
- S. Hu, Y. Li, Y. Zheng and L. Chen, Effect of solutes on dislocation motion—a phase-field simulation, Int. J. Plast., 2004, 20(3), 403–425 CrossRef.
- P. Wynblatt and D. Chatain, Anisotropy of segregation at grain boundaries and surfaces, Metall. Mater. Trans. A, 2006, 37(9), 2595–2620 CrossRef.
- N. Ma, C. Shen, S. Dregia and Y. Wang, Segregation and wetting transition at dislocations, Metall. Mater. Trans. A, 2006, 37(6), 1773–1783 CrossRef.
- K. Grönhagen and J. Ågren, Grain-boundary segregation and dynamic solute drag theory—a phase-field approach, Acta Mater., 2007, 55(3), 955–960 CrossRef.
- S. G. Kim and Y. B. Park, Grain boundary segregation, solute drag and abnormal grain growth, Acta Mater., 2008, 56(15), 3739–3753 CrossRef CAS.
- G. Gottstein and L. S. Shvindlerman, Grain boundary migration in metals: thermodynamics, kinetics, applications, CRC Press, 2009 Search PubMed.
- P. Lejček, Grain boundaries: description, structure and thermodynamics, Springer, 2010 Search PubMed.
- S. G. Kim, J. S. Lee and B.-J. Lee, Thermodynamic properties of phase-field models for grain boundary segregation, Acta Mater., 2016, 112, 150–161 CrossRef CAS.
- Y. Mishin, Solute drag and dynamic phase transformations in moving grain boundaries, Acta Mater., 2019, 179, 383–395 CrossRef CAS.
- J. D. van der Waals, The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density, J. Stat. Phys., 1979, 20(2), 200–244 CrossRef.
- J. W. Cahn and J. E. Hilliard, Free energy of a nonuniform system. I. Interfacial free energy, J. Chem. Phys., 1958, 28(2), 258–267 CrossRef CAS.
- J. W. Cahn, Critical point wetting, J. Chem. Phys., 1977, 66(8), 3667–3672 CrossRef CAS.
- N. Ma, S. Dregia and Y. Wang, Solute segregation transition and drag force on grain boundaries, Acta Mater., 2003, 51(13), 3687–3700 CrossRef CAS.
- R. Kobayashi, J. A. Warren and W. C. Carter, A continuum model of grain boundaries, Physica D, 2000, 140(1–2), 141–150 CrossRef.
- M. Tang, W. C. Carter and R. M. Cannon, Diffuse interface model for structural transitions of grain boundaries, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(2), 024102 CrossRef.
- M. Tang, W. C. Carter and R. M. Cannon, Grain boundary order–disorder transitions, J. Mater. Sci., 2006, 41(23), 7691–7695 CrossRef CAS.
- M. Tang, W. C. Carter and R. M. Cannon, Grain boundary transitions in binary alloys, Phys. Rev. Lett., 2006, 97(7), 075502 CrossRef PubMed.
- T. W. Heo, S. Bhattacharyya and L.-Q. Chen, A phase field study of strain energy effects on solute–grain boundary interactions, Acta Mater., 2011, 59(20), 7800–7815 CrossRef CAS.
- S. J. Dillon, M. P. Harmer and J. Luo, Grain boundary complexions in ceramics and metals: an overview, Jom, 2009, 61(12), 38–44 CrossRef.
- W. D. Kaplan, D. Chatain, P. Wynblatt and W. C. Carter, A review of wetting versus adsorption, complexions, and related phenomena: the rosetta stone of wetting, J. Mater. Sci., 2013, 48(17), 5681–5717 CrossRef CAS.
- P. R. Cantwell, M. Tang, S. J. Dillon, J. Luo, G. S. Rohrer and M. P. Harmer, Grain boundary complexions, Acta Mater., 2014, 62, 1–48 CrossRef CAS.
- A. P. Sutton and R. W. Balluffi, Interfaces in Crystalline Materials, 1995 Search PubMed.
- P. E. J. Flewitt and R. K. Wild, Grain Boundaries: Their Microstructure and Chemistry, ed. P. E. J. Flewitt and R. K. Wild, Wiley-VCH, 2001, p. 338, ISBN 0-471-97951-1 Search PubMed.
- M. K. Miller, Atom probe tomography: analysis at the atomic level, Springer Science & Business Media, 2012 Search PubMed.
- L. Huber, R. Hadian, B. Grabowski and J. Neugebauer, A machine learning approach to model solute grain boundary segregation, npj Comput. Mater., 2018, 4(1), 64 CrossRef.
- T. A. Sharp, S. L. Thomas, E. D. Cubuk, S. S. Schoenholz, D. J. Srolovitz and A. J. Liu, Machine learning determination of atomic dynamics at grain boundaries, 2018, arXiv:1803.01416.
- L. Li, R. Darvishi Kamachali, Z. Li and Z. Zhang, Grain boundary energy effect on grain boundary segregation in an equiatomic high-entropy alloy, Phys. Rev. Mater., 2020, 4, 053603 CrossRef.
- R. Darvishi Kamachali, A. K. da Silva, E. McEniry, D. Ponge, B. Gault, J. Neugebauer and D. Raabe, Segregation-Assisted Spinodal and Transient-Spinodal at Grain Boundaries, 2019, arxiv:1905.07970, submitted.
- J. M. Haile, Molecular Dynamics Simulation: Elementary Methods, Wiley, 1997 Search PubMed.
- K. Binder, Spinodal decomposition, Systems Far from Equilibrium, Springer, 1980, pp. 76–90 Search PubMed.
- K. Binder and P. Fratzl, Spinodal decomposition, Phase transformations in materials, 2001, pp. 409–480 Search PubMed.
- I. Steinbach, Phase-field models in materials science, Modell. Simul. Mater. Sci. Eng., 2009, 17(7), 073001 CrossRef.
- L.-Q. Chen, Phase-field models for microstructure evolution, Annu. Rev. Mater. Res., 2002, 32(1), 113–140 CrossRef CAS.
- W. J. Boettinger, J. A. Warren, C. Beckermann and A. Karma, Phase-field simulation of solidification, Annu. Rev. Mater. Res., 2002, 32(1), 163–194 CrossRef CAS.
- D. A. Porter, K. E. Easterling and M. Sherif, Phase Transformations in Metals and Alloys (Revised Reprint), CRC Press, 2009 Search PubMed.
- A. K. da Silva, R. Darvishi Kamachali, D. Ponge, B. Gault, J. Neugebauer and D. Raabe, Thermodynamics of grain boundary segregation, interfacial spinodal and their relevance for nucleation during solid–solid phase transitions, Acta Mater., 2019, 168, 109–120 CrossRef.
- V. Grolier and R. Schmid-Fetzer, Experimental study of Au–Pt–Sn phase equilibria and thermodynamic assessment of the Au–Pt and Au–Pt–Sn systems, J. Electron. Mater., 2008, 37(3), 264–278 CrossRef CAS.
- A. T. Dinsdale, SGTE data for pure elements, Calphad, 1991, 15(4), 317–425 CrossRef CAS.
- D. MacLean, Grain boundaries in metals, 1957 Search PubMed.
- F. Abdeljawad, P. Lu, N. Argibay, B. G. Clark, B. L. Boyce and S. M. Foiles, Grain boundary segregation in immiscible nanocrystalline alloys, Acta Mater., 2017, 126, 528–539 CrossRef CAS.
- C. O'Brien, C. Barr, P. Price, K. Hattar and S. Foiles, Grain boundary phase transformations in PtAu and relevance to thermal stabilization of bulk nanocrystalline metals, J. Mater. Sci., 2018, 53(4), 2911–2927 CrossRef.
- A. K. Da Silva, D. Ponge, Z. Peng, G. Inden, Y. Lu, A. Breen, B. Gault and D. Raabe, Phase nucleation through confined spinodal fluctuations at crystal defects evidenced in Fe–Mn alloys, Nat. Commun., 2018, 9(1), 1137 CrossRef PubMed.
- S. Sankaran, K. Kumar, H. Rösner, V. A. Esin, S. Divinski and G. Wilde, Grain boundary diffusion and grain boundary structures of a Ni–Cr–Fe-alloy: evidences for grain boundary phase transformations, 2019, arXiv:1912.09184.
- X. Zhou, X.-x. Yu, T. Kaub, R. L. Martens and G. B. Thompson, Grain boundary specific segregation in nanocrystalline Fe (Cr), Sci. Rep., 2016, 6, 34642 CrossRef CAS PubMed.
- H. Aaron and G. Bolling, Free volume as a criterion for grain boundary models, Surf. Sci., 1972, 31, 27–49 CrossRef CAS.
- L. Shvindlerman, G. Gottstein, V. Ivanov, D. Molodov, D. Kolesnikov and W. Łojkowski, Grain boundary excess free volume—direct thermodynamic measurement, J. Mater. Sci., 2006, 41(23), 7725–7729 CrossRef CAS.
- E.-M. Steyskal, B. Oberdorfer, W. Sprengel, M. Zehetbauer, R. Pippan and R. Würschum, Direct experimental determination of grain boundary excess volume in metals, Phys. Rev. Lett., 2012, 108(5), 055504 CrossRef PubMed.
- V. Ivanov, D. A. Molodov, L. S. Shvindlerman, G. Gottstein, D. Kolesnikov and W. Łojkowski, Excess Free Volume of High Angle Grain Boundaries in Aluminium, Mater. Sci. Forum, 2006, 1557–1562 CAS.
- M. A. Tschopp, G. Tucker and D. McDowell, Structure and free volume of 〈110〉 symmetric tilt grain boundaries with the E structural unit, Acta Mater., 2007, 55(11), 3959–3969 CrossRef CAS.
- A. Seki, D. N. Seidman, Y. Oh and S. Foiles, Monte Carlo simulations of segregation at [001] twist boundaries in a Pt (Au) alloy—I. Results, Acta Metall. Mater., 1991, 39(12), 3167–3177 CrossRef CAS.
- A. Seki, D. N. Seidman, Y. Oh and S. Foiles, Monte Carlo simulations of segregation at [001] twist boundaries in a Pt (Au) alloy—II. Discussion, Acta Metall. Mater., 1991, 39(12), 3179–3185 CrossRef CAS.
- D. N. Seidman, Solute-atom segregation at internal interfaces on an atomic scale: atom-probe experiments and computer simulations, Mater. Sci. Eng., 1991, 137, 57–67 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab
*ab
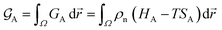
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is the atomic density field equivalent to the inverse molar volume field (Vm(
) is the atomic density field equivalent to the inverse molar volume field (Vm(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ))−1, HA is enthalpy per unit mole with HA = KA + EA + pVA (KA: kinetic energy, EA: potential energy and pVA: mechanical energy), and SA is entropy per unit mole, respectively. van der Waals has shown43 that the potential energy of a heterogeneous system depends on the (local) density as well as (nonlocal) density gradients. In this study, we consider a symmetric flat GB separating two infinitely large homogeneous grains. For this system, breaking the symmetry only normal to the GB plane, the interactions can be realized considering only one spatial dimension. The potential energy density will be
))−1, HA is enthalpy per unit mole with HA = KA + EA + pVA (KA: kinetic energy, EA: potential energy and pVA: mechanical energy), and SA is entropy per unit mole, respectively. van der Waals has shown43 that the potential energy of a heterogeneous system depends on the (local) density as well as (nonlocal) density gradients. In this study, we consider a symmetric flat GB separating two infinitely large homogeneous grains. For this system, breaking the symmetry only normal to the GB plane, the interactions can be realized considering only one spatial dimension. The potential energy density will be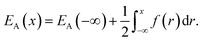
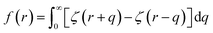
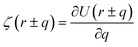 .
.
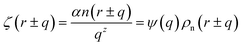
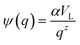 . Eqn (4) with z ≫ 1 is inspired by interatomic force relations in the absence of the long-range electrostatic interactions.62 Here VL is the characteristic coarse-graining volume over which the mesoscale atomic density field is measured by
. Eqn (4) with z ≫ 1 is inspired by interatomic force relations in the absence of the long-range electrostatic interactions.62 Here VL is the characteristic coarse-graining volume over which the mesoscale atomic density field is measured by 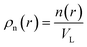 . Similar coarse-graining descriptions are worked out in defining mesoscale free energy formulations.63,64 The specific form of ψ(q) can be obtained from atomistic simulations. The second- or higher-order dependencies of the interaction forces on the atomic density (including repulsive atomic interactions) can also be assumed. In the current treatment, however, we limit ourselves to the simplest first-order linear approximation as in eqn (4).
. Similar coarse-graining descriptions are worked out in defining mesoscale free energy formulations.63,64 The specific form of ψ(q) can be obtained from atomistic simulations. The second- or higher-order dependencies of the interaction forces on the atomic density (including repulsive atomic interactions) can also be assumed. In the current treatment, however, we limit ourselves to the simplest first-order linear approximation as in eqn (4).
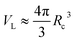 which can relate the atomistic simulation length-scale with the current mesoscale density-based formulation. Inserting eqn (4) in eqn (3), and integrating by part we can write
which can relate the atomistic simulation length-scale with the current mesoscale density-based formulation. Inserting eqn (4) in eqn (3), and integrating by part we can write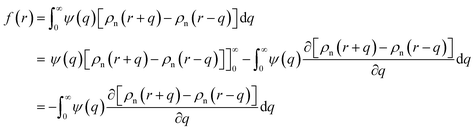
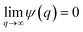 and
and 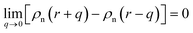 . Applying the Taylor expansions
. Applying the Taylor expansions 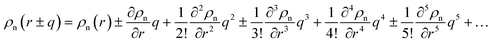 , eqn (5) gives
, eqn (5) gives 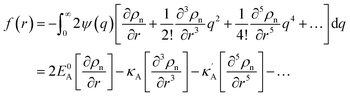
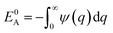 ,
, 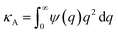 and
and 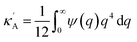 . Using eqn (2) and (6) with the boundary values EA(−∞) = E0Aρn(−∞),
. Using eqn (2) and (6) with the boundary values EA(−∞) = E0Aρn(−∞), 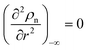 and
and 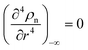 , we obtain the potential energy as a function of atomic density:
, we obtain the potential energy as a function of atomic density: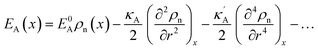
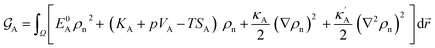
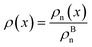 with ρBn = ρn(−∞) and writing
with ρBn = ρn(−∞) and writing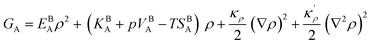
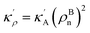 , KBA = KAρBn, pVBA = pVAρBn, SBA = SAρBn and, the Gibbs free energy of the homogeneous bulk phase (for ρ = 1) recovers as
, KBA = KAρBn, pVBA = pVAρBn, SBA = SAρBn and, the Gibbs free energy of the homogeneous bulk phase (for ρ = 1) recovers as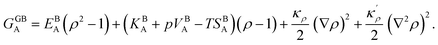
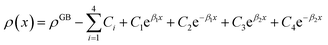
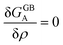 with
with 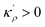 . The coefficients Cis need to fulfill boundary conditions ρ(x = 0) = ρGB, ρ(x = η) = 1 and the continuity conditions
. The coefficients Cis need to fulfill boundary conditions ρ(x = 0) = ρGB, ρ(x = η) = 1 and the continuity conditions 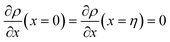 . Here
. Here  ,
,  and η is the GB half width. For a simpler case, assuming
and η is the GB half width. For a simpler case, assuming 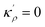 , the equilibrium density profile across the GB region reads
, the equilibrium density profile across the GB region reads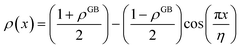
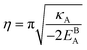 . Eqn (12) or (13) give a continuous atomic density profile across the GB. For more details on these equations see Appendix A. The continuity of atomic density profile across the GB region is confirmed by atomistic simulations.61 Fig. 1 compares the atomic density profile eqn (13) versus previous phase-field models for GBs47–50 (Fig. 1(c)) as well as the classical phase-field profile across an interface65–67 (Fig. 1(d)). Using eqn (13) with
. Eqn (12) or (13) give a continuous atomic density profile across the GB. For more details on these equations see Appendix A. The continuity of atomic density profile across the GB region is confirmed by atomistic simulations.61 Fig. 1 compares the atomic density profile eqn (13) versus previous phase-field models for GBs47–50 (Fig. 1(c)) as well as the classical phase-field profile across an interface65–67 (Fig. 1(d)). Using eqn (13) with 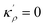 , the GB energy
, the GB energy 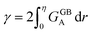 can be analytically obtained as
can be analytically obtained as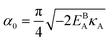 . This equation approximates the direct relation between γ and ρGB for an equilibrium density profile across the GB. Fig. 1(e) shows the normalized value
. This equation approximates the direct relation between γ and ρGB for an equilibrium density profile across the GB. Fig. 1(e) shows the normalized value 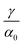 as a function of ρGB. In the following, ρGB, the average relative atomic density within the GB plane, will be referred to as ‘GB density’. The significance of the GB density and its relationship with the GB character is discussed in Section 4.2.
as a function of ρGB. In the following, ρGB, the average relative atomic density within the GB plane, will be referred to as ‘GB density’. The significance of the GB density and its relationship with the GB character is discussed in Section 4.2.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XA + XB
XA + XB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) XB]
XB]
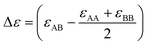 is bonding energy in which εij is the bonding energy between atoms i and j and XA (XB) is the mole fraction of atoms A (B). In principle, the mixing energy terms in eqn (15) can be assumed to follow the same scaling found in eqn (9). The effect of changing the coordination number Z on the GB enthalpy of mixing and GB segregation has been previously discussed (see for instance ref. 40, 46 and 69 and references therein). While the coordination number is proportional to the local density, the stretch in the bonding energy Δε is also expected to change with the density in the limit of linear elasticity. Considering these facts and neglecting the dependency of configurational entropy for the sake of simplicity, we can write
is bonding energy in which εij is the bonding energy between atoms i and j and XA (XB) is the mole fraction of atoms A (B). In principle, the mixing energy terms in eqn (15) can be assumed to follow the same scaling found in eqn (9). The effect of changing the coordination number Z on the GB enthalpy of mixing and GB segregation has been previously discussed (see for instance ref. 40, 46 and 69 and references therein). While the coordination number is proportional to the local density, the stretch in the bonding energy Δε is also expected to change with the density in the limit of linear elasticity. Considering these facts and neglecting the dependency of configurational entropy for the sake of simplicity, we can write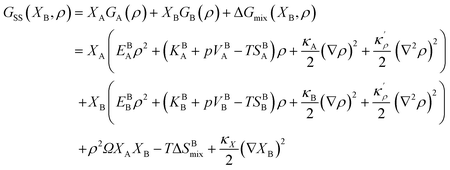
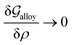 and
and 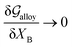 with
with 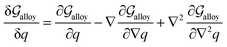 and
and 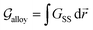 . A numerical solution of these equations can provide information about the spatiotemporal evolution of phases in the GB region. This has been quantitatively demonstrated in a parallel study on the Mn segregation in Fe–Mn system.61 The aim of the current study, however, is to provide analytical descriptions for equilibrium GB thermodynamics. Hence, in the following, we rather investigate a single material point at the GB center where spatial gradients of the atomic density field vanish, i.e. ∇ρ(x = 0) = 0. We further assume that for this point the concentration gradient and higher-order density gradients can be neglected. Thus, with ρ(x = 0) = ρGB and XB(x = 0) = XGBB, the density-based Gibbs free energy description at this material point simplifies to
. A numerical solution of these equations can provide information about the spatiotemporal evolution of phases in the GB region. This has been quantitatively demonstrated in a parallel study on the Mn segregation in Fe–Mn system.61 The aim of the current study, however, is to provide analytical descriptions for equilibrium GB thermodynamics. Hence, in the following, we rather investigate a single material point at the GB center where spatial gradients of the atomic density field vanish, i.e. ∇ρ(x = 0) = 0. We further assume that for this point the concentration gradient and higher-order density gradients can be neglected. Thus, with ρ(x = 0) = ρGB and XB(x = 0) = XGBB, the density-based Gibbs free energy description at this material point simplifies to![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 + 8.3104T and L1 = −12
625 + 8.3104T and L1 = −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 616 + 5.8186T [J mol−1] for the FCC Pt–Au solid solution. The rest of the thermodynamic data for pure Pt and Au are extracted from SGTE compilation by Dinsdale.71 Inserting these values in eqn (21) and (22), one obtains the Gibbs free energy as a function of GB density and composition. Fig. 2 shows a 3D map of the Gibbs free energy for the Pt–Au system at 300 K as a function of composition XAu and GB density ρGB. We found that as the GB density decreases, the Gibbs free energy increases and deviates larger from the corresponding bulk values. Fig. 3 compares bulk and GB Gibbs free energy for ρGB = 0.75 at different temperatures.
616 + 5.8186T [J mol−1] for the FCC Pt–Au solid solution. The rest of the thermodynamic data for pure Pt and Au are extracted from SGTE compilation by Dinsdale.71 Inserting these values in eqn (21) and (22), one obtains the Gibbs free energy as a function of GB density and composition. Fig. 2 shows a 3D map of the Gibbs free energy for the Pt–Au system at 300 K as a function of composition XAu and GB density ρGB. We found that as the GB density decreases, the Gibbs free energy increases and deviates larger from the corresponding bulk values. Fig. 3 compares bulk and GB Gibbs free energy for ρGB = 0.75 at different temperatures.


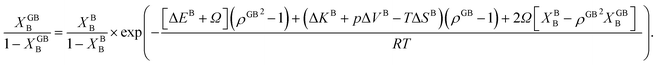
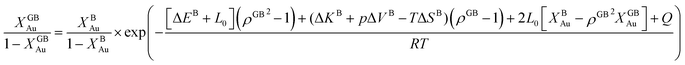
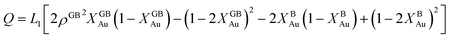 , ΔEB = EBAu − EBPt, ΔKB = KBAu − KBPt, pΔVB = pVBAu − pVBPt, and ΔS = SBAu − SBPt. Eqn (23) and (24) use GB density and bulk thermodynamic data as the inputs and give the corresponding GB segregation isotherms.
, ΔEB = EBAu − EBPt, ΔKB = KBAu − KBPt, pΔVB = pVBAu − pVBPt, and ΔS = SBAu − SBPt. Eqn (23) and (24) use GB density and bulk thermodynamic data as the inputs and give the corresponding GB segregation isotherms.

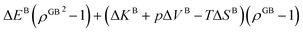 that is analogous to the segregation driving force in Langmuir–McLean isotherm.72 If we neglect the energetic contributions due to the mixing (Ω = 0), we obtain a density-based version of Langmuir–McLean relation as:
that is analogous to the segregation driving force in Langmuir–McLean isotherm.72 If we neglect the energetic contributions due to the mixing (Ω = 0), we obtain a density-based version of Langmuir–McLean relation as: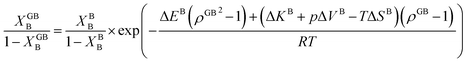
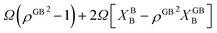 due to the mixing which contains a term with the GB concentration XGBB. The two contributions discussed above can have cooperative or competitive effects on the segregation level, depending on the magnitude and sign of Ω and ΔEB.
due to the mixing which contains a term with the GB concentration XGBB. The two contributions discussed above can have cooperative or competitive effects on the segregation level, depending on the magnitude and sign of Ω and ΔEB.
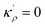 is assumed. It is observed that GBs with higher energies, i.e., lower GB densities, attract more solute content during the segregation.77 Using eqn (14) and (20), the GB Gibbs free energy of a regular solution can be written as a function of its initial GB energy. Accordingly, we can rewrite eqn (23) as
is assumed. It is observed that GBs with higher energies, i.e., lower GB densities, attract more solute content during the segregation.77 Using eqn (14) and (20), the GB Gibbs free energy of a regular solution can be written as a function of its initial GB energy. Accordingly, we can rewrite eqn (23) as
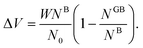
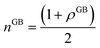 (where nB = 1) and the relative difference (with respect to the bulk) will be
(where nB = 1) and the relative difference (with respect to the bulk) will be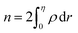 is the (relative) total number of atoms in the GB. Comparing eqn (27) and (28) one can find the one-to-one relationship between Δn and ΔV, where we can identify ΔV ∝ (1 − ρGB). Extensive works have been devoted to calculate and measure GB excess free volume (see for instance ref. 79–81). Aaron and Bolling78 have shown that the energy of different types of GBs can be associated with their excess free volume which can be extended as well for the GB density parameter ρGB.
is the (relative) total number of atoms in the GB. Comparing eqn (27) and (28) one can find the one-to-one relationship between Δn and ΔV, where we can identify ΔV ∝ (1 − ρGB). Extensive works have been devoted to calculate and measure GB excess free volume (see for instance ref. 79–81). Aaron and Bolling78 have shown that the energy of different types of GBs can be associated with their excess free volume which can be extended as well for the GB density parameter ρGB.
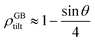 with the GB misorientation θ, and the edge dislocation core density ρD ≈ 0.75. For a larger misorientation angle, the GB density will be smaller, deviating larger from bulk properties. We also obtain a misorientation-dependent
with the GB misorientation θ, and the edge dislocation core density ρD ≈ 0.75. For a larger misorientation angle, the GB density will be smaller, deviating larger from bulk properties. We also obtain a misorientation-dependent 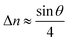 and thus a corresponding GB excess free volume ΔV ∝ sin
and thus a corresponding GB excess free volume ΔV ∝ sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ that is consistent with the previous studies.78,82 GB segregation as a function of GB misorientation has been studied in the Pt–Au system. Seki et al.83,84 and Seidman85 studied Au segregation to twist boundaries and have shown that although the GB segregation is not homogeneous, its average level increases as the misorientation angle increases (with the exception of special GBs). These observations confirm the results from the current density-based model where a higher misorientation angle corresponds to a lower GB density. An in-depth study of LAGBs requires consideration of elastic energy contributions which is left for a future study.
θ that is consistent with the previous studies.78,82 GB segregation as a function of GB misorientation has been studied in the Pt–Au system. Seki et al.83,84 and Seidman85 studied Au segregation to twist boundaries and have shown that although the GB segregation is not homogeneous, its average level increases as the misorientation angle increases (with the exception of special GBs). These observations confirm the results from the current density-based model where a higher misorientation angle corresponds to a lower GB density. An in-depth study of LAGBs requires consideration of elastic energy contributions which is left for a future study.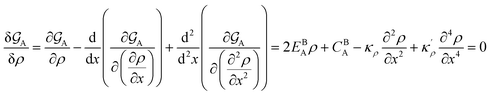
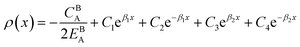
 and
and  . We also obtain
. We also obtain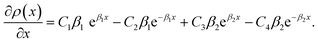
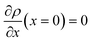 and
and 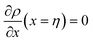 , we obtain
, we obtain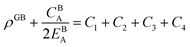
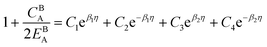
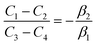
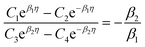
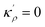 , we find another general solution for eqn (A.1):
, we find another general solution for eqn (A.1):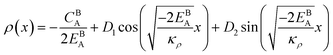
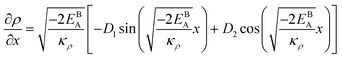
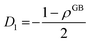
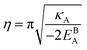
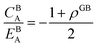
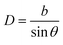
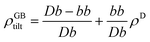
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ.
θ.
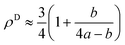 where a is the interatomic distance normal to the edge dislocation line – here we neglect the effect of elastic energy of the dislocation on its core density. Neglecting the second term inside the parenthesis then we have ρD ≈ 0.75 that gives the atomic density of a tilt GB as
where a is the interatomic distance normal to the edge dislocation line – here we neglect the effect of elastic energy of the dislocation on its core density. Neglecting the second term inside the parenthesis then we have ρD ≈ 0.75 that gives the atomic density of a tilt GB as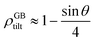

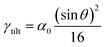
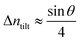 and thus the corresponding average GB excess free volume will be proportional to the misorientation angle as ΔV ∝ sin
and thus the corresponding average GB excess free volume will be proportional to the misorientation angle as ΔV ∝ sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. Fig. 8(b) and (c) show the variation of GB density and energy as a function of the misorientation angle according to this analysis.
θ. Fig. 8(b) and (c) show the variation of GB density and energy as a function of the misorientation angle according to this analysis.