Tailoring nanoscale polarization patterns and transport properties in ferroelectric tunnel junctions by octahedral tilts in electrodes

Abstract

Oxygen octahedral tilts are known for the ability to tailor polarization patterns in perovskites. We propose a way to manipulate nanoscale polarization patterns in ferroelectric tunnel junctions (FTJs) by oxygen octahedral tilts in electrodes combined with interface engineering. Here the electrode is epitaxial SrRuO₃ on SrTiO₃, and the ferroelectric barrier is a BaTiO₃/CaTiO₃ superlattice. The octahedral tilt mismatch between electrodes and the barrier is found to be eliminated at one of the two most stable interfaces by the imprinting of in-phase oxygen octahedral tilt from electrodes into the barrier, which further results in anti-polar order in the barrier, while uniform polar order is retained for another stable interface. Further analysis of electronic transport properties shows an increased transmission in FTJ with anti-polar order, which is mainly caused by octahedral tilt induced out-of-plane ferroelectric domain walls. Our results indicate that the oxygen octahedral tilts in electrodes can be used to manipulate polarization patterns and create charged domain walls in FTJs, which further expand the application prospects of FTJ-based devices.

---

1. Introduction

Ferroelectric tunnel junctions (FTJs) continue to draw tremendous interest due to their applications in non-volatile data storage devices.^1,2 An FTJ consists of two electrodes sandwiching a ferroelectric thin film (FTF), and its tunneling transport properties can be strongly modulated by polarization direction, thus resulting in different resistance states that can be used to store binary data. The above application is generally based on uniform polarization states in FTJs, but recent investigations also reported non-uniform polarization states in FTJs,^3–6 especially in multiferroic tunnel junctions (MFTJs) with ferromagnetic electrodes.^7,8 FTJs and MFTJs with non-uniform polarization states also have potential applications in a variety of devices such as domain wall memories⁹ and resonant tunneling transistors,^10,11 which expand their applications to broader fields.

Currently, numerous methods to tailor polarization patterns in epitaxial FTFs are reported, e.g. interface engineering,^12,13 mechanical bending,¹⁴ inserting functional dielectric layers¹⁵ or interface-engineered oxygen octahedral coupling (OOC) between FTFs and substrates.^16,17 In perovskite heterostructures, the corner-shared arrangement of BO₆ octahedra can be disrupted at some types of interfaces (i.e. the rocksalt interfaces in Ruddlesden–Popper structures), but it can be retained at perovskite interfaces. Due to the corner-shared feature of BO₆ octahedral networks, OOC between two different perovskites are established, thus antiferroelectric distortions include AFD_z modes (i.e. in-plane oxygen octahedral rotations (OORs) around the out-of-plane axis) and AFD_xy modes (i.e. out-of-plane oxygen octahedral tilts (OOTs) around the in-plane axis) can travel through perovskite heterointerfaces and drastically alter the lattice structures of FTFs. However, this effect is much less considered in FTJs. For example, strontium ruthenate (SrRuO₃) is a commonly used electrode material in FTJs. It has a Pnma structure with an a⁺b⁻b⁻ octahedral tilt system in Glazer's notation.¹⁸ Nevertheless, many studies adopted tetragonal phases without octahedral tilts for SrRuO₃ electrodes in FTJs.^19–22 This is because SrRuO₃ electrodes are often practically or fictitiously grown on high symmetry perovskite substrates such as SrTiO₃, and lattice distortions in their bulk counterparts are suppressed by octahedral coupling with the substrate. In the past decade, some researchers have carefully examined the structures of epitaxial SrRuO₃ thin films on SrTiO₃, and the suppression of octahedral tilts are found to decrease with increasing film thickness.^23–25 Recently, ferroelectric-like off-centering distortion is also found in ultrathin epitaxial SrRuO₃ on the SrTiO₃ substrate, which is a result of the proximity effect from ferroelectric BaTiO₃ top-layer.²⁶ All these findings suggested that epitaxial SrRuO₃ thin films on SrTiO₃ still exhibit abundant lattice distortions. As a result, the role of electrode octahedral tilts in determining the properties of FTJs needs further investigation.

Based on the above discussions, it is clear that octahedral rotations and tilts can appear in the experimentally prepared FTJs with SrRuO₃ electrodes on Pm3̄m SrTiO₃ substrate, especially when the thickness of the SrRuO₃ electrode is above 18 uc.^23–25 It is noteworthy that octahedral rotations can change abruptly at perovskite heterointerfaces, while octahedral tilts generally have longer relaxation lengths.²⁷ As octahedral tilts exist in SrRuO₃ thin films on SrTiO₃, their impact on FTF barriers can not be ignored. On the other hand, if the tilt system of the FTF barrier is different from SrRuO₃ electrodes, an octahedral tilt mismatch is created in the FTJ. This is a particularly interesting situation that will be explored in the following. One type of octahedral tilt mismatches includes an FTF barrier without octahedral rotational distortions grown on a SrRuO₃ electrode, such as commonly used BaTiO₃. But previous research has suggested BaTiO₃ is resistant to octahedral rotations and tilts,²⁸ thus it may suppress the tilt distortions in SrRuO₃ electrodes and produce ordinary FTJs that have been intensively studied.^18–22 Another type of octahedral tilt mismatches includes an FTF barrier with both ferroelectric and octahedral rotational distortions, while its tilt system is different from SrRuO₃. Perovskites with the coexistence of ferroelectric and antiferroic distortions are rare, one important class includes multiferroic perovskites such as BiFeO₃ which has an R3̄c structure at room temperature which includes the coexistence of a⁻a⁻a⁻ tilt system and ferroelectric distortion along the [111] direction. However, the polarization in BiFeO₃ is generally not a direct result of octahedral tilts but a result of the lone-pair mechanism. Recent developed ferroelectric superlattices are another kind of noticeable structure with the coexistence of ferroelectric and antiferrodistortive distortions, and the BaTiO₃/CaTiO₃ superlattices among them are reported to exhibit a Pc structure that is similar to BiFeO₃,^29,30 while the polarization strongly depends on octahedral tilts. In this work, we perform a systematic first-principle investigation on FTJs constructed by BaTiO₃/CaTiO₃ ferroelectric barriers and SrRuO₃ electrodes to reveal how octahedral tilts in electrodes would change the properties of FTF barriers in FTJs. Our work could have a certain significance to theoretical studies and applications of perovskite-based FTJs in the future.

2. Methods

Ground-state calculations for simulated FTJs are performed with the VASP code utilizing a plane-wave basis set.^31,32 The energy cutoff is set to 500 eV to ensure convergences. The exchange–correlation is treated in the generalized gradient approximation with the Perdew–Burke–Ernzerhof parametrization (GGA-PBE).³³ Integrations over the first Brillouin zone are performed by discrete k-points sampling. A 3 × 3 × 1 Monkhorst–Pack mesh³⁴ is used in this step, which is well-converged for total energy, lattice constant, and polarization results. The atomic structures are fully relaxed until Hellmann–Feynman forces are less than 0.01 eV Å⁻¹ and stress components along z-direction are less than 0.1 GPa. After relaxations, Space-groups for SrRuO₃ and BaTiO₃/CaTiO₃ superlattices are determined by the FINDSYM code.³⁵

Transport calculations for simulated FTJs are performed using the QuantumATK package utilizing a linear combination of atomic orbitals (LCAO) basis set.³⁶ The exchange–correlation is treated in the generalized gradient approximation with the Perdew–Burke–Ernzerhof parametrization (GGA-PBE).³³ To ensure accuracy, the numerical atomic orbital is set to be double zeta polarized. The Brillouin zone of the system is sampled by a 10 × 10 × 100 k-point mesh for the self-consistent calculations and 50 × 50 k-point mesh for the transmission calculations. The electron temperature in the electrodes is set to 300 K.

3. Results and discussions

3.1 Atom configurations of simulated FTJs

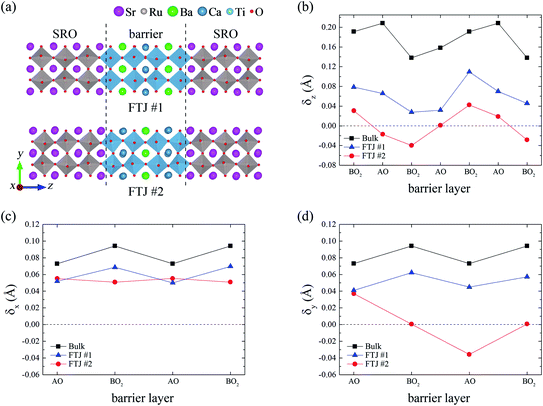
Our simulated FTJs are schematically shown in Fig. 1a. The open-circuit approach is used to exclude direct OOC between the bottom and top electrodes, which would not happen in experiments. Each repeat unit contains the FTJ structure and a 15 Å thick vacuum layer between the electrodes, forming an isolated geometry. In the in-plane direction, the supercells contain 2 × 2 perovskite unit cells to contain octahedral tilts. All simulated systems are epitaxially grown on fictitious SrTiO₃ substrates.

Fig. 1 (a) Schematic illustrations of FTJs in our investigation. From top to bottom is FTJ #1 with SrO/TiO₂–BaO interface and FTJ #2 with SrO/TiO₂–CaO interface. A 15 Å vacuum layer is added to the supercell to separate the top and bottom electrodes. (b)–(d) show layer RACDs for bulk 1 : 1 BaTiO₃/CaTiO₃ superlattice, barrier layers in fully relaxed FTJ #1 and #2 along z, x and y-directions respectively. The distribution of A–O and B–O displacements in the barrier are depicted, where A corresponds to Ba or Ca ions, and B corresponds to Ti ions.

When building FTJs, we first calculated bulk structures of all building blocks. For the substrate, our calculation with GGA-PBE exchange–correlation predicts the lattice parameter for Pm3̄m SrTiO₃ to be 3.94 Å, which is close to the previous GGA-PBE predictions.^37,38 As a result, in-plane lattice parameters for all simulated systems are fixed to two times the theoretical lattice constant of Pm3̄m SrTiO₃ (7.88 Å). For electrodes, in-plane lattice parameters for Pnma SrRuO₃ are calculated to be 7.89 Å and 7.90 Å, thus the substrate would introduce an in-plane compressive strain to SrRuO₃ electrodes. This effect is simulated by constraining the in-plane lattice parameters of SrRuO₃ to 7.88 Å and relax its structure again. An a⁺b⁻b⁻ tilt system is induced in the initial structure according to the bulk symmetry of SrRuO₃,^23–25 and it is found to be retained in the relaxed structure. Under the above conditions, relaxed SrRuO₃ on SrTiO₃ shows a P2₁/m structure with a⁺b⁻c⁻ tilt system. For the ferroelectric barrier, in-plane lattice parameters for periodic 1 : 1 BaTiO₃/CaTiO₃ superlattice are calculated to be 7.98 Å, thus the substrate would introduce −1.2% of in-plane compressive strain to the barrier. According to ref. 29, an a⁻a⁻c⁻ tilt system is induced in the initial structure of BaTiO₃/CaTiO₃ superlattice on SrTiO₃ under such misfit strain, and the relaxed structure shows a Pc structure with a⁻a⁻c⁻ tilt system and ferroelectric distortions along x, y and z-directions. Competitive phases include Pm structure with a⁺b⁻c⁻ tilt system and Cm structure with a⁺a⁺c⁻ tilt system are also calculated, and their energies are found to be higher than Pc structure: the calculated DFT total energy is −317.37 eV for 40 atoms cell of BaTiO₃/CaTiO₃ superlattice with Pc structure, while it is −317.34 eV for Pm structure and −317.28 eV for Cm structure. On the other hand, the P4mm structure which includes no octahedral rotations and tilts has the highest total energy of −316.12 eV. Our results indicate that the most stable structure of 1 : 1 BaTiO₃/CaTiO₃ superlattice on SrTiO₃ is the Pc structure, which is in good agreement with ref. 29.

In the next step, SrRuO₃ with P2₁/m structure and 1 : 1 BaTiO₃/CaTiO₃ superlattice with Pc structure are stacked to build FTJs and relaxed as a whole, and cohesive energies are calculated to determine the most stable interface between electrodes and the barrier. Fig. 1a shows the FTJs with the predicted 2 most stable interfaces (computational details are in the ESI†): FTJ #1 with SrO/TiO₂–BaO heterointerfaces and FTJ #2 with SrO/TiO₂–CaO interface. These interfaces have higher DFT cohesive energies than other interfaces, which indicates that they are likely to form under most experimental conditions. Ferroelectric distortions in these FTJs can be reflected by relative anion–cation displacements (RACDs) for atom layers which are calculated by [small delta, Greek, macron]_α = ū^A/B_α − ū^O_α, where [small delta, Greek, macron]_α is the averaged RACD in the α-direction, ū^A/B_α is the averaged position coordinates of A-site or B-site cations in the α-direction, and ū^O_α is the averaged position coordinates of oxygen anions in the α-direction. 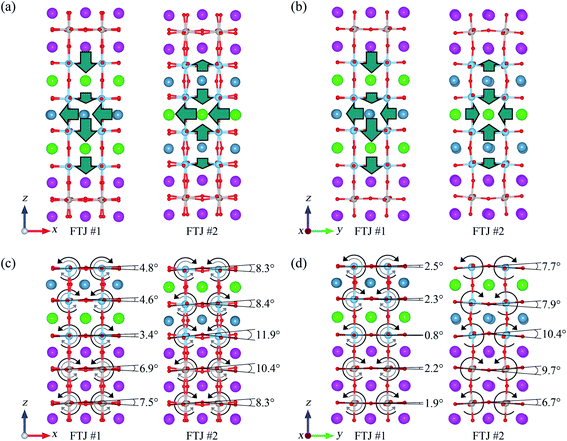A summation of [small delta, Greek, macron]_α for the atomic layers in the barrier shows the overall ferroelectric distortion of the FTJ in the α-direction, and a non-zero total [small delta, Greek, macron]_α indicates the existence of a net polarization. Averaged layer RACDs of barriers in FTJ #1 and #2 are shown in Fig. 1b–d. Fig. 1b shows layer RACDs in the z-direction with bulk superlattice values depicted as reference. It can be seen that in both bulk BaTiO₃/CaTiO₃ superlattice and FTJ #1, uniform polarization in the z-direction is formed, corresponding to a ferroelectric monodomain structure. Since the polarization in BaTiO₃/CaTiO₃ superlattice on SrTiO₃ is proper ferroelectricity,²⁹ it can be concluded that FTJ #1 behaves like ordinary FTJs. While in FTJ #2, complex anti-polar order in the z-direction is formed, which includes two in-plane tail-to-tail (TT) domain walls near interfaces and one in-plane head-to-head (HH) domain wall in the middle of the barrier. As a result, the total polarization in the z-direction for FTJ #2 is suppressed. In the x and y-directions, the situation is more interesting. As shown in Fig. 1c and d, layer RACDs for FTJ #1 and #2 in the x-direction are very similar, i.e. both FTJs have monodomain structure in the x-direction. Nevertheless, in the y-direction, an out-of-plane HH domain wall that parallels to the (100) plane is formed in FTJ #2, while a monodomain structure is retained in FTJ #1 in the y-direction. Distributions of RACDs for atom layers in FTJ #1 and #2 are further shown in Fig. 2a and b, in which the monodomain and antipolar states can be clearly seen. Consider the a⁻b⁻c⁻ tilt system in FTJ #1 and a⁺b⁻c⁻ tilt system in FTJ #2, it can be concluded that the in-phase octahedral tilt in the x-direction (i.e. the a⁺b⁰b⁰ mode) in 1 : 1 BaTiO₃/CaTiO₃ superlattice disfavors uniform polarization states in the y-direction, and anti-polar orders are formed in the direction, which comes down to the imprinting of the electrode octahedral tilt system into the barrier under the specific type of interface. These results indicate that the octahedral tilt in the electrode plays an important role in determining ferroelectric distortions in simulated FTJs.

Fig. 2 Schematic illustrations of layer polarizations for barrier layers in fully relaxed FTJ #1 and #2 along (a) x-direction and (b) y-direction, and octahedral tilt angles near bottom heterointerfaces in fully relaxed FTJ #1 and #2 around (c) y-axis and (d) x-axis. Black arrows mark the directions of octahedral tilts. For out-phase tilts, gray arrows mark the directions of tilts for the second layer of octahedra.

Besides ferroelectric distortions discussed above, another concerned lattice distortion is octahedral tilts in FTJ #1 and #2, Fig. 2 also provides insight into them. As mentioned above, the bulk 1 : 1 BaTiO₃/CaTiO₃ superlattice has a Pc structure with a⁻a⁻c⁻ tilt system, thus octahedral tilts in x, y and z-directions are all out-phase. However, as shown in Fig. 2d, octahedral tilts around the x-direction in the barrier in FTJ #2 are in-phase, which is different from its bulk counterpart. It is obvious that this new tilt system comes from the SrRuO₃ electrode as it has a⁺b⁻c⁻ tilt system, and OOC at the interface has enabled the imprinting of in-phase tilt in the x-direction into the barrier. Nevertheless, as shown in Fig. 2c and d, out-phase octahedral tilts in the barrier are retained in FTJ #1, thus the imprinting of the electrode tilt system into the barrier is suppressed in FTJ #1. This conclusion is also reflected from the octahedral tilt angles of each perovskite layer in the barrier. As shown in Fig. 2c and d, octahedral tilt angles in the barrier increase as the distance from the interface increases in FTJ #1, and octahedral tilts at the interface are negligible, which reveals that the SrO/TiO₂–BaO heterointerface disfavors octahedral tilts. As the distance from the interface increases, the bulk structure of 1 : 1 BaTiO₃/CaTiO₃ superlattice gradually restores, thus tilt angles increases and an a⁻b⁻c⁻ tilt system appears, which results in the Pc-like structure. Nevertheless, the situation in FTJ #2 is completely the opposite, in which octahedral tilt angles in the barrier decrease as the distance from the interface increases, and tilt system in the barrier is changed to a Pm-like structure with a⁺b⁻c⁻ tilt system, which indicates the strong structural modulation from the SrRuO₃ bottom electrode through the interface. The cause of different behaviors of SrO/TiO₂–BaO and SrO/TiO₂–CaO heterointerfaces can be analyzed from their different structures. As shown in Fig. 2c and d, SrO/TiO₂–BaO and SrO/TiO₂–CaO heterointerfaces are both composed of one SrO layer and one TiO₂ layer, the only difference is that the layer adjacent to the interfacial TiO₂ layer in the barrier is BaO layer in FTJ #1 and CaO layer in FTJ #2. It is well known that octahedral rotational instabilities are suppressed in BaTiO₃ due to the large ionic radius of Ba,³⁹ while CaTiO₃ has a Pnma ground state with a⁺b⁻b⁻ tilt system that is similar to SrRuO₃.⁴⁰ This is due to octahedral tilts required in-plane off-centering displacements for oxygen atoms in BO layers of perovskites, and B ions with large radius would suppress this distortion, thus the BaO layer adjacent to the SrO/TiO₂–BaO heterointerface has excluded octahedral tilts at the interface and results in discontinuity of tilt systems between the barrier and electrodes. While in FTJ #2, the CaO layer adjacent to the SrO/TiO₂–CaO heterointerface not only allows significant octahedral tilts at the interface but also supports new tilt modes that include in-phase tilts around the x-axis. These results indicate that BO layers near perovskite heterointerfaces play important roles in determining octahedral tilt distortions in perovskite heterostructures, and the transmission of octahedral tilts across the interface can be manipulated by choosing appropriate heterointerface.

3.2 Polarizations of simulated FTJs

The relationship between ferroelectric polarization and octahedral tilts in perovskites has long been an intriguing matter of discussion. Besides the improper ferroelectricity resulted from the trilinear coupling between ferroelectric and antiferrodistortive modes, octahedral tilts can also change polarization patterns, e.g. the a⁺b⁻b⁻ tilt system would results in anti-polar order in some perovskites.⁴¹ In the previous we have shown that the SrRuO₃ electrode can tailor octahedral tilts and ferroelectric distortions in the ferroelectric barrier in our simulated FTJs, it's natural to suggest that polarizations in simulated FTJs can also be tailored by the electrodes. Thus investigations on polarizations of barriers in simulated FTJs are performed to show effects from octahedral tilts in electrodes. In the following, polarizations are calculated by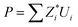 , where 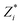is the Born effective charge of the ith ion and U_i is the displacement of the ith ion from its position in the paraelectric phase (i.e. the P4/mmm phase). Ionic Born effective charges are calculated by using the density functional perturbation theory (DFPT) implemented in VASP. Firstly, the polarization of bulk 1 : 1 BaTiO₃/CaTiO₃ superlattice with in-plane lattice parameters fixed to 3.94 Å is calculated. The calculated total polarization is 60.89 μC cm⁻², which is about 2 times of LDA result of 32.8 μC cm⁻² presented in ref. 28. Under LDA-CA exchange–correlation, the calculated total polarization for 1 : 1 BaTiO₃/CaTiO₃ superlattice using DFPT method is 35.72 μC cm⁻², which is in close agreement with ref. 28. It is known that GGA-PBE exchange–correlation treatment tends to obtain larger polarization than LDA, e.g. reported GGA-PBE spontaneous polarization for tetragonal BTO is 47.0 μC cm⁻², which is also about 2 times of LDA result of 24.3 μC cm⁻².⁴² This is not related to the method for calculating spontaneous polarization in the VASP code (i.e. Berry-phase or DFPT method), but a result of the GGA-PBE treatment of exchange–correlation itself. However, LDA is not suitable for our work as we found it severely underestimates lattice constants of SrRuO₃. Although both LDA and GGA calculations cannot reproduce experimental lattice constants for SrRuO₃ and SrTiO₃, the type of misfit strain (i.e. compressive or tensile) should at least be correct. Our calculations using LDA predicts a = 5.461 Å and b = 5.431 Å for the pseudocubic cell of Pbnm-phase SrRuO₃, and a = 7.710 Å for Pm3̄m-phase SrTiO₃. As a result, the LDA result of misfit strain for SrRuO₃ grown on SrTiO₃ is about 0.12% along the ab-direction, which is different from the experimental value of −0.44%²³ in sign. A tensile misfit strain could produce a new a⁺a⁻c⁰ tilt system in SrRuO₃,²³ which was not observed in SrRuO₃ thin film on the SrTiO₃ substrate. On the other hand, our PBE calculations predict a = 5.583 Å and b = 5.563 Å for the pseudocubic cell of Pbnm-phase SrRuO₃, and a = 7.874 Å for Pm3m-phase SrTiO₃. Thus the PBE misfit strain is about −0.08% along the ab-direction, which is consistent with the experimental result of compressive misfit strain. As a result, GGA-PBE exchange–correlation is used for the following simulations. In FTJ #1, total polarization under GGA-PBE approximation is decreased to 32.89 μC cm⁻², and it is further reduced to 16.04 μC cm⁻² in FTJ #2. In FTJ #1, the decrease of polarization relative to the bulk counterpart of the barrier is likely due to the depolarization field resulted from incomplete charge screening from electrodes, as the polarization in BaTiO₃/CaTiO₃ superlattice is reported to be proper ferroelectricity²⁹ and the depolarization field would have a significant effect on it. The same effect also exists in FTJ #2, however, its polarization is only about half of FTJ #1, which reveals the existence of mechanisms other than the depolarization field. Two possible mechanisms are interface effect and octahedral tilt. While FTJ #2 has the same SrO/TiO₂ interface as FTJ #1, it can be concluded that different octahedral tilt systems in FTJ #1 and #2 play a major role in their different polarizations. As mentioned above, the Pm-like structure with a⁺b⁻c⁻ tilt system in FTJ #2 can create anti-polar order and reducing total polarization, and it is necessary to further study the components of polarization rather than total polarizations in simulated FTJs to reveal the change of polarization patterns. Calculated components of polarizations for bulk BaTiO₃/CaTiO₃ superlattice, FTJ #1 and #2 are listed in Table 1, it can be seen that polarization components for FTJ #2 in the y and z-direction drastically decrease to negligible. Based on the previous discussion of RACDs, the suppression of polarization in the y-direction indicates the appearance of anti-polar order rather than paraelectric phases, and the disappearance of polarization in the z-direction is also due to complex anti-polar state in the z-direction. As FTJ #1 and #2 have very similar heterointerfaces and FTJ #1 has a significant polarization in the z-direction, the suppression of polarization for FTJ #2 in the z-direction is not due to increased depolarization field, but a result of the in-phase octahedral tilt around the x-axis in FTJ #2 that disfavors uniform polarization state in the z-direction. These results have revealed how octahedral tilts in the simulated FTJs can drastically change their polarization patterns, and eventually results in their different ferroelectric properties and application prospects.

Table 1 Calculated components along x, y and z-directions of polarizations for bulk 1 : 1 BaTiO₃/CaTiO₃ superlattice, BaTiO₃/CaTiO₃ barrier in FTJ #1 and #2

Superlattice	Px (μC cm^−2)	Py (μC cm^−2)	Pz (μC cm^−2)
Bulk	26.43	26.44	48.06
FTJ #1	19.19	16.43	21.06
FTJ #2	15.99	0.07	−1.31

---

3.3 Transport properties

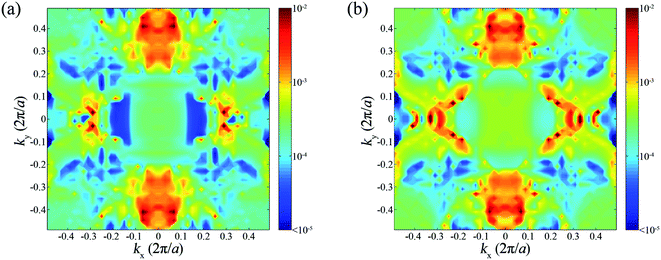
It is known that ferroelectric domain walls in perovskites would significantly increase their conductivity, and this effect is closely related to domain wall types and misfit strains.⁴³ As there are different polarization patterns in our simulated FTJs, especially the existence of abundant domain walls in FTJ #2, it's natural to suggest that they have different electronic transport properties. The calculated transmission spectra near the Fermi level of FTJ #1 and #2 are depicted in Fig. 3, which reflects the tunneling conductivities under small external bias along the z-direction. It is clear that FTJ #2 generally has higher transmissions than FTJ #1 in the depicted range of energy, and the difference in transmission reaches the maximum at the Fermi level. Nevertheless, the mechanism of the enhancement of transmission in FTJ #2 is not clear. To get more insight into this, we calculated the k_‖ resolved transmission by projecting the transmission at the Fermi level onto the 2D Brillouin zone perpendicular to the transport direction for FTJ #1 and #2, as shown in Fig. 4a and b. Results show a significant difference in the distribution of transmission probabilities along x and y-directions for both FTJ #1 and #2. The difference in FTJ #2 is apparently due to the lattice structure of the P2₁/m phase SrRuO₃ and the Pm-like phase BaTiO₃/CaTiO₃ barrier, as they both have a⁺b⁻c⁻ octahedral tilt system. The in-phase tilt along the x-axis and out-phase tilt along the y-axis result in inequivalent atomic configurations along x and y-directions, as shown in Fig. 2, which further results in anisotropic distributions of transmission probabilities along x and y-directions. The same mechanism also exists in FTJ #1, although BaTiO₃/CaTiO₃ barrier in FTJ #1 has a Pc-like phase which has equivalent atomic configurations along x and y-directions (i.e. coexistence of a⁻a⁻c⁻ tilt system and ferroelectric distortion along both x and y-directions), but the SrRuO₃ electrode still has a P2₁/m phase. The discontinuity of octahedral tilts at the interface results in local lattice reconstruction, which drastically reduces tilt angles near the interface in FTJ #1, as shown in Fig. 2. As a result, the Pc phase only appears in the middle part of the barrier, and the inequivalence of atomic configurations along x and y-directions still exists in other parts of the FTJ, thus the distribution of transmission probabilities along x and y-directions are also different from each other.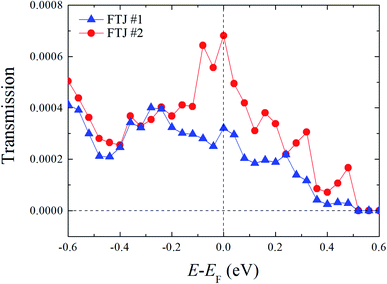

Fig. 3 Dependence of transmission spectra on the energy for FTJ #1 and #2. The Fermi level is set to zero.

Fig. 4 k_‖ resolved transmission at the Fermi level for (a) FTJ #1 and (b) FTJ #2.

Another noteworthy result is the enhancement of transmission near the Fermi level for FTJ #2 relative to FTJ #1. Based on the previous results, we suggest there are several possible mechanisms for this enhancement: (1) the in-plane HH domain wall in FTJ #2 enables resonant tunneling, (2) improved contact between the barrier and electrodes in FTJ #2 due to the more stable heterointerface and (3) the out-of-plane HH domain wall in FTJ #2 opens new conductive channels. From Fig. 4, it can be seen that the enhancement of transmission in FTJ #2 is generally due to hot spots scattered in the x-direction, while the distribution of transmission probabilities in the y-direction is very similar to FTJ #1. This result indicates that the effect from mechanism (1) and (2) are not obvious in FTJ #2, as they would significantly increase the distributions of transmissions in both x and y-directions. While the out-of-plane HH domain wall in the (100) plane plays an important role in determining the distribution of transmission probabilities in the x-direction. This result also implies that charged domain walls parallel to the transport direction have a bigger impact on the tunneling conductance than charged domain walls perpendicular to the transmission direction. We suggest the tunneling conductance in FTJ #2 can be further improved by carrier injection via doping.

4. Conclusions

In summary, we have explored electronic and transport properties of ferroelectric tunnel junctions built by SrRuO₃ electrodes and ferroelectric 1 : 1 BaTiO₃/CaTiO₃ superlattice barrier, and the octahedral tilts in electrodes are taken into consideration to simulate the relatively large thickness of electrodes in the experiment. The SrO/TiO₂ interface is found to be the most stable one. However, depending on whether the atom layer in the barrier next to the TiO₂ interface layer is BaO layer or CaO layer in simulated FTJs, two SrO/TiO₂ interfaces result in completely different lattice reconstructions: the SrO/TiO₂–BaO interface causes discontinuity of octahedral tilt for electrodes and barrier in FTJ #1, while the SrO/TiO₂–CaO interface allows the imprinting of electrode tilt system into the barrier which retains the continuity of octahedral tilts in FTJ #2. Different octahedral tilt systems further result in different polarization patterns in FTJ #1 and #2, as uniform polarizations along x, y, and z-directions are formed in FTJ #1, while abundant ferroelectric domain walls are formed in FTJ #2. As a result, FTJ #2 has higher tunneling conductance than FTJ #1, which is mainly caused by the out-of-plane HH ferroelectric domain wall in it. These observations about the interactions between octahedral tilt systems of barriers and electrodes in FTJs provides further understanding of the importance of octahedral tilts in determining a variety of properties of FTJs. As a result, we suggest that possible octahedral tilts in electrodes for FTJs cannot be ignored in both theoretical and experimental studies. They have also revealed the octahedral tilt in perovskite electrode to be used as a way to create or manipulate new polarization orders and charged domain walls in the barrier, which is of interest for FTJ-based ferroelectric memristors, transistors and photovoltaic devices. It is worth mentioning that our results depend on the thicknesses of electrodes and ferroelectric barriers. Discussions of size effects (e.g. critical thicknesses for FE and AFD orders and dependencies of order parameters on film thickness) requires a large number of simulations for plenty of different FTJs, which is beyond the scope of this paper, while the results will not change our current conclusions. We hope to discuss size effects in future works.

Conflicts of interest

There are no conflicts to declare.

References

1. S. Slesazeck and T. Mikolajick, Nanotechnology, 2019, 30, 35.
2. L. Wang, C. Yang, J. Wen, S. Gai and Y. Peng, J. Mater. Sci.: Mater. Electron., 2015, 26, 4618.
3. P. V. Yudin, A. K. Tagantsev, E. A. Eliseev, A. N. Morozovska and N. Setter, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 134102.
4. R. K. Behera, C. W. Lee, D. Lee, A. N. Morozovska, S. B. Sinnott, A. Asthagiri, V. Gopalan and S. R. Phillpot, J. Phys.: Condens. Matter, 2011, 23, 175902.
5. M. Li, Y. Gu, Y. Wang, L. Chen and W. Duan, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 054106.
6. Y. S. Oh, X. Luo, F. Huang, Y. Wang and S. Cheong, Nat. Mater., 2015, 14, 407–413.
7. J. J. P. Peters, G. Apachitei, R. Beanland, M. Alexe and A. M. Sanchez, Nat. Commun., 2016, 7, 13484.
8. W. Huang, Y. Liu, Z. Luo, C. Hou, W. Zhao, Y. Yin and X. Li, J. Phys. D: Appl. Phys., 2018, 51, 23.
9. P. Sharma, et al., Sci. Adv., 2017, 3, e1700512.
10. G. Sanchez-Santolino, et al., Nat. Nanotechnol., 2017, 12, 655–662.
11. M. Li, L. L. Tao, J. P. Velev and E. Y. Tsymbal, Phys. Rev. B, 2018, 97, 155121.
12. C.-G. Duan, R. F. Sabirianov, W.-N. Mei, S. S. Jaswal and E. Y. Tsymbal, Nano Lett., 2006, 6, 483–487.
13. M.-G. Han, et al., Nat. Commun., 2016, 5, 4693.
14. G. Dong, et al., Science, 2019, 366, 475–479.
15. C. Lichtensteiger, S. Fernandez-Pena, C. Weymann, P. Zubko and J. Triscone, Nano Lett., 2014, 14, 4205–4211.
16. L. Bellaiche and J. Íñiguez, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 014104.
17. Z. Liao, et al., Nat. Mater., 2016, 15, 425–432.
18. A. M. Glazer and H. D. Megaw, Philos. Mag., 1972, 26, 995–1014.
19. J. P. Velev, C.-G. Duan, J. D. Burton, A. Smogunov, M. K. Niranjan, E. Tosatti, S. S. Jaswal and E. Y. Tsymbal, Nano Lett., 2009, 9, 427–432.
20. N. M. Caffrey, T. Archer, I. Rungger and S. Sanvito, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 125409.
21. E. Y. Tsymbal, A. Gruverman, V. Garcia, M. Bibes and A. Barthélémy, MRS Bull., 2012, 37, 138–143.
22. W. J. Chen, Y. Zheng, X. Luo, B. Wang and C. H. Woo, J. Appl. Phys., 2013, 114, 064105.
23. A. Vailionis, H. Boschker, W. Siemons, E. P. Houwman, D. H. A. Blank, G. Rijnders and G. Koster, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 064101.
24. S. H. Chang, Y. J. Chang, S. Y. Jang, D. W. Jeong, C. U. Jung, Y.-J. Kim, J.-S. Chung and T. W. Noh, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 104101.
25. D. Kan, R. Aso, H. Kurata and Y. Shimakawa, Adv. Funct. Mater., 2013, 23, 1129–1136.
26. L. Wang, et al., Nat. Mater., 2018, 17, 1087–1094.
27. Q. He, et al., ACS Nano, 2015, 9, 8412–8419.
28. H. F. Li, G. H. Zhang, Y. Zheng, B. Wang and W. J. Chen, Acta Mater., 2014, 76, 472–481.
29. X. Z. Lu, X. G. Gong and H. J. Xiang, Comput. Mater. Sci., 2014, 91, 310–314.
30. H. Wang, et al., Phys. Rev. X, 2016, 6, 011027.
31. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
32. G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
34. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
35. H. T. Stokes and D. M. Hatch, FINDSYM, 2004, http://stokes.byu.edu/isotropy.html.
36. S. Smidstrup, et al., J. Phys.: Condens. Matter, 2019, 32, 1.
37. H. Guhl, W. Miller and K. Reuter, Surf. Sci., 2010, 604, 372–376.
38. E. Ertekin, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195460.
39. Y. Xie, H. Yu, G. Zhang and H. Fu, J. Phys.: Condens. Matter, 2008, 20, 21.
40. H. Moriwake, A. Kuwabara, C. A. J. Fisher, H. Taniguchi, M. Itoh and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 104114.
41. N. A. Benedek and C. Fennie, J. Phys. Chem. C, 2013, 117, 13339.
42. Y. Zhang, J. Sun, J. P. Perdew and X. Wu, Phys. Rev. B, 2017, 96, 035143.
43. J. Seidel, et al., Nat. Mater., 2009, 8, 229–234.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra04740f

---