Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The structure and vibrational spectroscopy of cryolite, Na3AlF6
Stewart F. Parker *a,
Anibal J. Ramirez-Cuesta
*a,
Anibal J. Ramirez-Cuesta b and
Luke L. Daemenb
b and
Luke L. Daemenb
aISIS Facility, STFC Rutherford Appleton Laboratory, Chilton, Didcot, Oxon OX11 0QX, UK. E-mail: stewart.parker@stfc.ac.uk
bSpallation Neutron Source, Neutron Spectroscopy Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831-6475, USA
First published on 8th July 2020
Abstract
Cryolite, Na3[AlF6], is essential to commercial aluminium production because alumina is readily soluble in molten cryolite. While the liquid state has been extensively investigated, the spectroscopy of the solid state has been largely ignored. In this paper, we show that the structure at 5 K is the same as that at room temperature. We use a combination of infrared and Raman spectroscopies together with inelastic neutron scattering (INS) spectroscopy. The use of INS enables access to all of the modes of Na3[AlF6], including those that are forbidden to the optical spectroscopies. Our spectral assignments are supported by density functional theory calculations of the complete unit cell.
Introduction
Cryolite, Na3[AlF6], occurs naturally as a rare mineral.1 Historically, it was used as a source of aluminium but this has been superseded by bauxite (a mixture of the Al2O3 containing minerals boehmite, diaspore and gibbsite), largely because of the higher Al content of bauxite (∼50%) vs. cryolite (13%) and the scarcity of the latter. However, cryolite remains essential to aluminium production because alumina is readily soluble in molten cryolite. This is crucial to the economics of aluminium production because cryolite melts at 1012 °C whereas alumina melts at 2072 °C. As the melt is ionic, it also conducts electricity efficiently making the electrolytic reduction of alumina feasible. This is the basis of the Hall–Héroult process, which was invented independently by Hall and Héroult in 1886 and it is still the method of production today.2The liquid phase of cryolite has been extensively investigated by a variety of techniques including multinuclear (19F, 23Na, 27Al) NMR,3–5 Raman spectroscopy6–8 and quasielastic neutron scattering.9,10 There are also a large number of molecular dynamics studies e.g.11–15, some of which calculate the Raman spectra13,14 in the melt. Surprisingly, the solid state has been much less investigated, with only one paper on the infrared spectroscopy of Na3[AlF6]16 and one on that of the isostructural K3[AlF6].17 Cryolite is the end member of the elpasolite family,18 the archetype is K2Na[AlF6], and this is the most abundant prototype in the Inorganic Crystal Structure Database.19 The spectroscopy of elpasolite itself has been studied,20 as has Cs2Na[AlF6].21 Materials of the type Li3[InX6] (X = Cl,22 Br23) are of current interest as lithium ion conductors.24
In view of the technological importance of cryolite, we have carried out a comprehensive spectroscopic investigation and report new infrared and Raman spectra over extended temperature and spectral ranges and the inelastic neutron scattering (INS) spectrum. The last of these is observed for the first time and enables access to all of the modes of Na3[AlF6]. Our spectral assignments are supported by density functional theory calculations of the complete unit cell.
Results
Structure
At room temperature cryolite crystallizes in the monoclinic α-phase, space group P21/n (no. 14) with two formula units in the primitive cell,25–27 Fig. 1. The non-standard setting is used because it highlights the relationship to the high temperature (above 823 K) face centered cubic β-phase, Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (no. 225).27,28
m (no. 225).27,28
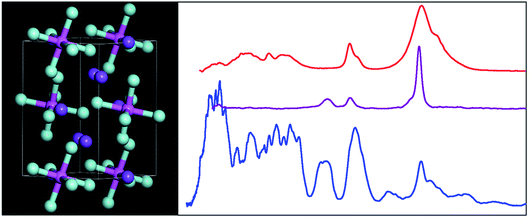 | ||
| Fig. 1 The room temperature structure of cryolite in the monoclinic space group P21/n (no. 14).26 Key: Na1 = orange, Na2 = purple, Al = magenta, F = turquoise. | ||
The structure in the α-phase is shown in Fig. 1 and it can be seen that there are two types of sodium ion: one (Na1, orange) on the Wyckoff site 2c and two (Na2, purple) on the Wyckoff site 4e. These are six- and eightfold coordinated by fluorine atoms, respectively. The [AlF6]3− ion is on the Wyckoff site 2d and has Ci symmetry. Thus the compound is better formulated as: (Na2)(Na)[AlF6] and is an example of a double perovskite.27
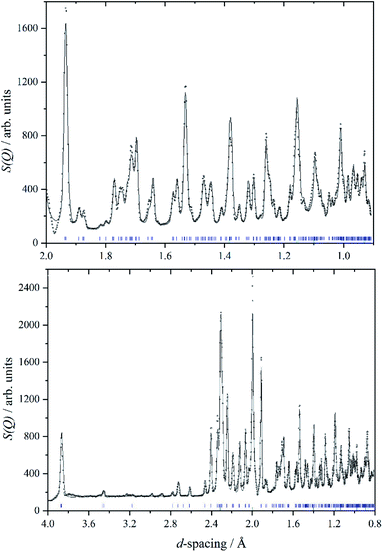
We are unaware of any structural studies below room temperature. Heat capacity measurements from 7–350 K,29 do not show any evidence of a phase transition in that range, apart from the melting of a liquid inclusion at 268 K in the natural sample of cryolite that was used. However, the INS spectrometer used in this work, VISION,30 also has a neutron diffraction capability. Fig. 2 shows a two-phase (cryolite plus the aluminium can) Rietveld fit of the neutron diffractogram measured at 5 K. Scale factors were refined for both phases in obtaining the fit to the data. Lattice parameters have been allowed to refine, to allow for cell contraction, but atomic positions have been held at the room temperature values.25 An excellent fit to the data is obtained, even though the atomic positions and temperatures factors of the cryolite have not been refined. Table 1 lists the lattice parameters determined here together with room temperature and estimated values. It is apparent that, apart from the expected lattice contraction on cooling, that the P21/n structure is retained to at least 5 K.
| 5a K | 0b K | 0c K | 295d K | 295 Ke | |
|---|---|---|---|---|---|
| a This work.b Extrapolated from ref. 25 by ref. 14.c Calculated by molecular dynamics.14d From ref. 25.e From ref. 26. | |||||
| a/Å | 5.3917(5) | 5.381 | 5.42 | 5.4139(7) | 5.4054(1) |
| b/Å | 5.6010(5) | 5.581 | 5.63 | 5.6012(5) | 5.5934(1) |
| c/Å | 7.7556(8) | 7.693 | 7.83 | 7.7769(8) | 7.7672(1) |
| α/° | 90.000 | 90.000 | 90.0 | 90.000 | 90.000 |
| β/° | 90.253(8) | 90.285 | 90.2 | 90.183(3) | 89.81(1) |
| γ/° | 90.000 | 90.000 | 90.0 | 90.000 | 90.000 |
| V/Å3 | 234.21(4) | 232.6 | 238.9 | 235.8 | 234.84 |
Table 2 compares selected observed and calculated bond distances (all of the cis F–Al–F bond angles are 90 ± 1°, all the trans angles are 180° by symmetry). As might be expected from the very small difference between the room temperature and 5 K lattice parameters there is little change in the interatomic distances. The calculation does slightly overestimate the Al–F distances. The Na–F distances are slightly shorter than found in NaF (2.318 Å (ref. 31)).
| Distance/Å | 295a K | 5 K initialb | 5 K optc |
|---|---|---|---|
| a From ref. 26.b Structure used for the fits in Fig. 2.c 5 K structure after geometry optimization. | |||
| Al–F | 2 × 1.799 | 2 × 1.812 | 2 × 1.825 |
| 2 × 1.820 | 2 × 1.825 | 2 × 1.834 | |
| 2 × 1.830 | 2 × 1.836 | 2 × 1.836 | |
| Na1–F | 2 × 2.211 | 2 × 2.205 | 2 × 2.219 |
| 2 × 2.271 | 2 × 2.256 | 2 × 2.257 | |
| 2 × 2.272 | 2 × 2.264 | 2 × 2.274 | |
| Na2–F (min) | 2.292 | 2.287 | 2.276 |
| (max) | 2.816 | 2.806 | 2.807 |
| (ave) | 2.498 | 2.494 | 2.564 |
Vibrational spectroscopy
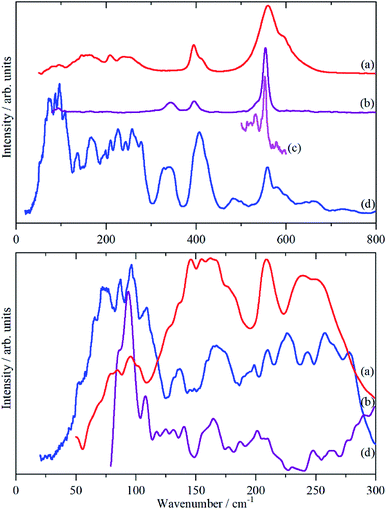
Fig. 3 shows the infrared, Raman and INS spectra of cryolite. The Raman spectrum at 13 K is seen in Fig. 3c, unfortunately, because of sample fluorescence, only the Al–F symmetric stretch mode at 554 cm−1 was observable. However, apart from a marked narrowing, there is no shift in transition energy or additional peaks apparent. The lattice mode region, shown in the lower part of Fig. 3, shows coincidences between the INS and the infrared and Raman data. Thus the vibrational spectroscopy suggests (but does not prove) that there is no phase change between room temperature and 5 K, consistent with the diffraction results.An isolated octahedral, Oh, [AlF6]3− ion has six Al–F stretch modes: ν1 (A1g), ν2 (Eg), ν3 (T1u) and nine F–Al–F bend modes: ν4 (T1u), ν5 (T2g), ν6 (T2u). ν1, ν2 and ν5 are Raman active, ν3 and ν4 are infrared active and ν6 is forbidden in both forms of spectroscopy.32 However, all of the modes are allowed in the INS spectrum. To go beyond this requires more detailed analysis and to this end we use the correlation method.33 The results are shown in Table 3.
| Ion | n | Free ion | Crystal | Factor group | Totala | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sitec | Translations | Librations | Intramolecular | |||||||||
| Sym.b | Rep. | Rep. | No. | Rep. | No. | Rep. | No. | C2h | ||||
| a Total is the product of the column “No.” and the factor group.b Sym. = symmetry, Rep. = irreducible representation of the point group, No. = number.c Symmetry of the site occupied by the ion in the crystal. | ||||||||||||
| Na1 | 2 | Ci | Au | 3 | (Au + Bu) | 3(Au + Bu) | ||||||
| Na2 | 4 | C1 | A | 3 | (Ag + Bg + Au + Bu) | 3(Ag + Bg + Au + Bu) | ||||||
| AlF6 | 2 | Oh | T1u | Ci | Au | 3 | (Au + Bu) | 3(Au + Bu) | ||||
| 2 | Oh | T1g | Ci | Ag | 3 | (Ag + Bg) | 3(Ag + Bg) | |||||
| 2 | Oh | A1g (ν1) | Ci | Ag | 1 | (Ag + Bg) | (Ag + Bg) | |||||
| 2 | Oh | Eg (ν2) | Ci | Ag | 2 | (Ag + Bg) | 2(Ag + Bg) | |||||
| 2 | Oh | T1u (ν3) | Ci | Au | 3 | (Au + Bu) | 3(Au + Bu) | |||||
| 2 | Oh | T1u (ν4) | Ci | Au | 3 | (Au + Bu) | 3(Au + Bu) | |||||
| 2 | Oh | T2g (ν5) | Ci | Ag | 3 | (Ag + Bg) | 3(Ag + Bg) | |||||
| 2 | Oh | T2u (ν6) | Ci | Au | 3 | (Au + Bu) | 3(Au + Bu) | |||||
With two formula units in the primitive cell, there are 20 atoms present hence there are 60 modes, which are given by the sum of the last column in Table 3: 12 Ag + 12 Bg + 18 Au + 18 Bu. This includes the three acoustic translational modes, which have Au + 2 Bu representations and have zero energy at the Brillouin zone Γ-point, where the infrared and Raman modes are observed. Modes that have Au or Bu symmetry are infrared active, those with Ag or Bg are Raman active. Two deductions are immediately obvious: all of the degeneracies are formally lifted and because the centre of symmetry is preserved, the free ion selection rules will still apply, except that ν6 is now allowed in the infrared spectrum. As stated earlier, all modes are allowed in the INS spectrum.
The analysis in Table 3 enables some of the modes to be assigned. The intense, broad mode at 559 cm−1 with shoulders at 596 and 608 cm−1 in the infrared spectrum must be ν3. Previous work16 on the infrared spectrum of cryolite found ν3 at 599 cm−1 with shoulders at 580 and 630 cm−1, the lower energy modes were not reported. We can only ascribe the difference in the transition energy of ν3 to either a calibration error in the older (pre-FTIR) work or that the natural sample of cryolite used there was impure.
The strong mode at 554 cm−1 in the Raman spectrum must be ν1 and the two weaker modes at 396 and 344 cm−1 in the Raman spectrum are ν2 and ν5 respectively. This is in excellent agreement with the previously reported Raman spectrum of cryolite.8 Cryolite melts6–8 show a strong band at ∼550 cm−1 assigned to ν1. In the infrared spectrum the mode at 396 cm−1 is assigned as ν4. The coincidence with ν2 is surprising because one is an Al–F stretch mode and the other an F–Al–F bending mode, but the selection rules are unambiguous. The assignment is supported by the INS spectrum, which shows a mode at 407 cm−1, that is much stronger than ν5, consistent with it being the unresolved sum of the two modes. The optically silent mode ν6 is not apparent, so it must occur below 300 cm−1.
It is only in the region <300 cm−1 in the INS spectrum that the low symmetry of the system is readily apparent. In the infrared spectrum, there are three weak features, which Table 3 shows must be ν6 and the translational modes of the ions, although there is no way to assign which is which. In the Raman spectrum there is a weak mode at 94 cm−1, which is presumably the [AlF6]3− ion librational mode.
Computational studies
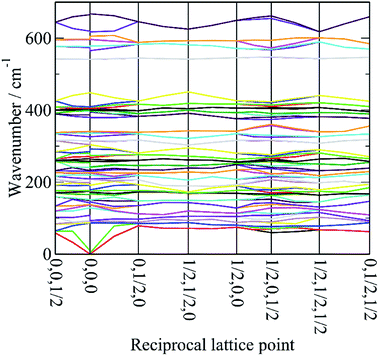
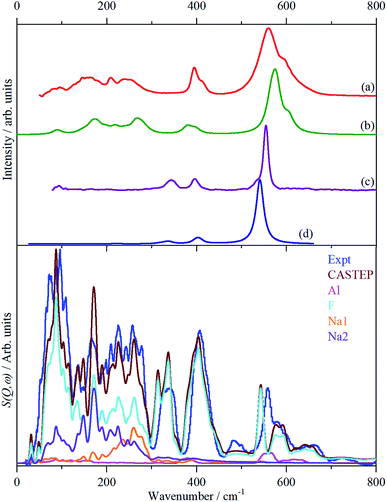
In order to assign the low energy region and to confirm the assignments for ν1 to ν5 we use periodic density functional theory (DFT) of the primitive cell and calculate the vibrational transition energies across the entire Brillouin zone (see: Materials and methods for details). The resulting dispersion curves are shown in Fig. 4 and the INS spectrum generated from the calculation is shown in Fig. 5.It can be seen that the calculated INS spectrum is in almost quantitative agreement with the experimental data. The Al–F stretch modes are calculated slightly softer than is observed, this is probably because the bond lengths are calculated slightly too long: observed:25–27 1.799, 1.820, 1.830 Å; calculated: 1.825, 1.834, 1.836 Å. However, the overall pattern of the experimental data is very well reproduced. In particular, the splitting of ν3 is clearly seen and Fig. 4 shows that this is the result of the combination of the site group and factor group splitting combined with significant vibrational dispersion (variation with wavevector). The dense manifold of modes below 300 cm−1 occurs because the low symmetry removes all the degeneracies and results in the complex structure seen experimentally.
The transition energies at the Brillouin zone Γ-point, (0,0,0), are given in Table 4 with the assignments based on visualization of the modes. This confirms the assignments for ν1 to ν5 and in particular that ν2 and ν4 are coincident. The “missing” mode ν6 is calculated at 254–288 cm−1 and is seen to occur weakly in the infrared spectrum at 239/253 cm−1. This is the first time that ν6 has been observed experimentally.
| CASTEP/cm−1 | Symb | IR int/km mol−1 | Raman int/Å4 amu−1 | Observeda | Descriptionb | ||
|---|---|---|---|---|---|---|---|
| INS/cm−1 | Raman/cm−1 | Infrared/cm−1 | |||||
| a s = strong, m = medium, w = weak, br = broad, sh = shoulder.b Lib = libration of [AlF6]3− ion, AlF6 = translation of [AlF6]3− ion, Na1 trans = translational mode of Na1, Na2 trans = translational mode of Na2. | |||||||
| 0 | Bu | 0 | 0 | Acoustic | |||
| 0 | Au | 0 | 0 | Acoustic | |||
| 0 | Bu | 0 | 0 | Acoustic | |||
| 86 | Ag | 0 | 0.02 | 75s | Lib + Na2 trans | ||
| 87 | Au | 13.62 | 0 | AlF6 trans | |||
| 90 | Bu | 103.00 | 0 | AlF6 trans | |||
| 92 | Ag | 0 | 0.02 | 87s | 86sh | Lib + Na2 trans | |
| 93 | Bg | 0 | 0 | 96s | 94w | Lib + Na2 trans | |
| 128 | Bg | 0 | 0 | 109s | 109w | Lib + Na2 trans | |
| 137 | Ag | 0 | 0.02 | 136m | Lib + Na2 trans | ||
| 138 | Bg | 0 | 0 | Lib + Na2 trans | |||
| 142 | Au | 32.79 | 0 | Na2 trans | |||
| 149 | Au | 9.73 | 0 | AlF6 trans | |||
| 150 | Bu | 36.73 | 0 | 146w | Na2 trans | ||
| 165 | Au | 55.50 | 0 | 154w | Na2 trans | ||
| 167 | Bu | 163.52 | 0 | 164s | 163w | Na2 trans | |
| 175 | Ag | 0 | 0.02 | Na2 trans + Lib | |||
| 175 | Bg | 0 | 0.01 | Na2 trans + Lib | |||
| 178 | Bu | 226.57 | 0 | 178w | Na2 trans | ||
| 191 | Au | 5.47 | 0 | 183w | Na1 trans | ||
| 198 | Au | 100.07 | 0 | Na2 trans | |||
| 209 | Bg | 0 | 0 | 198w | Na2 trans + Lib | ||
| 209 | Ag | 0 | 0.02 | 210m | Na2 trans + Lib | ||
| 219 | Au | 59.53 | 0 | 209m | 209w | Na1 trans | |
| 219 | Bu | 96.45 | 0 | Na1 trans | |||
| 225 | Bg | 0 | 0.02 | 226m | Na2 trans + Lib | ||
| 226 | Ag | 0 | 0.02 | Na2 trans + Lib | |||
| 232 | Au | 1.86 | 0 | 243m | Na1 trans | ||
| 240 | Bu | 37.39 | 0 | Na1 trans | |||
| 242 | Bu | 56.98 | 0 | 243w | Na1 trans | ||
| 258 | Au | 1.46 | 0 | 257m | 252w | ν6 | |
| 264 | Bu | 199.11 | 0 | ν6 | |||
| 268 | Bu | 73.93 | 0 | 265sh | ν6 | ||
| 271 | Au | 71.91 | 0 | ν6 | |||
| 280 | Au | 161.49 | 0 | 278sh | ν6 | ||
| 292 | Bu | 38.42 | 0 | ν6 | |||
| 304 | Ag | 0 | 0.01 | 325s | ν5 | ||
| 314 | Bg | 0 | 0.07 | ν5 | |||
| 326 | Ag | 0 | 0.18 | ν5 | |||
| 335 | Ag | 0 | 0.24 | ν5 | |||
| 341 | Bg | 0 | 0.16 | 336s,br | 343m | ν5 | |
| 341 | Bg | 0 | 0.08 | ν5 | |||
| 379 | Bu | 108.53 | 0 | ν4 | |||
| 380 | Au | 95.40 | 0 | ν4 | |||
| 397 | Bu | 129.31 | 0 | 396sh | 395m | ν4 | |
| 398 | Ag | 0 | 0.62 | 395m | ν2 | ||
| 400 | Bu | 0.62 | 0 | ν4 | |||
| 404 | Ag | 0 | 0.36 | ν2 | |||
| 405 | Au | 0.24 | 0 | ν4 | |||
| 408 | Bg | 0 | 0.50 | 407s | ν2 | ||
| 409 | Au | 2.09 | 0 | 413sh | ν4 | ||
| 448 | Bg | 0 | 0.05 | 425sh | ν2 | ||
| 541 | Ag | 0 | 13.80 | ν1 | |||
| 541 | Bg | 0 | 0 | 554s | ν1 | ||
| 565 | Bu | 562.08 | 0 | 559s | 559s | ν3 | |
| 574 | Au | 762.85 | 0 | ν3 | |||
| 578 | Bu | 657.32 | 0 | 580m | ν3 | ||
| 597 | Au | 21.77 | 0 | 601m | ν3 | ||
| 605 | Bu | 336.80 | 0 | 596sh | ν3 | ||
| 619 | Au | 21.74 | 0 | 608sh | ν3 | ||
Fig. 5 also includes the individual contributions to the INS spectrum from each element. As expected, the fluorine contribution accounts for most of the intensity and it confirms that the librational modes account for the peaks at ∼85–150 cm−1. However, the librations have the same symmetry, Ag and Bg, as some of the translational modes of Na2 which results in extensive mixing of the two vibrations. Thus the lower energy modes around 100 cm−1 are more librational in form while the higher energy ones around 210 cm−1 are more translational. Na2 has modes of both gerade and ungerade character, Table 3, and this results in the modes occurring in a broad band from 50–300 cm−1. In contrast, the Na1 modes are much more localized and largely occur in the narrower range of 200–300 cm−1. This is a consequence of the more regular coordination polyhedron of Na1: the Na–F distances vary by less than 0.06 Å, by contrast those around Na2 vary by nearly ten times as much, 0.5 Å (Table 2).
Discussion
This work provides the first complete assignment of the vibrational spectra of cryolite. In particular, the forbidden (in Oh symmetry) mode ν6 has been observed. This is very rare:32 (pp. 216–218) lists the spectra of over 30 [MF6]x− ions; for none of them is ν6 given, although it is known for a few neutral MF6 systems. Assignment of librational modes is equally rare. To our knowledge, the only examples for which this is known are for K2[MCl6] (M = Pt, Ir,34 Re35) where the librational transition energies are 55 cm−1 (Pt), 48 cm−1 (Ir) and 28 and 68 cm−1 (Re). Making the naive assumption that it is only the difference in the moment of inertia between the [AlF6]3− and [PtCl6]2− ions that accounts for the difference in transition energy would predict that [AlF6]3− occurs at 87 cm−1. This is on the lowest edge of the band of the librational modes (Table 4) and suggests that other factors are also relevant, the most likely being the difference in charge of the ions.The only unassigned band in the spectra shown in Fig. 3 is the shoulder at 533 cm−1 on the low energy side of ν1 that is clearly resolved at 13 K. We considered the possibility that it may be the Bg symmetric Al–F stretch mode that was miscalculated, however, there is no corresponding mode in the INS spectrum, which also argues against it being an overtone or combination. The calculated Raman intensity of this mode is almost zero which also militates against this assignment. Inspection of the Raman spectra of cryolite in the literature4,6,8 does not show the band in the solid or liquid phase. This suggests that it is an impurity, despite the stated purity being >99%, and the most likely candidate is chiolite, Na5Al3F14. This mineral occurs naturally with cryolite36 and consists of sheets of corner-sharing AlF6 octahedra,37 it has a very strong totally symmetric Al–F stretch mode at 530 cm−1.38
Materials and methods
Cryolite, Na3[AlF6], (>99%) was purchased from Sigma-Aldrich (Gillingham, Dorset, UK) and used as received.INS spectra were recorded at 5 K using the VISION30 spectrometer at the Spallation Neutron Source (SNS) (Oak Ridge, Tennessee, USA). An empty aluminium sample can has been subtracted from the measured INS data. Infrared spectra (50–4000 cm−1, 4 cm−1 resolution, 64 scans) were recorded at room temperature with a Bruker Vertex 70 Fourier transform infrared spectrometer using a Bruker Platinum single reflection attenuated total internal reflection accessory. The FT-Raman spectrum was recorded at room temperature a from the sample inside a quartz cuvette with a Bruker MultiRam spectrometer using 1064 nm excitation (500 mW laser power and 1024 scans at 4 cm−1 resolution). Variable temperature (13–300 K) Raman spectra were recorded with a modified Renishaw InVia spectrometer using 785 nm excitation.39
Dispersion corrected periodic density functional theory (DFT-D) calculations were carried out with CASTEP (version 17.21).40 On-the-fly generated norm conserving pseudopotentials with a plane-wave cut-off of 870 eV were used with the PBE41 functional with the Tkatchenko–Scheffler (TS) dispersion correction scheme42 within the generalized gradient approximation (GGA). Brillouin zone sampling of electronic states was performed on a 10 × 8 × 9 Monkhorst–Pack grid (180 k-points). The starting structure was that determined here at 5 K. The equilibrium structure, an essential prerequisite for lattice dynamics calculations, was obtained by BFGS geometry optimization after which the residual forces were converged to |0.00097| eV Å−1. A second calculation that optimised both the lattice parameters and the geometry resulted in a 5.9% increase in the volume of the unit cell. Phonon frequencies were obtained by diagonalization of the dynamical matrix, computed using density-functional perturbation theory,43 to compute the dielectric response and the Born effective charges, and, from these, the mode oscillator strength tensor and infrared absorptivity were calculated. Raman intensities were calculated by a finite displacement method.44 In addition to the calculation of transition energies at zero wavevector, phonon dispersion was also calculated along high symmetry directions throughout the Brillouin zone. For this purpose, dynamical matrices were computed on a regular grid of wavevectors throughout the Brillouin zone, and Fourier interpolation was used to extend the computed grid to the desired fine set of points along the high-symmetry paths.45 The atomic displacements in each mode, that are part of the CASTEP output, enable visualization of the modes in Materials Studio46 to aid assignments and are also all that is required to generate the INS spectrum using the program ACLIMAX (version 6.0.0 LE).47 It is emphasised that, for the calculated spectra and dispersion curves shown, the transition energies have not been scaled.
Conclusions
In this work we have shown that the structure of cryolite is the same at 5 K as previously determined at room temperature.25–27 We have used a combination of vibrational spectroscopies to observe all of the modes for the first time, including those that are infrared and Raman forbidden under octahedral symmetry.This work also allows some assignments to be made for elpasolite20 and Cs2Na[AlF6].21 For the former, the Raman bands at 561, 330 and 138 cm−1 are ν1, ν5 and the librational mode, the infrared bands at 590, 401 and 238 cm−1 are ν3, ν4 and a Na+ translation. For Cs2Na[AlF6] the Raman bands at 520 and 364 cm−1 are ν1 and ν2, those at 316, 310 and 307 cm−1 are from ν5.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors gratefully acknowledge the invaluable assistance of Professor Kenneth Shankland (University of Reading) with the analysis of the diffraction data. This research benefited from the use of the VISION beamline at the Spallation Neutron Source, Oak Ridge National Laboratory (ORNL), which is supported by the Scientific User Facilities Division, Office of Basic Energy Sciences, US Department of Energy (DOE). Computing resources (time on the SCARF computer cluster for the CASTEP calculations) was provided by STFC's e-Science facility. This research has been performed with the aid of facilities at the Research Complex at Harwell, including the FT-Raman spectrometer. The authors would like to thank the Research Complex for access and support to these facilities and equipment.References
- R. V. Gaines, H. C. W. Skinner, E. E. Foord, B. Mason and A. Rosenzweig, Dana's New Mineralogy: The System of Mineralogy of James Dwight and Edward Salisbury, Wiley-Blackwell, Oxford, UK, 8th edn, 1997 Search PubMed.
- J. Thonstad, P. Feller, G. M. Haarberg, J. Hiveš, H. Kvande and Å. Sterten, Aluminium Electrolysis. Fundamentals of the Hall–Héroult Process, Aluminium-Verlag, Dusseldorf, Germany, 3rd edn, 2001 Search PubMed.
- V. Lacassagne, C. Bessada, B. Ollivier, D. Massiot, P. Florian and J.-P. Coutures, C. R. Acad. Sci., Ser. IIb: Mec., Phys., Astron., 1997, 325, 91–98 CAS.
- E. Robert, V. Lacassagne, C. Bessada, D. Massiot, B. Gilbert and J.-P. Coutures, Inorg. Chem., 1999, 38, 214–217 CrossRef CAS.
- V. Lacassagne, C. Bessada, P. Florian, S. Bouvet, B. Ollivier, J.-P. Coutures and D. Massiot, J. Phys. Chem. B, 2002, 106, 1862–1868 CrossRef CAS.
- M. H. Brooker, J. J. Johnson, A. A. Shabana and J. Wang, in Proceedings of the 9th International Symposium on Molten Salts, ed. C. L. Hussey, D. S. Newman, G. Mamantov and Y. Ito, Electrochemical Society, Pennington, NJ, USA, 1994, vol. 94–13, pp. 227–234 Search PubMed.
- B. Gilbert, E. Robert, E. Tixhon, J. E. Olsen and T. Østvold, Inorg. Chem., 1996, 35, 4198–4210 CrossRef CAS PubMed.
- M. H. Brooker, R. W. Berg, J. H. von Barner and N. J. Bjerrum, Inorg. Chem., 2000, 39, 3682–3689 CrossRef CAS PubMed.
- S. Jahn, J. Ollivier and F. Demmel, Solid State Ionics, 2008, 179, 1957–1961 CrossRef CAS.
- F. Demmel, T. Seydel and S. Jahn, Solid State Ionics, 2009, 180, 1257–1260 CrossRef CAS.
- Z. Akdeniz and P. A. Madden, J. Phys. Chem. B, 2006, 110, 6683–6691 CrossRef CAS PubMed.
- L. Foy and P. A. Madden, J. Phys. Chem. B, 2006, 110, 15302–15311 CrossRef CAS PubMed.
- S. Cikit, Z. Akdeniz and P. A. Madden, J. Phys. Chem. B, 2014, 118, 1064–1070 CrossRef CAS PubMed.
- T. Bučko and F. Šimko, J. Chem. Phys., 2016, 144, 064502 CrossRef PubMed.
- K. Machado, D. Zanghi, V. Sarou-Kanian, S. Cadars, M. Burbano, M. Salanne and C. Bessada, J. Phys. Chem. C, 2017, 121, 10289–10297 CrossRef CAS.
- J. Bondam, Acta Chem. Scand., 1971, 25, 3271–3276 CrossRef CAS.
- M. J. Reisfeld, Spectrochim. Acta, Part A, 1973, 29, 1923–1926 CrossRef.
- R. H. Mitchell, M. D. Welch and A. R. Chakhmouradian, Mineral. Mag., 2017, 81, 411–461 CrossRef CAS.
- A. Belsky, M. Hellenbrandt, V. L. Karen and P. Luksch, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 364–369 CrossRef PubMed.
- L. R. Morss, J. Inorg. Nucl. Chem., 1974, 36, 3876–3878 CrossRef CAS.
- H. N. Bordallo, R. W. Henning, L. P. Sosman, R. J. M. da Fonseca, A. D. Tavares, K. M. Hanif and G. F. Strouse, J. Chem. Phys., 2001, 115, 4300–4305 CrossRef CAS.
- X. Li, J. Liang, N. Chen, J. Luo, K. R. Adair, C. Wang, M. N. Banis, T.-K. Sham, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li and X. Sun, Angew. Chem., 2019, 131, 16579–16584 CrossRef.
- K. Yamada, K. Iwaki, T. Okuda and Y. Tomita, in Solid State Ionics Trends in the New Millennium, ed. B. V. R. Chowdari, S. R. S. Prabaharan, M. Yahaya and I. A. Talib, World Scientific, Singapore, Singapore, 2002, pp. 621–628 Search PubMed.
- A. Zevgolis, B. C. Wood, Z. Mehmedovic, A. T. Hall, T. C. Alves and N. Adelstein, APL Mater., 2018, 6, 047903 CrossRef.
- H. Yang, S. Ghose and D. M. Hatch, Phys. Chem. Miner., 1993, 19, 528–544 CrossRef CAS.
- K. C. Ross, R. H. Mitchell and A. R. Chakhmouradian, J. Solid State Chem., 2003, 172, 95–101 CrossRef CAS.
- Q. Zhou and B. J. Kennedy, J. Solid State Chem., 2004, 177, 654–659 CrossRef CAS.
- Ľ. Smrčok, M. Kucharík, M. Tovar and I. Žižak, Cryst. Res. Technol., 2009, 44, 834–840 CrossRef.
- L. M. Anovitz, B. S. Hemingway, E. F. Westrum Jr, G. W. Metz and E. J. Essene, Geochim. Cosmochim. Acta, 1987, 51, 3087–3103 CrossRef CAS.
- Science and Discovery: Neutron Sciences, https://neutrons.ornl.gov/vision Search PubMed.
- Y. Shirako, Y. G. Shi, A. Aimi, D. Mori, H. Kojitani, K. Yamaura, Y. Inaguma and M. Akaogi, J. Solid State Chem., 2012, 191, 167–174 CrossRef CAS.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part A, Wiley-Interscience, New York, USA, 5th edn, 1997 Search PubMed.
- W. G. Fateley, F. R. Dollish, N. I. McDevitt and F. E. Bentley, Infrared and Raman Selection Rules for Molecular and Lattice Vibrations: The Correlation Method, Wiley-Interscience, New York, USA, 1972 Search PubMed.
- S. F. Parker and J. B. Forsyth, J. Chem. Soc., Faraday Trans., 1998, 94, 1111–1114 RSC.
- G. P. O' Leary and R. G. Wheeler, Phys. Rev. B: Solid State, 1970, 1, 4409–4439 CrossRef.
- H. Pauly, Bull. Geol. Soc. Den., 1985, 34, 145–150 Search PubMed.
- C. Jacoboni, A. Leble and J. J. Rousseau, J. Solid State Chem., 1981, 36, 297–304 CrossRef CAS.
- P. Rocquett, M. Couzi, A. Tressaudi, J. P. Chaminadei and C. Hauw, J. Phys. C: Solid State Phys., 1985, 18, 6555–6569 CrossRef.
- M. A. Adams, S. F. Parker, F. Fernandez-Alonso, D. J. Cutler, C. Hodges and A. King, J. Appl. Spectrosc., 2009, 63, 727–732 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. Cryst. Mater., 2005, 220, 567–570 CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- V. Milman, A. Perlov, K. Refson, S. J. Clark, J. Gavartin and B. Winkler, J. Phys.: Condens. Matter, 2009, 21, 485404 CrossRef PubMed.
- D. V. Porezag and M. R. Pederson, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 7830–7836 Search PubMed.
- X. Gonze, J.-C. Charlier and M. P. Teter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 13035–13038 CrossRef PubMed.
- BIOVIA Materials Studio, https://www.3dsbiovia.com/products/collaborative-science/biovia-materials-studio/ Search PubMed.
- A. J. Ramirez-Cuesta, Comput. Phys. Commun., 2004, 157, 226–238 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |