Open Access Article
Open Access ArticleRedox and structural properties of accessible actinide(II) metallocalixarenes (Ac to Pu): a relativistic DFT study†
Shuai Niu‡
,
Hong-Xue Cai‡,
Hong-Bo Zhao,
Li Li and
Qing-Jiang Pan *
*
Key Laboratory of Functional Inorganic Material Chemistry of Education Ministry, School of Chemistry and Materials Science, Heilongjiang University, Harbin 150080, China. E-mail: panqjitc@163.com
First published on 17th July 2020
Abstract
The redox properties of actinides play a significant role in manipulating organometallic chemistry and energy/environment science, for being involved in fundamental concepts (oxidation state, bonding and reactivity), nuclear fuel cycles and contamination remediation. Herein, a series of trans-calix[2]pyrrole[2]benzene (H2L2) actinide complexes (An = Ac–Pu, and oxidation states of +II and +III) have been studied by relativistic density functional theory. Reduction potentials (E0) of [AnL2]+/[AnL2] were computed within −2.45 and −1.64 V versus Fc+/Fc in THF, comparable to experimental values of −2.50 V for [UL1e]/[UL1e]− (H3L1e = (Ad,MeArOH)3mesitylene and Ad = adamantyl) and −2.35 V for [U(CpiPr)2]+/[U(CpiPr)2] (CpiPr = C5iPr5). The E0 values show an overall increasing trend from Ac to Pu but a break point at Np being lower than adjacent elements. The arene/actinide mixed reduction mechanism is proposed, showing arenes predominant in Ac–Pa complexes but diverting to metal-centered domination in U–Pu ones. Besides being consistent with previously reported those of AnIII/AnII couples, the changing trend of our reduction potentials is corroborated by geometric data, topological analysis of bonds and electronic structures as well as additional calculations on actinide complexes ligated by tris(alkyloxide)arene, silyl-cyclopentadiene and octadentate Schiff-base polypyrrole in terms of electron affinity. The regularity would help to explore synthesis and property of novel actinide(II) complex.
1. Introduction
In-depth understanding of fundamental concepts like oxidation state, bonding and electronic structures has helped to reveal structures of related complexes and properties and rationalize existing/potential applications.1–5 In this respect, Evans and co-workers conducted a pioneering work in that an isolable U(II) complex, [K(2.2.2-cryptand)]·[UL3] (L3 stands for three Cp′ (C5H4SiMe3) ligands, in Chart 1), was crystallographically identified.6 This extended uranium oxidation state to +II with respect to commonly recognized +III to +VI. Studies of the same group further had access to several U(II) complexes ligated by various substituted cyclopentadienyls (Cp)7–10 and even a more electron-donating N(SiMe3)2.10 The Meyer's group increased one member into the U(II) complex family, [K(2.2.2-cryptand)]·[UL1e] (H3L1e = (Ad,MeArOH)3mesitylene and Ad = adamantyl).11 Very recently, two neutral U(II) complexes have been found, [U(NHAriPr6)] (AriPr6 = 2,6-(2,4,6-iPr3C6H2)2C6H3)12 and [U(CpiPr)2] (CpiPr = C5iPr5).13 Interestingly, actinide(II) complexes such as Th,14,15 Np16–18 and Pu19 have been synthetically accessible, most of which are accommodated by Cp-derived ligands.14–17,19 | ||
| Chart 1 Ligand structures of (a) tris(alkyloxide)arene, (b) trans-calix[2]pyrrole[2]benzene, (c) silylcyclopentadiene, and (d) octadentate Schiff-base polypyrrolic macrocycle. | ||
It is worth noting that aforementioned U(II) complexes have some similarity and difference.6–21 Firstly, a low-temperature synthetic route was developed by applying potassium graphite (KC8) to reduce respective U(III) parent. Secondly, it is found that the stability of complex was partially contributed by δ back-bonds between U and Ar/Cp. Thirdly, these two kinds of δ bonds have subtle difference in strength, which may come from the symmetric matching extent of δ[U(5f)] and π*(Ar/Cp).22 Additionally, U(II) complexes show uranium ground-state electronic configuration of 5f3(6d/7s)1 while being ligated by substituted-Cp ligands, in contrast to 5f4 by Ar-derived ones. In brief, it is crucial to explore redox, metal–ligand bonding and electronic properties, which will guide the synthesis of more novel U(II) complexes and even other actinide(II) ones to enrich actinide coordination chemistry.
The redox property is of great importance in manipulating the actinide chemistry of coordination, energy and environment, for it is involved in processing nuclear fuel, spent fuel and nuclear waste as well as remedying environmental contamination that highly radiotoxic actinides create.1–5,23 However, relevant techniques remain greatly challenging. For example, reports about reduction potentials of U(II) complexes are very rare, which may be restricted by experimental difficulties such as safe handling of high radioactivity, sample stability/scarcity and applicable solvent shortage.5,24–27 So far, only two examples were recorded, i.e., [UL1e]/[UL1e]− and [U(CpiPr)2]+/[U(CpiPr)2] showing reduction potentials at −2.50 and −2.35 V versus Fc+/Fc in THF, respectively.13,25 In this regard, theoretical computation becomes appealing for it has been applied in many studies to successfully predict and confirm structural and redox properties of actinide-containing complexes.22,28–34
Ligand is the key to prepare stable actinide(II) complexes and explore their properties. It also plays a significant role in determining electronic structures and bonding. Recently, a versatile trans-calix[2]pyrrole[2]benzene (H2L2, Chart 1)35 has been exploited to fabricate complexes of AnIII and AnVI (An = Th, U and Np)18,36–38 and even a NpII one18 although being unstable chemically. Apparently, H2L2 is able to stabilize various valence and sorts of actinide. Thus, it is desirable to carry out a comprehensive and systematic study involving early and middle actinides in low oxidation states.
In the work, a series of actinide complexes of H2L2 were designed and probed by relativistic density functional theory (DFT). Metals is crossed from cis-uranium (Ac, Th and Pa) to uranium (U) to trans-uranium (Np and Pu), and oxidation states involve +II and +III. Comparison was made with complexes of other three ligands (Chart 1) which have been known to encapsulate low-valent actinide ions. Redox properties were addressed in terms of reduction potentials (E0) and electron affinity (EA). Structural, electron-transfer and An–ligand bonding properties were discussed.
2. Computational details
Herein, we centered on the highest electron-spin state (ESS) of all complexes with the exception of L1 ones. Various geometric isomers were optimized for the complex [UL2] representatively. Along with relevant description, computed various relative energies and geometry parameters were collected in Tables S1–S4 of ESI† and structures of L2 complexes illustrated in Fig. 1.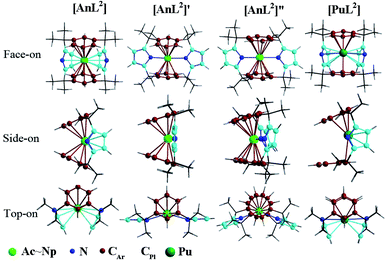 | ||
| Fig. 1 Structures of [AnL2] (An = Ac–Np) and [PuL2] that slightly differs on the side-on view, along with two geometric isomers of [UL2] that are labeled as [UL2]′ and [UL2]′′. | ||
Unless otherwise noted, structures of all complexes were optimized by the Priroda code (version 6.0).39–42 No symmetry constraints were adopted. The scalar relativistic all-electron (AE)43 was used, which came from full Dirac equation with spin–orbit projected out and neglected.44 The Perdew–Burke–Ernzerhof (PBE)45 functional was applied, along with all-electron Gaussian basis sets (labeled as B-I).46 Frequency calculations approved the minimum nature of optimized structure and attained thermodynamic data (zero-point vibrational energy, enthalpy and free energy) at 298.15 K simultaneously. Electron-spin density and Mulliken atomic charge were computed, compared with those of the ADF code.
Later, we computed solvation and spin–orbit coupling (SOC) energies using the ADF code (2014 version).47–49 Electronic structures in solution were described in terms of density of states (DOSs). An integration parameter of 6.0 was applied. We did not re-optimize structures in the ADF calculations, for the ADF-optimized results are comparable to those of Priroda in molecular properties (Tables S5 and S6†) and geometry parameters (Tables S7 and S8†). This also agrees with previous studies.32,50–56 The scalar relativistic zeroth-order regular approximation (ZORA) method,57–60 PBE functional and Slater-type TZP basis sets (labeled as B-II) were used. The conductor-like screening model (COSMO)61,62 was employed to simulate environmental effects of THF, where the dielectric constant of 7.58 and Esurf-type cavity were taken.
To explore An–ligand bonding nature, we carried out the quantum theory of atoms in molecule (QTAIM).63,64 Firstly, calculations with the Gaussian 09 code65 were performed to obtain checkpoint files. We employed PBE functional and combined basis sets (B-III). The quasi-relativistic small-core effective core potentials (SC-ECPs) were used to treat actinide atoms along with corresponding basis sets, and the Pople basis sets of 6-31G(d) for other atoms. Secondly, with the Multiwfn 3.4.1 software,66 we computed QTAIM data and related parameters at the bond critical point (BCP).
3. Results and discussion
3.1 Reduction reactions
According to synthetic route, divalent actinide complexes have been accessible via reducing their trivalent parents at low temperature. To shed light into these processes, we theoretically explored single-electron reduction reactions from [AnL2]+ to [AnL2] (An = Ac–Pu). And then, reduction potentials (E0 in V) were calculated with respect to the reference electrode ferrocenium/ferrocene (Fc+/Fc) in THF in conjunction with following reaction and equations| Reaction: [AnL2]+ + Fc → [AnL2] + Fc+ |
| ΔrG(sol) = ΔrG + ∑Gsol(reagent) | (1) |
| ΔrG(sol–so) = ΔrG + ∑Gsol(reagent) + ∑Gso(reagent) | (2) |
| E0 = −ΔrG/F | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1. Accordingly E0(sol) and E0(sol–so) were computed, showing close values (Table 1). In the work we will focus on E0(sol–so).
485 C mol−1. Accordingly E0(sol) and E0(sol–so) were computed, showing close values (Table 1). In the work we will focus on E0(sol–so).
| Couples | ΔrEa | ΔrE0a | ΔrGa | ΔrG(sol)a | ΔrG(sol–so)a | E0(sol)b | E0(sol–so)b |
|---|---|---|---|---|---|---|---|
| a See their explanation in text.b ΔrG(sol) and ΔrG(sol–so) of the reference electrode Fc+/Fc were calculated to be −5.40 eV. | |||||||
| [AcL2]+/0 | −3.90 | −4.05 | −4.02 | −2.96 | −2.98 | −2.45 | −2.42 |
| [ThL2]+/0 | −4.21 | −4.31 | −4.34 | −3.27 | −3.26 | −2.14 | −2.14 |
| [PaL2]+/0 | −4.44 | −4.52 | −4.50 | −3.44 | −3.47 | −1.96 | −1.93 |
| [UL2]+/0 | −4.54 | −4.62 | −4.61 | −3.53 | −3.50 | −1.87 | −1.90 |
| [NpL2]+/0 | −4.08 | −4.21 | −4.24 | −3.15 | −3.19 | −2.25 | −2.21 |
| [PuL2]+/0 | −4.84 | −4.90 | −4.89 | −3.76 | −3.67 | −1.64 | −1.73 |
The computed E0(sol–so) fall within −2.42 and −1.73 V, showing an overall increasing trend from Ac to Pu in Fig. 2a. The one of [NpL2]+/[NpL2], however, is lower than adjacent U and Pu couples. Consequently, E0 follows the order of Ac < Np < Th < Pa < U < Pu. This implies that the Ac(II) complex may be the most difficult to prepare among these actinides via a route of reducing their parents. So far, divalent Th, U, Np and Pu complexes ligated by substituted cyclopentadienyls have been synthesized by applying the potassium graphite reductant.6,7,14,16,19 And [Np(Cp′′)3]− (Cp′′ = C5H3(SiMe3)2)16 is the last experimentally identified one, which seems to support our computed results. Additionally, −1.90 V E0(sol–so) of [UIIIL2]+/[UIIL2] is larger than experimentally determined values of −2.50 V for [UL1e]/[UL1e]− (ref. 25) and −2.35 V for [U(CpiPr)2]+/[U(CpiPr)2].13 When only considering the E0 value, [UIIL2] would be synthetically accessible using similar approach in previous studies, as well as other actinide(II) complexes.6–19
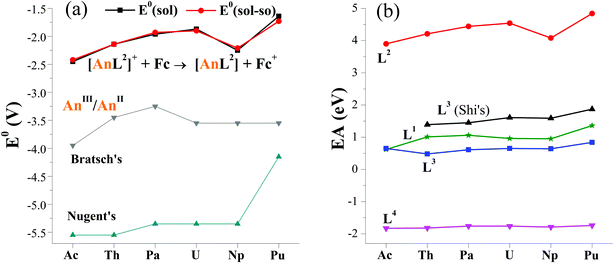 | ||
| Fig. 2 (a) Reduction potentials (E0 in V) of [AnL2]+/[AnL2] (An = Ac–Pu) versus Fc+/Fc in THF, along with previously reported values for AnIII/AnII.26,27 Noting that the solvation energy is included in E0(sol) while additional spin–orbit coupling energy in E0(sol–so). (b) Calculated electron affinity (EA) of actinide complexes with various ligands (Ln, n = 1–4), where those of L3 in THF come from Shi's ref. 31. | ||
As seen in Fig. 2a, the trend obtained in the work is approximately the same as those of previous studies of Bratsch27 and Nugent.26 One can note that these E0 values have a large difference in the magnitude. In general, the order follows ours > Bratsch > Nugent. It is caused by factors like ligand (i.e. coordination and chemical environment), solvent sort and approach. For example, our results came from diarene organic ligand and THF solvent, while others used water–acid solution in that halides were included; these results also differ in approaches, theoretical calculation for ours, thermodynamic prediction in Bratsch work and absorption-based calculation for Nugent study.
Additionally, thermodynamic reaction was calculated to probe the experimentally accessible possibility of actinide(II) complex. Referring to experimental route of U(II) complexes and cyclopentadienyl An(II) ones, the actinide(III) parent complex was reduced by the potassium graphite. In the calculations, a sp2-conjugated arene, formulated as C24H12 was utilized to model the graphite. As seen in Table S9,† the plutonium complexes show the smallest formation reaction free energy (ΔrG(sol)) of −0.15 eV, indicating the easiest production of [PuL2]. In contrast, the formation of [AnL2] is the most difficult because of the largest ΔrG(sol) of 0.65 eV, but it still can be accessible from a thermodynamic perspective. While adding SOC energy, exactly the same trend was obtained for this actinide series of complexes.
3.2 Electron-transfer mechanism
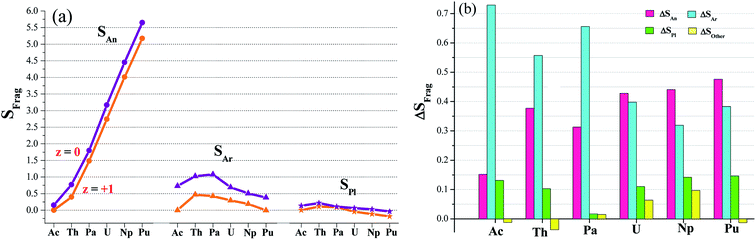
Electron-spin density (S) calculations (Table S5†) found have two types of redox active sites, arenes and metal center. This was visually depicted in Fig. 3a. Furthermore, we plotted in Fig. 3b the spin difference of various fragments (ΔSFrag) while single-electron reduction takes place. It is clear to observe that the reduction mainly occur in Ar fragments and actinide; and other parts (including pyrroles) are almost redox-inactive. The arenes gain the percent of the reduced electron ranging from 31% to 73%, and the metal accounts for 15–48%. Change in pyrroles is relatively small, ΔSPl < 15%. ΔSother can be negligible due to its absolute value less than 10%. So we proposed an arene and actinide mixed mechanism for the single-electron reduction reaction. Moreover, the arene moieties are predominant in complexes of Ac, Th and Pa; in contrast, it diverts to the metal-based reduction for U, Np and Pu ones.Computed charge of actinide in [AnL2] ranges from 1.76 to 2.00, comparable to the supposed +II oxidation state. Although metal charge shows 0.04–0.16 increase in [AnL2]+, apparently those within 1.92 and 2.10 still have some deviation from the expected +III metal valence. Charges computed by the ADF code are greatly different, taking metal for instance, 0.36–0.97 for [AnL2] and 0.053–0.90 for [AnL2]+, Table S6.† However, electron spin holds close value for Priroda and ADF code, suggesting that it is a more reliable and reasonable indicator for the electron-transfer mechanism.
3.3 Factors of affecting reduction
To analyze factors to determine E0, we firstly plotted data of various reduction energies of [AnL2]+ + e = [AnL2] in Fig. S1.† For convenient comparison, we used their negative values. Exactly the same trend is found. So it is concluded that the inclusion of solvation, spin–orbit coupling, entropy and zero-point vibration energies has almost no effect. This can simplify our computational procedures by only calculating gas-phase reaction total energy ΔrE. One can note that its opposite value (−ΔrE) is right the commonly-used important indicator for redox reaction, i.e., electron affinity (EA), which is equal to the energy of [AnL2]+ subtracting [AnL2] at their respective optimized geometry.To rule out the effect of different computational codes on redox property, the ADF code was used to optimize complexes of [AnL2]z (An = Ac–Pu; z = 0 and +1). The computed EA is increasing from Ac to U, then decreases at Np and increases at Pu. This obviously gives the same trend as those calculated the Priroda code.
In terms of EA and sticking to the Priroda code, we will compare effects of different ligands (Chart 1). Referring to experimentally known ligands that suit for actinide(II) ion, arene (L1) and cyclopentadiene (L3) ligands were chosen. Relative to these organic ligands, we also selected a “so-called” inorganic ligand, Schiff-base octadentate polypyrrolic macrocycle (L4). It is very versatile to encapsulate one UIV ion experimentally,67 and to render actinide of various sorts (U and Np), valences (III–VI) and number (one and two).3,68 As shown in Fig. 2b, the order of computed EA values is L2 > L3–L1 > L4, where those of L3 come from Wu and Shi's work.31 Interestingly, it right follows their charges from −2 to −3 to −4. They may have some correlation. Certainly, the An–ligand bond nature and strength are also different from ligand to ligand, where L2, L3–L1 and L4 feature bonds of An–Ar/N, An–Cp–An–Ar/O and An–N, respectively. Notably, all EA values of various ligands show similar trend while changing metal center from Ac to Pu.
3.4 Structural and bonding properties
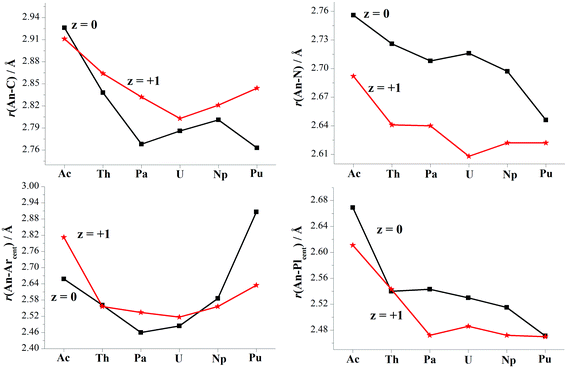
Optimizations show similar general structures for [AnL2]z (An = Ac–Pu; z = 0 and +1) in Fig. 1. Computed angles of C(t)–An–C(t) (α1) and N–An–N (α2) range from 168° to 180° (Table S7†), indicating that the L2 renders the metal almost at the center. The angles of metal and centroids of Ar or Pl (β) are close to 120°. [PuL2] is a little different from the side-on view, having much smaller interplanar angle between two pyrrolides (γ1 = 20°). Being analogous to [UL2]+, complexes [UL2(BH4)] and [UL2(I)], have been experimentally synthesized and structurally characterized.36,37 As shown in Tables S7 and S8,† optimized geometry parameters are comparable to experimental ones, which indicate that the theoretical approach used is reliable for current study. Due to the omission of counter anion, the uranium of [UL2]+ would favor to be situated at the center of the ligand over [UL2(BH4)] and [UL2(I)]. This consequently causes difference for some geometry parameters such as U–N distance and N–An–N (α2) angle.Reduction from [AnL2]+ to [AnL2] results in some regular changes, Fig. 4 and Table S8.† One can note that An–N distance is lengthening, while An–C is shortening except for Ac complexes. Almost the same trend is found for An–Plcent as An–N. However, it is not the case for An–Arcent distance, where the contraction is found for Ac, Pa and U, and the elongation for Th, Np and Pu. The largest difference for Pu complex is due to change of orientation of one arene of [PuL2] (side-on view of Fig. 1). The change of An–Arcent distance is caused by two effects. One is the formation of δ(An–Ar) bond(s), which would result in shortening. The other is ionic radius of metal in different valence; An(II) is supposed to be bigger than An(III), responsible for the elongation upon reduction. Obviously, the two opposite effects, to a different extent, contribute to above changes of An–Arcent.
Along the actinide change (Ac–Pu), we will focus on the difference of distance between An and ligand induced by the reduction, i.e. Δr(An–ligand), aiming to connect with the redox behavior. One can observe that the trend of Δr(An–Arcent) from Ac to Pu is similar to that of redox potential (Fig. 2a), but the subtle difference is that the former has those of Pa–Np at the lower end. This similarity is consistent with the An/Ar mixed reduction mechanism in that the reducing electron is mainly localizing around area of metal and arenes. A good connection is found for the negative values of Δr(An–C), while no same manner for Δr(An–N/Plcent). So far, [UCp′]− and [AnCp′′]− (An = Th, U, Np and Pu) were structurally characterized.6,7,14,16,19 Because of lack of the number of trivalent complexes (only [UCp′] and [ThCp′′]), it is not conclusive for the changing trend of Δr(An–Cpcent).
Previous studies indicate that QTAIM is reliable for classifying chemical bond involving actinide metal.18,28,69–73 Here, we will use this density-based approach to analyze An–ligand bonding. The computed parameters at the An–C BCP for L2 complexes are presented in Table 2. Values of ρ(r) < 0.05, 0 < ∇2ρ(r) < 0.11 and H(r) < 0 indicate a dative or electron-transfer bond. Associated with electron-spin density presented in Fig. 3a and Table S5,† An–C is attributed to a dative bond for [PuL2]+ and an electron-transfer one for others. The An–C bond is a weak single bond, evidenced by δ(An, C) (denoted as bond order) that ranges from to 0.14–0.30 and Eint (kind of bond energy) from −0.28 to −0.61 eV. Relative to those of respective [AnL2]+, values of ρ(r)/H(r)/δ(An, C)/Eint (absolute values) of [AnL2] increase, which agrees with the shortening of An–C distances upon the reduction. These all indicate that the reduction strengthens the An–C bonding, consistent with the An/Ar mixed reduction mechanism again. Regarding changes of QTAIM data along the actinide series (Ac–Pu), we do observe similar trend to that of E0 in Fig. 2a. For example, the difference of electron density ρ(r) between [AnL2] and [AnL2]+ was computed to ascend from Ac to U, descend at Np and then ascend at Pu.
| Complexes | ρ(r) | ∇2ρ(r) | H(r)b | V(r)a | G(r)b | δ | Eintc |
|---|---|---|---|---|---|---|---|
| a QTAIM data (in au) include electron density ρ(r), Laplacian density ∇2ρ(r) and energy density H(r).b H(r) is the sum of potential V(r) and kinetic G(r) energy density.c The interaction energy (in eV) is calculated from Eint = −0.5 × V(r). | |||||||
| [AcL2] | 0.0287 | 0.0762 | −0.0010 | −0.0212 | 0.0199 | 0.1628 | −0.29 |
| [ThL2] | 0.0342 | 0.0858 | −0.0027 | −0.0268 | 0.0241 | 0.2085 | −0.36 |
| [PaL2] | 0.0356 | 0.0999 | −0.0027 | −0.0304 | 0.0277 | 0.2526 | −0.41 |
| [UL2] | 0.0373 | 0.1015 | −0.0039 | −0.0332 | 0.0293 | 0.2697 | −0.45 |
| [NpL2] | 0.0319 | 0.0960 | −0.0013 | −0.0266 | 0.0253 | 0.2219 | −0.36 |
| [PuL2] | 0.0493 | 0.1072 | −0.0089 | −0.0446 | 0.0357 | 0.2944 | −0.61 |
| [AcL2]+ | 0.0298 | 0.0738 | −0.0012 | −0.0209 | 0.0197 | 0.1400 | −0.28 |
| [ThL2]+ | 0.0330 | 0.0775 | −0.0024 | −0.0243 | 0.0218 | 0.2029 | −0.33 |
| [PaL2]+ | 0.0334 | 0.0934 | −0.0020 | −0.0273 | 0.0253 | 0.1752 | −0.37 |
| [UL2]+ | 0.0359 | 0.0968 | −0.0033 | −0.0308 | 0.0275 | 0.2280 | −0.42 |
| [NpL2]+ | 0.0315 | 0.0562 | −0.0014 | −0.0253 | 0.0239 | 0.1879 | −0.34 |
| [PuL2]+ | 0.0301 | 0.0860 | −0.0011 | −0.0236 | 0.0225 | 0.1742 | −0.32 |
We plotted density of states (DOSs) of α-spin orbitals (Fig. 5, and S2–S4). [AnL2] (An = U, Np and Pu) have three types of high-lying occupied orbitals, An(5f), δ(An–Ar) and π(An–Pl/Ar), but ones of Ac, Th and Pa only have the second two. As seen in Fig. 5 (DOSs for each fragment), there is a large separation between the second type and the third. One can see the energetic separation becomes smaller from Ac to Pu, agreeing with more core-like An(5f) in Pu than in Pa–Np. Comparatively, there is considerable 6d participation in δ(An–Ar) while An = Ac and Th. Focusing on HOMO of each [AnL2] that is supposed to populate the reducing electron, the energetic change seems to correlate with the trend of E0. Metal contribution to HOMO increases from Th to Pu, while arene participation decreases; HOMOs of [NpL2] and [PuL2] are almost metal-dominated. Frontier orbitals of [AnL2]+ show similar character to their reduced products, apart from the Ac complex that is a closed-shell system.
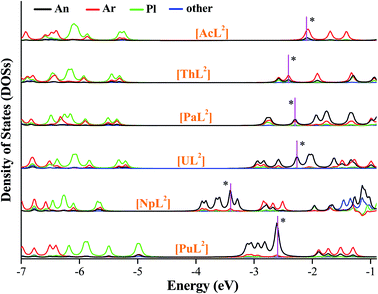 | ||
| Fig. 5 Density of states of each fragment of [AnL2] (An = Ac–Pu), where the α-spin orbitals are plotted and HOMO of each complex is marked with a star. | ||
4. Conclusions
To shed light into the prevailing route to prepare divalent actinide complex via reducing its trivalent parent, low-valent actinide complexes [AnL2]z (An = Ac–Pu; z = 0 and +1) as well as Ln (n = 1, 3 and 4) ligated ones have been computationally investigated. Some important points have been come to.Computed reduction potentials of [AnL2]+/[AnL2] range from −2.45 to −1.64 V versus Fc+/Fc in THF while including solvation and spin–orbit coupling effects. Considering experimentally determined values of −2.50 V for [UL1e]/[UL1e]− and −2.35 V for [U(CpiPr)2]+/[U(CpiPr)2] and commonly-used reactant (potassium graphite), our L2-accommodated An(II) complex would be synthetically accessible by reducing respective An(III) parent.
It is found that the electron-spin density mainly resides in parts of arene and metal of [AnL2]z. The single-electron reduction is proposed as an arene and actinide mixed mechanism. The arene moieties dominate in the early-actinide complexes (Ac–Pa), while the metal-based contribution becomes more significant in uranium and trans-uranium ones (U–Pu).
The E0 values of [AnL2]+/[AnL2] show an overall increasing trend from Ac to Pu but a break point at Np whose E0 is lower than adjacent U and Pu. This trend well reproduces previously reported E0 of AnIII/AnII ions. In terms of electron affinity (EA), almost the same change is found for actinide complexes of Ln (n = 1–4). Geometry parameters, analyses of An–C bonds and electronic structures of L2 complexes further corroborate the E0 trend.
In summary, the study is expected to provide an in-depth understanding of low-valent metallocene of actinide, particularly for redox and actinide–ligand bonding properties. Due to their importance in organometallic chemistry as well as energy/environment area, the fundamental concepts such oxidation state, bonding and reactivity would help to efficiently process nuclear fuel, spent fuel and nuclear waste and remedy environmental contamination.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work is supported by the Natural Science Foundations of China (21671060) and Heilongjiang Province (LH2019B029). The Heilongjiang Touyan Innovation Team Program is appreciated. The author (QJP) is grateful to Dr Dimitri Laikov for providing the Priroda code.References
- B. E. Cowie, J. M. Purkis, J. Austin, J. B. Love and P. L. Arnold, Chem. Rev., 2019, 119, 10595–10637 CrossRef CAS PubMed.
- D. Schaedle and R. Anwander, Chem. Soc. Rev., 2019, 48, 5752–5805 RSC.
- P. L. Arnold, M. S. Dutkiewicz and O. Walter, Chem. Rev., 2017, 117, 11460–11475 CrossRef CAS PubMed.
- D. Wang, W. F. van Gunsteren and Z. Chai, Chem. Soc. Rev., 2012, 41, 5836–5865 RSC.
- W.-Q. Shi, L.-Y. Yuan, C.-Z. Wang, L. Wang, L. Mei, C.-L. Xiao, L. Zhang, Z.-J. Li, Y.-L. Zhao and Z.-F. Chai, Adv. Mater., 2014, 26, 7807–7848 CrossRef CAS PubMed.
- M. R. MacDonald, M. E. Fieser, J. E. Bates, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2013, 135, 13310–13313 CrossRef CAS PubMed.
- C. J. Windorff, M. R. MacDonald, K. R. Meihaus, J. W. Ziller, J. R. Long and W. J. Evans, Chem.–Eur. J., 2016, 22, 772–782 CrossRef CAS PubMed.
- S. A. Moehring and W. J. Evans, Chem.–Eur. J., 2020, 26, 1530–1534 CrossRef CAS PubMed.
- D. N. Huh, J. W. Ziller and W. J. Evans, Inorg. Chem., 2018, 57, 11809–11814 CrossRef CAS PubMed.
- A. J. Ryan, M. A. Angadol, J. W. Ziller and W. J. Evans, Chem. Commun., 2019, 55, 2325–2327 RSC.
- H. S. La Pierre, A. Scheurer, F. W. Heinemann, W. Hieringer and K. Meyer, Angew. Chem., Int. Ed., 2014, 53, 7158–7162 CrossRef CAS PubMed.
- B. S. Billow, B. N. Livesay, C. C. Mokhtarzadeh, J. McCracken, M. P. Shores, J. M. Boncella and A. L. Odom, J. Am. Chem. Soc., 2018, 140, 17369–17373 CrossRef CAS PubMed.
- F.-S. Guo, N. Tsoureas, G.-Z. Huang, M.-L. Tong, A. Mansikkamaeki and R. A. Layfield, Angew. Chem., Int. Ed., 2020, 59, 2299–2303 CrossRef CAS PubMed.
- R. R. Langeslay, M. E. Fieser, J. W. Ziller, F. Furche and W. J. Evans, Chem. Sci., 2015, 6, 517–521 RSC.
- R. R. Langeslay, M. E. Fieser, J. W. Ziller, F. Furche and W. J. Evans, J. Am. Chem. Soc., 2016, 138, 4036–4045 CrossRef CAS PubMed.
- J. Su, C. J. Windorff, E. R. Batista, W. J. Evans, A. J. Gaunt, M. T. Janicke, S. A. Kozimor, B. L. Scott, D. H. Woen and P. Yang, J. Am. Chem. Soc., 2018, 140, 7425–7428 CrossRef CAS PubMed.
- M. S. Dutkiewicz, C. Apostolidis, O. Walter and P. L. Arnold, Chem. Sci., 2017, 8, 2553–2561 RSC.
- M. S. Dutkiewicz, J. H. Farnaby, C. Apostolidis, E. Colineau, O. Walter, N. Magnani, M. G. Gardiner, J. B. Love, N. Kaltsoyannis, R. Caciuffo and P. L. Arnold, Nat. Chem., 2016, 8, 797–802 CrossRef CAS PubMed.
- C. J. Windorff, G. P. Chen, J. N. Cross, W. J. Evans, F. Furche, A. J. Gaunt, M. T. Janicke, S. A. Kozimor and B. L. Scott, J. Am. Chem. Soc., 2017, 139, 3970–3973 CrossRef CAS PubMed.
- W. J. Evans, Organometallics, 2016, 35, 3088–3100 CrossRef CAS.
- G. Meyer, Angew. Chem., Int. Ed., 2014, 53, 3550–3551 CrossRef CAS PubMed.
- H.-B. Zhao, M. Zheng, G. Schreckenbach and Q.-J. Pan, Dalton Trans., 2018, 47, 2148–2151 RSC.
- Y. Sun, Z.-Y. Wu, X. Wang, C. Ding, W. Cheng, S.-H. Yu and X. Wang, Environ. Sci. Technol., 2019, 53, 11613 CrossRef CAS PubMed.
- W. J. Evans and S. A. Kozimor, Coord. Chem. Rev., 2006, 250, 911–935 CrossRef CAS.
- H. S. La Pierre, H. Kameo, D. P. Halter, F. W. Heinemann and K. Meyer, Angew. Chem., Int. Ed., 2014, 53, 7154–7157 CrossRef CAS PubMed.
- L. J. Nugent, R. D. Baybarz, J. L. Burnett and J. L. Ryan, J. Phys. Chem., 1973, 77, 1528–1539 CrossRef CAS.
- S. G. Bratsch and J. J. Lagowski, J. Phys. Chem., 1986, 90, 307–312 CrossRef CAS.
- N. Kaltsoyannis, Inorg. Chem., 2013, 52, 3407–3413 CrossRef CAS PubMed.
- Y.-L. Wang, H.-S. Hu, W.-L. Li, F. Wei and J. Li, J. Am. Chem. Soc., 2016, 138, 1126–1129 CrossRef CAS PubMed.
- Y.-J. Zhang, J.-H. Lan, L. Wang, Q.-Y. Wu, C.-Z. Wang, T. Bo, Z.-F. Chai and W.-Q. Shi, J. Hazard. Mater., 2016, 308, 402–410 CrossRef CAS PubMed.
- Q. Y. Wu, J. H. Lan, C. Z. Wang, Z. P. Cheng, Z. F. Chai, J. K. Gibson and W. Q. Shi, Dalton Trans., 2016, 45, 3102–3110 RSC.
- H.-S. Hu, F. Wei, X. Wang, L. Andrews and J. Li, J. Am. Chem. Soc., 2014, 136, 1427–1437 CrossRef CAS PubMed.
- Z. Bao, H.-B. Zhao, N. Qu, G. Schreckenbach and Q.-J. Pan, Dalton Trans., 2016, 45, 15970–15982 RSC.
- J.-N. Tian, M. Zheng, L. Li, G. Schreckenbach, Y.-R. Guo and Q.-J. Pan, New J. Chem., 2019, 43, 1469–1477 RSC.
- J. L. Sessler, W. S. Cho, V. Lynch and V. Kral, Chem.–Eur. J., 2002, 8, 1134–1143 CrossRef CAS.
- P. L. Arnold, J. H. Farnaby, R. C. White, N. Kaltsoyannis, M. G. Gardiner and J. B. Love, Chem. Sci., 2014, 5, 756–765 RSC.
- P. L. Arnold, C. J. Stevens, J. H. Farnaby, M. G. Gardiner, G. S. Nichol and J. B. Love, J. Am. Chem. Soc., 2014, 136, 10218–10221 CrossRef CAS PubMed.
- P. L. Arnold, J. H. Farnaby, M. G. Gardiner and J. B. Love, Organometallics, 2015, 34, 2114–2117 CrossRef CAS.
- D. N. Laikov and Y. A. Ustynyuk, Russ. Chem. Bull., 2005, 54, 820–826 CrossRef CAS.
- D. N. Laikov, Chem. Phys. Lett., 1997, 281, 151–156 CrossRef CAS.
- D. N. Laikov, Chem. Phys. Lett., 2005, 416, 116–120 CrossRef CAS.
- D. N. Laikov, J. Comput. Chem., 2007, 28, 698–702 CrossRef CAS PubMed.
- D. N. Laikov, An Implementation of the Scalar Relativistic Density Functional Theory for Molecular Calculations with Gaussian Basis Sets, DFT2000 Conference, Menton, France, 2000 Search PubMed.
- K. G. Dyall, J. Chem. Phys., 1994, 100, 2118–2127 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- D. N. Laikov, PhD dissertation, Moscow State University, 2000.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- E. J. Baerends, T. Ziegler, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, L. Deng, R. M. Dickson, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, C. Fonseca Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, J. W. Kaminski, G. van Kesse, F. Kootstra, A. Kovalenko, M. V. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, J. I. Rodríguez, P. Ros, P. R. T. Schipper, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Swart, D. Swerhone, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF; SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2014 Search PubMed.
- G. A. Shamov and G. Schreckenbach, J. Am. Chem. Soc., 2008, 130, 13735–13744 CrossRef CAS PubMed.
- G. A. Shamov, G. Schreckenbach, R. L. Martin and P. J. Hay, Inorg. Chem., 2008, 47, 1465–1475 CrossRef CAS PubMed.
- Q. J. Pan and G. Schreckenbach, Inorg. Chem., 2010, 49, 6509–6517 CrossRef CAS PubMed.
- G. A. Shamov, G. Schreckenbach and T. N. Vo, Chem.–Eur. J., 2007, 13, 4932–4947 CrossRef CAS PubMed.
- Y.-X. Zhong, Y.-R. Guo and Q.-J. Pan, Chem. Phys. Lett., 2016, 646, 75–80 CrossRef CAS.
- J. P. Dognon, C. Clavaguéra and P. Pyykkö, J. Am. Chem. Soc., 2009, 131, 238–243 CrossRef CAS PubMed.
- P. Tecmer, A. S. P. Gomes, U. Ekström and L. Visscher, Phys. Chem. Chem. Phys., 2011, 13, 6249–6259 RSC.
- E. van Lenthe, A. Ehlers and E. J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610 CrossRef CAS.
- E. van Lenthe, J. Snijders and E. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396–408 Search PubMed.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, OUP, Oxford, 1990 Search PubMed.
- C. F. Matta and R. J. Boyd, In The Quantum Theory of Atoms in Molecules, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2007 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. P. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- P. L. Arnold, N. A. Potter, C. D. Carmichael, A. M. Z. Slawin, P. Roussel and J. B. Love, Chem. Commun., 2010, 46, 1833–1835 RSC.
- B. E. Cowie, J. M. Purkis, J. Austin, J. B. Love and P. L. Arnold, Chem. Rev., 2019, 119, 10595–10637 CrossRef CAS PubMed.
- R. F. W. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- P. L. Arnold, A. Prescimone, J. H. Farnaby, S. M. Mansell, S. Parsons and N. Kaltsoyannis, Angew. Chem., Int. Ed., 2015, 54, 6735–6739 CrossRef CAS PubMed.
- N. Kaltsoyannis, Dalton Trans., 2016, 45, 3158–3162 RSC.
- L. Tian, C. Zhang, N. Qu, Y. Bi, H. Zhang and Q. Pan, Chem. J. Chin. Univ., 2018, 39, 749–757 CAS.
- I. Kirker and N. Kaltsoyannis, Dalton Trans., 2011, 40, 124–131 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Plots of various energies of reduction reaction (Fig. S1) and diagrams of density of states (S2–S4). Tables of relative energies in various electron-spin states and geometric isomers (Tables S1–S3), geometry parameters (S4, S7 and S8), and spin and charges (S5 and S6). See DOI: 10.1039/d0ra05365a |
| ‡ The two authors contributed to the work equally. |
| This journal is © The Royal Society of Chemistry 2020 |