Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A coumarin derivative-Cu2+ complex-based fluorescent chemosensor for detection of biothiols†
Nguyen Khoa Hien‡
 a,
Mai Van Bay‡bc,
Phan Diem Trana,
Nguyen Tan Khanhd,
Nguyen Dinh Luyenb,
Quan V. Vo
a,
Mai Van Bay‡bc,
Phan Diem Trana,
Nguyen Tan Khanhd,
Nguyen Dinh Luyenb,
Quan V. Vo e,
Dang Ung Vanf,
Pham Cam Nam
e,
Dang Ung Vanf,
Pham Cam Nam *g and
Duong Tuan Quang
*g and
Duong Tuan Quang *b
*b
aMientrung Institute for Scientific Research, Vietnam Academy of Science and Technology, Hue 530000, Vietnam
bUniversity of Education, Hue University, Hue 530000, Vietnam. E-mail: dtquang@hueuni.edu.vn
cThe University of Danang −University of Science and Education, Danang 550000, Vietnam
dFaculty of Pharmacy, Hue University of Medicine and Pharmacy, Hue 530000, Vietnam
eFaculty of Chemical Technology-Environment, The University of Danang−University of Technology and Education, 48 Cao Thang, Danang 550000, Vietnam
fHoa Binh University, Hanoi 100000, Vietnam
gThe University of Danang −University of Science and Technology, Danang 550000, Vietnam. E-mail: pcnam@dut.udn.vn
First published on 1st October 2020
Abstract
Herein, a novel fluorescent sensor has been developed for the detection of biothiols based on theoretical calculations of the stability constant of the complex between a Cu2+ ion and (E)-3-((2-(benzo[d]thiazol-2-yl)hydrazono)methyl)-7-(diethylamino) coumarin (BDC) as a fluorescent ligand. In this study, on the basis of density functional theory method, the Gibbs free energy of ligand-exchange reaction and the solvation model were carried out using thermodynamic cycles. The obtained results are in good agreement with the experimental data. The BDC–Cu2+ complex can be used as a fluorescent sensor for the detection of biothiols in the presence of non-thiol containing amino acids, with a detection limit for cysteine at 0.3 μM. Moreover, theoretical calculations of excited states were used to elucidate variations in the fluorescence properties. The computed results show that the excited doublet states D2 and D1 are dark doublet states, which quench the fluorescence of the complex.
1. Introduction
Cysteine (Cys), homocysteine (Hcy), and glutathione (GSH) are thiol biomolecules that play an important role in human biological processes. Some diseases are believed to be related to abnormalities in the concentrations of these compounds in biological systems. A low level of Cys may cause a decline in the immune system, resulting in diseases such as infections, cancer, Parkinson's, Alzheimer's, retarded growth, liver damage, and skin lesions.1–4 A high level of Hcy is believed to be associated with heart disease, thromboembolic disease, stroke, atherosclerosis, renal and thyroid dysfunction, psoriasis, diabetes, and cancer.5,6 Disturbances in GSH homeostasis are associated with some diseases including immune diseases, inflammatory, cancer, metabolic diseases, diseases of aging, cystic fibrosis, cardiovascular, and neurodegenerative diseases.1,7 As a result, the development of selective and sensitive detection methods for biothiols has been attracting the attention of scientists. In particular, analytical methods based on fluorescence technique have been widely developed due to their outstanding advantages.8,9 This technique, in particular, can be used to detect biothiols in living cells.10,11 A number of fluorescent sensors have been reported based on various interactions with biothiols, such as Michael addition,12,13 addition-cyclization with acrylates or aldehydes,14,15 cleavage reactions of sulfonamide, sulfonate ester, disulfides,16–18 substitution reactions,19 and disulfide exchange reactions.20 Recently, sensors for biothiols have been widely synthesized and reported; their working mechanism is based on the reactions between biothiols and complexes of fluorescent ligands with metal ions.21,22 This approach has opened a new research direction taking advantage of complexes between fluorescent sensors and metal ions towards the detection of biothiols. These works become more convenient if the stability constants of complexes can be determined. Recently, some theoretical computational models for determining the stability constants of complexes have been proposed with the aim of replacing traditional experimental methods.23–25 However, the accuracy of these models needs to be verified before their application. This problem can be effectively solved by combining theoretical calculations and empirical investigations to determine the stability constant of complexes.In the present study, a complex between a Cu2+ ion and a fluorescent ligand is reported as a novel chemosensor for the detection of biothiols based on complex exchange reactions. The stability constant of the complex, also known as the complexation equilibrium constant in aqueous solutions, was calculated using the Gibbs free energy of the ligand-exchange reaction determined by a solvation model based on density (SMD), a density functional theory (DFT) method, and thermodynamic cycles.26,27 The calculated results are in good agreement with the experimental data obtained by a nonlinear curve-fitting method.28,29 From the value of the stability constant, the applicability of the complex as a fluorescent sensor for the detection of biothiols based on the complex exchange reaction was predicted. This was further confirmed by the experimental data obtained by applying this complex as a fluorescent sensor. In addition, herein, theoretical calculations of the excited states were used to explain the fluorescence properties of the substances.
2. Materials and methods
2.1 Instruments
The Shimadzu RF-5301 spectrofluorophotometer, Shimadzu UV-1800 UV-Vis spectrophotometer, Varian Unity NMR instruments (200 MHz), and electrospray ionization mass spectrometer (ESI MS) were used to obtain the fluorescence spectra, UV-Vis absorption spectra, NMR spectra, and MS spectra, respectively.2.2 Reagents
All chemicals were purchased from Aldrich and used directly without further purification. In particular, 4-(diethylamino)salicylaldehyde, 2-hydrazinobenzothiazole, diethyl malonate, and triethylamine were synthesis grade reagents. Cysteine, glutathione, homocysteine, alanine, aspartic acid, arginine, glycine, glutamic acid, isoleucine, leucine, lysine, methionine, threonine, serine, tyrosine, tryptophan, valine, histidine, HEPES, acetic acid, HCl, NaOH, POCl3, and nitrate salts of K+, Ca2+, Na+, Mg2+, Zn2+, Fe3+, Ni2+, Pb2+, Hg2+, Co2+, Cd2+, and Cu2+ were analytical-grade reagents.All solvents were purchased from Merck. Ethanol was HPLC-grade without fluorescent impurities and used without further purification. DMF was also HPLC-grade; however, it was re-distilled before use. H2O was two times distilled water.
2.3 Computational methodology
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β), is calculated by the Gibbs free energies of ligand-exchange reactions determined using thermodynamic cycles, the DFT theory method, and the SMD solvent model (Scheme 1).23–27 Accordingly, the complexation equilibrium constant in aqueous solutions (log
β), is calculated by the Gibbs free energies of ligand-exchange reactions determined using thermodynamic cycles, the DFT theory method, and the SMD solvent model (Scheme 1).23–27 Accordingly, the complexation equilibrium constant in aqueous solutions (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) is calculated by the following equation:
β) is calculated by the following equation:
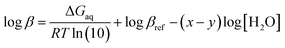 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βref is the experimental equilibrium constant in the aqueous solution of [CuLref(H2O)2]2+, which was used as a reference complex for calculation. ΔGaq is the Gibbs free energy of the ligand-exchange reaction in the aqueous solution, which was determined by Scheme 1 and calculated using eqn (2):
βref is the experimental equilibrium constant in the aqueous solution of [CuLref(H2O)2]2+, which was used as a reference complex for calculation. ΔGaq is the Gibbs free energy of the ligand-exchange reaction in the aqueous solution, which was determined by Scheme 1 and calculated using eqn (2): | ΔGaq = ΔGg + ΔΔGsolv | (2) |
| ΔGg = ∑(Δ0 + Gcorr)products − ∑(Δ0 + Gcorr)reactants | (3) |
| ΔΔGsolv = (x − y)ΔGsolv(H2O2)g + ΔGsolv([CuL(H2O)y]g2+) + ΔGsolv(Lref)g − ΔGsolv(L)g −ΔGsolv([CuLref(H2O)x]g2+) | (4) |
| Cu2+ + L = [CuL]2+ | (5) |
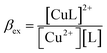 | (6) |
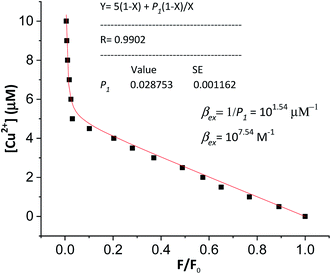
According to this method, the experimental complexation equilibrium constant (βex) is detected by the nonlinear curve-fitting method based on the relationship between the two quantities y = CM and x = F/F0, as shown below (see details in the ESI†):
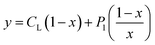 | (7) |
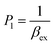 | (8) |
CM is the total concentration of the Cu2+ ions added to the solution, F0 is the fluorescence intensity of the free L solution (concentration of L is CL) at the time when the concentration of Cu2+ ions was zero, and F is the fluorescence intensity of the L solution at the time when the concentration of Cu2+ ions was CM.
3. Results and discussion
3.1 Characterization of the fluorescent ligand and its complex with a metal ion
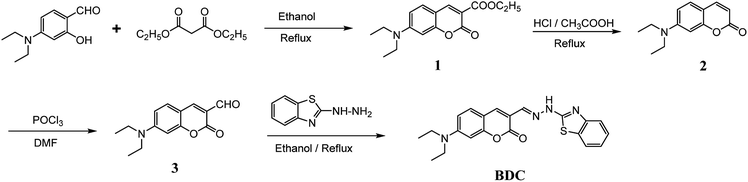
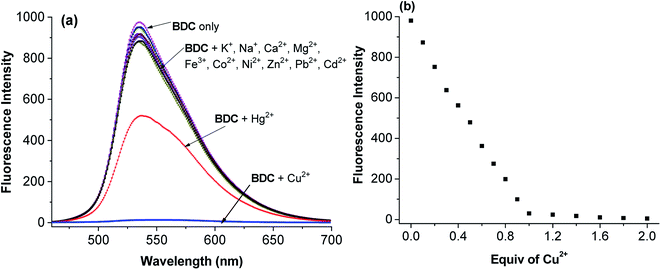
(E)-3-((2-(Benzo[d]thiazol-2-yl)hydrazono)methyl)-7-(diethylamino) coumarin (BDC) was synthesized in about 30% overall yield using 4-(diethylamino)salicylaldehyde via the four steps shown in Fig. 1. The structural characteristics of BDC were confirmed by the 1H NMR, 13C NMR, and mass spectra (ESI†).The experimental results show that the free ligand BDC is a fluorescent compound. It exhibits a characteristic emission band peaked at 536 nm, with a fluorescence quantum yield (Φ) of 0.11 calculated using fluorescein in 0.1 N NaOH (Φ = 0.85) as a ref. 50. When 1 equivalent of Cu2+ was added to the BDC solution, the fluorescence intensity of the solution was almost completely quenched, over 95%. However, the fluorescence intensity of the BDC solution was quenched only about 40% when 1 equivalent of Hg2+ was added. On the other hand, the addition of 1 equivalent of other metal ions, i.e. K+, Ca2+, Na+, Mg2+, Zn2+, Fe3+, Ni2+, Pb2+, Co2+, and Cd2+ ions, hardly changed the fluorescence spectra of the BDC solution (Fig. 2a). The fluorescence titration spectra of BDC with the gradual addition of Cu2+ ions, as shown in Fig. 2b, indicated that the reaction between BDC and Cu2+ occurred in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry. In another experiment, when 1 equivalent of EDTA was added to the solution obtained after adding 1 equivalent of Cu2+ to the BDC solution, the fluorescence intensity was almost restored to the original fluorescence intensity of the free ligand BDC. These results indicated that the reaction between Cu2+ ions and BDC was a reversible reaction and led to the formation of a complex with a 1
1 stoichiometry. In another experiment, when 1 equivalent of EDTA was added to the solution obtained after adding 1 equivalent of Cu2+ to the BDC solution, the fluorescence intensity was almost restored to the original fluorescence intensity of the free ligand BDC. These results indicated that the reaction between Cu2+ ions and BDC was a reversible reaction and led to the formation of a complex with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry.
1 stoichiometry.
The optimization of the geometries of BDC and its 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with Cu2+ was performed using the PBE0 functional with the 6-31+G(d) basis set. The calculated results are presented in Fig. 3 and 4 and Tables S1–S7.†
1 complex with Cu2+ was performed using the PBE0 functional with the 6-31+G(d) basis set. The calculated results are presented in Fig. 3 and 4 and Tables S1–S7.†
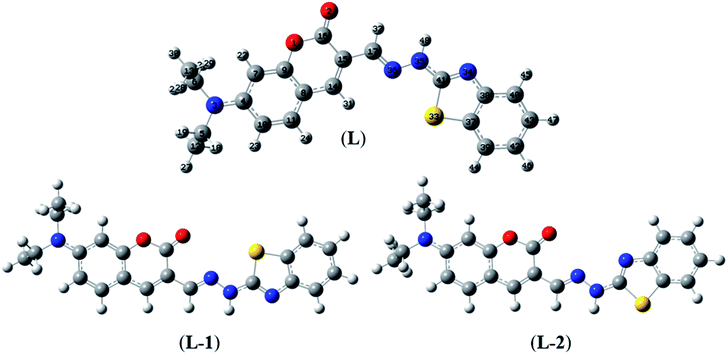
Herein, three optimized geometries of BDC were defined and denoted as L, L-1, and L-2. In each of these geometries, most atoms are in the same plane except for the atoms of the ethylamino groups. In the L geometry, the configuration of the two chain bonds C16–C15–C17–N36 and N36–N35–C41–N34 is similar to trans–trans configuration. Moreover, in the L-1 geometry, the configuration of these two chain bonds is similar to cis–trans configuration. In the L-2 geometry, the configuration of these two chain bonds is similar to cis–cis configuration. The calculated results show that L is the most energetically favorable geometry. Consequently, the L geometry was used to define the configuration of the complex as well as calculate the Gibbs free energy of the ligand-exchange reaction in the aqueous solution.
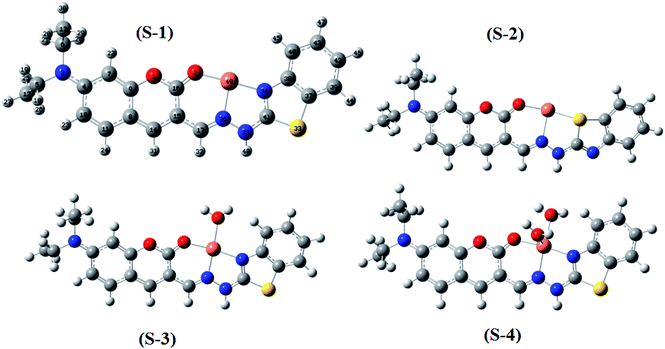
Moreover, four optimized geometries of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes between L and Cu2+ ion were defined and denoted as S-1, S-2, S-3, and S-4. The molecular formulas of the S-1, S-2, S-3, and S-4 geometries are [Cu(L)]2+, [Cu(L)]2+, [Cu(L)(H2O)]2+, and [Cu(L)(H2O)2]2+, respectively. The calculated results show that the reactions for the formation of S-1, S-2, S-3, and S-4 geometries are energetically favorable (Table S8†).
1 complexes between L and Cu2+ ion were defined and denoted as S-1, S-2, S-3, and S-4. The molecular formulas of the S-1, S-2, S-3, and S-4 geometries are [Cu(L)]2+, [Cu(L)]2+, [Cu(L)(H2O)]2+, and [Cu(L)(H2O)2]2+, respectively. The calculated results show that the reactions for the formation of S-1, S-2, S-3, and S-4 geometries are energetically favorable (Table S8†).
The molecular structures of the S-1, S-2, S-3, and S-4 geometries are presented in Table S9,† including bond lengths, bond angles, and dihedral bond angles, and the coordination numbers of the S-1, S-2, S-3, and S-4 geometries are 3, 3, 4, and 5, respectively. These values are consistent with those reported in previous studies.41,51–54 All contact distances of the coordination bonds are significantly shorter than the sum of the van der Waals radii of relevant atoms (Cu: 1.40 Å, N: 1.55 Å, O: 1.52 Å, and S: 1.80 Å). All the four complexes have three coordination bonds between a Cu atom and three atoms of the L ligand. These four atoms are roughly on the same plane, forming the bond angles of approximately 180° and 90°. The formation of complexes mainly leads to changes in the configurations of the two chain bonds C16–C15–C17–N36 and N36–N35–C41–N34 in the BDC moieties. The configurations of the S-2 and S-1, S-3, and S-4 geometries are similar to “cis–trans” and “cis–cis” configurations, respectively.
The complexation equilibrium constants in the aqueous solutions of the S-1, S-2, S-3, and S-4 complex configurations were calculated via the Gibbs free energies of ligand-exchange reactions determined using the thermodynamic cycles, DFT theory method, and SMD solvent model (Scheme 1). Herein, the reference complex [CuLref(H2O)2]2+ was used for calculation, which is a complex between the Cu2+ ions and histamine (Lref) as a ligand, and the experimental equilibrium constant in the aqueous solution (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βref) of this complex was 9.55 (ref. 55 and 56) (the optimized geometry of histamine (Lref) and cartesian coordinate are presented in Fig. S5, S6 and Tables S10 and S11 in the ESI†). The calculation results presented in Table 1 indicate that S-1 is the most stable configuration with a calculated complexation equilibrium constant of 107.16. Consequently, the S-1 configuration was used for all subsequent studies of the BDC–Cu2+ complex.
βref) of this complex was 9.55 (ref. 55 and 56) (the optimized geometry of histamine (Lref) and cartesian coordinate are presented in Fig. S5, S6 and Tables S10 and S11 in the ESI†). The calculation results presented in Table 1 indicate that S-1 is the most stable configuration with a calculated complexation equilibrium constant of 107.16. Consequently, the S-1 configuration was used for all subsequent studies of the BDC–Cu2+ complex.
| ΔGsolv | ΔΔGsolv | ΔGg | ΔGaq | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βref βref |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β β |
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | ||||||
| a A: [CuLref(H2O)x](g)2+, B: L(g), C: [CuL(H2O)y](g)2+, D: H2O(g), E: Lref(g). | ||||||||||
| S-1 | −201.61 | −15.35 | −172.79 | −8.84 | −13.50 | 12.99 | −14.47 | −1.48 | 9.55 | 7.16 |
| S-2 | −201.61 | −15.35 | −152.85 | −8.84 | −13.50 | 32.93 | −2.08 | 30.85 | 9.55 | −16.56 |
| S-3 | −201.61 | −15.35 | −157.3 | −8.84 | −13.50 | 37.32 | −34.03 | 3.29 | 9.55 | 5.40 |
| S-4 | −201.61 | −15.35 | −148.75 | −8.84 | −13.50 | 54.71 | −42.46 | 12.25 | 9.55 | 0.57 |
In order to verify the calculated complexation equilibrium constant before studying the applications of the complex, the experimental complexation equilibrium constant was also determined by a nonlinear curve-fitting method. The fluorescent titration and nonlinear curve-fitting results are shown in Fig. 5. Accordingly, the experimental complexation equilibrium constant was determined to be 107.15 (M−1).
This result is in good agreement with the above calculated complexation equilibrium constant. These results provide further important evidence confirming the correctness of the proposed method for the determination of the complexation equilibrium constants in aqueous solutions using DFT theory and the SMD solvent model.
In terms of application, this value of the complexation equilibrium constant of Cu2+ ions with BDC is significantly smaller than that of the Cu2+ ions with biothiols. For example, the Cu2+ ions react with Cys to form a [CuX2]2+ complex with an equilibrium constant of 1016.57,58 Moreover, the Cu2+ ions react with Hcy to form a [CuHY]2+ complex with an equilibrium constant of 1013.5.59 Compared to the abovementioned reactions, the reactions between the Cu2+ ions and GSH are more complicated. In particular, the main reaction occurs between the Cu2+ ions and GSH to generate a complex of Cu+ ions with GSH in the form of [CuZ2]+ and introduce the GSSG (oxidized glutathione). Herein, the stability constant of the [CuZ2]+ complex is substantially large, equal to 1038.8.60–62 Based on these results, it can be anticipated that the complex of BDC with the Cu2+ ions can be used as a fluorescent sensor for the detection of biothiols based on the complex exchange reactions.
3.2 Application of the BDC–Cu2+ complex in the detection of biothiols
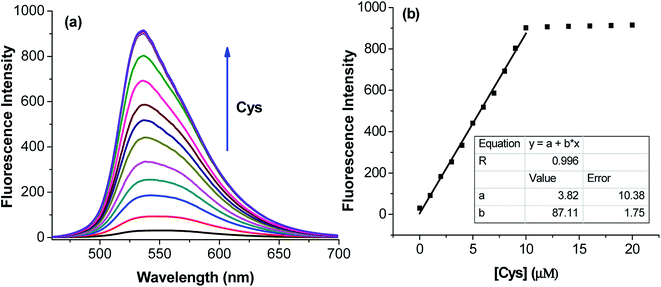
The application of the BDC–Cu2+ complex as a fluorescent sensor for the detection of cysteine was investigated. As shown in Fig. 6, when Cys was gradually added to the solution of the BDC–Cu2+ complex, the fluorescence intensity at 536 nm accordingly changed and increased. It almost restored to the original fluorescence intensity of free BDC when Cys was added to the solution at a concentration greater than or equal to twice that of the BDC–Cu2+ complex. These results show that the stoichiometry of the reaction between Cys and the BDC–Cu2+ complex is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and this reaction leads to the formation of the [CuX2]2+ complex (X: Cys) and the release of free BDC, resulting in the restoration of fluorescence intensity (Fig. 7). This result is also consistent with those reported in previous studies on the composition of the complex of Cys and Cu2+ ion.57,58
1, and this reaction leads to the formation of the [CuX2]2+ complex (X: Cys) and the release of free BDC, resulting in the restoration of fluorescence intensity (Fig. 7). This result is also consistent with those reported in previous studies on the composition of the complex of Cys and Cu2+ ion.57,58
To use the BDC–Cu2+ complex as a fluorescent sensor for the determination of Cys, the interactions of the BDC–Cu2+ complex with H2S and other amino acids were also investigated. The experimental results in Fig. 8 show that thiol-containing amino acids, such as GSH and Hcy, also cause fluorescence recovery. Moreover, H2S and non-thiol containing amino acids, such as alanine (Ala), arginine (Arg), aspartic acid (Asp), glutamic acid (Glu), glycine (Gly), histidine (His), isoleucine (Ile), leucine (Leu), lysine (Lys), methionine (Met), serine (Ser), threonine (Thr), tyrosine (Tyr), tryptophan (Trp) and valine (Val), did not cause any changes in the fluorescence spectrum of the BDC–Cu2+ solution. These results indicate that the BDC–Cu2+ complex can be used as a fluorescent sensor for the detection of thiol-containing amino acids in the presence of H2S and non-thiol containing amino acids in the concentration range from 0 to 10 μM (from 0 to 2 equivalent). In addition, the experimental results show that the presence of H2S at concentrations greater than 10 μM affects the performance of BDC–Cu2+ in the detection of biothiols (Fig. S7†).
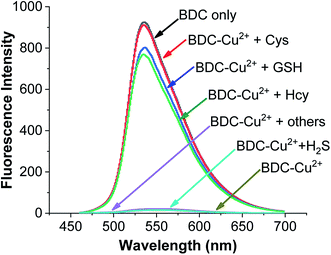 | ||
| Fig. 8 Fluorescence spectra of BDC (5 μM); BDC (5 μM)+Cu2+ (5 μM); BDC (5 μM)+ Cu2+ (5 μM) + Cys/Hcy/GSH/Ala, Asp, Arg, Gly, Glu, Ile, Leu, Lys, Met, Thr, Ser, Tyr, Trp, Val, His, and H2S (10 μM). | ||
Similar to the cases of previous studies reported on fluorescent sensors based on complex exchange reactions,63,64 the BDC–Cu2+ complex also reacted with thiols, including Cys, Hcy, and GSH, and provided similar results. However, in many actual samples, these thiols do not occur simultaneously. For example, in human whole blood, the concentration of reduced glutathione is significantly higher (up to 1 mM) than that of the other thiols. Furthermore, in human plasma, the total concentration of Cys species is up to 250 μM, whereas the concentrations of GSH and Hcy are almost negligible.65–67 Therefore, the BDC–Cu2+ complex can be used as a fluorescent sensor for the detection of Cys, HCy, or GSH depending on the actual cases.
The applicability of the BDC–Cu2+ complex as a fluorescent sensor for the quantification of Cys was also investigated. As shown in Fig. 6b, there is a good linear relationship between the fluorescence intensity of the BDC–Cu2+ solution and the concentration of Cys when Cys is added to the BDC–Cu2+ solution (5 μM). In the Cys concentration range from 0 to 10 μM, the calibration curve equation was determined as follows: FI536 = (3.8 ± 10.4) + (87.1 ± 1.8) × [Cys], R = 0.996. The limit of detection (LOD) and the limit of quantitation (LOQ) of the method were also evaluated by the linear regression method using a calibration curve with a range of low concentrations of Cys (0–5 μM).68 The values of these parameters were 0.3 and 1.1 μM, (Fig. S8†). Moreover, the intracellular concentration of Cys was 30–200 μM.63 These results indicate that the BDC–Cu2+ complex can be used as a fluorescent sensor for the quantification of intracellular Cys and has greater sensitivity than that of the similar previously reported sensors.69,70
3.3 Theoretical investigation of the changes in the fluorescence properties of the complexes and ligands
The fluorescence properties of the ligand and complex were investigated based on the electronic excited states using time-dependent density-functional theory (TD-DFT) at the PBE0/6-31+G(d) level. The obtained results are presented in Table 2 and Fig. 9.| Compound | State | E (eV) | Λ (nm) | f | Contribution of orbital transition | |
|---|---|---|---|---|---|---|
| Composition | Percentage contribution (%) | |||||
| BDC | S0 → S1 | 2.74 | 452.9 | 1.2659 | HOMO → LUMO | 98.58 |
| S0 → S2 | 3.60 | 346.4 | 0.0585 | HOMO−1 → LUMO | 97.59 | |
| S0 → S3 | 3.98 | 311.6 | 0.3340 | HOMO → LUMO+1 | 80.64 | |
| S0 → S4 | 4.12 | 301.1 | 0.1155 | HOMO−3 → LUMO | 69.20 | |
| S0 → S5 | 4.14 | 299.2 | 0.0325 | HOMO−2→LUMO | 90.33 | |
| S0 → S6 | 4.40 | 281.8 | 0.0293 | HOMO−3 → LUMO | 15.72 | |
| HOMO → LUMO+2 | 18.96 | |||||
| HOMO → LUMO+3 | 49.74 | |||||
| BDC–Cu2+ | D0 → D1 | 0.92 | 1350.8 | 0.0054 | HOMOβ → SOMOβ | 87.88 |
| D0 → D2 | 1.44 | 861.9 | 0.0099 | HOMO−2β → SOMOβ | 15.15 | |
| HOMO−1β → SOMOβ | 42.81 | |||||
| D0 → D3 | 1.83 | 676.7 | 0.0011 | SOMOα → LUMOα | 30.25 | |
| HOMOβ → LUMOβ | 27.33 | |||||
| D0 → D4 | 1.86 | 666.2 | 0.0025 | HOMO−3β → SOMOβ | 47.21 | |
| D0 → D5 | 1.94 | 637.3 | 0.0124 | HOMO−2β → SOMOβ | 21.27 | |
| HOMO−1β → SOMOβ | 34.64 | |||||
| D0 → D6 | 2.14 | 579.3 | 0.0035 | HOMO−21β → SOMOβ | 32.03 | |
| D0 → D7 | 2.16 | 574.2 | 0.0019 | HOMO−28β → SOMOβ | 15.67 | |
| HOMO−21β → SOMOβ | 26.27 | |||||
| D0 → D8 | 2.27 | 545.6 | 0.0021 | HOMO−2β → SOMOβ | 40.68 | |
| D0 → D9 | 2.68 | 462.4 | 0.0014 | SOMOα → LUMO+1α | 24.45 | |
| HOMOβ → LUMO+1β | 23.65 | |||||
| D0 → D10 | 2.88 | 430.7 | 1.2645 | SOMOα → LUMOα | 39.49 | |
| HOMOβ → LUMOβ | 41.68 | |||||
| D0 → D11 | 2.89 | 428.7 | 0.1655 | HOMO−3β → SOMOβ | 63.47 | |
| D0 → D12 | 2.97 | 417.9 | 0.0949 | HOMO−4β → SOMOβ | 66.61 | |
| D0 → D13 | 3.13 | 396.5 | 0.0001 | HOMOα → LUMOα | 22.56 | |
| SOMOα → LUMO+1α | 17.29 | |||||
| HOMO−1β → LUMOβ | 21.26 | |||||
| HOMOβ → LUMO+1β | 16.81 | |||||
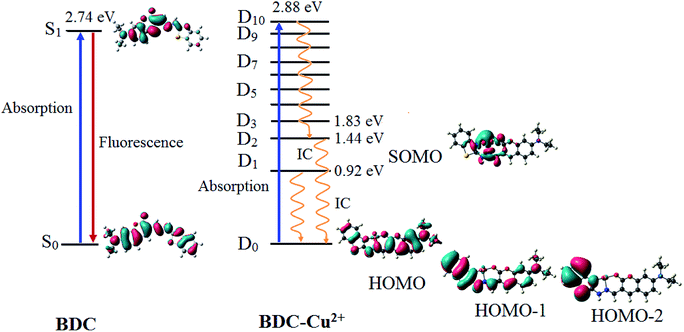 | ||
| Fig. 9 The characteristics of the main transition between the electron excited states and ground states of BDC and BDC–Cu2+ at the PBE0/6-31+G(d) level. | ||
The results provided in Table 2 indicate that in BDC, the S0 → S1 transition plays a key role in all the singlet electronic transitions from ground state (S0) to excited states (Sn). This is due to the fact that the oscillator strength (f) of this transition is 1.2659, substantially larger than those of the other transitions. The S0 → S1 transition energy is 2.74 eV (452.9 nm). The calculated result is completely consistent with the empirical investigations, indicating that BDC exhibits a maximum absorption peak at 460 nm. The HOMO → LUMO transition plays a key role in all the orbital transitions from S0 to S1, with a percentage contribution of 98.58%. This transition occurs between two adjacent MOs. Therefore, it can be firmly affirmed that photoinduced electron transfer (PET) does not occur in BDC, and the abovementioned transition leads to a green emission at 536 nm, as observed via empirical investigations.71,72
The formation of the BDC–Cu2+ complex leads to a significant decrease in the energy gap between the ground state and the excited states of BDC. As a result, the energy gap between the excited state and the D0 state reaches 2.88 eV (430.7 nm) only when the D10 excited state is attained. The D0 → D10 transition has an oscillator strength of 1.2645, significantly bigger than that of the other transitions; therefore, this transition plays a key role in all the electronic transitions. The D0 → D10 transition is mainly contributed by the SOMO → LUMO and HOMO → LUMO transitions, with the percentage contributions of 39.49% and 41.68%, respectively. These transitions are believed to lead to a strong absorption spectrum, as observed in the experiments. Regarding the fluorescence properties of the BDC–Cu2+ complex, on the basis of Kasha's rule, the fluorescence occurs from the lowest-lying electron excited state D1,73,74 in which the D1 → D0 transition is mainly contributed by the LUMO → SOMO. However, the lack of overlapping between the LUMO and SOMO makes the radiation transition D1 → D0 strongly forbidden. Instead, the internal conversion process occurs from D1 to D0 as a radiationless transition. Considering the exceptions of the Kasha rule, from the D2 state to the D10 state, the energy gap between adjacent excited states is quite small, less than 0.42. Thus, according to the energy gap law for radiationless transitions, the internal conversion processes from the excited states at higher energy level to the excited state at adjacent low energy levels quickly occur, competing with the fluorescent radiation process, which quenches the Dn → D0 fluorescence (n > 2).75,76 Only the energy gap between the D2 and D1 states is quite large, 0.52 eV, which should be considered. The D2 → D0 transition is mainly contributed by the SOMO → HOMO−2 and SOMO → HOMO−1 transitions. However, the lack of overlapping between the SOMO and HOMO−2 or HOMO−1 makes the radiation transition D2 → D0 strongly forbidden. As a result, the IC process is also preferred over the fluorescent radiation process, which quenches the D2 → D0 fluorescence. In summary, in the BDC–Cu2+ complex, since the energy gap between adjacent excited states is small, the transitions from the excited states Dn (n > 2) to the excited state D2 are dominated by the internal conversion processes. Moreover, due to the lack of overlapping between MOs during each transition, the D1 → D0 and D2 → D0 transitions are dominated by the internal conversion processes. The D2 and D1 states are dark doublet states that quench the fluorescence.77
4. Conclusions
In summary, herein, a complex exchange reaction-based fluorescent chemosensor was investigated for the detection of biothiols. This sensor was designed based on the theoretical calculations of the stability constants of the complex between the Cu2+ ions and fluorescent ligands. The obtained results are completely consistent with the experimental results. The BDC–Cu2+ complex can be used for the detection of biothiols in the presence of non-thiol containing amino acids. The limit of detection and the limit of quantitation of the proposed chemosensor for Cys are 0.3 and 1.1 μM, respectively. This result opens a new research direction toward the utilization of the complexes between metal ions and fluorescent ligands for the detection of biothiols based on the theoretical calculations of the stability constants.In this study, the theoretical calculations of the excited states were also used to elucidate the changes in the fluorescence properties of compounds. The quenching of the fluorescence of the BDC–Cu2+ complex occurred because the internal conversion processes dominated the fluorescence process due to the small energy gap between adjacent excited states, from the excited states Dn (n > 2) to the excited state D2. Moreover, the D2 and D1 states are dark doublet states because of the lack of overlapping between MOs during each transition.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 104.06-2016.32 (Nguyen Khoa Hien).References
- P. Ghezzi, Int. J. Gen. Med., 2011, 4, 105 CrossRef CAS.
- S. Hasanbasic, A. Jahic, E. Karahmet, A. Sejranic and B. Prnjavorac, Mater. Soc. Med., 2016, 28, 235 CrossRef.
- C. B. Pocernich and D. A. Butterfield, Biochim. Biophys. Acta, Mol. Basis Dis., 2012, 1822, 625–630 CrossRef CAS.
- S. Shahrokhian, Anal. Chem., 2001, 73, 5972–5978 CrossRef CAS.
- P. Ganguly and S. F. Alam, Nutr. J., 2015, 14, 1–10 CrossRef.
- D. Faeh, A. Chiolero and F. Paccaud, Swiss Med. Wkly., 2006, 136, 745–756 CAS.
- N. Ballatori, S. M. Krance, S. Notenboom, S. Shi, K. Tieu and C. L. Hammond, Biol. Chem., 2009, 390, 191–214 CAS.
- D. T. Quang and J. S. Kim, Chem. Rev., 2010, 110, 6280–6301 CrossRef CAS.
- N. K. Hien, P. T. Quy, N. T. Trung, V. Vien, D. Van Khanh, N. T. A. Nhung and D. T. Quang, Chem. Lett., 2014, 43, 1034–1036 CrossRef CAS.
- X. Chen, Y. Zhou, X. Peng and J. Yoon, Chem. Soc. Rev., 2010, 39, 2120–2135 RSC.
- C. Yin, F. Huo, J. Zhang, R. Martínez-Máñez, Y. Yang, H. Lv and S. Li, Chem. Soc. Rev., 2013, 42, 6032–6059 RSC.
- X. Zhang, Y. Yan, Y. Hang, J. Wang, J. Hua and H. Tian, Chem. Commun., 2017, 53, 5760–5763 RSC.
- Y.-Q. Sun, M. Chen, J. Liu, X. Lv, J.-f. Li and W. Guo, Chem. Commun., 2011, 47, 11029–11031 RSC.
- F. Kong, R. Liu, R. Chu, X. Wang, K. Xu and B. Tang, Chem. Commun., 2013, 49, 9176–9178 RSC.
- J. Shi, Y. Wang, X. Tang, W. Liu, H. Jiang, W. Dou and W. Liu, Dyes Pigm., 2014, 100, 255–260 CrossRef CAS.
- S. Ji, H. Guo, X. Yuan, X. Li, H. Ding, P. Gao, C. Zhao, W. Wu, W. Wu and J. Zhao, Org. Lett., 2010, 12, 2876–2879 CrossRef CAS.
- X.-D. Jiang, J. Zhang, X. Shao and W. Zhao, Org. Biomol. Chem., 2012, 10, 1966–1968 RSC.
- M. Wei, P. Yin, Y. Shen, L. Zhang, J. Deng, S. Xue, H. Li, B. Guo, Y. Zhang and S. Yao, Chem. Commun., 2013, 49, 4640–4642 RSC.
- Y.-S. Guan, L.-Y. Niu, Y.-Z. Chen, L.-Z. Wu, C.-H. Tung and Q.-Z. Yang, RSC Adv., 2014, 4, 8360–8364 RSC.
- M. H. Lee, J. H. Han, P.-S. Kwon, S. Bhuniya, J. Y. Kim, J. L. Sessler, C. Kang and J. S. Kim, J. Am. Chem. Soc., 2012, 134, 1316–1322 CrossRef CAS.
- Y. Bao, Q. Li, B. Liu, F. Du, J. Tian, H. Wang, Y. Wang and R. Bai, Chem. Commun., 2012, 48, 118–120 RSC.
- D. T. Nhan, N. K. Hien, H. Van Duc, N. T. A. Nhung, N. T. Trung, D. U. Van, W. S. Shin, J. S. Kim and D. T. Quang, Dyes Pigm., 2016, 131, 301–306 CrossRef.
- D. Devarajan, P. Lian, S. C. Brooks, J. M. Parks and J. C. Smith, ACS Earth Space Chem., 2018, 2, 1168–1178 CrossRef CAS.
- O. Gutten and L. Rulisek, Inorg. Chem., 2013, 52, 10347–10355 CrossRef CAS.
- S. Vukovic, B. P. Hay and V. S. Bryantsev, Inorg. Chem., 2015, 54, 3995–4001 CrossRef CAS.
- R. Flores, L. I. Reyes-García, N. Rodríguez-Laguna and R. Gómez-Balderas, Theor. Chem. Acc., 2018, 137, 125 Search PubMed.
- A. T. Afaneh, G. Schreckenbach and F. Wang, J. Phys. Chem. B, 2014, 118, 11271–11283 CrossRef CAS.
- J.-S. Wu, F. Wang, W.-M. Liu, P.-F. Wang, S.-K. Wu, X. Wu and X.-H. Zhang, Sens. Actuators, B, 2007, 125, 447–452 CrossRef CAS.
- Y. H. Lee, M. H. Lee, J. F. Zhang and J. S. Kim, J. Org. Chem., 2010, 75, 7159–7165 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, G. Z. J. Bloino, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- T. Weymuth, E. P. Couzijn, P. Chen and M. Reiher, J. Chem. Theor. Comput., 2014, 10, 3092–3103 CrossRef CAS.
- W. Zhang, D. G. Truhlar and M. Tang, J. Chem. Theory Comput., 2013, 9, 3965–3977 CrossRef CAS.
- S. Dohm, A. Hansen, M. Steinmetz, S. Grimme and M. P. Checinski, J. Chem. Theor. Comput., 2018, 14, 2596–2608 CrossRef CAS.
- D. Jacquemin, V. Wathelet, E. A. Perpete and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435 CrossRef CAS.
- J. Moon, H. Baek and J. Kim, J. Phys. Chem. A, 2017, 121, 6531–6537 CrossRef CAS.
- L. s. F. Pašteka, T. Rajsky and M. Urban, J. Phys. Chem. A, 2013, 117, 4472–4485 CrossRef.
- V. Srinivasadesikan, Y.-C. Chen and S.-L. Lee, J. Mol. Graph. Model., 2018, 85, 270–280 CrossRef CAS.
- T. A. Hamlin, B. J. Levandowski, A. K. Narsaria, K. N. Houk and F. M. Bickelhaupt, Chem.–Eur. J., 2019, 25, 6342–6348 CrossRef CAS.
- S. A. Hosseini-Yazdi, P. Samadzadeh-Aghdam and R. Ghadari, Polyhedron, 2018, 151, 221–232 CrossRef CAS.
- P. Zarabadi-Poor and J. Barroso-Flores, J. Phys. Chem. A, 2014, 118, 12178–12183 CrossRef CAS.
- N. K. Hien, N. C. Bao, N. T. A. Nhung, N. T. Trung, P. C. Nam, T. Duong, J. S. Kim and D. T. Quang, Dyes Pigm., 2015, 116, 89–96 CrossRef CAS.
- A. Ali, M. I. Rafiq, Z. Zhang, J. Cao, R. Geng, B. Zhou and W. Tang, Phys. Chem. Chem. Phys., 2020, 22, 7864–7874 RSC.
- I. d. L. de Sousa, V. F. Ximenes, A. R. de Souza and N. H. Morgon, J. Mol. Struct., 2019, 1192, 186–191 CrossRef.
- J. R. Pliego Jr, Chem. Phys. Lett., 2003, 381, 246–247 CrossRef.
- V. S. Bryantsev, M. S. Diallo and W. A. Goddard Iii, J. Phys. Chem. B, 2008, 112, 9709–9719 CrossRef CAS.
- C. J. Cramer and D. G. Truhlar, Accounts Chem. Res., 2008, 41, 760–768 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- O. Gutten, I. Beššeová and L. Rulíšek, J. Phys. Chem. A, 2012, 116, 8407 CrossRef CAS.
- L. Xu and M. Coote, J. Phys. Chem. A, 2019, 123, 7430 CrossRef CAS.
- K. N. More, T.-H. Lim, J. Kang, H. Yun, S.-T. Yee and D.-J. Chang, Molecules, 2019, 24, 3206 CrossRef CAS.
- P. L. Holland and W. B. Tolman, J. Am. Chem. Soc., 1999, 121, 7270–7271 CrossRef CAS.
- D. W. Randall, S. D. George, P. L. Holland, B. Hedman, K. O. Hodgson, W. B. Tolman and E. I. Solomon, J. Am. Chem. Soc., 2000, 122, 11632–11648 CrossRef CAS.
- B. A. Jazdzewski, P. L. Holland, M. Pink, V. G. Young, D. J. Spencer and W. B. Tolman, Inorg. Chem., 2001, 40, 6097–6107 CrossRef CAS.
- P. Frank, M. Benfatto, R. K. Szilagyi, P. D'Angelo, S. Della Longa and K. O. Hodgson, Inorg. Chem., 2005, 44, 1922–1933 CrossRef CAS.
- B. Mickel and A. Andrews, J. Am. Chem. Soc., 1955, 77, 5291–5292 CrossRef CAS.
- J. Schubert, V. Sharma, E. White and L. S. Bergelson, J. Am. Chem. Soc., 1968, 90, 4476–4478 CrossRef CAS.
- G. Berthon, Pure Appl. Chem., 1995, 67, 1117–1240 CAS.
- H. Tavallali, G. Deilamy-Rad, M. A. Karimi and E. Rahimy, Anal. Biochem., 2019, 583, 113376 CrossRef CAS.
- J. M. Murphy, A. A. Gaertner, T. Williams, C. D. McMillen, B. A. Powell and J. L. Brumaghim, J. Inorg. Biochem., 2019, 195, 20–30 CrossRef CAS.
- M. E. Aliaga, C. López-Alarcón, R. Bridi and H. Speisky, J. Inorg. Biochem., 2016, 154, 78–88 CrossRef CAS.
- H. Speisky, C. López-Alarcón, C. Olea-Azar, C. Sandoval-Acuña and M. E. Aliaga, Bioinorgan. Chem. Appl., 2011, 2011 Search PubMed.
- R. Österberg and R. Ligaarden, J. Inorg. Biochem., 1979, 10, 341–355 CrossRef.
- H. Jia, M. Yang, Q. Meng, G. He, Y. Wang, Z. Hu, R. Zhang and Z. Zhang, Sensors, 2016, 16, 79 CrossRef CAS.
- G. He, J. Li, L. Yang, C. Hou, T. Ni, Z. Yang, X. Qian and C. Li, PLoS One, 2016, 11, e0148026 CrossRef.
- X. Fu, S. A. Cate, M. Dominguez, W. Osborn, T. Özpolat, B. A. Konkle, J. Chen and J. A. López, Sci. Rep., 2019, 9, 1–9 CrossRef.
- P. Hallman, D. Perrin and A. E. Watt, Biochem. J., 1971, 121, 549–555 CrossRef CAS.
- P. M. Ueland, H. Refsum, S. P. Stabler, M. R. Malinow, A. Andersson and R. H. Allen, Clin. Chem., 1993, 39, 1764–1779 CrossRef CAS.
- J. C. Miller and J. N. Miller, Statistics for Analytical Chemistry. (Reprinted with Corrections 1989), Ellis Horwood, 1988 Search PubMed.
- M. Yang, L. Ma, J. Li and L. Kang, RSC Adv., 2019, 9, 16812–16818 RSC.
- Y. Yang, H. Wang, Y.-L. Wei, J. Zhou, J.-F. Zhang and Y. Zhou, Chin. Chem. Lett., 2017, 28, 2023–2026 CrossRef CAS.
- A. P. De Silva, T. S. Moody and G. D. Wright, Analyst, 2009, 134, 2385–2393 RSC.
- D. T. Nhan, N. T. A. Nhung, V. Vien, N. T. Trung, N. D. Cuong, N. C. Bao, D. Q. Huong, N. K. Hien and D. T. Quang, Chem. Lett., 2017, 46, 135–138 CrossRef CAS.
- P. Klán and J. Wirz, Photochemistry of organic compounds: from concepts to practice, John Wiley & Sons, 2009 Search PubMed.
- N. K. Hien, D. T. Nhan, W. Y. Kim, M. Van Bay, P. C. Nam, D. U. Van, I.-T. Lim, J. S. Kim and D. T. Quang, Dyes Pigm., 2018, 152, 118–126 CrossRef.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS.
- M. Bixon and J. Jortner, J. Chem. Phys., 1968, 48, 715–726 CrossRef CAS.
- J. Andreas, B. Dnyaneshwar and S. Th, Phys. Chem. Chem. Phys., 2017, 19, 26255–26264 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra05651k |
| ‡ These authors contributed equally to the work. |
| This journal is © The Royal Society of Chemistry 2020 |