Open Access Article
Open Access ArticleIndividual control of singlet lifetime and triplet yield in halogen-substituted coumarin derivatives
Katrin E. Oberhofera,
Mikayel Musheghyana,
Sebastian Wegscheidera,
Martin Wörlea,
Eleonora D. Iglevac,
Rositca D. Nikolovab,
Reinhard Kienbergera,
Petko St. Pekov *b and
Hristo Iglev
*b and
Hristo Iglev *a
*a
aPhysics Department E11, Technical University of Munich, James-Franck-Str., 85748 Garching, Germany. E-mail: hristo.iglev@tum.de
bFaculty of Chemistry and Pharmacy, University of Sofia, J. Bouchier 1, 1164 Sofia, Bulgaria. E-mail: ppetkov@chem.uni-sofia.bg
cW. L. Gore & Associates GmbH, Hermann-Oberth-Str. 2285640 PutzbrunnGermany
First published on 21st July 2020
Abstract
The photophysical properties of three 3-diethylphosphonocoumarin derivatives are studied by transient absorption spectroscopy and DFT calculations. The measured lifetime of the first excited singlet state changes upon halogen substitution at the 6-position from 40 ps for the unsubstituted compound to 100 ps for Cl and 24 ps for Br. This observation is in clear contradiction with the estimated singlet–triplet quantum yield, which increases with atomic weight of the substituted atom and is usually referred as a heavy-atom effect. The DFT calculations give evidence that the main reason for this behavior is the different composition of the HOMO, while the LUMO is similar for all three compounds. The optical excitation leads to intramolecular charge transfer from the halogen lone pairs to the π* molecular orbital and thus to a significant change in the molecular dipole moment. Hence, the latter phenomenon in combination with the heavy-atom effect enables an independent control of singlet lifetime and singlet–triplet quantum yield in the studied 3-diethylphosphonocoumarin derivatives.
1 Introduction
The ability to control photophysical key properties of organic molecules such as fluorescence lifetime and singlet–triplet quantum yields (QYs) bears huge potential for the synthesis of new substances, in particular for applications in biochemistry and medical science. Suitable candidates can be found in coumarin derivatives because of their large application spectrum in these fields.1–11 It is widely known that triplet states are involved in many photochemical reactions.12 Aside their role in the use of coumarins as oxygen sensors,4,5 photosensitizers6 and photolabile protecting groups,7,8 long-lived triplet states are crucial for photodynamic therapy of cancer9,10 and for enantioselective photocycloaddition reactions.11 The triplet QY hence is an essential parameter for controlling these reactions. The same applies for the lifetime of the first excited singlet state, which usually correlates with the fluorescence QY. Emission lifetime and triplet QY can be effectively influenced by the so called heavy-atom effect (HAE), which is mediated by spin–orbit interactions and thus enhanced by halogen substitution.12,13 Therefore decreased lifetimes and increased triplet QY are obtained. Different studies8,14 report on utilization of the HAE for azacoumarin photolabile protecting groups. They show that 6-substitution of iodine instead of chlorine or bromine enhances the reaction rate and the photolytic efficiency dramatically.In general, coumarin derivatives feature a couple of triplet states energetically close to the lowest excited singlet states, which are shifted upon substitution.15–20 Although this tends to result in a complex nature of the photophysical properties, it facilitates a targeted design of compounds with applications involving reactions that proceed through the triplet state. Here we report on 6-substituted 3-diethylphosphonocoumarin. The 3-position of coumarin becomes important for adding larger functional groups for various applications. For example, an electron-accepting substituent on 3- or 4-position in combination with an electron-donating substituent on 7-position leads to high fluorescence QY due to intramolecular charge transfer. The latter was intensively used for the application of coumarin derivatives as laser dyes.20,21 In other approaches the comparably small coumarin moiety was used to study the attached functional groups.22–24 In our case the 3-substituted diethylphosphono and phosphono groups are commonly known for their enzyme inhibiting abilities.25,26 The electron withdrawing effect of the diethylphosphono group on the conjugated aromatic coumarin structure reduces the electron density stronger on 7 with respect to 6-position. This is also confirmed by the calculated natural bond orbital charges on carbon atoms at 6- and 7-position, which are −0.218 and −0.151, respectively. Thus, the interaction between position 3 and 7 is enhanced with respect to the 3-and 6-position in diethylphosphonocoumarin. Therefore, this suggests a relatively weak influence of the 6-substituent on the photophysical properties of the molecule.
In the present study we investigated how the substituents Cl or Br at the 6-position can be used for fine-tuning of the fluorescence lifetime and singlet–triplet QY. According to the HAE,12 one would expect a slight fluorescence quenching and an increased intersystem-crossing rate. However, the compounds exhibit an anomalous HAE, which we examine by use of femtosecond transient absorption spectroscopy together with conventional fluorescence and absorption measurements. We give a detailed analysis of the experimental observations and performed DFT calculations in order to explain the underlying processes.
2 Experimental
The synthesis of the studied coumarin derivatives is described elsewhere,27 while their chemical structure is shown in the inset of Fig. 1A. We present a detailed investigation of three 3-diethylphosphonocoumarins, which differ in their substituent at 6-position (H, Cl, or Br). Compounds labelled with 6-Cl and 6-Br are derived from 3-diethylphosphonocoumarins (6-H) by substituting H at the 6-position of the coumarin by chlorine or bromine, respectively. In addition, a second group of similar compounds, substituted in 6-position with Cl or Br coumarin-3-phosphonic acid, was also investigated. For our studies we used a polar and aprotic solvent acetonitrile (99.5%, Sigma Aldrich). Conventional absorption (Lambda 19 UV/Vis spectrometer, PerkinElmer) and fluorescence spectroscopy are performed in acetonitrile solution at a concentration of 80 μM in a 1 cm thick UV grade fused silica cell (Suprasil, Hellma). The excitation wavelength of the spectrofluorometer (FP-6500, Jasco) was set to the respective absorption maximum of each molecule. Fluorescence quantum yields ΦF were determined according to Brouwer et al.28 with coumarin 120 as reference.29The femtosecond spectrometer is based on a Ti:sapphire laser system (CPA-2010, Clark-MXR) delivering 1 mJ pulses at 775 nm with a repetition rate of 1 kHz. A fraction of the laser beam is used to pump a two-stage non-collinear optical parametric amplifier (NOPA).30 The NOPA generates sub-50 fs pulses at 660 nm. These pulses are frequency-doubled in a 200 μm BBO to provide 330 nm pump pulses with an energy of 0.2 μJ. Super-octave white light continuum generated by focusing the 1150 nm output of a second two-stage NOPA onto a CaF2-plate is used as a probe pulse. The latter is focused onto the sample with a parabolic mirror at an angle below 10° with respect to the incident pump beam. The transmitted probe light is recollimated with a second parabolic mirror and detected via a Czerny–Turner spectrometer (MicroHR Imaging, Horiba) and a CCD-camera (Series 2000, Stresing). The transient change in the optical density of the sample can be obtained by ΔOD = −log(T/T0), wherein T is the transmitted light through the sample with pre-excitation by the pump pulse, and T0 without (pump pulse blocked). The detection bandwidth of this setup reaches from 430 to 800 nm. The pump and probe pulses are linearly polarized and oriented in an angle of 54.6° (“magic-angle”) in order to detect isotropic signals. The studied coumarins are dissolved in acetonitrile at a concentration of about 1 mM. The liquid sample is measured in a 1 mm thick glass cuvette (Suprasil, Hellma).
3 Computational details
The geometry optimization of the studied coumarin molecules in ground state was performed with Density Functional Theory (DFT) employing the range-separated hybrid exchange–correlation functional CAM-B3LYP31 with triple-ζ basis set quality including polarisation and diffuse functions (6-311+G(d,p)) as it is implemented in Gaussian09 suite.32 To obtain the vertical excitation energies, dipole moments, and the geometry of the coumarin molecules at the first excited state, a time-dependent DFT (TD-DFT)33–38 formalism was applied with the same functional and basis set as for the ground state calculations. Such range-separated hybrid exchange–correlation functionals are capable to describe systems with charge transfer states with satisfying accuracy. Moreover, the same functional was successfully applied to study the intramolecular charge transfer in coumarin molecules39,40 and also a charge transfer from coumarin to the solvent molecules.22 The solvent effects were considered with a polarizable continuum model (PCM).41 In PCM formalism the solvent is described as a homogeneous dielectric medium, which is polarized by the solute. The solvation model used in the calculations is the PCM with the default parameters implemented in Gaussian 09 suite.32 In the PCM model a reaction field calculation with the integral equation formalism model (IEFPCM) was applied.42 The solvent used in the PCM model is acetonitrile with dielectric constant 35.688. The pressure used to calculate the thermochemistry parameters is 1 atm. The cavity was determined by scaled vdW surface (van der Waals surface), with scaling factor a = 1.100. The calculated excitation wavelengths were scaled by factor 1.125 estimated as a ratio of the experimentally measured absorption maximum and a calculated value for the 6-H coumarin molecule. The factor obtained from this ratio was applied to the other calculated excitation energies.4 Results and discussion
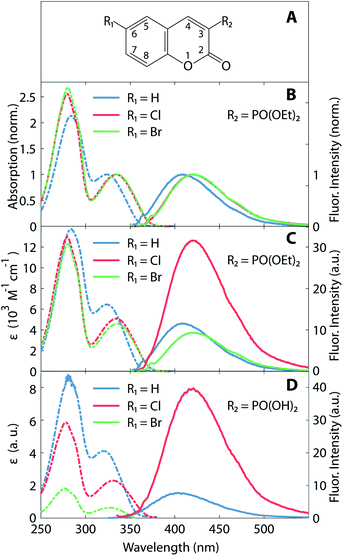
Absorption and fluorescence spectra of the coumarin derivatives in acetonitrile solution are depicted in Fig. 1. Fig. 1B and C illustrate the spectra of the three 3-diethylphosphonocoumarin substituted in 6-position as follows: 6-H, 6-Cl and 6-Br. The normalized spectra (Fig. 1B) show similar spectral shape in the absorbance and fluorescence bands. 6-H exhibits its energetically lowest absorbance maximum at 324 nm. The corresponding maxima of 6-Cl and 6-Br are slightly red-shifted by 10–12 nm, and this effect is attributed to the electron-withdrawing inductive effect of halogen substitution and to the charge-transfer character of the HOMO–LUMO transition (see also Fig. 4).8,43 Likewise, the fluorescence maximum of 6-Cl is red-shifted by 10 nm (13 nm for 6-Br) with respect to the maximum of 6-H at 410 nm. The observed Stokes shifts of 85–90 nm are typical for coumarin derivatives.15Fig. 1B shows the molar absorption coefficients, ε, and the corresponding fluorescence intensities, which represent each an average over several individually prepared solutions (see also Table 1). The molar absorption coefficients are retrieved from the absorption maxima in the wavelength range above 300 nm, shown in Fig. 1C. The molar absorption coefficient of 6-H (ε = 6400 M−1 cm−1) is the largest of all three compounds. 6-Cl and 6-Br exhibit slightly smaller values of 5000 and 4600 M−1 cm−1, respectively. Since the width of the low-energy absorption bands are similar in all three compounds (Fig. 1B), the relation of oscillator strengths, which are proportional to the surface below the absorption spectrum, is expected to be in agreement with ε.
| Compound | 6-H | 6-Cl | 6-Br |
| λabs (nm) | 324 | 334 | 336 |
| λfluo (nm) | 410 | 420 | 423 |
| ε (M−1 cm−1) | 6400 ± 100 | 5000 ± 400 | 4600 ± 350 |
| ΦF (%) | 0.34 ± 0.02 | 1.01 ± 0.05 | 0.32 ± 0.03 |
Fluorescence intensities are depicted in the right part in Fig. 1C (see solid lines and right ordinate scale). Cl-substitution increases the fluorescence signal threefold and fourfold with respect to 6-H and 6-Br, respectively. The fluorescence quantum yield ΦF (see Table 1) also has a larger value for 6-Cl (1.01%) than for 6-H (0.34%) and 6-Br (0.27%). However, all three compounds show very low fluorescence QY. This implicates a large rate of nonradiative relaxation from the first excited state. The stronger fluorescence of 6-Cl with respect to the unsubstituted compound 6-H is unusual, as due to the HAE one would expect a reduction of this parameter upon halogen substitution. In contrast, 6-Br shows at least a decrease of the fluorescence QY with respect to 6-H and 6-Cl. A similar HAE anomaly is observed for the second group of compounds, 3-substituted with a phosphono group (see Fig. 1D). Molar absorption coefficients decrease strongly from the unsubstituted compound to the Cl- and the Br-substituted compound. The Cl-compound reveals a four-fold enhanced fluorescence intensity with respect to the unsubstituted compound. The fluorescence of the Br-compound was even weaker than the latter and overlaps with the Raman scattered excitation light.
Femtosecond transient absorption spectroscopy elucidates the dynamics of singlet and triplet excited states. Fig. 2 shows the transient spectra recorded at various delay times after excitation at 330 nm of 6-H (A), 6-Cl (B) and 6-Br (C). Due to a similar temporal evolution of the coumarin-3-phosphonic acid (Fig. 1D, transient data not shown) we limit the following discussion to the 3-diethylphosphonocoumarins. The data in Fig. 2 indicate similar dynamics for all three studied samples. A broad absorption band centered around 640 nm, assigned to excited state absorption (ESA) of the first singlet state S1, is rising within the first picosecond. The ESA band is ranging from about 500 nm up to beyond our detection limit at 800 nm. For the spectral range below 500 nm a negative signal becomes visible, which is likewise reaching its maximum within 1 ps. The negative signals are assigned to stimulated emission (SE), since this spectral range overlaps with the steady-state fluorescence spectra (see Fig. 1). In contrast, the ground state bleaching is expected to be at wavelengths below 375 nm. Moreover, ESA and SE spectrally overlap. At the blue end of our detection range in Fig. 2B the SE band approaches zero, although significant steady state fluorescence can be detected for wavelengths between 400 and 450 nm. Presumably this effect is caused by the low intensity of the probe below 450 nm, which reduces our sensitivity in this spectral range.
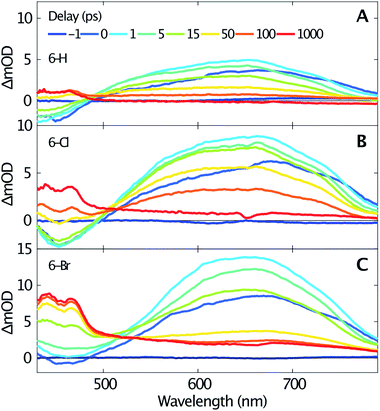 | ||
| Fig. 2 Transient spectra measured for selected time delays (see inset in A) after excitation at 330 nm of 6-H (A), 6-Cl (B) and 6-Br (C) dissolved in acetonitrile. | ||
The transient spectra beyond 1 ps, shown in Fig. 2, indicate a clear isosbestic point at 490 nm for 6-H, which shifts to 505 nm for 6-Cl and 515 nm for 6-Br, respectively. These isosbestic points suggest an intramolecular relaxation from the excited singlet state into a lower-lying excited state with longer lifetime. For delay times larger than 50 ps the SE vanishes and gives rise to an absorption band with two distinct maxima at 440 and 465 nm and a flat low-frequency wing ranging to wavelengths beyond 800 nm. Taking into account the results of the DFT calculations (see below), this can be assigned to triplet–triplet absorption (TTA). The assumption agrees with earlier studies on coumarins,17–19 where TTA in the range from 400 to 500 nm have been reported. The spacing between the two maxima of the TTA band (≈1400 cm−1) is comparable to the C–C stretching mode. Such vibrational spacing is often observed in TTA.17,18
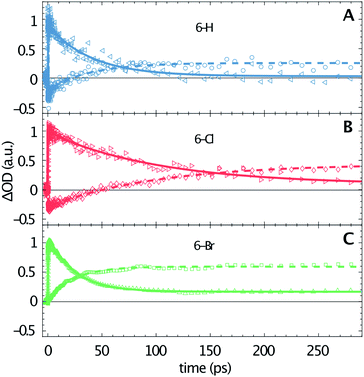
The transient data are analysed via a global fitting procedure based on a rate equation model. This data analysis indicates four subsequent relaxation steps. The initially excited Franck–Condon state relaxes to a “hot” excited singlet state within the first <200 fs, which is followed by vibrational cooling on the few picosecond time scale.44,45 The pronounced isosbestic points in Fig. 2 give strong evidence for intramolecular singlet to triplet transition via intersystem-crossing. Hence, the corresponding time-constant is equal to the lifetime of S1. Because non-radiative relaxation in unsubstituted coumarin is mediated by internal conversion through a conical intersection,46 this process presumably cannot be neglected as contribution to the lifetime of S1. Hence, the respective third transition rate includes contributions by intersystem-crossing, internal conversion and also stimulated emission. In order to keep our model simple, we desisted from including multiple simultaneous pathways. Fig. 3 illustrates the singlet–triplet relaxation in the three studied compounds. Time-scans measured at 640 nm trace the S1 population (triangles, solid lines), while the triplet state is monitored at 465 nm (circles, dashed lines). Note that for delay times shorter than 150 ps the latter signals overlap with SE from S1. The lifetime of the triplet state goes beyond our time window of 1.3 ns. Most important, Fig. 3 shows a significant variation of the S1 lifetime upon halogen substitution. This lifetime increases from 40 ps for 6-H to 100 ps for 6-Cl, and then decreases to 24 ps for 6-Br. This observation agrees with the extracted fluorescence QY (see Table 1), however, seems to be in contradiction to the HAE, where a shorter singlet lifetime would be expected for molecules including heavier halogen atoms. The overall low lifetimes and fluorescence QY can be related to a strong contribution of internal conversion as nonradiative relaxation process.
Fig. 2 shows that the ESA amplitudes increase going from 6-H to 6-Cl and 6-Br (note the transient spectra measured at 1 ps). The TTA, which dominated the long-time transient spectra (see red lines in Fig. 2), rises even stronger under halogen substitution. Fig. 3 enables a rough estimation of the relative change of singlet–triplet QY upon halogen substitution. Here the signal amplitudes are normalized to the respective ESA maximum at 640 nm for each molecule. Thus, the 465 nm signal at large delay times directly represents the ratio between TTA and ESA amplitudes. The latter numbers (0.25 for 6-H; 0.45 for 6-Cl; and 0.65 for 6-Br) could serve as a relative measure for the singlet–triplet QY. Hence, the triplet yield increases for Cl and Br substitution, as predicted by the HAE.
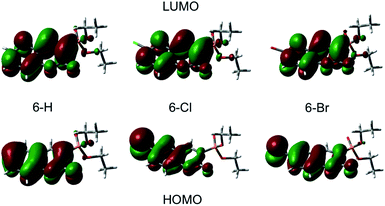
A qualitative comparison of the S1-lifetimes with the fluorescence QYs (Table 1) reveals a strong correlation, i.e. clearly enhanced values for 6-Cl, and thus manifests itself in an anomaly of the HAE. In contrast, the estimated singlet–triplet QY grows according to the atomic number of the 6-substituted atom, reflecting exactly the HAE. We used DFT calculations to elucidate this unexpected phenomenon. Our calculations show that the lowest excitation energies for the three coumarin molecules are associated mostly (94%) to a HOMO → LUMO transition. The absorption wavelengths, scaled by the factor of 1.125, and the corresponding oscillator strengths are calculated according to a vertical transition (molecular structure optimized to the ground state) and shown in Table 2. We emphasize that the scaling of the calculated wavelengths leads to almost perfect matching between calculated and experimentally measured absorption wavelengths for all three compounds (cf. Tables 1 and 2), which additionally validates the DFT results.
| λscaled (nm) | f | μ (D) | Δμ (D) | |
|---|---|---|---|---|
| 6-H | 324 | 0.305 | 5.10 | +2.0 |
| 6-Cl | 334 | 0.223 | 2.72 | +4.12 |
| 6-Br | 335 | 0.213 | 2.68 | +4.65 |
Plots of the HOMO and LUMO are shown on Fig. 4. The illustrated LUMO represent the excited state minima. The analysis of the molecular orbitals in the three coumarins indicates that the main reason for the different behaviour of the halogen-substituted compounds is the composition of the HOMO. Fig. 4 indicates that the electron density at HOMO is shifted from the carbonyl O (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) towards the halogen and the inductive effect of Cl is stronger than the one of Br, as it is expected form the electronegativity difference. The lone pair orbitals from Cl or Br, which are normal to the molecular plane, are taking part in HOMO formation. In contrast, the LUMO does not change significantly upon halogen substitution. The halogen substituent at 6-position reduces the oscillator strengths for excitation by almost 30% (see Table 2) in agreement with the experimentally observed change in the molar extinction coefficients (Table 1).
O) towards the halogen and the inductive effect of Cl is stronger than the one of Br, as it is expected form the electronegativity difference. The lone pair orbitals from Cl or Br, which are normal to the molecular plane, are taking part in HOMO formation. In contrast, the LUMO does not change significantly upon halogen substitution. The halogen substituent at 6-position reduces the oscillator strengths for excitation by almost 30% (see Table 2) in agreement with the experimentally observed change in the molar extinction coefficients (Table 1).
Most interesting, the ground state molecular dipole moment is lowered from 5.10 D for 6-H to 2.72 D and 2.78 D for 6-Cl and 6-Br, respectively. The optical excitation leads to a partial intramolecular charge transfer from the lone pairs of the heavy atom (Cl, Br) to the π* molecular orbital and thus, to significant extension of the π* system and corresponding change in the dipole moment. The change in the dipole moment upon excitation Δμ increases by factor 2 upon halogen substitution at 6-position. Recent studies on π-conjugated systems reported a correlation between fluorescence QY and extension in the conjugated π-system.47,48 Moreover, intramolecular charge-transfer processes, which are common in coumarins,22,49,50 lead to large changes in dipole moment between ground and excited state accompanied by a significant increase of the fluorescence intensity.47,50 Accordingly, the rise of Δμ from 2.0 D to 4.12 D and 4.65 D going form 6-H to 6-Cl and 6-Br, respectively, suggests an increase of the fluorescence QY in the same way. However, the superposition of this phenomenon with the enhanced intersystem-crossing rate upon Cl- and Br-6-substitution results in an anomalous heavy-atom behaviour. For 6-Cl the effect caused by the large Δμ is stronger than the influence of the HAE leading to larger ΦF and S1 lifetime compared to 6-H. In contrast, the HAE dominates for 6-Br leading to weaker fluorescence and shorter S1 lifetime. The latter is supported by the observed increase of the triplet yield as a direct cause of the stronger influence of the HAE with atomic number of the 6-substituted atom.
We emphasize that we found an exception to the “normal” HAE reported for different Cl- and Br-substituted coumarin derivatives at the 6-position,51 which occurs in PO2 containing 3-substituted coumarins. Note that little changes in substitutions and functional groups can cause large differences in the photophysical properties of coumarins due to their complex electronic structure.15,16 Thus our results should not be understood as a general refutation of the HAE.
5 Conclusions
We report on the influence of Cl and Br substituents at 6-position in 3-diethylphosphonocoumarin on the molecular photophysical properties. Using conventional fluorescence and absorption spectroscopy we observe an anomalous heavy-atom effect (HAE), namely an enhanced fluorescence quantum yield, ΦF, for the Cl-derivative. Absorption and fluorescence spectroscopy in Cl- and Br-6-substituted coumarin-3-phosphonic acids confirm the occurrence of this anomaly in a more general frame for PO2 containing 3-substitutions. Femtosecond transient absorption spectroscopy shows that the lifetime of the singlet excited state changes from 40 ps for the unsubstituted compound, 6-H, to 100 ps for 6-Cl and 24 ps for 6-Br. The results are in strong correlation with the extracted ΦF and point towards an anomalous HAE. The performed DFT calculations are in a good agreement with the experimental results and give evidence that the main reason for this anomalous behavior is the different composition of the HOMO, while the LUMO is very similar for all compounds. The optical excitation leads to partial intramolecular charge transfer from the nonbonding orbitals of the heavy atom (Cl, Br) to the π* molecular orbital, and thus to a much larger change in the dipole moment (Δμ). The doubling of Δμ upon halogen substitution is expected to cause a significant increase in ΦF for 6-Cl and 6-Br, however, the enhanced intersystem-crossing rates due to the HAE quench their fluorescence. The latter effect is stronger for Br, which explains the shorter lifetime measured in 6-Br. Hence, the results reveal two superimposing effects displaying contradictory photophysical properties, which enable an independent control of singlet lifetime and singlet–triplet quantum yield in the studied 3-diethylphosphonocoumarin derivatives.Conflicts of interest
There are no conflict of interest to declarate.Acknowledgements
We acknowledge the Deutsche Forschungsgemeinschaft (DFG) for the financial support via the Cluster of Excellence “Munich-Centre of Advanced Photonics MAP”. P. St. P. and R. D. N. are grateful to Operational programme “Science and Education for Smart Growth”, project BG05M2OP001-2.009-0028 and the Bulgarian National Science Fund project KP-06-N-39/15.Notes and references
- D. Egan, R. O'Kennedy, E. Moran, D. Cox, E. Prosser and R. D. Thornes, Drug Metab. Rev., 1990, 22, 503–529 CrossRef CAS PubMed.
- P. Anand, B. Singh and N. Singh, Bioorg. Med. Chem., 2012, 20, 1175–1180 CrossRef CAS PubMed.
- D. Wöhrle, M. W. Tausch and W. D. Stohrer, Photochemie: Konzepte, Methoden, Experimente, Wiley-VCH, 2005 Search PubMed.
- H. Sun, H. Guo, W. Wu, X. Liu and J. Zhao, Dalton Trans., 2011, 40, 7834–7841 RSC.
- D. Hara, H. Komatsu, A. Son, S. I. Nishimoto and K. Tanabe, Bioconjugate Chem., 2015, 26, 645–649 CrossRef CAS PubMed.
- X. Yi, C. Zhang, S. Guo, J. Ma and J. Zhao, Dalton Trans., 2014, 43, 1672–1683 RSC.
- N. Senda, A. Momotake, Y. Nishimura and T. Arai, Bull. Chem. Soc. Jpn., 2006, 79, 1753–1757 CrossRef CAS.
- H. Takano, T. Narumi, W. Nomura, T. Furuta and H. Tamamura, Org. Lett., 2015, 17, 5372–5375 CrossRef CAS PubMed.
- R. Nomula, X. Wu, J. Zhao and N. R. Munirathnam, Mater. Sci. Eng., C, 2017, 79, 710–719 CrossRef CAS PubMed.
- Q. Zou, Y. Fang, Y. Zhao, H. Zhao, Y. Wang, Y. Gu and F. Wu, J. Med. Chem., 2013, 56, 5288–5294 CrossRef CAS PubMed.
- R. Brimioulle, A. Bauer and T. Bach, J. Am. Chem. Soc., 2015, 137, 5170–5176 CrossRef CAS PubMed.
- K. N. Solov'ev and E. A. Borisevich, Phys.-Usp., 2005, 48, 231–253 CrossRef.
- D. S. McClure, J. Chem. Phys., 1949, 17, 905–913 CrossRef CAS.
- T. Furuta, S. S. H. Wang, J. L. Dantzker, T. M. Dore, W. J. Bybee, E. M. Callaway, W. Denk and R. Y. Tsien, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 1193–1200 CrossRef CAS PubMed.
- J. S. Seixas de Melo, R. S. Becker and A. L. Macanita, J. Phys. Chem., 1994, 98, 6054–6058 CrossRef CAS.
- J. Seixas de Melo, R. S. Becker, F. Elisei and A. L. Maçanita, J. Chem. Phys., 1997, 107, 6062–6069 CrossRef CAS.
- B. R. Henry and R. V. Hunt, J. Mol. Spectrosc., 1971, 39, 466–470 CrossRef CAS.
- B. R. Henry and E. A. Lawler, J. Mol. Spectrosc., 1973, 48, 117–123 CrossRef CAS.
- T. G. Pavlopoulos and D. G. Taylor, Spectrochim. Acta, 1985, 41, 1357–1358 CrossRef.
- G. Jones, W. R. Jackson, C. Y. Choi and W. R. Bergmark, J. Phys. Chem., 1985, 89, 294–300 CrossRef CAS.
- G. A. Reynolds and K. H. Drexhage, Opt. Commun., 1975, 13, 222–225 CrossRef CAS.
- M. S. Wagner, E. D. Ilieva, P. S. Petkov, R. D. Nikolova, R. Kienberger and H. Iglev, Phys. Chem. Chem. Phys., 2015, 17, 9919–9926 RSC.
- G. J. Zhao and K. L. Han, J. Phys. Chem. A, 2007, 111, 2469–2474 CrossRef CAS PubMed.
- K. Khemakhem, M. Soulié, R. Brousses, H. Ammar, S. Abid and S. Fery-Forgues, Chem.–Eur. J., 2015, 21, 7927–7937 CrossRef CAS PubMed.
- J. Parrish, L. Tong, M. Wang, X. Chen, E. B. Lansdon, C. Cannizzaro, X. Zheng, M. C. Desai and L. Xu, Bioorg. Med. Chem. Lett., 2013, 23, 1493–1497 CrossRef CAS PubMed.
- J. M. Boilevin and J. L. Reymond, Synth, 2018, 50, 2631–2654 CrossRef CAS.
- A. Bojilova, R. Nikolova, C. Ivanov, N. A. Rodios, A. Terzis and C. P. Raptopoulou, Tetrahedron, 1996, 52, 12597–12612 CrossRef CAS.
- A. M. Brouwer, Pure Appl. Chem., 2011, 83, 2213–2228 CAS.
- M. L. Horng, J. A. Gardecki, A. Papazyan and M. Maroncelli, J. Phys. Chem., 1995, 99, 17311–17337 CrossRef CAS.
- U. Megerle, I. Pugliesi, C. Schriever, C. F. Sailer and E. Riedle, Appl. Phys. B, 2009, 96, 215–231 CrossRef CAS.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010 Search PubMed.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
- M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449 CrossRef CAS.
- G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi and V. Barone, J. Chem. Phys., 2006, 124, 094107 CrossRef PubMed.
- F. Furche and R. Ahlrichs, Chem. Phys., 2002, 117, 7433–7447 CAS.
- C. Van Caillie and R. D. Amos, Chem. Phys. Lett., 1999, 308, 249–255 CrossRef CAS.
- R. E. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224 CrossRef CAS.
- D. Yang, Y. Liu, D. Shi and J. Sun, Comput. Theor. Chem., 2012, 984, 76–84 CrossRef CAS.
- A. Pedone, J. Chem. Theory Comput., 2013, 9, 4087–4096 CrossRef CAS PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef PubMed.
- M. J. S. Dewar and P. J. Grisdale, J. Am. Chem. Soc., 1962, 84, 3539 CrossRef CAS.
- A. Pigliucci and E. Vauthey, CHIMIA International Journal for Chemistry, 2003, 57, 200–203 CrossRef CAS.
- J. Y. Liu, W. H. Fan, K. K. Han, W. Q. Deng, D. L. Xu and N. Q. Lou, J. Phys. Chem. A, 2003, 107, 10857–10861 CrossRef CAS.
- Y. Gan, et al., Phys. Chem. Chem. Phys., 2017, 19, 12094–12106 RSC.
- M. Humbert-Droz, C. Piguet and T. A. Wesolowski, Phys. Chem. Chem. Phys., 2016, 18, 29387–29394 RSC.
- Y. Yamaguchi, Y. Matsubara, T. Ochi, T. Wakamiya and Z. I. Yoshida, J. Am. Chem. Soc., 2008, 130, 13867–13869 CrossRef CAS PubMed.
- H. Zhang, et al., Synth. Met., 2010, 160(15–16), 1642–1647 CrossRef CAS.
- S. Phukan, M. Saha, K. A. Pal, A. C. Bhasikuttan and S. Mitra, J. Photochem. Photobiol., A, 2015, 303–304, 67–79 CrossRef CAS.
- X. Ni, Y. Guo, H. Bu, J. An and D. En, J. Chin. Chem. Soc., 2012, 59, 1439–1445 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |