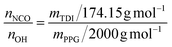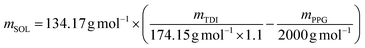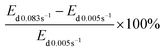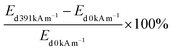Open Access Article
Open Access ArticleMagneto-induced rheological properties of magnetorheological gel under quasi-static shear with large deformation
Runsong Mao ,
Huixing Wang,
Guang Zhang
,
Huixing Wang,
Guang Zhang ,
Xudan Ye and
Jiong Wang*
,
Xudan Ye and
Jiong Wang*
School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China. E-mail: wjiongz@njust.edu.cn
First published on 27th August 2020
Abstract
Magnetorheological gel (MRG) is a kind of magneto-sensitive smart material mainly composed of soft magnetic particles and polyurethane, which can decrease or even avoid the severe sedimentation problem appearing in MR fluids. In this work, the rheological properties of MRG under quasi-statically monotonic and cyclic loading with large deformation were investigated, respectively. The results could provide effective guidance for the design of MR devices that are often subjected to quasi-static loading. Firstly, MRG was fabricated by mixing carbonyl iron particles (CIPs) with the polyurethane matrix. Then, variations of normal force with time and magnetic field for MRG were tested and discussed. Moreover, the influences of CIPs content, shear rate, shear strain amplitude and magnetic field on the energy dissipation density of MRG were analyzed. The results showed the magneto-induced damping performance of MRG is highly relevant to the CIPs content and magnetic field, i.e. the magneto-induced enhancement of energy dissipation density of MRG with 60% CIPs content could reach up to 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900% when the external magnetic strength increases to 391 kA m−1. Furthermore, the related mechanisms, from the perspective of microstructure, were proposed to qualitatively explain the various mechanical phenomena occurring in shear stress and normal force.
900% when the external magnetic strength increases to 391 kA m−1. Furthermore, the related mechanisms, from the perspective of microstructure, were proposed to qualitatively explain the various mechanical phenomena occurring in shear stress and normal force.
1. Introduction
Magnetorheological (MR) materials are a novel type of intelligent material whose rheological properties can be controlled rapidly and reversibly by adjusting the external magnetic field.1,2 To date, liquid-like MR fluid3,4 (MRF) and solid-like MR elastomer5,6 (MRE) are the two most famous MR materials and have been widely investigated in devices such as dampers and isolators, etc. However, there are few reports on the commercialization of MR applications based on MRF or MRE. The reason for this is that, for MR fluids, the soft magnetic particles dispersed in the liquid matrix (mineral oil or water, etc.) are easy to settle due to the huge density difference between them.7,8 This defect will give rise to some severe problems such as reduction of the stability and lifetime of the devices. On the other hand, the solid matrix based MRE could thoroughly avoid the sedimentation problem. However, MRE has comparatively low MR effect9,10 because the movement of particles is restricted by the rigid matrix (natural or synthetic rubber, etc.). Different from MRF and MRE, MR gel possesses excellent sedimentation stability and a relatively high MR effect due to the existence of the polymer matrix, which has attracted many researchers' attention in recent years.11–13 Moreover, MRG also has many other prominent features,14–16 such as electric property, acoustic property, which are not possessed by MRF and MRE. Overall, the occurrence of MRG may realize the commercialization of MR materials in the practical devices, such as MR dampers,17–19 magnetic-controlled sensor and actuators.20The rheological properties, e.g. viscosity, yield stress, are important factors in the design of the MR devices. Until now, researchers conducted a series of experiments on the rheological properties of MRG. Xu et al.21 investigated the time-dependent stress relaxation behavior of MRG under different magnetic fields. It found that the instantaneous and stable modulus of MRG with ordered chain-like microstructures are larger than those of MRG with unordered microstructures in the absence of a magnetic field.21 Zhang et al.22 carried out the static and dynamic shear tests to study the rheological properties of polyurethane-based MRG. The static experiments indicated that, compared with other factors, the magnetic field has a stronger influence on the rheological properties. Also, the tendency with magnetic strength can be divided into initial increment, the linear increment and the saturate tendency. The dynamic oscillation tests show the maximum loss modulus of the MRG with 80% CIPs content could reach 0.626 MPa and the corresponding strain amplitude was 0.526%. As known, the exterior loading applied to MR materials are basically categorized into three kinds: static loading, dynamic loading and quasi-static loading.23–25 However, the current experiments on the rheological properties of MRG are almost conducted under the static and dynamic shear. To the best of our knowledge, the investigation on the rheological properties of MRG under quasi-static shear has never been reported. For PU-based MR gels, in the absence of a magnetic field, the movement of soft segments in the polymer matrix is the primary contribution to the rheological performance compared with that of the magnetic particles. However, in the presence of a magnetic field, the magneto-induced rheological properties under quasi-static shear are highly relevant to the coupling effects between the particle chains and the polymeric matrix. Particle chains were continuously recovered while being destroyed by shearing under the continuous application of a magnetic field and quasi-static shear with a small shear rate. Simultaneously, the polymer matrix is also continually recovering due to the thixotropic properties of the matrix. At this time, the continuously recovered particle chains and polymer matrix are further coupled with each other, resulting in a more complex microstructure. These phenomena inevitably lead to different rheological properties.26,27 Therefore, it is urgent to investigate the magneto-mechanical performance of MRG under quasi-static shear with and without magnetic field.
The purpose of this study is to investigate the magneto-induced rheological properties of MRG with different CIPs content under quasi-statically loading and large shear deformation. Firstly, MRG with 40%, 60%, and 70% CIPs content were prepared, respectively. Then, the magnetic field-dependent deformation of MRG was tested and the corresponding magneto-induced normal force of sample is analyzed. Finally, the magneto-induced rheological properties and damping performance of MRG under monotonic and cyclic shearing code with different shear rates, CIPs content, strain amplitudes and magnetic fields are discussed.
2. Experimental
2.1 Raw materials
Table 1 presents the details of the raw materials used for the preparation of MRG. Toluene diisocyanate (TDI; 2,4- ≈ 80%, 2,6- ≈ 20%, Tokyo Chemical Industry Co., Ltd, Japan) and polypropylene glycol (PPG-2000, Mn = 2000, Sigma-Aldrich (Shanghai) Trading Co., Ltd, China) were selected as the two main reactants to fabricate the PU matrix. Dipropylene glycol (SOL, Sigma-Aldrich (Shanghai) Trading Co., Ltd, China) was selected as the chain extender. Stannous octoate (Sinopharm Chemical Reagent Co., Ltd, China) was selected as a catalyst. Carbonyl iron powder (CIPs, type CN, BASF, Germany with an average particle size of about 6 μm) was selected as the soft magnetic particles.| Raw materials | Usage | Producer |
|---|---|---|
| Toluene diisocyanate (TDI) | Main reactant | Tokyo Chemical Industry Co., Ltd, Japan |
| Polypropylene glycol (PPG-2000) | Main reactant | Sigma-Aldrich (Shanghai) Trading Co., Ltd, China |
| Dipropylene glycol (SOL) | Chain extender | Sigma-Aldrich (Shanghai) Trading Co., Ltd, China |
| Stannous octoate | Catalyst | Sinopharm Chemical Reagent Co., Ltd, China |
| Carbonyl iron powder (CIP) | Magnetic particle | BASF, Germany |
The weight ratio of TDI to PPG was decided by the following formula:
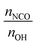 was selected as 3
was selected as 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 according to the paper of Wei28 and Zhang.29 Meanwhile, the weight of SOL was decided by the following formula:
1 according to the paper of Wei28 and Zhang.29 Meanwhile, the weight of SOL was decided by the following formula:where, the mSOL represents the weight of SOL.
2.2 Fabrication of MRG
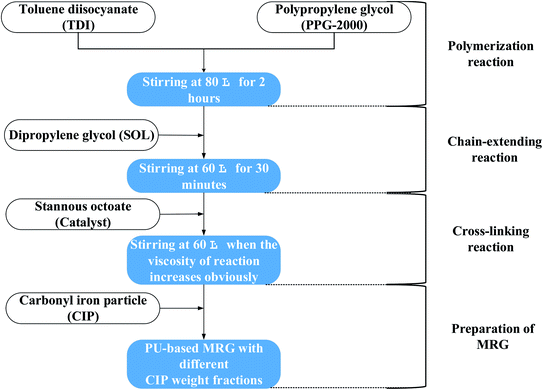
There are three steps in the fabrication of the PU matrix (as shown in Fig. 1). Firstly, PPG was evaporated at 100 °C in the loft drier for about one hour. Then, TDI and PPG were agitated in a 250 mL three-necked round bottom flask with a mechanical stirrer and the reaction was kept at 80 °C. Two hours later, SOL was added into the flask and the temperature of the reaction was simultaneously dropped to 60 °C. Finally, moderate stannous octoate was added into the flask at the same temperature. The stirrer agitated at high speed during the whole reaction.After the fabrication of the PU matrix, the CIPs was added into it immediately before the matrix chilled down. Moreover, stirring vigorously for a long enough time to make sure the iron particles and matrix mixed adequately. Then, the geometry of the self-developed MRG is presented in Fig. 2. The microstructure of MRG is observed with a digital microscope (type VHX-100, Keyence) and the shining white points shown in Fig. 2(b) represents magnetic particles. In this paper, three kinds of MRG with different CIPs weight percentages were synthesized and the samples were named as MRG-40, MRG-60, MRG-70 individually (Table 2).
| Samples | CIP (wt%) | PU (wt%) |
|---|---|---|
| MRG-40 | 40 | 60 |
| MRG-60 | 60 | 40 |
| MRG-70 | 70 | 30 |
2.3 Experimental and test
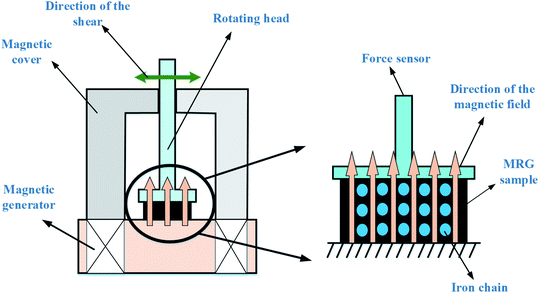
A commercial rheometer (Type MCR 302, Anton Paar Co., Graz, Austria) equipped with the magnetorheological module (Type MRD180, Anton Paar Co., Austria) was used to conduct a series of experiments to study the rheological properties of MRG under monotonic and cyclic loading. The schematic diagram of MCR 302 is shown in Fig. 3. During the process of the experiment, MRG was laid between the magnetic generator and rotating head. The bottom plate of the rotating head has a diameter of 20 mm and the gap distance between the two plates was set as 1 mm. A magnetic cover is employed to intensify the magnetic field and make it identical in the distance where MRG is placed. The shear stress and normal force of MRG were firstly measured with the strain-controlled mode and then the data was recorded and processed with a data acquisition board (DAQ) and computer. The direction along the direction of magnetic field (i.e. vertical to bottom plate) is defined as the normal direction.As shown in Fig. 4, the quasi-static shear test is conducted under two different mode,30 i.e. monotonic shear mode and cyclic shear mode. The test fundamental of monotonic shear mode is presented in Fig. 4(a). The shear strain grows linearly from 0% to 100% in four different times (i.e. 200 s, 50 s, 25 s and 12 s). Thus, the corresponding shear rates are 0.005 s−1, 0.02 s−1, 0.04 s−1 and 0.083 s−1, respectively. Fig. 4(b) presents the test fundamental of cyclic shear mode. The shear strain that applied on MRG varies in a triangular wave, and the shear time and corresponding shear rates are the same as those under monotonic shear mode. Furthermore, all the experiments were carried out at a temperature of 25 °C.
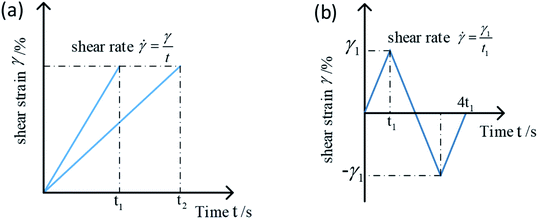 | ||
| Fig. 4 Schematic diagram of quasi-static shear mode: monotonic shear mode (a) and cyclic shear mode (b). | ||
3. Results and discussion
3.1 Magneto-induced normal force of MRG under large deformation
To investigate the quasi-static properties of MRG under large deformation, MRG-70 was chosen as an experimental sample and placed directly between the two plates of rheometer, as shown in Fig. 5(a). Then, a uniform 740 kA m−1 magnetic strength was applied to the sample and lasted 60 seconds. An obvious change can be found from Fig. 5(a) to Fig. 5(b). Flower-like structures are observed in Fig. 5(b), and feel rigid when we touched them. The flower-like structures started to ‘fade’, and felt softer than the former state when the magnetic field returns to 0. This phenomenon authenticates the fact that the unordered particle microstructures in the absence of a magnetic field will change into powerful chain-like or column-like microstructures in the presence of a magnetic field. Moreover, when the external magnetic field is removed, the needle-like shape (Fig. 5(c)) retained for a while and did not return to the original state (Fig. 5(a)) immediately, which has not been reported in MR fluid and elastomer.Fig. 6 displayed the variations of normal force Fn with magnetic field for MRG with different CIPs content. The magnetic strength increases linearly from 0 kA m−1 to 740 kA m−1 during the experiments. The normal force increases rapidly first and then slowly with the magnetic strength. Besides, MRG with more magnetic particles appears larger normal force. It is worthwhile to note here that there are three critical values (as shown in Fig. 6, i.e. C40, C60 and C70, respectively) that divide the Fn–H curves into two sections. When the magnetic strength is smaller than the critical values, the slopes of the Fn–H curves will increase gradually along with the magnetic strength. When the magnetic strength is larger than the critical value, the slopes of the Fn–H curves will occur progressive decreasing trends. Furthermore, the critical values increase with the CIPs content, i.e. C40 < C60 < C70. This phenomenon indicates that the ability, which the normal force increases rapidly with the magnetic field, will decrease moderately when the excited magnetic strength exceeds a critical value. This phenomenon may be ascribed to the transformation of interior microstructures in MRG. The interior magnetic particles in MRG transfer from unordered particle structures to chain-like structures with the growing of magnetic field, resulting the dramatic and drastic changes of normal force of MRG. The chain-like structures gradually form such stable column-like or cluster-like structures that the normal force of MRG saturates with the continuous increasing of magnetic strength.
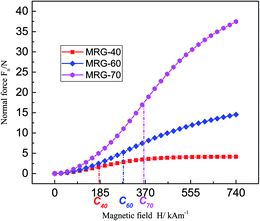 | ||
| Fig. 6 The normal force of Fn of MRG in the condition where the magnetic field changes linearly from 0 kA m−1 to 740 kA m−1 (i.e. from 0 A to 4 A). | ||
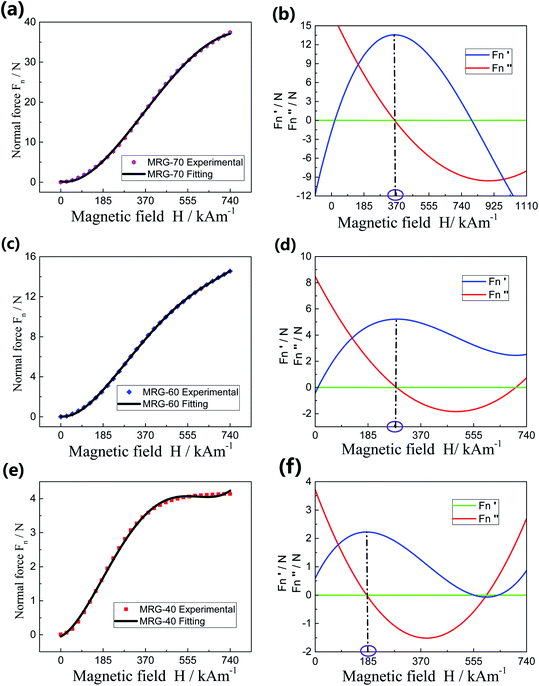
Furthermore, calculations of the three critical values are presented as follow. A polynomial fitting method (i.e. Fn = B1H + B2H2 + B3H3 + B4H4 + intercept) was adopted to fit the experimental data of the normal force (Fn) of MRG-40, MRG-60 and MRG-70 and the parameters were listed in Table 3. It can be seen from Fig. 7(a), (c) and (e) that the fitting curves could be well matched the experimental data. Then the slopes of Fn 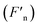 of MRG-40, MRG-60 and MRG-70, and their derivatives
of MRG-40, MRG-60 and MRG-70, and their derivatives 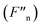 were respectively calculated (presented in Fig. 7(b), (d) and (f)). According to the above-mentioned discussion, the critical magnetic fields should be theoretically corresponding to the maximum of the
were respectively calculated (presented in Fig. 7(b), (d) and (f)). According to the above-mentioned discussion, the critical magnetic fields should be theoretically corresponding to the maximum of the 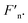 Therefore, we let
Therefore, we let 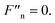 Consequently, the critical magnetic fields were calculated (i.e. 179 kA m−1 for MRG-40, 285 kA m−1 for MRG-60, and 360 kA m−1 for MRG-70), and marked with purple circles in Fig. 7(b), (d) and (f)).
Consequently, the critical magnetic fields were calculated (i.e. 179 kA m−1 for MRG-40, 285 kA m−1 for MRG-60, and 360 kA m−1 for MRG-70), and marked with purple circles in Fig. 7(b), (d) and (f)).
| Samples | Parameters | ||||
|---|---|---|---|---|---|
| B1 | B2 | B3 | B4 | Intercept | |
| MRG-40 | 0.59369 | 1.86021 | −0.82782 | 0.09815 | −0.04965 |
| MRG-60 | −0.43329 | 4.24101 | 1.28976 | 0.12086 | 0.04139 |
| MRG-70 | −1.75589 | 8.60307 | −1.8466 | 0.09546 | 0.21036 |
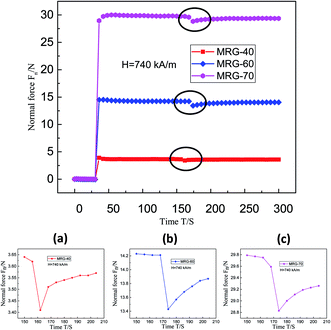
To investigate the transient properties of MRG, MRG with different CIPs content were selected as the samples and then applied a transient 740 kA m−1 magnetic field at the 30th second. From the upper series in Fig. 8, the normal force appears a sudden increase first and then saturates when the magnetic field of 740 kA m−1 is applied. Moreover, the more the magnetic particles are, the larger the normal force is. However, it is of great necessity to note that the normal force occurs an abrupt drop between 160th second and 180th second (as shown in the lower series of Fig. 8) and then increases gradually to a constant level. An explanation for the sudden drop may be due to the evolution of the internal particle microstructures in MRG. The sudden drop phenomenon possibly results from the fracture of unstable chain-like particle aggregations in MRG. Initially, the magnetic particles are randomly dispersed in MRG in the absence of a magnetic field (Fig. 9(a)). However, the magnetic particles will immediately aggregate into some short chains in the presence of a magnetic field. Then, these short chains will progressively gather together and evolve into long chains due to the continuous application of the magnetic field (Fig. 9(b)). However, these long chains are not so stable that interfacial slipping and extrusion between the particles will happen. The contribution of magnetic attractive force between particles to normal force is positive while the contribution of interfacial slipping and extrusion between particles to normal force is negative. Therefore, the normal force will occur an abrupt drop at some point when the effect of magnetic attractive force is weaker than that of slipping. However, the unstable particle chains will finally aggregate together to form stable cluster-like microstructures (Fig. 9(c)) or complex network-like microstructures, resulting in the gradual increase of normal force with the increment of time. Besides, the magnitude of the normal force could achieve as high as 30 N (about 95.49 kPa) and the weight fractions of CIP have a significant impact on the magnitude of the normal force. From the above-mentioned tests, one can conclude that it is promising for MRG to be employed in the devices like MR force sensor and actuator.31,32
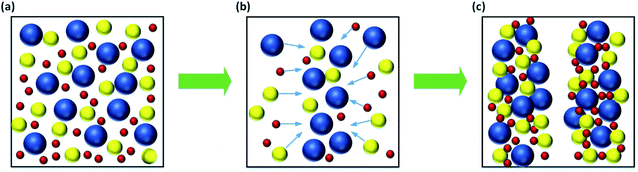 | ||
| Fig. 9 The microscopic particle structures of the MRG evolve from the initial unordered structure (a) to an unstable chain-like structure (b) and then to a stable cluster-like structure (c). | ||
3.2 Frequency sweep
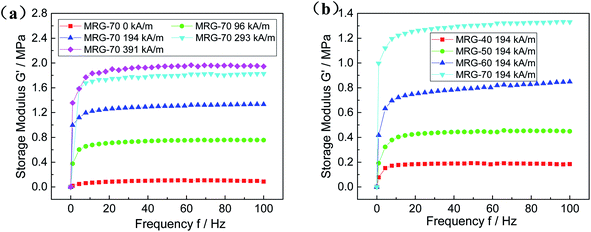
Storage modulus G′ is a significant factor to characterize the elastic feature of viscoelastic materials. It also represents the capacity of storing the deformation energy during shearing, and the stored energy could be thoroughly available when the exterior shearing is uploaded.33 Thus, a series of experiments of frequency sweep were conducted on MRG at a constant strain amplitude of 0.01%, and the frequency was changed from 0 to 100 Hz. Fig. 10 presents the influence of magnetic fields and CIP contents on the storage modulus of MRG. The results presented in Fig. 10(a) reveal that frequency has a weak influence on the storage modulus of MRG, neither with nor without applied magnetic fields. For example, the storage modulus of MRG-70 almost keeps constant when the frequency approximately exceeds 10 Hz. Moreover, it could be seen from Fig. 10(a) that the influence of magnetic fields on the storage modulus of MRG shows a decreasing trend with increasing of magnetic fields, resulting from the gradually saturated magnetic particles in MRG.34 Therefore, the gaps between the steady-state value of storage modulus decrease progressively with the increasing of magnetic fields.35 On the other hand, taking MRG-40 for example, storage modulus appears a rising trend with the enlargement of frequency at first and then gets a plateau gradually. Fig. 10(b) also demonstrates that the CIP contents of MRG have a strong effect on the storage modulus, i.e. MRG with more magnetic particles usually achieves a larger storage modulus.3.3 Quasi-static properties of MRG under monotonic shear mode
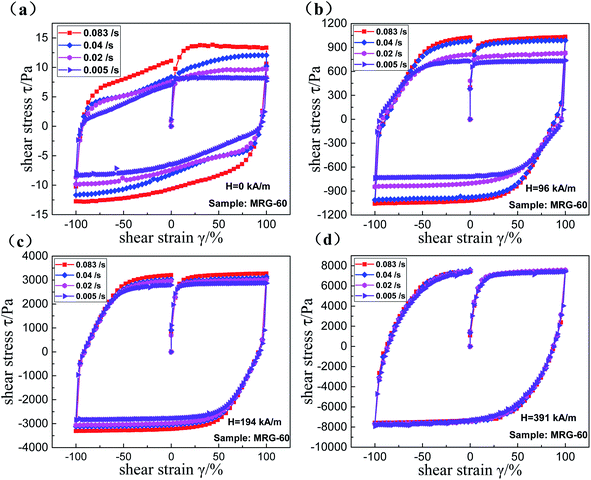
To understand the shear rate-dependent properties of MRG, MRG-60 was selected as a test sample. The variations of shear stress with shear strain for MRG-60 under four different shear rates and constant magnetic fields are displayed in Fig. 11. In the absence of a magnetic field, the shear stress appears an abrupt increment firstly and then gets a gradual plateau with the increasing of shear strain when the shear rates are set as 0.005 s−1 and 0.02 s−1. However, the shear stress gets up to a maximum value firstly and then decreases to a steady-state value which is slightly smaller than the maximum value when the shear rates are set as 0.04 s and 0.083 s−1. These phenomena indicate that there is a threshold between the 0.02 s−1 and 0.04 s−1. However, these phenomena will disappear in the presence of a magnetic field, i.e. the shear stress evenly trends stable after a sudden increment, which is different from the MR grease36 and MR plastomer.37 Another notable characteristic is that the influence of shear rate on the shear stress will be negligible gradually with the increasing of the external magnetic field. There is almost no discrepancy between the shear stress under different shear rates (Fig. 11(d)) at the 391 kA m−1 magnetic strength and it is not the phenomena of wall slip after confirmations. This may be ascribed to the formation of the similar column-like or cluster-like microstructures and the high damping performance originated from the microstructures in MRG when the magnetic field is strong enough.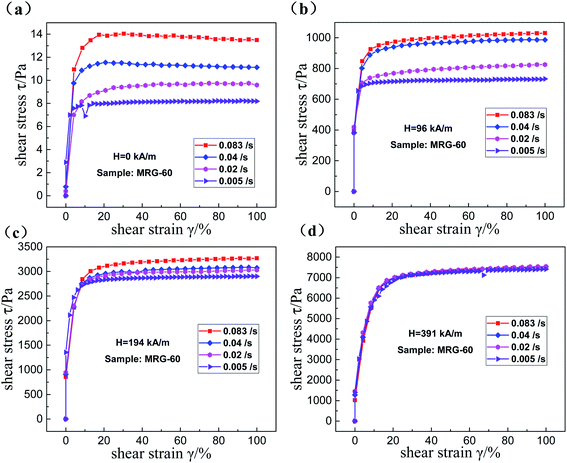 | ||
| Fig. 11 The shear stress–strain curves of MRG-60 under different shear rates with 0 kA m−1 (a); 96 kA m−1 (b); 194 kA m−1 (c) and 391 kA m−1 (d). | ||
3.4 Magneto-induced damping performance of MRG under cyclic shear mode
In this section, the influence of CIPs content, shear rate and shear strain amplitude on the damping performance of MRG under different magnetic fields will be discussed. As mentioned before, MRG is promising to be used in vibration control devices such as MR damper. MRG can dissipate the energy and attenuate the damage when it is exposed to the vibration caused by external motivation. Therefore, it is necessary to study the energy dissipation density under quasi-statically and cyclically shearing conditions. As known, the area surrounded by the shear stress–strain curve represents the energy dissipation density of MRG. The larger the area is, the larger the energy dissipation density is, and the better the damping performance of MRG is.38 The area of shear stress–strain curve could be quantitatively calculated using the following integral formula:| Ed = ∮τdγ | (1) |
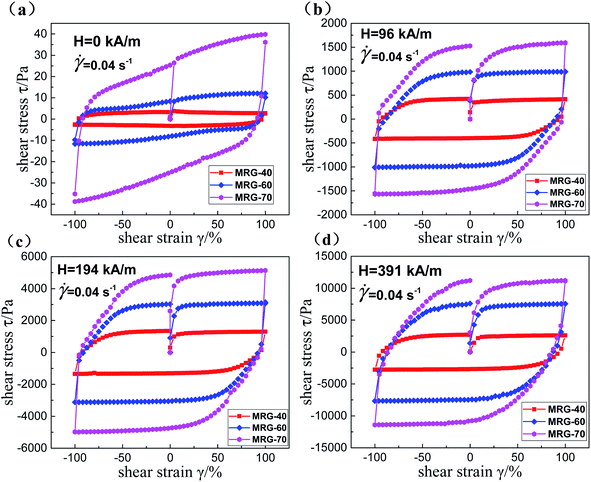 | ||
| Fig. 12 The shear stress–strain curves of MRG with different CIP contents under constant shear rate of 0.04 s−1. 0 kA m−1 (a); 96 kA m−1 (b); 194 kA m−1 (c) and 391 kA m−1 (d). | ||
Taking MRG-70 for example, the changing regularity of the field-dependent shapes of shear stress–strain curves under four constant magnetic fields is shown in Fig. 13. The shear stress–strain curve displays a closed parallelogram-like shape in the absence of a magnetic field while it displays a gapped polygon-like shape and a gapped ellipse-like shape in the presence of a magnetic field (marked by the blue dotted lines in Fig. 13). Moreover, the shear stress appears a sudden decrease (or increase) immediately during the transition from loading to unloading (i.e. the shear strain changes from 100% to 0% or −100% to 0%) in the presence of a magnetic field, as marked by the green dotted lines in Fig. 13(b)–(d). However, MRG gets a delayed decrease (or increase) in the absence of a magnetic field, as marked by a green dotted line in Fig. 13(a). To the best of our knowledge, this phenomenon has not found in MR fluid and MR elastomer.
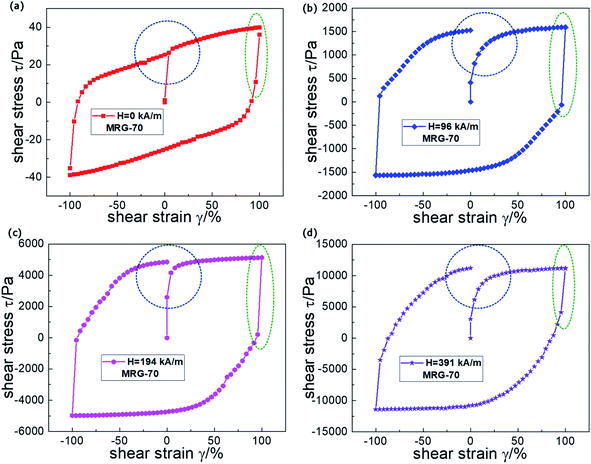 | ||
| Fig. 13 The shear stress–strain curves of MRG-70 under constant shear rate of 0.04 s−1 with 0 kA m−1 (a); 96 kA m−1 (b); 194 kA m−1 (c) and 391 kA m−1 (d). | ||
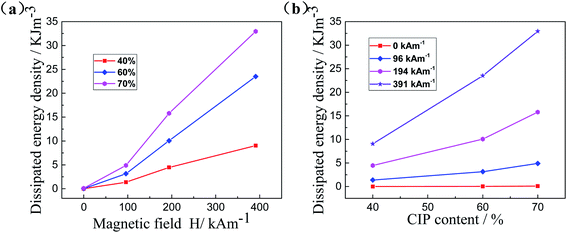
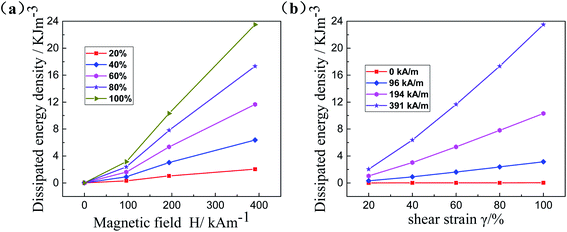
To evaluate the damping performance of MRG, the energy dissipation density (i.e. the area of the shear stress–strain curve) of MRG with different CIPs content under different magnetic fields is calculated, as presented in Fig. 14. The energy dissipation densities are 0.01, 0.03 and 0.09 kJ m−3 for MRG-40, MRG-60 and MRG-70, respectively. In other words, there is almost no difference between the energy dissipation densities of MRG with different CIPs content in the absence of a magnetic field. It demonstrates that the CIPs content have weak effects on the damping performance of MRG when the excited magnetic field is not applied. However, the energy dissipation density of MRG with constant CIPs content increases dramatically with the increasing of the magnetic field, as displayed in Fig. 14(a). This is because the application of a magnetic field will lead to the generation of the magnetic interaction between soft magnetic particles, resulting in the particle chains being rather stiff and hard to be demolished. At this time, the demolition of the particle chains (restraint to magnetic interaction and interface slipping between particles) is the main mechanism of energy dissipation behavior. Therefore, more energy is needed to destroy the particle chains in the presence of a magnetic field. The magnetic interaction between particles increases with the magnetic field, which demonstrates that the energy dissipation density is highly dependent on the excited magnetic field. Fig. 14(b) also implies that MRG with larger CIPs content usually possesses larger energy dissipation density and better magneto-induced damping performance when the excited magnetic field is constant. Apparently, the larger the CIPs content of MRG is, the more particle chains will form under a constant magnetic field. Therefore, it will consume more energy to break the particle chains. More energy is dissipated by MRG with higher CIPs content. Moreover, the dissipated energy density of MRG-70 reaches as high as 32.95 kJ m−3 under the magnetic field of 391 kA m−1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900% under the shear rate of 0.005 s−1, which is nearly twice than that under the shear rate of 0.083 s−1. A time-dependent explanation could be used to interpret this phenomenon. When the shear rate (i.e. 0.005 s−1) is relatively small, the magnetic field is given long enough time (i.e. 200 s) to drive the transformation of microstructures from unordered state to steady state. However, under a relatively larger shear rate of 0.083 s−1, the transformation of the microstructures is mainly driven by the shear-induced deformation instead of the magnetic field. It is because the magnetic field can only drive the transformation of microstructure partly due to relatively less time (i.e. 12 s). As discussed in 3.4.1, the magnetic field is the primary influencing factor in the evolution of interior microstructures. Thus, the microstructures do not evolve completely due to the limitation of time when the shear rate is relatively larger. Consequently, the magneto-induced enhancing effect on damping performance decreases with the increase of shear rate.
900% under the shear rate of 0.005 s−1, which is nearly twice than that under the shear rate of 0.083 s−1. A time-dependent explanation could be used to interpret this phenomenon. When the shear rate (i.e. 0.005 s−1) is relatively small, the magnetic field is given long enough time (i.e. 200 s) to drive the transformation of microstructures from unordered state to steady state. However, under a relatively larger shear rate of 0.083 s−1, the transformation of the microstructures is mainly driven by the shear-induced deformation instead of the magnetic field. It is because the magnetic field can only drive the transformation of microstructure partly due to relatively less time (i.e. 12 s). As discussed in 3.4.1, the magnetic field is the primary influencing factor in the evolution of interior microstructures. Thus, the microstructures do not evolve completely due to the limitation of time when the shear rate is relatively larger. Consequently, the magneto-induced enhancing effect on damping performance decreases with the increase of shear rate.
 | ||
| Fig. 15 The shear stress–strain curves of MRG-60 under different shear rates. 0 kA m−1 (a); 96 kA m−1 (b); 194 kA m−1 (c) and 391 kA m−1 (d). | ||
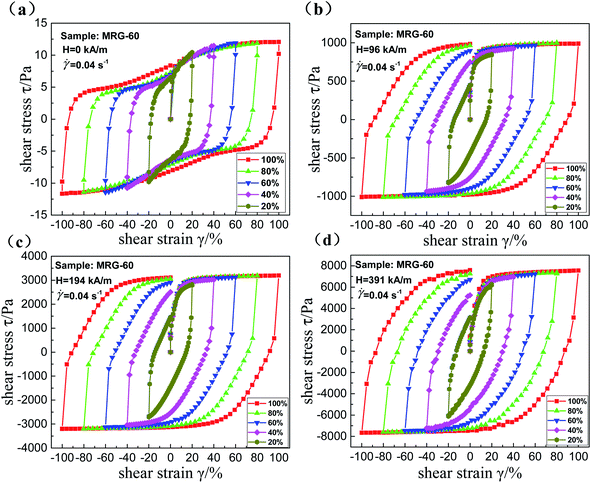 | ||
| Fig. 16 The shear stress–strain curves of MRG-60 under different shear strain amplitude. 0 kA m−1 (a); 96 kA m−1 (b); 194 kA m−1 (c) and 391 kA m−1 (d). | ||
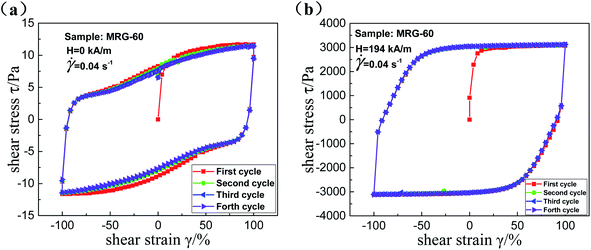 | ||
| Fig. 18 The shear stress–strain curves of MRG-60 with a constant shear rate of 0.04 s−1 under numerous cyclic shear 0 kA m−1 (a); 194 kA m−1 (b). | ||
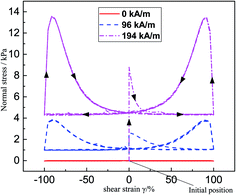
Besides, we particularly pay attention to the relationship between normal stress and shear strain under a constant shear rate of 0.04 s−1 and different magnetic fields, as shown in Fig. 19. The black arrows represent the evolution process of normal stress. In the absence of a magnetic field, the normal stress–strain curve behaves a straight line-like shape and the normal stress is almost zero. However, the normal stress changes from 0.98 kPa to 3.85 kPa under 96 kA m−1-field condition. And it appears a much larger variation range from 4.27 kPa to 13.54 kPa under 96 kA m−1-field condition, resulting from the contribution of the magneto-induced enhancing effect. On the other hand, the normal stress gets a sudden increase immediately as soon as a magnetic field is applied due to the contribution of magneto-induced cluster-like structures. This proves that the randomly dispersed particles in MRG will change into ordered particle chain microstructure within milliseconds. Then, normal stress begins to decrease and plateaus to a minimum value (0.98 and 4.27 kPa in the magnetic field of 96 kA m−1 and 194 kA m−1, respectively). The rebuilding and fracture of the internal particle chain microstructures carry out simultaneously and their contributions to the normal stress are contrary. When the influence of the fracture (such as the gradually enlarged gap between particles and the incline of the particle chain, etc.) is larger than that of the rebuilding, the normal stress will fall. On the contrary, normal stress will move up when the influence of rebuilding is larger than that of fracture. Then, the internal particle chain microstructure starts to rebuild and contribute to the increasing of normal stress again when the shear strain inversely approaches 0% after it reaches 100%. However, the reconstructive internal microstructure will be destroyed again due to the gradual change of the shearing deformation, resulting in the emergence of peaks of normal stress (i.e. 3.85 and 13.54 kPa under a magnetic field of 96 and 194 kA m−1, respectively).
4. Conclusion
In this paper, two kinds of experiments, (i.e., magneto-induced large deformation shear and magneto-induced damping performance under quasi-statically and cyclically condition, respectively), were conducted to investigate the rheological properties of MRG. The excited magnetic field has a strong effect on the shear stress and normal force by transforming the interior microstructure in MRG, which indirectly results in the magneto-induced large deformation and enhancing damping performance. The magneto-induced normal force increases with the increment of the magnetic field, and the speed of the increment firstly increases rapidly and then slows down gradually. The normal force of MRG-70 could be adjusted in a large range from 0 to 30 N (95.4 kPa) in the magnetic strength of 740 kA m−1. In the quasi-static monotonic shear test, the influence of shear rate on magneto-induced shear stress is nearly negligible when the magnetic field is strong enough. From the discussion on the energy dissipation density of MRG under the cyclic shear mode, the shape-changing regularity of shear stress–strain curve is mainly influenced by the external magnetic field. Magneto-induced damping performance of MRG is highly relevant to the external actuating conditions (i.e. CIP content, shear rate, shear strain amplitude and magnetic field). The magneto-induced enhanced damping performance of MRG-60 could attain 104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900% in the magnetic strength of 391 kA m−1 while it will significantly reduce with the increasing of shear rate. Besides, one can conclude that the larger the shear strain amplitude, the larger the energy dissipation density, the better the damping performance of MRG. This work will provide effective guideline for the design of MR devices used for vibration controlling (such as dynamic vibration absorber), which is our main work of the next stage.
900% in the magnetic strength of 391 kA m−1 while it will significantly reduce with the increasing of shear rate. Besides, one can conclude that the larger the shear strain amplitude, the larger the energy dissipation density, the better the damping performance of MRG. This work will provide effective guideline for the design of MR devices used for vibration controlling (such as dynamic vibration absorber), which is our main work of the next stage.
Conflicts of interest
There is no conflict to declare.Acknowledgements
The work of this paper has been supported by a National Natural Foundation of China (No. 51675280).Reference
- T. Shiga, A. Okada and T. Kurauchi, J. Appl. Polym. Sci., 1995, 58, 787–792 CrossRef CAS.
- G. Zhang, Y. C. Li, H. X. Wang and J. Wang, Front. Mater., 2019, 6(56) DOI:10.3389/fmats.2019.00056.
- N. Dogdu, I. Uslan, S. Yuksel and Z. Parlak, J. Mech. Sci. Technol., 2019, 33, 3885–3893 CrossRef.
- Y. Rabbani, M. Ashtiani and S. H. Hashemabadi, Soft Matter, 2015, 11, 4453–4460 RSC.
- J. K. Wu, X. L. Gong, Y. C. Fan and H. S. Xia, Smart Mater. Struct., 2010, 19(10) DOI:10.1088/0964-1726/19/10/105007.
- G. J. Liao, Y. G. Xu, F. J. Wang, F. Y. Wei and Q. Wan, Mater. Lett., 2016, 174, 79–81 CrossRef CAS.
- M. Ashtiani, S. H. Hashemabadi and A. Ghaffari, J. Magn. Magn. Mater., 2015, 374, 716–730 CrossRef CAS.
- S. H. Kwon, H. S. Jung, H. J. Choi, Z. Strecker and J. Roupec, Colloids Surf. A, 2018, 555, 685–690 CrossRef CAS.
- M. Bunoiu and J. Bica, J. Ind. Eng. Chem., 2016, 37, 312–318 CrossRef CAS.
- Y. C. Li, J. C. Li, W. H. Li and B. Samali, Smart Mater. Struct., 2013, 22(3) DOI:10.1088/0964-1726/22/3/035005.
- R. Ahamed, S. B. Choi and M. M. Ferdaus, J. Intel. Mat. Syst. Str., 2018, 29, 2051–2095 CrossRef.
- L. R. Wang, M. Yu, J. Fu and S. Qi, Smart Mater. Struct., 2018, 27(10) DOI:10.1088/1361-665X/aadf3e.
- P. Dhar, A. Katiyar, A. Pattamatta and S. K. Das, Colloids Surf. A, 2017, 530, 218–226 CrossRef CAS.
- C. L. Sun, H. M. Pang, S. H. Xuan and X. L. Gong, Mater. Lett., 2019, 256 DOI:10.1016/j.matlet.2019.126611.
- M. Yu, H. P. Luo, J. Fu and P. A. Yang, J. Intel. Mat. Syst. Str., 2018, 29, 24–31 CrossRef CAS.
- M. Yu, P. A. Yang, J. Fu, S. Z. Liu and S. B. Choi, Sens. Actuators, A, 2016, 245, 127–134 CrossRef CAS.
- M. Rahman, Z. C. Ong, S. Julai, M. M. Ferdaus and R. Ahamed, J. Zhejiang Univ., Sci., A, 2017, 18, 991–1010 CrossRef.
- I. I. M. Yazid, S. A. Mazlan, T. Kikuchi, H. Zamzuri and F. Imaduddin, Mater. Des., 2014, 54, 87–95 CrossRef.
- Y. Yu, Y. C. Li, J. C. Li, X. Y. Gu and S. Royel, Int. J. Struct. Stab. Dy., 2018, 18(8) DOI:10.1142/S0219455418400072.
- S. Kaluvan, Y. D. Park and S. B. Choi, Sens. Actuators, A, 2016, 238, 19–24 CrossRef CAS.
- Y. G. Xu, T. X. Liu, G. J. Liao and G. Lubineau, Smart Mater. Struct., 2017, 26(11) DOI:10.1088/1361-665X/aa89ac.
- G. Zhang, H. X. Wang, J. Wang, J. J. Zheng and Q. Ouyang, RSC Adv., 2019, 9, 10124–10134 RSC.
- O. Kuwano, R. Ando and T. Hatano, Powders and Grains, 2013, 1542, 32–37 Search PubMed.
- J. C. L. Perez, C. Y. Kwok, C. O'Sullivan, X. Huang and K. J. Hanley, Soils Found., 2016, 56, 152–159 CrossRef.
- H. X. Wang, G. Zhang and J. Wang, RSC Adv., 2019, 9, 27167–27175 RSC.
- S. Qi, M. Yu, J. Fu, P. D. Li and M. Zhu, Smart Mater. Struct., 2016, 25(1) DOI:10.1088/0964-1726/25/1/015020.
- Y. G. Xu, X. L. Gong, S. H. Xuan, W. Zhang and Y. C. Fan, Soft Matter, 2011, 7, 5246–5254 RSC.
- B. Wei, X. L. Gong, W. Q. Jiang, L. J. Qin and Y. C. Fan, J. Appl. Polym. Sci., 2010, 118, 2765–2771 CrossRef CAS.
- G. Zhang, H. X. Wang, J. Wang, J. J. Zheng and Q. Ouyang, Colloids Surf. A, 2019, 580 DOI:10.1016/j.colsurfa.2019.123596.
- G. J. Liao, X. L. Gong, S. H. Xuan, C. Y. Guo and L. H. Zong, Ind. Eng. Chem. Res., 2012, 51, 3322–3328 CrossRef CAS.
- S. Ryu, J. H. Koo, T. H. Yang, D. Pyo, K. U. Kyung and D. S. Kwon, J. Intel. Mat. Syst. Str., 2016, 27, 1967–1975 CrossRef CAS.
- T. H. Yang, H. J. Kwon, S. S. Lee, J. An, J. H. Koo, S. Y. Kim and D. S. Kwon, Sens. Actuators, A, 2010, 163, 180–190 CrossRef CAS.
- X. L. Gong, Y. G. Xu, S. H. Xuan, C. Y. Guo, L. H. Zong and W. Q. Jiang, J. Rheol., 2012, 56, 1375–1391 CrossRef CAS.
- H. Wang, Y. Li, G. Zhang and J. Wang, Smart Mater. Struct., 2019, 28(3) DOI:10.1088/1361-665X/aaf32b.
- G. Zhang, H. Wang, J. Wang, J. Zheng and Q. Ouyang, RSC Adv., 2019, 9, 10124–10134 RSC.
- H. X. Wang, G. Zhang and J. Wang, Materials, 2019, 12(15) DOI:10.3390/ma12152431.
- T. X. Liu, X. L. Gong, Y. G. Xu, H. M. Pang and S. H. Xuan, Smart Mater. Struct., 2014, 23(10) DOI:10.1088/0964-1726/23/10/105028.
- Y. G. Xu, T. X. Liu, Q. Wan, X. L. Gong and S. H. Xuan, Mater. Lett., 2015, 158, 406–408 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |