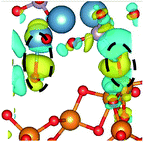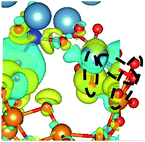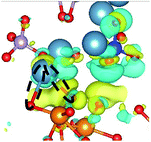Open Access Article
Open Access ArticleEffect of van der Waals interactions on the adhesion strength at the interface of the hydroxyapatite–titanium biocomposite: a first-principles study†
Irina Yu. Grubova *a,
Maria A. Surmeneva
*a,
Maria A. Surmeneva a,
Roman A. Surmenev
a,
Roman A. Surmenev *a and
Erik C. Neyts
*a and
Erik C. Neyts b
b
aResearch Center for Physical Materials Science and Composite Materials, Research School of Chemistry & Applied Biomedical Sciences, National Research Tomsk Polytechnic University, Lenin Avenue, 30, 634050 Tomsk, Russia. E-mail: rodeo_88@mail.ru; rsurmenev@gmail.com
bDepartment of Chemistry, PLASMANT Research Group, NANOlab Center of Excellence, University of Antwerp, Universiteitsplein 1, B-2610 Wilrijk, Antwerp, Belgium
First published on 14th October 2020
Abstract
Hydroxyapatite (HAP) is frequently used as biocompatible coating on Ti-based implants. In this context, the HAP-Ti adhesion is of crucial importance. Here, we report ab initio calculations to investigate the influence of Si incorporation into the amorphous calcium-phosphate (a-HAP) structure on the interfacial bonding mechanism between the a-HAP coating and an amorphous titanium dioxide (a-TiO2) substrate, contrasting two different density functionals: PBE-GGA, and DFT-D3, which are capable of describing the influence of the van der Waals (vdW) interactions. In particular, we discuss the effect of dispersion on the work of adhesion (Wad), equilibrium geometries, and charge density difference (CDD). We find that replacement of P by Si in a-HAP (a-Si-HAP) with the creation of OH vacancies as charge compensation results in a significant increase in the bond strength between the coating and substrate in the case of using the PBE-GGA functional. However, including the vdW interactions shows that these forces considerably contribute to the Wad. We show that the difference (Wad − Wad(vdW)) is on average more than 1.1 J m−2 and 0.5 J m−2 for a-HAP/a-TiO2 and a-Si-HAP/a-TiO2, respectively. These results reveal that including vdW interactions is essential for accurately describing the chemical bonding at the a-HAP/a-TiO2 interface.
Introduction
In recent years, ceramics based on hydroxyapatite (HAP, Ca10(PO4)6(OH)2) are commonly considered as coating materials on metallic implants and scaffolds for tissue engineering because of their biocompatible and osteoconductive properties.1,2 The most commonly used substrates for HAP coating deposition are titanium (Ti) and its alloys, which are clinically used as metal implants due to their good bulk properties, such as relatively low modulus, good fatigue strength, and high corrosion resistance.3–5 By properly selecting the processing parameters of coating formation, a strong bonding of the ceramic coating to the substrate can be achieved. Nevertheless, during the surgical implantation and clinical use of a high-loaded bone implant, the ceramic coating can chip or delaminate from the metal surface for a number of reasons, which might cause the implant rejection. From a clinical perspective, this is to be avoided at all cost. As a result, improving the adhesion of such kind of metal-ceramic interfaces remains an important problem. There are some commonly accepted guidelines regarding how to enhance the adhesion at the HAP/Ti interface,5 including a denser microstructure and thinner HAP coatings resulting in high bonding strength,6,7 reducing the residual stress,8 doping HAP with other elements such as Si, Sr, and Ag,6,9 controlling the Ti substrate surface texture and compositions,10,11 and controlling the choice of deposition method and its operating conditions.12,13Although the large number of research groups actively work in the field of studying and applying thin biocompatible ceramic coatings, it is nevertheless still difficult to quantitatively comprehend the detailed interatomic interaction mechanism at the Ti-ceramic coating interface by conventional experimental methodologies.
Nevertheless, various theoretical approaches, such as density functional theory (DFT) can provide complementary understanding of the interfacial structure and the electronic properties of the interface, which no experimental technique can directly reach.
In standard DFT approaches, such as local-density approximation (LDA) and the generalized gradient approximation (GGA), the functionals provide an accurate description of physical properties of many atoms, molecules, and solids. However, these approximations fail to reproduce non-local dispersive forces, generally denoted as van der Waals (vdW) interactions, whose role is obviously important for the study of the interactions at the interfaces.
In recent years, several functionals were developed to consider vdW forces for the description of the adhesion mechanism correctly. The most successful and commonly used approaches are the dispersion-corrected DFT (DFT-D)14–24 and the vdW density functional (vdW-DF).25 Among them, the so-called DFT-D3 method was successfully used in both molecular and solid-state applications.26 The main advantage of DFT-D3 is that it is obtained at negligible computational cost, which makes it particularly attractive in applications to large systems.27 The DFT-D3 method,26 proposed by Grimme et al. in 2010, suggests to define the dispersion correction energy between two atoms i and j as:
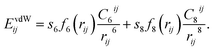 | (1) |
In this formalism, damping of the following form is used:
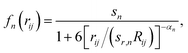 | (2) |
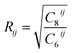 is the cutoff radius associating with the pair of atoms i and j.
is the cutoff radius associating with the pair of atoms i and j.
This paper is a continuation of our previous ab initio study28 of interface interactions in HAP/Ti composites that was concentrated foremost on the effect of substitutional Si doping in the amorphous calcium-phosphate (a-HAP) structure on the work of adhesion (Wad), integral charge transfer, charge density difference (CDD) and theoretical tensile strengths between an a-HAP coating and amorphous titanium dioxide (a-TiO2) substrate.
The results revealed that the presence of Si dopants in the a-HAP (a-Si-HAP) structure strongly alters not only the bioactivity and resorption rates, but also the mechanical properties of the studied interface.
However, despite the obtained insight gained into the nature of the adhesion mechanism between a-HAP and a-TiO2, the effect of the vdW forces on the adhesion mechanism is still unclear, because of the GGA functional limitations, and further study of the description of vdW interaction within the DFT approach is needed.
Although numerous studies have been devoted to the atomistic simulation of HAP properties, only a few theoretical studies have analyzed the mechanism of the HAP interaction with Ti at the coating/substrate interface. Moreover, no studies to date have examined how the incorporation of Si affects such nanoscale properties as vdW interactions, which can be critical to the determination of the interfacial adhesion mechanism of the HAP/Ti composites and cannot be reached by experimental approach.
Therefore, here we focus on the a-HAP/a-TiO2 and a-Si-HAP/a-TiO2 interface interactions with the aim of comparing results obtained with a reliable vdW functional to the results obtained with the PBE-GGA functional, which are conventionally used to describe only chemical bonding.
Thus, this paper aims to describe the adhesion mechanism with a rigorous treatment of non-local interactions as well as the effect of dispersion forces on the equilibrium geometries of studied interfaces and the role of these forces in the binding mechanism.
Calculation method
Our calculations are based on DFT as implemented in VASP (Vienna Ab initio Simulation Package).29–36 VASP is a complex package for simulation of many-electron systems at an atomic scale, which is widely applied for the numerical solution of the challenges of quantum mechanical molecular dynamics and calculations related to the electronic structure. The exchange-correlation interactions are treated at the GGA level, employing the Perdew–Burke–Ernzerhof (PBE) functional34,35 using plane-wave basis sets and the projector-augmented wave method as implemented in VASP.33,36 The plane-wave cutoff is set to 550 eV, valence electrons are 1s1 for hydrogen, 3s23p3 for phosphorus, 3s23p64s2 for calcium, 2s22p4 for oxygen, 3s23p2 for silicon, and 3d34s1 for Ti. The total energy in the calculations is converged to within 0.01 eV, and a 6 × 6 × 1 Γ-centered k-point grid is used for k-point sampling. The DFT-D3 method is used to account for dispersion corrections. A detailed description of the construction of the considered interfaces and the amorphization procedure can be found in our previous works28,37 and ESI.† The atomic structures are visualized by the VESTA 3 program.38Results and discussion
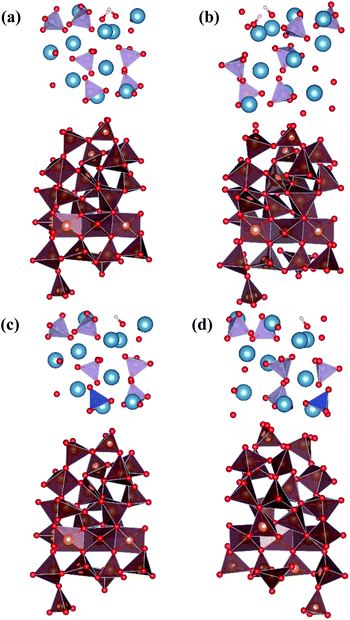
In our previous work,28 we studied the effects of Si-doping on the adhesion mechanism and ideal tensile strength of fully relaxed a-HAP/a-TiO2 interface structures using a GGA functional. For creating the Si substituted interfaces we used the a-HAP/a-TiO2 model with two possible stacking positions, which resulted in the best interatomic interaction.37In this study, the aim is to improve our understanding of the interaction between the a-HAP coating and the a-TiO2 substrate. For this purpose, we focus on the comparison of the results obtained for two best stacking positions of each considered interfaces, and calculated with normal GGA and dispersion-corrected DFT-D3 functionals. The initial geometry of the studied interfaces are presented in Fig. 1.
Initially, the preferred configuration of the interfaces was determined by quantifying the adhesion interaction, which is characterized by the Wad, within the GGA approximation. By neglecting diffusion and plastic deformation, Wad of an interface can be defined by eqn (3):39
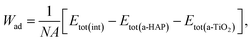 | (3) |
The results are shown in Table 1. As can be seen in the table, including dispersion interactions in our calculations via the DFT-D3 functional significantly changes the obtained values of Wad. The higher the absolute value of the obtained Wad is, the more stable the interfacial bonds.
| Functional | Wad (J m−2) | |||
|---|---|---|---|---|
| System | a-HAP/a-TiO2 | a-Si-HAP/a-TiO2 | ||
| Stacking position | I | II | I | II |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Functional | ||||
| PBE | −0.690 | −2.030 | −1.370 | −2.855 |
| DFT-D3 | −1.740 | −0.930 | −0.870 | −2.315 |
The first feature to highlight is that for the PBE functional we can observe that the Si substitution strongly increases the interaction at the interface for both stacking positions, indicating that the Si-doped a-HAP surface is more reactive. The increase of Wad is about 50% and 30% for stacking I and II, respectively. The obtained data are in good agreement with experimental results,40 where doping the HAP structure by Si was shown to lead to a decrease in crystal size and an increase in their specific surface, which in turn determined the improvement in the sorption properties of HAP. Also to note is the discrepancy between the results obtained with the different DFT functionals considered in this work. The less negative Wad were computed with the DFT-D3 approach for the a-Si-HAP/a-TiO2. However, in the case of a-HAP/a-TiO2, DFT-D3 correction lead to the Wad larger than those obtained from the PBE-GGA scheme for the stacking I and lower for the stacking II.
Thus, the semi-empirical method proposed by Grimme describes the effect of dispersion forces on the interatomic interaction at the considered interfaces. Analysis of the calculated data shows that the contribution of the vdW interactions is rather high, since the value of (Wad − Wad(vdW)) is on average more than 1.1 J m−2 and 0.5 J m−2 for a-HAP/a-TiO2 and a-Si-HAP/a-TiO2, respectively.
Interactions at the interface lead to charge redistribution due to electronic hybridization between the orbitals of the coating and the substrate. Therefore, for gaining a better insight in the influence of Si doping in the a-HAP structure with and without dispersion DFT on the electronic interactions at the studied interfaces, the CDD was evaluated as follows:41
| Δρ(r) = ρa-HAP/a-TiO2(r) − ρa-HAP(r) − ρa-TiO2(r), | (4) |
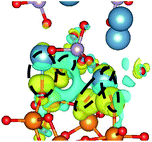
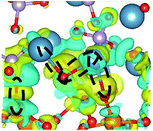
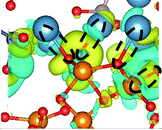
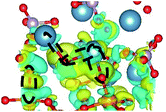
CDD with isosurface values of ±0.002 eV Å−3 for a-HAP/a-TiO2 and a-Si-HAP/a-TiO2 systems plotted for both functionals (PBE, DFT-D3) are shown in Table 2. The isosurfaces of charge redistribution at the interface indicate that the electron charge was mainly localized in two near-boundary layers. The plotted CDD helps to understand the chemical bonding mechanism at the constructed interfaces. The yellow and the blue areas represent the depletion and accumulation of electrons, respectively. For all interfaces, we observe a charge depletion near the O atoms from the a-TiO2 slabs and a charge accumulation near the Ca atoms, which means that covalent Ca–O bonds are formed. The same character of the charge transfer is observed between O atoms from the PO4 groups and Ti atoms along the Ti–O direction at the interface.
Further, it can be seen that Ti and Ca atoms act as electrons acceptors (Lewis acid), whereas O atoms from the coating and the a-TiO2 slab act as electrons donors (Lewis base). The obtained results are consistent with those reported in our previous DFT studies.
The calculations show that the character of interactions at the a-HAP/a-TiO2 strongly depends on Si dopants and the used DFT functionals. Based on the visualization of CDD, for a-HAP/a-TiO2 there is one Ti–O bonds for both stacking positions in the range of 1.83–2.03 Å. Moreover, three covalent Ca–O bonds in the range of 2.36–2.61 Å were detected in the case of using the DTF-D3 approach (for both stacking positions) and PBE functional (for stacking position II) for a-HAP/a-TiO2. Nevertheless, a-HAP/a-TiO2 with the stacking position I calculated with the PBE method shows only one covalent Ca–O bond (2.29 Å) (Table 2).
As for the a-Si-HAP/a-TiO2 case for both stacking positions, the use of the DFT-D3 functional leads to the reduction of the amount of bonds, which in turn decreases the adhesion strength at the interface. The a-Si-HAP/a-TiO2 interface (stacking I, PBE) shows one Ti–O bond and two Ca–O bonds with lengths less than 2.58 Å. One Ti–O bond (1.99 Å) and three Ca–O bonds in the range of 2.19–2.49 Å were generated across the a-Si-HAP/a-TiO2 (stacking II, PBE) interface, showing the quite strong chemical bonding at the interface (Table 2).
The structural picture of the interaction at the a-Si-HAP/a-TiO2 (stacking I, DFT-D3) shows two Ca–O bonds of about 2.40 ± 0.03 Å. One Ti–O bond (2.76 Å) and two Ca–O bonds (2.29 and 2.25 Å) formed at the a-Si-HAP/a-TiO2 (stacking II, DFT-D3) interface. Thus, this structural analysis reveals that the dispersion forces induce the observed change in the Wad values. The change in adhesion at the interface depends not only on the composition, but also on the stacking positions. The bond lengths are mainly determined by a balance between the long-range attractive vdW forces and the short-range Pauli repulsion.
Conclusion
In this study, first-principles calculations are performed to investigate the influence of Si dopants on the interfacial adhesion of the a-HAP/a-TiO2 interface, contrasting two different density functionals: PBE-GGA, and DFT-D3, which is capable of describing the influence of the dispersion forces on the interfacial bonding mechanism. The Wad value of various interface models with different stacking configurations and compositions are evaluated. Our calculations indicate that the Si-doping in the HAP crystal has a large impact on the adhesion properties of the a-HAP/a-TiO2 interface. In the case of a-Si-HAP/a-TiO2 the use of the DFT-D3 functional yields less negative values for Wad than the PBE-GGA functional. However, in the case of a-HAP/a-TiO2 interface, the final adhesion at the interface depends also on the stacking position. Moreover, the adhesion mechanism is mainly supported by the formation of covalent (polar) Ca–O and Ti–O bonds across the interface.Thus, we can conclude that dispersion interactions play a significant role in altering the adhesion mechanism and charge distribution, and accounting for such interactions is critical in molecular simulations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge financial support from the Russian president's grant MK-330.2020.8 and BOF Fellowships for International Joint PhD students funded by University of Antwerp (UAntwerp, project number 32545). The work was carried out at Tomsk Polytechnic University within the framework of Tomsk Polytechnic University Competitiveness Enhancement Program grant and in part using the Turing HPC infrastructure of the CalcUA core facility of the UAntwerp, a division of the Flemish Supercomputer Centre (VSC), funded by the Hercules Foundation, the Flemish Government (department EWI) and the UAntwerp, Belgium.References
- A. Vladescu, M. A. Surmeneva, C. M. Cotrut, R. A. Surmenev and I. V. Antoniac, Bioceramic Coatings for Metallic Implants, Handbook of Bioceramics and Biocomposites, 2016, 703–733 CrossRef.
- R. A. Surmenev, M. A. Surmeneva and A. A. Ivanova, Significance of Calcium Phosphate Coatings for the Enhancement of New Bone Osteogenesis – a Review, Acta Biomater., 2014, 10, 557–579 CrossRef CAS.
- Y. Li, S. Zou, D. Wang, G. Khan, C. Bao and J. Hu, The Effect of Hydrofluoric Acid Treatment on Titanium Implant Osseointegration in Ovariectomized Rats, Biomaterials, 2010, 31, 3266–3273 CrossRef CAS.
- M. R. Khan, N. Donos, V. Salih and P. M. Brett, The Enhanced Modulation of Key Bone Matrix Components by Modified Titanium Implant Surfaces,, Bone, 2012, 50, 1–8 CrossRef CAS.
- B. León and J. A. Jansen, Thin Calcium Phosphate Coatings for Medical Implants, Springer, New York, 2009 Search PubMed.
- X. Wei, C. Fu, K. Savino and M. Z. Yates, Fully Dense Yttrium-Substituted Hydroxyapatite Coatings with Aligned Crystal Domains, Cryst. Growth Des., 2012, 12, 217–223 CrossRef CAS.
- F. J. Garciasanz, M. B. Mayor, J. L. Aris, J. Pou and B. León, Peréz-Amor, M. Hydroxyapatite Coatings a Comparative Study between Plasma-Spray and Pulsed Laser Deposition Techniques, J. Mater. Sci.: Mater. Med., 1997, 8, 861–865 CrossRef CAS.
- B. Cofino, P. Fogarassy, P. Millet and A. Lodini, Thermal Residual Stresses Near the Interface Between Plasma-Sprayed Hydroxyapatite Coating and Titanium Substrate: Finite Element Analysis and Synchrotron Radiation Measurements, J. Biomed. Mater. Res., 2004, 70, 20–27 CrossRef CAS.
- J. Terra, E. R. Dourado, J. G. Eon, D. E. Ellis, G. Gonzalez and A. M. Rossi, The Structure of Strontium-Doped Hydroxyapatite: An Experimental and Theoretical Study, Phys. Chem. Chem. Phys., 2009, 11, 568–577 RSC.
- I. Y. Grubova, M. A. Surmeneva, A. A. Ivanova, K. Kravchuk, O. Prymak, M. Epple, V. Buck and R. A. Surmenev, The Effect of Patterned Titanium Substrates on the Properties of Silver-Doped Hydroxyapatite Coatings, Surf. Coat. Technol., 2015, 276, 595–601 CrossRef CAS.
- I. Grubova, T. Priamushko, E. Chudinova, M. Surmeneva, O. Korneva, M. Epple, O. Prymak, I. Shulepov and R. Surmenev, Formation and Characterization of Crystalline Hydroxyapatite Coating with the (002) Texture, IOP Conf. Ser.: Mater. Sci. Eng., 2016, 116, 012016 Search PubMed.
- A. A. Ivanova, M. A. Surmeneva, I. Y. Grubova, A. A. Sharonova, V. F. Pichugin, M. V. Chaikina, V. Buck, O. Prymak and M. Epple, Surmenev. R. A. Influence of the Substrate Bias on the Stoichiometry and Structure of RF-Magnetron Sputter-Deposited Silver-Containing Calcium Phosphate Coatings, Materialwiss. Werkstofftech., 2013, 44, 218–225 CrossRef CAS.
- R. A. A. Surmenev, Review of Plasma-Assisted Methods for Calcium Phosphate-Based Coatings Fabrication, Surf. Coat. Technol., 2012, 206, 2035–2056 CrossRef CAS.
- S. Grimme, Accurate Description of van der Waals Complexes by Density Functional Theory Including Empirical Corrections, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS.
- S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- F. Ortmann, F. Bechstedt and W. G. Schmidt, Semiempirical van der Waals Correction to the Density Functional Description of Solids and Molecular Structures, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205101 CrossRef.
- Q. Wu, Q. Wu and W. Yang, Empirical Correction to Density Functional Theory for van der Waals Interactions, J. Chem. Phys., 2002, 116, 515–524 CrossRef CAS.
- A. D. Becke and E. R. Johnson, Exchange-Hole Dipole Moment and the Dispersion Interaction, J. Chem. Phys., 2005, 122, 154104 CrossRef.
- A. D. Becke and E. R. Johnson, A Density-Functional Model of the Dispersion Interaction, J. Chem. Phys., 2005, 123, 154101 CrossRef.
- E. R. Johnson and A. D. Becke, A Post-Hartree–Fock Model of Intermolecular Interactions, J. Chem. Phys., 2005, 123, 024101 CrossRef.
- T. Sato and H. Nakai, Density Functional Method Including Weak Interactions: Dispersion Coefficients Based on the Local Response Approximation, J. Chem. Phys., 2009, 131, 224104 CrossRef.
- P. L. Silvestrelli, Van der Waals Interactions in DFT Made Easy by Wannier Functions, Phys. Rev. Lett., 2008, 100, 053002 CrossRef.
- A. Tkatchenko and M. Scheffler, Accurate Molecular van der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data, Phys. Rev. Lett., 2009, 102, 073005 CrossRef.
- M. Dion, H. Rydberg, E. Schrödinger, D. C. Langreth and B. I. Lundqvist, Van der Waals Density Functional for General Geometries, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS.
- K. Lee, E. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Higher-Accuracy van der Waals Density Functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- L. A. Goerigk, Comprehensive Overview of the DFT-D3 London-Dispersion Correction. Non-Covalent Interactions in Quantum Chemistry and Physics, Elsevier, 2017, pp. 195–219 Search PubMed.
- I. Y. Grubova, M. A. Surmeneva, S. Huygh, R. A. Surmenev and E. C. Neyts, Effects of Silicon Doping on Strengthening Adhesion at the Interface of the Hydroxyapatite–Titanium Biocomposite: A First-Principles Study, Comput. Mater. Sci., 2019, 159, 228–234 CrossRef CAS.
- G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Hafner, Norm-Conserving and Ultrasoft Pseudopotentials for First-Row and Transition Elements, J. Phys.: Condens. Matter, 1994, 6, 8245–8257 CrossRef CAS.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Improved Tetrahedron Method for Brillouin-Zone Integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef.
- I. Y. Grubova, M. A. Surmeneva, S. Huygh, R. A. Surmenev and E. C. Neyts, Density Functional Theory Study of Interface Interactions in Hydroxyapatite/Rutile Composites for Biomedical Applications, J. Phys. Chem. C, 2017, 121, 15687–15695 CrossRef CAS.
- K. Momma and F. Izumi, VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- M. W. Finnis, The Theory of Metal-Ceramic Interfaces, J. Phys.: Condens. Matter, 1996, 8, 5811–5836 CrossRef CAS.
- M. A. Trubitsyn, N. G. Gabruk, L. van Thuan and D. van Dat, The Comparative Characteristic of Physical, Chemical and Bioactive Properties of the Synthesized Hydroxyapatites, Global J. Pharmacol., 2013, 7, 342–347 Search PubMed.
- J. P. Sun, J. Dai, Y. Song, Y. Wang and R. Yang, Affinity of the Interface between Hydroxyapatite (0001) and Titanium (0001) Surfaces: A First-Principles Investigation, ACS Appl. Mater. Interfaces, 2014, 6, 20738–20751 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Two views of the phase-pure HA unit cell with the labelled phosphate and hydroxyl groups, Fig. S1. The calculated Wad for 24 constructed interfaces between aSiHA and aTiO2, Table S1. See DOI: 10.1039/d0ra06006b |
| This journal is © The Royal Society of Chemistry 2020 |