Open Access Article
Open Access ArticleNovel tetrahedral cobalt(II) silanethiolates: structures and magnetism†
Daria Kowalkowska-Zedlera,
Natalia Nedelkob,
Katarzyna Kazimierczuka,
Pavlo Aleshkevychb,
Renata Łyszczekc,
Anna Ślawska-Waniewska*b and
Agnieszka Pladzyk *a
*a
aDepartment of Inorganic Chemistry, Faculty of Chemistry, Gdańsk University of Technology, Narutowicza Str. 11/12, 80-233 Gdańsk, Poland. E-mail: agnieszka.pladzyk@pg.edu.pl
bInstitute of Physics, Polish Academy of Sciences, Aleja Lotników 32/46, 02-668 Warsaw, Poland
cDepartment of Coordination and General Chemistry and Crystallography, Institute of Chemical Sciences, Faculty of Chemistry, Maria Curie-Skłodowska University in Lublin, M.C. Skłodowska Sq. 2, 20-031 Lublin, Poland
First published on 6th August 2020
Abstract
Three heteroleptic complexes of Co(II) tri-tert-butoxysilanethiolates have been synthesized with piperidine [Co{SSi(OtBu)3}2(ppd)2] 1, piperazine [Co{SSi(OtBu)3}2(NH3)]2(μ-ppz)·2CH3CN 2, and N-ethylimidazole [Co{SSi(OtBu)3}2(etim)2] 3. The complexes have been characterized by a single-crystal X-ray, revealing their tetrahedral geometry on Co(II) coordinated by two nitrogen and two sulfur atoms. Complexes 1 and 3 are mononuclear, whereas 2 is binuclear. The spectral properties and thermal properties of 1–3 complexes were established by FTIR spectroscopy for solid samples and TGA. The magnetic properties of complexes 1, 2, and 3 have been investigated by static magnetic measurements and X-band EPR spectroscopy. These studies have shown that 1 and 3, regardless of the similarity in structure of CoN2S2 cores, demonstrate different types of local magnetic anisotropy. Magnetic investigations of 2 reveal the presence of weak antiferromagnetic intra-molecular Co(II)–Co(II) interactions that are strongly influenced by the local magnetic anisotropy of individual Co(II) ions.
Introduction
The search for new materials with novel magnetic properties and application options is one of the most developed fields of science. In this area, mononuclear coordination complexes based on transition metals are promising due to properties they exhibit as single-molecule magnets (SMMs), also referred to as single-ion magnets (SIMs).1–5 It is an intriguing group of compounds that is able to retain spin direction after the removal of an external magnetic field, and this particular feature is important to improving data storage and quantum computing devices.6 The essential attribute of SIM complexes is a single-ion magnetic anisotropy, which generates an energy barrier for spin reversal and many works are aimed at finding the principles of its controlled modification.In the search for potential 3d SIM materials, complexes containing high-spin cobalt(II) ions (S = 3/2) are one of the most explored.1–4 Interestingly, such Co(II) mononuclear complexes can exhibit a slow magnetic dynamic, typical of SIMs, for both types of single-ion magnetic anisotropy, easy axis and easy plane. In both cases, the magnetic bistability of Co(II) ground state is achieved through the Zero-Field Splitting effect (ZFS), arising from strong spin–orbit couplings (if ligand-field symmetry is lower than cubic). ZFS parameters, D and E, and consequently the local magnetic anisotropy of Co(II) ions, can be changed via modification of ligand-field symmetry and/or ligand strength.7
The breakthrough work of Zadrozny et al. showed that in mononuclear compound [PPh4]2[Co(SPh)4], low-coordinated tetrahedral Co(II) complexes possess a large negative ZFS parameter D, −70 cm−1, and exhibit SIM behaviour in a zero static magnetic field.8 Thereupon, the magneto-structural correlations of this and a few similar four-coordinated homoleptic Co(II) complexes have been thoroughly studied, and the intricate relations between the ZFS and ligand-field parameters have been revealed and explained.9–14 Unfortunately, the developed models that predict anisotropy parameters for homoleptic complexes cannot be simply extended to heteroleptic complexes. Different ligands around Co(II) ions contribute to the ZFS parameters in a different manner, and, for each type of heteroleptic complexes, individual analysis of the magneto-structural relations is required.
So far, one of the problems concerning low-coordinated Co(II) complexes is their low stability in atmospheric conditions, which excluded them from magnetic tests. Our research group has significant experience in syntheses of tetrahedral cobalt(II) silanethiolates that show noticeable resistance towards hydrolysis.15–21
Moreover, our previous research has demonstrated that some of them exhibit high responsiveness in single-ion magnetic anisotropy to even small changes in coordination environments around Co(II) ions.22
The results obtained so far motivated us to further explore this subject for the purpose of finding the relationship between the coordination arrangement on Co(II) and its magnetic properties. Therefore, we have synthesized a new group of heteroleptic Co(II) silanethiolates with tetrahedral geometry on a metallic center. In our syntheses, we have used tri-tert-butoxysilanethiol (tBuO)3SiSH (TBST) as a S-donor ligand, which has the characteristic and an almost distinctive resistance among thiols that enables syntheses under atmospheric conditions.
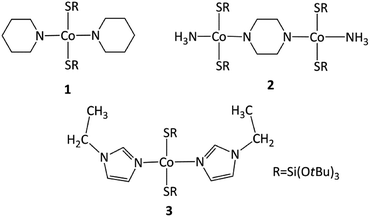
Here, we describe three new tetrahedral Co(II) silanethiolates with piperidine ppd, piperazine ppz and N-ethylimidazole etim as N-donor ligands, and their structural, spectral, thermal, and magnetic characterization.
Results
Synthesis and crystal structure characterization
As expected, the use of piperidine ppd, piperazine ppz and N-ethylimidazole etim in reactions with Co(II) tri-tert-butoxysilanethiolate [Co{SSi(OtBu)3}2(NH3)]2 resulted in blue monocrystals of [Co{SSi(OtBu)3}2(ppd)2] 1, [Co2{SSi(OtBu)3}4(μ-ppz)(NH3)2·2CH3CN] 2 and [Co{SSi(OtBu)3}2(etim)2] 3, respectively (Scheme 1). All three complexes are stable in atmospheric conditions.Compound 1 crystallizes in the monoclinic system in the space group I2/a with eight molecules in the unit cell (Fig. S1, Table S1, ESI†). The asymmetric unit contains one Co(II), two coordinated piperidine molecules arranged side to side and two tri-tert-butoxysilanethiolate residues (Fig. 1). The angles on Co(II) ion are in the range of 99.22(3)–128.000(14)° (Table S2, ESI†) signalizing some deviations from the ideal tetrahedron confirmed by geometric parameters τ4 = 0.82 and 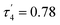 .23,24
.23,24
However these deviations do not influence on the Co–N and Co–S bond distances which are generally in agreement with those of the previously reported tetrahedral cobalt silanethiolates (Table S2, ESI†).15–21 The spatial arrangement of all ligands around metallic center enables the formation of two intramolecular Nppd–H⋯Osilanethiolate hydrogen bonds with N-bonded hydrogen atom of piperidine ring and (tBuO)3SiS− residues (Fig. 1 and Table S3, ESI†). Due to the crystal packing of 1 the Co(II) atoms are separated in the range distance 7.8741(8)–14.2009(9) Å.
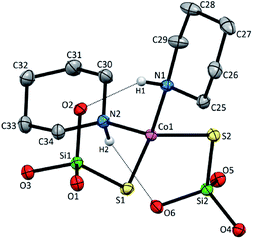
Compound 2 crystallizes as binuclear molecule in P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group in the triclinic system with two molecules of acetonitrile in the unit cell. The molecule of 2 is centrosymmetric with the inversion center located at the midpoint of the piperazine ring which links two Co(II) centers (Fig. 2 and S2, Table S1, ESI†). The tetrahedral coordination sphere of each Co(II) atom complete two silanethiolate residues and one molecule of ammonia (Fig. 2). This compound, in opposition to the previously synthesized with ammonia as the additional ligand, shows significant stability in atmospheric conditions.16,17,19,25–29 Co(II) based angles in 2 vary from 102.31(11) to 119.34(5)° (Table S2, ESI†) indicating some distortions of tetrahedral geometry verified by τ4 and
space group in the triclinic system with two molecules of acetonitrile in the unit cell. The molecule of 2 is centrosymmetric with the inversion center located at the midpoint of the piperazine ring which links two Co(II) centers (Fig. 2 and S2, Table S1, ESI†). The tetrahedral coordination sphere of each Co(II) atom complete two silanethiolate residues and one molecule of ammonia (Fig. 2). This compound, in opposition to the previously synthesized with ammonia as the additional ligand, shows significant stability in atmospheric conditions.16,17,19,25–29 Co(II) based angles in 2 vary from 102.31(11) to 119.34(5)° (Table S2, ESI†) indicating some distortions of tetrahedral geometry verified by τ4 and 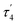 (Table S4†).23,24 Nonetheless, the distortion are smaller than those observed in 1 and do not influence the Co–N as well as Co–S bond distances which still are comparable with those found in other tetrahedral Co(II) silanethiolate complexes.15,30 Co(II) cores are bridged by the piperazine molecule separating them apart at 6.041(1) Å distance. Recently, we have described another binuclear and tetrahedral Co(II) silanethiolate [Co{SSi(tBuO)3}2(μ-3AMP)]2 bridged by 3-aminomethylpyridine with metallic centers distanced at 6.483(3) Å.22 The deeper structural analysis of 2 allows to suspect that the distortions appear to be due to the presence of a dense and woven net of intermolecular and intramolecular non-covalent interactions. The two shortest hydrogen bonding interactions are intramolecular N2ppz–H2⋯O6silanethiolate and N1ammonia–H1B⋯O1silanethiolate (D⋯A are 2.941(5) and 3.007(6) Å, respectively) (Table S3, ESI†). The molecule of ammonia as a triple donor of N–H hydrogen bonding forms next intramolecular N1ammonia–H1B⋯O4silanethiolate interaction weaker than the two described above and N1ammonia–H1C⋯N3acetonitrile (D⋯A are 3.292(5) and 3.108(7) Å, respectively) (Table S3, ESI†). The non-covalent interactions are not limited to these just described. The crucial role in their formation play four molecules of CH3CN solvent which are trapped between molecules of complex 2. They are engaged as a donors in the formation of Cacetonitrile–H⋯Ssilanethiolate (D⋯A are 3.723(8) and 3.8146(1) Å, respectively) and as acceptors of Cppz–H⋯Nsilanethiolate and Cacetonitrile–H⋯Nacetonitrile interactions with the neighboring solvent molecule (D⋯A are 3.340(1) and 3.656(9) Å, respectively). All this lead to the formation of 2D regular lattice of molecules of complex 2 with Co(II) ions distanced at 14.159(1) Å within the same chain and 10.491(1) Å between the neighboring ones (Fig. S3, ESI†).
(Table S4†).23,24 Nonetheless, the distortion are smaller than those observed in 1 and do not influence the Co–N as well as Co–S bond distances which still are comparable with those found in other tetrahedral Co(II) silanethiolate complexes.15,30 Co(II) cores are bridged by the piperazine molecule separating them apart at 6.041(1) Å distance. Recently, we have described another binuclear and tetrahedral Co(II) silanethiolate [Co{SSi(tBuO)3}2(μ-3AMP)]2 bridged by 3-aminomethylpyridine with metallic centers distanced at 6.483(3) Å.22 The deeper structural analysis of 2 allows to suspect that the distortions appear to be due to the presence of a dense and woven net of intermolecular and intramolecular non-covalent interactions. The two shortest hydrogen bonding interactions are intramolecular N2ppz–H2⋯O6silanethiolate and N1ammonia–H1B⋯O1silanethiolate (D⋯A are 2.941(5) and 3.007(6) Å, respectively) (Table S3, ESI†). The molecule of ammonia as a triple donor of N–H hydrogen bonding forms next intramolecular N1ammonia–H1B⋯O4silanethiolate interaction weaker than the two described above and N1ammonia–H1C⋯N3acetonitrile (D⋯A are 3.292(5) and 3.108(7) Å, respectively) (Table S3, ESI†). The non-covalent interactions are not limited to these just described. The crucial role in their formation play four molecules of CH3CN solvent which are trapped between molecules of complex 2. They are engaged as a donors in the formation of Cacetonitrile–H⋯Ssilanethiolate (D⋯A are 3.723(8) and 3.8146(1) Å, respectively) and as acceptors of Cppz–H⋯Nsilanethiolate and Cacetonitrile–H⋯Nacetonitrile interactions with the neighboring solvent molecule (D⋯A are 3.340(1) and 3.656(9) Å, respectively). All this lead to the formation of 2D regular lattice of molecules of complex 2 with Co(II) ions distanced at 14.159(1) Å within the same chain and 10.491(1) Å between the neighboring ones (Fig. S3, ESI†).
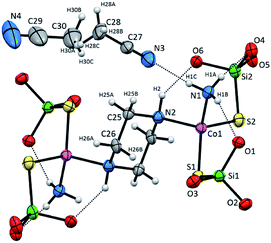 | ||
| Fig. 2 Molecular structure of 2 with atom labeling scheme and hydrogen bond interaction (shown as dashed line), tBu groups omitted for clarity. Thermal ellipsoids are drawn at 30% probability. | ||
Mononuclear complex 3 crystallizes in C2/c space group in the monoclinic system and consist of four molecules in a unit cell with no other than van der Waals interactions between them (Fig. S4 and Table S1, ESI†). The asymmetric unit contains Co(II) ion, one coordinated etim molecule and one (tBuO)3SiS− residue. The complex has the 2-fold rotation axis that goes through the metallic center lying in a distorted tetrahedral CoN2S2 geometry with Co(II) coordinated by two silanethiolate residues (tBuO)3SiS− and two N-ethylimidazole molecules (Fig. 3, Table S4, ESI†). Co(II) based angles vary from 104.66(17) to 125.1(4)° and only the S2–Co1–S2 angle has the closest value to the ideal tetrahedral geometry angles (109.55(11)°). The bond distances are comparable to those found in other tetrahedral Co(II) silanethiolates with imidazole ligands obtained so far (Table S2, ESI†).15,31,32
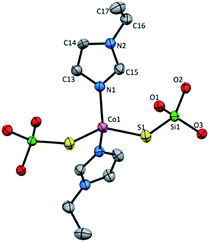 | ||
| Fig. 3 Molecular structure of 3 with atom labeling scheme, tBu groups omitted for clarity. Thermal ellipsoids are drawn at 30% probability. | ||
FT-IR spectroscopy
The FT-IR spectra were recorded for complexes 1–3 in the solid state (Fig. S5, ESI†).They are consistent with their crystal structures and confirm the presence of the ligands used in the syntheses.33
In general, the spectra of 1–3 are comparable and contain strong intensity bands in the range of 2970–2858 cm−1 attributed to symmetric and asymmetric C–H stretching modes of methylene groups of ppd and ppz rings, ethyl group from etim ligand and methyl groups from (tBuO)3SiS− residues. The imidazole ring in 3 shows strong band at 3139 cm−1 for vibrations of C–H bonds and bands of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretching vibrations in the region 1670–1320 cm−1. The Si–O–C bonding of silanethiolate residue is represented by the characteristic bands observed at 1100–980 cm−1. Heterocyclic compounds and ammonia molecule exhibit the stretching vibrations of N–H in the range of 3500–3200 cm−1 and the out-of-plane or in-plane-mode of N–H vibrations in the regions 780–800 cm−1 and 1440–1480 cm−1, respectively.34 The positions of particular vibrations depends strongly upon their additional engagement in hydrogen bonding formation. The mentioned vibrations appear in complex 1 at 3191 and 3176 cm−1 as two sharp absorption bands, and additional vibration at 1452 cm−1, whereas compound 2 exhibits a broad band at 3157 cm−1 and sharp one at 1460 cm−1. Other vibrations typical for the cyclic amine ligands appear at about 1261 and 1238 cm−1 for 1 as well as 1237 cm−1 for 2 and correspond to vibrations of C–N bonds.
N stretching vibrations in the region 1670–1320 cm−1. The Si–O–C bonding of silanethiolate residue is represented by the characteristic bands observed at 1100–980 cm−1. Heterocyclic compounds and ammonia molecule exhibit the stretching vibrations of N–H in the range of 3500–3200 cm−1 and the out-of-plane or in-plane-mode of N–H vibrations in the regions 780–800 cm−1 and 1440–1480 cm−1, respectively.34 The positions of particular vibrations depends strongly upon their additional engagement in hydrogen bonding formation. The mentioned vibrations appear in complex 1 at 3191 and 3176 cm−1 as two sharp absorption bands, and additional vibration at 1452 cm−1, whereas compound 2 exhibits a broad band at 3157 cm−1 and sharp one at 1460 cm−1. Other vibrations typical for the cyclic amine ligands appear at about 1261 and 1238 cm−1 for 1 as well as 1237 cm−1 for 2 and correspond to vibrations of C–N bonds.
Thermal behaviour of complexes
To estimate thermal stability in nitrogen atmosphere as well as pathway of thermal decomposition of 1–3 complexes, the thermogravimetric analysis (TG) coupled with Fourier transform infrared spectroscopy (FTIR) were performed. The TG curves of complexes are inserted in Fig. S6, ESI.† All investigated complexes exhibit stability up to 99 °C. Further heating of complexes 1 and 3 leads to the decomposition process with significant mass losses of 77.24 and 82.05%, respectively. For complex 1, some solid intermediate product is formed at 256 °C. At higher temperature, slowly mass loss of 10% up to 700 °C takes place. The final solid product of thermal decomposition of complex 3 is formed at 387 °C.The decomposition of complex 2 occurs in slightly different way. In the temperature range 100–127 °C, mass loss of 1.74% is observed. This stage can be related to evolution of ammonia molecules due to the presence of weak bands at 966 cm−1 and 930 cm−1 in the FTIR spectra of volatile products of complex decomposition (Fig. S7, ESI†). The solid product is stable up to 50 °C, followed by mass loss of 3.11% to 198 °C. Total decomposition of 2 takes place in the narrow temperature range 200–243 °C with mass loss of 75.63%. All compounds degrade with formation of cobalt, cobalt oxides and carbon mixture.35
The main mass loss on TG curves of complexes corresponds to the tert-butyl alcohol release.36 The FTIR spectra show bands at 3725, 2980, 1472, 1369, 1236, 1192 and 1074 cm−1 assigned to vibrations of OH, CH3 and COH groups (Fig. S7, ESI†). Additionally, some compounds from N-ligand decomposition as well as tri-tert-butoxysilyl moieties, carbon oxides and water are evolved.
Magnetic and EPR spectroscopy studies
The results of static magnetic measurements of sample 1 are shown in Fig. 4a: variable temperature molar magnetic susceptibility, χ = Mmol/H, measured at the applied dc magnetic field H = 1 kOe, is given as χT vs. T; the inset shows magnetization curves measured at 2, 5, 10, and 20 K (experimental data are represented by symbols). At room temperature, χT = 2.33 cm3 K mol−1, which is consistent with the presence of magnetically isolated high-spin Co(II) ions with an orbital angular momentum contribution to the total magnetic moment, χT = 2.3 cm3 K mol−1 for g = 2.22. Upon cooling, χT(T) initially changes very weakly, but below ∼50 K begins to fall clearly and in the ∼20–2 K range drops rapidly down to 1.46 cm3 K mol−1. Thermal dependence of the inverse susceptibility shows linearity over the whole measured range (Fig. S8, ESI†), and fitting χ(T) data to the Curie–Weiss law (χ = C/(T − θ)) gives the Curie constant C = 2.37 cm3 K mol−1 and Weiss constant θ = −1.85 K.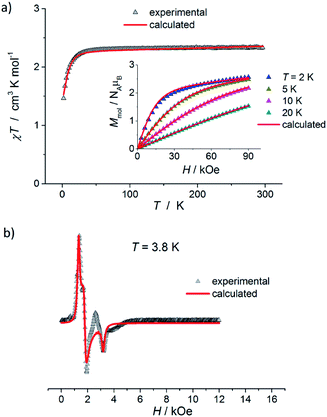 | ||
| Fig. 4 (a) Temperature dependence of χT for 1, measured at 1 kOe. Inset: isothermal magnetization curves measured at 2, 5, 10, and 20 K for 1. (b) X-band EPR powder spectrum of 1 recorded at 3.8 K. In (a) and (b), the symbols represent experimental data whereas solid lines correspond to best-fitting calculated curves according to eqn (1), with parameters described in the text. | ||
The magnetization isotherm at 2 K, Fig. 4a inset, demonstrates a Brillouin-like shape with no magnetic hysteresis. The near-saturation magnetic moment measured at 90 kOe M9T = 2.56 μB per molecule, which is slightly below the expected value of ∼3.3 μB per Co for a Brillouin S = 3/2 model (giso = 2.22). Structural analysis reveals that in complex 1, the cobalt ion resides in a distorted tetrahedral geometry, and there are no covalent bonds between the molecules (the shortest intermolecular Co–Co distance is ∼7.87 Å). Therefore, we suppose that the observed magnetic behavior of 1 results from the presence of paramagnetic high-spin Co(II) centers, the magnetic properties of which are strongly affected by Zero Field Splitting (ZFS) within the ground state spin multiplet.37–39 The ZFS effect explains the observed rapid decrease of χT upon cooling below ∼20 K, as well as the unsaturation of M(H) in 90 kOe at 2 K and the lack of superposition of the reduced magnetization curves, M(H/T), measured at 2, 5, 10, and 20 K (Fig. S9a, ESI†).
To complement the dc magnetic studies, X-band EPR measurements have been performed. The EPR powder spectrum of 1 recorded at 3.8 K is shown in Fig. 4b (by symbols). The observed characteristic resonance absorption in the ∼1–4 kOe field range is common for paramagnetic high-spin Co(II) complexes in distorted tetrahedral geometry;40,41 the anisotropic effective g′ factors were determined to be 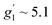 ,
, 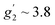 and
and 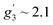 .
.
Accordingly, we performed quantitative analysis of all of the above presented experimental data on the basis of a spin Hamiltonian for a mononuclear S = 3/2 system that includes the Zeeman and ZFS terms:
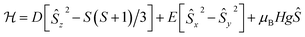 | (1) |
In Fig. 5, the results of dc magnetic measurements of binuclear Co(II) complexes 2 are presented. χ(T) dependence measured at H = 1 kOe exhibits a small maximum at Tmax ≈ 2.5 K that is indicative of weak antiferromagnetic (AFM) couplings between the cobalt ions in this compound, Fig. 5a. Furthermore, χ(T) above ∼25 K obeys the Curie–Weiss law with C = 5.24 cm3 K mol−1 and θ = −4.41 K (Fig. S8, ESI†). The room temperature χT value, 5.26 cm3 K mol−1, Fig. 5b, shows the presence of two non-interacting Co(II) ions with S = 3/2 and g > 2.0 (χT = 5.2 cm3 K mol−1 for g = 2.36). χT(T) smoothly decreases with temperature in the 300 to ∼50 K range, then drops rapidly to a value of 1.01 cm3 K mol−1 at 2 K. Such a decrease in χT is too sharp to be attributed only to the ZFS effect of individual Co(II) ions (as in 1), but can be explained by the presence of Co⋯Co AFM interactions. Magnetic measurements reveal that there is no long-range magnetic ordering in sample 2: χZFC and χFC thermal dependences measured in ZFC and FC regimes are superimposed, Fig. 5a, and the isothermal magnetization curves measured at 2, 3, 5, and 10 K demonstrate zero coercivity, Fig. 5b inset. M(H) at 2 K does not show the standard shape of a Brillouin function typical for magnetically isolated Co(II) ions. Instead, in the low field range, we observe a relatively slow increase of M(H) and the dynamic is maintained up to a quite high field, ∼20 kOe, Fig. 5b inset and S10 (ESI†); above ∼20 kOe, the growth rate of M(H) increases slightly, forming a characteristic inflection point on the magnetization curve, usually observed for AFM systems. At the highest fields, M(H) is unsaturated and M9T = 5.43 μB per molecule. The reduced magnetization curves, M(H/T), measured at 2, 3, 5, 10, and 20 K exhibit significant splitting (Fig. S9b, ESI†), which is more pronounced compared to that observed for mononuclear compound 1 (Fig. S9a, ESI†).
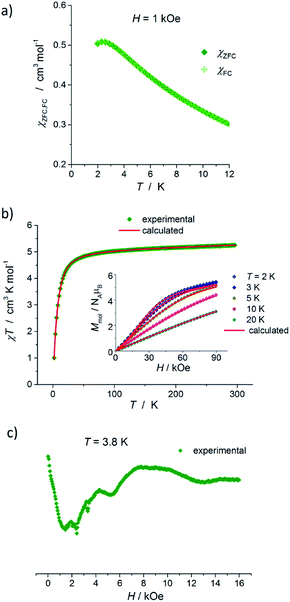 | ||
| Fig. 5 (a) Variable-temperature χZFC and χFC molar magnetic susceptibilities of 2, measured at 1 kOe. (b) Plot of χT versus T at 1 kOe, and magnetization curves (inset) at 2, 3, 5, 10, and 20 K for 2. Solid lines represent best-fitting simulation results with model described by eqn (2), in which anisotropic spin–spin interaction has been considered, see text for details. (c) X-band EPR powder spectrum of 2 recorded at 3.8 K. | ||
Compound 2 consists of a binuclear complex in which tetrahedrally coordinated Co(II) ions are bridged by piperazine ligands and Co⋯Co separation equal to 6.04 Å. Moreover, the binuclear molecules with the shortest intermolecular Co⋯Co distance of ∼10.49 Å seem to be well magnetically separated. Therefore, the observed low-temperature magnetic behavior of 2 can be attributed to Co(II)–Co(II) AFM couplings in the molecules. The X-band EPR powder spectrum of 2 recorded at 3.8 K confirms the presence of AFM Co(II)–Co(II) pairs (Fig. 5c). We observe a very wide and extremely weak absorption line at a near zero magnetic field and the resonance absorption is two orders of amplitude smaller compared to that observed in 1. The first attempt to analyze the experimental magnetic data of 2 was carried out using a regular spin–spin model with isotropic magnetic exchange interactions 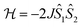 , but it did not provide a satisfactory result (especially at the lowest temperatures). We suppose that this disagreement is due to the contribution of single-ion magnetic anisotropy.
, but it did not provide a satisfactory result (especially at the lowest temperatures). We suppose that this disagreement is due to the contribution of single-ion magnetic anisotropy.
In 2, Co(II) ions reside in a distorted tetrahedral geometry, very similar to that in complex 1, and a similar absolute value of ZFS parameter D, ∼10 cm−1 (∼14.4 K), can be expected. Therefore, to describe the magnetic data of 2, we used a model in which the spin–spin interaction, J, as well as the ZFS term D, have been included (the single-ion anisotropy term D is presumed to be identical for each Co(II) ion within a molecule):
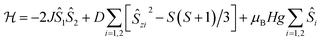 | (2) |
This approach agrees quite well with the experimental data for the following parameters: Jiso = −0.62 cm−1, D = 10.02 cm−1, giso = 2.33 and χTIP = 7.0 × 10−4 cm3 mol−1 (see Fig. S11, ESI,† solid lines). It should be noted here that the sign of the estimated parameter D is quite uncertain, as we do not have an informative-enough EPR spectrum (Fig. 5c). Moreover, attempts to include in the analysis the ZFS E component, as well as the anisotropic g-factor values, gx, gy, gz, did not improve the goodness of fit and had a negligible effect on the values of other parameters.
The obtained value of the |Jiso/D| ratio, 0.06, indicates that local single-ion anisotropy dominates the interaction term J. In such circumstances, anisotropy of magnetic exchange interactions, arising from strong spin–orbit coupling of Co(II) ions, can be expected.38,43 Hence, we also carried out a fitting procedure with eqn (2) while assuming an anisotropic exchange parameter: 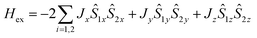 .42 As a result, a visible improvement in goodness of fit has been achieved, see Fig. 5b (solid lines). The best-fit parameters are: Jx = −0.0025 cm−1, Jy = −1.24 cm−1, Jz = −0.84 cm−1, D = 9.43 cm−1, giso = 2.33 and χTIP = 7.0 × 10−4 cm3 mol−1.
.42 As a result, a visible improvement in goodness of fit has been achieved, see Fig. 5b (solid lines). The best-fit parameters are: Jx = −0.0025 cm−1, Jy = −1.24 cm−1, Jz = −0.84 cm−1, D = 9.43 cm−1, giso = 2.33 and χTIP = 7.0 × 10−4 cm3 mol−1.
In Fig. 6a, the results of dc magnetic measurements of mononuclear Co(II) complexes 3 are presented. The high temperature χT value, 2.45 cm3 K mol−1, corresponds to the presence of magnetically isolated high-spin Co(II) ions with considerable orbital contribution, χT = 2.48 cm3 K mol−1 for g = 2.3. With a decrease in temperature, χT remains nearly constant until ∼50 K, then decreases smoothly and below ∼20 K drops rapidly to 1.75 cm3 K mol−1 at 2 K. χ(T) obeys the Curie–Weiss law with C = 2.50 cm3 K mol−1 and θ = −2.25 K (Fig. S8, ESI†). M(H) isotherm at 2 K reveals no hysteresis and a Brillouin-like shape; the near-saturation magnetic moment is 2.30 μB per Co ion, Fig. 6a inset.
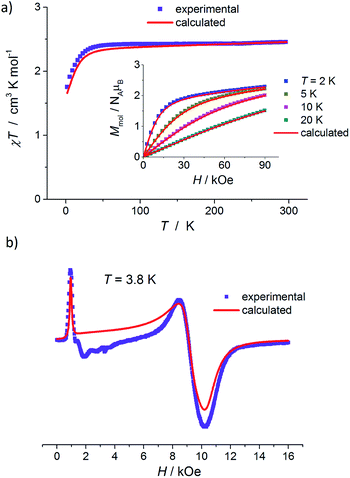 | ||
| Fig. 6 (a) Plot of χT versus T for 3, measured at 1 kOe. Inset: magnetization curves measured at 2, 5, 10, and 20 K for 3. (b) X-band EPR powder spectrum of 3 at 3.8 K. In both panels, symbols represent the experimental data whereas solid red lines – best-fit simulation results according to eqn (1), with parameters given in the text. | ||
M(H/T) dependences at 2, 5, 10, and 20 K do not superimpose on a single master curve (Fig. S9c, ESI†). In general, magnetic properties of mononuclear compound 3 are similar to those observed for 1 and indicate a paramagnetic behavior of Co(II) ions with significant contribution of ZFS splitting at the lowest temperatures. This is in agreement with the structural data of 3: the Co(II) ion is coordinated in a distorted tetrahedral geometry, the molecules are well isolated and the shortest Co⋯Co distance is 9.4 Å.
Fig. 6b shows an EPR powder spectrum of 3 observed at 3.8 K. It exhibits two major resonance absorptions, in the low-field and high-field area, H < ∼4 kOe and H > ∼6 kOe, respectively. In addition, the signal intensity of the low-field resonance component is much lower compared to that of the high field. We fitted the EPR spectrum to obtain apparent g′-values, which are: 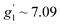 ,
, 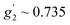 and
and 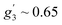 . Such a pattern of an X-band EPR spectrum is characteristic of distorted tetrahedral Co(II) complexes with D < 0 and a non-zero rhombic ZFS parameter E.41,44,45 Taking into account the structure and magnetic behavior of 3, the experimental data of this complex have been analyzed in a similar way to that of sample 1: a spin Hamiltonian model presented by eqn (1) has been used; M(H) at 2, 5, 10, and 20 K and χ(T) data were fitted simultaneously (with PHI software42). The obtained set of best-fit spin Hamiltonian parameters is: D = −17.0 cm−1, E = 1.89 cm−1, gx = 2.38, gy = 1.88, gz = 2.39 and χTIP = 4.0 × 10−4 cm3 mol−1. These parameters describe well the experimental magnetic susceptibility, magnetization and EPR spectra, and the corresponding calculated curves are presented by solid red lines in Fig. 6. It should be noted here that an attempt at analyzing the experimental data with positive D value did not lead to reasonable results.
. Such a pattern of an X-band EPR spectrum is characteristic of distorted tetrahedral Co(II) complexes with D < 0 and a non-zero rhombic ZFS parameter E.41,44,45 Taking into account the structure and magnetic behavior of 3, the experimental data of this complex have been analyzed in a similar way to that of sample 1: a spin Hamiltonian model presented by eqn (1) has been used; M(H) at 2, 5, 10, and 20 K and χ(T) data were fitted simultaneously (with PHI software42). The obtained set of best-fit spin Hamiltonian parameters is: D = −17.0 cm−1, E = 1.89 cm−1, gx = 2.38, gy = 1.88, gz = 2.39 and χTIP = 4.0 × 10−4 cm3 mol−1. These parameters describe well the experimental magnetic susceptibility, magnetization and EPR spectra, and the corresponding calculated curves are presented by solid red lines in Fig. 6. It should be noted here that an attempt at analyzing the experimental data with positive D value did not lead to reasonable results.
In the case of tetrahedral Co(II) complexes, the sign of the estimated ZFS parameter D shows which Kramers doublet of 4A2 ground state has lower energy – with mS = ±1/2 if D > 0 (easy-plane anisotropy) or with mS = ±3/2 if D < 0 (easy-axes anisotropy). In the framework of perturbation theory, ZFS anisotropy of four-coordinated Co(II) ions correlates with an energy pattern of d-orbitals, which in turn strongly depends on the ligand field.7,39 For 1 and 3, D parameters of opposite signs were obtained. Structurally, the CoN2S2 cores of 1 and 3 are very similar: both show almost identical bond lengths and moderate deviation from the ideal tetrahedral geometry. Additionally, for these two compounds, the dihedral angles between the two planes formed by the atoms (S, Co, S) and (N, Co, N) are practically the same, 88.79° and 88.68° for 1 and 3, respectively. Regarding the first coordination sphere of Co(II) ions, the most significant difference between 1 and 3, is related to S–Co–S bond angles, 128.00° (for 1) and 109.58° (for 3). Accordingly, the calculated values of the parameter δ, which measures the deviation of coordination tetrahedrons from the ideal Td geometry, are −25.85° and −15.44° for 1 and 3, respectively (δ = 2Td − (α + β), α and β are the S–Co–S and N–Co–N bond angles, respectively, and Td = 109.5°). Larger δ of 1 (absolute value) suggests that its symmetry is lower than that of 3. The question arise whether this is enough to change the type of anisotropy? On the other hand, local magnetic anisotropy of Co(II) ions can also be influenced by peripheral groups,9,11–14,46–49 particularly in the case of four-coordinated complexes with π-anisotropic S-donor ligands.9,11,12,46 Therefore, we also compared S–Co–S–Si spatial configurations in 1 and 3. We see a significant diversity in regular torsion angles: for 1 ∠S1–Co1–S2–Si2 = 60.07° and ∠S2–Co1–S1–Si1 = 167.12°, whereas for 3 ∠S1–Co1–S1–Si1 = −171.02° (see also Table S6, ESI†). Accordingly, the torsion angle between the (Co, S, Si) planes is 52.75° and 14.66° for 1 and 3, respectively. There are several publications in the literature explaining the influence of ligand positions on ZFS parameters.9,11,14,46 In particular, ligand-field calculations based on the angular overlap model have shown that torsion angle variations affect the directions of Co–S π and off-axis σ-interactions, and thus modify energy splitting of d-orbitals.46 The explicit importance of Co–S π-anisotropy in modulating Co(II) ZFS parameters has also been confirmed and explored extensively with ab initio quantum chemical methods by Neese and co-workers.9,11 Regarding our samples, at this stage of research, it cannot be clearly determined whether the observed anisotropy switching is mainly induced by changes in the first or second coordination sphere. More experimental and theoretical studies, supported by ab initio calculations, are required and will be taken.
Conclusions
The magnetic properties of complexes 1, 2, and 3 have been investigated by static magnetic measurements and X-band EPR spectroscopy. Both mononuclear compounds 1 and 3 show paramagnetic behaviour of cobalt ions with significant influence of Zero-Field Splitting within a ground-state spin multiplet. The ZFS parameters of 1 and 3 were determined from experimental magnetic susceptibility, magnetization isotherms, and EPR spectra. The obtained results show that these mononuclear complexes, regardless of similarity in structure of the CoN2S2 cores, have different types of local magnetic anisotropy, easy-plane and easy-axis for 1 and 3, respectively. For dinuclear complex 2, a tentative interpretation of the experimental data reveals that intra-molecular spin carriers are weakly antiferromagnetically coupled and that the ZFS effect of individual Co(II) ions dominates.Experimental section
Materials and methods
The elemental analyses for complexes 1–3 (C, H, S, N contents) were performed on an Elemental Analyser EA 1108 (Carlo Erba Instruments). The FTIR spectra were measured for crystalline compounds 1–3 in the range of 4000 to 400 cm−1 with a Nicolet iS50 FTIR spectrometer equipped with the Specac Quest single-reflection diamond attenuated total reflectance (ATR) accessory. Single crystal X-ray diffraction data of compounds 1–3 were collected at 120(2) K on a Stoe IPDS-2T diffractometer with graphite-monochromated Mo-Kα radiation. Data collection and image processing was performed with X-Area 1.75 (STOE & Cie GmbH, 2015).50 Intensity data were scaled with LANA (part of X-Area) in order to minimize differences of intensities of symmetry-equivalent reflections (multi-scan method). In all case crystals were cooled using a Cryostream 800 open flow nitrogen cryostat (Oxford Cryosystems). The structures were solved with direct methods and were refined with the SHELX-2016/4 program package51 with the full-matrix least squares procedure based on F2. The Olex52 and Wingx53 program suites were used to prepare the final version of CIF files. Mercury54 was used to prepare the figures. All non-hydrogen atoms were refined anisotropically. Hydrogen atoms were refined in geometrically idealised position with isotropic temperature factors 1.2 times the equivalent isotropic temperature factors Ueq of their attached atoms (1.5 for CH3 groups). The crystallographic data and some details of the structural refinement are summarized in Table S1, ESI.† Structural details of hydrogen bonding are collected in Table S3, ESI.†The crystal 3 studied is non-merohedral twin consisting of two components (domains). The twinning law is 180° rotation about the [100] reciprocal lattice vector. The twinning was resolved with the aid of the programs ROTAX55 and ROTWIN.56 The partially overlapped reflections were rejected, resulting in a low data completeness value of 93.5%.
Crystallographic data for structures of 1–3 reported in this paper have been deposited with the Cambridge Crystallographic Data Center as supplementary publications no. CCDC 2010158 (1), CCDC 2010156 (2) and CCDC 2010160 (3).†
The TG-FTIR coupled measurements for 1–3 have been carried out using Q5000 (TA Instruments) thermal analyser coupled with the Nicolet 6700 (Thermo Scientific) spectrophotometer. The samples of about 30 mg were heated up to 700 °C at a heating rate 20 °C min−1 in flowing nitrogen atmosphere in open platinum crucibles.
Magnetic measurements were performed with a Quantum Design PPMS magnetometer equipped with a 9 T magnet. Magnetization curves were measured at selected temperatures in the accessible field range. Direct current (dc) magnetization (M) was determined as a function of temperature (T) (in the range 2–298 K) in both zero-field-cooled (ZFC) and field-cooled (FC) regimes at 1 kOe applied magnetic field. The measurements were performed on polycrystalline powdered samples that have been packed in specialized capsules. The background signal of the sample holders was checked independently and subtracted from the measured data. The magnetic measurements data were also corrected for molecular diamagnetism using standard procedures.57
EPR spectra were collected with an EMX Bruker ER083CS spectrometer operating at a fixed frequency in X-band (9.382 GHz) and equipped with a liquid-helium cryostat. The powdered sample was wrapped in a polyethylene membrane and fixed to the quartz holder.
Synthetic procedure
[Co{SSi(OtBu)3}2(NH3)]2 were obtained according to procedures described previously.25 All other reagents were obtained commercially with no further purification. Complexes 1–3 were obtained according the same synthetic procedure: to a solution of [Co{SSi(OtBu)3}2(NH3)]2 (0.127 g, 0.1 mmol) dissolved in 20 mL of light petroleum (1 and 3) or acetonitrile (2), the respective N-donor ligand (1 0.04 mL, 0.4 mmol of ppd, 2 0.035 g, 0.4 mmol of ppz; 3, 0.021 mL, 0.02 mmol of etim) was added.Conflicts of interest
There are no conflicts to declare.References
- G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135 RSC.
- A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346 CrossRef CAS.
- J. M. Frost, K. L. Harriman and M. Murugesu, Chem. Sci., 2016, 7, 2470 RSC.
- S. Tripathi, A. Dey, M. Shanmugam, R. S. Narayanan and V. Chandrsekhar, Cobalt(II) Complexes Single-Ion Magnets, in Topics in Organometallic Chemistry, Springer, Berlin/Heidelberg, 2018 Search PubMed.
- F. S. Guo, A. K. Bar and R. A. Layfield, Chem. Rev., 2019, 119, 8479 CrossRef CAS.
- J. Bartolomé, F. Luis and J. F. Fernandez, Molecular Magnets: Physics and Applications, Springer-Verlag, Berlin/Heidelberg, 2014 Search PubMed.
- S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289, 379 CrossRef.
- J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732 CrossRef CAS.
- D. Maganas, S. Sottini, P. Kyritsis, E. J. J. Groenen and F. Neese, Inorg. Chem., 2011, 50, 8741 CrossRef CAS.
- J. M. Zadrozny, J. Telser and J. R. Long, Polyhedron, 2013, 64, 209 CrossRef CAS.
- E. A. Suturina, D. Maganas, E. Bill, N. Atanasov and F. Neese, Inorg. Chem., 2015, 54, 9948 CrossRef CAS.
- S. Vaidya, S. Tewary, S. K. Singh, S. K. Langley, K. Murray, Y. Lan, W. Wernsdorfer, G. Rajaraman and M. Shanmugam, Inorg. Chem., 2016, 55, 9564 CrossRef CAS.
- S. Sottini, G. Poneti, S. Ciattini, N. Levesanos, E. Ferentinos, J. Krzystek, L. Sorace and P. Kyritsis, Inorg. Chem., 2016, 55, 9537 CrossRef CAS.
- E. A. Suturina, J. Nehrkorn, J. M. Zadrozny, J. Liu, M. Atanasov, T. Weyhermueller, D. Maganas, S. Hill, A. Schnegg, E. Bill, J. R. Long and F. Neese, Inorg. Chem., 2017, 56, 3102 CrossRef CAS.
- B. Becker, A. Zalewska, A. Konitz and W. Wojnowski, Polyhedron, 2001, 20, 2567 CrossRef CAS.
- B. Becker, A. Pladzyk, A. Konitz and W. Wojnowski, Appl. Organomet. Chem., 2002, 16, 517 CrossRef CAS.
- A. Pladzyk and K. Baranowska, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, m1594 CrossRef CAS.
- A. Pladzyk, K. Baranowska and P. Hapter, Transition Met. Chem., 2010, 35, 373 CrossRef CAS.
- A. Pladzyk, J. Olszewska, K. Baranowska and A. M. Dziurzyńska, Transition Met. Chem., 2010, 35, 821 CrossRef CAS.
- A. Pladzyk, Ł. Ponikiewski, A. Dołęga, K. Słowy, A. Sokołowska, K. Dziubińska and Z. Hnatejko, Chem.–Asian J., 2015, 10, 2388 CrossRef CAS.
- D. Kowalkowska, A. Dołęga, N. Nedelko, Z. Hnatejko, Ł. Ponikiewski, A. Matracka, A. Ślawska-Waniewska, A. Strągowska, K. Słowy, M. Gazda and A. Pladzyk, CrystEngComm, 2017, 19, 3506 RSC.
- D. Kowalkowska-Zedler, A. Dołęga, N. Nedelko, R. Łyszczek, P. Aleshkevych, I. Demchenko, J. Łuczak, A. Ślawska-Waniewska and A. Pladzyk, Dalton Trans., 2020, 49, 697 RSC.
- L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955 RSC.
- A. Okuniewski, D. Rosiak, J. Chojnacki and B. Becker, Acta Crystallogr., Sect. C: Struct. Chem., 2017, 73, 52 CrossRef CAS.
- B. Becker, A. Zalewska, A. Konitz and W. Wojnowski, Z. Anorg. Allg. Chem., 2001, 627, 271 CrossRef CAS.
- A. Pladzyk, K. Baranowska, D. Gudat, S. Godlewska, M. Wieczerzak, J. Chojnacki, M. Bulman, K. Januszewicz and A. Dołęga, Polyhedron, 2001, 30, 1191 CrossRef.
- A. Pladzyk and K. Baranowska, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, o4773 CrossRef.
- A. Dołęga, A. Jabłońska, A. Pladzyk, L. Ponikiewski, W. Ferenc, J. Sarzyński and A. Herman, Dalton Trans., 2014, 43, 12766 RSC.
- A. Eichhofer and G. Buth, Dalton Trans., 2016, 45, 17382 RSC.
- A. Pladzyk and K. Baranowska, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m2602 CrossRef CAS.
- A. Dołęga, K. Baranowska, A. Pladzyk and K. Majcher, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2008, 64, m259 CrossRef.
- A. Dołęga, A. Pladzyk, K. Baranowska and J. Jezierska, Inorg. Chim. Acta, 2009, 362, 5085 CrossRef.
- K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, Wiley, Hoboken, NY, 5th edn, 1997 Search PubMed.
- N. Prabavathi, N. S. Nayaki and V. Krishnakumar, Pharm. Anal. Acta, 2015, 6, 1000391 Search PubMed.
- N. Deb, P. K. Gogoi and N. N. Dass, J. Therm. Anal., 1989, 35, 27 CrossRef CAS.
- P. K. Kipkemboi, P. C. Kiprono and J. J. Sanga, Bull. Chem. Soc. Ethiop., 2003, 17, 211 CAS.
- R. L. Carlin, Magnetochemistry, Springer-Verlag, 1986 Search PubMed.
- O. Kahn, Molecular Magnetism, VCH Publishers, Inc., 1993 Search PubMed.
- R. Boča, Coord. Chem. Rev., 2004, 248, 757 CrossRef.
- J. R. Pilbrow, J. Magn. Reson., 1978, 31, 479 CAS.
- L. Banci, A. Bencini, C. Benelli, D. Gatteschi and C. Zanchini, Struct. Bonding, 1982, 52, 37 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164 CrossRef CAS.
- T. Gupta and G. Rajaraman, Chem. Commun., 2016, 52, 8972 RSC.
- H. Drulis, K. Dyrek, K. P. Hoffmann, S. K. Hoffmann and A. Wesełucha-Birczyńska, Inorg. Chem., 1985, 24, 4009 CrossRef CAS.
- K. Fukui, H. Ohya-Nishinuchi and N. Hirota, Bull. Chem. Soc. Jpn., 1991, 64, 1205 CrossRef CAS.
- K. Fukui, H. Masuda, H. Ohya-Nishiguchi and H. Kamada, Inorg. Chim. Acta, 1995, 238, 73 CrossRef CAS.
- Y. Peng, V. Mereacre, C. E. Anson, Y. Zhang, T. Bodenstein, K. Fink and A. K. Powell, Inorg. Chem., 2017, 56, 6056 CrossRef CAS.
- M. Böhme, S. Ziegenbalg, A. Aliabadi, A. Schnegg, H. Görls and W. Plass, Dalton Trans., 2018, 47, 10861 RSC.
- S. Vaidya, P. Shukla, S. Tripathi, E. Rivière, T. Mallah, G. Rajaraman and M. Shanmugam, Inorg. Chem., 2018, 57, 3371 CrossRef CAS.
- STOE & Cie GmbH, X-Area 1.75, software package for collecting single-crystal data on STOE area-detector diffractometers, for image processing, scaling reflection intensities and for outlier rejection, Darmstadt, 2015 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2014, 64, 112 CrossRef; G. M. Sheldrick, SHELXL-2014, University of Göttingen and Bruker AXS, Karlsruhe, Germany, 2014 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339 CrossRef CAS.
- L. J. Farrugia, J. Appl. Crystallogr., 2012, 45, 849 CrossRef CAS.
- C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2012, 45, 849 CrossRef.
- R. I. Cooper, R. O. Gould, S. Parson and D. J. Watkin, J. Appl. Crystallogr., 2002, 35, 168 CrossRef CAS.
- M. Pink and V. G. Young Jr, ROTWIN, University of Minnesota, USA, 2000 Search PubMed.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic data, crystal structures, FTIR, magnetic and thermal data. CCDC 2010156, 2010158 and 2010160. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0ra06036d |
| This journal is © The Royal Society of Chemistry 2020 |