Open Access Article
Open Access ArticleCooperative physisorption and chemisorption of hydrogen on vanadium-decorated benzene†
Li-Juan Ma‡
 *,
Ting Han‡,
Jianfeng Jia
*,
Ting Han‡,
Jianfeng Jia and
Hai-Shun Wu
and
Hai-Shun Wu
Key Laboratory of Magnetic Molecules & Magnetic Information Materials Ministry of Education, School of Chemical and Material Science, Shanxi Normal University, No. 1, Gongyuan Street, Linfen, China 041004. E-mail: malijuan19852223@163.com; malijuan@sxnu.edu.cn
First published on 13th October 2020
Abstract
3d TM-decorated carbon composites have been proved to be a new generation of hydrogen storage materials. However, detailed hydrogen storage mechanisms are still unclear. Investigation of the H2 dissociation and H migration on the 3d TM-decorated six-membered carbocycles is very critical for better understanding the hydrogen storage mechanism. In this paper, the processes of chemisorption and physisorption of multiple H2 molecules on synthesized VC6H6 were simultaneously investigated for the first time. The Gibbs free energy calculations show that the optimal chemisorption pathway with the hydrogen storage capacity of 5.97 wt% is exothermic by 2.83 kcal mol−1. Both the continuous hydrogenation giving the product of VC6H11–3H and reverse dehydrogenation could run smoothly at room temperature. The physisorption with a hydrogen storage capacity of 4.48 wt% will be exothermic by 13.49 kcal mol−1. The H2 molecules can be physisorbed at any temperature under 416 K and readily desorbed above 480 K at 1 atm. In summary, physisorption and chemisorption synergistically boost the hydrogen storage property of complex VC6H6. Our study provides a comprehensive picture of the interaction between hydrogen and VC6H6 and opens a new window for optimizing the future hydrogen storage materials.
1. Introduction
To satisfy the increasing global energy demands and solve serious environmental problems, renewable energy sources need to be researched to replace fossil-based fuels.1 Hydrogen energy is reversible, recyclable, and pollution-free.2,3 With the rapid progress of energy transformation, the value of hydrogen energy is further highlighted.4–9 However, the hydrogen energy industry chain, especially the basic research on hydrogen storage links, faces many difficulties currently. Although many hydrogen storage methods10–12 have their advantages in some aspects, they are not enough to meet the practical requirements of hydrogen energy in transportation. Generally, hydrogen is attached by physisorption or chemisorption. In physisorption, hydrogen remains in a molecular state and is weakly bound to the surface. In chemisorption, H2 molecules dissociate into double H atoms and even migrate to the material forming chemical bonds, which are strong.6 Kubas-type orbital interaction13,14 is similar to physisorption, in which the H–H bond in an H2 molecule is elongated but not broken. It improves the hydrogen adsorption energy of transition metals (TMs)-decorated carbon composites (0.10–0.80 eV)6 and makes most of the hydrogen gravimetric storage capacities satisfy the target of the U.S. Department of Energy (∼6.5 wt%).15 Then, TM-decorated carbon composites grew up to be a new generation of hydrogen storage materials.16–19 Interestingly, the dissociation of the first H2 was spontaneous on most of Sc/Ti/V-decorated carbon nanostructures.20–22 The dissociation of the H2 increases the probability of H migration. The question then arises: whether hydrogen molecules are adsorbed only or migrate to form C–H bonds? If dissociation and even migration take place and TM-H/C–H bond is formed, the adsorption of H2 on transition-metal-decorated nanomaterials will change from physisorption to chemisorption. Investigation of the H2 dissociation and H migration is very important for better understanding the hydrogen storage mechanism on the 3d transition metal-decorated carbon nanostructures. While physisorption was mainly focused on and chemisorptions was always neglected.On the other hand, the spillover mechanism is another promising mechanism for enhancing the H2 uptake in carbon-based materials.23–25 Hydrogen spillover following three processes: (1) the dissociation of H2 molecules on the TM sites; (2) the migration of the atomic hydrogen from TM sites to the carbon surface and (3) the diffusion of atomic hydrogen on the carbon surface eventually forming a stable C–H bond. Understanding these three key steps is necessary to fully understand the hydrogen spillover process. Most theoretical studies on the mechanism of hydrogen spillover on carbon adsorbent have been carried out on graphene.26–30 The metal catalyst is an important factor affecting storage by hydrogen spillover. So far, the dissociation sources for hydrogen spillover have been long known for TMs such as Pt, Pd, Ru, Ni, and Ti.31–34 The experimental progress of Kubas-type H2-storage materials always confirmed by V-containing polymers.35 Then, could monatomic V be used as a source of dissociation sources for hydrogen spillover?
Six-membered carbocycle isan important linker in some metal organic frameworks36,37 and covalent organic frameworks38 but also a basic unit of C60,39,40 graphene,41,42 and carbon nanotubes.43–46 In this regard, Ti/Sc/V-benzene complexes as representative units of high-capacity hydrogen storage materials have received great attention.47–50 In this study, based on first-principles calculations, the adsorption behavior of hydrogen on the synthesized VC6H6 (ref. 51–54) is focused on to further address the hydrogen storage mechanism. Previously, Weck,47 Ajay,48 and Li49 reported that VC6H6 could adsorb three hydrogen molecules, but the only physisorption was considered. Here, a systematic study of both physisorption and chemisorption is investigated. The mechanism of dissociative adsorption and even the migration of the H atoms on VC6H6 is investigated. It was found that physisorption and chemisorption synergistically boost the hydrogen storage property of complex VC6H6. Most of our findings would have a great significance for the study of hydrogen storage on TM-decorated carbon composites.
2. Computational methods and details
All geometry optimizations were carried out by using the density functional theory (DFT) method at B3LYP55/6-31+G(d,p) level. The whole calculations employed the Gaussian 09 suite of programs.56 The optimization was carried out without any symmetry constraint and different spin multiplicities were considered. The optimized geometric coordinates and energies were listed in the ESI.† Frequency calculations were performed to confirm that there was no imaginary frequency in the stable structure, and one imaginary frequency in the transition states. Ab initio molecular dynamics (MD) simulations based on atom density matrix propagation (ADMP)57–61 were performed to confirm part of the favorable dissociation paths.Consecutive adsorption energies with ZPEs (ΔEn) and Gibbs free energy corrections (ΔGn) at 298.15 K were obtained using the following formula:
| ΔEn = E(VC6H6(H2)n−1) + E(H2) − E(VC6H6(H2)n) | (1) |
| ΔGn = G(VC6H6(H2)n−1) + G(H2) − G(VC6H6(H2)n) | (2) |
In the equilibrium state, various conformations of VC6H6(H2)n have different energy and proportion. The proportion of conformation (Pi) was calculated according to the Boltzmann distribution:
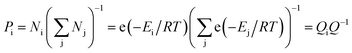 | (3) |
Spin multiplicity, vibrational frequencies, ionization energy, and electron affinity of VC6H6 were calculated to test the reliability of our calculations. The range-separated hybrid DFT method (wB97XD)57 was used. The larger Pople-style orbital basis sets 6-311G++(3df,3pd) and diffuse functions in standard basis set aug-cc-pVTZ for C, H, and large-core relativistic Stuttgart–Dresden effective core potential(SDD)58 basis set for V atom were included.
As shown in Table 1, both the results using B3LYP/6-31G+(d,p) and wB97XD/6-311G++(3df,3pd) show that VC6H6 is quartet state and the vibrational frequencies of VC6H6 are in good agreement with the experimental values.48 The ionization energies and electron affinities of VC6H6 in Table 2 using B3LYP/6-31G+(d,p), B3LYP/aug-cc-pVTZ and wB97XD/6-311G++(3df,3pd) are in good agreement with the experimental values in ref. 51 and 53. The C–C bond lengths and the C–H bond lengths of VC6H6 using B3LYP/6-31+g(d,p) are 1.40–1.56 Å and 1.08–1.10 Å, respectively, which coincide well with the theoretical results by Duncan.54 These values indicate the scheme of B3LYP/6-31+g(d,p) is a good compromise between accuracy and computational effort.
| Functional | Multi. | Δ (eV) | νo-p(CH)a | νs(CC) | νi-p(CH) | ν(CC) |
|---|---|---|---|---|---|---|
| a Vibrational modes: νo-p(CH) = C–H out of plane bending; νs(CC) = symmetric C–C stretching; νi-p(CH) = C–H in-plane rocking; ν(CC) = asymmetric C–C stretching. | ||||||
| B3LYP/6-31G+(d,p) | 2 | 0.07 | ||||
| 4 | 0.00 | 769.05 | 956.3 | 1319.34 | 1420.15 | |
| B3LYP/6-311G++(3df,3pd) | 2 | 0.30 | ||||
| 4 | 0.00 | 734.10 | 924.20 | 1368.27 | 1507.34 | |
| B3LYP/aug-cc-pVTZ | 2 | 0.11 | ||||
| 4 | 0.00 | 679.54 | 928.29 | 1341.32 | 1500.48 | |
| wB97XD/6-311G++(3df,3pd) | 2 | 2.64 | ||||
| 4 | 0.00 | 760.51 | 947.81 | 1329.71 | 1426.20 | |
| wB97XD/aug-cc-pVTZ | 2 | 1.61 | ||||
| 4 | 0.00 | 781.87 | 974.09 | 1348.03 | 1506.89 | |
| Experiments54 | 758.00 | 958.00 | 1306.00 | 1460.00 | ||
Moreover, the adsorption processes of H2 molecules on TM decorated carbon nanomaterials include Kubas-type bonding, H2 dissociation, H atom migration, and even strong C–H bonds producing. Both our previous researches52 and other group's reports59–61 prove that the B3LYP method is appropriate for obtaining both reliable structures and potential energy surfaces. Firstly, B3LYP functional is very valid for estimating the H2 storage property of Ti-acetylene/ethylene compounds.59–61 Secondly, the B3LYP method employing a 6-31+G(d,p) basis set was used to study the hydrogen storage capacity of alkali metal ion decorated boric acid.62 Thirdly, the investigation of the stepwise adsorption energies of hydrogen on TiC6H6 showed the M06-2X functional was not preferred and the B3LYP functionals with 6-31+g(d,p) basis sets gave an impressive agreement with the accurate results.
3. Results and discussion
3.1 Optimized configurations of VC6H6(H2)n (n = 1–4)
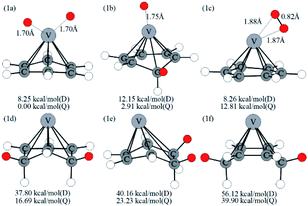
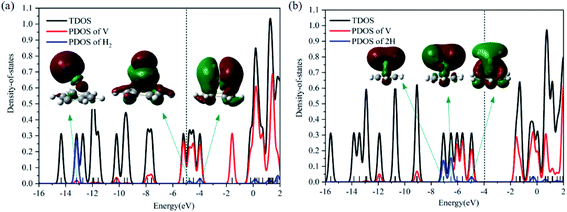
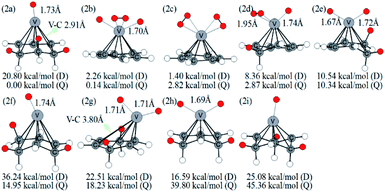
Optimized configurations of VC6H6(H2)n (n = 1–4) and relative free energies at 298.15 K and 1 atm are presented in Fig. 1, 3–5, respectively. Thermodynamic data show that the configurations in the quartet state are lower in energy than the corresponding doublet state except for 1c. The most stable structure is the 1a(Q), which is 8.25 kcal mol−1 lower in energy than the doublet state. 1a with the dissociated H2 molecule is mentioned in ref. 31 1b with the CH2 group is more stable than the 1c with molecular H2. It indicates hydrogen dissociation, H migration, and even formation of the C–H bond are favorable thermodynamically. Chemisorption forming C–H or V–H bonds is usually stronger than physisorption forming V–H2 unit. Then, it's easy to understand that structure 1a with V–H bonds and 1b with a C–H bond is more stable than structure 1c. The configurations of 1d, 1e, and 1f have two CH2 groups. The original C6H6 has a little deformation and the longest V–C bond length increases from 2.32 Å to 2.94 Å due to the formation of the CH2 groups. Obviously, the forming of the C–H bond causes a great deformation of the C6H6 unit. The preferred site of one H atom in VC6H6 is determined by comparing the two structures in Fig. S2.† The binding energy of H to the V site is 2.83 eV, which is larger than that of H to the C site (1.82 eV). This indicates that the H atoms prefer to bind at the on-top V site. That's maybe why 1a with the V–H bonds is more stable than 1b with a C–H bond.The dissociation of the first H2 was spontaneous on most of Sc/Ti/V decorated carbon nanostructures.35–42 To understand the dissociation process, Fig. 2 shows the partial orbital density state (PDOS) of V and adsorbed H2 in 1c (VC6H6(H2)), and 1a (VC6H6(2H)). Effective intermolecular bonding leads to bonding orbits have lower energies. Two parts interact strongly when electrons filling in these bonding orbits. The three principles of effective bonding include matching symmetry, energy proximity, and maximum overlap between orbits. For 1c, the orbital in the energy of −13.00 eV mainly comes from the s orbits of H2 and the other orbitals of VC6H6 are almost unaffected by the hydrogen molecule. The larger energy difference between the orbitals from V and the H2 causes weak interaction. For 1a, the localized 3d orbits of V in VC6H6 mix with s orbits from hydrogen atoms easily in energies of −6.00–7.50 eV. So, VC6H6 has a strong interaction with the H atoms rather than a hydrogen molecule.
The structures in Fig. 3 include the configurations with one CH2 group (2d), two CH2 groups (2e, 2g, 2h), and three CH2 groups (2a, 2f, 2i). The 2b structure contains an activated hydrogen molecule and two V–H bonds, which was mentioned in previous literature.40 2a and 2b structures have an energy difference of only 0.14 kcal mol−1 at the B3LYP level.
 | ||
| Fig. 3 Optimized configurations of various isomers of VC6H6–2H2 at the B3LYP/6-31+G(d,p) level and relative Gibbs free energies at 298.15 K (in kcal mol−1). The red circle means adsorbed hydrogen. | ||
This little energy difference indicates 2b inclines to form more stable 2a. For the structure shown in Fig. 3, the bond length of the V–H bond is 1.67–1.74 Å for isomers with one H atom but is 1.90–1.95 Å for isomers with H2, which is longer than the former. This means that the single H atom has a stronger interaction with metal V. The distance of C–C neighboring CH2 is lengthened to 1.50–1.56 Å. Besides, the V–C bond adjacent to three CH2 groups in 2a is stretched from 2.28 Å to 2.91 Å, and causing the metal V atom is tilted to one side.
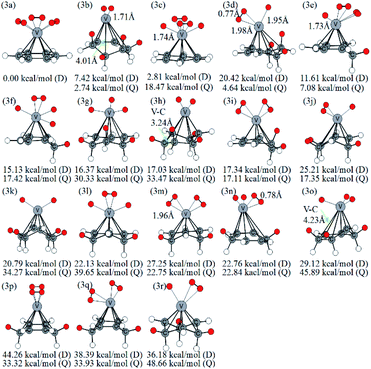
The optimized VC6H6(H2)3 are displayed in Fig. 4. Notably, the 3a with not CH2 groups is the most stable doublet isomer due to its higher symmetry (C3V). From the perspective of overlooking, it can be seen that the position of H2 molecules corresponds to the C–C bond in the six-membered ring. There are two configurations with one CH2 group (3e, 3f), six configurations with two CH2 groups (3i, 3l, 3m, 3n, 3p, 3q), five configurations with three CH2 groups (3d, 3g, 3j, 3o, 3r), and three configurations with four CH2 groups (3b, 3h, 3k). Thus, the structures with the adjacent CH2 groups are more stable.
 | ||
| Fig. 4 Various configurations of VC6H6–3H2 at the B3LYP/6-31+G(d,p) level and relative Gibbs free energies at 298.15 K (in kcal mol−1). The red circle means adsorbed hydrogen. | ||
A complex containing dissociated H2 molecules (with V–H bond) is always more stable than the corresponding complex with activated H2 molecules. For example, 1a with the dissociated H2 molecule is more stable than the 1c with molecular H2; the 2b structure contains an activated hydrogen molecule and two V–H bonds is more stable than the 2c with two molecular H2 and so on. However, the reverse appears in the VC6H6(H2)3 isomers. Firstly, calculations at different theoretical levels confirm our results. As shown in Table S2,† both the results using B3LYP/6-31G+(d,p), B3LYP/6-311G++(3df,3pd), B3LYP/aug-cc-pVTZ, wB97XD/6-311G++(3df,3pd) and wB97XD/6-311G++(3df,3pd) show that 3a with three molecular H2 molecules is more stable than the 3c with the dissociated H2 molecule. Secondly, detailed analyses of the symmetry and energy of deformation are carried out to comment on why this is the case. The symmetry of optimized VC6H6(D) is C6V. As shown in Table S2,† the VC6H6 unit in structure 3a is C6V symmetry while that in structure 3c is C2 symmetry. That's mean, after adsorbing 3H2, the VC6H6 unit in structure 3a is nearly no change. Therefore, the energy of deformation (ΔGR) of VC6H6 and hydrogen binding energy between the VC6H6 unit and 3H2 unit in 3a and 3c (ΔGH) are defined.
| ΔGR = G(VC6H6 unit in 3a/3c) − G(VC6H6) |
| ΔGH = [G(VC6H6 unit in 3a/3c) + G (3H2 unit in 3a/3c) − G(3a/3c)]/3 |
The values of ΔGR and ΔGH are listed in Table S3.† The deformation energy of 3c is 0.28 eV, which is greater than that of 3a (0.23 eV). When deformation energy is not taken into account, the hydrogen binding energy between the VC6H6 unit in 3c and 2H2–2H unit is 2.52 eV, which is greater than that between the VC6H6 unit in 3a and 3H2(0.72 eV). This is consistent with the common understanding.
Similarly, Fig. 5 lists several optimized isomers of VC6H6–4H2 complexes. Notably, the structure with four activated hydrogen molecules is very unstable. The most stable configuration 4a is composed of four adjacent CH2 groups with an activated hydrogen molecule and two H atoms. Among many other configurations, 4c, 4d, and 4f have one CH2 group are, 4e, 4i, 4k, 4m, and 4p have two CH2 groups, 4b, 4g, 4h, 4n, 4o, and 4s have three CH2 groups, 4a, 4l, and 4r have four CH2 groups, 4j has five CH2 groups, and 4q has six CH2 groups. The energy difference between 4g and 4h is 3.05 kcal mol−1, though both have three CH2 groups and two activated hydrogen molecules. It indicates that the energy of structures also depends on the direction of the activated hydrogen molecule. 4q and 4j have six and five consecutive CH2 groups, respectively, but their energy is not the lowest. This may be due to the steric hindrance effect formed by the consecutive CH2 groups. For VC6H6–nH2 (n = 1, 3), the most stable isomers have no CH2 group. For VC6H6–nH2 (n = 2,4), the most stable isomers have CH2 groups, and in which CH2 groups are adjacent. These prompt us to think strongly about whether the C–H bond could be formed easily.
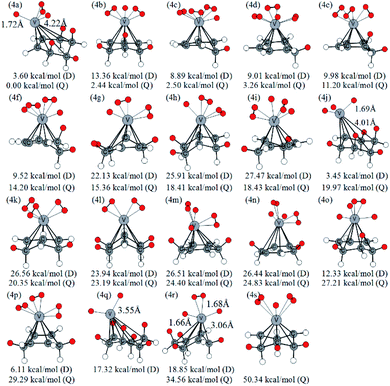 | ||
| Fig. 5 Optimized configurations of various isomers of VC6H6–4H2 at the B3LYP/6-31+G(d,p) level and relative Gibbs free energies at 298.15 K (in kcal mol−1). The red circle means adsorbed hydrogen. | ||
3.2 The optimal chemisorption pathway of multiple H2 molecules on the VC6H6
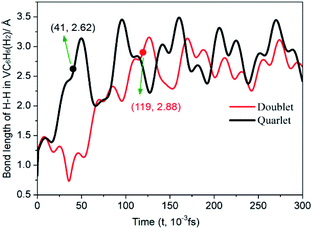 | ||
| Fig. 7 Time evolution trajectories of the H–H in VC6H6(H2) at 300 K. The bond lengths are given in Å. | ||
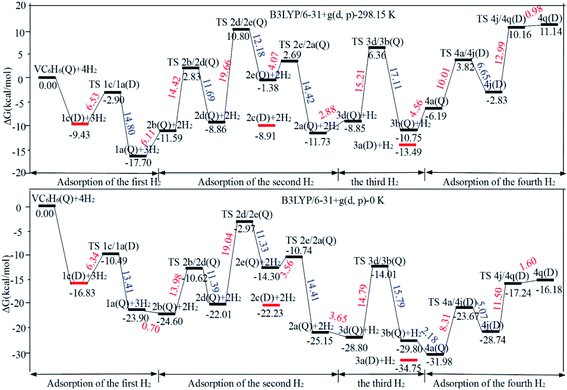
One of the dissociated H atoms in 1a(Q) will migrate to form CH2 group with a barrier of 21.79 kcal mol−1, which is endothermic by 2.91 kcal mol−1 and slow. At 298.15 K, the overall conformation analysis shows that the 1a(Q) and 1b(Q) of VC6H6–H2 are 99.3% and 0.70%, respectively. IR stability calculations ensure that the structures 1a(Q) and 1b(Q) are energy minima without imaginary frequency (see Fig. S4 of the ESI†). Two main H modes for 1a(Q) are symmetric and antisymmetric stretching vibrations, respectively corresponding frequencies of 1606.48 and 1645.80 cm−1. One main H mode vibration frequency for 1b(S) is 1582.26 cm−1. The three unique modes should be present in the Raman/IR spectra of a successfully synthesized material.
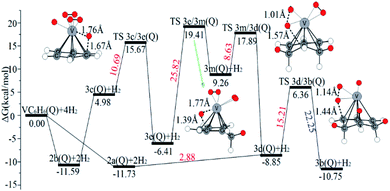 | ||
| Fig. 9 The Gibbs free energy profiles of the third H2 molecule adsorption on the VC6H6 complex. The energy barriers are highlighted in red for the forward reaction and blue for the backward reaction. | ||
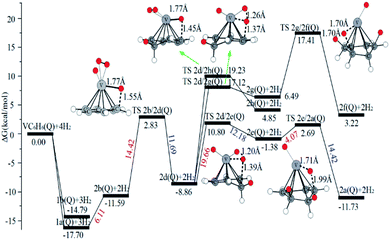
When the fourth H2 molecule continues to approach the structure 3b(Q), the consecutive adsorption energies (ΔEn-ZPE) is 2.18 kcal mol−1 (0.09 eV). The 4a(Q) forms 4j(D) through a spin crossover. When 4j(D) is used as a reactant, it is unfavorable to generate 4q(D) (Fig. 10).
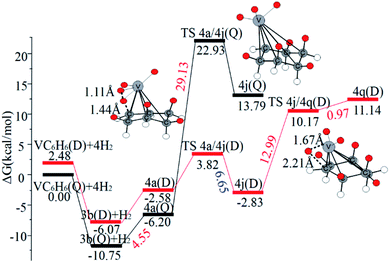 | ||
| Fig. 10 The Gibbs free energy profiles of the fourth H2 molecule adsorption on VC6H6. The energy barriers are highlighted in red for the forward reaction and blue for the backward reaction. | ||
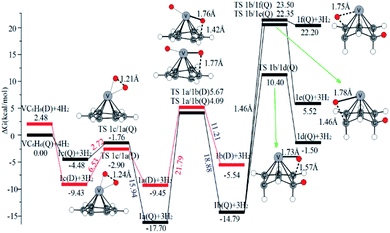
The optimal chemisorption pathways of H2 molecules on VC6H6 are shown in Fig. 11. (More detailed information regarding optimized cartesian coordinates and computed sum of electronic and thermal free energies of mentioned structures see the ESI†). When the pressure of hydrogen increases, H2 molecules adhering to VC6H6 can migrate continuously to form CH2 groups, and finally VC6H11–3H (4j) is formed. Gibbs free energy calculations show that the whole reaction is exothermic by 2.83 kcal mol−1 at 298.15 K. The generation of 4q(D) is endothermic by 11.14 kcal mol−1, which is unfavorable in thermodynamics. The dissociation and migration of the second H2 is the rate-determining step in the whole reaction with a barrier of 19.66 kcal mol−1. In turn, the complex VC6H11–3H will dehydrogenate continuously until VC6H6 when the hydrogen pressure decreases. The energy barrier of the critical speed step (the migration of H atom in 3d(Q)) is 17.11 kcal mol−1. Hence the hydrogen chemisorption adsorption and desorption on the VC6H6 complex could run smoothly with the hydrogen storage of 5.97 wt%, simply regulated by increasing/decreasing the hydrogen pressure.
As the discussion above, the chemisorptions pathway of H2 molecules on VC6H6 at 298.15 K indicates that: (1) H2 molecules attached to VC6H6 can be dissociated, and H atoms migrate continuously to form CH2 groups. (2) Spin crossover mainly occurs in the pathway of adsorption of the first and fourth hydrogen molecules. (3) The optimal chemisorption pathway should be VC6H6(Q) → 1c(D) → 1a(Q) → 2b(Q) → 2d(Q) → 2e(Q) → 2a(Q)→ 3d(Q) → 3b(Q)→ 4a(Q) → 4j(D) (VC6H11–3H). (4) Gibbs free energy calculations show that the overall reaction to give the hydrogenation product 4j (VC6H11–3H) is exothermic by 2.83 kcal mol−1 and has an energy barrier of 19.66 kcal mol−1.
3.3 Physisorption of multiple H2 molecules on the VC6H6
Fig. 12a shows the optimal physical adsorption path of multiple H2 molecules on the VC6H6 complex. The free energy profile is shown in Fig. S5.† For n = 1, H2 dissociates into two H atoms via the transition state TS. Though the single H2 dissociation on VC6H6 is exothermic, the dissociation barrier is 6.34 kcal mol−1. Moreover, 3a is more stable than 3c. So, the adsorption pathway along VC6H6 → 1c(D) → 2c(Q) → 3a(Q) pathway will be more favorable thermodynamically.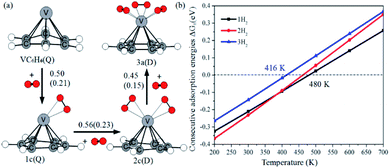 | ||
| Fig. 12 (a) The consecutive adsorption energies ΔEn (ΔGn) of multiple H2 molecules on the VC6H6 (in eV), (b) temperature dependence of ΔGn at p = 1 atm. | ||
When all the three hydrogen molecules are adsorbed in molecular form, the consecutive adsorption energies are 0.50, 0.56, 0.45 eV, respectively. And the average hydrogen adsorption energy for VC6H6(H2)3 is 0.50 eV, which is between physisorption and chemisorption (0.20–0.60 eV). As shown in Fig. 11, the physisorption of the three hydrogen molecules is exothermic by 13.49 kcal mol−1 at 298.15 K, and need no energy barrier. The hydrogen storage capacity of VC6H6 is 4.48 wt%. Based on the van't Hoff equation: TD= (Ea/kB)(ΔS/R − ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P)−1,63 the three H2 can be adsorbed at any temperature under 421 K and 1 atm. Notably, spin multiplicity and the Gibbs free energy correction fully considered here. The temperatures at which ΔG = 0 eV/H2 for 1c(Q), 2c(Q), 3a(D) are 480 K, 462 K, and 416 K, respectively (Fig. 12b). It also indicates that three H2 molecules can be spontaneously adsorbed on VC6H6 forming 3a below 416 K. And three H2 can be readily desorbed above 480 K under atmospheric pressure.
P)−1,63 the three H2 can be adsorbed at any temperature under 421 K and 1 atm. Notably, spin multiplicity and the Gibbs free energy correction fully considered here. The temperatures at which ΔG = 0 eV/H2 for 1c(Q), 2c(Q), 3a(D) are 480 K, 462 K, and 416 K, respectively (Fig. 12b). It also indicates that three H2 molecules can be spontaneously adsorbed on VC6H6 forming 3a below 416 K. And three H2 can be readily desorbed above 480 K under atmospheric pressure.
4. Conclusions
TM-decorated carbon composites grew up to be a new generation of hydrogen storage materials. Most of these researches reported that the dissociation of the first H2 was spontaneous on most of Sc/Ti/V-decorated carbon nanostructures. As known that H migration easily occurs on metal sites. Then hydrogenation reaction would also occur during the hydrogen storage on 3d TM-decorated organic complexes. To further address this issue, the process of hydrogen adsorption on synthesized VC6H6 is focused on answering the question that whether hydrogen molecules are absorbed only or migrate to form C–H bonds.Optimized configurations of VC6H6(H2)n (n = 1–4) and relative Gibbs free energies at 298.15 K and 1 atm were presented. For VC6H6–nH2 (n = 1, 3), the most stable isomers have no CH2 group. For VC6H6–nH2 (n = 2,4), the most stable isomers have adjacent CH2 groups. The chemisorptions pathway of H2 molecules on VC6H6 at 298.15 K indicates that H2 molecules attached to VC6H6 can be dissociated, and H atoms migrate continuously to form CH2 groups. Gibbs free energy calculations show that the overall reaction giving the hydrogenation product 4j (D) (VC6H11–3H) is exothermic by 2.83 kcal mol−1 and has an energy barrier of 19.66 kcal mol−1. Hence the hydrogen chemisorption adsorption and desorption on the VC6H6 complex could run smoothly with the hydrogen storage of 5.97 wt%, simply regulated by increasing/decreasing the hydrogen pressure. The physisorption along VC6H6 → 1c(D) → 2c(Q) → 3a(Q) will be exothermic by 13.49 kcal mol−1. The three H2 can be adsorbed at any temperature under 416 K and readily desorbed above 480 K at 1 atm. The corresponding hydrogen storage capacity is 4.48 wt%. In summary, both physisorption and chemisorption tend to occur in certain circumstances.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financially supported by the National Natural Science Foundation of China (21805176), the 1331 Engineering, and Education Reform Project (J2019098) and Youth Science and Technology Research Foundation (201901D211394) of Shanxi Province of China, the Doctor Fund (0505/02070359) of Shanxi Normal University.Notes and references
- I. L. R. Gomes, H. M. I. Pousinho, R. Melicio and V. M. F. Mendes, Energy, 2017, 124, 310–320 CrossRef.
- S. Niaz, T. Manzoor and A. H. Pandith, Renewable Sustainable Energy Rev., 2015, 50, 457–469 CrossRef CAS.
- A. G. Stern, Int. J. Hydrogen Energy, 2018, 43, 4244–4255 CrossRef CAS.
- K. T. Møller, T. R. Jensen, E. Akiba and H.-w. Li, Prog. Nat. Sci.: Mater. Int., 2017, 27, 34–40 CrossRef.
- M. Hirscher, V. A. Yartys, M. Baricco, J. M. B. Von Colbe, D. Blanchard, R. C. Bowman, D. P. Broom, C. E. Buckley, F. Chang and P. Chen, J. Alloys Compd., 2020, 827, 153548 CrossRef CAS.
- E. S. Hanley, J. P. Deane and B. P. Ó. Gallachóir, Renewable Sustainable Energy Rev., 2018, 82, 3027–3045 CrossRef.
- N. Z. A. K. Khafidz, Z. Yaakob, K. L. Lim and S. N. Timmiati, Int. J. Hydrogen Energy, 2016, 41, 13131–13151 CrossRef.
- H. Wang, H. Lin, W. Cai, L. Z. Ouyang and M. Zhu, J. Alloys Compd., 2016, 658, 280–300 CrossRef CAS.
- P. E. Dodds, I. Staffell, A. Hawkes, F. G. N. Li, P. Grunewald, W. McDowall and P. Ekins, Int. J. Hydrogen Energy, 2015, 40, 2065–2083 CrossRef CAS.
- J. B. von Colbe, J.-R. Ares, J. Barale, M. Baricco, C. Buckley, G. Capurso, N. Gallandat, D. M. Grant, M. N. Guzik and I. Jacob, Int. J. Hydrogen Energy, 2019, 44, 7780–7808 CrossRef.
- R. Moradi and K. M. Groth, Int. J. Hydrogen Energy, 2019, 44, 12254–12269 CrossRef CAS.
- Y. Gao, N. Zhao, J. Li, E. Liu, C. He and C. Shi, Int. J. Hydrogen Energy, 2012, 37(16), 11835–11841 CrossRef CAS.
- G. J. Kubas, Chem. Rev., 2007, 107, 4152–4205 CrossRef CAS.
- C. Chung, J. Ihm and H. Lee, J. Korean Phys. Soc., 2015, 66, 1649–1655 CrossRef CAS.
- U.S. Department of Energy, https://www.energy.gov/eere/fuel%20cells/doe-technical-targets-onboard-hydrogen-storage%20light%20–%20duty%20-vehicles.
- L. Ma, J. Zhang and K. Xu, Appl. Surf. Sci., 2014, 292, 921–927 CrossRef CAS.
- H. He, X. Chen, W. Zou and R. Li, Int. J. Hydrogen Energy, 2018, 43, 2823–2830 CrossRef CAS.
- S. Kumar, M. Samolia and T. J. Dhilip Kumar, ACS Appl. Energy Mater., 2018, 1, 1328–1336 CrossRef CAS.
- S. Nachimuthu, P. Lai and J. Jiang, Carbon, 2014, 73, 132–140 CrossRef CAS.
- L. Yang, L. L. Yu, H. W. Wei, W. Q. Li, X. Zhou and W. Q. Tian, Int. J. Hydrogen Energy, 2019, 44, 2960–2975 CrossRef CAS.
- P. Tavhare, N. Wadnerkar, V. G. Kalamse and A. Chaudhari, Acta Phys. Pol., A, 2016, 129, 1257–1262 CrossRef CAS.
- S. Cui, N. Zhao, C. Shi, C. Feng, C. He, J. Li and E. Liu, J. Phys. Chem. C, 2014, 118, 839–844 CrossRef CAS.
- A. Lueking and R. T. Yang, J. Catal., 2002, 206, 165–168 CrossRef CAS.
- A. J. Lachawiec, G. Qi and R. T. Yang, Langmuir, 2005, 21, 11418–11424 CrossRef CAS.
- D. S. Pyle, E. M. Gray and C. J. Webb, Int. J. Hydrogen Energy, 2016, 41, 19098–19113 CrossRef CAS.
- M. Blanco-Rey, J. I. Juaristi, M. Alducin, M. J. López and J. A. Alonso, J. Phys. Chem. C, 2016, 120, 17357–17364 CrossRef CAS.
- C. M. Ramos-Castillo, J. U. Reveles, M. E. Cifuentes-Quintal, R. R. Zope and R. de Coss, J. Phys. Chem. C, 2016, 120, 5001–5009 CrossRef CAS.
- D. H. Chung, H. Guk, D. Kim, S. S. Han, N. Park, K. Choi and S.-H. Choi, RSC Adv., 2014, 4, 9223–9228 RSC.
- S. Nachimuthu, P.-J. Lai and J.-C. Jiang, Carbon, 2014, 73, 132–140 CrossRef CAS.
- A. D. Lueking, G. Psofogiannakis and G. E. Froudakis, J. Phys. Chem. C, 2013, 117, 6312–6319 CrossRef CAS.
- C.-Y. Wang, J. L. Gray, Q. Gong, Y. Zhao, J. Li, E. Klontzas, G. Psofogiannakis, G. Froudakis and A. D. Lueking, J. Phys. Chem. C, 2014, 118, 26750–26763 CrossRef CAS.
- T.-Y. Chung, C.-S. Tsao, H.-P. Tseng, C.-H. Chen and M.-S. Yu, J. Colloid Interface Sci., 2015, 441, 98–105 CrossRef CAS.
- J. L. Blackburn, C. Engtrakul, J. B. Bult, K. Hurst, Y. Zhao, Q. Xu, P. A. Parilla, L. J. Simpson, J.-D. R. Rocha, M. R. Hudson, C. M. Brown and T. Gennett, J. Phys. Chem. C, 2012, 116, 26744–26755 CrossRef CAS.
- H. Chen and R. T. Yang, Langmuir, 2010, 26, 15394–15398 CrossRef CAS.
- T. K. A. Hoang, A. Hamaed, G. Moula, R. Aroca, M. L. Trudeau and D. M. Antonelli, J. Am. Chem. Soc., 2011, 133, 4955–4964 CrossRef CAS.
- P. García-Holley, B. Schweitzer, T. Islamoglu, Y. Liu, L. Lin, S. Rodriguez, M. H. Weston, J. T. Hupp, D. A. Gómez-Gualdrón, T. Yildirim and O. K. Farha, ACS Energy Lett., 2018, 3, 748–754 CrossRef.
- G. Li, H. Kobayashi, J. M. Taylor, R. Ikeda, Y. Kubota, K. Kato, M. Takata, T. Yamamoto, S. Toh, S. Matsumura and H. Kitagawa, Nat. Mater., 2014, 13, 802–806 CrossRef CAS.
- P. Pachfule, A. Acharjya, J. Roeser, T. Langenhahn, M. Schwarze, R. Schomäcker, A. Thomas and J. Schmidt, J. Am. Chem. Soc., 2018, 140, 1423–1427 CrossRef CAS.
- T. Mashoff, M. Takamura, S. Tanabe, H. Hibino, F. Beltram and S. Heun, Appl. Phys. Lett., 2013, 103, 013903 CrossRef.
- H. Ren, C. Cui, X. Li and Y. Liu, Int. J. Hydrogen Energy, 2017, 42, 312–321 CrossRef CAS.
- A. A. Ensafi, M. Jafariasl, A. Nabiyan, B. Rezaei and M. Dinari, Energy, 2016, 99, 103–114 CrossRef CAS.
- Y. Zhou, W. Chu, F. Jing, J. Zheng, W. Sun and Y. Xue, Appl. Surf. Sci., 2017, 410, 166–176 CrossRef CAS.
- K. Wenelska, B. Michalkiewicz, X. Chen and E. Mijowska, Energy, 2014, 75, 549–554 CrossRef CAS.
- S. Ghosh and V. Padmanabhan, Int. J. Energy Res., 2017, 41, 1108–1117 CrossRef CAS.
- M. S. Yahya and M. Ismail, J. Phys. Chem. C, 2018, 122, 11222–11233 CrossRef CAS.
- D. Silambarasan, V. J. Surya, V. Vasu and K. Iyakutti, ACS Appl. Mater. Interfaces, 2013, 5, 11419–11426 CrossRef CAS.
- P. F. Weck, T. J. Dhilip Kumar, E. Kim and N. Balakrishnan, J. Chem. Phys., 2007, 126, 094703 CrossRef.
- A. Deshmukh, R. Konda, V. Kalamse and A. Chaudhari, RSC Adv., 2016, 6, 47033–47042 RSC.
- P. Li, S. H. Deng, G. H. Liu, L. Zhang, J. Huang and J. Y. Yu, J. Power Sources, 2012, 211, 27–32 CrossRef CAS.
- R. Y. Sathe, S. Kumar and T. J. Dhilip Kumar, Int. J. Hydrogen Energy, 2019, 44, 6663–6673 CrossRef CAS.
- M. P. Andrews, S. M. Mattar and G. A. Ozin, J. Phys. Chem., 1986, 90, 744–753 CrossRef CAS.
- P. Tavhare and A. Chaudhari, Indian J. Pure Appl. Phys., 2018, 56, 341–345 Search PubMed.
- K. Judai, M. Hirano, H. Kawamata, S. Yabushita, A. Nakajima and K. Kaya, Chem. Phys. Lett., 1997, 270, 23–30 CrossRef CAS.
- D. van Heijnsbergen, G. von Helden, G. Meijer, P. Maitre and M. A. Duncan, J. Am. Chem. Soc., 2002, 124, 1562–1563 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford, 2009 Search PubMed.
- R. Car and M. Parrinello, Phys. Rev. Lett., 1985, 55, 2471–2474 CrossRef CAS.
- G. Martyna, C. Cheng and M. L. Klein, J. Chem. Phys., 1991, 95, 1318–1336 CrossRef CAS.
- B. G. Lippert and J. H. Parrinello, Mol. Phys., 1997, 92, 477–488 CrossRef.
- G. Lippert and H. M. Parrinello, Theor. Chem. Acc., 1999, 103, 124–140 Search PubMed.
- H. B. Schlegel, S. S. Iyengar, X. Li, J. M. Millam, G. A. Voth, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 2002, 117, 8694–8704 CrossRef CAS.
- J. Chai and M. Headgordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- Ea is the average adsorption energy, kB is the Boltzmann constant1.38 × 10−23 J K−1, R is the gas constant 8.31 J K−1 mol−1, and P is the equilibrium pressure 1 atm, ΔS is the change of the H2 entropy from gas to liquid phase.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra06057g |
| ‡ These authors contributed equally to this work and should be considered co-first authors. |
| This journal is © The Royal Society of Chemistry 2020 |