 Open Access Article
Open Access ArticleFirst-principles study on the effects of N and Al doping on the mechanical properties and electronic structures of TiC†
Zhinan Caoa,
Na Jin *a,
Jinwen Ye
*a,
Jinwen Ye a,
Xu Dua and
Ying Liuab
a,
Xu Dua and
Ying Liuab
aCenter for Rare Earth & Vanadium-titanium Based Materials, School of Materials Science & Engineering, Sichuan University, Chengdu, 610065, China. E-mail: jinna319@163.com
bKey Laboratory of Advanced Special Material & Technology, Ministry of Education, Chengdu, 610065, China
First published on 2nd October 2020
Abstract
First-principles calculations are carried out by DFT within the CASTEP plane wave code to investigate the mechanical properties and electronic structure of N and Al doped TiC. The results show that the co-doping of nitrogen and aluminum narrows the lattice constant and nitrogen could enhance the stability of TiC, however, aluminum makes the compound unstable. The calculated elastic constants and elastic moduli reveal that aluminum reduces the elastic constants, bulk modulus B, shear modulus G and Young's modulus E, but nitrogen can enhance them. The results of B/G and C12–C44 indicate that aluminum could significantly increase the ductility of TiC. Meanwhile, the electronic structure calculations reveal that strong p–d covalent bonds exist among C-p, N-p, Ti-d and Al-p states and Al-doping causes DOS peak transfer to a higher energy level and increases the DOS above the Fermi level. The hardness is estimated by a semi-empirical model that is based on the Mulliken overlap population and bond length. The addition of Al sharply reduces the hardness of the TiC-based alloys due to the weakest bond taking a determinative role in the hardness of materials, which is the C–Al bond in those compounds.
Introduction
Titanium carbide, a typical transition metal carbide, has been applied in cutting tools,1 hard coatings,2,3 grain inhibitors4 as well as a catalyst5–7 for years. It is not only due to its desirable physical properties such as high hardness, high melting points, low density and corrosion resistance but also the chemical stability and low thermal expansion coefficient draw huge attention in manufacturing industries. However, it is still limited to niche applications due to its intrinsic brittleness.8,9 Thus, many researchers have been making efforts to improve the toughness of TiC, for instance by doping some other elements like N, W, Mo, Ta.10–14 In recent years, some research has focused on improving the mechanical properties of TiC by Al-doping. Several experimental studies investigated the microstructure, physical properties of Al-doped TiC and testified that Al is an ideal dopant for TiC-based compounds, which was applied on coatings.15–19 Moreover, since 1970s Kieffer and Ettmayer introduced N into TiC-based cermets, N doping enhanced the toughness of cermets significantly, resulting in the Ti(C,N)-based cermets gradually replaced WC–Co hardmetals in machining process, especially those related to high-speed cutting. Based on the consideration of cooperation between N and Al, some works tried adding AlN or Al into Ti(C,N)-based cermets, which was proved to be able to enhance the fracture toughness and hardness by strengthening the rim phase and binder phase.20,21First-principles calculations with density functional theory (DFT) is an effective way to model and bridge the gap between crystal structure and properties for many materials.22 Although many experimental studies on cermets proved that Al doping provides a remarkable enhancement in TiC-based or Ti(C,N)-based compounds, the fundamental researches of them based on DFT methods are still rare. Chen and Zhao23 investigated the elastic properties and electronic structures of Ti0.75X0.25C (X = W, Mo, Ta, V, Al, etc.) by using ab initio DFT calculations and found that aluminum could significantly promote the ductility and slightly reduce the hardness. However, it still lacks comparable works on how the Al and N effects comprehensive properties of these compounds.
In this work, TiC0.75N0.25, Ti0.75Al0.25C and Ti0.75Al0.25C0.75N0.25 were chosen to investigate the effects of addition of N and Al on the lattice parameters, elastic properties, density of states (DOS) and Mulliken population and hardness of TiC-based carbonitrides using DFT methods with generalized gradient approximation (GGA) exchange potential. Additionally, properties of TiC, TiN were also calculated for clarifying the effects of N and Al doping.
Methods of calculation
In this study, the calculation was carried out by the DFT within the Cambridge Serial Total Energy Package (CASTEP) plane wave code.24–26 The interaction between ionic core and valance was treated by ultrasoft pseudopotentials.27 The GGA of Perdew–Burke–Ernzerhof functional was utilized to investigate the exchange and correlation terms.28,29 The status of valence electrons in this study were considered as 3s23p63d24s2 for Ti, 3s23p1 for Al, 2s22p2 for C and 2s22p3 for N. In order to assure the convergence of total energy and elastic moduli of our work, different cut-off energy (450 eV, 600 eV) and Monkhorst–Pack -point meshes30 (6 × 6 × 6, 10 × 10 × 10, 14 × 14 × 14) were carefully checked. Finally, the cut-off energy was set as 700 eV and Brillouin-zone integration was chosen 14 × 14 × 14 as
-point meshes30 (6 × 6 × 6, 10 × 10 × 10, 14 × 14 × 14) were carefully checked. Finally, the cut-off energy was set as 700 eV and Brillouin-zone integration was chosen 14 × 14 × 14 as  -points parameters. During the calculation process, all calculations were considered converged when the maximum force on atom below 0.01 eV Å−1, the maximum stress was below 0.02 GPa, the maximum displacement between cycles was below 0.0005 Å and the energy difference was less than 5 × 10−6 eV per atom.
-points parameters. During the calculation process, all calculations were considered converged when the maximum force on atom below 0.01 eV Å−1, the maximum stress was below 0.02 GPa, the maximum displacement between cycles was below 0.0005 Å and the energy difference was less than 5 × 10−6 eV per atom.
In the calculations, the unit cell of all models was based on NaCl-type face centered cubic with Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (no. 225).31–33 TiC and TiN contain four Ti atoms and four C(N) atoms. The structures of TiC0.75N0.25, Ti0.75Al0.25C, Ti0.75Al0.25C0.75N0.25 was replaced one C atom by N atom, one Ti atom by Al atom and then one C atom by N atom, respectively. All structures are shown in Fig. 1.
m space group (no. 225).31–33 TiC and TiN contain four Ti atoms and four C(N) atoms. The structures of TiC0.75N0.25, Ti0.75Al0.25C, Ti0.75Al0.25C0.75N0.25 was replaced one C atom by N atom, one Ti atom by Al atom and then one C atom by N atom, respectively. All structures are shown in Fig. 1.
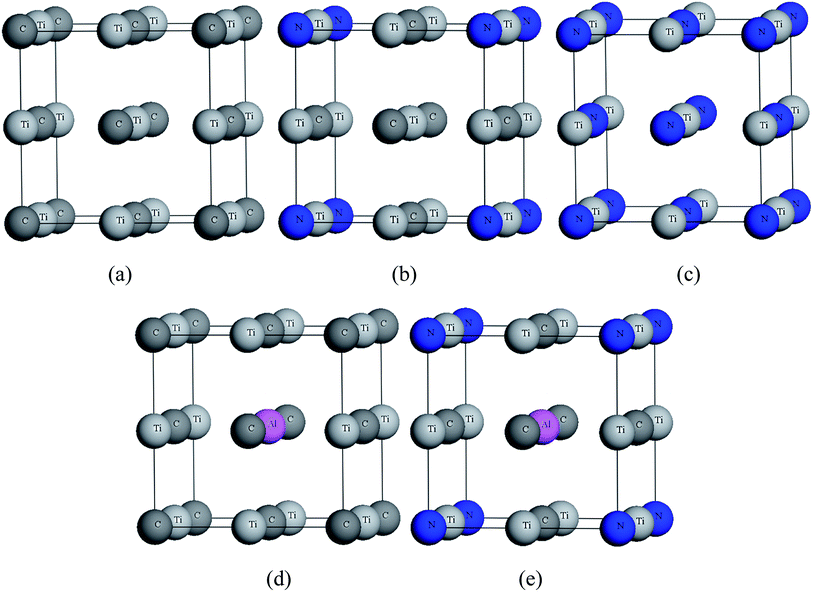 | ||
| Fig. 1 Crystal structures of (a) TiC, (b) TiC0.75N0.25, (c) TiN, (d) Ti0.75Al0.25C, (e) Ti0.75Al0.25C0.75N0.25. | ||
Results and discussion
Crystal structures
In order to get the most stable structure, it is necessary to conduct the geometry optimizations for TiC, TiC0.75N0.25, TiN, Ti0.75Al0.25C, Ti0.75Al0.25C0.75N0.25. Table 1 presents the optimized lattices parameters along with other experimental and theoretical results. According to Table 1, the calculations results are in a good agreement with other experimental and theoretical results. In this work, the lattice constants of all structures present a trend as following: TiN < Ti0.75Al0.25C0.75N0.25 < TiC0.75N0.25 < Ti0.75Al0.25C < TiC. This reveals that the doping of aluminum shrink the crystal lattice of TiC and the nitrogen plays the same role. It could be explained by that the covalent radius of Al atom (1.26 Å) is smaller than Ti atom (1.36 Å) and N atom (0.71 Å) is smaller than C atom (0.75 Å). Moreover, the presented lattice constant of Ti0.75Al0.25C 4.322 Å is perfectly matched the experiment data from P. S. Mukherjee,44 indicating the calculation results in this work are accurate.| Lattice constant a (Å) | |||
|---|---|---|---|
| Present | Experiment | Calculation | |
| a Ref. 34.b Ref. 35.c Ref. 36.d Ref. 23.e Ref. 37.f Ref. 38.g Ref. 39.h Ref. 40.i Ref. 31.j Ref. 41.k Ref. 42.l Ref. 43.m Ref. 44.n Ref. 23. | |||
| TiC | 4.331 | 4.33a, 4.328b | 4.3311c, 4.3428d, 4.33e, 4.3317f, 4.31g |
| TiC0.75N0.25 | 4.307 | 4.306h | 4.307i |
| TiN | 4.246 | 4.24j, 4.238k | 4.246c, 4.2468f, 4.266l |
| Ti0.75Al0.25C | 4.322 | 4.322m | 4.3313n |
| Ti0.75Al0.25C0.75N0.25 | 4.292 | — | — |
Cohesive energy and formation energy
To investigate the relative stability of the solid solutions, the cohesive and formation energy of TiC, TiN, TiC0.75N0.25, Ti0.75Al0.25C, Ti0.75Al0.25C0.75N0.25 have been interpreted in this section. The cohesive and formation energy for TikAllCmNn can be presented by the following formulae:
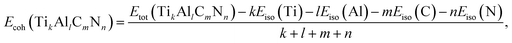 | (1) |
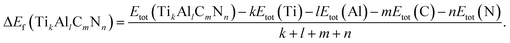 | (2) |
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), C with diamond structure (Fd
m), C with diamond structure (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) and N with gaseous N2 structure (one N2 molecule in the center of a fixed cubic lattice).
m) and N with gaseous N2 structure (one N2 molecule in the center of a fixed cubic lattice).
The calculated results of cohesive and formation energies of this work are presented in Table 2 and the negative values of energies demonstrate the relative stability of compounds. From Table 2, it could be found that the results of this work match well with the values of other literatures. In the perspective of cohesive energy, nitrogen could enhance the stability of TiC, however, aluminum plays an opposite role, which could be demonstrated by comparing the absolute value of cohesive energy of TiC (8.63 eV per atom) and TiC0.75N0.25 (8.78 eV per atom) between the one of Ti0.75Al0.25C (7.87 eV per atom) and Ti0.75Al0.25C0.75N0.25 (8.05 eV per atom), it could be seen that both Al-doped compounds are more unstable than Al free compounds. From the point of view of formation energy which is more determinative on stability of compounds, it could be found that the formation energy values of TiC, TiN, TiC0.75N0.25, Ti0.75Al0.25C, Ti0.75Al0.25C0.75N0.25 are −0.891 eV per atom, −1.961 eV per atom, −1.191 eV per atom, −0.484 eV per atom, −0.812 eV per atom, respectively, which are consistent with the results of cohesive energy, indicating that Al-doping makes the compound unstable.
Elastic properties
For cubic symmetry system, there are three independent elastic constants (C11, C12, C44) determine the elastic behavior of crystals.45 Thus, in order to investigate the elastic behavior of TiC, TiN, TiC0.75N0.25, Ti0.75Al0.25C, Ti0.75Al0.25C0.75N0.25, the elastic constants were calculated by applying external stress and strain forces on the optimized crystal structures of these compounds based on the generalized Hooke's law.46 Otherwise, the mechanical stability could be confirmed by C11 > 0, C44 > 0, C11–C12 > 0 and C11 + 2C12 > 0 (ref. 47 and 48) and all compounds in this work were proved mechanically stable. The bulk modulus B, isotropic shear modulus G, Young's modulus E and Poisson's ratio v are vital parameters to describe elastic behaviors. The bulk modulus is the inverse of the compressibility and measures the resistance of the material to a uniform hydrostatic pressure and can be derived from the elastic constants by the following equation:
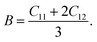 | (3) |
Otherwise, the isotropic shear modulus G, Young's modulus E and Poisson's ratio v are bridged by bulk modulus to evaluate the elasticity properties of materials. In this work they are presented by following equations, where we assume the shear modulus by the average of Voigt and Reuss bounds, which offers the best mechanical properties estimation of polycrystalline materials from known elastic constants.49
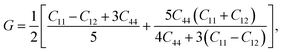 | (4) |
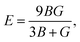 | (5) |
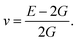 | (6) |
The calculated elastic constants, elastic constants, bulk modulus, shear modulus, Young's modulus of this work are listed in Table 3. The calculated results for TiC, TiN and TiC0.75N0.25 are matched well with other DFT predicted values31,33,36,36,54 and experimental results.50–53 In addition, the mechanical stability of this work was examined by eqn (3) which is satisfied by calculated elastic constants of each compound in this work. It means all presented compounds are mechanically stable.
| Alloy | C11 | C12 | C44 | B | G | E | v | B/G | C12–C44 | A′ | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TiC | Present | 518 | 120 | 174 | 253 | 184 | 443 | 0.207 | 1.38 | −54.0 | 0.87 |
| Cal. (ref. 33) | 517 | 117 | 174 | 251 | 184 | 443 | 0.205 | 1.36 | −56.3 | 0.87 | |
| Cal. (ref. 31) | 518 | 115 | 183 | 249 | 190 | 455 | 0.197 | 1.31 | −67.4 | 0.91 | |
| Cal. (ref. 37) | 523 | 116 | 207 | 251 | 206 | 481 | 0.181 | 1.22 | — | — | |
| Exp. (ref. 50) | 513 | 106 | 178 | ||||||||
| Exp. (ref. 51) | 500 | 113 | 175 | 242 | 182 | 437 | 0.199 | — | — | 0.91 | |
| Exp. (ref. 52) | 233 | 184 | 436 | 0.187 | |||||||
| TiN | Present | 590 | 122 | 161 | 278 | 187 | 458 | 0.225 | 1.49 | −38.7 | 0.69 |
| Cal. (ref. 33) | 588 | 121 | 161 | 277 | 187 | 457 | 0.225 | 1.48 | −39.5 | 0.69 | |
| Cal. (ref. 31) | 578 | 128 | 180 | 278 | 196 | 477 | 0.182 | 1.42 | −51.2 | 0.80 | |
| Cal. (ref. 36) | 579 | 129 | 180 | 279 | 197 | 477 | 0.21 | 1.42 | −51 | ||
| Exp. (ref. 50) | 625 | 165 | 163 | ||||||||
| Exp. (ref. 53) | 507 | 96 | 163 | 233 | 179 | 427 | 0.19 | ||||
| TiC0.75N0.25 | Present | 532 | 122 | 191 | 259 | 196 | 470 | 0.197 | 1.32 | −68.2 | 0.93 |
| Cal. (ref. 33) | 532 | 123 | 191 | 259 | 196 | 471 | 0.198 | 1.32 | −68.2 | 0.93 | |
| Cal. (ref. 54) | 533 | 112 | 184 | ||||||||
| Ti0.75Al0.25C | Present | 456 | 118 | 132 | 230 | 146 | 361 | 0.239 | 1.58 | −14.5 | 0.78 |
| Ti0.75Al0.25C0.75N0.25 | Present | 460 | 133 | 174 | 242 | 170 | 413 | 0.215 | 1.42 | −41.7 | 1.06 |
It is well known that the relationships between hardness and modulus are not identical for different materials.55,56 Therefore, in this section, only elastic modulus is discussed. The hardness of compounds will be analyzed independently in Section 3.5. In this work, the bulk modulus B experiences a substantial increase from 250 to 279 with addition of nitrogen. However, Al-doping decreases the bulk modulus comparing with non-doping, the bulk modulus of co-doping Al and N (i.e. (Ti0.75,Al0.25)(C0.75,N0.25)) is still less than non-doped compound. It is known that the bulk modulus could be utilized to describe the average atomic bonding strength as a measure, which is due to the strong correlation with the cohesive energy or binding energy of atoms in crystals.57 Therefore, Al could dramatically decrease the atomic bonding strength of TiC-based compounds and N plays an adverse role, which could be explained by the weak carbide-forming ability of Al.15 TiN have the largest shear modulus (G) value and the largest Young's modulus (E) value.
Poisson's ratio reflects the volume change of crystal during uniaxial deformation, the lower Poisson's ratio (v), the larger volume change occurs when the elastic deformation of crystal happens and if v = 0.5 means no volume changes. In this work, the v of TiC0.75N0.25 is smaller than the v of TiC, which means N-doping increases the volume change of TiC during uniaxial deformation. The v of Ti0.75Al0.25C0.75N0.25 is larger than that of TiC0.75N0.25, indicating that Al-doping could decrease the volume change of TiC0.75N0.25 during uniaxial deformation. Moreover, Poisson's ratio has been proved associated with the central-force solids,58 the upper limit of which is v = 0.5 and lower limit is v = 0.25, which corresponds to infinite elastic anisotropy.59 The calculation results of this work suggest that the interatomic forces for TiC, Ti0.75Al0.25C, Ti0.75Al0.25C0.75N0.25, TiC0.75N0.25 and TiN are non-central.
Pugh60 proposed an empirical criterion associated the ratio of B/G of compounds with malleability and brittleness to analyze ductile (brittle) behavior of materials. It is worthy to note that a high B/G value presents a ductile manner of materials and a low value predicates the reverse. Many studies for metallic compounds of cubic and hexagonal symmetry reveals a critical value as 1.75 to separate ductility and brittleness. If B/G < 1.75, the material presents brittleness.61–63 As shown in Table 3, the B/G value of compounds in this work could be classified as brittle. The B/G for Ti0.75Al0.25C, Ti0.75Al0.25C0.75N0.25 are both higher than TiC0.75N0.25 which indicates that the Al-doping could improve the ductility of Ti(C,N). Otherwise, TiC0.75N0.25 and Ti0.75Al0.25C0.75N0.25 have lower B/G value than TiC and Ti0.75Al0.25C, which means the addition of nitrogen presents a contrary effect.
Additionally, Cauchy pressure C12–C44 could also be considered as a parameter to appraise ductility and brittleness. Cauchy pressure describes the angular characteristics of atomic bonds in materials and compounds.64 A positive Cauchy pressure reveals the bonding is metallic characteristic and a negative Cauchy pressure suggests an angular or directional character in bonding. Moreover, the bonds are less mobile and more directional with the more negative Cauchy pressure. As shown in Table 3, it could be observed a similar trend for Cauchy pressure as found in B/G, Cauchy pressure increases monotonously following the order TiC0.75N0.25, TiC, Ti0.75Al0.25C0.75N0.25, and Ti0.75Al0.25C, indicating that Al-doping improves the ductility while nitrogen plays the adverse role.
The Zener anisotropy ratios (A′) were also calculated and presented in Table 3. This parameter could reveal the deviation from elastic isotropy in cubic crystals. The more Zener anisotropy ratio differs from 1, the more elastically anisotropic the crystalline structure is. The A′ of TiC0.75N0.25 is 7.95% higher than TiC, and that of Ti0.75Al0.25C is 6.82% lower than TiC, both of which presents a small change on elastic anisotropy comparing with TiC. However, the A′ of Ti0.75Al0.25C0.75N0.25 is 15.91% higher than that of TiC and close to 1, indicating the co-doping of Al and N leads to elastic isotropy.
Electronic structure
In order to get a comprehensive understanding of the studied compounds, it is necessary to investigate the electronic origin of the composition effects on elastic behavior of the studied compounds. The total and partial density of states of TiC, TiN, TiC0.75N0.25, Ti0.75Al0.25C and Ti0.75Al0.25C0.75N0.25 were calculated and presented in Fig. 2. For highlighting the DOS near the Fermi level, a dash line was plotted on the Fermi level (0 eV).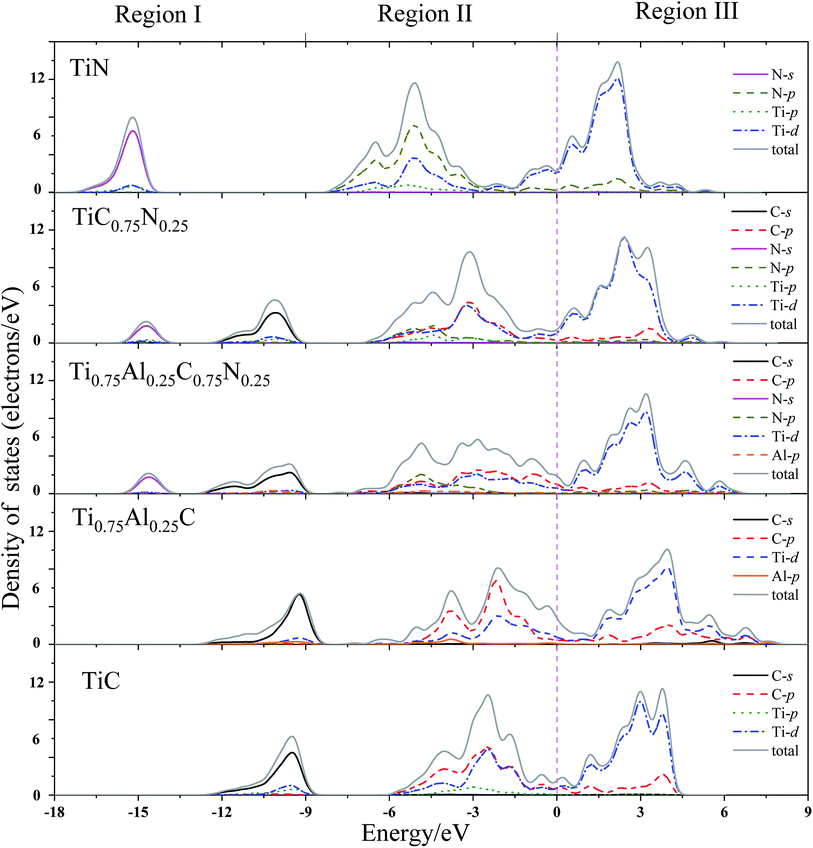 | ||
| Fig. 2 Total and partial density of states (DOS) for TiC, TiN, TiC0.75N0.25, Ti0.75Al0.25C, Ti0.75Al0.25C0.75N0.25. 0 eV is the Fermi level (dash line). | ||
From Fig. 2, it could be noted that the distribution of DOS of the studied crystals are very similar. They could be divided into three main energy regions. The first region starts at −18 eV and ends up with −9 eV, it contains nonmetal C(N)-s states with a small contribution of Ti-d and Al-p states, representing the core electronic structure. A strongly hybridizing between C(N)-p, Ti-d and Al-p is introduced in region II, from −9 eV to the Fermi level (0 eV). These states demonstrate the strong covalent bonding. Region III (above the Fermi level) predominately consists of Ti-d with a small fraction of p orbitals of Al and C(N). These states contribute to metal–metal bonds between next-nearest-neighbor metal atoms.
In region I, the addition of N introduces two separate N-s and C-s peaks to TiC0.75N0.25 and Ti0.75Al0.25C0.75N0.25, since the long distance peak location between N-s for TiN and C-s for TiC. The locations of the peaks of C-s and N-s are −10.06 eV, −14.69 eV for TiC0.75N0.25 and −9.56 eV, −14.58 eV for Ti0.75Al0.25C0.75N0.25, respectively. Moreover, the peaks of C-s state of TiC and Ti0.75Al0.25C are located in −9.50 eV and −9.20 eV, respectively. This suggests the Al-doping leads the C-2s orbitals moving towards to a higher energy.
For DOS in region II, it was mainly composed by C-p, N-p, Ti-d and Al-p states, which can form the p–d covalent bonds. Comparing with TiC, the DOS in region II for Ti0.75Al0.25C becomes broader and separates to two peaks which may contribute negatively to the hardness of materials.23,65 The addition of Al causes the DOS peaks transfer to a higher energy level in this region. Additionally, region III mainly consists metal–metal bonding, and addition of Al expands the area of DOS in region III which may bring negative effects to the hardness of material. Meanwhile, a minimum shape of the DOS exists at 0 eV (nearby the Fermi level) for TiC which indicates the bands are full filled with eight valence electrons. For TiC0.75N0.25, the minimum transfers to the lower energy. However, the minimum DOS of Ti0.75Al0.25C and Ti0.75Al0.25C0.75N0.25 moves towards the higher energy and that of Ti0.75Al0.25C locates at higher energy than that of Ti0.75Al0.25C0.75N0.25. This demonstrates that Al-doping increases the DOS near Fermi level by introducing more p-electrons. This may improve the elastic properties of TiC.21
Hardness
In this work, to investigate the hardness information of the presented alloys, the linear combination of atomic orbitals basis sets was used to obtain the Mulliken population which is broadly applied to analyze the electronic structure and to assess the covalent or ionic nature of a bond with providing an objective criterion for bonding between atoms.66,67 A low value of the bond population suggests an ionic interaction while a high one implies a covalent bond. According to the data in Table 4, it can be found that there are 12 C(N)–Ti(Al) bonds in each studied cell of TiC, TiN, TiC0.75N0.25, Ti0.75Al0.25C and Ti0.75Al0.25C0.75N0.25. The number of bonds is proportional to the atom fraction in each cell. As shown in Table 4, the C–Ti bonds are more covalent than N–Ti bonds for TiC0.75N0.25 and Ti0.75Al0.25C0.75N0.25, and the C–Ti bonds are more covalent than C–Al bonds for Ti0.75Al0.25C0.75N0.25. It may indicate that C–Ti bonds are stronger than N–Ti and C–Al bonds. But the C–Ti1 bonds for Ti0.75Al0.25C is weaker than that for TiC0.75N0.25, it could be the effect of Al addition.| Alloy | Bond | Population | Length (Å) | νμb (Å3) | Hv cal |
|---|---|---|---|---|---|
| a Ref. 31.b Ref. 33.c Ref. 69.d Ref. 37. | |||||
| TiC | C–Ti(12) | 0.82 | 2.17 | 6.72 | 25.4 (24.8a, 25.03b, 24.7c, 25.0d) |
| TiN | N–Ti(12) | 0.70 | 2.12 | 6.35 | 23.8 (23.6a,b) |
| TiC0.75N0.25 | C–Ti1(3) | 0.77 | 2.15 | 6.66 | 24.2 |
| C–Ti2(6) | 0.84 | 26.4 | |||
| N–Ti(3) | 0.72 | 22.6 | |||
| Ti0.75Al0.25C | C–Al(3) | 0.82 | 2.16 | 6.73 | 25.3 |
| C–Ti1(3) | 0.73 | 22.5 | |||
| C–Ti2(6) | 1.04 | 32.4 | |||
| Ti0.75Al0.25C0.75N0.25 | C–Al(3) | 0.79 | 2.15 | 6.59 | 25.2 |
| C–Ti2(6) | 1.13 | 36.1 | |||
| N–Ti(3) | 0.64 | 20.5 | |||
Based on the previous works of Gao,68 the hardness could be characterized by the strength of bonding and the number of bonds per unit area. So the hardness of TiC, TiN, TiC0.75N0.25, Ti0.75Al0.25C and Ti0.75Al0.25C0.75N0.25 was evaluated and the calculation formula could be expressed as follows:
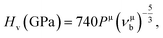 | (7) |
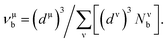 | (8) |
Conclusion
In this work, we have performed the DFT with ultrasoft pseudopotentials to calculate and investigate the crystal structure, elastic properties, electronic structure and hardness of TiC, TiC0.75N0.25, TiN, Ti0.75Al0.25C, Ti0.75Al0.25C0.75N0.25. The results show that doping nitrogen reduces the lattice constant and enhances the stability of TiC while doping aluminum shrinks the lattice and reduces the stability of compound. It is also found that in the studied compounds, aluminum reduces the bulk modulus B, shear modulus G and Young's modulus E but nitrogen can enhance them. The results of B/G and C12–C44 indicate aluminum could significantly increase the ductility of TiC. Meanwhile, the electronic structure calculations reveal that a strong p–d covalent bonds exists among C-p, N-p, Ti-d and Al-p states and Al-doping causes the DOS peaks transfer to a higher energy level and increases the DOS above the Fermi level, which may bring negative effects to the hardness of material. The Mulliken population results show C–Al bonds could weaken C(N)–Ti bonds and the addition of Al sharply reduces the hardness of the TiC-based material.Conflicts of interest
There are no conflicts to declare for this article.Acknowledgements
This work is supported by the National Key Research and Development Plan of China (Grant No. 2017YFB0305900).Notes and references
- S. Zhang, Mater. Sci. Eng., A, 1993, 163(1), 141–148 CrossRef.
- H. Feng, J. K. Yu and W. Tan, Mater. Chem. Phys., 2010, 124(1), 851–855 CrossRef CAS.
- Y. T. Pei, C. Q. Chen, K. P. Shaha, J. T. M. De Hosson, J. W. Bradley, S. A. Voronin and M. Cada, Acta Mater., 2008, 56(4), 696–709 CrossRef CAS.
- C. W. Morton, D. J. Wills and K. Stjernberg, Int. J. Refract. Met. Hard Mater., 2005, 23(4–6), 287–293 CrossRef CAS.
- F. Viñes, J. A. Rodriguez, P. Liu and F. Illas, J. Catal., 2008, 260(1), 103–112 CrossRef.
- C. Jimenez-Orozco, E. Florez, F. Viñes, J. A. Rodriguez and F. Illas, ACS Catal., 2020, 10, 6213–6222 CrossRef CAS.
- M. López, F. Viñes, M. Nolan and F. Illas, J. Phys. Chem., 2020, 124(29), 15969–15976 Search PubMed.
- X. B. Zhang, N. Liu, C. L. Rong and J. Zhou, Ceram. Int., 2009, 35(3), 1187–1193 CrossRef CAS.
- X. Zhang, N. Liu and C. Rong, Microstructure and fracture toughness of TiC–ZrC–WC–Mo–Ni cermets, Int. J. Refract. Met. Hard Mater., 2008, 26(4), 346–356 CrossRef CAS.
- P. C. Rong, Y. Liu, J. W. Ye, Y. C. Qiu, Q. Cao and A. R. Liu, J. Alloys Compd., 2017, 718, 425–432 CrossRef CAS.
- H. J. Yu, Y. Liu, Y. Z. Jin and J. W. Ye, Int. J. Refract. Met. Hard Mater., 2011, 29(5), 586–590 CrossRef CAS.
- E. Chicardi, J. M. Córdoba, M. J. Sayagués and F. J. Gotor, Int. J. Refract. Met. Hard Mater., 2012, 31, 39–46 CrossRef CAS.
- E. Chicardi, J. M. Córdoba, M. J. Sayagués and F. J. Gotor, Int. J. Refract. Met. Hard Mater., 2012, 33, 38–43 CrossRef CAS.
- J. M. Córdoba, E. Chicardi, R. Poyato, F. J. Gotor, V. Medri, S. Guicciardi and C. Melandri, Chem. Eng. J., 2013, 230, 558–566 CrossRef.
- M. Lindquist, O. Wilhelmsson, U. Jansson and U. Wiklund, Wear, 2009, 266(3–4), 379–387 CrossRef CAS.
- H. A. Chaliyawala, G. Gupta, P. Kumar, G. Srinivas, Siju and H. C. Barshilia, Surf. Coat. Technol., 2015, 276, 431–439 CrossRef CAS.
- X. H. Zhang, J. Q. Jiang, Z. Yuqiao, J. L. Lin, F. L. Wang and J. J. Moore, Surf. Coat. Technol., 2008, 203(5–7), 594–597 CrossRef CAS.
- J. Soldán, J. Musil and P. Zeman, Plasma Processes Polym., 2007, 4(S1), S6–S10 CrossRef.
- Q. Yang, L. R. Zhao, F. Cai, S. Yang and D. G. Teer, Surf. Coat. Technol., 2008, 202(16), 3886–3892 CrossRef CAS.
- W. Zhou, Y. Zheng, Y. J. Zhao, Y. P. Ma and W. H. Xiong, Ceram. Int., 2015, 41(3), 5010–5016 CrossRef CAS.
- X. J. Ni and L. H. Qi, Key Eng. Mater., 2008, 368–372, 1110–1112 CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140(4A), A1133 CrossRef.
- K. Y. Chen and L. R. Zhao, J. Phys. Chem. Solids, 2007, 68(9), 1805–1811 CrossRef CAS.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14(11), 2717 CrossRef CAS.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64(4), 1045 CrossRef CAS.
- V. Milman, B. Winkler B, J. A. White, C. J. Pickard, M. C. Payne, E. V. Akhmatskaya and R. H. Nobes, Int. J. Quantum Chem., 2015, 77(5), 895–910 CrossRef.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892 CrossRef.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(23), 16533 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 16(12), 1748–1749 Search PubMed.
- B. Wang, Y. Liu, Y. Liu and J. W. Ye, Phys. B, 2012, 407(13), 2542–2548 CrossRef CAS.
- S. J. Yi, H. Q. Yin, J. Zheng, D. F. Khan and X. H. Qu, Comput. Mater. Sci., 2013, 79, 417–423 CrossRef CAS.
- S. Q. Ma, Y. Liu, J. W. Ye and B. Wang, Commun. Theor. Phys., 2014, 62(6), 895 CrossRef CAS.
- A. Dunand, H. D. Flack and K. D. Yvon, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31(4), 2299 CrossRef CAS.
- A. N. Christensen, Acta Chem. Scand., Ser. A, 1978, 32, 89–90 CrossRef.
- Y. Yang, H. Lu, C. Yu and J. M. Chen, J. Alloys Compd., 2014, 485(1–2), 542–547 CrossRef.
- Y. Z. Liu, Y. H. Jiang, R. Zhou and J. Feng, J. Alloys Compd., 2014, 582, 500–504 CrossRef CAS.
- W. X. Feng, S. X. Cui, H. Q. Hu, G. Q. Zhang and Z. T. Lv, Phys. B, 2011, 406(19), 3631–3635 CrossRef CAS.
- M. Guemmaz, A. Mosser, R. Ahujab and B. Johansson, Solid State Commun., 1999, 110(6), 299–303 CrossRef CAS.
- M. Guemmaz, G. Moraitis, A. Mosser, M. A. Khan and J. C. Parlebas, J. Phys.: Condens. Matter, 1997, 9(40), 8453 CrossRef CAS.
- V. P. Zhukov, V. A. Gubanov, O. Jepsen, N. E. Christensen and O. K. Andersen, J. Phys. Chem. Solids, 1988, 49(7), 841–849 CrossRef CAS.
- N. Schönberg N, Acta Chem. Scand., 1954, 8, 213–220 CrossRef.
- Z. Gao and S. Kang, Solid State Commun., 2013, 156, 25–30 CrossRef CAS.
- P. S. Mukherjee, K. Gupta, A. Sen, H. Dutta, S. K. Pradhan and A. K. Meikap, Phys. B, 2014, 447, 1–6 CrossRef CAS.
- W. S. Slaughter, The linearized theory of elasticity, Birkhäuser, Boston, 2002 Search PubMed.
- B. B. Karki, L. Stixrude, S. J. Clark, M. C. Warren, G. J. Ackland and J. Crain, Am. Mineral., 1997, 82(1–2), 51–60 CAS.
- M. Mattesini, R. Ahuja and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 184108 CrossRef.
- Y. F. Li, Y. M. Gao, B. Xiao, T. Min, Z. J. Fan, S. Q. Ma and L. L. Xu, J. Alloys Compd., 2010, 502(1), 28–37 CrossRef CAS.
- E. Schreiber, O. L. Anderson and N. Soga, J. Appl. Mech., 1973, 42(3), 747–748 CrossRef.
- R. Ahuja, O. Eriksson, J. M. Wills and B. Johansson, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53(6), 3072 CrossRef CAS.
- J. J. Gilman and B. W. Roberts, J. Appl. Phys., 1961, 32(7), 1405 CrossRef CAS.
- S. P. Dodd, M. Cankurtaran and B. James, J. Mater. Sci., 2003, 38(6), 1107–1115 CrossRef CAS.
- W. J. Meng and G. L. Eesley, Thin Solid Films, 1995, 271(1–2), 108–116 CrossRef CAS.
- V. I. Ivashchenko, P. E. A. Turchi, A. Gonis, L. A. Ivashchenko and P. L. Skrynskii, Metall. Mater. Trans. A, 2006, 37(12), 3391–3396 CrossRef.
- Q. Yang, W. Lengauer, T. Koch, M. Scheerer and I. Smid, J. Alloys Compd., 2000, 309(1–2), L5–L9 CrossRef CAS.
- H. L. Liu, J. C. Zhu, Y. Liu and Z. H. Lai, Mater. Lett., 2008, 62(17–18), 3084–3086 CrossRef CAS.
- D. G. Clerc and H. M. Ledbetter, J. Phys. Chem. Solids, 1998, 59(6–7), 1071–1095 CrossRef CAS.
- W. Kosterand and H. Franz, Metall. Rev., 1961, 6(1), 1–56 Search PubMed.
- R. P. Reed, A. F. Clark and L. G. Rubin, Phys. Today, 1983, 37(3), 97 CrossRef.
- S. F. Pugh, Philos. Mag., 1954, 45(367), 823–843 CAS.
- K. Haddadi, A. Bouhemadou, L. Louail and M. Maamache, Intermetallics, 2011, 19(4), 476–485 CrossRef CAS.
- I. R. Shein and A. L. Ivanovskii, J. Phys.: Condens. Matter, 2008, 20(41), 415218 CrossRef.
- B. Minisini, J. Roetting and F. Tsobnang, Comput. Mater. Sci., 2008, 43(4), 812–817 CrossRef CAS.
- C. L. Fu and M. H. Yoo, Philos. Mag. Lett., 1990, 62(3), 159–165 CrossRef CAS.
- S. H. Jhi, J. Ihm, S. G. Louie and M. L. Cohen, Nature, 1998, 399(6732), 132–134 CrossRef.
- R. S. Mulliken, J. Chem. Phys., 2004, 23(10), 1841–1846 CrossRef.
- S. M. Aouadi, J. Appl. Phys., 2006, 99(5), 053507 CrossRef.
- F. M. Gao, J. L. He, E. D. Wu, S. M. Liu, D. L. Yu, D. C. Li, S. Y. Zhang and Y. J. Tian, Phys. Rev. Lett., 2003, 91(1), 015502 CrossRef.
- A. Šimůnek and J. Vackář, Phys. Rev. Lett., 2006, 96(8), 085501 CrossRef.
- F. M. Gao, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(13), 132104 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra06630c |
| This journal is © The Royal Society of Chemistry 2020 |
