Open Access Article
Open Access ArticleExploring the effect of a peptide additive on struvite formation and morphology: a high-throughput method†
Jacob D. Hostert ,
Olivia Kamlet,
Zihang Su
,
Olivia Kamlet,
Zihang Su ,
Naomi S. Kane and
Julie N. Renner
,
Naomi S. Kane and
Julie N. Renner *
*
Case Western Reserve University, Department of Chemical and Biomolecular Engineering, 2102 Adelbert Road, Cleveland, Ohio 44106, USA. E-mail: julie.renner@case.edu
First published on 27th October 2020
Abstract
Precipitation of struvite (MgNH4PO4·6H2O), a slow-release fertilizer, provides a means of recycling phosphate from wastewater streams. In this work, a high-throughput struvite precipitation method is developed to investigate the effects of a peptide additive. The reactions occurred in small volumes (300 μL or less) in a 96-well plate for 45 minutes. The formation of struvite was monitored by fitting absorbance at 600 nm over time to a first order model with induction time, with the addition of peptide inducing significant changes to the yield parameter and formation constant in that model. The impact of struvite seed dosing was also investigated, highlighting the importance of optimization when peptide is present. The composition of the precipitate was confirmed through Fourier-transform infrared spectroscopy, while morphology and crystal size were analyzed through optical microscopy. Crystals had a higher aspect ratio when precipitated with the peptide. Finally, the utility of the high-throughput platform was demonstrated with a 25 full factorial design to capture the effects and interactions of: magnesium dose, mixing time, seed dose, pH, and temperature. Overall, this study quantifies novel effects of a sequence-defined peptide on struvite formation and morphology via a newly developed high throughput platform.
Introduction
Phosphate rock is a non-renewable resource, yet is the source of nearly all phosphate used in commercial fertilizers.1 The demand for phosphate rock will continue to increase as the global population and food demand increases, which will likely lead to supply shortage within a century.1 Additionally, up to 40% of applied phosphorus fertilizer is lost due to runoff into rivers, lakes and streams.2 Aside from being wildly inefficient, the excess phosphorus contributes significantly to eutrophication and algae blooms that harm aquatic life.3 The necessity of recovering lost phosphorus is often overlooked in treating wastewater streams, where the phosphorus is seen as a contaminant rather than a valuable resource.4 The impending phosphorus crisis will be fully realized unless this attitude is changed, and technologies are rapidly developed to recover phosphorus.Struvite (MgNH4PO4·6H2O) formation is one promising way to recover phosphorus from waste streams.4–7 Life cycle assessment studies have shown struvite precipitation from wastewater is comparable or better economically than that of conventional wastewater treatment processes with the added benefit of recovering a useful product while simultaneously removing excess phosphorus and nitrogen from water systems.8 Struvite is a slow release fertilizer that precipitates readily out of solution at basic pH according to the following equation.
| Mg2+ + NH4+ + HnPO43−n + 6H2O → MgNH4PO4·6H2O + nH+ | (1) |
The slow release character of struvite fertilizer is valuable because it allows for lower amounts of phosphorus runoff. However, struvite can also be viewed as a nuisance because it is often found in alkaline streams of wastewater treatment plants where struvite growth can occlude pipes and cause damage. Currently struvite is formed via chemical precipitation from wastewater, where magnesium salts are often added and the pH adjusted with sodium hydroxide or aeration.6 Ammonia and phosphate are typically at high enough concentrations such that no salt supplements need to be added.10 The addition of chemicals (i.e. salts or hydroxide) adds cost to the process which can be undesirable, however, there is evidence that precipitation can occur at more moderate pH than more typical basic pH (i.e. 8–10) and some waste streams have sufficiently high magnesium content such that no additional chemicals need to be added. Understanding how to control struvite growth is beneficial not only for recovering phosphorus, but also for preventing precipitation in unwanted areas. Recovered phosphorus is currently more expensive than mined phosphorus, but other simultaneously recovered products like energy (e.g. through biogas production) and nitrogen species can make phosphorus recycling economically viable.11
Struvite growth is typically modeled via first order kinetics, although more complex models have been investigated.12–15 A typical feature of struvite nucleation is an initial lag period, known as induction time. Kinetics are often examined by monitoring pH, as pH tends to decrease as precipitation proceeds. Absorbance measurements have also been implemented to qualitatively probe reaction processes, but never to quantitatively model struvite formation.16 Monitoring absorbance has the potential to enable high-throughput experiments, where reactions can be performed in a 96-well plate with a reaction volume of 200 μL or less. A high throughput platform thus allows for minimal use of expensive additives as their impact on precipitation is probed. Additionally, a high throughput platform allows for facile modulation of many process parameters at once, drastically reducing experimental time.
One possible way to control the precipitation of struvite is through the use of peptides. Peptides are short polymeric chains of amino acids, which if arranged in a specific sequence can have high binding specificity for a ligand or material. There is ample evidence in the literature of specific peptide sequences modulating the precipitation of various inorganic compounds, however peptides are rarely applied to struvite precipitation.17,18 Polyaspartic acid, a peptide made only of aspartic acid, has been shown to influence the morphology and yield of struvite precipitate, which gives potential insight into the impact on thermodynamics, but influence on kinetics has not yet been examined.19 Insight into kinetics is an integral part of process design and scaling-up struvite formation.20 Another study on bacterial mineralization has shown that low molecular weight naturally occurring peptides are a driving factor in production of struvite, but a specific amino acid sequence has not been explored.21 One promising peptide to use that has not yet been explored in struvite precipitation is an amelogenin-derived sequence (shADP5) shown to play a role in the remineralization of enamel (largely hydroxyapatite) through an unknown mechanism. The primary sequence of shADP5 is SYENSHSQAINVDRT (see Fig. S1† for the skeletal structure).18 This peptide is promising due to the presence of phosphate in both struvite and hydroxyapatite along with chemical similarities between the magnesium in struvite and the calcium in hydroxyapatite – if the peptide interacts with one of these groups on hydroxyapatite, we propose it may play a role in struvite mineralization as well.
In this work, a high throughput method for probing struvite growth based on absorbance was developed to quantify the impact of a peptide additive. To our knowledge, no quantitative studies on struvite formation kinetics have been performed in this way. Previous studies using absorbance focus on monitoring induction time or qualitatively monitoring precipitation.16,20,22,23 Reactions were performed until equilibrium, when the absorbance stopped changing significantly, which also had the potential to give insight into system thermodynamics and yield. After equilibrium was achieved, the identity of resultant crystals was assigned using FTIR, and morphology was studied via optical microscopy. After establishing the high-throughput platform, we analyzed the impact of shADP5 as an additive on struvite precipitation and morphology. The utility of the assay was also highlighted in the implementation of a 25 factorial design. Overall, the outcome of the study shows that: (1) the high-throughput platform is useful in simplifying precipitation experiments; (2) shADP5 is a promising additive for modulating struvite growth; and (3) process parameters can be optimized using the high-throughput platform to increase final struvite yield.
Methodology
Materials
Deionized water was obtained from Western Reserve Water Systems mixed deionizer tanks (10 MΩ). Nitrogen gas (N2) was obtained from Airgas (99.99%). Ammonium phosphate monobasic (NH4H2PO4, 98%) and magnesium chloride hexahydrate (MgCl2·6H2O, 99.0–102%) were obtained from VWR. Hydrochloric acid (HCl, 1 N) and sodium hydroxide pellets (NaOH) for pH adjustment were obtained from Fisher Chemical. 47 mm 0.45 μm polyvinylidene fluoride (PVDF) membranes were obtained from MilliporeSigma.High-throughput struvite precipitation
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 Mg2+
2 Mg2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NH4+
NH4+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PO43− ratio.12,16 This ratio was selected from the literature because magnesium is often more scarce than ammonium or phosphate and can help shift the equilibrium so more of the added magnesium precipitates out. A 14 mM ammonium phosphate stock solution was prepared using NH4H2PO4 and deionized water, while a 7 mM magnesium stock solution was prepared using MgCl2·6H2O and deionized water. The resulting solutions were adjusted to pH 9.2 with 1 M NaOH and 100 mM NaOH before being vacuum filtered through a 0.45 μm PVDF membrane to eliminate particulates from the solutions. While low-solubility magnesium sources have been shown to be of increasing economic importance,24 a simple solution was selected to allow for facile detection of differences.
PO43− ratio.12,16 This ratio was selected from the literature because magnesium is often more scarce than ammonium or phosphate and can help shift the equilibrium so more of the added magnesium precipitates out. A 14 mM ammonium phosphate stock solution was prepared using NH4H2PO4 and deionized water, while a 7 mM magnesium stock solution was prepared using MgCl2·6H2O and deionized water. The resulting solutions were adjusted to pH 9.2 with 1 M NaOH and 100 mM NaOH before being vacuum filtered through a 0.45 μm PVDF membrane to eliminate particulates from the solutions. While low-solubility magnesium sources have been shown to be of increasing economic importance,24 a simple solution was selected to allow for facile detection of differences.To determine the impact of seed dosage, the seed amount was set to 5.0, 12.9, and 27.9 μL of stock. For these experiments, peptide addition at 5 μL of stock was tested alongside no peptide addition. To maintain the same total volume as the previous experiments, the sum volume of deionized water, peptide stock solution, and seed stock was fixed at 32.9 μL per well, and the same about of ammonium phosphate and magnesium stock solutions were used throughout all tests (84 μL of each stock, total volume set at 200.9 μL).
Struvite precipitate characterization
 | (2) |
Kinetic modelling
Kinetic modelling of the precipitation monitored via the plate reader with time was performed using nonlinear least squares curve fitting on MATLAB® (please see Note 1 in the ESI† for MATLAB® code used). The kinetic growth curves were fit to a first order model with induction time:
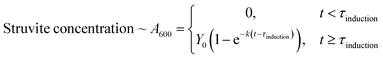 | (3) |
It is well known that struvite follows first order growth kinetics and has notable induction time.5,12,13,32,33 The first term of the equation represents the initial lag due to induction time – τinduction, with units of seconds. This is commonly ascribed to nucleation prior to crystal growth.12,34 The second term represents exponential growth of the crystals on the nucleation sites. Y0 is referred to as the yield parameter, an estimate of how much total struvite at the end of the experiment – this is the horizontal asymptote, with units of absorbance (i.e. A.U.). The formation constant (k) describes how fast the growth curve reaches the horizontal asymptote, with units of s−1. A second order fit was also attempted (eqn (S1)†), but the fits were poor, as shown in Fig. S3 and Table S2.†
25 factorial design experiment
A two-level full factorial design was performed in triplicate to analyze the effect of magnesium dose (at 2.75 and 3.5 mM), mixing time (at 5 and 10 s), seed dose (at 5 and 12.9 μL), pH (at 9.2 and 9.6), and temperature (at 22 and 37 °C) on the final struvite yield. The precipitations were carried out as above, however the data were not fit to eqn (3). For simplicity, the endpoint absorbance was used as the response in the data analysis. Endpoints were measured at sufficient time to ensure the reaction came to equilibrium, and indicates the total yield of the precipitation. The factorial design was generated and analyzed using Minitab.Statistical analysis
Statistical hypothesis testing was performed using Minitab with α = 0.05. To determine if the struvite seed vs. absorbance calibration curve was statistically significant, a linear regression was performed.Kinetic precipitation monitoring was performed with at least thirteen repeats, with fitting parameters determined by nonlinear regression using MATLAB®. Any fitting parameter outliers were discarded using Dixon's Q ratio. Normality (Anderson–Darling test) and equal variance testing (Levene's test) were conducted using Minitab to determine if non-parametric testing was necessary, and if equal-variance could be assumed. Thus, to determine if experimental conditions (e.g. peptide vs. no peptide) had a significant impact on formation parameters determined by kinetic modelling, single factor analysis of variance (ANOVA) without assuming equal variance was conducted on the resultant data. Games–Howell nonparametric post hoc tests were performed to compare means of formation parameters determined by kinetic modelling.
For struvite morphology data, Anderson–Darling tests were used to determine if the data are normally distributed. No data were normally distributed (p < 0.005), thus the Mann–Whitney nonparametric test was conducted for significance.
For the factorial design, normality and constant variance assumptions were examined via residual plots and a histogram. Interactions above a two-way interaction were pooled in the estimate of error. Significance was determined at α = 0.05 with an ANOVA. Further details on statistical tests can be found elsewhere.35
Results and discussion
Absorbance measurements to investigate struvite formation
To determine if absorbance could be used to quantify struvite formation, known amounts of struvite were added to solution and the absorbance was measured via a plate reader. Fig. 1a shows the impact of known amounts of struvite on absorbance at 600 nm. The data were fit to a linear model to create a calibration curve. The linear relationship between struvite concentration and absorbance at 600 nm was significant (p < 0.005) with a slope of 0.873 mL mg−1 and a y-intercept of −0.118 (see Table S1 in ESI† for ANOVA table from linear regression). The x-intercept of the linear regression for struvite calibration was 0.14 mg mL−1, which corresponds to the solubility of struvite and is within nearly 20% of values reported.36 The difference could be ascribed to slight differences in temperature and pH, as our experiment was carried out at 3 °C colder conditions than literature values.36 The scattering seen is due to heterogeneous distribution of struvite crystals in the well – taking the average over multiple data points gives a representative absorbance for a given concentration of struvite crystals. Thus, the linear model was validated with known struvite properties, and the absorbance measurements can be easily converted to concentration or mass using the linear model's slope and intercept.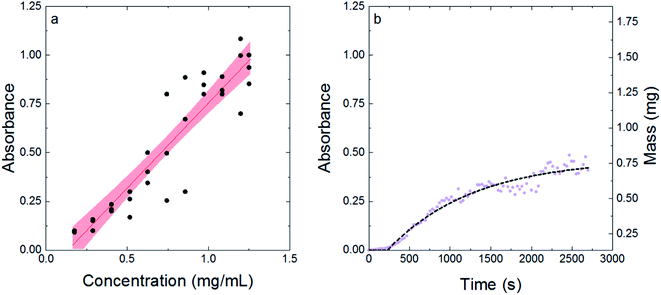 | ||
| Fig. 1 Struvite concentration can be quantified and modeled by measuring absorbance. (a) The calibration curve generated from measuring absorbance of known amounts of struvite. The red line is the linear fit and the shaded red region shows the 95% confidence interval of the fit. (b) A representative precipitation experiment. The purple dots are the raw data collected in the experiment, and the black dotted line is the fit to eqn (3). | ||
Fig. 1b shows a representative precipitation experiment, with the purple dots corresponding to the raw data, and the dashed black line corresponding to the model shown in eqn (3). The horizontal asymptote corresponds to the yield parameter (i.e., the absorbance corresponding to the maximum mass of struvite that can be made). The formation constant corresponds to how fast the reaction reaches the maximum level of struvite. The initial lag before exponential growth is defined as the induction time. The first order kinetic model with induction time fit the data well, with a representative set of conditions (57 μM of peptide and 27.9 μL of seed) having an average R2 = 0.87 ± 0.04 across 12 trials (see Table S2† for R2 values from each trial). This is in agreement with literature, with a first order model being a common way to examine struvite growth.12,33 Thus, Fig. 1 shows that absorbance can be used to easily model kinetic struvite growth and formation with time according to eqn (3).
The effect of peptide on struvite formation and growth kinetics
Using absorbance to monitor struvite formation in the 96-well plate, eqn (3) was used to estimate the average induction time, formation constant, and yield parameter for each well. Fig. 2 displays the averaged estimated model parameters, with no peptide additives shown in bars filled in with lines, and with peptide shown as solid bars. ANOVA results showed that peptide significantly impacted each parameter (p < 0.05, see Tables S3 and S4† for ANOVA results, and post hoc testing). Without peptide, the yield parameter in absorbance was 0.16 ± 0.01 A.U. (0.32 ± 0.15 mg mL−1) the formation constant was 4.6 × 10−3 ± 0.4 × 10−3 s−1, and the induction time was 170 ± 20 s. Generally, presence of peptide significantly increased the yield parameter (Fig. 2a), indicating a larger amount of struvite present at the end of the experiment. The increase in the yield parameter was not significantly dependent on the peptide dose at the levels tested. At 133 μM peptide, the yield parameter in terms of absorbance reached 0.43 ± 0.04 A.U. (0.63 ± 0.18 mg mL−1) a nearly 3× increase over experiments with no peptide. The increase in yield shows a thermodynamic effect of peptide addition. We speculate the peptide binds to specific faces of struvite crystals, with previous literature showing complex changes in local oversaturation and free energy occur when peptides bind to crystals.37–39 The formation constant decreased when the experiment was conducted in the presence of any amount of peptide within the concentration range of the study (Fig. 2b), indicating that the reaction reached steady-state at a slower rate than the no peptide case. The formation constant dropped to 2.4 × 10−3 ± 0.5 × 10−3 s−1 at 113 μM peptide added, a roughly 2× decrease compared to the no peptide case. The induction time increased only when the peptide dose became comparatively large, with no significant difference between moderate peptide dose and no peptide case as seen in Fig. 2c. At 113 μM peptide added, the induction time spikes to 490 ± 1![[0 with combining macron]](https://www.rsc.org/images/entities/char_0030_0304.gif) 0 s – an increase of about 3× when compared to no peptide added. We speculate that at high doses the peptide could be increasing the free energy barrier for early crystal nucleation and growth, thus leading to a higher induction time. Thus, it can be seen that using shADP5 as an additive in struvite precipitation induces changes in formation kinetics.
0 s – an increase of about 3× when compared to no peptide added. We speculate that at high doses the peptide could be increasing the free energy barrier for early crystal nucleation and growth, thus leading to a higher induction time. Thus, it can be seen that using shADP5 as an additive in struvite precipitation induces changes in formation kinetics.
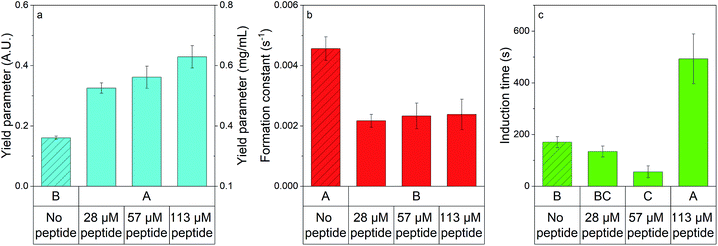 | ||
| Fig. 2 The high-throughput platform identified significant changes in the formation parameters determined by kinetic modelling of struvite when peptide was present. (a) Yield parameter (blue bars), (b) formation constant (red bars), and (c) induction time (green bars) were investigated when no peptide was present (bars with filler) and when 28, 57, and 113 μM of peptide were present. All data are represented by the average ± standard error. Statistical groupings are shown below each bar by performing ANOVA and the Games–Howell post hoc test – bars that do not share a letter within a graph are statistically different at the 95% confidence level. Note that equal variance tests are shown in Table S5.† | ||
Other additives such as humic acid,40 calcium,16 a polyaspartic acid peptide,19 and citric acid41 have been explored in the context of struvite precipitation – largely having the effect of inhibiting crystal growth or changing morphology. While a previous study by Li et al. showed that a peptide of undetermined sequence produced naturally by bacteria influenced the growth of struvite,21 to our knowledge, our study is the first to show that a specific peptide sequence can increase the yield of struvite. With the high-throughput method established, future work will examine more complex water matrices and investigate competing ions that could coprecipitate with struvite.
The formation constants found in this study are on the same order of magnitude as those reported by Le Corre et al., with deviation likely due to differences in mixing and the inclusion of seed crystals in this study.12 The induction times have been reported elsewhere as long as 2 days for static systems to 60 seconds for well-mixed systems.6 The system in this study falls between a static system and a well-mixed system, so the induction times seen in Fig. 2c are reasonable. The addition of seed also contributes to lowering the induction time of the system by giving the crystals nuclei on which to grow.14
Confirmation of composition via Fourier transform infrared spectroscopy and analysis of crystal morphology via optical microscopy
ATR-FTIR was performed to confirm the identity of precipitates on a PVDF membrane as a backing (Fig. 3a). Some PVDF peaks are visible in the spectra of precipitation samples with and without peptide, so the bare membrane spectrum is shown in gray on Fig. 3a for comparison. Also included for comparison is a standard struvite spectrum obtained from the RRUFF database (blue).42 For the struvite sample spectra (shown in pink, green, and red), a broad asymmetric peak centered around 2800 cm−1 was attributed the O–H/NH stretching of the water and ammonium molecules present in the struvite crystal structure.43 The peak associated with bending vibrations of water and ammonium ions at roughly 1450 cm−1 was partially obfuscated by the presence of a PVDF peak in a similar location, but present in all struvite sample spectra, and present in the standard. The peaks around 1000 cm−1 and 570 cm−1 in the struvite sample spectra were associated with phosphate present in the crystal structure, while the peaks around 800 cm−1 were attributed to water vibrational bands.43 Overall, FTIR confirms that the seed stock used in precipitation is struvite while the precipitation products with and without peptide are also struvite. More complete assignments including PVDF peaks can be found in Fig. S4.†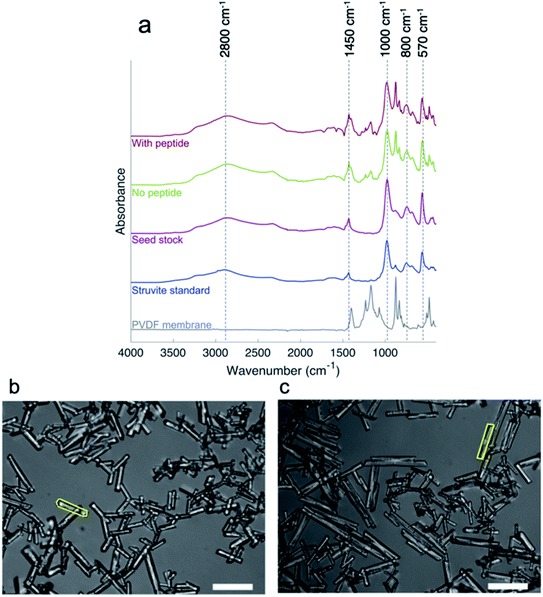 | ||
| Fig. 3 The composition and morphology of struvite crystals. (a) FTIR spectra confirm the identity of struvite throughout precipitation experiments. Spectra of samples of precipitate from reactions performed with peptide (red) without peptide (green) and the seed stock (pink) are shown. The struvite standard spectrum (blue) is from the RRUFF database and represents struvite analyzed by ATR-FTIR.42 Dashed lines are to draw attention to peaks and their locations. The presence of shADP5 peptide has a significant effect on the dimensions of struvite crystals. (b) Crystals precipitated in absence of peptide have a smaller width and aspect ratio compared to (c) crystals precipitated in presence of peptide. Representative crystals are shown traced as an example of the analysis conducted via ImageJ. The scale bar represents 100 μm. | ||
Microscopy and image analysis were conducted on precipitated struvite crystals after formation in the 96-well plate to determine if the peptide had an effect on crystal morphology. A total of 1006 crystals were analyzed, 490 with no peptide and 516 with addition of peptide at a representative concentration of 57 μM. Table 1 summarizes the results of the image analysis. First, the data were tested for normality via the Anderson–Darling test, determining the data were not normally distributed. The area, perimeter, and length are all statistically the same at p < 0.05, using a Mann–Whitney nonparametric test. However, the width and aspect ratio of the struvite crystals formed in the presence and absence of peptide are statistically different at p < 0.05 using a Mann–Whitney test. The crystals precipitated in the presence of shADP5 had a larger aspect ratio than the crystals not exposed to peptide. This could be seen visually, as shown in Fig. 3b and c. This result can be used to explain the differences seen in Fig. 2 and 4, where the peptide is found to induce changes in the formation constant versus no peptide conditions. It has been shown previously that flat crystals correspond to high growth kinetics and stick-like crystals correspond to slower growth kinetics.44 This can be seen in this study as well, as precipitation without shADP5 promotes a lower aspect ratio crystal and has faster growth kinetics. Li et al. used a simple polyaspartic acid peptide in struvite precipitation, but this served to inhibit growth and reduce crystal size – distinctly different than the results of this study.19 The exact mechanism by which the peptide is acting is unknown, but it has been suggested elsewhere that different peptides can anchor to specific crystal faces to mediate growth – inducing changes in morphology and aspect ratio.19,37 As shown in ESI (Fig. S5–S7†), there is no evidence that the peptide binds strongly to component ions in solution. Thus, exploring a direct interaction between shADP5 and the struvite crystals is the subject of future work to begin to understand the mechanism by which the peptide influences struvite morphology, kinetics, and yield. Understanding this interaction would enable a clear understanding of how the peptide will operate in more complex water matrices. Additionally, the crystals sizes seen in this study are on the same order of magnitude as other bench-scale operations.16,45,46 Further processing of the crystals formed could be employed to create pellets to use as fertilizer.47
| Treatment | Measured property | ||||
|---|---|---|---|---|---|
| Area (μm2) | Perimeter (μm) | Length (μm) | Width (μm) | Aspect ratio | |
| No peptide | 530 ± 20 | 120 ± 0 | 56 ± 1 | 11 ± 0* | 5.2 ± 0.1* |
| With peptide | 560 ± 20 | 130 ± 0 | 59 ± 1 | 1![[0 with combining macron]](https://www.rsc.org/images/entities/char_0030_0304.gif) ± 0* ± 0* |
5.8 ± 0.1* |
The effect of seed on struvite formation and growth kinetics
The impact of seed concentration on struvite precipitation kinetic parameters was investigated in the absence and presence of peptide (Fig. 4). Significance was determined by conducting an ANOVA with α = 0.05 and assigning statistical groupings with the Games–Howell post hoc test (see Tables S3 and S4† for full ANOVA tables, and results of post hoc testing). The yield parameter, seen in Fig. 4a increases with increasing seed dosage in the presence of peptide, while in the absence of peptide an increase occurs between 12.9 and 27.9 μL seed added. Previous literature has stated that less energy is required to grow a crystal on a seed than is required to nucleate a crystal, with increasing seed concentration increasing struvite recovery due to a lower energy barrier.25 The presence of peptide increases the yield at high enough seed loadings – further suggesting an interaction between shADP5 and faces of struvite crystals. Fig. 4b shows that seed has no impact on formation constant in the presence of peptide but shows that formation constant is significantly dependent on seed dose in the absence of peptide. Fig. 4c shows that no clear trends exist for induction time regardless of whether or not peptide was introduced. Overall, the data shown in Fig. 4 highlights the need to explore potential interactions when additives are present to achieve the desired results.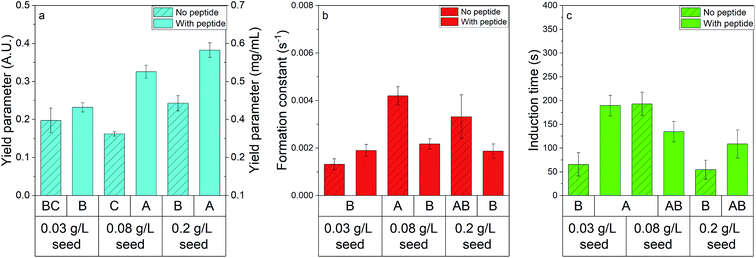 | ||
| Fig. 4 The impact of seed on precipitation shows synergistic effects with peptide presence. (a) Yield parameter (blue bars), (b) formation constant (red bars), and (c) induction time (green bars) were investigated when no peptide was present (bars with filler) and when 57 μM of peptide was present. All data are represented by the average ± standard error. Statistical groupings are shown below each bar by performing ANOVA and the Games–Howell post hoc test – bars that do not share a letter within a graph are statistically different at the 95% confidence level. Note that equal variance tests are shown in Table S5.† | ||
Induction time has been shown to decrease with increasing struvite seeding,14,26 however, this was not explicitly seen in this study. This discrepancy may be due to the low concentration of seed used (estimated 0.03–0.2 g L−1) which limited the range where a significant difference could be observed. Liu et al. also assert that seed addition increases the apparent reaction rate, which we also see in the case of no peptide additives.26 The increase in reaction rate with seed concentration disappears in the reactions performed in the presence of peptide, indicating that peptide does not act as a seed itself. The increase in yield between the two highest seed doses with no peptide is likely due to an increase in nucleation sites. A significant increase in yield parameter is not present between the lowest two seed doses in the experiments without peptide, however it is present between the two lowest seed doses when the peptide is present. Overall, the effect of seed dose on yield parameter changes in the presence of peptide, with higher yield occurring at lower concentrations of seed when the peptide is present, further suggesting there may be a potential interaction between the peptide and struvite crystals.
Factorial design experiment
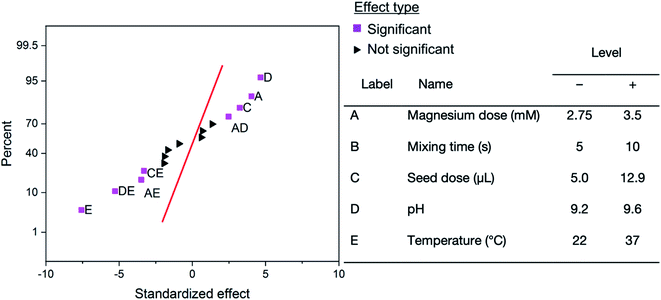
To further highlight the utility of the high-throughput platform, a two-level full factorial design was conducted (n = 3) to analyze the effect of magnesium dose, mixing time, seed dose, pH, and temperature on the final struvite yield. Fig. 5 shows the normal probability plot of standardized effects.As seen in Fig. 5, the results of the factorial design show there is a strong negative influence of temperature. As the temperature increases, the yield of struvite decreases. This can be readily explained by the increasing solubility of struvite with increased temperature.36,48 Temperature shows synergistic negative effects with pH, magnesium dose, and seed dose. This is likely due to the effect temperature has on each individual parameter where (1) the pH of a solution depends on temperature as given by the Nernst equation, (2) the seed is more soluble at higher temperatures, and (3) the mean ionic activity coefficient is lower at higher temperatures.49 The synergistic effects with temperature imply that if raising the temperature of the reaction (e.g. on hot versus cold days) the pH, seed, or magnesium dose would need to be increased to serve as extra driving force to induce the same struvite precipitation yield. Magnesium dose has a positive impact on struvite yield because it is the limiting factor in precipitation – occurring in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of Mg2+
2 ratio of Mg2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) PO43−
PO43−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NH4. Increasing the amount of magnesium increases the theoretical and actual amounts of struvite that can be made in this system. Increasing the pH leads to a positive effect on struvite growth, as struvite is less soluble with increasing pH leading to increased amounts precipitating out of solution.6 The combination of decreased solubility (as pH increases) and increased precipitation (as magnesium increases) leads to a positive interaction between magnesium dose and pH. Increasing the amount of seed also increases the final yield of struvite, as previously observed.25 As shown in Fig. S8,† there is no apparent trend between oversaturation and endpoint absorbance. Thus, these interactions could not be explained only by oversaturation – potentially due to the low range of oversaturation tested. Notably, the mixing time was determined to not be a significant factor in struvite growth at the levels tested. Preliminary tests showed that no mixing led to minimal crystal growth, while mixing led to consistent crystal growth. The lack of dependence on mixing time shows that minimal mixing is sufficient to get suitable struvite growth. The remainder of the combinations did not fall far enough from the standard normal distribution, as seen in Fig. 5, indicating that at α = 0.05 the effect on struvite precipitation is not significant. Table S6† reports every coefficient in the empirical model found via regression. These coefficients can be used to predict a struvite yield in the high-throughput platform based on the levels chosen in a specific experiment. The model uses coded units – i.e. the levels are either −1 or +1, as shown in Fig. 5. The reduced model with only significant factors is shown at the bottom of Table S6.† Using this model, several contour maps were generated (Fig. S9†) to illustrate how the high throughput platform combined with design of experiments could be useful in rapidly identifying optimal reaction conditions. While design of experiments has been applied in struvite formation, this study is the first to examine the simultaneous impacts of magnesium dose, mixing time, seed dose, pH, and temperature on struvite yield.25,41,45 To our knowledge, all interactions aside from temperature–pH41 have not been shown in previous factorial design experiments. The high-throughput platform developed in this study is conducive to further factorial experiments as many factor combinations can be run simultaneously. Overall, the factorial design identified some of the known key parameters affecting struvite formation and shows how the high throughput platform can be used to optimize conditions.
NH4. Increasing the amount of magnesium increases the theoretical and actual amounts of struvite that can be made in this system. Increasing the pH leads to a positive effect on struvite growth, as struvite is less soluble with increasing pH leading to increased amounts precipitating out of solution.6 The combination of decreased solubility (as pH increases) and increased precipitation (as magnesium increases) leads to a positive interaction between magnesium dose and pH. Increasing the amount of seed also increases the final yield of struvite, as previously observed.25 As shown in Fig. S8,† there is no apparent trend between oversaturation and endpoint absorbance. Thus, these interactions could not be explained only by oversaturation – potentially due to the low range of oversaturation tested. Notably, the mixing time was determined to not be a significant factor in struvite growth at the levels tested. Preliminary tests showed that no mixing led to minimal crystal growth, while mixing led to consistent crystal growth. The lack of dependence on mixing time shows that minimal mixing is sufficient to get suitable struvite growth. The remainder of the combinations did not fall far enough from the standard normal distribution, as seen in Fig. 5, indicating that at α = 0.05 the effect on struvite precipitation is not significant. Table S6† reports every coefficient in the empirical model found via regression. These coefficients can be used to predict a struvite yield in the high-throughput platform based on the levels chosen in a specific experiment. The model uses coded units – i.e. the levels are either −1 or +1, as shown in Fig. 5. The reduced model with only significant factors is shown at the bottom of Table S6.† Using this model, several contour maps were generated (Fig. S9†) to illustrate how the high throughput platform combined with design of experiments could be useful in rapidly identifying optimal reaction conditions. While design of experiments has been applied in struvite formation, this study is the first to examine the simultaneous impacts of magnesium dose, mixing time, seed dose, pH, and temperature on struvite yield.25,41,45 To our knowledge, all interactions aside from temperature–pH41 have not been shown in previous factorial design experiments. The high-throughput platform developed in this study is conducive to further factorial experiments as many factor combinations can be run simultaneously. Overall, the factorial design identified some of the known key parameters affecting struvite formation and shows how the high throughput platform can be used to optimize conditions.
Conclusion
In conclusion, a high-throughput platform was created to study the formation and morphology of struvite with and without peptide additives. The formation was modeled by a first order kinetic model with induction time to allow for quantitative assessment of kinetic parameters. Future work will focus on more complex models explored elsewhere.15,50 It was seen that the presence of the peptide increased the yield and decreased the formation constant in a non-dose dependent way in the concentration range tested. The morphological study revealed slower precipitation corresponded to narrower crystals with peptide present. To confirm the identity of the crystals, FTIR was performed, aligning well with previous literature. The impact of struvite seed on the formation parameters determined by kinetic modelling was then probed with and without peptide, showing a synergistic effect occurring between the peptide and struvite seed crystals, increasing the yield. Together, it can be seen that the shADP5 peptide is a promising additive for struvite growth as the yield increases with its presence. We anticipate that the general technique investigated can be applied to more complex water matrices, with purity investigated spectroscopically or through other high throughput assays. Future work will focus on identifying the mechanism by which the peptide acts. The use of a sequence-defined peptide paves the way for further developments in favorably modifying struvite formation and growth. With the effects of shADP5 documented, other similar peptides can be explored via either computational simulations or experimentation to modulate the quality and yield of struvite – potentially increasing its value as a fertilizer. Further computational studies also need to be explored to elucidate the exact mechanism by which shADP5 modulates the thermodynamics of struvite crystallization. Finally, a 25 factorial design experiment was performed to highlight the utility of the platform developed and explore many of the parameters said to influence struvite growth. The results of the factorial design experiment can be used to optimize struvite precipitation with respect to magnesium dose, mixing time, seed dose, pH, and temperature. Overall, the method developed shows broad applicability for future tests of potential additives for struvite growth and future optimization experiments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the United States Department of Agriculture (Award No. 2018-68011-28691) and the National Science Foundation (Award No. 1739473). We thank the CWRU School of Medicine Light Microscopy Core Facility for assistance in gathering images. The CWRU School of Medicine Light Microscopy Core Facility acknowledges NIH Grant S10-RR021228. We also thank Dr Harihara Baskaran for use of his microplate reader and Dr Smarajit Bandyopadhyay at the Case Western Reserve University Molecular Biotechnology Core Facility for assistance with circular dichroism.References
- D. Cordell and S. White, Sustainability, 2011, 3, 2027–2049 CrossRef.
- M. R. Hart, B. F. Quin and M. L. Nguyen, J. Environ. Qual., 2004, 33, 1954–1972 CrossRef CAS.
- V. H. Smith, G. D. Tilman and J. C. Nekola, Environ. Pollut., 1999, 100, 179–196 CrossRef CAS.
- L. E. de-Bashan and Y. Bashan, Water Res., 2004, 38, 4222–4246 CrossRef CAS.
- N. C. Bouropoulos and P. G. Koutsoukos, J. Cryst. Growth, 2000, 213, 381–388 CrossRef CAS.
- J. D. Doyle and S. A. Parsons, Water Res., 2002, 36, 3925–3940 CrossRef CAS.
- J. D. Doyle, R. Philp, J. Churchley and S. A. Parsons, Process Saf. Environ. Prot., 2000, 78, 480–488 CrossRef CAS.
- M. Sena and A. Hicks, Resour., Conserv. Recycl., 2018, 139, 194–204 CrossRef.
- K. S. Le Corre, E. Valsami-Jones, P. Hobbs and S. A. Parsons, Crit. Rev. Environ. Sci. Technol., 2009, 39, 433–477 CrossRef CAS.
- D. Crutchik and J. M. Garrido, Water Sci. Technol., 2011, 64, 2460–2467 CrossRef CAS.
- B. K. Mayer, L. A. Baker, T. H. Boyer, P. Drechsel, M. Gifford, M. A. Hanjra, P. Parameswaran, J. Stoltzfus, P. Westerhoff and B. E. Rittmann, Environ. Sci. Technol., 2016, 50, 6606–6620 CrossRef CAS.
- K. S. Le Corre, E. Valsami-Jones, P. Hobbs and S. A. Parsons, Environ. Technol., 2007, 28, 1317–1324 CrossRef CAS.
- N. O. Nelson, R. L. Mikkelsen and D. L. Hesterberg, Bioresour. Technol., 2003, 89, 229–236 CrossRef CAS.
- S. Agrawal, J. S. Guest and R. D. Cusick, Water Res., 2018, 132, 252–259 CrossRef CAS.
- B. Elduayen-Echave, I. Lizarralde, G. S. Larraona, E. Ayesa and R. Grau, Water Res., 2019, 155, 26–41 CrossRef CAS.
- K. S. Le Corre, E. Valsami-Jones, P. Hobbs and S. A. Parsons, J. Cryst. Growth, 2005, 283, 514–522 CrossRef CAS.
- T. Nonoyama, H. Ogasawara, M. Tanaka, M. Higuchi and T. Kinoshita, Soft Matter, 2012, 8, 11531–11536 RSC.
- S. Dogan, H. Fong, D. T. Yucesoy, T. Cousin, C. Gresswell, S. Dag, G. Huang and M. Sarikaya, ACS Biomater. Sci. Eng., 2018, 4, 1788–1796 CAS.
- H. Li, Q. Z. Yao, Y. Y. Wang, Y. L. Li and G. T. Zhou, Sci. Rep., 2015, 5, 1–8 CAS.
- K. S. Le Corre, E. Valsami-Jones, P. Hobbs, B. Jefferson and S. A. Parsons, Water Res., 2007, 41, 2449–2456 CrossRef CAS.
- H. Li, Q. Z. Yao, S. H. Yu, Y. R. Huang, X. D. Chen, S. Q. Fu and G. T. Zhou, Am. Mineral., 2017, 102, 381–390 CrossRef.
- I. Kabdasli, S. A. Parsons and O. Tunay, Croat. Chem. Acta, 2006, 79, 243–251 CAS.
- M. Fromberg, M. Pawlik and D. S. Mavinic, Powder Technol., 2020, 360, 715–730 CrossRef CAS.
- E. Kirinovic, A. R. Leichtfuss, C. Navizaga, H. Y. Zhang, J. D. S. Christus and J. Batrusaitis, ACS Sustainable Chem. Eng., 2017, 5, 1567–1577 CrossRef CAS.
- W. L. Song, Z. P. Li, F. Liu, Y. Ding, P. S. Qi, H. You and C. Jin, Environ. Sci. Pollut. Res., 2018, 25, 628–638 CrossRef CAS.
- Z. G. Liu, Q. L. Zhao, L. L. Wei, D. L. Wu and L. M. Ma, J. Chem. Technol. Biotechnol., 2011, 86, 1394–1398 CrossRef CAS.
- B. Li, W. Yu, H. M. Huang, E. Lim, I. Boiarkina and B. Young, J. Environ. Chem. Eng., 2019, 7, 1–8 Search PubMed.
- S. Polat and P. Sayan, J. Cryst. Growth, 2020, 531, 1–11 CrossRef.
- Z. L. Ye, S. H. Chen, M. Lu, J. W. Shi, L. F. Lin and S. M. Wang, Water Sci. Technol., 2011, 64, 334–340 CrossRef CAS.
- A. Sinha, A. Singh, S. Kumar, S. K. Khare and A. Ramanan, Water Res., 2014, 54, 33–43 CrossRef CAS.
- A. Rabinovich, A. A. Rouff, B. Lew and M. V. Ramlogan, ACS Sustainable Chem. Eng., 2018, 6, 652–659 CrossRef CAS.
- A. N. Kofina and P. G. Koutsoukos, Cryst. Growth Des., 2005, 5, 489–496 CrossRef CAS.
- M. Quintana, E. Sanchez, M. F. Colmenarejo, J. Barrera, G. Garcia and R. Borja, Chem. Eng. J., 2005, 111, 45–52 CrossRef CAS.
- S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, Cryst. Growth Des., 2016, 16, 6663–6681 CrossRef CAS.
- D. C. Montgomery, Statistical Quality Control, Wiley, 7th edn, 2012 Search PubMed.
- M. I. H. Bhuiyan, D. S. Mavinic and R. D. Beckie, Environ. Technol., 2007, 28, 1015–1026 CrossRef CAS.
- S. Farmanesh, J. H. Chung, R. D. Sosa, J. H. Kwak, P. Karande and J. D. Rimer, J. Am. Chem. Soc., 2014, 136, 12648–12657 CrossRef CAS.
- C. Rodriguez-Navarro, M. Rodriguez-Gallego, K. Ben Chekroun and M. T. Gonzalez-Munoz, Appl. Environ. Microbiol., 2003, 69, 2182–2193 CrossRef CAS.
- G. Fu, S. R. Qiu, C. A. Orme, D. E. Morse and J. J. De Yoreo, Adv. Mater., 2005, 17, 2678–2683 CrossRef CAS.
- L. Wei, T. Q. Hong, K. P. Cui, T. H. Chen, Y. F. Zhou, Y. X. Zhao, Y. D. Yin, J. F. Wang and Q. Zhang, Chem. Eng. J., 2019, 378, 1–8 CrossRef.
- S. Polat and P. Sayan, Adv. Powder Technol., 2019, 30, 2396–2407 CrossRef CAS.
- B. Lafuente, R. T. Downs, H. Yang and N. Stone, in Highlights in Mineralogical Crystallography, 2016, pp. 1–29 Search PubMed.
- V. Stefov, B. Soptrajanov, I. Kuzmanovski, H. D. Lutz and B. Engelen, J. Mol. Struct., 2005, 752, 60–67 CrossRef CAS.
- F. Abbona and R. Boistelle, J. Cryst. Growth, 1979, 46, 339–354 CrossRef CAS.
- S. G. Barbosa, L. Peixoto, B. Meulman, M. M. Alves and M. A. Pereira, Chem. Eng. J., 2016, 298, 146–153 CrossRef CAS.
- S. Shaddel, S. Ucar, J. P. Andreassen and S. W. Osterhus, J. Environ. Chem. Eng., 2019, 7, 1–9 Search PubMed.
- F. Degryse, R. Baird, R. C. da Silva and M. J. McLaughlin, Plant Soil, 2017, 410, 139–152 CrossRef CAS.
- M. Ronteltap, M. Maurer and W. Gujer, Water Res., 2007, 41, 977–984 CrossRef CAS.
- P. Atkins and J. de Paula, Atkins' Physical Chemistry, OUP, Oxford, 2010 Search PubMed.
- A. Stanclik, N. Hutnik, K. Piotrowski and A. Matynia, Chem. Pap., 2019, 73, 555–563 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Methods and results, Fig. S1–S9 and Tables S1–S6. See DOI: 10.1039/d0ra06637k |
| This journal is © The Royal Society of Chemistry 2020 |