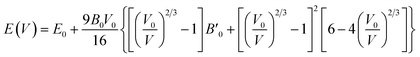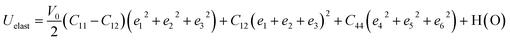New ferromagnetic half-metallic perovskites for spintronic applications: BaMO₃ (M = Mg and Ca)

Abstract

Herein, first principles computer-based simulations were performed to predict the ground-state structure, mechanical stability, and magneto-electronic properties of BaMO₃ (M = Mg and Ca) perovskites, which have not been experimentally synthesized to date. Structural optimization authenticate the stability in the cubic structure for BaMO₃ perovskites having symmetry of the Pm3m space group. The tolerance factor and cohesive energy further validate the stability of BaMO₃ in the cubic phase. Moreover, mechanical stability was confirmed by the positive elastic constants, satisfying the necessary stability conditions. The band structure and density of states at the optimized lattice constants revealed the ferromagnetic half-metallic character of BaMO₃ materials, with O–p states playing a prominent role. The half-metallic character originates from the partial filling of the O–p states in the spin-down channel. Spatial charge distribution indicated the dominant ionic character of bonding. No change in the magnetic moment of perovskites was observed upon changing the M-site atoms. Various elastic parameters suggested that these perovskites are ductile in nature with highly anisotropic character. The three-dimensional graphical representation of different elastic moduli revealed that the linear compressibility is isotropic, whereas the shear modulus, Young's modulus, and Poisson's ratio of these perovskites are highly anisotropic. The results obtained in this study are in agreement with those reported in the literature for other similar perovskites.

---

Introduction

Via integrated circuit (IC) technology, a number of minute transistors can be mounted on a single microchip (normally composed of silicon) to fabricate faster and economic circuits. According to Moore, the number of transistors on an integrated chip doubles at regular intervals; thus, the speed and capability of electronic devices increases, leading to high performance of these devices at lower cost.¹ Although an IC transfers information at high speed and has excellent reliability, but it has volatile memory storage and thus loses information upon power cut-off.^2,3 On the other hand, the magnetic drives store data in the magnetically polarized small patches of surface coating. The magnetic hard disk IBM 350 was developed in 1956, which had 2000 bit per square inch areal density. However, in the year 2015, hard drives with a density of 1.34 terabyte (TB) per square inch, i.e., 600 million-fold that of the IBM 350, were introduced. The storage capacity of these drives is expected to increase further in the near future.^2,4 The main advantage of magnetic memory devices is that they have non-volatile data storage. These devices are fabricated from spintronic materials with high spin polarization.^5,6

Spintronics is emerging as a key technology for next generations and has enabled the utilization of electron spin for various applications.^7–9 Spin-polarized currents do not dissipate energy as heat, and thereby resolve the heat problems very often confronted in IC and other electronic devices. For application in spintronic technology, materials must have high spin polarization, high magnetic moment, and high magnetic phase transition temperature (at least close to room temperature). The ratio of the density of states (DOS) of spin-up and -down channels at the Fermi level quantifies the magnitude of spin polarization (SP); SP = |DOS_↑ − DOS_↓|/|DOS_↑ + DOS_↓|.¹⁰ Diamagnetic and paramagnetic materials have symmetric DOS of the spin-up and -down channels; therefore, they do not exhibit spin polarization. However, ferromagnetic materials demonstrate asymmetric DOS; thus, their SP is always greater than zero but less than unity. Contrarily, in half-metallic ferromagnetic materials, the band structure in one spin channel is metallic, indicating the presence of states at the Fermi level, whereas the band structure in the other spin channel is semiconducting/insulating.¹¹ Therefore, these materials demonstrate 100% spin polarization at the Fermi level and are considered suitable candidates for spintronic technology.

Over the last few years, large number of compounds, including Heusler alloys (half, full, as well as quaternary^12,13), transition metal oxides (CrO₂ (ref. 14)), dilute magnetic semiconductors (Cu-doped ZnO¹⁵), spinels (Fe₃O₄ (ref. 16)), perovskites (BaBkO₃ (ref. 17)), double perovskites (Ba₂CoUO₆ (ref. 18)), halide double perovskites (Cs₂NaMCl₆; M = Ti, V, Mn, Co, and Ni^5,19), with different chemical compositions and structural symmetries have been reported to show half-metallic character. One of the most important family of compounds among them is oxide perovskites with the stoichiometric composition ABO₃, where A is mostly an s-block element, B is a transition/inner-transition element or can rarely be an sp-element, and O is oxygen. Exploration of new members of perovskites and their modification/tailoring to achieve desired properties are an active area of research. These materials have been the focus of various studies because of their better oxidation resistance and diverse physical properties. In addition, half-metallic perovskites have been reported to demonstrate ferroelectricity,²⁰ piezoelectricity,²¹ ionic conductivity,²² good thermoelectric performance,²³ superconductivity,²⁴ and colossal magnetoresistance.²⁵ Due to these unparallel properties, perovskites are suitable for various fascinating technological applications including optoelectronics, waste heat encapsulation, solid oxygen fuel cells, spintronics, gas sensing, and shape memory devices.^26–29

Recently, Mahmood et al. have reported half-metallic ferromagnetic character in XBeO₃ (X = Mg, Ca, Sr, and Ba) perovskites with diamagnetic/paramagnetic constituents.³⁰ The stability of these perovskites was estimated via the optimization of their structure and evaluation of their formulation energy. The X-site atom remains neutral in characterizing the electronic structure of these perovskites, as no change in the magneto-electronic character was observed upon changing X from Mg to Ba. Half-metallicity was maintained even when Sr and Ca partially occupied the X-site in XBeO₃.³¹ However, the magnetic moment increased by unity (1 μ_B) when the first group element K occupied the X-site.³² In the present study, we have investigated the possible changes in the magneto-electronic profile of XBeO₃ that might occur if the Be-site atom is replaced by other alkaline earth elements. Therefore, herein study based on the DFT calculations, we have analyzed the structural, electronic, magnetic, and thermophysical properties of BaMO₃ (M = Mg and Ca) perovskites.

Computational details

The ground-state structures and electronic and magnetic properties of the BaMO₃ (M = Mg and Ca) perovskites were explored by iteratively solving the Kohn–Sham (K–S) equation via spin-polarized calculations using the Wien2k simulation code.³³ Computationally, the stability and ground-state structure can be determined by minimizing the crystal energy with respect to volume. The Birch–Murnaghan equation of state was incorporated to optimize the structure:^34,35
here E₀, B₀, V₀, and 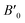represent the energy, bulk modulus, volume, and pressure derivative of B₀, respectively, in the relaxed state. The potential from the core as well as of valence electrons was considered for solving the K–S equation. The exchange–correlation effects were estimated by the well-known generalized gradient approximation (GGA).³⁶ Moreover, the Tran–Blaha-modified Becke–Johnson potential (mBJ) was used to analyse the magneto-electronic property of perovskites.³⁷ The unit cell volume is shared between muffin-tin spheres (with the radii R_MT) surrounding the atomic sites and interstitial space. A linearized augmented plane wave basis set was used to describe the behaviour of electrons within the muffin-tin sphere as well as in the interstitial space. The atomic-like wave functions within spheres were extended up to l_Max = 10, whereas in the interstitial space, the plane wave cut-off was set to R_MTK_Max = 7. A k-mesh of 2500 points was used to integrate the irreducible Brillouin zone, and the separation between the core and valence states was set to −6.0 Ry. The convergence criteria used for energy was 0.0001 Ry, whereas the charge was converged up to 0.0001e.

Structural properties

In order to predict the stable structural configuration of the BaMO₃ (M = Mg, Ca) perovskites, which have not been experimentally synthesized to date, we first evaluated the tolerance (τ) factor. The τ-factor is an empirical parameter widely used to predict the possible stable structure of new perovskites.³⁸ In the ideal perovskite (ABO₃) structure, the ionic radii follow the relation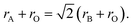 According to this relation, tolerance factor is defined as 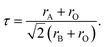The ideal perovskite structure free from any bonding strain follows the symmetry of the Pm3m space group when τ = 1. When τ is not equal to 1, the system has different strain effects on its bonds. To overcome these stresses and enhance bonding among constituents, the system allows tilting of BO₆ octahedra. This distortion results in fascinating magneto-electronic features. The divergence of the tolerance factor from unity decreases the probability of the formation of a cubic structure as the stable phase, whereas increases the probability of the formation of less symmetric states. However, the cubic structure is stable over a range of τ = 0.9–1.³⁸ The τ-values calculated for the BaMO₃ perovskites are provided in Table 1, confirming the stability of the cubic structure. After ascertaining the tolerance factor, we evaluated the cubic lattice constant for the BaMO₃ systems using ionic radii based on the following relation: r = α + β(r_Ba + r_O) + γ((r_M + r_O)), where α = 0.064, β = 0.4912, and γ = 1.2921 are constants.³⁹ Subsequently, using these computed lattice constants, we optimized the Pm3m symmetric cubic structure via spin-polarized calculations. The parabolic nature of the optimization curves depicted in Fig. 1 suggests that the perovskites are stable in Pm3m structure. The minimum in the curve shows the optimized energy corresponding to the relaxed lattice constant. The optimized parameters of the cubic phase are presented in Table 1. The unit cell structure is also shown in Fig. 1. The constituents Ba, B, and O within the cell are cited at the 4a (corners), 4b (centre), and 3d (faces) Wyckoff positions following the symmetry m3m, m3m, and 4/mmm, respectively. In order to ensure that these perovskites can be experimentally synthesized, we determined the enthalpy of formation (H_f) of these perovskites from their optimized energy and energy of the constituent elements in their stable phases.³⁰ The enthalpy of formations were below zero, as shown in Table 1. The negative H_f signifies that the BaMO₃ materials can be experimentally prepared. Moreover, we determined the cohesive energy (E_Coh) of the perovskites to confirm their stability in the cubic phase. The positive E_Coh signifies that energy is required to rupture the bonds, verifying the stability of the BaMO₃ (M = Mg and Ca) perovskites.

Table 1 Ground-state structural parameters viz bond distance (in Å), tolerance factor (τ), lattice constant (a in Å), crystal energy (E₀ in eV), cohesive energy (E_Coh in eV), and enthalpy of formation (H_f in eV)

Perovskite	Bond distance		τ		a		E0	ECoh	Hf
	Ba–O	M–O	Ionic radii	Bond distance	Analytical	Optimized
BaMgO3	2.92	2.06	1.0	1.0	4.16	4.12	−232984.47	22.45	−1.63
BaCaO3	3.15	2.22	0.9	1.0	4.55	4.44	−246041.86	22.52	−1.46
BaBeO3 (ref. 30)			1.03		3.81				−1.85

---

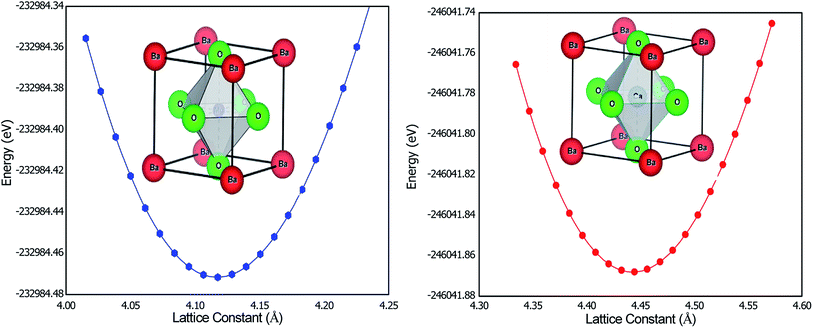Fig. 1 Optimization curves along with the unit cell structure of BaMO₃ (M = Mg and Ca) perovskites determined via spin-polarized calculations.

Mechanical stability and anisotropic character

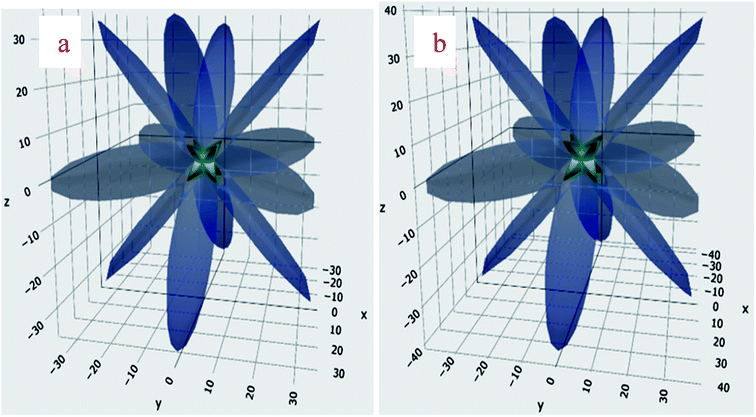
To further investigate the mechanical stability of the titled perovskites, the elastic constants were computed. If a system is arbitrarily deformed under equilibrium conditions through a small strain “e”, the change in energy would be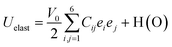 ; (HO) is used for higher-order strain terms.⁴⁰ Symmetry reduces the number of independent elastic constants that could completely reveal the mechanical behavior of a system. Only C₁₁, C₁₂, and C₄₄ are required to completely describe the mechanical behavior of a cubic symmetric system. Therefore, the above mentioned equation for the cubic system reduces to

The system would be dynamically stable if and only if the deformed system is at higher energy i.e., U_elast should be positive. This condition restricts the values of elastic constants, which have been mathematically outlined as necessary stability conditions by Born.^41,42 The cubic structure is dynamically stable if and only if C₁₁ > 0; C₁₁ − C₁₂ > 0; C₄₄ > 0; and C₁₁ + 2C₁₂ > 0 are followed.

The elastic constants of the titled perovskites were computed by applying tetrahedral and rhombohedral distortions to the optimized structure under a constant volume constraint. The computed values of the elastic constants presented in Table 2 are positive and follow the stability criteria, thereby authenticating the stability of the perovskites. Moreover, the magnitude of elastic constants for the BaMO₃ (M = Mg and Ca) perovskites decreases in the order C₁₁ > C₁₂ > C₄₄, signifying that these perovskites offer higher resistance towards unidirectional deformation than pure shear deformation.

Table 2 Elastic constants determined by DFT calculations and the maximal and minimal values along with anisotropies of various elastic moduli

Perovskite	Cij (GPa)			A^U	Y (GPa)			G (GPa)			σ
	C11	C12	C44		Ymin	Ymax	AY	Gmin	Gmax	AG	σmin	σmax	Aσ
BaMgO3	151.2	52.4	3.08	16.96	9.1	124.2	13.6	3.08	49.42	16.0	0.024	0.92	37.7
BaCaO3	135.3	25.7	3.8	14.99	11.2	127.1	11.4	3.8	54.79	14.8	0.018	0.90	19.6
KMgO3 (ref. 22)	121.5	32.5	9.03

---

Using these elastic constants, we have analyzed the anisotropic character of the perovskites by evaluating the universal anisotropic index (A^U). The deviation of A^U from zero, as shown in Table 2, signifies the presence of anisotropy. The elastic matrices were supplied to the ‘ELATE: elastic tensor analysis’ tool to visualize the three-dimensional orientation dependence of various elastic moduli.⁴³

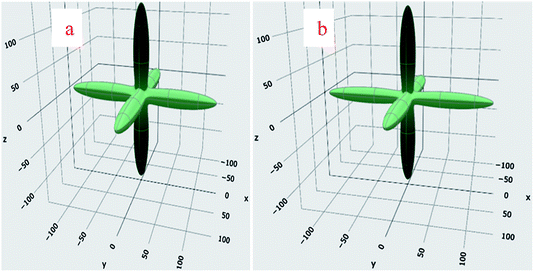
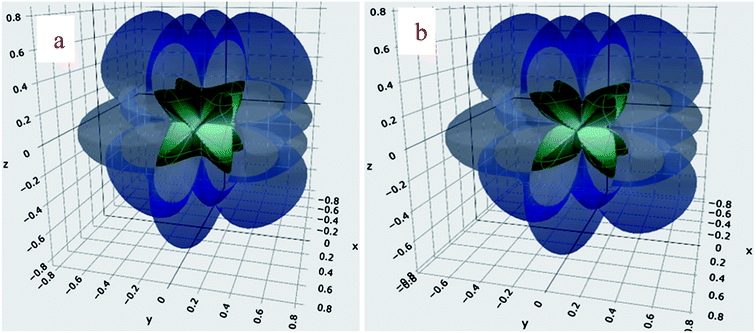
The graphical representation of the Young's modulus (Y) of BaMgO₃ and BaCaO₃ is shown in Fig. 2. The maximum values of Y reached 124.2 (127.1) along the [100], [001], and [010] directions and reduced to the minimum value 9.1 (11.2) along the body diagonals for the Mg (Ca)-based perovskites. The ratio A_Y = E_max/E_min is about 13.6 and 11.4 for BaMgO₃ and BaCaO₃, respectively, and characterize the anisotropy in the Y-modulus. The anisotropy originates from the large difference in the longitudinal and shear elastic constants. The directional deformation of shear modulus is illustrated in Fig. 3. The star-like behavior of shear modulus, exhibiting different values along different directions, reveals the anisotropic character of the perovskites. The highest and lowest values of G are provided in Table 2 along with the shear anisotropy (A_G) ratio. The maximum value of G is equal to C′ = (C₁₁ − C₁₂)/2, representing the resistance to shear in the (110) plane. On the other hand, G_min = C₄₄ represents the resistance to shear in the (100) plane.⁴⁴

Fig. 2 Directional dependence of Young's modulus for (a) BaMgO₃ and (b) BaCaO₃.

Fig. 3 Angular dependence of shear modulus for (a) BaMgO₃ and (b) BaCaO₃.

Poisson's ratio σ = −e_j/e_i is the ratio of transverse to axial strain. The ratio varies over −1 < σ < 0.5 range.⁴⁵ The angular dependence of σ for the BaMO₃ framework is shown in Fig. 4(a and b). The ranges over which σ varies for the titled perovskites as well as anisotropy A_σ are shown in Table 2. For a ductile solid, σ is usually larger than 0.26, and the average of σ_max and σ_min is greater than 0.26, indicating ductile character of the perovskites.

Fig. 4 Three-dimensional graphical representation of Poisson's ratio for (a) BaMgO₃ and (b) BaCaO₃.

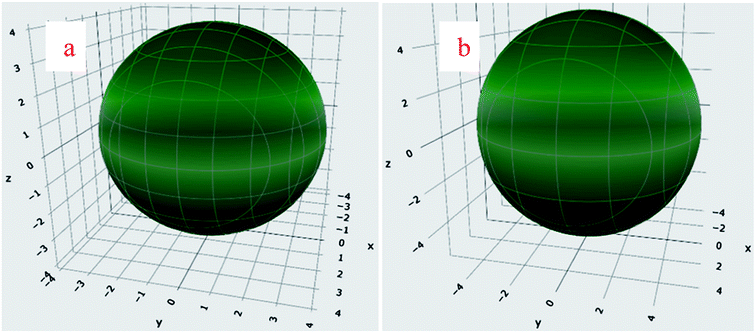
The mean values of the bulk (B) and shear (G) moduli of these highly anisotropic perovskites were estimated by adopting the Voigt–Reuss–Hill-scheme using elastic constants and are provided in Table 3.^42,45 The same values of B_V, B_R, and B_H signify that the bulk modulus is isotropic. The isotropy of B can also be confirmed from the spherical shape of linear compressibility shown in Fig. 5(a and b), reflecting angular independence. The Pugh's ratio (B/G) and σ are often used to characterize the mechanical behavior of ductility or brittleness. The index values of these parameters are 1.75 and 0.26. If the value of these parameters is above the index value, the perovskite is most likely to have a ductile character. The calculated values of these decisive parameters signified that the BaMO₃ perovskites are highly ductile in nature.

Table 3 Mean elastic parameters of BaMO₃ perovskites

Perovskites	B			G			Y			σ			B/G
	BV	BR	BH	GV	GR	GH	YG	YR	YH	σV	σR	σH
BaMgO3	85.42	85.42	85.42	21.61	4.92	13.27	59.80	14.50	37.95	0.38	0.47	0.42	6.4
BaCaO3	62.31	62.31	62.31	24.19	6.05	15.12	64.27	17.59	41.97	0.32	0.45	0.38	4.12
KMgO3 (ref. 22)	62.22			23.21			49.84			0.36			2.68

---

Fig. 5 Orientation dependence of linear compressibility for (a) BaMgO₃ and (b) BaCaO₃.

Electronic and magnetic properties

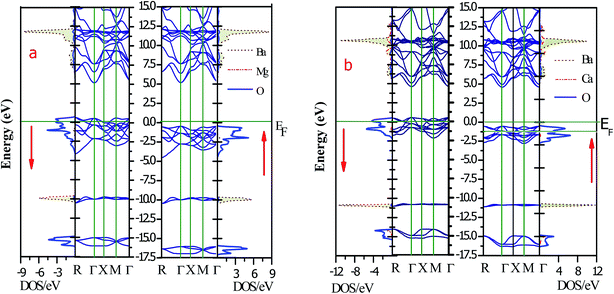
The magneto-electronic behavior of the titled perovskites was investigated based on the optimized lattice constant. The exchange–correlation potential was approximated by the generalized gradient approximation, which works well for systems with sp-electrons. However, we also added the mBJ potential to GGA in order to more precisely describe the electron profile. The spin-polarized electronic band structures determined via the GGA approximation are shown in Fig. 6(a and b). The energy bands of the spin-down channel clearly reflect the metallic character as the bands crosses over the Fermi level. Contrarily, in the spin-up channel, the Fermi level remained vacant. The wide band gap separating the top of the valence band (VBM) and minimum of the conduction band (CBM) indicates insulating nature of the respective spin channel. The presence of bands at the Fermi level in one spin channel and the vacant Fermi level in the other spin channel signify that these perovskites have 100% spin polarization at the Fermi level. The band structure also indicates the presence of large pseudo-gaps. The spin-flip (half-metallic) gap is determined from the energy difference between the Fermi level (zero energy) and VBM because of its closeness to the Fermi level than to the CBM for a semiconducting channel. This expresses the minimum energy required to flip an electron from the top of the occupied valence to the Fermi level.⁴⁶ The HM gap is a significant parameter to determine the minimum energy required for spin excitation to induce holes in the minority spin channel. The wider HM gap suggested that the BaMO₃ materials are suitable HM ferromagnets for potential spintronic applications. The mBJ band structure also demonstrated half-metallic electronic character of the BaMO₃ (M = Mg and Ca) perovskites. However, the band gap in the spin-up channel and spin-splitting values were modified, as presented in Table 4. The effect of mBJ on the energy states can be determined from the density of states illustrated in Fig. 7, where it is evident that the energy states show a marginal shift away from the Fermi level in the spin-up channel. However, the energy bands at the Fermi level in the spin-down state did not shift, thereby maintaining the half-metallicity. In order to exploit and extract more information from the band structure and understand hybridization within perovskites, we plotted projected density of states (PDOS), which can indicate both quantitative as well as qualitative behavior of states at a particular energy value. Since both perovskites have a similar band and DOS profiles, herein, we have shown only the pDOS of BaMgO₃ in Fig. 8. The distribution of the valence states reveals that the oxygen p-states are responsible for the half-metallicity of these perovskites as they occupy the Fermi level in the spin-down channel. The presence of the oxygen p-states at different energy values in the spin-up and down channels indicates that the electrons in these channels do not cancel each other's magnetic moment and thereby lead to ferromagnetic character. However, the presence of Ba and M-atom states at the same energy value in the spin-up and down channels reflects symmetric character of the valence states of these atoms. This implies complete cancellation of the magnetic moment of these constituents. The valence s-states of the Ba and Mg-site atoms are in the conduction band, whereas their inner lying p-states constitute the DOS peaks in the valence band, as can be observed in the pDOS plots shown in Fig. 8.

Fig. 6 Spin-polarized band structure and density of states determined via GGA calculations: (a) BaMgO₃ and (b) BaCaO₃. The distribution of energy bands reflects the semi-conducting character of the spin-up channel and metallic character of the spin-down channel.

Table 4 Band gap (eV), half-metallic gap (eV), spin-splitting gap (↓_VBM − ↑_VBM in eV), and magnetic moment (μ_B) of the BaMO₃ perovskites determined via the GGA and mBJ approximation

Parameter	Band gap		Half-metallic gap		↓VBM − ↑VBM		Magnetic moment
Approximation	GGA	mBJ	GGA	mBJ	GGA	mBJ	GGA	mBJ
BaMgO3	5.67	7.61	0.49	0.62	1.08	2.75	2.0	2.0
BaCaO3	5.16	7.16	0.58	0.60	1.09	2.47	2.0	2.0

---

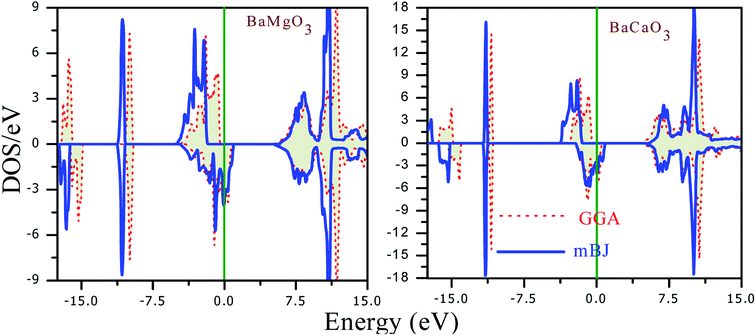Fig. 7 Total density of states of BaMgO₃ and BaCaO₃ perovskites obtained through the GGA and mBJ methods. The energy peaks depict a slight shift with the mBJ potential.

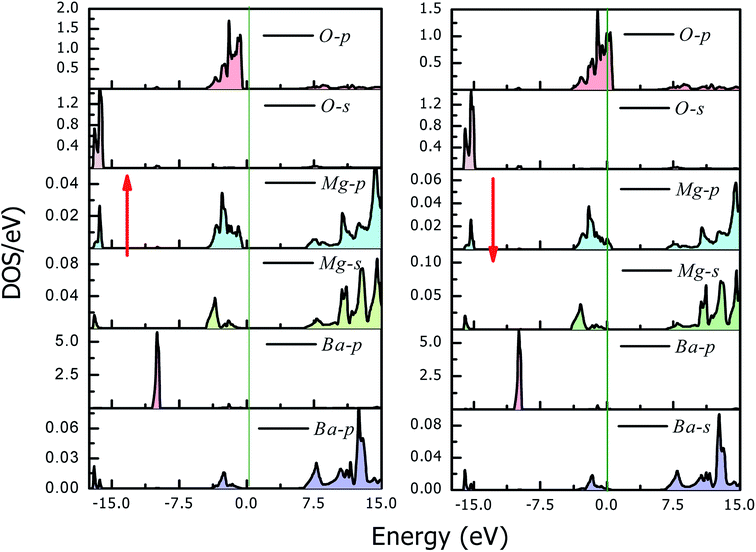Fig. 8 Projected density of states for BaMgO₃. It is evident that the O–p states are responsible for the ferromagnetic half-metallic character of these perovskites.

The total spin magnetic moment and individual contributions to it are presented in Table 2. The magnetic moment for any system originates from the number of unpaired electrons with each unpaired electron contributing 1 μ_B. Perovskites mostly demonstrate A²⁺B⁴⁺O₃²⁻ or A³⁺B³⁺O₃²⁻ oxidation states, in which all the oxygen atoms are in the −2 oxidation state. However, in BaMO₃, the Ba and M-site atoms belong to the II group of the periodic table and have +2 oxidation state. Therefore, to maintain charge stability, individual oxygen atoms demonstrate different oxidation states. Among the three oxygen atoms per formula, two have the oxidation state of −1 and one oxygen atom depicts the oxidation state of −2. Accordingly, the oxidation state of oxygen in the BaMO₃ perovskites is 4/3. The average oxidation state was obtained by summing the different oxidation states of the oxygen atoms and dividing the obtained value by the total oxygen atoms per formula. This configuration reveals the presence of two unpaired electrons at the oxygen sites partially filling the p-states in the spin-down channel. The unpaired electrons would lead to the magnetic character of perovskites with a magnetic moment of 2 μ_B. Upon replacing the Ba-atom with potassium (K), K¹⁺Mg²⁺O₃¹⁻ can be obtained. The number of unpaired electrons as well as the magnetic moment increases to three. The partial filling of the p-states in the spin-down channel pushes the valence band to cross over the Fermi level. Thus, the valence band maxima (VBM) in the spin-up and down channels are obtained at different values. Therefore, we evaluated the spin-splitting gap (↓_VBM − ↑_VBM), which is reported in Table 2.

Charge density and characteristic bonding

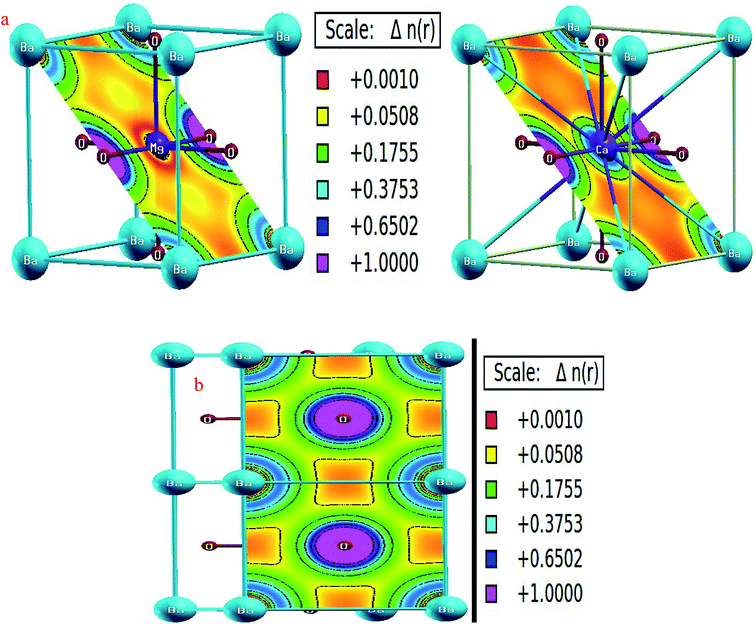
The constituent atoms within a perovskite can be linked together by different kinds of bonds with different spatial charge distribution. Covalent bonds are characterized by the mutual sharing of electrons and therefore have non-zero charge density along the bond distance. However, in ionic bonding, the inter-atomic distances are free from any type of charge density owing to the complete transfer of charge from one atom to another. For the titled perovskites, we have analyzed charge distribution in the (011) and (001) planes, as shown in Fig. 9. The O-atoms are nearest neighbors to the Ba and M-site atoms; therefore, we examined the bonding among them. The charge distribution around the three constituents is almost spherical, indicating ionic bonding. However, the charge distribution around Mg and Ca is typically different, as shown in Fig. 9(a). Charge accumulation around Ca is more as compared to that around Mg because of higher number of electrons in Ca due to which the charge of Ca extends to almost up to the charge of O. Nevertheless, almost negligible charge at half of the distances from the centers of the Ca and O atoms conveys ionic character of the Ca–O bonds. The ionic character of bonding is dominant because alkaline earth metals have highly electropositive character, whereas oxygen is one of the most electronegative elements.

Fig. 9 Charge density distribution in the (a) [011] and (b) [001] planes.

Thermodynamic properties

Within the regimes of the quasi-harmonic approximation, we deduced the thermodynamic parameters using the GIBBS2 code.⁴⁷ The variation in the various thermodynamic properties against temperature and pressure can be evaluated using this program with the aid of fitted input E–V data-generated from Birch–Murnaghan equation. The advantage of deriving the thermodynamic properties under different temperature and pressure conditions from the DFT calculations is the ease in modeling these parameters under extreme conditions, which could be harsh experimentally. The variation in the specific heat at constant volume (C_V) is illustrated in Fig. 10(a). The specific heat abruptly increases at low temperatures, following the Debye T³-law. However, at higher temperatures, C_V tends towards a constant value of 3nR = 121 J mol⁻¹ K⁻¹, where R is the gas constant. C_V shows a rapid increase with an increase in T from absolute zero possibly due to an increase in thermal vibrations at elevated temperatures. However, all vibration modes are thermally excited at higher temperatures, corresponding to the Dulong–Petit limit for specific heat. With an increase in temperature, the atoms start vibrating vigorously, and thus, the inter-atomic distances are increased, leading to thermal expansion. Almost all the solids expand to some extent with an increase in temperature; however, materials with weak inter-atomic bonding show greater degree of expansion. The ratio of change in the length to the original length is known as thermal coefficient (α), and the variation in this coefficient with temperature is shown in Fig. 10(b). At higher temperatures, the value of α tends towards a saturation value. However, at lower temperatures, it sharply increases, exhibiting similar character as C_V.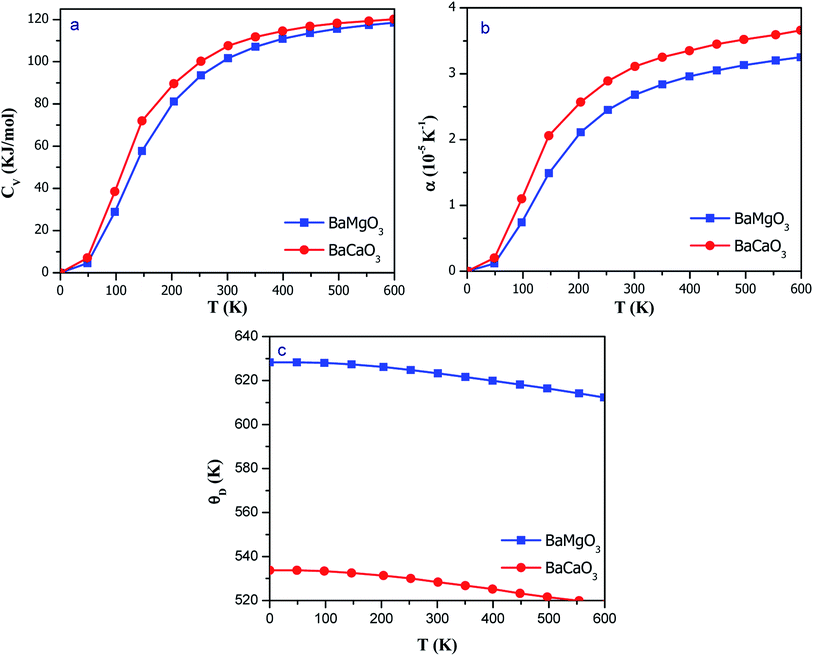

Fig. 10 Variation in the thermodynamic properties of perovskites against temperature: (a) specific heat; (b) thermal expansion; and (c) Debye temperature.

Debye temperature (θ_D) is one of the important thermoelastic parameters of solids. It represents the highest value of temperature up to which the constituents exhibit coupled vibrations and the vibrations reach the maximum possible modes. It is a good indicator of the hardness of materials; materials with high θ_D exhibit high hardness and are comparatively rigid than the materials with low θ_D. The θ_D as a function of temperature is shown in Fig. 10(c); it is clear that θ_D decreases with an increase in temperature. At low temperatures, the thermal expansion as well as anharmonicity are small, resulting in an almost constant Debye temperature. The high-frequency modes can be considered frozen at low temperatures, i.e., only the acoustic modes are excited. The θ_D decreases with an increase in temperature; thus, the vibration spectra of the atoms change with an increase in temperature. The room-temperature values of Debye temperature are 623.2 and 528.3 K for BaMgO₃ and BaCaO₃, respectively. The high value of the Debye temperature suggests that the perovskites can be used for application purposes even at higher temperatures.

Conclusion

In the study, we successfully established the structural and mechanical stabilities of BaMO₃ (M = Mg and Ca) perovskites. The structural optimization, tolerance factor, cohesive energy, and stability criteria indicate the stability of these perovskites in the cubic symmetric Pm3m structure. The electronic profile demonstrates 100% spin polarization at the Fermi level with a wide band gap in the spin-up channel. Both the perovskites show a magnetic moment of 2 μ_B with sole contribution from the oxygen p-electrons. Using quasi-harmonic approximation, we demonstrated the variation in thermodynamic properties against temperature. The magnitude of the bulk and shear moduli suggests higher these paerovskites show higher resistance towards volumetric deformation as compared to shape deformation. The Pugh's ratio and Poisson's ratio signify highly ductile character of these perovskites. The high anisotropy of these perovskites was verified by analysing 3D graphical representation of various elastic parameters. Our successful prediction of structural and mechanical stability would be helpful for the synthesis of these novel perovskites.

Funding

The research work is not funded by any agency.

Data availability

The datasets generated during and/or analyzed during the current study would be available from the corresponding author on reasonable request.

Author contributions

All the authors have significantly contributed to the research. Shabir Ahmad Mir: conceptualization, methodology (partially), writing – original draft, revision; Ab Quyoom Seh: methodology (partially), editing write-up; and Dinesh C. Gupta: supervision, software, validation, writing – review & modification.

Conflicts of interest

The authors declare that they have no conflict of interest for this work.

Acknowledgements

The authors are greatly thankful to Jiwaji University for providing the facilities to carry out the research work.

References

1. R. R. Schaller, Moore's law: past, present and future, IEEE Spectrum, 1997, 34, 52–59,  DOI:10.1109/6.591665.
2. S. J. Pearton, C. R. Abernathy, D. P. Norton, A. F. Hebard, Y. D. Park, L. A. Boatner and J. D. Budai, Advances in wide bandgap materials for semiconductor spintronics, Mater. Sci. Eng., R, 2003, 40, 137–168,  DOI:10.1016/s0927-796x(02)00136-5.
3. T. Endoh and H. Honjo, A Recent Progress of Spintronics Devices for Integrated Circuit Applications, Journal of Low Power Electronics and Applications, 2018, 8, 1–17,  DOI:10.3390/jlpea8040044.
4. L. D. Stevens, The Evolution of Magnetic Storage, IBM J. Res. Dev., 1981, 25, 663–676,  DOI:10.1147/rd.255.0663.
5. S. A. Mir and D. C. Gupta, Systematic investigation of the magneto-electronic structure and optical properties of new halide double perovskites Cs₂NaMCl₆ (M = Mn, Co and Ni) by spin polarized calculations, RSC Adv., 2020, 10, 26277–26287,  10.1039/d0ra02817g.
6. C. Chappert, A. Fert and F. N. V. Dau, The emergence of spin electronics in data storage, Nat. Mater., 2007, 6, 813–823,  DOI:10.1038/nmat2024.
7. S. D. Sarma, Spintronics, Am. Sci., 2001, 89, 516–523,  DOI:10.1511/2001.6.516.
8. V. K. Joshi, Spintronics: a contemporary review of emerging electronics devices, Eng. Sci. Technol. Int J., 2016, 19, 1503–1513,  DOI:10.1016/j.jestch.2016.05.002.
9. S. A. Wolf, Spintronics: A Spin-Based Electronics Vision for the Future, Science, 2001, 294, 1488–1495,  DOI:10.1126/science.1065389.
10. S. Kokado, Y. Sakuraba and M. Tsunoda, Spin polarization ratios of resistivity and density of states estimated from anisotropic magnetoresistance ratio for nearly half-metallic ferromagnets, Jpn. J. Appl. Phys., 2016, 1–3,  DOI:10.7567/jjap.55.108004.
11. R. A. de Groot, F. M. Mueller, P. G. van Engen and K. H. J. Buschow, New Class of Materials: Half-Metallic Ferromagnets, Phys. Rev. Lett., 1983, 50, 2024–2027,  DOI:10.1103/physrevlett.50.2024.
12. S. Yousuf and D. C. Gupta, Insight into half-metallicity, spin-polarization and mechanical properties of L2 1 structured MnY₂Z (Z = Al, Si, Ga, Ge, Sn, Sb) Heusler alloys, J. Alloys Compd., 2018, 735, 1245–1252,  DOI:10.1016/j.jallcom.2017.11.239.
13. A. Q. Seh and D. C. Gupta, Exploration of highly correlated Co-based quaternary Heusler alloys for spintronics and thermoelectric applications, Int. J. Energy Res., 2019, 43, 8864–8877,  DOI:10.1002/er.4853.
14. K. Schwarz, CrO₂ predicted as a half-metallic ferromagnet, J. Phys. F: Met. Phys., 1986, 16, L211–L215,  DOI:10.1088/0305-4608/16/9/002.
15. L. H. Ye, A. J. Freeman and B. Delley, Half-metallic ferromagnetism in Cu-doped ZnO: density functional calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 033203,  DOI:10.1103/physrevb.73.033203.
16. Q. Mahmood, B. U. Haq, M. Rashid, N. A. Noor, S. AlFaify and A. Laref, First-principles study of magnetic and thermoelectric properties of SnFe₂O₄ and SnCo₂O₄ spinels, J. Solid State Chem., 2020, 286, 1–8,  DOI:10.1016/j.jssc.2020.121279.
17. M. Nabi, T. M. Bhat and D. C. Gupta, Magneto-Electronic, Thermodynamic, and Thermoelectric Properties of 5f-Electron System BaBkO₃, J. Supercond. Novel Magn., 2018, 32, 1751–1759,  DOI:10.1007/s10948-018-4872-8.
18. S. A. Mir and D. C. Gupta, Exploration of Uranium Double Perovskites Ba₂MUO₆ (M = Co, Ni) for Magnetism, Spintronic and Thermoelectric Applications. Journal of Magnetism and Magnetic Materials, J. Magn. Magn. Mater., 2019, 493, 1–12,  DOI:10.1016/j.jmmm.2019.165722.
19. S. A. Mir and D. C. Gupta, Analysis of cage structured halide double perovskites Cs₂NaMCl₆ (M = Ti, V) by spin polarized calculations, J. Alloys Compd., 2020, 854, 1–10,  DOI:10.1016/j.jallcom.2020.156000.
20. R. E. Cohen, Origin of ferroelectricity in perovskites, Nature, 1992, 358, 136–138,  DOI:10.1038/358136a0.
21. K. Uchino, Glory of of piezoelectric perovskites, Sci. Technol. Adv. Mater., 2015, 16, 046001,  DOI:10.1088/1468-6996/16/4/046001.
22. J. C. Boivin and G. Mairesse, Recent Material Developments in Fast Oxide Ion Conductors, Chem. Mater., 1998, 10, 2870–2888,  DOI:10.1021/cm980236q.
23. A. H. Reshak, Transport properties of the n-type SrTiO₃LaAlO₃ interface, Phys. Chem. Chem. Phys., 2016, 6, 92887–92895,  10.1039/c6ra21929b.
24. R. J. Cava, B. Batlogg, J. J. Krajewski, R. Farrow, L. W. Rupp Jr, A. E. White, K. Short, W. F. Peck and T. Kometani, Superconductivity near 30 K without copper: the Ba_0.6K_0.4BiO₃ perovskite, Nature, 1988, 814–816,  DOI:10.1038/332814a0.
25. B. Raveau, A. Maignan, C. Martin and M. Hervieu, Colossal Magnetoresistance Manganite Perovskites:  Relations between Crystal Chemistry and Properties, Chem. Mater., 1998, 10, 2641–2652,  DOI:10.1021/cm9801791.
26. E. A. R. Assirey, Perovskite synthesis, Properties and their related biochemical and industrial application, Saudi Pharm. J., 2019, 27, 817–829,  DOI:10.1016/j.jsps.2019.05.003.
27. S. Das, S. Gholipour and M. Saliba, The Versatile Application Range of Perovskite Optoelectronics, Energy Environ. Mater., 2019, 2, 144–151,  DOI:10.1002/eem2.12044.
28. Y. Inaguma, L. Chen, M. Itoh and T. Nakamura, Candidate compounds with perovskite structure for high lithium ionic conductivity, Solid State Ionics, 1994, 70–71, 196–202,  DOI:10.1016/0167-2738(94)90309-3.
29. Y. Tokura and N. Nagaosa, Orbital Physics in Transition-Metal Oxides, Science, 2000, 288, 462–468,  DOI:10.1126/science.288.5465.462.
30. Q. Mahmood, M. Hassan, M. Yaseen and A. Laref, Half-metallic ferromagnetism and optical behavior in alkaline-earth metals based Beryllium perovskites: DFT calculations, Chem. Phys. Lett., 2019, 729, 11–16,  DOI:10.1016/j.cplett.2019.05.011.
31. R. Singla and M. K. Kashyap, First-Principles Study of Electronic Properties and Robust Half Metallicity of Mixed Sr_1−xCa_xBeO₃ (x = 0.25) Perovskite, Journal of Advances and Scholarly Researches in Allied Education, 2019, 16, 299–302,  DOI:10.29070/jasrae.
32. M. Hamlat, K. Boudia, K. Amara, F. Khelfaoui and N. Marbouh, Half-Metallic Stability of the Cubic Perovskite KMgO₃, Computational Condensed Matter, 2020, 23, e00456,  DOI:10.1016/j.cocom.2020.e00456.
33. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, J. Luitz, R. Laskowsk, F. Tran, L. Marks and L. Marks, WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Techn. Universitat, Vienna, Austria, 2019, p. 287.
34. F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev., 1947, 71, 809–824,  DOI:10.1103/physrev.71.809.
35. F. D. Murnaghan, The Compressibility of Media under Extreme Pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247,  DOI:10.1073/pnas.30.9.244.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868,  DOI:10.1103/physrevlett.77.3865.
37. F. Tran and P. Blaha, Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential, Phys. Rev. Lett., 2009, 102, 226401,  DOI:10.1103/physrevlett.102.226401.
38. S. A. Khandy and D. C. Gupta, Investigation of the transport, structural and mechanical properties of half-metallic REMnO₃ (RE = Ce and Pr) ferromagnets, RSC Adv., 2016, 6, 97641–97649,  10.1039/c6ra19448f.
39. R. Ubic, Revised Method for the Prediction of Lattice Constants in Cubic and Pseudocubic Perovskites, J. Am. Ceram. Soc., 2007, 90, 3326–3330,  DOI:10.1111/j.1551-2916.2007.01881.x.
40. G. Grimvall, B. M. Köpe, V. Ozoliņš and K. A. Persson, Lattice instabilities in metallic elements, Rev. Mod. Phys., 2012, 84, 945–986,  DOI:10.1103/revmodphys.84.945.
41. M. Born, On the stability of crystal lattices. I, Math. Proc. Cambridge Philos. Soc., 1940, 36, 160,  DOI:10.1017/s0305004100017138.
42. S. A. Mir, S. Yousuf, T. M. Bhat, S. Singh, Ab Q. Seh, S. A. Khandy, S. A. Sofi, Z. Saleem and D. C. Gupta, Structural and elasto-mechanical properties of ordered double perovskite Ba₂LuSbO₆, AIP Conf. Proc., 2019, 2115,  DOI:10.1063/1.5113176.
43. R. Gaillac, P. Pullumbi and F.-X. Coudert, ELATE: an open-source online application for analysis and visualization of elastic tensors, J. Phys.: Condens. Matter, 2016, 28, 275201,  DOI:10.1088/0953-8984/28/27/275201.
44. G. Feng, X. Jiang, W. Wei, P. Gong, L. Kang, Z. Li, Y. Li, X. Li, X. Wu, Z. Lin, W. Li and P. Lu, High pressure behaviour and elastic properties of a dense inorganic–organic framework, Dalton Trans., 2016, 45, 4303–4308,  10.1039/c5dt03505h.
45. S. A. Mir and D. C. Gupta, Understanding the origin of half-metallicity and thermophysical properties of ductile La₂CuMnO₆ double perovskite, Int. J. Energy Res., 2019, 43, 4783–4796,  DOI:10.1002/er.4620.
46. B. Cai, X. Chen, M. Xie, S. Zhang, X. Liu, J. Yang, W. Zhou, S. Guo and H. Zeng, A class of Pb-free double perovskite halide semiconductors with intrinsic ferromagnetism, large spin splitting and high Curie temperature, Mater. Horiz., 2018, 5, 961,  10.1039/c8mh00590g.
47. A. Otero-de-la-Roza, D. Abbasi-Pérez and V. Luaña, Gibbs2: a new version of the quasiharmonic model code. II. Models for solid-state thermodynamics, features and implementation, Comput. Phys. Commun., 2011, 182, 2232–2248,  DOI:10.1016/j.cpc.2011.05.009.

---