Open Access Article
Open Access ArticleA universal strategy to continuously tune the properties of materials through internal strain
Chengyuan Liu*a,
Wenlian Li*b,
Yuan Yua and
Yuying Hao *a
*a
aCollege of Physics and Optoelectronics, Taiyuan University of Technology, Taiyuan 030024, China. E-mail: 553505626@qq.com; haoyuyinghyy@sina.com
bState Key Laboratory of Luminescence and Applications, Changchun Institute of Optics, Fine Mechanics and Physics (CIOMP), Chinese Academy of Sciences, Changchun 130033, China. E-mail: wenlianli@aliyun.com
First published on 2nd November 2020
Abstract
We proposed a universal strategy to continuously and precisely tune the properties of materials. Atoms or molecules would be inserted into a nano tuner, which is a nano container with inwalls linked by molecular springs. Interactions between core materials and nanocontainers can be precisely and continuously tuned by changing the types and amount of molecular springs. The fact is that most properties of atoms or molecules depend on their environments. This strategy can be applied universally to numerous materials. It could raise the performances of many materials significantly, even up to their theoretical limits.
Energy and materials are the bases for the survival and development of human society. Researches on related topics, such as transistors,1 photovoltaics,2,3 photodetection,4 thermoelectricity,5 electroluminescence,6 catalysis,7 lithium batteries,8 hydrogen storage,9 superconductivity,10 magnetic materials,11 target drugs12 and so on, are extremely important. Although lots of progress have been made, there is still much room for improvement.
For example, the power conversion efficiency (PCE) of a photovoltaic cell under the standard radiation condition of the global air mass 1.5 (AM 1.5G) spectrum has a theoretical limit of 87% (concentrator cell).3 However, the highest record of PCE was 47% of 6-junction III–V tandem cells (concentrator cell) up to now.13 It is important to raise the PCE of photovoltaic cells high enough at a low cost for the future energy requirement of mankind. The key to getting high PCE is to synthesize a range of materials with high carrier mobilities and different energy gaps (the energy gap distribution or optical absorption bands should be narrow), covering the entire solar spectrum. The former mentioned 6-junction tandem cell has 140 materials with different energy gaps as photo absorption materials, electron transport materials and hole transport materials. Metal–organic chemical vapor deposition (MOCVD), the key technology to manufacture quality inorganic materials, is a high energy-consuming, high environment polluting, expensive and complex method. Besides, due to the limited variety of suitable chemical materials, these very high-cost cells may be already close to the limit of traditional material-based photovoltaic cells. The nano tuner-modified technology will raise PCEs of photovoltaic cells to the theoretical limit at a much lower cost.
Structure of nano tuners
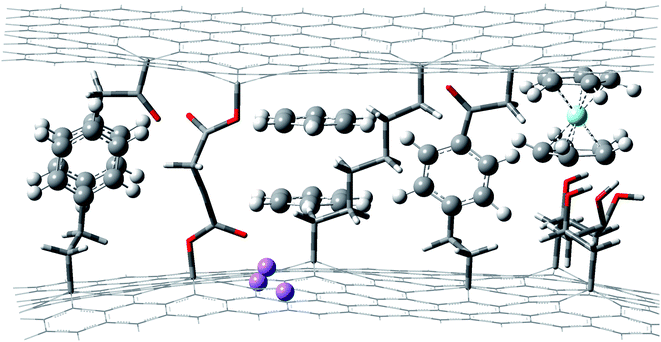
Strain dependence of the energy gap has been extensively and deeply studies. It is common sense in solid-state physics14,15 that strong interactions and weak interactions work together to determine the properties of materials. The strain of strong interactions16 and weak interactions17 would inevitably affect the properties of materials. We focused on the study of strains with weak interactions in this paper. Weak interaction depending on the energy gap, which is called the solvent effect in numerous cases, has been studied and applied in many fields.18 Isolated atoms or molecules have thread-like isolated energy levels, while crystals have wide energy bands. The differences in crystal energy bands compared to the isolated atom or molecule energy levels are mainly energy band broadening and red-shift, which are caused by the degeneracies of energy levels. The energy bandwidths are usually less than 100 meV. In the amorphous materials, the influence of the irregular atom or molecular environments on the energy levels generally conform to the Gaussian distribution, and the range of mean square deviation is 80–120 meV.19 We designed a nano tuner to tune the interactions imposed on the atoms or molecules precisely and continuously. The schematic structure of a nano tuner based on graphene is shown in Fig. 1.In Fig. 1, Li atoms, ferrocene complex and benzene molecules (including single benzene molecules and benzene dimers) are inserted between two graphene layers.10,23 Li atoms were absorbed into the graphene lattices. A benzene molecule is linked to both sides of the graphene layers by organic chains. A pair of benzenes is parallel to the graphene layers. Interaction between them and the graphene layers is π–π interaction. Another pair is linked to the graphene layers. The two graphene layers are linked by two organic chains, which are called molecular springs here. Some chemical groups (such as 2,3,3′,4 tetrahydroxy heptane in Fig. 1) can be attached to graphene layers to tune the environments of core materials or work as molecular recognizing sites. Nanocontainers and molecular springs have a wide range of options. Nanocontainers can be layered materials (such as graphene, MOFs, g-C3N4, and inorganic frame of perovskites20), nanotubes (such as carbon nanotubes, α-CuSCN nanotubes), nanospheres (such as C60 (ref. 12)), phospholipid bilayers, and others. Molecular springs can be almost any type as long as they can attach to nanocontainers without any ill effects on core materials. Bonding interactions between nanocontainers and molecular springs can be either strong interactions (such as covalent interactions) or weak interactions (such as hydrogen bonding interactions, π–π interactions, CH–π interactions, anion–π and coordination interactions).21 Interactions between the core material and nano container can be changed by replacing chemical groups between them.
Working principle of energy gap tuning
Weak interactions (π–π interaction here) imposed on the core material can be calculated. For most general cases, it is assumed that there is a certain number (n) of types of interactions, such as the carbon–carbon single bond, the carbon–nitrogen double bond, and π–π interactions, which is denoted by i. To a first approximation, bond energy is a quadratic function of the bond length, as the first nonzero term of Taylor series expansion for the Morse potential curve of a chemical bond is a quadratic term:
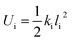 | (1) |
| Fi = kijyi,sj | (2) |
According to the balance of forces,
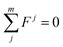 | (3) |
When the forces are balanced, the lengths of all the chains are the same.
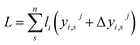 | (4) |
The change in the value of each interaction in each chain can be obtained from the above equations. Strain is defined to be: ε ≡ Δyi,sj/yi,sj. Tensile and compression correspond to positive and negative strains, respectively. The mole ratio of chains linked to both sides of the nanocontainer with and without core material is r. Then, we find that the strain imposed on the core material is a reverse ratio function of r. In principle, r can take any value in a certain range of positive rational numbers. It can be seen as continuous in practical applications, which means that weak interactions between the core material and nanocontainers can be tuned precisely and continuously. The properties of the material can be tuned precisely and continuously at the same time as a function of strain.
The bond energy of the C–C single bond is 82.9 kcal mol−1. The value of the benzene dimer π–π bond is 3.2 kcal mol−1. In a spring model, one straight chain molecule comprising eight C–C single bonds have a stiffness coefficient equal to about 7.7, which is parallel to the benzene dimers (π–π bond). Zavitsas investigated the relationship between C–C bond lengths (R) and their bond dissociation energies (BDEs) and reported an excellent linear relationship between R and BDEs, from which a maximum bond length of 0.1748 nm for an unsupported C–C single bond was predicted (BDE = 0 kcal mol−1).22 That means a corresponding strain of 13.5% since the average length of the C–C single bond is about 0.154 nm.
The above analysis is based on some idealized assumptions, such as the deformation of graphene layers is neglected. In practical design and calculation, the results of numerical simulation and experiment should be brought into consideration.
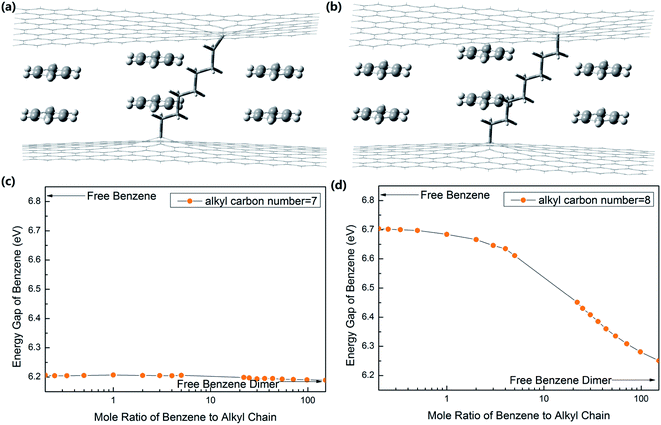
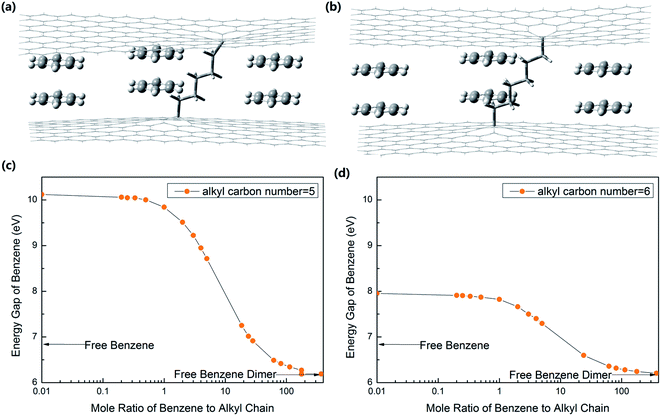
To show how nano tuners work, we took a simple case as an example. Nano tuners are alkyl chain-linked graphene layers,10,23 as shown in Fig. 2(a) and (b).
We calculated the interaction energy and bond length of the benzene dimer–graphene10,23 complex by Gaussian 09 (B97-D3/TZV(2d,2p)) with the counterpoise-corrected. The results agreed with other reported values.23 Then, we calculated the energy gaps of the system with different ratios of (CH2)82+, (CH2)72+, (CH2)62+ and (CH2)52+ groups, functioning as molecular springs (Gaussian 09, B3LYP/6-31++G(2d,2p)). The results are shown in Fig. 2 and 3.
The total energy and molecular distance curves of the graphene–benzene dimer system could be obtained by scanning the potential energy surface. Then, the graphene–single alkane chain system is scanned, and the relationship curve of energy with the graphene sheet distance is obtained. The equilibrium positions of the benzene dimer–graphene–alkane chain in any ratio of the benzene dimer to alkane chain can be obtained. The molecular structures of the benzene dimer–graphene system were optimized at each given equilibrium position one by one. Then, the graphene sheets are removed, and the energy level structures of optimized benzene dimers are then calculated. The results would be the energy structures of benzene dimers in graphene–alkane chain nano tuners.
Fig. 2(a) and (b) are the schematics of nano tuner-modified benzene dimers with molecule springs of (CH2)72+ and (CH2)82+, respectively. As shown in Fig. 2(c) and (d), the energy gaps of free benzene molecules and benzene dimers are 6.82 eV and 6.19 eV, respectively. The latter one being lower than the former one is a result of energy level degeneracy. When the molecule springs are (CH2)72+ and (CH2)82+, the strain applied to benzene dimers is tensile strain. Strain is so minute with a molecule spring of (CH2)72+. The energy gap of benzene molecules changes continuously in the range from 6.19 eV to 6.21 eV, with the mole ratio (Rm) of benzene dimers to (CH2)72+ springs changing from ∞ to 0. The corresponding ranges of value will be from 6.22 eV to 6.71 eV when the molecule springs are replaced with (CH2)82+, as shown in Fig. 2(d). When Rm is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the internal tensile strain in benzene dimers is about 27%, and the corresponding energy gap of benzene molecules is 6.68 eV. When Rm is 1
1, the internal tensile strain in benzene dimers is about 27%, and the corresponding energy gap of benzene molecules is 6.68 eV. When Rm is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22, the strain is about 10%, and the energy gap of benzene is 6.45 eV.
22, the strain is about 10%, and the energy gap of benzene is 6.45 eV.
The strain imposed on benzene molecules is compression when the carbon number of molecule springs is less than 6. As shown in Fig. 3(d), the energy gap of benzenes changes continuously in the range from 6.17 eV to 7.97 eV with Rm of benzene to (CH2)62+ springs changing from ∞ to 0. The energy gap of benzene is 10.13 eV, when Rm of benzene dimers to (CH2)52+ springs is 0, as shown in Fig. 3(c). The compression strain imposed on benzene continuously increases with the increase in Rm. The corresponding energy gap reduces steadily at the same time. When the strain becomes too large, the (CH2)52+ springs will break (BDE = 0 kcal mol−1) when Rm is as large as 177.40. The energy gap of benzene falls to about 6.19 eV, almost equal to the value of the benzene dimer.
The above results are all based on the numerical results of the Gaussian program. There are some very high values, such as the energy gap of benzene increasing to 10.13 eV, when Rm of benzene dimers to (CH2)52+ springs is 0. Although we are not sure whether these numerical simulation results are reliable, at least from the changing trend, the simulation results are in line with the theoretical law.
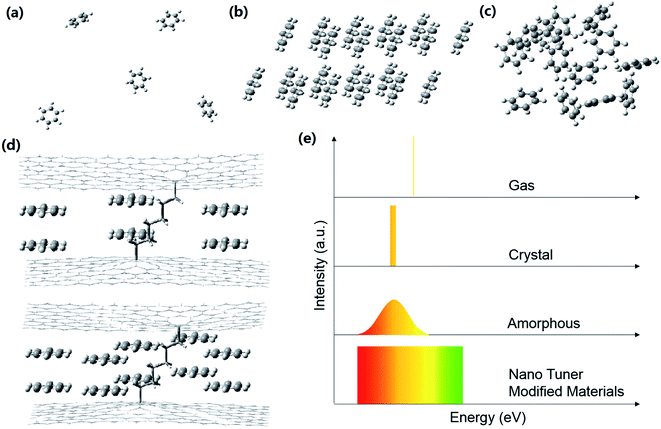
Fig. 4 shows differences in molecular environments and the corresponding absorption spectra of the same molecules in the gas, crystal, amorphous and nano tuner-modified materials. It is important to note that the absorption spectrum of nano tuner-modified materials is a superposition result of an almost infinite number of different thread-like absorption spectra. Each of the thread-like spectra corresponds to one or more nano tuner-modified materials. It is known that the absorption spectrum width of the same molecules in different condensates depends on the degree of degeneracy. The degeneracy of our nano tuner-modified benzene dimer is 2. The absorption spectrum width of other kinds of nano tuner-modified materials would be as narrow as that of molecular gas, according to the degree of degeneracy. The red- or blue-shift of the absorption spectrum can be tuned by changing the mole ratio of core materials to molecular springs precisely and continuously. Nano tuner-modified materials act like tunable molecule gases. Their tuning range is wider than the variation range of amorphous.
Discussion
We acknowledged that graphene, with a very narrow energy gap, will absorb most optical radiation injected into the above nano tuner-modified materials. Besides, the absorption spectra of the above materials fall out of the visible light region. This system is just a simplified example to show how the nano tuner works and its performance potential.Considering the fact that more than 99.9% energy of solar radiation AM 1.5G is in the range from 0.50 eV to 4.13 eV, we need only a few materials and their hundreds of nano tuner-modified derivatives to cover this spectrum. Then, photovoltaic cells with a PCE nearing 87% (concentrator cell) can be obtained. This is the first strategy that has the potential to reach the theoretical limits of photovoltaic cells. Besides, the synthesis of the nano tuner would be low cost because it can be synthesized by a solution process. In comparison, the manufacture of the inorganic multi heterojunction is highly difficult technically, high energy-consuming and environment-polluting. The application of nano tuner-based photovoltaic cells is of great promise.
Taking the application in the photovoltaic cell as an example, we showed the advantages of materials tuned by nano tuners. The results can be easily transplanted to numerous other fields, such as catalysis (include solar fuels, artificial photosynthesis and photocatalysis),24 electroluminescence,25–27 mechanoluminescence,28 thermoelectricity29 lithium batteries, hydrogen storage,30 superconductivity,31 magnetic materials,32 and drugs,33 since numerous studies have shown applications of strain on them. For example, aggregation-induced emission (AIE)34 and clusteroluminescence35 would have a new tool if a nano tuner was introduced because the two phenomena are the direct results of intermolecular interaction. In general, lasers are required for appropriate metastable energy levels to realize population inversion.36 Thermally activated delayed fluorescence (TADF) requires materials whose triplet of the first excited state is close to the singlet.37 Doping, lattice mismatch, molecular design and numerous other methods are applied to get competent materials. Now, we can achieve this goal in a simpler way.
In these researches, strains applied to the materials are mostly external strain and of minute values, thus greatly limiting the applications of strains on them. The strains in our proposed nano tuners are internal strains, with a big range of change. They can be easily and precisely tuned by changing the composition and proportion of molecule springs, causing the properties as a function of composition and proportion of molecule springs of materials to be changed precisely and continuously.
Tuning the properties of materials through internal strain has been researched and applied extensively in either inorganic materials or organic materials. However, these applications are limited. Our strategy using nano tuners to bring about internal strain is universal, robust and low cost. The proof of this strategy is based on ab initio calculations. The synthesis of nano container tuned materials still is a challenge. Other applications of this strategy remain to be explored.
Author contributions
C. Y. Liu designed the project, carried out the calculations, and wrote the paper. Y. Y. Hao and W. L. Li provided guidance and supervision. All authors contributed to the discussions of the results.Conflicts of interest
The authors declared that there were no competing interests.Acknowledgements
We acknowledge funding from the National Natural Scientific Foundation of China (U1710115, 61274056), the Key Research and Development (International Cooperation) Program of Shanxi (201603D421042), Platform and Base Special Project of Shanxi (201605D131038), and Shanxi Natural Scientific Foundation (201801D121097).References
- K. He, C. Poole, K. F. Mak and J. Shan, Nano Lett., 2013, 13, 2931–2936 CrossRef CAS.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- A. Marti and G. L. Araújo, Sol. Energy Mater. Sol. Cells, 1996, 43, 203–222 CrossRef CAS.
- B. Nabet, Photodetectors: materials, devices and applications in communications and imaging technologies, Elsevier Science & Technology, 2015 Search PubMed.
- P. Gorai, V. Stevanović and E. S. Toberer, Nat. Rev. Mater., 2017, 2, 17053 CrossRef CAS.
- X. R. Xu and M. Z. Su, Luminescence and luminescent materials, Chemical Industry Press, 2004 Search PubMed.
- R. Schlogl, Angew. Chem., Int. Ed., 2015, 54, 2–58 CrossRef.
- Nanotechnology for lithium-ion batteries, ed. Y. Abu-Lebdeh and I. Davidson, Springer Science & Business Media, 2012 Search PubMed.
- A. Züttel, Mater. Today, 2003, 6, 24–33 CrossRef.
- R. C. Haddon, Acc. Chem. Res., 1992, 25, 127–133 CrossRef CAS.
- K. H. J. Buschow and F. R. Boer, Physics of magnetism and magnetic materials, Kluwer Academic/Plenum Publishers, 2003 Search PubMed.
- P. Nguyen-Tri, T. O. Do, T. A. Nguyen and A. A. Assadi, Smart Nanocontainers, Elsevier, 2020 Search PubMed.
- J. F. Geisz, R. M. France, K. L. Schulte, M. A. Steiner and T. Moriarty, Nat. Energy, 2020, 5(4), 326–335 CrossRef CAS.
- Strain and its implications in organic chemistry: organic stress and reactivity, ed. A. De Meijere and S. Blechert, Springer Science & Business Media, 2012, vol. 273 Search PubMed.
- H. Jiang, P. Hu, J. Ye, K. K. Zhang, Y. Long, W. Hu and C. Kloc, J. Mater. Chem. C, 2018, 6, 1884–1902 RSC.
- Z. Dai, L. Liu and Z. Zhang, Adv. Mater., 2019, 31, 1805417 CrossRef CAS.
- J. Y. Lin, B. Liu, M. N. Yu, X. H. Wang, L. B. Bai, Y. M. Han, C. J. Ou, L. H. Xie, F. Liu, W. S. Zhu, X. W. Zhang, H. F. Ling, P. N. Stavrinou, J. P. Wang, D. D. C. Bradley and W. Huang, J. Mater. Chem. C, 2018, 6, 1535–1542 RSC.
- V. Antonov, B. Harmon and A. Yaresko, Electronic Structure and Magneto-Optical Properties of Solids, Springer Science & Business Media, 2004 Search PubMed.
- H. Bässler, Phys. Status Solidi B, 1981, 107, 9 CrossRef.
- C. L. Tan, X. H. Cao, X. J. Wu, Q. Y. He, J. Yang, X. Zhang, J. Z. Chen, W. Zhao, S. K. Han, G.-H. Nam, M. Sindoro and H. Zhang, Chem. Rev., 2017, 117, 6225–6633 CrossRef CAS.
- A. S. Mahadevi and G. N. Sastry, Chem. Rev., 2016, 116, 2775–2825 CrossRef CAS.
- A. A. Zavitsas, J. Phys. Chem. A, 2003, 107, 897–898 CrossRef CAS.
- E. Munusamy and S. E. Wheeler, J. Chem. Phys., 2013, 139, 094703 CrossRef.
- M. Luo and S. Guo, Nat. Rev. Mater., 2017, 2, 1–13 Search PubMed.
- H. Fukunaga, D. G. Fedorov, M. Chiba, K. Nii and K. Kitaura, J. Phys. Chem. A, 2008, 112, 10887–10894 CrossRef CAS.
- J. Cornil, D. Beljonne, D. A. D. Santos, J. P. Calbert, Z. Shuai and J. L. Brédas, C. R. Acad. Sci., Ser. IV: Phys., Astrophys., 2000, 1, 403–408 CrossRef CAS.
- M. Chen, J. Liu, F. Liu, H. Nie, J. Zeng, G. W. Lin, A. J. Qin, M. Tu, Z. K. He, H. H. Y. Sung, I. D. Williams, J. W. Y. Lam and B. Z. Tang, Adv. Funct. Mater., 2019, 29, 1903834 CrossRef.
- Z. Xie, T. Yu, J. Chen, E. Ubba, L. Wang, Z. Mao, T. T. Su, Y. Zhang, M. P. Aldreda and Z. G. Chi, Chem. Sci., 2018, 9, 5787–5794 RSC.
- W. Shi, T. Deng, G. Wu, K. Hippalgaonkar, J. S. Wang and S. W. Yang, Adv. Mater., 2019, 31, 1901956 CrossRef.
- M. Cason, The stress and strain behavior of materials for energy storage and production, Doctoral dissertation, The University of Illinois at Urbana-Champaign, 2015.
- M. Suda, Y. Kawasugi, T. Minari, K. Tsukagoshi, R. Kato and H. M. Yamamoto, Adv. Mater., 2014, 26, 3490–3495 CrossRef CAS.
- S. A. Safran and F. J. DiSalvo, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 4889 CrossRef CAS.
- A. Zhang, K. Jung, A. Li, J. Liu and C. Boyer, Prog. Polym. Sci., 2019, 101164 CrossRef CAS.
- Y. Chen, J. W. Lam, R. T. Kwok, B. Liu and B. Z. Tang, Mater. Horiz., 2019, 6, 428–433 RSC.
- H. Zhang, Z. Zhao, P. R. McGonigal, R. Ye, S. Liu, J. W. Lam, R. T. K. Kwok, W. Z. Yuan, J. P. Xie, A. L. Rogach and B. Z. Tang, Mater. Today, 2019, 32, 275–292 CrossRef.
- Tunable lasers handbook, ed. F. J. Duarte, Elsevier, 1996 Search PubMed.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2020 |