Open Access Article
Open Access ArticleEffect of the loading amount and arrangement of iodine chains on the interfacial thermal transport of carbon nanotubes: a molecular dynamics study†
Hanying Zou,
Yanhui Feng *,
Lin Qiu* and
Xinxin Zhang
*,
Lin Qiu* and
Xinxin Zhang
School of Energy and Environmental Engineering, University of Science and Technology Beijing, Beijing, 100083, China. E-mail: yhfeng@me.ustb.edu.cn; qiulin@ustb.edu.cn
First published on 15th December 2020
Abstract
Due to their excellent electrical and thermal conductivity properties, the nano-scale characteristics of carbon nanotubes (CNTs) are expected to be suitable for very large-scale integrated circuits and for next-generation micro interconnected devices. Consequently, CNT–metal composite materials have been widely researched, and have shown excellent performance in terms of thermal conductivity, electrical conductivity, thermal expansion, and adaptability to microelectronic devices. However, there are few studies on halogen–CNT composite materials with characteristics similar to CNT–metal composites, including regarding the remarkable electrical compatibility of the halogen and CNT and the large number of low-frequency phonons that are beneficial for thermal transport. In this work, iodine chains were considered to explore the halogen effect on CNTs. Variation of the interfacial thermal conductance of CNTs as a function of the iodine chains loading amount and arrangement was explored by a molecular dynamics method. The heat transfer mechanism was further analyzed based on the phonon state difference. This research is expected to provide a new pathway for the application of CNT composite materials in the field of next-generation microelectronics.
1. Introduction
With the development of device processing accuracy and the uniformity of semiconductor material doping, the bottleneck of metal interconnect devices represented by copper has become more and more obvious, due to the difficult device production process. The performance of metals deteriorates significantly at the micro-scale, whereas carbon nanotube assembly structures have great advantages at this scale. In addition to possessing high electrical conductivity, which is higher than that of copper, CNTs have excellent thermal conductivity, which can support good thermal management and heat dissipation. Another important aspect for CNTs is related to the unique characteristics of their solder and ability to work at high frequency. The nanosoldering technique involves a local heating of CNT fibers to generate crosslinked fibers.1,2 Based on this technology, various structures, including 2D networks and 3D cages, can be built by CNT fibers, and programmable circuits can be produced. Also, CNTs can work with high performance at high frequencies of 40 GHz or higher,3 which represent limitations in metals that cannot be overcome due to their nature. In addition, heat dissipation has become a major bottleneck restricting the development of electronic circuit technology, so CNTs offer promise in addressing this problem.In application, higher integration leads to a reduction in the heat dissipation area and an increase in components that produce heat, resulting in a high-density structure with a local heat flux of up to 300–1000 W cm−2.4–6 Hence, transferring heat effectively from the source component to the radiator, eliminating local hot spots, and achieving effective thermal management can improve the reliability and life of devices, and these also represent the bottleneck challenges for developing the next generation of microelectronics. However, the nanometer-scale size also hinders the current application of carbon nanotubes, and the assembly of materials based on CNTs is critical for the application of CNTs due to their larger scale size. Therefore, breaking through the performance degradation of CNT assembly structures and exploring the application of carbon nanotube assembly materials have attracted researchers' attention.
The control of the heat conduction between CNTs and metals has attracted researchers for a long time.7–13 For example, Xu et al.7 considered two cases where CNTs were embedded inside a copper block and adsorbed onto the copper surface. Xu reported that the unconventional high thermal conductivity between CNTs and metals confirmed their excellent compatibility. On the other hand, enhancing the energy transfer between metal nanoparticles and CNTs is also of great interest to researchers, owing to their facile preparation process and potential for large-scale industrial production.
The principle behind the energy transfer enhancement of metal guest particles between tubes is mainly based on the assembly of materials such as CNT fibers and thin films in most cases, and the weak coupling between the tubes is a determining factor in material performance. Therefore, strengthening the energy transfer between CNTs is a shortcut to greatly improving the performance of the assembled materials. Particles loaded between CNTs have been shown to lead to an amazing improvement in the thermal conductivity of nanofluids14,15 and in the infrared absorption of CNT thin films.16 Compared with the non-Ag-loaded material, a Ag-loaded nanopaper/glass fiber composite material prepared by Chu et al.16 showed a significantly reduced infrared emissivity at 3–5 mm. In terms of heat transfer, the CNT-based nanofluid prepared by Jha14 et al. show that its thermal conductivity could be increased by about 23% after loading metal particles compared with the CNT nanofluid. The increase in the specific surface area of nanoparticles in the fluid is an important reason for the increased heat transfer. Farbod et al.15 loaded 4 wt% Ag onto CNTs, and found the boundary scattering and heat flow resistance were reduced, enabling it to achieve an 8% thermal conductivity improvement compared to CNT nanofluids.
Interestingly, the interaction between halogens and CNTs also exhibits similar characteristics to the CNT–metal interaction, both of them strengthen the electrical conductivity of CNTs and aid the transport of numerous low-frequency phonons. This means that halogens can also regulate the performance of CNTs, allowing the CNT composite materials to meet the standards for application in electronic circuits. For example, iodine-doped double-walled CNT cables were prepared by Zhao et al.16 and could achieve an extremely high current-carrying capacity in the order of 104 to 105 A cm−2, and the change in the conductivity with temperature was five times smaller than that of copper. These results confirmed that CNT cables have the potential to replace copper cables. Recently, research on CNT–halogen composite materials has mainly focused on electrical aspects, and exploration of the thermal performance is rarely reported. Furthermore, exploration of the heat transport mechanism is currently performed mainly through Raman curve analysis, lacking an analysis based on the nature of the material and in-depth research at the most basic atomic level. Filho et al.17 prepared CNT composite materials with Br2 physical absorption on the CNT wall. The change of the G peak during the physical adsorption and desorption of Br2 on the surface with resonance Raman scattering showed that the loaded Br2 affected the surface carbon atoms' vibration, which affected the double phonon scattering process, whereas the structure of the carbon tube itself was not affected. Nascimento et al.18 placed CNTs in I2 vapor and Br2 vapor, respectively, to load halogen particles on the CNT surface. The change in the shape and position of the G peak confirmed that the loaded halogen affect the interfacial heat transfer of intertube.
Based on the similar characteristics of halogens and metal particles in their action on CNTs, and the enhancement effect of metal particles, in order to discover a new way to make CNTs applicable for next-generation microelectronic interconnect devices, it is important to explore the enhancement mechanism of the halogen particles effect on the CNTs, and to propose a new strategy to control the performance of CNTs. Therefore, this article takes iodine particles as an example to explore the thermal enhancement mechanism of the halogen's effect on the CNTs. The effects of the amount and arrangement of iodine particles on the interfacial heat transfer between CNTs were studied based on molecular dynamics (MD) simulations. The vibration density of states (VDOS) and phonon overlap energy were used to analyze the changes in the atomic vibration and phonon state during the heat transfer process, and to explore the induced effect of the loaded low-frequency vibration iodine particles on the interfacial carbon atoms and on the strengthening of the interface force. In addition, in the heat transfer process, we considered the non-planar curved surface heat transfer of the CNT interface and the thermal repeater function of the interfacial iodine chains, and proposed an additional heat transfer channel induced by iodine chains for analyzing the interfacial heat transfer.
2. Materials and methods
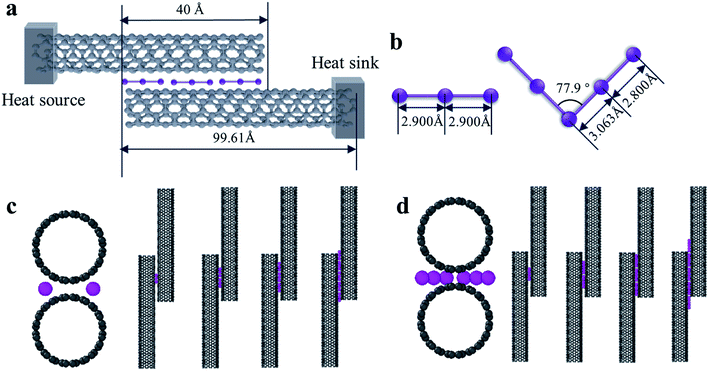
In order to ensure that the calculations were correct, we first established a model based on the related past reported research. Placing the carbon nanotube fibers in iodine vapor at a certain temperature can allow the iodine to be uniformly adsorbed on the surface of the CNTs while maintaining its structure.19 In other words, the iodine can penetrate deeply between the CNTs of the fiber as an intercalation structure. Through X-ray photoelectron spectroscopy, Raman spectroscopy, and UV-Vis-NIR optical absorption spectroscopy characterization of the experimental samples of CNT-I, it was observed that I3− and I5− chains were the main forms of iodine on the surface of the CNTs.20,21 Hence, we built a calculation model for loading I3 and I5 between the tubes. The loaded I3− particles had a linear structure with a bond length of 2.9 Å,22 while the I5− particles had a symmetrical V-shaped structure with an inclusion angle of 77.9°. The bond lengths from the center of symmetry to both sides were 3.063 and 2.800 Å, respectively.23In the simulation, the interfacial thermal conductance between two CNTs was calculated, which represented armchair CNTs with a chirality of (10,10), length of 99.61 Å, and the C–C bond length of 1.42 Å. The spacing between the two CNTs was 3.4 Å with an overlap length of about 40 Å and the iodine chains were loaded at the groove of the interface of two CNTs. A schematic diagram of the calculation models is shown in Fig. 1a, c and d. The iodine chains were placed in the vertical axial interface and the number of chains was continuously increased in the axial direction to explore the effect of different loadings on the interfacial heat transfer (Fig. 1c and d).
In order to accurately simulate the atomic interactions of CNTs, the adaptive intermolecular reactive empirical bond order (AIREBO) potential24 has been used to describe the bonding force and the non-bonding van der Waals force of carbon atoms. This potential function has been widely applied in the thermal transport state of CNTs.25,26 The iodine atom was described by a universal force field (UFF),27 and its bond effect was used in the form of a Morse potential function.28,29 The non-bonding forces between iodine chains and between iodine chains and CNTs could be described by 12–6 Lennard–Jones potentials,30 and its parameters were calculated using the Lorentz–Berthelot combination rules.31 All the thermal conductance calculations were performed by NEMD simulations based on Fourier's law using LAMMPS software.32
In the calculation models, two narrow layers were sited at the end of two CNTs that were near the boundaries while the carbon atoms in the layers were fixed as walls, so that the atoms did not move during the entire simulation. Next to the fixed walls, there was a heat source and heat sink region and the temperature was set at 320 K and 280 K, respectively, and the temperature difference was 40 K. The temperatures of the heat source and heat sink were controlled by a Nosé–Hoover thermostat (NVT).33 The heat flow for the calculation cell was generated from a high-temperature heat source and flowed to the heat sink through the overlap interface of two CNTs. The settings for the heat bath were reported in previous papers34,35 to avoid the additional influence of the heat bath, which enabled studying the variation of the thermal conductivity as a function of the position and length of the heat bath. In order to calculate the interface temperature difference, the whole cell was partitioned axially into 16 slabs for recording the temperature of each CNT, and the temperature of the atoms in each slab were averaged every N ps. The unit length interfacial thermal conductance (G) is defined by 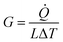 which is based on Fourier's law, where J is the heat flux, L is the overlap length of two CNTs, and ΔT is the temperature difference of the overlap interface. Due to the establishment of a temperature gradient, the influence of the initial atomic velocity was eliminated and so did not need to be considered.
which is based on Fourier's law, where J is the heat flux, L is the overlap length of two CNTs, and ΔT is the temperature difference of the overlap interface. Due to the establishment of a temperature gradient, the influence of the initial atomic velocity was eliminated and so did not need to be considered.
In order to explore the mechanism of the iodine chain boosting the heat transfer at the CNT interface, the VDOS was calculated to show the changes in the atomic vibration frequency and phonon mode in the system. The VDOS was calculated by Fourier transform of the atomic velocity autocorrelation function (VACF).36–38 Also, for the phonon mode of frequency v, VDOS was defined as follow:
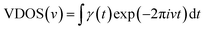 | (1) |
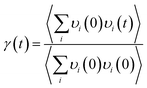 | (2) |
The matching degree between the VDOS is the main mechanism that affects the transport and scattering of phonons. The degree of matching between the two atomic VDOS can be quantitatively expressed by the overlap energy. The phonon overlap energy is calculated by using the frequency integration of the overlapping area, which is the overlapping vibrational dynamic density of the two types of atoms. The overlap area means there are a number of phonons at the same frequency, which enables efficient energy transfer since the closer the atoms' vibrations, the easier the energy transfer between them. The overlap energy is defined as follows:39
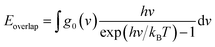 | (3) |
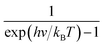 represents the Bose–Einstein distribution.
represents the Bose–Einstein distribution.
3. Results and discussion
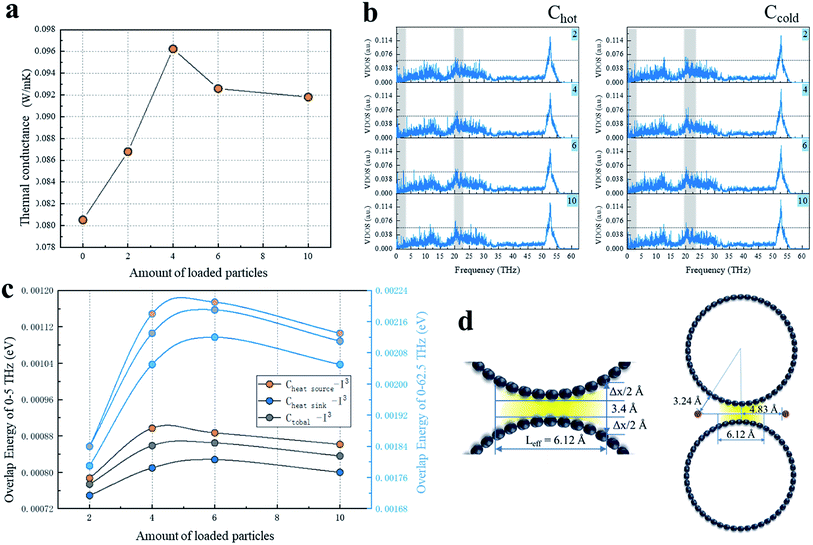
We calculated for the overlapping CNTs' system that the groove of the CNTs interface was loaded with I3− chains numbering 2, 4, 6, 10 (Fig. 2a). It could be observed that G showed a marked rise until it peaked at 4 chains loaded and then slightly decreased with the increasing number of iodine chains loaded. Moreover, the G values of all the iodine-loaded systems were higher than their no-loaded counterparts. In order to investigate the mechanism behind the enhancement of G, the VDOS of the overlapped carbon atoms was calculated to analyze the phonon motion difference in the heat transfer process with all the loaded and non-loaded CNT systems.For the interfacial carbon atoms (Chot) belonging to the CNT system that included a heat source and the other that was Ccold, the VDOS results of Chot and Ccold of I3− chains of the loaded on cases are illustrated in Fig. 2b. With the increase in the amount of I3− chains loaded, the VDOS of Chot for the six-I3− chains system was high and concentrated in the low-frequency of 0–3 THz, while second was the four-I3− chains case with a small concentration that appeared at 1 THz. The system with the decorated amount of 10 chains had the lowest concentration of phonons at the low-frequency portion of 0–3 THz, while a significantly high peak appeared at 20–23 THz, which indicated that the atomic vibrations of Chot were significantly blue-shifted, which means that the atoms as a whole tended to vibrate at a higher frequency. For the phonon density of state of Ccold, in the frequency of 0–3 THz, the 4-loaded system was significantly stronger than the other systems, followed by the system with 2 and 10 chains loaded for the relatively dense phonon state. Additionally, the 6-loaded case had fewer phonons in this band, but it was slightly stronger than the 2- and 10-loaded chains systems at 20–24 THz.
It is known that the long wavelength of low-frequency phonons results in a higher heat transfer capacity than that of high-frequency short-wave phonons. Therefore, it can be seen from the results of the existing VDOS that the low-frequency phonon states clearly had an advantage over other systems when the loaded amount was 4 since that case had the strongest phonon state density and heat transport capacity. In order to further clarify the heat transfer differences with the other three loaded systems, we calculated the phonon overlap energy of the four loaded systems at 0–5 THz and 0–62.5 THz, respectively, and compared the phonon energy between the systems to evaluate the phonon mismatch level in a semi-quantitative way.
The overlap energy of C–I of all the I3− chains-loaded systems in the range of 0–5 THz and 0–62.5 THz are shown in Fig. 2c. The two diagrams show a similar variation of the VDOS as a function of frequency, with a little amplitude of the changes. Due to the few introduced chains, there were fewer carbon atoms available to vibrate at lower frequency resonated by iodine chains, and these carbon atoms vibrated at a lower frequency, which was close to the frequency of iodine, resulting in the low C–I phonon matching level in the 2-chains-loaded system. In addition, with the increasing number of loaded iodine chains, the more carbons atoms were resonated by iodine chains and the more atoms (carbon and iodine atoms) vibrated at close frequencies, resulting in the higher C–I phonon matching level. Therefore, the maximum capacity in the axial direction between the CNTs was approached by the introduction of 6 chains, and thus the 6-loaded system showed the highest phonon matching degree of C–I. When the loaded iodine chain number was increased to 10, part of the I3− chains located at the end of the CNTs overlap the interface and can affect the atoms on the edge of the CNTs' overlap. The positive induction effect of the edge atoms was very limited due to the slight resonance induction being limited to only a few carbons and it was greatly inferior to that of the iodine chains in the middle position. However, the phonon scattering effect caused by heteroatoms was not reduced, resulting in a decrease in low-frequency phonons and a decrease in the matching level. In addition, in the 0–5 THz region, the system with a loading of 4 was equivalent to the 6-loaded system, and neither Chot–I nor Ctotal–I in the 4-loaded system was weaker than in the 6-loaded system. In the 0–62.5 THz region, the system with the loading of 4 was inferior to the 6-loaded system, which indicated a stronger effect on the low-frequency carbon atoms from the introduced iodine, while the phonon scattering caused by heterogeneous iodine atoms mainly occurs at higher frequencies.
In addition to introducing low-frequency phonons and inducing carbon atom resonance, more importantly, the iodine chains can also serve as effective thermal repeaters for the interfacial heat transfer. Different from the normal interfacial heat transfer, the CNT interface is composed of two curved surfaces instead of planes. Due to the variation of the interface distances, the intertube non-bonding forces is a function of the distance and there is a great difference in the intertube strength. When the distance increases from the equilibrium distance of 3.4 Å, the van der Waals force can rapidly decrease. When the distance is increased by 1 Å, its effect can be reduced by half.40 Hence, the effect of the interface distance changes on the heat transfer cannot be neglected. Based on a continuous model of the binding energy between two parallel CNTs,41 the surface area of the attraction curve above the reduced equilibrium distance was integrated to obtain the normalized intertube distance. Then the effective separation of the van der Waals force of the (10,10) chiral CNTs in this work was calculated as Δx = 1.46 Å, and the corresponding effective action length between the tubes was Lefftive = 6.12 Å (Fig. 2d). It can be considered that beyond the effective length, the corresponding excessively high separation interface causes the heat flow to dissipate in a vacuum and thus it cannot be transferred to another CNT.
In this study, the chains were placed 4.83 Å from the center line of the two CNTs, which was greater than 1/2Lefftive, and the corresponding distance of iodine from the CNTs was 2.98 Å and within the van der Waals force range of C–I (Fig. 2d). The introduced iodine chains acted as a thermal repeater at the interface and created an additional heat transfer channel, so that the heat flow that could not be transmitted through the C–C path was transmitted to the destination through C–I–C. With the increase in the loading, the increasing number of heat transfer channels caused an enhancement in the heat transfer capability, and the interface thermal conductance reached a peak when the loading was 4. With further increasing the loaded chains, the additional thermal channel effect of the newly introduced I3− chains was weaker than the phonon scattering effect, so G then began to decrease. The slowdown in the increase of the overlap energy also proved the effect of scattering. When the number of loaded iodine chains was 10, only a small part of the iodine chains was at the overlapping interfacial edges, and the repeater effect was effectively powerless, while the newly introduced phonon scattering was not weakened, so G was slightly lower than in the case of the 6-loaded system.
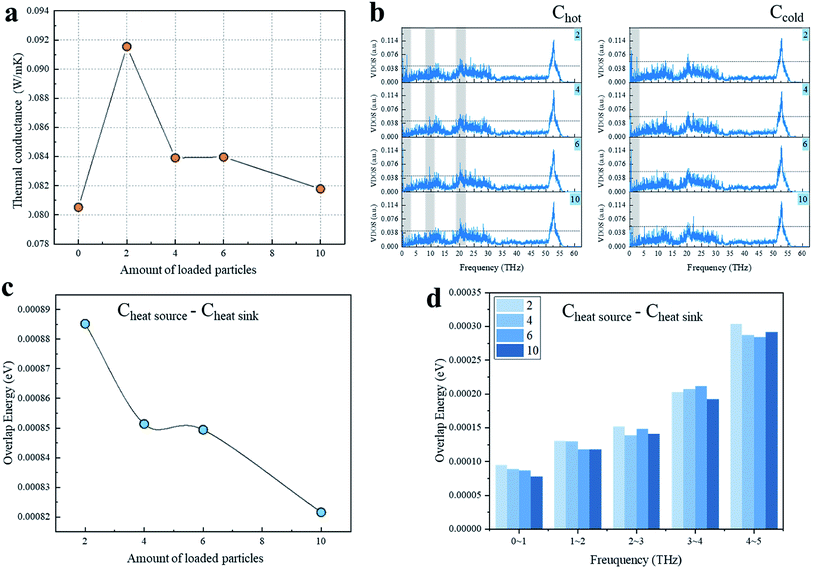
Currently, the iodine-loaded CNT samples obtained in the experiments generally contained I3− and I5− chains, so we also explored the enhancement effect of I5− chains loaded at the CNTs' interface (Fig. 3). Fig. 3a shows the variation of G of the CNT interface as a function of the number of I5− chains loaded. It can be clearly seen that after I5− chains were added between the CNTs, G increased sharply and then decreased significantly, and the difference between I3− and I5− chains was obvious, which may be due to the differences in the structure and volume of the chains. In order to investigate the mechanism for the thermal conductance difference, the VDOS of the overlapping carbon atoms was obtained (Fig. 3b). As can be observed in this plot, the VDOS of the Chot and Ccold of the system with 2-loaded chains were highly concentrated in the low-frequency part of 0–3 THz, resulting in a strong interatomic heat transfer. For the VDOS of the hot-end carbon atoms, there was no significant difference in the low-frequency region among the 4-, 6-, and 10-loaded chains systems, where their phonon modes were mainly located at 0–3 THz, while their higher frequency part showed a blue-shift of the vibration frequency as the loading amount increased. For example, the peaks around 10 THz for the 4- and 6-loaded systems did not appear in the 10-loaded chains system, but the strength of the VDOS peak around 20 THz followed the order: 10 > 6 > 4.
Since the long-wave phonon mode dominates heat transfer, the overlap energy of the Chot–Ccold from 0 to 5 THz and the overlap energy of each frequency segment are important and are shown in Fig. 3c and d. As can be observed from Fig. 3c, with the loaded amount increasing, the overlap energy decreased as per the stepped curve, and the variation trend was very close to the interfacial thermal conductance shown in Fig. 3a. Fig. 3d illustrates a comparison between the overlap energy and the loading number of iodine chains. It can be seen that as the loading amount increased, the more atoms tended to vibrate at lower frequency. Unlike other examples, the overlap energy of the 10-loaded chains case was lower than for the others, which may be caused by the shape of I5− chains. Although the placement position distance between I5− chains and CNT is smaller than for the I3− chains, where the distance range was 1.88–3.90 Å for I5− chains and 2.98 Å for I3− chains, only a part of the I5− chains can directly receive and transfer heat as a repeater, and it cannot make the entire chain act as an effective heat transfer medium. Moreover, due to the large chain weight, the scattering effect introduced by I5− is more significant. In short, the interfacial heat transport increased significantly when the first two I5− chains were introduced, and then decreased significantly when more chains were introduced.
According to the calculation results for the I3− and I5− cases, the number and distribution of iodine chains have an obvious effect on the thermal transport of the interface. Therefore, we used I3− chains as an example to illustrate its effect on the interface heat transfer. These models and the thermal conductance of the three cases are summarized in Fig. 4. The distance to the center I3− chains was 2.98 Å according to the CNT, the upper and lower distance was 3.04 Å and the distance between the chains with each other was 3.5 Å. In the system, besides the original C–C path to transfer heat flow, additional C–I–C and C–I–I–C channels were added for heat transfer in the system with three chains on each side, while the system with one molecule on both sides only added C–I–C channels.
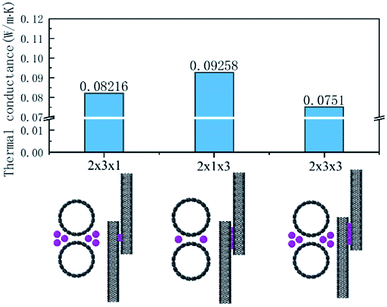 | ||
| Fig. 4 Thermal conductance of the three cases with the iodine arrangements: 2 × 3 × 1, 2 × 1 × 3, and 2 × 3 × 3. | ||
Comparing the calculations for the same numbers of chains, as shown in Fig. 4, the heat transfer of the 2 × 1 × 3 arrangement of single chains on both sides was slightly higher than that for the 2 × 3 × 1 arrangement of the three chains on each side. The worst heat transfer case was the 2 × 2 × 3 arrangement case, where there were three chains on each side and three groups of chains in the axial direction. As can be observed from Fig. 5 regarding the VDOS of Chot, the 2 × 1 × 3 case had a large number of phonon states at 0–5 THz, while the phonon mode in the 2 × 3 × 1 case was rigid and more low-frequency shifted to 7–13 THz, and a blue-shift of the phonon mode was more significant in the 2 × 3 × 1 case, whereby fewer low-frequency and strong peaks were found at 18–25 THz. For the VDOS of Ccold, the results showed that the difference between the three cases was small. The greater the number of atoms along the axis of the CNT, the more carbon atoms there are that tend to vibrate at higher frequencies. For instance, the 2 × 3 × 3 had less phonons at 0–3 THz than the 2 × 3 × 1 case, and a more intense VDOS appeared at 4–8 THz. When the chains on both sides were increased, the phonon scattering effect was more obvious. The 2 × 1 × 3 case was more concentrated at low frequencies; for example, the 0–3 THz part was relatively flat, while the 2 × 3 × 1 and 2 × 3 × 3 cases had obvious grooves and a higher phonon mode appeared at 10–13 THz.
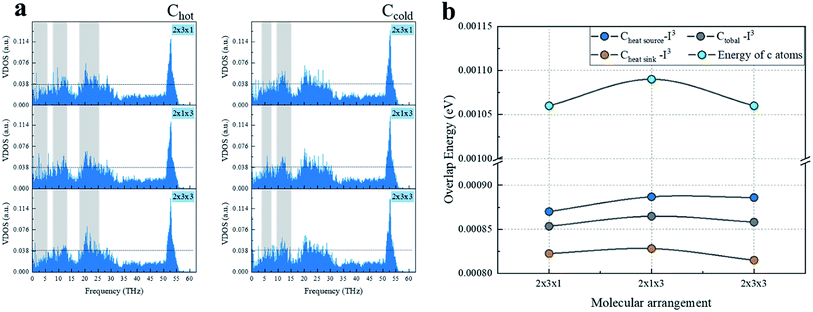 | ||
| Fig. 5 Heat transfer mechanism calculation of the three arrangement cases: (a) VDOS of carbon atoms of CNT with a heat source and heat sink, (b) phonon overlap energy and atomic energy. | ||
Further, comparing the overlap energy at 0–5 THz of C–I atoms and the energy of C atoms, it can be seen that the energy of carbon atoms in the 2 × 1 × 3 system was the highest, and when the chains on both sides were further increased (2 × 3 × 1 and 2 × 3 × 3 cases), the introduced heteroatoms reduced the atomic power energy. The overlap energy of C–I and the low overlap energy of the 2 × 3 × 3 case showed that the heterogeneous effect of the additional I3− chains on both sides was far greater than from the resonance induction of CNT atoms. As more I3− chains were added along the axis, a more negative effect was produced. From all the results of VDOS and the overlap energy discussed above, it is clear that for the 2 × 3 × 1 and 2 × 3 × 3 cases of three chains on both sides of the CNT@(10,10), the amount of atoms exceeded the effective capacity of this CNT. That resulted in carbon atoms resonance by the iodine chains being far away from the effective interface, and thus the enhancement of heat transfer energy was mainly transmitted through the C–I–I–C path, which was weaker than the C–I–C path; while along the axial unit length, the heterogeneous atom scattering effect resulted from the atomic mass and vibration mismatch, where the phonon scattering of the 2 × 3 × 1 arrangement was twice as high as that of the 2 × 1 × 3 arrangement.
4. Conclusion
In this work, the thermal conductance of the two-CNTs' interface showed a tendency to increase to a peak first and then decreased as the loading increased, owing to the additional heat channels and greater low-frequency phonon mode brought about by the loaded iodine chains. Unlike planar surfaces, the heat transfer of a curved interface is limited in a certain range since the farther from the center, the greater the distance. This work calculated the effective transfer distance of CNT@(10,10) based on the interfacial force and this value was 6.12 Å. Placing the iodine chains outside the original heat transfer length of the CNT interface and a C–I distance less than the van der Waals force ensure energy transfer will happen. The part of the heat flow that is out of the CNT effective range at 6.12 Å can be transferred to the other side through the C–I–C and C–I–I–C paths, so that more heat is transferred by the additional channels. Furthermore, iodine chains with a low-frequency phonon mode and induced carbon atoms tend to vibrate at a lower frequency to transfer more heat flow. Also, the heat transfer benefit brought about by a small amount of iodine loading can completely offset the phonon scattering caused by its heteroatoms effect. In this work, based on the effective range of the non-bonding force between carbon nanotubes, we raised concerns about additional thermal channels, and proposed an analysis method for interfacial heat transfer enhancement by tuning the arrangement of the particles. In addition, the results of the CNT-I calculation can provide a theoretical basis for the thermal design of CNT fibers and films. This work also provides new ideas for the design and application of CNT assemblies, and proposes the possibility of applying CNT–iodine materials to electronic circuits.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key R&D Program of China (No. 2018YFA0702302), National Natural Science Foundation of China (No. 51876007 and 51876008), Beijing Natural Science Foundation (No. 3202020), Interdisciplinary Research Project for Young Teachers of USTB (Fundamental Research Funds for the Central Universities) (No. FRF-IDRY-19-004) and Fundamental Research Funds for the Central Universities (No. FRF-TP-19-002B2).References
- J. Do, D. Estrada, X. Xie, N. N. Chang, J. Mallek and G. S. Girolami, et al., Nanosoldering Carbon Nanotube Junctions by Local Chemical Vapor Deposition for Improved Device Performance, Nano Lett., 2013, 13, 5844–5850, DOI:10.1021/nl4026083.
- J. Zou, X. Zhang, C. Xu, J. Zhao, Y. T. Zhu and Q. Li, Soldering carbon nanotube fibers by targeted electrothermal-induced carbon deposition, Carbon, 2017, 121, 242–247, DOI:10.1016/j.carbon.2017.05.091.
- C. Brun, C. C. Yap, D. Tan, S. Bila, S. Pacchini and D. Baillargeat, et al., Flip Chip Based on Carbon Nanotube–Carbon Nanotube Interconnected Bumps for High-Frequency Applications, IEEE Trans. Nanotechnol., 2013, 12, 609–615, DOI:10.1109/TNANO.2013.2264534.
- R. Mahajan, C. Chiu and G. Chrysler, Cooling a Microprocessor Chip, Proceedings of the IEEE, 2006, 94, 1476–1486, DOI:10.1109/JPROC.2006.879800.
- R. S. Prasher, J. Chang, I. Sauciuc, S. Narasimhan, D. Chau and G. Chrysler, et al., Nano and Micro Technology-Based Next-Generation Package-Level Cooling Solutions, Intel Technology Journal, 2005, 9, 285–296, DOI:10.1535/itj.0904.03.
- W. Haensch, E. J. Nowak, R. H. Dennard, P. M. Solomon, A. Bryant and O. H. Dokumaci, et al., Silicon CMOS devices beyond scaling, IBM J. Res. Dev., 2006, 50, 339–361, DOI:10.1147/rd.504.0339.
- Z. Xu and M. J. Buehler, Nanoengineering Heat Transfer Performance at Carbon Nanotube Interfaces, ACS Nano, 2009, 3, 2767–2775, DOI:10.1021/nn9006237.
- L. Qiu, H. Zou, X. Wang, Y. Feng, X. Zhang and J. Zhao, et al., Enhancing the interfacial interaction of carbon nanotubes fibers by Au nanoparticles with improved performance of the electrical and thermal conductivity, Carbon, 2019, 141, 497–505, DOI:10.1016/j.carbon.2018.09.073.
- L. Qiu, H. Zou, N. Zhu, Y. Feng, X. Zhang and X. Zhang, Iodine nanoparticle-enhancing electrical and thermal transport for carbon nanotube fibers, Appl. Therm. Eng., 2018, 141, 913–920, DOI:10.1016/j.applthermaleng.2018.06.049.
- L. Qiu, N. Zhu, Y. Feng, E. E. Michaelides, G. Zyła and D. Jing, et al., A review of recent advances in thermophysical properties at the nanoscale: From solid state to colloids, Phys. Rep., 2020, 843, 1–81, DOI:10.1016/j.physrep.2019.12.001.
- L. Qiu, K. Scheider, S. A. Radwan, L. S. Larkin, C. B. Saltonstall and Y. Feng, et al., Thermal transport barrier in carbon nanotube array nano-thermal interface materials, Carbon, 2017, 120, 128–136, DOI:10.1016/j.carbon.2017.05.037.
- L. Qiu, P. Guo, Q. Kong, C. W. Tan, K. Liang and J. Wei, et al., Coating-boosted interfacial thermal transport for carbon nanotube array nano-thermal interface materials, Carbon, 2019, 145, 725–733, DOI:10.1016/j.carbon.2019.01.085.
- C. Subramaniam, Y. Yasuda, S. Takeya, S. Ate, A. Nishizawa and D. Futaba, et al., Carbon nanotube-copper exhibiting metal-like thermal conductivity and silicon-like thermal expansion for efficient cooling of electronics, Nanoscale, 2014, 6, 2269–2674, 10.1039/c3nr05290g.
- N. Jha and S. Ramaprabhu, Thermal conductivity studies of metal dispersed multiwalled carbon nanotubes in water and ethylene glycol based nanofluids, J. Appl. Phys., 2009, 106, 083417, DOI:10.1063/1.3240307.
- M. Farbod and A. Ahangarpour, Improved thermal conductivity of Ag decorated carbon nanotubes water based nanofluids, Phys. Lett. A, 2016, 380, 4044–4048, DOI:10.1063/1.3240307.
- H. Chu, Z. Zhang, Y. Liu and J. Leng, Silver particles modified carbon nanotube paper/glassfiber reinforced polymer composite material for high temperature infrared stealth camouflage, Carbon, 2016, 98, 557–566, DOI:10.1016/j.carbon.2015.11.036.
- Y. Zhao, J. Wei, R. Vajtai, P. M. Ajayan and E. V. Barrera, Iodine doped carbon nanotube cables exceeding specific electrical conductivity of metals, Sci. Rep., 2011, 1, 83, DOI:10.1038/srep00083.
- A. G. Filho, M. Endo, H. Muramatsu, T. Hayashi, Y. A. Kim and E. B. Barros, et al., Resonance Raman scattering studies in Br2-adsorbed double-wall carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235413, DOI:10.1103/PhysRevB.73.235413.
- G. M. do Nascimento, T. Hou, Y. A. Kim, H. Muramatsu, T. Hayashi and M. Endo, et al., Behavior of the high frequency Raman modes of double-wall carbon nanotubes after doping with bromine or iodine vapors, Carbon, 2011, 49, 3585–3596, DOI:10.1016/j.carbon.2011.04.061.
- Y. Zhao, J. Wei, R. Vajtai, P. M. Ajayan and E. V. Barrera, Iodine doped carbon nanotube cables exceeding specific electrical conductivity of metals, Sci. Rep., 2001, 1, 00083, DOI:10.1038/srep00083.
- A. A. Tonkikh, E. D. Obraztsova, E. A. Obraztsova, A. V. Belkin and A. S. Pozharov, Optical spectroscopy of iodine-doped single-wall carbon nanotubes of different diameter, Phys. Status Solidi B, 2012, 249, 2454–2459, DOI:10.1002/pssb.201200153.
- K. N. Robertson, T. S. Cameron and O. Knop, Polyhalide anions in crystals. Part 2. I3-asymmetry and N—H⋯I bonding: triiodides of the Me2NH2+, Ph2I+, tropanium, N,N,N′,N′-Me4-1,2-ethanediammonium, N,N,N′,N′-Me4-1,3-propanediammonium, N-Me-piperazinium(2+), and N,N′-Me2-piperazinium(2+) cations, and Me2NH2I, Can. J. Chem., 1996, 74, 1572–1591, DOI:10.1139/v96-174.
- K. F. Tebbe and R. Buchem, Studies on polyhalides. 30 - On decamethylferriciniumpolyiodides [(Me5C5Fe]Ix with x=3, 5, 6.5: preparation and crystal structures of a triiodide (DMFc)I3, a pentaiodide (DMFc)I5 and a hexacosaiodide (DMFc)4I26, Z. Anorg. Allg. Chem., 1998, 624, 671–678 Search PubMed.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, A reactive potential for hydrocarbons with intermolecular interactions, J. Chem. Phys., 2000, 112, 6472–6486, DOI:10.1063/1.481208.
- A. M. Marconnet, M. A. Panzer and K. E. Goodson, Thermal conduction phenomena in carbon nanotubes and related nanostructured materials, Rev. Mod. Phys., 2013, 85, 1295–1326, DOI:10.1103/RevModPhys.85.1295.
- L. Zhu and B. Li, Low thermal conductivity in ultrathin carbon nanotube (2, 1), Sci. Rep., 2015, 4, 4917, DOI:10.1038/srep04917.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skid, UFF, a Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations, J. Am. Chem. Soc., 1992, 114, 10024–10039 Search PubMed.
- P. M. Morse, Diatomic Molecules According to the Wave Mechanics II. Vibrational Lavels, Phys. Rev., 1929, 34, 57–64 Search PubMed.
- R. D. Verma, Ultraviolet Resonance Spectrum of the Iodine Molecule, J. Chem. Phys., 1960, 32, 738–749, DOI:10.1063/1.1730793.
- J. E. Lennard-Jones, On the Determination of Molecular Fields, Proc. R. Soc. London, Ser. A, 1924, 106, 463–477, DOI:10.1098/rspa.1924.0082.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, New York, 1989 Search PubMed.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19, DOI:10.1006/jcph.1995.1039.
- D. J. Evans and B. L. Holian, The Nose–Hoover thermostat, J. Chem. Phys., 1985, 83, 4069–4074, DOI:10.1063/1.449071.
- R. N. Salaway and L. V. Zhigilei, Molecular dynamics simulations of thermal conductivity of carbon nanotubes: Resolving the effects of computational parameters, Int. J. Heat Mass Transfer, 2014, 70, 954–964, DOI:10.1016/j.ijheatmasstransfer.2013.11.065.
- J. Shiomi and S. Maruyama, Molecular dynamics of diffusive-ballistic heat conduction in single-walled carbon nanotubes, Jpn. J. Appl. Phys, 2008, 47, 2005–2009, DOI:10.1143/JJAP.47.2005.
- T. Coquil, J. Fang and L. Pilon, Molecular dynamics study of the thermal conductivity of amorphous nanoporous silica, Int. J. Heat Mass Transfer, 2011, 54, 4540–4548, DOI:10.1016/j.ijheatmasstransfer.2011.06.024.
- G. Balasubramanian, I. K. Puri, M. C. Böhmb and F. Leroy, Thermal conductivity reduction through isotope substitution in nanomaterials: predictions from an analytical classical model and nonequilibrium molecular dynamics simulations, Nanoscale, 2011, 3, 3714–3720, 10.1039/C1NR10421G.
- X. Zhang, M. Hu, K. Giapis and D. Poulikakos, Schemes for and Mechanisms of Reduction in Thermal Conductivity in an nanostructured Thermoelectrics, J. Heat Transfer., 2012, 134(10), 102402, DOI:10.1115/1.4006750.
- X. Zhang, M. Hu and D. Tang, Thermal rectification at silicon/horizontally aligned carbon nanotube interfaces, J. Appl. Phys., 2013, 113, 194307, DOI:10.1063/1.4804071.
- B. I. Yakobson and L. S. Couchman, Persistence Length and Nanomechanics of Random Bundles of Nanotubes, J. Nanopart. Res., 2006, 8, 105–110 Search PubMed.
- L. A. Girifalco, M. Hodak and R. S. Lee, Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 13104, DOI:10.1103/PhysRevB.62.13104.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra06870e |
| This journal is © The Royal Society of Chemistry 2020 |