First-principles study of structural, elastic and electronic properties of naphyne and naphdiyne

Abstract

The structural, elastic and electronic properties of 2D naphyne and naphdiyne sheets, which consist of naphthyl rings and acetylenic linkages, are investigated using first-principles calculations. Both naphyne and naphdiyne belong to the orthorhombic lattice family and exhibit the Cmmm plane group. The structural stability of naphyne and naphdiyne are comparable to those of experimentally synthesized graphdiyne and graphtetrayne, respectively. The increase of acetylenic linkages provides naphdiyne with a larger pore size, a lower planar packing density and a lower in-plane stiffness than naphyne. Naphyne is found to be an indirect semiconductor with a band gap of 0.273 eV, while naphdiyne has no band gap and has a Dirac point. The band gaps of naphyne and naphdiyne are found to be modified by applied strain in the elastic range. These facts make naphyne and naphdiyne potential candidates for a wide variety of membrane separations and for fabrication of soft and strain-tunable nanoelectronic devices.

---

1 Introduction

It is well known that carbon has three different hybridizations (i.e., sp, sp² and sp³). This leads to the formation of different covalent bonds between carbon atoms, resulting in a wide variety of carbon allotropes.¹ In nature, carbon basically exists in the form of diamond or graphite, containing sp³ or sp² hybridized carbon atoms, respectively. Moreover, some novel carbon allotropes, such as C₆₀,² carbon nanotubes (CNTs),³ and graphene⁴ have been successfully synthesized since the 1980s. Typically, graphene is the first fabricated 2D carbon allotrope. Graphene consists of benzene rings forming a monolayer structure. That makes graphene have very high in-plane strength and excellent electron mobility.^5,6 Since graphene was successfully synthesized by Geim and Novoselov et al.⁴ using a micro-mechanical stripping method in 2004, it has rapidly become a research hotspot in condensed matter physics, materials science, electronics, chemistry and other fields.^7–10

Inspired by the research craze on graphene, the search for carbon allotropes with multiple hybrid states continues. Among the carbon family, the acetylenic carbon materials (ACMs), a new kind of carbon allotropes contained sp-hybridized carbon atoms, is the most imaginative, and their architecture is a challenging subject.^11,12 One of the most representative ACMs is graphyne (GY), which was proposed by Baughman et al.¹³ in 1987. GY is a general name of a series of carbon grid structures composed of sp² and sp hybrid carbon atoms, including graphyne, α-graphyne, and 6,6,12-graphyne etc.¹⁴ Another representative ACM is graphdiyne (GDY) proposed by Haley et al.,¹⁵ which contains two acetylenic linkages between two carbon hexagons. The networks of GY and GDY both contain sp and sp² hybridized carbon atoms and they are thought to consist of graphene (sp² type carbon atom) and carbyne (sp type carbon atom).¹¹ The flat carbon networks and the presence of acetylenic linkages make GY and GDY become promising monatomic carbon allotropes.^16–21 They exhibit possible applications in separation of component,²² energy storage,^23,24 electrode material,²⁵ and catalysts.²⁶

At present, the ACMs represented by GY and GDY have become a scientific research field. The search for ACMs containing multiple hybridized states continues. For instance, Cui et al.^27,28 reported the research of preparing ACMs by wet ball grinding of calcium carbide, and investigated the electrochemical properties of the obtained acetylene carbon material. Casco et al.²⁹ explored the mechanical reaction of calcium carbide and hexachlorobenzene to produce ACMs. However, it is worth noting that so far only phenyl carbon materials (hexachlorobenzene) are used to prepare ACMs. Other carbon materials (such as octachloronaphthalene, tetrabromothiophene, etc.) are rarely reported to be used to synthesize ACMs. Very recently, we just reported the architecture and electrochemical performance of naphyne on experiment.³⁰ Thus, it is believed that more 2D ACMs will be prepared by ball-grinding calcium carbide with different non-phenyl carbon materials (halogenated or oligomer substructures).

In the study, two novel 2D ACMs, namely naphyne (NY)³⁰ and naphdiyne (NDY), are proposed. We present an study on the structures, mechanical and electronic properties of NY and NDY by means of first-principles calculations. Once the stable geometries and structural properties for these two ACMs are studied, the mechanical properties are calculated and compared with those of graphene and graphyne. Then, the electronic properties of NY and NDY are studied by means of electronic band structures and density of states. NY possesses a indirect band gap of 0.273 eV. NDY has no band gap with a Dirac point located on the line from Y to Γ. In addition, it is found that the band gap of NY and NDY can be tuned continuously under small biaxial strain.

2 Computational methodology

The Vienna ab initio package (VASP)^31,32 was used to perform all first-principles calculations within the projector augmented wave (PAW) method.³³ The Perdew–Burke–Ernzerhof (PBE) functional of generalized gradient approximation (GGA) is applied for the exchange-correlation functional.³⁴ It is known that HSE and GW methods give much better band gaps than GGA method, but the computational cost is much larger.^35–37 Although stand GGA functional always underestimates the band gap of semiconductors, it can give acceptable structural, elastic, and electronic results. All of the structure models were fully relaxed until the forces exerted on each atom are smaller than 0.01 eV Å⁻¹. The kinetic energy cutoff for plane-wave expansion was set to 550 eV. For the geometric optimization of NY and NDY, the Brillouin zones were sampled using 7 × 11 × 1 and 5 × 9 × 1 Monkhorst–Pack k-points grid, respectively.³⁸ For preventing the interaction between these 2D layered structures, a vacuum layer of 25 Å was added along the z direction. To verify the structural stabilities of NY and NDY, the calculations of phonon band dispersion and first-principles molecular dynamics simulations were performed. The calculation of phonon band dispersion was performed within the Phonopy package, while the first-principles molecular dynamics simulation was performed using the CP2K package in the NVT ensemble for 10 ps.

3 Results and discussion

3.1 Structural properties

Structural models of NY and NDY are shown in Fig. 1. The planar, layered NY and NDY, containing both naphthyl rings and acetylenic linkages, are named for their relationship to naphthalene and acetylenic components. Interestingly, for both NY and NDY, the repeating α-sites of naphthyl rings bond with each other by acetylenic linkages and the repeating β-sites of naphthyl rings also bond with each other by acetylenic linkages. However, NY and NDY differ from each other in the percentage of acetylenic linkages in their structures. There is one acetylenic linkage between the repeating naphthyl rings in NY and it has two in NDY. Due to the near distance of these two acetylenic linkages among the repeating α-sites of naphthyl rings in NY (diacetylenic linkages in NDY), the repulsive interaction between them makes these two acetylenic linkages not in a straight line. As a result, the internal repulsion caused by adjacent acetylenic linkages increases the total energy of NY and NDY.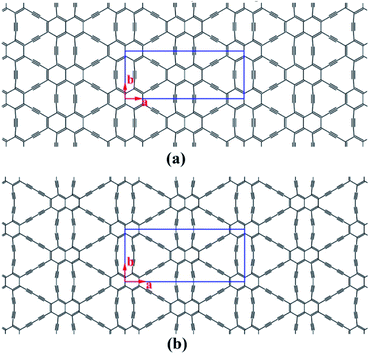

Fig. 1 Schematic representation of (a) naphyne, and (b) naphdiyne. The conventional cell is labeled by blue line.

For verifying the stability and experimental feasibility of NY and NDY, we thus examined their cohesive energy, formation energy, and phonon band dispersion. The cohesive energy is defined as the energy required to form isolated atoms from their condensed phase. Hence, the cohesive energies of NY and NDY are calculated using eqn (1).

E_c = (E_sheet − nE_C,atom)/n (1)

where E_sheet means the total energy of NY or NDY and E_C,atom means the total energy of carbon atom at ground state, respectively (Table S1†), and n denote the number of carbon atoms present in the system. The cohesive energies are reported in Table 1.

Table 1 The cohesive energy (E_c) and formation energy (E_form) of naphyne and naphdiyne

C allotrope	Ec (eV per atom)	Eform (eV per atom)
a Ref. 38.b Ref. 16.c Ref. 39.d Ref. 40.
Naphyne	−7.25	0.60
Naphdiyne	−7.12	0.73
Graphite	−7.95^a	0.01^a
Graphene	−7.97^a, −8.11^b	0.00^a
γ-Graphyne	−7.33^a, 7.21^c	0.64^a
Graphdiyne	−7.20^a, −7.65^d	0.76^a
Graphtetrayne	−7.11^a	0.86^a

---

It is found that NY and NDY have lower cohesive energies than graphite or graphene, which indicates that NY and NDY are less stable than graphite or graphene. However, the cohesive energy of NY is close to that of γ-graphyne or graphdiyne, which demonstrates that the stability of NY is comparable to γ-graphyne (theoretically most stable graphyne)⁴¹ and experimentally synthesized graphdiyne.⁴² In addition, NDY also exhibits comparable stability to experimentally synthesized graphtetrayne considering they have similar cohesive energies.⁴³ Comparing NY and NDY, it is found that the cohesive energy of NY is higher than that of NDY. This fact can be attributed to the different number of acetylenic linkages among the repeating α-sites of naphthyl rings. There is one acetylenic linkage among the repeating α-sites of naphthyl rings in NY and it has two in NDY.

Subsequently, the repulsive interaction between these two adjacent diacetylenic linkages that linking repeating α-sites of naphthyl rings increases the instability of NDY.

The formation energy is another important base to judge the stability of the ordered structure system. In this study, the formation energies of NY and NDY are calculated using eqn (2).

E_form = (E_sheet − nμ_C,atom)/n (2)

where E_sheet and n have the same meaning with those in eqn (1), and μ_C,atom means the chemical potential of carbon atom (Table S1†). The calculated formation energies are also reported in Table 1. It can be seen from Table 1 that the formation energies of NY (0.60 eV per atom) and NDY (0.73 eV per atom) are higher than those of graphite and graphene, but lower than those of graphdiyne⁴² and graphtetrayne,⁴³ respectively. Based on this fact, it can be concluded that although NY and NDY are far less stable than graphite and graphene, they are energetically more favorable than experimentally synthesized graphdiyne and graphtetrayne.

Phonon band dispersion spectra calculations are discussed in this part to judge structure instability.⁴⁴ Obviously, there is no imaginary frequencies in the calculated phonon results of NY and NDY, as can be seen from Fig. 2. This characteristic demonstrates that NY and NDY are kinetically very stable. Furthermore, the stability of NY and NDY at 300 K are assessed using first-principles molecular dynamics (MD) simulations (Fig. S1†). It can be seen from Fig. S1† that throughout the whole MD simulations of NY and NDY, both total energies and temperatures are well maintained (fluctuating around a constant value).

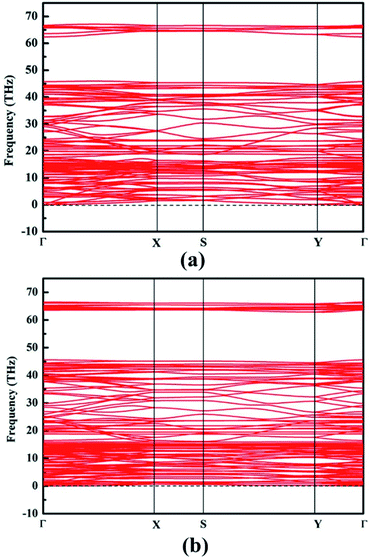Fig. 2 Phonon band dispersions of (a) naphyne and (b) naphdiyne, which exhibit outstanding kinetic stability.

The optimized structural parameters for the rectangular unit cells of NY and NDY are presented in Table 2 along with the bond lengths (detailed bond length information is shown in Fig. S2†). Both NY and NDY belong to the orthorhombic lattice family and exhibit the Cmmm plane group. The calculated lattice constants of NY and NDY are a = 16.993 Å, b = 6.860 Å and a = 21.455 Å, b = 9.408 Å, respectively. The NY and NDY comprise 36 and 52C atoms, respectively. As it can be seen from Fig. S2† that it has three different bonds in NY and NDY, aromatic bond, single bond and triple bond. Due to π-conjugation between the alkyne units and the naphthyl rings, the aromatic bonds are extended and single bonds contracted relative to typical values (ca. 1.40 and 1.54 Å, respectively⁴⁵). The triple bonds, in where the electron is localized, are the shortest bonds and similar to those in acetylene.⁴⁶ The aromatic bonds are found to be the longest bonds, which are similar to those in graphene (i.e., 1.42 Å (ref. 16)). Affected by the π-conjugation between the alkyne units and the naphthyl rings, the bond lengths of single bond fall in between aromatic bond and triple bond. The calculated bond lengths of single bond are found to be in agreement with other published works.^17,41,47

Table 2 Calculated lattice parameters and equilibrium bond lengths

	Naphyne	Naphdiyne
Lattice constant
a (Å)	16.993	21.455
b (Å)	6.860	9.408
Bond length (Å)
Aromatic	1.414–1.447	1.423–1.446
Single	1.396–1.408	1.336–1.396
Triple	1.223–1.226	1.233–1.235

---

It is well known that the pore size and the pore surface concentration can modify the specific surface are, and thus they play important role in heterogeneous catalysis, gas filtration and storage. Due to the import of acetylenic linkages and the replacement of benzene ring by naphthyl ring, the pores in NY and NDY become much large than those in graphene. As can be seen from Fig. 1 that it has three different pores in NY or NDY, hexagonal, extended hexagonal and truncated triangular pores. For calculating the dimensions of these three different pores, C atoms are considered as single points here. The calculated hexagonal, extended hexagonal and truncated triangular pore areas of NY are 5.30, 12.27 and 17.70 Ų (17.8 Ų of γ-graphyne),⁴¹ respectively; corresponding to pore concentrations of 3.43 × 10¹⁴, 1.72 × 10¹⁴ and 3.43 × 10¹⁴ pores per cm², respectively. The calculated hexagonal, extended hexagonal and truncated triangular pore areas of NDY are 5.32, 20.65 and 34.82 Ų, respectively; leading to pore concentrations of 1.98 × 10¹⁴, 0.99 × 10¹⁴ and 1.98 × 10¹⁴ pores per cm², respectively. The planar packing density is defined as the mass per unit of surface, and it is the inverse of the specific surface area. NY has a planar packing density of 0.62 mg m⁻² and NDY has a planar packing density of 0.51 mg m⁻² (0.58 mg m⁻² of γ-graphyne).⁴¹

3.2 Elastic properties

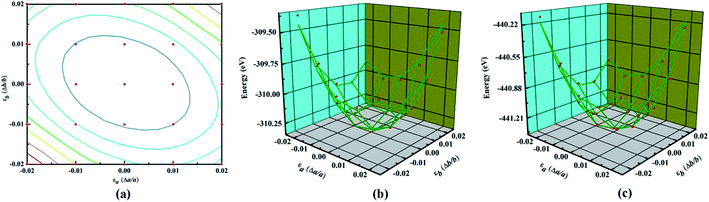
The main text of the article should appear here with headings as appropriate. Young's modulus (Y) and Poisson's ratio (υ) are usually used to evaluate the elastic properties of 3D materials. However, in the cases of NY or NDY, the thickness h is not well defined, which leads to unreasonable equilibrium volume for Y calculation. Therefore, the in-plane stiffness (C) calculation is preferred in the cases of NY and NDY instead of Y. The in-plane stiffness is given by C = (1/A₀)(∂²E/∂ε²), where A₀ is area of the unstrained system, E is total energy of the strained system and ε is uniaxial strain-ratio. The Poisson's ratio can be defined straightforwardly as υ = −ε_trans/ε_axial.

To calculate the elastic properties of NY and NDY, their conventional unit cell (as shown in Fig. 1) are used. Strain is applied to the unit cell in the method of changing the lattice constants in the range from −0.02 to 0.02 for each direction. Thus, we obtain 25 data points by changing the strain with an increment of 0.01, as shown in Fig. 3a. At each point, the atomic positions of the strained system are fully relaxed and then we obtain the dependence of energy vs. strain. The red balls in Fig. 3b and c show the calculated results. In order to obtain the in-plane stiffness and Poisson's ratio, we use the method described in ref. 48 and 49, in which the elastic properties of graphene and graphyne are well predicted. Based on this, the results of energy vs. strain are fitted by the formula E = c₁ε_a² + c₂ε_b² + c₃ε_aε_b + E₀, where c_1, c₂, and c₃ are the fitting parameters, and E₀ is the total energy of the unstrained system. Accordingly, the in-plane stiffness can be calculated by C = (1/A₀)(2c₁ − c₂²/2c₁), and the Poisson's ratio can be calculated by υ = c₂/2c₁. Hence, the calculated in-plane stiffness of NY and NDY are 128 N m⁻¹ and 91 N m⁻¹, and their Poisson's ratio are 0.61 and 0.64, respectively. The in-plane stiffness of NY is 62% less stiffer than that of graphene (340 + 50 N m⁻¹, experimentally).⁵⁰ However, compared with the in-plane stiffness of graphyne (166 N m⁻¹), the value of NY is only 23% less stiffer.⁴⁹ This characteristic can be explained by the different planar packing densities of these three different type of 2D materials. The planar packing density of NY (0.62 mg m⁻²) are closer to that in graphyne (0.582 mg m⁻²), but smaller than that in graphene (0.756 mg m⁻²).⁴¹ As to NDY, the increase of acetylenic linkages reduces its planar packing density, which in turn reduces the in-plane stiffness. The Poisson's ratio values obtained for NY and NDY are similar with each other. Both of them are larger than those values (0.18 and 0.42, respectively) of graphene and graphyne.⁴¹

Fig. 3 (a) The mesh of data points used for the total energy calculations. The three-dimensional plot of ε_a,ε_b and corresponding total energy values of (b) naphyne, and (c) naphdiyne. The red balls are actual points and the green lines are the fitted formula.

3.3 Electronic properties

In this section, we focus on the intrinsic electronic properties of NY and NDY. The band structure and density of state (DOS) for NY and NDY are discussed and the corresponding results are shown in Fig. 4 and 5, respectively. It can be seen from Fig. 4 that there exists a indirect band gap and a Dirac point in the band structures of NY and NDY, respectively. For NY, the lowest unoccupied conduction band (LUCB) and the highest occupied valence band (HOVB) degenerate at two different k points. The valence band maximum (VBM) is located on the line from Γ to X, and the conduction band minimum (CBM) is located on the high-symmetry S-points. That makes NY possess a narrow indirect band gap of 0.273 eV, different from the band gap of γ-graphyne (0.46 eV).⁴¹ For NDY, the HOVB and the LUCB are degenerate at one off-symmetry k-point (located on the line from Y to Γ) on the Fermi level. The linearly dispersive HOVB and LUCB bands around the contact point form two Dirac cones. The contacting point is known as Dirac point, which indicates that NDY is semiconductor with zero DOS in the Fermi level.^51,52 That makes NDY differentiable in the band gap with graphdiyne, which has a direct band gap of 0.46 eV obtained from DFT calculation.⁵³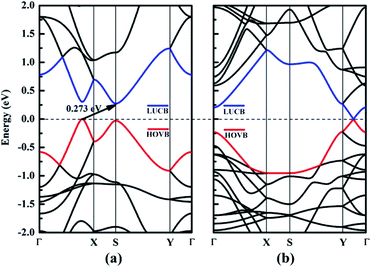

Fig. 4 Electronic band structures of (a) naphyne and (b) naphdiyne. The Fermi level has been shifted to zero, and the HOVB and LUCB are labeled by blue and red lines, respectively.

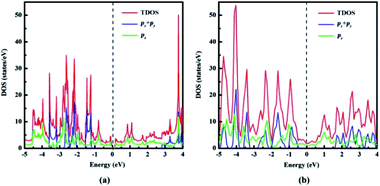Fig. 5 Total density of states (TDOS) and partial density of states (PDOS) of (a) naphyne, (b) naphdiyne.

With the aid of total density of state (TDOS) and partial density of states PDOS, we can obtain deeper insight into the bands near the Fermi level. As can be seen from Fig. 5 that the valence and conduction bands near the Fermi level in both NY and NDY are mainly attributed to the p_z bonding and antibonding orbitals. In the energy ranges of −1.2 to −2.8 eV and −3.1 to 3.6 eV, the contribution of p_x and p_y orbitals becomes prominent, but mixed with p_z orbital for NY. This result demonstrates that corresponding bonds in these two regions are the π bonds of triple bonds. Similarly, in the energy ranges of −0.4 to −2.8 eV and −3.2 to −4.9 eV, the TDOS of NDY are composed of p_x, p_y, and p_z orbitals, also corresponding to the π bonds of triple bond. However, the area where p_x, p_y, and p_z orbitals overlap in NDY is larger than NY, which indicates different electronic localization in these two 2D ACMs. This feature in the DOS of NY and NDY can be attributed to the different concentration of acetylenic linkages. The double acetylenic linkages between the repeating naphthyl rings in NDY makes two π(p_x, p_y) bonding, then leading to more p_x, p_y, and p_z orbitals overlapping. What is more, the π bands mainly contributed by p_z orbital show a wider energy distribution in DOS than those contributed by p_x, p_y orbitals. Considering this, we can get the conclusion of a much higher delocalization of the π(p_z) states than π(p_x, p_y) states. which can be attributed to conjugation between aromatic bonds and triple bonds. Contrarily, the type of π(p_x, p_y) bonds only exist in triple bands, which are separated by naphthyl rings.

It is well known that an external strain can be applied to 2D materials by mechanical loading or lattice mismatch on experiment, which is an effective way to tune the band gap.^54,55 Here, a biaxial strain (−5–10%), which is critically small, is imposed to NY and NDY. The corresponding changes in band gap is presented in Fig. 6 (for details, see Fig. S3 and S4†). Under tensile strain, the band gaps of NY gradually decrease first and then increase, and it gets the minimum value (0 eV) at the biaxial tensile strain of 6%. Under 1% tensile strain, the VBM of NY remains on the line from Γ to X (Fig. S3†). However, further increasing the strain up to 2% shifts the VBM to the S high-symmetry point, which rapidly transforms NY into a direct band-gap semiconductor. The changes of CBM make the band gaps of NY gradually decrease first and then increase with the tensile strain increase. As to NDY, the band gaps remain zero under the tensile strain of 7%. Interestingly, when the tensile strain is increased to 8%, the band gap of NDY changes to 0.08 eV. The band gaps gradually increase with further increasing the tensile strain, which transforms NDY into a semiconductor. Keeping the tensile strain below 6%, the Dirac point remains on the line from Y to Γ (Fig. S4†). However, further increasing the strain up to 7%, the Dirac point is shifted to the Γ high-symmetry point. When applying compressive strain on NY or NDY, it is found that it has no influence on the band gap regulation of NY or NDY.

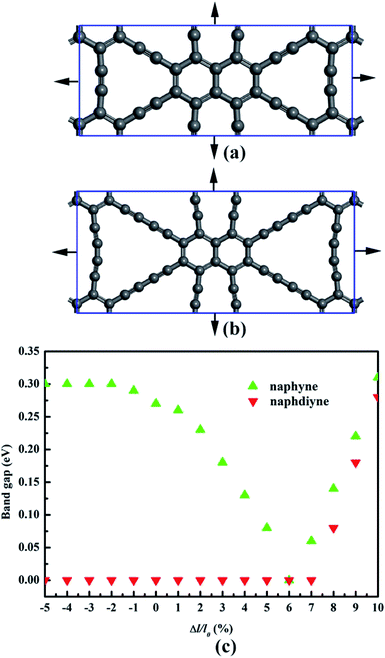Fig. 6 Schematic representation of (a) naphyne and (b) naphdiyne under biaxial tensile strain. (c) Changes in the band gap of naphyne and naphdiyne with increasing biaxial tensile strain.

4 Conclusions

In conclusion, we have reported two 2D acetylenic carbon materials NY and NDY sheets with distinguished structural, elastic and electronic properties. Both NY and NDY belong to the orthorhombic lattice family and exhibit the Cmmm plane group. The calculated lattice constants of NY and NDY are a = 16.993 Å, b = 6.860 Å and a = 21.455 Å, b = 9.408 Å, respectively. Based on the calculations of cohesive energy and formation energy, it is concluded that the stability of NY and NDY are comparable to those of experimentally synthesized graphdiyne and graphtetrayne, respectively. The results of phonon calculations and first principle MD simulations shown that NY and NDY are kinetically very stable. NY and NDY differ from each other in the percentage of acetylenic linkage in their structures, which makes these two 2D ACMs have different structural, elastic and electronic properties. The increase of acetylene bond makes NDY have a larger pore size and a lower planar packing density than NY. The in-plane stiffness of NY and NDY are 128 N m⁻¹ and 91 N m⁻¹, and their Poisson's ratio are 0.61 and 0.64, respectively. Both NY and NDY are softer than graphene, but comparable to graphyne. This fact can be explained by the reduced planar packing densities of the two materials compared with graphene and graphyne. The calculated band structures indicate that NY is an indirect semiconductor with a band gap of 0.273 eV and NDY has no band gap with a Dirac point located on the line from Y to Γ. Upon tensile strain, NY undergo an indirect band-gap to Dirac point, and then direct band-gap transition, while NDY undergo a Dirac point to direct band-gap transition. NY and NDY are reported for the first time, and are energetically more favorable than the synthesized graphdiyne and graphtetrayne. We believe that these novel materials will be synthesized in the laboratory in the very near future and these findings will be helpful for the application of NY and NDY.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Innovation and Entrepreneurship Project of Anhui Science and Technology University (No. S201910879303), the Scientific Research Project of Education Department of Anhui Province (No. KJ2020A0053) and the Academic Subsidy Project for Top Academic Talents in Universities (gxbjZD28).

Notes and references

1. A. Hirsch, Nat. Mater., 2010, 9, 868.
2. H. W. Kroto, J. R. Obrien, S. C. Obrien, R. F. Cur and R. E. Smalley, Nature, 1985, 318, 162.
3. S. Iijima, Nature, 1991, 354, 56.
4. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Gregoneva and A. A. Firzov, Science, 2004, 306, 666.
5. B. K. I. olotin, K. J. Sikes, J. Hone, H. L. Stormer and P. Kim, Phys. Rev. Lett., 2008, 101, 096802.
6. Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201.
7. M. Xu, T. Liang, M. Shi and H. Chen, Chem. Rev., 2013, 113, 3766.
8. Y. E. L. Bai, L. Fan, M. Han, X. Zhang and S. Yang, J. Mater. Chem., 2011, 21, 819.
9. L. Huang, B. Wu, G. Yu and Y. Liu, J. Mater. Chem., 2011, 21, 919.
10. T. Wassmann, A. P. Seitsonen, A. M. Saitta, M. Lazzeri and F. Mauri, J. Am. Chem. Soc., 2010, 132, 3440.
11. Y. Li, L. Xu, H. Liu and Y. Li, Chem. Soc. Rev., 2014, 43, 2572.
12. F. Diederich and M. Kivala, Adv. Mater., 2010, 22, 803.
13. R. H. Baughman, H. Eckhardt and M. Kertesz, J. Chem. Phys., 1987, 87, 6687.
14. J. M. Chen, J. Y. Xi, D. Wang and Z. G. Shuai, J. Phys. Chem. Lett., 2013, 4, 1443.
15. M. M. Haley, S. C. Brand and J. J. Pak, Angew. Chem., Int. Ed. Engl., 1997, 36, 836.
16. V. O. Özçelik and S. Ciraci, J. Phys. Chem. C, 2013, 117, 2175.
17. J. M. Ducéré, C. Lepetit and R. Chauvin, J. Phys. Chem. C, 2013, 117, 21671.
18. H. Sevinçli and C. Sevik, Appl. Phys. Lett., 2014, 105, 223108.
19. G. Wang, M. Si, A. Kumar and R. Pandey, Appl. Phys. Lett., 2014, 104, 213107.
20. Q. Yue, S. Chang, J. Kang, S. Qin and J. Li, J. Phys. Chem. C, 2013, 117, 14804.
21. Z. Li, M. Smeu, A. Rives, V. Maraval, R. Chauvin, M. A. Ratner and E. Borguet, Nat. Commun., 2015, 6, 6321.
22. M. Alaghemandi, Chem. Phys. Lett., 2015, 629, 65.
23. Y. Liu, W. Liu, R. Wang, L. Hao and W. Jiao, Int. J. Hydrogen Energy, 2014, 39, 12757.
24. R. Lu, D. Rao, Z. Meng, X. Zhang, G. Xu, Y. Liu, E. Kan, C. Xiao and K. Deng, Phys. Chem. Chem. Phys., 2013, 15, 16120.
25. Q. Tang, Z. Zhou and Z. Chen, Nanoscale, 2013, 5, 4541.
26. P. Wu, P. Du, H. Zhang and C. Cai, Phys. Chem. Chem. Phys., 2015, 17, 1441.
27. C. Yang, Y. Li, Y. Chen, Q. Li, L. Wu and X. Cui, Small, 2019, 15, 1804710.
28. Q. Li, C. Yang, L. Wu, H. Wang and X. Cui, J. Mater. Chem. A, 2019, 7, 5981.
29. M. E. Casco, F. Badaczewski, S. Grätz, A. Tolosa, V. Presser, B. M. Smarsly and L. Borchardt, Carbon, 2018, 139, 325.
30. Y. Li, Y. Li, P. Lin, J. Gu, X. He, M. Yu, X. Wan, C. Liu and C. Li, ACS Appl. Mater. Interfaces, 2020, 12, 33076.
31. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
32. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
35. S. Pari, A. Cuéllar and B. M. Wong, J. Phys. Chem. C, 2016, 120, 18871.
36. J. Kim, S. Kang, J. Lim and W. Y. Kim, ACS Appl. Mater. Interfaces, 2019, 11, 2677.
37. J. Kang, Z. Wei and J. Li, ACS Appl. Mater. Interfaces, 2019, 11, 2692.
38. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
39. N. V. Rao Nulakani and V. Subramanian, J. Mater. Chem. C, 2018, 6, 7626.
40. H. Bu, M. Zhao, A. Wang and X. Wang, Carbon, 2013, 65, 341.
41. A. R. Puigdollers, G. Alonso and P. Gamallo, Carbon, 2016, 96, 879.
42. G. Li, Y. Li, H. Liu, Y. Guo, Y. Li and D. Zhu, Architecture of graphdiyne nanoscale films, Chem. Commun., 2010, 46, 3256–3258.
43. J. Gao, J. Li, Y. Chen, Z. Zuo, Y. Li, H. Liu and Y. Li, Nano Energy, 2018, 43, 192.
44. Y. F. Li, Y. L. Liao and Z. F. Chen, Angew. Chem., Int. Ed., 2014, 53, 7248.
45. J. Carper, Library Journal, 1999, 124, 192.
46. S. Zou and J. M. Bowman, Chem. Phys. Lett., 2003, 368, 421.
47. H. Bai, Y. Zhu, W. Qiao and Y. Huang, RSC Adv., 2011, 1, 768.
48. J. Kang, J. Li, F. Wu, S. S. Li and J. B. Xia, J. Phys. Chem. C, 2011, 115, 20466.
49. M. Topsakal, S. Cahangirov and S. Ciraci, Appl. Phys. Lett., 2010, 96, 091912.
50. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385.
51. V. K. Arora and A. Bhattacharyya, Nanoscale, 2013, 5, 10927.
52. Z. Wang, X. F. Zhou, X. Zhang, Q. Zhu, H. Dong, M. Zhao and A. R. Oganov, Nano Lett., 2015, 15, 6182.
53. M. Long, L. Tang, D. Wang, Y. Li and Z. Shuai, ACS Nano, 2011, 5, 2593.
54. J. Feng, X. F. Qian, C. W. Huang and J. Li, Nat. Photonics, 2012, 6, 866.
55. P. Miró, M. Ghorbani-Asl and T. Heine, Angew. Chem., Int. Ed., 2014, 53, 3015.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0ra07214a

---